低密度奇偶校验码(low density parity check,LDPC codes)是一种具有稀疏矩阵的线性分组码。伽罗华域GF(q)上的非二进制LDPC码(non-binary low density parity check,NB-LDPC codes),即多元LDPC码,在1998年首次被提出[1]。与二进制LDPC码相比,多元LDPC码表现出更好的纠错性能[2]。然而,基于置信传播思想译码的多元LDPC码高阶伽罗华域GF(q)的算法随着域的维数q的增加而复杂化。为了减少这个问题,基于快速傅立叶变换(fast fourier transformation,FFT)的置信传播(belief propagation,BP)译码算法,即FFT-BP译码算法[3]和多元LDPC码的对数域BP译码算法[4]相继被提出。在对数域BP译码算法的基础上,复杂度更低的拓展最小和(extended min-sum,EMS)算法[5]被提出,它即是二进制LDPC码最小和算法的扩展,并且量化精度要求低,有利于硬件实现。我们基于EMS算法进行多元LDPC码译码算法改进,降低计算复杂度,对于多元LDPC码的硬件实现有重要意义。
在这些译码算法的基础上,又出现了大量的研究分别从优化算法自身结构[6]和引入其他思想[7]改进两方面来降低多元LDPC码在计算和硬件实现中复杂度。其中,遗传算法是快速搜索和优化算法,在LDPC码中最开始是被用来搜索性能良好且易于硬件实现的LDPC码[8]。而A.G.Scandurra等[9]的研究成功将遗传算法应用到LDPC译码中。在此基础上,邓泽荣等[10]首次在BP算法中应用了遗传算法。而近来在FFT-BP译码算法[11]和大数逻辑译码算法[12]中也已尝试使用了遗传算法并取得成功。基于这些研究,本文将这种思想引入到了EMS算法中。
本文研究了多元LDPC码的EMS译码算法,采用遗传算法的思想对其进行了改进,提出了基于遗传思想的EMS算法(genetic extended min-sum,G-EMS)。相比原EMS算法,G-EMS算法通过制定约束条件筛选高度可靠的变量节点,针对这些特殊节点增加采用修正参数放大消息判决位符号置信度的方法,优化了对应的变量节点向校验节点发送的消息矢量,加快了收敛速度,节省了计算资源。
1 EMS算法 1.1 多元LDPC码相关定义多元LDPC码由稀疏的奇偶校验矩阵H来定义,可以由Tanner(或因子)图表示[13-14],如图 1。对于一个M行和N列的矩阵H,它的每行对应于一个q进制奇偶校验方程,即一个Tanner图的校验节点(CN),每列对应到码字的一个GF(q)符号,即一个Tanner图的变量节点(VN)。符号dc 表示校验节点的度,dv表示变量节点的度。
|
Download:
|
| 图 1 LDPC码Tanner图 | |
假设矩阵H是满秩的,则码率定义为R=(N-M)/M。令{hvc}v, c表示q进制矩阵H中的元素,它们是伽罗华域GF(q)中的值,任意校验节点对应的校验方程可以表示为
| $ \mathop \sum \limits_{v = 1}^{{d_c}} {h_{vc}}{x_v} = 0\;{\rm{in}}\;{\rm{GF}}(q) $ | (1) |
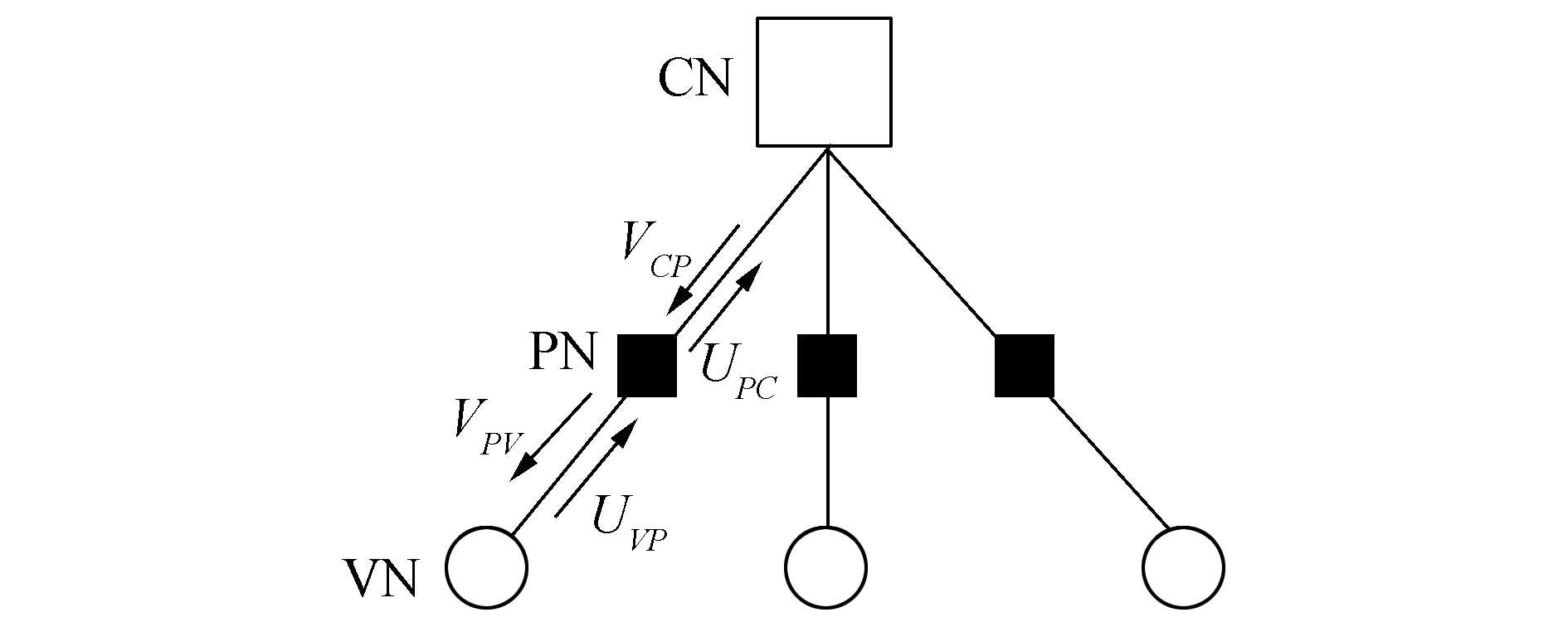
式中xv(v=1, 2, …, dc)是该校验方程涉及变量节点的码字符号。多元LDPC码译码采用的是迭代消息译码,其中消息被定义为q维矢量。多元LDPC码Tanner图中的消息传递事宜图如图 2所示。
|
Download:
|
| 图 2 多元LDPC码Tanner图中的消息传递 | |
除了变量节点和校验节点,多元LDPC码的Tanner图还包括置换节点(PN),用来体现H矩阵中非二进制值的作用[6]。令Vpv(p=1, …, dv)表示进入的度数dv的变量节点v的消息矢量,Uvp是v的输出消息矢量。消息矢量中的Uvp[β]表示变量节点v取值为β∈ GF(q)的置信度为Uvp[β]。符号vp表示消息从VN流向PN,pv表示消息的方向相反。同理对于一个度为dc校验节点,定义了类似的矢量消息Upc和Vcp。
1.2 EMS算法流程根据上述定义,EMS算法的基本步骤如下:
1) 初始化。将信道输出的对数似然比(log-likelihood ratio,LLR)消息矢量存储到图中的变量节点消息矢量中。多元码迭代译码中消息采用对数似然比(LLR)的形式表示。对于GF(q)上的随机变量z,L[i]=log(P(z=αi)/P(z=0))是z取值为αi∈GF(q)的似然比,则对应的LLR信息矢量可以表示为L(z=(L[0], L[1], …, L[q-1])。其中P(z=αi)是z取值为αi∈ GF(q)的概率,取值依赖于信道的统计特性。而信道输出的LLR消息也可以用一个q维的矢量Lch来表示。
2) 消息置换。由于Tanner图的每条边上非二进制元素hvc的影响,在译码时,需要执行矢量信息的置换。变量节点输出的消息传至置换节点后,经置换再发送至校验节点,消息置换可表示为
| $ {\mathit{\boldsymbol{U}}_{pc}}\left[\beta \right] = {U_{vp}}\left[{{\boldsymbol{h}}_{_{vc}}^{^{-1}}\beta } \right]\;\;\;\;\beta \in {\rm{GF}}\left( q \right), p = 1, 2, \cdots, {d_v} $ | (2) |
3) 校验节点更新。在EMS算法中,对每个变量节点传递的消息矢量只选择nm个最可靠的消息值用来更新,消息矢量长度由q被截短为nm [5, 15]。在[6]中,作者引入了配置集的概念以减少校验节点更新的复杂性。配置集定义为
| $ \begin{array}{l} \;\;\;{\rm{con}}f\left( {{n_m}} \right) = \{ {\beta _k} = {\left[{\beta _{_1}^{^{{k_1}}}, \beta _{_2}^{^{{k_2}}}, \cdots \beta _{_{{d_c}-1}}^{^{{k_{{d_c}-1}}}}} \right]^{\rm{T}}}:\\ \forall \mathit{\boldsymbol{K}} = {\left[{{k_1}, {k_2}, \cdots, {k_{{d_c}-1}}} \right]^{\rm{T}}} \in {\{ 1, 2, \cdots, {n_m}\} ^{{d_c} -1}}\} \end{array} $ | (3) |
在配置集中,ki指校验节点第i个传入消息矢量置信度大小排序在第k的值。集合中任意一个有dc-1个域元素βiki 的矢量即为一个配置。配置集conf(1)是只包含一个最可靠的输出配置,也被称为0阶配置。为了进一步减少校验节点更新的配置数量,将与0阶配置的最大偏差数限制为nc。更新与校验节点相连第dc个变量节点的输出消息时,其配置集为
| $ {\rm{con}}{f_\beta }\left( {{n_m}, {n_c}} \right) = \{ {\beta _K} \in {\rm{con}}f\left( {{n_m}, {n_c}} \right):\beta + \mathop \sum \limits_{p = 1}^{{d_c}-1} \beta _{_p}^{^{{k_p}}} = 0\} $ | (4) |
这个配置集用来计算第dc个输出消息矢量域值为β∈ GF(q)对应的消息。根据配置集的定义,校验节点的更新方程可以表示为
| $ {V_{c{d_c}}}\left[\beta \right] = \mathop {{\rm{max}}}\limits_{{\beta _K} \in {\rm{con}}{f_\beta }\left( {{n_m}, {n_c}} \right)} \mathop \sum \limits_{p = 1}^{{d_c} - 1} {U_{pc}}\left[{\beta _{_p}^{^{{k_p}}}} \right]\;\;\;\;\;\beta \in {\rm{GF}}\left( q \right) $ | (5) |
4) 消息逆置换。校验节点输出的消息经逆置换发送至变量节点,逆置换可表示为
| $ {\mathit{\boldsymbol{V}}_{pv}}\left[\beta \right] = {\mathit{\boldsymbol{V}}_{cp}}\left[{{h_{vc}}\beta } \right]\;\;\;\;\;\;\beta \in {\rm{GF}}\left( q \right), p = 1, 2, \cdots, {d_c} $ | (6) |
5) 变量节点更新。每个变量节点v有dv个输入消息Vpv(p=1, 2, …, dv)。结合外部输入消息和信道信息,变量节点v发送给与其相邻的置换节点的外部输出消息为:
| $ \begin{array}{l} {\mathit{\boldsymbol{U}}_{vp}}\left[\beta \right] = {L_v}\left[\beta \right] + \sum\limits_{t = 1, t \ne p}^{{d_v}} {{V_{tv}}\left[\beta \right]} \\ \beta \in {\rm{GF}}\left( q \right), p = 1, 2, \cdots, {d_v} \end{array} $ | (7) |
6) 判决。每个变量节点v的估计判决符号
| $ {{\hat C}_v} = \mathop {\arg \max }\limits_{\beta \in {\rm{GF}}\left( q \right)} \left( {{L_v}\left[\beta \right] + \sum\limits_{p = 1}^{{d_v}} {{V_{pv}}\left[\beta \right]} } \right) $ | (8) |
当N个变量节点的判决符号能满足全部校验方程或译码到达最大迭代次数则结束译码,否则返回步骤2)继续译码。
2 G-EMS算法的变量节点消息优化遗传的主要思想是选择高度可靠的变量节点并增大对应的变量节点向校验节点发送的消息值,它类似于在遗传算法中的遗传操作,即适应性强的个体被选择,它们的基因是为了适应环境而更新。G-EMS算法则是对筛选出的高度可靠的变量节点增大其向校验节点发送消息的可靠符号的置信值。
为了筛选高度可靠的变量节点,引入了2个约束:
1)
2)
在译码过程中,当译码迭代次数达到k次之前,节点仍按式(7)更新。
当译码达到k次迭代之后,通过约束筛选高可靠度的变量节点,这些节点发送的校验节点消息,需要经过修正值α进行优化,α>0。
增加的优化方程为
| $ {U^i}\left[\beta \right] = \left\{ \begin{array}{l} \;\;\;\;\;\;\;{U^i}\left[\beta \right] + a\;\;\;\;\;\;\;\beta = \hat C_n^i\\ {U^i}\left[\beta \right] + a/\left( {q -1} \right)\;\;\;\beta \ne \hat C_n^i \end{array} \right. $ | (9) |
即对一个满足约束的变量节点,等于当前迭代判决码字的元素符号对应的置信值经过修正被放大,而其他置信值相对变小。
随着信噪比的增加,大部分变量节点消息矢量的判决符号在几次迭代之后就是正确的,而剩下的迭代只要纠正余下的少量符号[11]。来自还未纠正的变量节点的消息是不准确的。如果不采取措施,这些不准确的信息将在迭代过程中循环传播,会导致译码算法的纠错性能不佳。但是如果优化这些符号正确的变量节点发出的消息的权重,增大正确符号的置信值,那么符号不正确的消息产生的影响将被大大抑制,这样就有利于在后面的迭代过程中更快地纠正错误的消息。在继续译码的过程中,上述增加优化方程的操作就会形成良性循环。
而关于迭代门限k的选取标准,对与环长为g的LDPC码,如果将Tanner图扩展为树[16],那么可以了解到消息在前g/2次迭代中是独立传递,在这种情况下不需要增加消息更新方程。当迭代次数大于g/2时,码字符号大部分被正确译出,此时通过约束条件筛选出的变量节点的判决符号极有可能就是最终判决符号,因此选择的门限k取值应大于g/2。
3 仿真分析本节通过公式及仿真结果全面地对G-EMS算法的性能进行分析,需要通过与原EMS算法的对比,证明改进的G-EMS算法的优越性。关于算法复杂度,EMS算法一次迭代的计算量可表示为Ndcq+2Mdcnmq,而G-EMS算法一次迭代增加的计算量xq+ydcdv。其中,N>y>x。
在高斯白噪声信道条件下,采用四进制LDPC码进行G-EMS算法与EMS算法的性能仿真,码长为400,度分布为(dc, dv)=(2, 4)。根据EMS算法的收敛速度、采用的H矩阵及仿真测试结果,本文初始的最大迭代次数设为20次。由于k取值应大于g/2,而LDPC码在构造时消除了4环,即g>4,得到k>2,在仿真中选择门限k为5次。
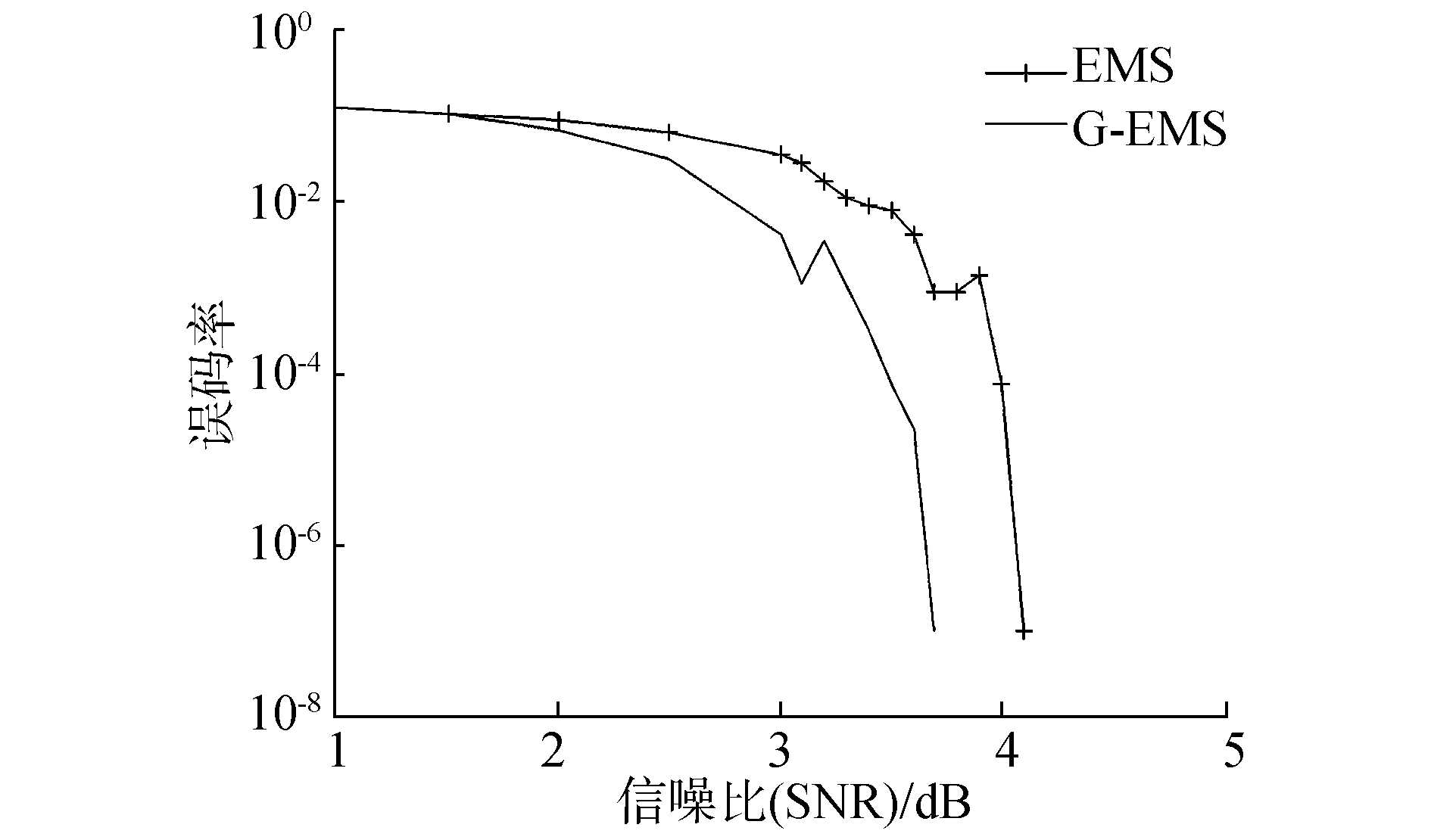
根据图 3的仿真曲线,由于G-EMS算法的通过增加更新方程加快了译码迭代的收敛速度,因此在设置相同最大迭代次数时,同一信噪比条件下G-EMS有更大的几率能够纠正全部的错误信息。因而相比于EMS,G-EMS的译码纠错性能有明显提高。
|
Download:
|
| 图 3 相同最大迭代次数下EMS与G-EMS性能比较 | |
但当采用精心构造的NB-LDPC码时,其性能普遍优秀,完全超出所需的准确度,而其缺点在于超高的计算量。因此我们的目标是降低算法的计算量,而G-EMS算法可以通过减少设置的最大迭代次数降低算法复杂度,因此在上述仿真结果的基础上,将G-EMS算法最大迭代次数减少为EMS算法的1/2,获得如图 4~5的仿真曲线。

|
Download:
|
| 图 4 不同最大迭代次数下EMS与G-EMS性能比较 | |
|
Download:
|
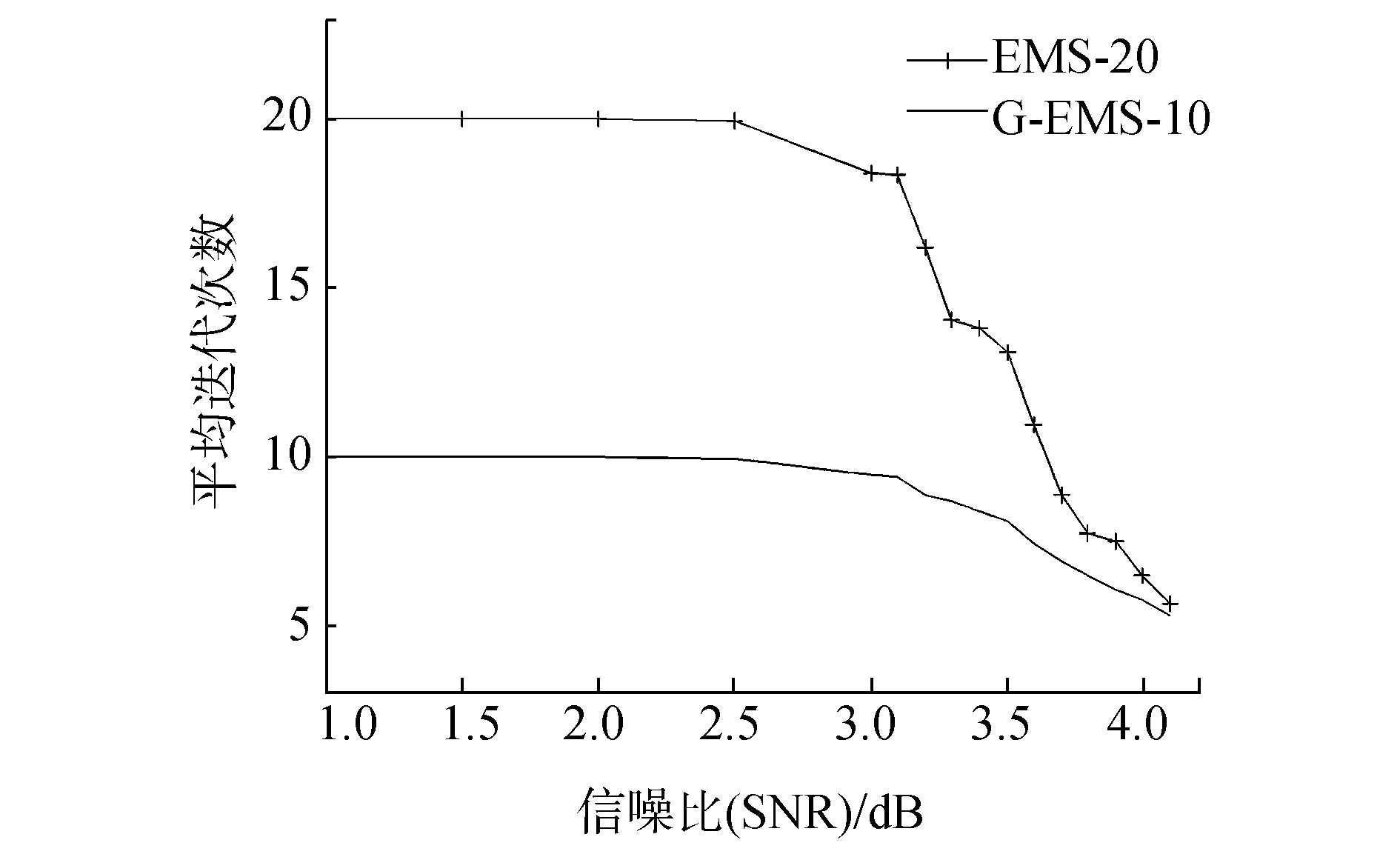
| 图 5 不同最大迭代次数下EMS与G-EMS译码平均迭代次数比较 | |
由图 4可知,当G-EMS算法采用较少的最大迭代次数时,与EMS算法的性能近似,带入仿真参数计算量计算简化为48N远远大于4x+8y,而通过图 5中的平均迭代次数可知,在大部分的仿真信噪比范围内,G-EMS算法的译码平均迭代次数都要远小于EMS算法,而仅在高信噪比误码率极低的区间略小于EMS算法。由于迭代门限k取值为5,由图 5可知,在信噪比到达3.9 dB前,G-EMS算法的平均迭代次数已经十分接近5次,即算法在迭代中进行节点选择的次数已经很少,结合附加计算量远小于算法计算量,可以认为G-EMS算法的计算量更少;而信噪比到达3.9 dB时,G-EMS算法的纠错性能已经接近完全译码,相比于原算法性能提升非常大,可以认为能通过调高k值以性能降低为代价减少计算量,即便k值增大使G-EMS算法附加计算实际不工作,此时G-EMS算法也可保持与原算法性能相同。
仿真结果可以说明在低信噪比性能较差阶段,只设置1/2最大迭代次数的G-EMS算法能够显著降低计算量;而在高信噪比阶段,G-EMS算法能在最大迭代次数之内以较少的迭代次数译码成功,其计算量也能大概率少于EMS算法。所以G-EMS算法可以在保持性能近似的情况下,通过降低最大迭代次数减少NB-LDPC码译码的计算量。
4 结束语本文通过设置约束筛选节点及进行消息优化,使G-EMS算法在EMS算法的基础上提升了译码性能。而通过对G-EMS算法设置更小的译码最大迭代次数,则可在不影响纠错性能的情况下减少译码计算量。综合仿真图分析,G-EMS算法能够实现减少计算量而不影响纠错性能的目的。这种改进对于多元LDPC码的硬件实现有重要意义,有利于多元LDPC码在通信系统中的实际应用。
| [1] |
DAVEY M C, MACKAY D. Low-density parity check codes over GF (q)[J]. IEEE communications letters, 1998, 2(6): 165-167. DOI:10.1109/4234.681360 ( 0) 0)
|
| [2] |
GALLAGER R G. Low-density parity-check codes[J]. IRE transactions on information theory, 1962, 8(1): 21-28. DOI:10.1109/TIT.1962.1057683 ( 0) 0)
|
| [3] |
DAVEY M C. Error-correction using low-density parity-check codes[D]. Cambridge: University of Cambridge, 1999.
( 0) 0)
|
| [4] |
WYMEERSCH H, STEENDAM H, MOENECLAEY M. Log-domain decoding of LDPC codes over GF (q)[C]//Proceedings of 2004 IEEE International Conference on Communications. Pairs, France: IEEE, 2004: 772-776. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1312606
( 0) 0)
|
| [5] |
DECLERCQ D, FOSSORIER M. Decoding algorithms for nonbinary LDPC codes over GF (q)[J]. IEEE transactions on communications, 2007, 55(4): 633-643. DOI:10.1109/TCOMM.2007.894088 ( 0) 0)
|
| [6] |
LI Erbao, DECLERCQ D, GUNNAM K. Trellis-based extended min-sum algorithm for non-binary LDPC codes and its hardware structure[J]. IEEE transactions on communications, 2013, 61(7): 2600-2611. DOI:10.1109/TCOMM.2013.050813.120489 ( 0) 0)
|
| [7] |
LACRUZ J O, GARCÍA-HERRERO F, VALLS J. Reduction of complexity for nonbinary LDPC decoders with compressed messages[J]. IEEE transactions on very large scale integration (VLSI) systems, 2015, 23(11): 2676-2679. DOI:10.1109/TVLSI.2014.2377194 ( 0) 0)
|
| [8] |
KU Mongkai, LI Huansheng, CHIEN Y H. Code design and decoder implementation of low density parity check code[C]//Proceedings of 2005 Emerging Information Technology Conference. Taipei, China: IEEE, 2005. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1544356
( 0) 0)
|
| [9] |
SCANDURRA A G, DAI PRA A L, ARNONE L, et al. A genetic-algorithm based decoder for low density parity check codes[J]. Latin American applied research, 2006, 36(3): 169-172. ( 0) 0)
|
| [10] |
DENG Zerong, LIU Xingcheng, TENG Man. Modified BP decoding algorithms combined with GA for low-density parity check codes[C]//Proceedings of 2008 International Conference on Computational Intelligence and Security. Suzhou, China: IEEE, 2008: 371-375. http://ieeexplore.ieee.org/document/4724676/
( 0) 0)
|
| [11] |
LIU Xingcheng, LIANG Chulong, ZHANG Yuanbin, et al. Decoding of non-binary low-density parity-check codes based on the genetic algorithm and applications over mobile fading channels[J]. IET communications, 2015, 9(16): 1941-1948. DOI:10.1049/iet-com.2015.0085 ( 0) 0)
|
| [12] |
YATRIBI A, BELKASMI M, AYOUB F, et al. Non-binary cyclic majority-logic decodable codes: an algebraic construction by using Genetic Algorithms[C]//Proceedings of 2016 International Conference on Advanced Communication Systems and Information Security (ACOSIS). Marrakesh, Morocco: IEEE, 2016: 1-9. http://ieeexplore.ieee.org/document/7843935/
( 0) 0)
|
| [13] |
TANNER R. A recursive approach to low complexity codes[J]. IEEE transactions on information theory, 1981, 27(5): 533-547. DOI:10.1109/TIT.1981.1056404 ( 0) 0)
|
| [14] |
KSCHISCHANG F R, FREY B J, LOELIGER H A. Factor graphs and the sum-product algorithm[J]. IEEE transactions on information theory, 2001, 47(2): 498-519. DOI:10.1109/18.910572 ( 0) 0)
|
| [15] |
VOICILA A, DECLERCQ D, VERDIER F, et al. Low-complexity decoding for non-binary LDPC codes in high order fields[J]. IEEE transactions on communications, 2010, 58(5): 1365-1375. DOI:10.1109/TCOMM.2010.05.070096 ( 0) 0)
|
| [16] |
HU Xiaoyu, ELEFTHERIOU E, ARNOLD D M. Regular and irregular progressive edge-growth tanner graphs[J]. IEEE transactions on information theory, 2005, 51(1): 386-398. DOI:10.1109/TIT.2004.839541 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


