2. 厦门大学 信息科学与技术学院 水声通信与海洋信息技术教育部重点实验室,福建 厦门 361005
2. Key Laboratory of Underwater Acoustic Communication and Marine Information Technology, Ministry of Education, School of Information Science and Technology, Xiamen University, Xiamen 361005, China
声学浮标是指布放于水中,主要完成海上各种声学要素测量的设备。海上声学要素主要包括海水声速、海洋环境噪声、海洋声传播损失、混响和海底声特性等。由于其布放与回收相对简便,经常用来进行海洋声学要素观测。在实际应用的过程中,受海面风、浪以及自身结构的影响,声学浮标会产生大量的自噪声和干扰,降低了信噪比,严重影响了其对海洋环境真实噪声和弱水声信号的测量效果。
一些研究表明,在这些大量的自噪声和干扰中,由海流引起的噪声占据很大的一部分[1-3]。当水流通过声学浮标线阵的水听器及其电缆时,在水听器线阵周围形成湍流边界层,湍流边界层脉动压力压迫水听器产生了噪声,一般称之为流致噪声,简称流噪声。声学浮标的流噪声,主要是由声学浮标线阵和海水间的垂直相对运动产生。
近年来,随着电子技术的发展,声学浮标在采样率、功耗、存储容量、电噪声等电子性能上有大幅度的提高和进步,但在声学浮标声学性能方面包括抗流降噪等依然还存在一些问题。在运用声学浮标进行海洋环境噪声测量时,数据质量常常不够好,干扰的成分比较多。国内的一些相关噪声研究主要是从早期简单的声学浮标系统的布设考虑[1, 4]。本文通过分析声学浮标流噪声的成因,借鉴较为成熟的水平拖曳线阵流噪声的理论模型,根据声学浮标自身的特点,建立声学浮标流噪声理论模型,并依此分析流噪声功率谱的大小和流噪声的相关关系。
1 声学浮标接收流噪声 1.1 拖曳线阵流噪声分析当水听器线列阵被拖着在海水中运动时,线阵的表面经受湍流边界层脉动压力的作用。流噪声产生的机理就是水听器收到的脉动压力的直接传递和脉动压力激起的机械振动,如图1所示。

|
Download:
|
| 图 1 水平线阵拖曳情况 | |
在柱对称情况下,在护套内某点(x,r)处,流噪声的声压为p(x,r,t),利用傅里叶积分,可得噪声场的声压表达式为[5-7]
| $p\left( {x,r,t} \right) = {{ }}{\left( {\frac{1}{{2\pi }}} \right)^2}\int {\int_{ - \infty }^\infty {{\phi _s}\left( {{k_x},\omega } \right)h\left( {{k_x},r,\omega } \right){{{e}}^{{{j}}\left( {{k_x}x - \omega t} \right)}}{{d}}{k_x}{{d}}\omega } } {{ }}$ |
拖线阵内水听器对TBL压力起伏的响应功率谱[8]为
| ${\phi _0}\left( \omega \right) = {{ }}\int_{ - \infty }^\infty {{\phi _s}\left( {{k_x},\omega } \right)|T\left( {{k_x},\omega } \right){|^2}{{\left| {\frac{{{J_0}\left( {{k_1}{r_0}} \right)}}{{{J_0}\left( {{k_1}b} \right)}}} \right|}^2}{{\left| {H\left( {{k_x}} \right)} \right|}^2}{{d}}{k_x}} $ | (1) |
式中:
| ${\varphi _s}({k_x},\omega ) = \frac{{{c^2}\rho _2^2v_{{*}}^3{R^2}\left[ {{{\left( {{k_x}R} \right)}^2} + 1/12} \right]}}{{{{\left[ {{{\left( {\omega R - {U_C}{k_z}R} \right)}^2}/{{\left( {h{v_{{*}}}} \right)}^2} + {{\left( {{k_x}R} \right)}^2} + 1/{b^2}} \right]}^{2.5}}}}$ |
式中:
因此,在已知拖曳线阵线缆护套表面TBL压力起伏波数−频率谱、护套传递函数前提下,即可对压力起伏激励下管内水听器流噪声谱进行预报。
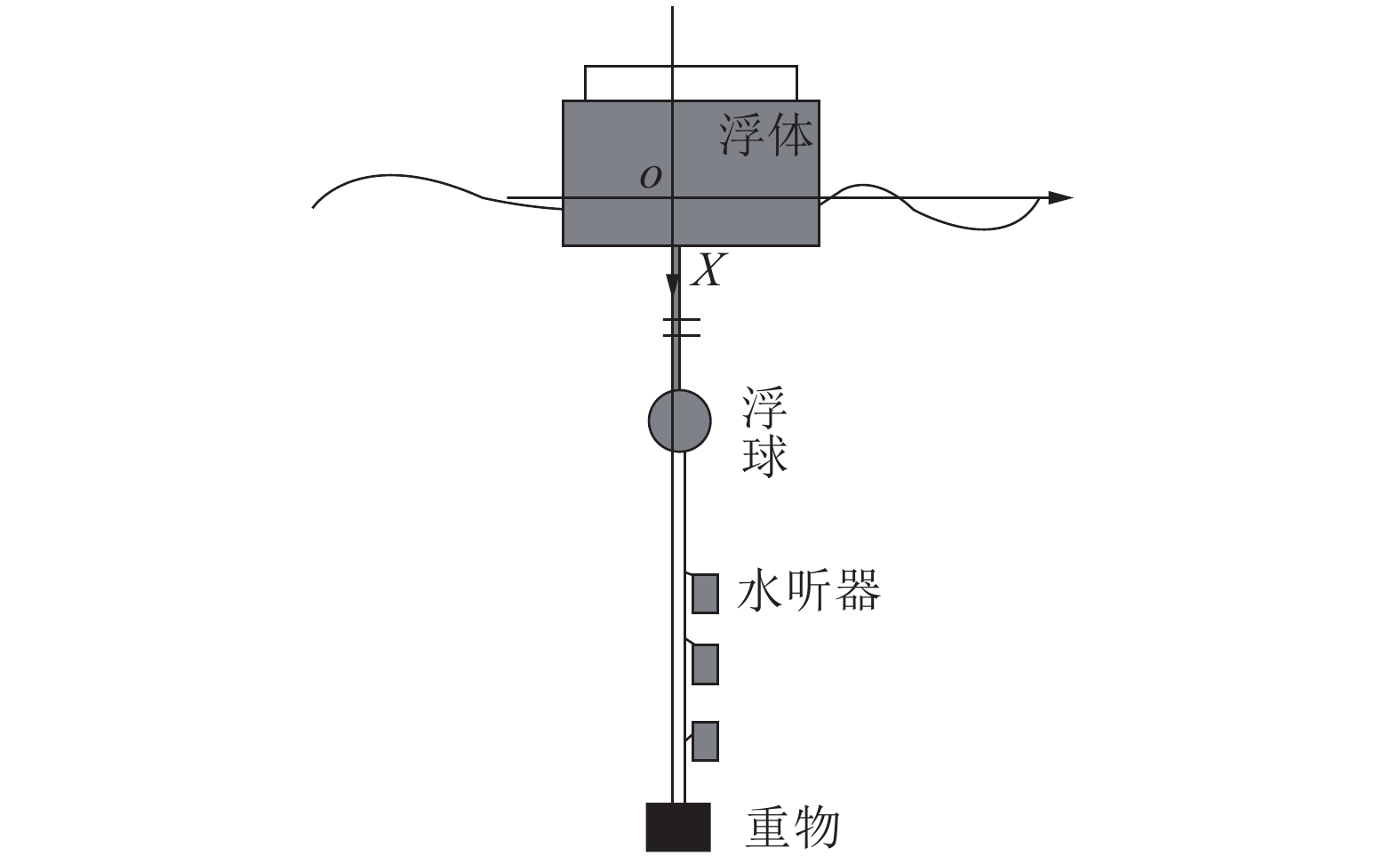
1.2 声学浮标运动状态分析声学浮标浮体漂浮于海面,水听器线阵悬在浮体上如图2所示。由于波浪的作用,浮体会上、下起伏。
|
Download:
|
| 图 2 声学测量浮标结构示意 | |
对声学浮标系统运动状态进行受力分析。根据牛顿第二定律,有
| $m\ddot x = F - f - c\dot x$ |
式中:m为浮标质量,F为波浪对浮标的作用力,f是浮标在水中所受的浮力,c是浮标在水中的阻尼系数,x为浮标的垂直位移。其中波浪对浮标的作用力F是时间的简谐函数,可表示为
| $F\left( t \right) = F{{cos}}\left( {\omega t} \right)$ |
将其带入公式,合并整理得
| $\ddot x + 2\delta {\omega _n}\dot x + \omega _n^2x = \omega _n^2H{{cos(}}\omega t{{)}}$ | (2) |
式中:δ是浮标的阻尼比,H是波高。式(2)是二阶常系数非齐次线性常微分方程,根据微分方程理论,它的解由两部分组成:一部分是与其对应的齐次方程的通解,式(2)左式作为通解,根是收敛的,即无论浮标投入的状态如何,经过一段时间,浮标在垂直方向上的自身扰动运动会逐渐消失。另一部分是特解,依照参考文献[10]有
| $\begin{gathered} x = H{{cos}}\left\{ {\omega t - \arctan \left\{ {\left( {2\delta \omega /{\omega _n}} \right)/\left[ {1 - {{\left( {\omega /{\omega _n}} \right)}^2}} \right]} \right\}} \right\}/ \hfill \\ \quad \quad {\left\{ {{{\left[ {1 - {{\left( {\omega /{\omega _n}} \right)}^2}} \right]}^2} + {{\left( {2\delta \omega /{\omega _n}} \right)}^2}} \right\}^{0.5}} \hfill \\ \end{gathered} $ |
由此可以看出,在波浪的简谐激励下,浮标在垂直方向的响应也是简谐振动。因此,在声学浮标作业过程中,达到稳态后,在垂直方向主要是由波浪激励引起的上、下垂直运动。这种垂直运动,一方面,会产生机械噪声,但这种噪声频率往往很低(小于10 Hz),但当速度达到一定的数值时,其在线缆的外面形成TBL湍流层,会产生较大的流噪声,这种流噪声正是由于线缆上、下运动的垂直速度引起,也就是上文分析的声学浮标垂直线阵的拖曳速度,因此其是影响流噪声大小的重要因素。
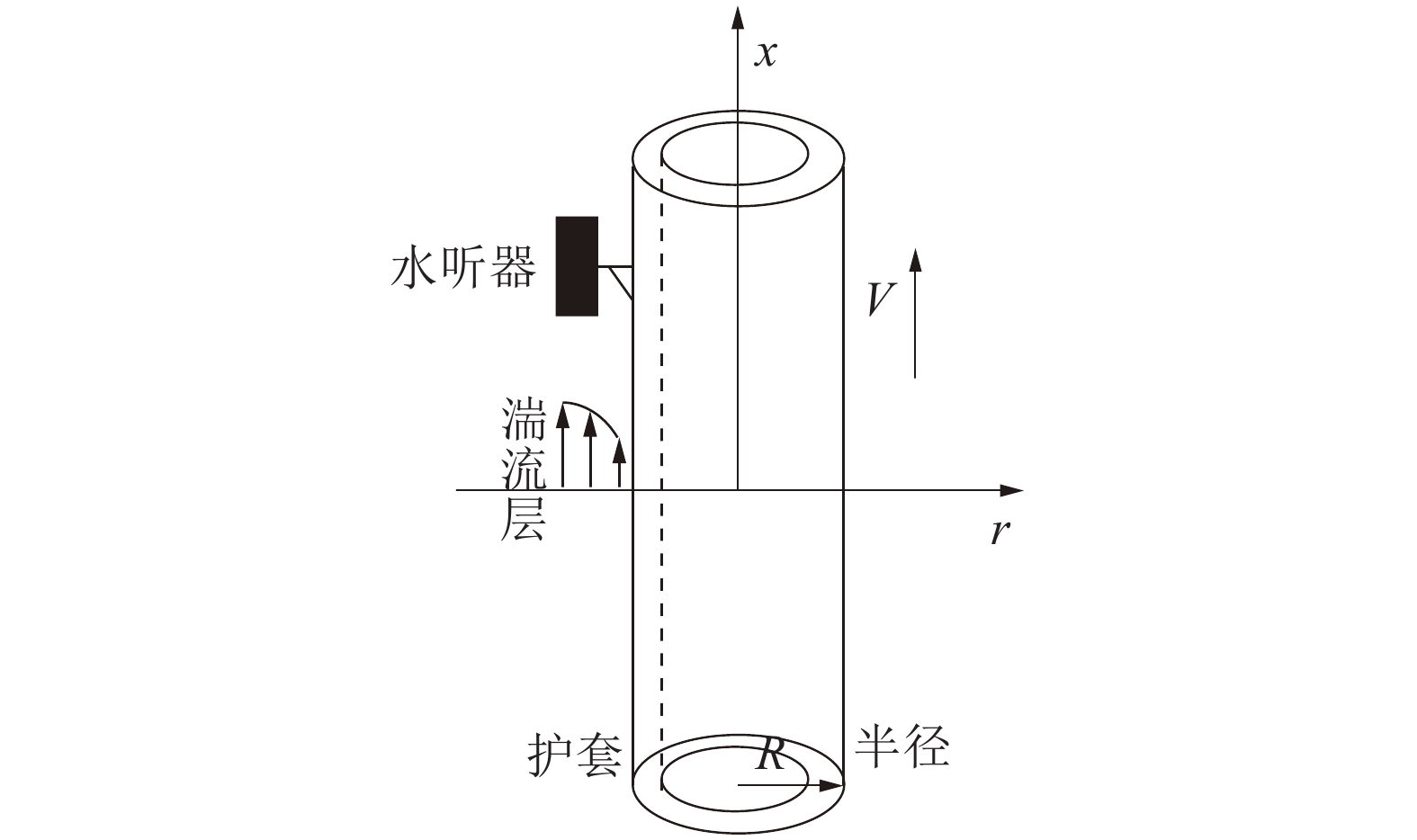
1.3 声学浮标流噪声功率谱理论模型声学浮标垂直线阵在线缆运动产生流噪声的机理上与一般的水平拖线阵是相同的,但它们在结构上有所不同:水平拖线阵的水听器一般位于护套线缆内,而声学浮标垂直阵的水听器直接位于线缆外侧,如图3所示。
|
Download:
|
| 图 3 声学浮标水听器分布 | |
这样,由于水听器布放于声学浮标垂直线阵线缆外侧,没有受到线缆管内传播的限制,不需考虑护套柱壳传递函数和径向传播约束,式(1)中系统的波数−频率谱传递函数,将只需要考虑水听器的响应函数,即
| $h\left( {{k_x},r,\omega } \right) = \frac{{\sin \left( {{k_x}l/2} \right)}}{{{k_x}l/2}}$ | (3) |
式中l为水听器长度,将其带入水听器对流的响应功率谱,
| ${\phi _0}\left( \omega \right) = \int_{ - \infty }^\infty {{\phi _{{s}}}\left( {{k_x},\omega } \right){{\left| {\frac{{\sin \left( {{k_x}l/2} \right)}}{{{k_x}l/2}}} \right|}^2}{{d}}{k_x}} $ |
即为声学浮标流噪声功率谱的理论模型。
由于声学浮标垂直线阵与水平拖线阵的运动方式和水听器布放不同,因此对于声学浮标来说,上述Carpenter&Kewley模型的修正模型中的修正参数c、h、b需要调整,其他参数保持不变。
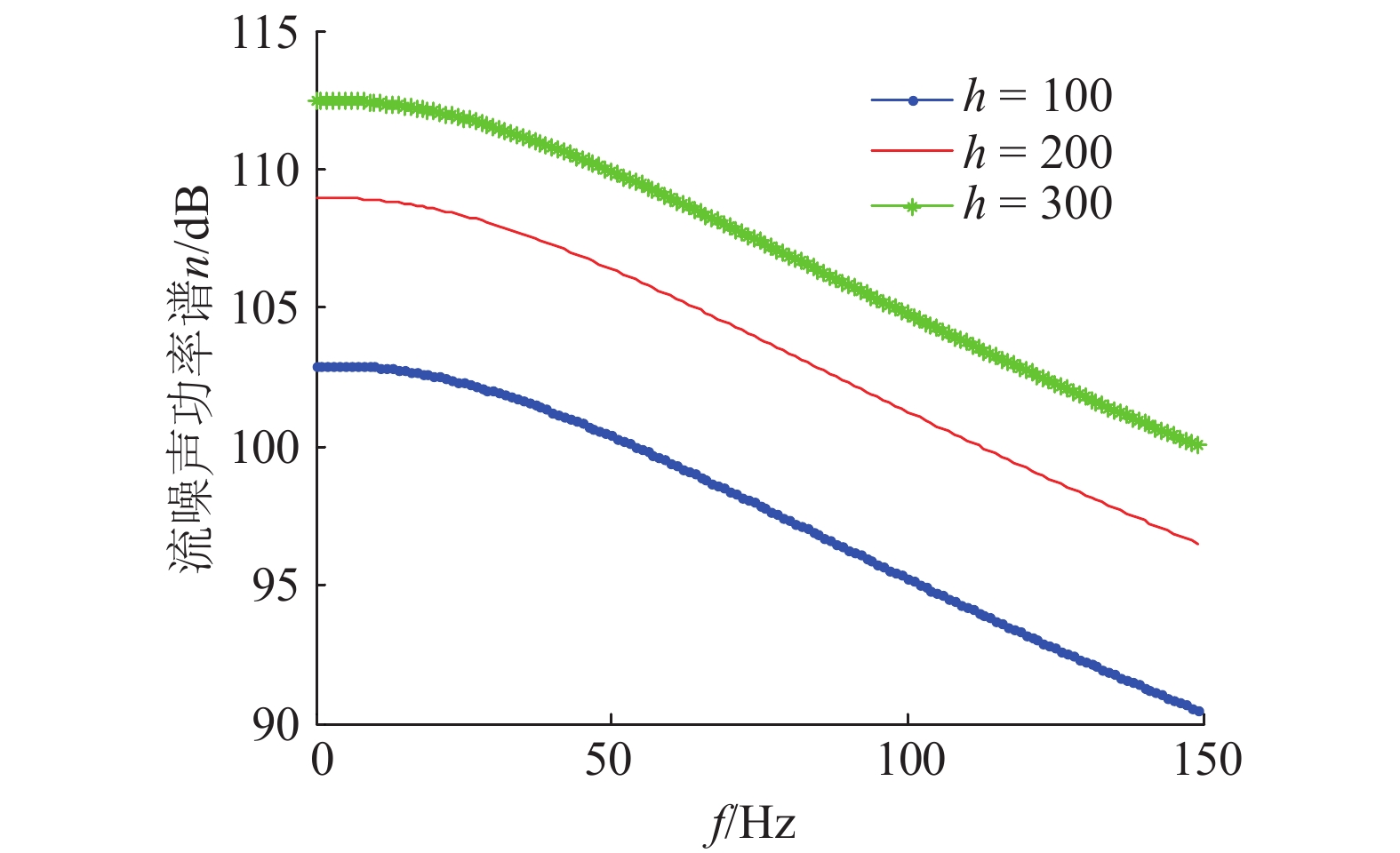
1.4 仿真分析 1.4.1 声学浮标流噪声功率谱参数修正调整声学浮标流噪声功率谱的理论模型修正参数c、h、b。当电缆半径R=0.02 m,水听器长度l=0.15 m时,得到不同参数c、h、b时的流噪声功率谱,见图4~6。
|
Download:
|
| 图 4 参数c与流噪声功率谱关系 | |
从图4可以看出,不同参数c时,流噪声功率谱曲线形状变化不大,大小随着参数c的增大而增大。
|
Download:
|
| 图 5 参数h与流噪声功率谱关系 | |
从图5可以看出,不同参数h时,流噪声功率谱曲线斜率发生变化,参数h越大,曲线越平坦。

|
Download:
|
| 图 6 参数b与流噪声功率谱关系 | |
从图6可以看出,参数b越大时,流噪声功率谱曲线在小于50 Hz低频部分斜率越大,相对值也越大。
综合上述分析,调整修正参数c、h、b值,并与参考文献[11]推导的海上实验中实测的流噪声数据进行比对,就可以得到符合实际的参数。经多次比较后,最后选定修正参数c=3 100、h=100、b=0.15。
将修正参数,电缆半径R=0.02 m,水听器长度l=0.15 m代入声学浮标流噪声功率谱的理论模型,得到水听器垂直速度和流噪声功率谱的关系,见图7。
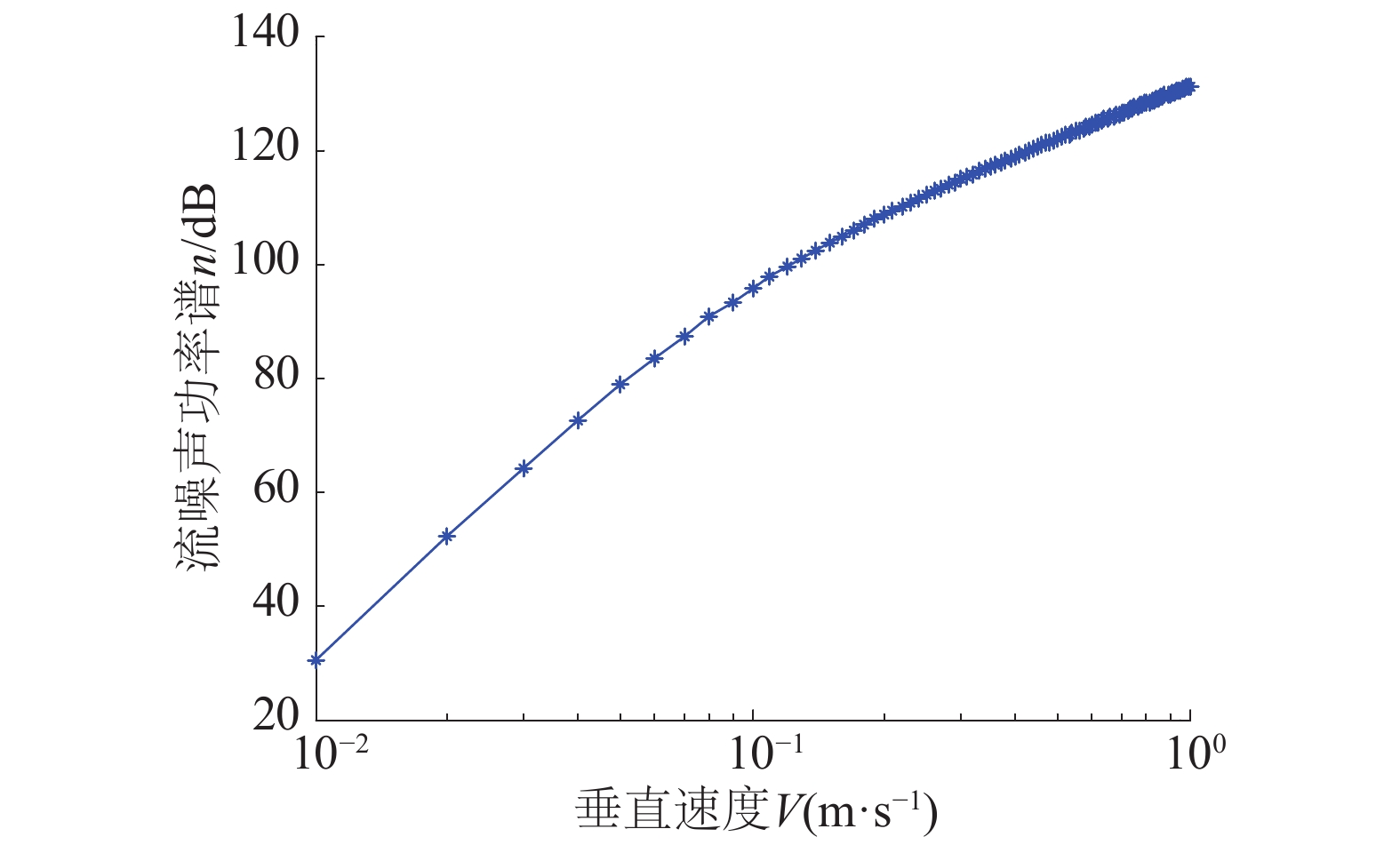
|
Download:
|
| 图 7 垂直速度和流噪声功率谱关系 | |
从图7可以看出,垂直速度和流噪声呈指数关系。经详细计算得出,当速度在V=0.2 m/s附近时,水听器垂直速度的对数值与流噪声功率谱的斜率近似在48左右,也就是说水听器垂直速度与流噪声功率谱为指数关系,且近似指数V4.8关系。Arakeri等[12]认为在对称体的驻点处有1/5的速度能量转化为流噪声,Lauchle[13]认为,这种情况下,流噪声和速度的指数关系在6~7.5;Legendre[14]认为,应该是1/6的能量转化为流噪声,所以指数小于6。这与我们所选的参数下,指数为4.85左右是吻合的。也就是说修正参数的选择是合理的。当V<0.2 m/s时,取V=0.1 m/s。依据声学浮标流噪声谱模型,垂直速度与流噪声功率谱的关系近似指数值超出7.5。有研究表明,当V<0.234 m/s时,流噪声功率谱为一个定值[11]。因此本模型将V<0.2 m/s时的流噪声功率谱看做定值。
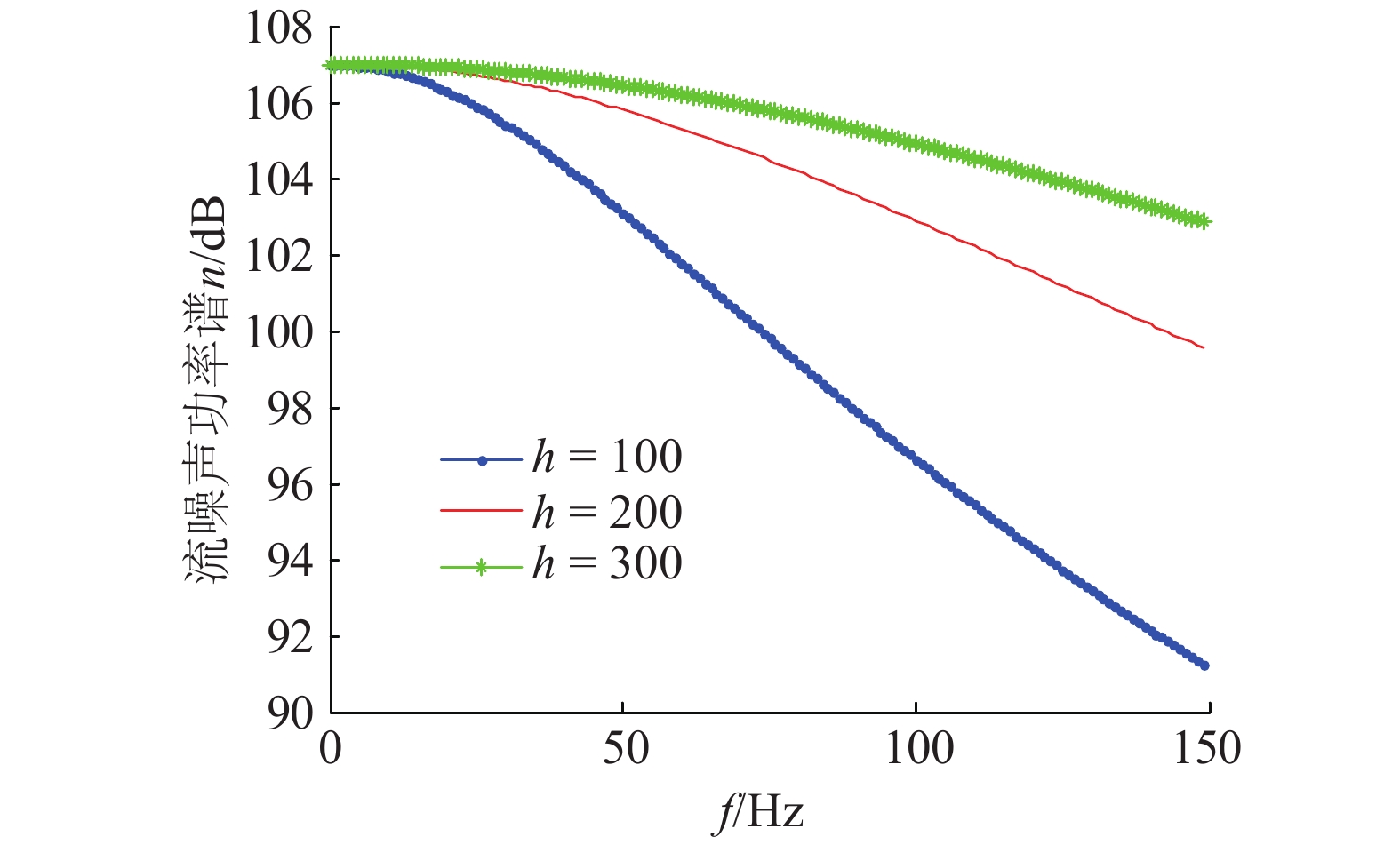
1.4.2 声学浮标流噪声功率谱特性将电缆半径R=0.02 m,水听器长度l=0.15 m,U=0.7 m/s带入式(3),带入已修正参数c、h、b;得到流噪声响应功率谱的被积函数TBL层压力起伏谱、水听器响应及它们之间的乘积与波数之间的关系如图8~9所示。图8中f=100 Hz,图9中 f=500 Hz。

|
Download:
|
| 图 8 f=100 Hz时,H(kx)、Φ(kx,ω)及它们的乘积和kx的关系 | |
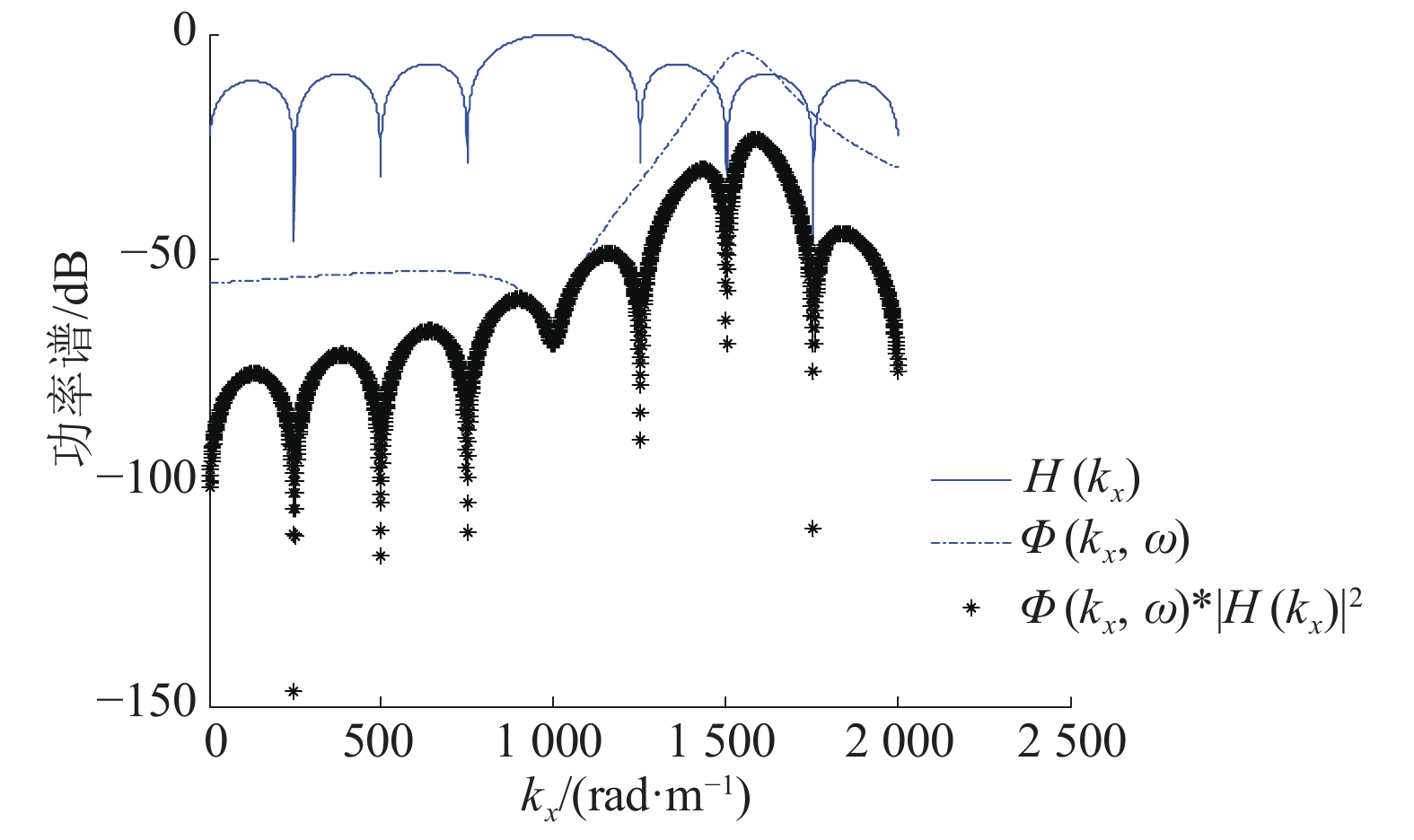
|
Download:
|
| 图 9 f=500 Hz时,H(kx)、Φ(kx,ω)及它们的乘积和kx的关系 | |
从图8~9可以看出,对积分式结果有较大影响的是TBL压力起伏谱。随着频率的增加,TBL压力起伏谱的迁移峰向高波数区域移动。
当垂直速度为0.3 m/s,其他系数维持不变。用数值积分法计算得到的积分结果,即流噪声功率谱图10。
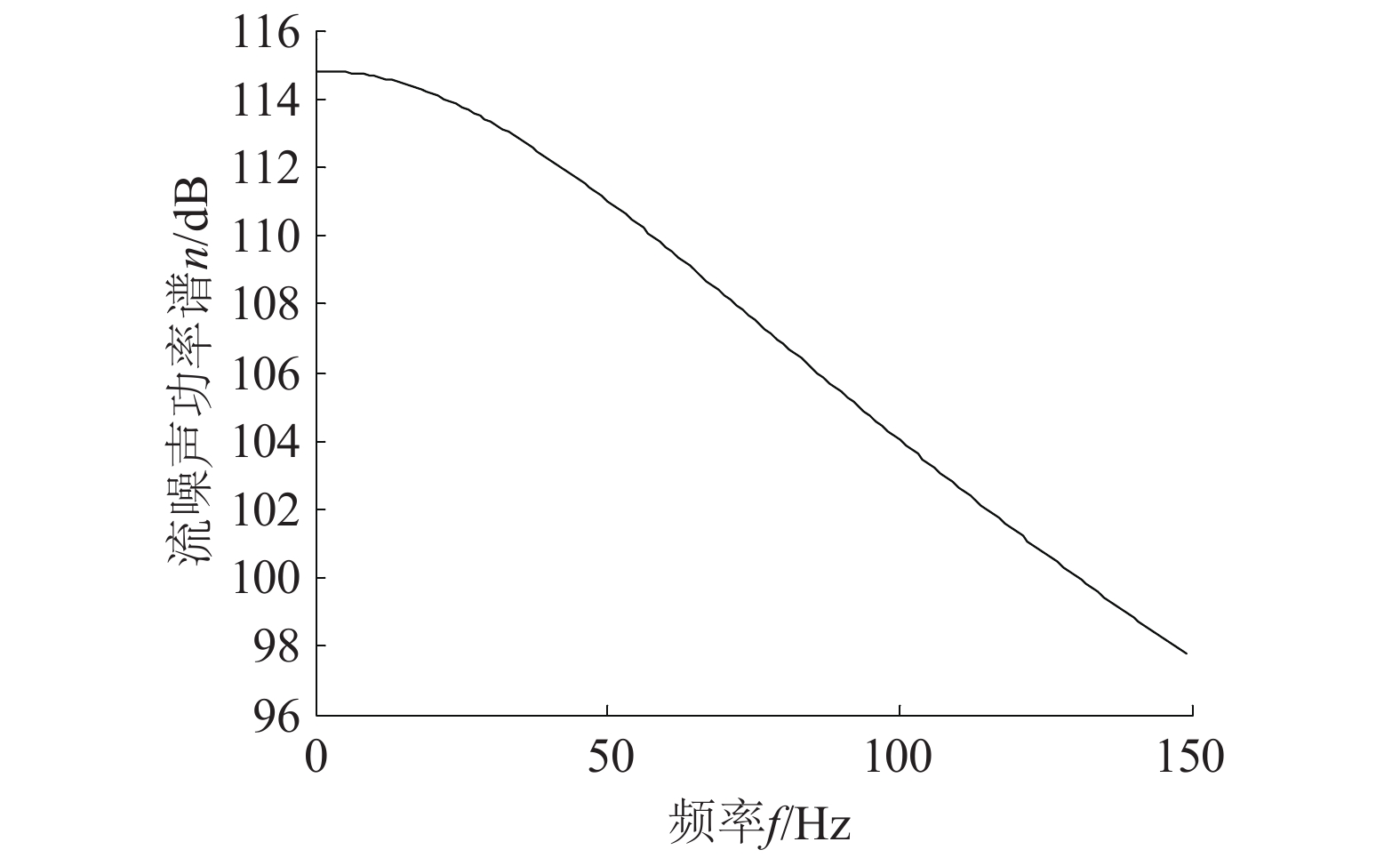
|
Download:
|
| 图 10 流噪声功率谱 | |
从图10可见,声学浮标水听器接收到的流噪声主要分布在低频段(平均速度为0.3 m/s,分布在150 Hz内)。谱级大小随频率的增高迅速下降,由此可知,在海浪级别较高,垂直速度相对较大的甚低频段,流噪声很大。
1.4.3 声学浮标流噪声相关特性声学浮标不同间距水听器接收流噪声的相关特性是声学浮标流噪声分析的基础,在指导声学浮标水听器布放上有重要的实际意义。根据前面对垂直线阵外水听器流噪声的分析,以及流噪声场归一化的时−空相关函数的定义,得到流噪声的相关函数R[7]为
| $\begin{gathered} R = {\left( {\frac{1}{{2{{\pi }}}}} \right)^2} \times \hfill \\ \int {\int_{ - \infty }^\infty {{\phi _s}\left( {{k_x},{{\omega }}} \right)h\left( {{k_x},{r_1},\omega } \right){h^{{*}}}\left( {{k_x},{r_2},\omega } \right){{{e}}^{{{j}}\left( {{k_x}l - \omega t} \right)}}{{d}}{k_x}{{d}}\omega } } \hfill \\ \end{gathered} $ | (4) |
式中r1、r2为水听器的轴向坐标。
本文只讨论轴向空间相关性,因此相关函数可简化为
| ${R_{\Delta \omega }}\left( {L,0} \right) = \int_{{\omega _0} - \frac{{\Delta \omega }}{2}}^{{\omega _0} + \frac{{\Delta \omega }}{2}} {\phi \left( {L,\omega } \right){{d}}\omega }$ |
归一化后,消去Δω,得到
| $R \approx \int_{ - \infty }^{{{ + }}\infty } {{\phi _s}\left( {{k_x},\omega } \right)|H\left( {{k_x}} \right){|^2}{{{e}}^{{{i}}{k_x}L}}{{d}}{k_x}} $ |
设它的平均速度为0.3 m/s,电缆半径R=0.018 m,水听器长度不同时带入式(4),经数值积分,计算得到频率f=150 Hz时,阵元间距与相关系数的关系如图11所示。

|
Download:
|
| 图 11 水听器长度不同时流噪声相关系数 | |
根据相关系数下降到1/e时,对应的间距为水听器流噪声的空间相关半径的定义。从图11可以看出,流噪声的相关半径与水听器长度有关,一般随着水听器长度的增大而增大。当水听器长度为0.10 m时,声学浮标流噪声的相关半径约为10 cm。改变流噪声的频率,经过仿真计算还可以得出不同频率下水听器流噪声的空间相关半径,如图12所示。
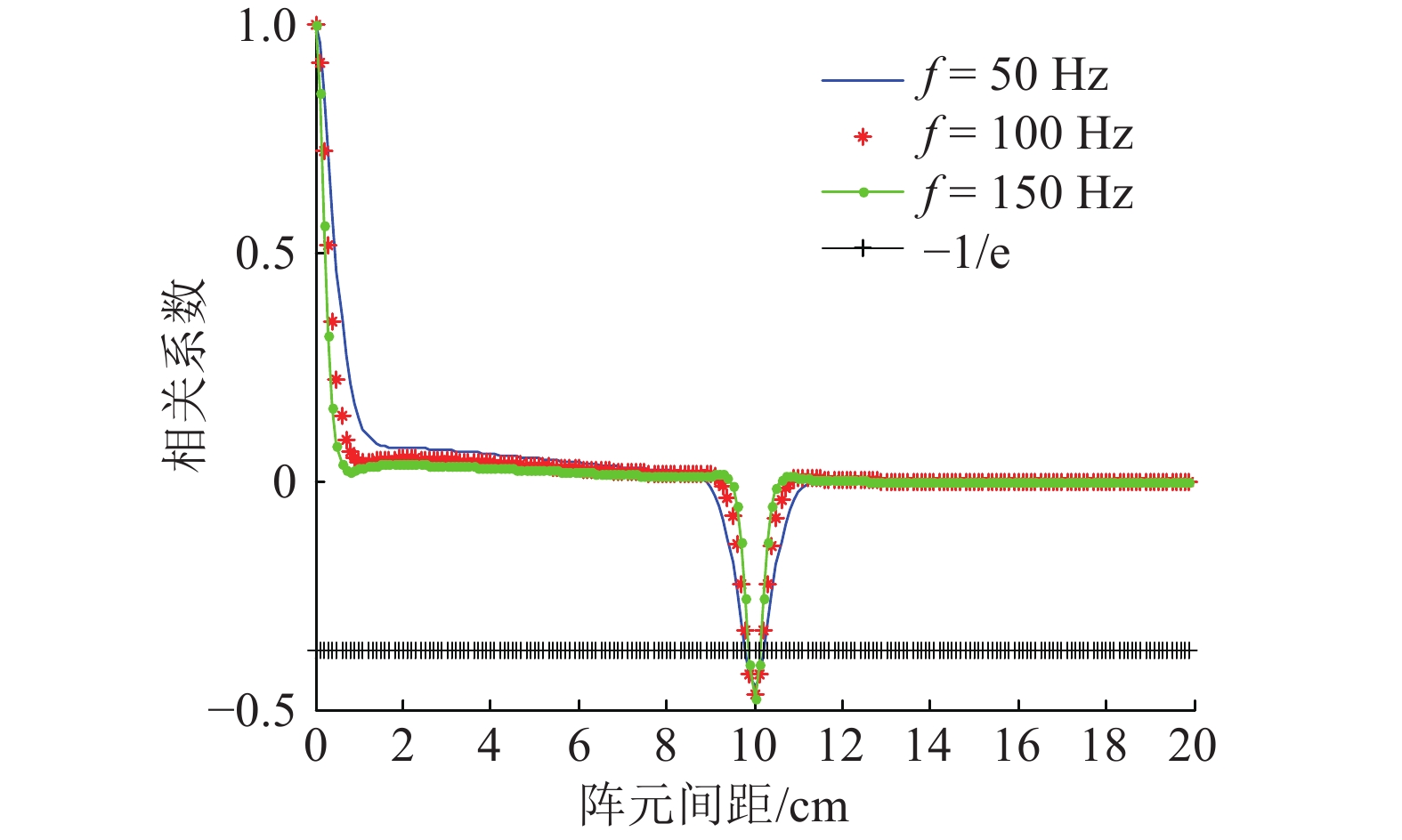
|
Download:
|
| 图 12 不同频率时流噪声相关系数 | |
从图12可以看出,声学浮标水听器流噪声的空间相关半径与流噪声的频率大小关系不大。一般情况下,当声学浮标水听器布放间距远大于流噪声相关半径时,两水听器接收的流噪声是互不相关的。
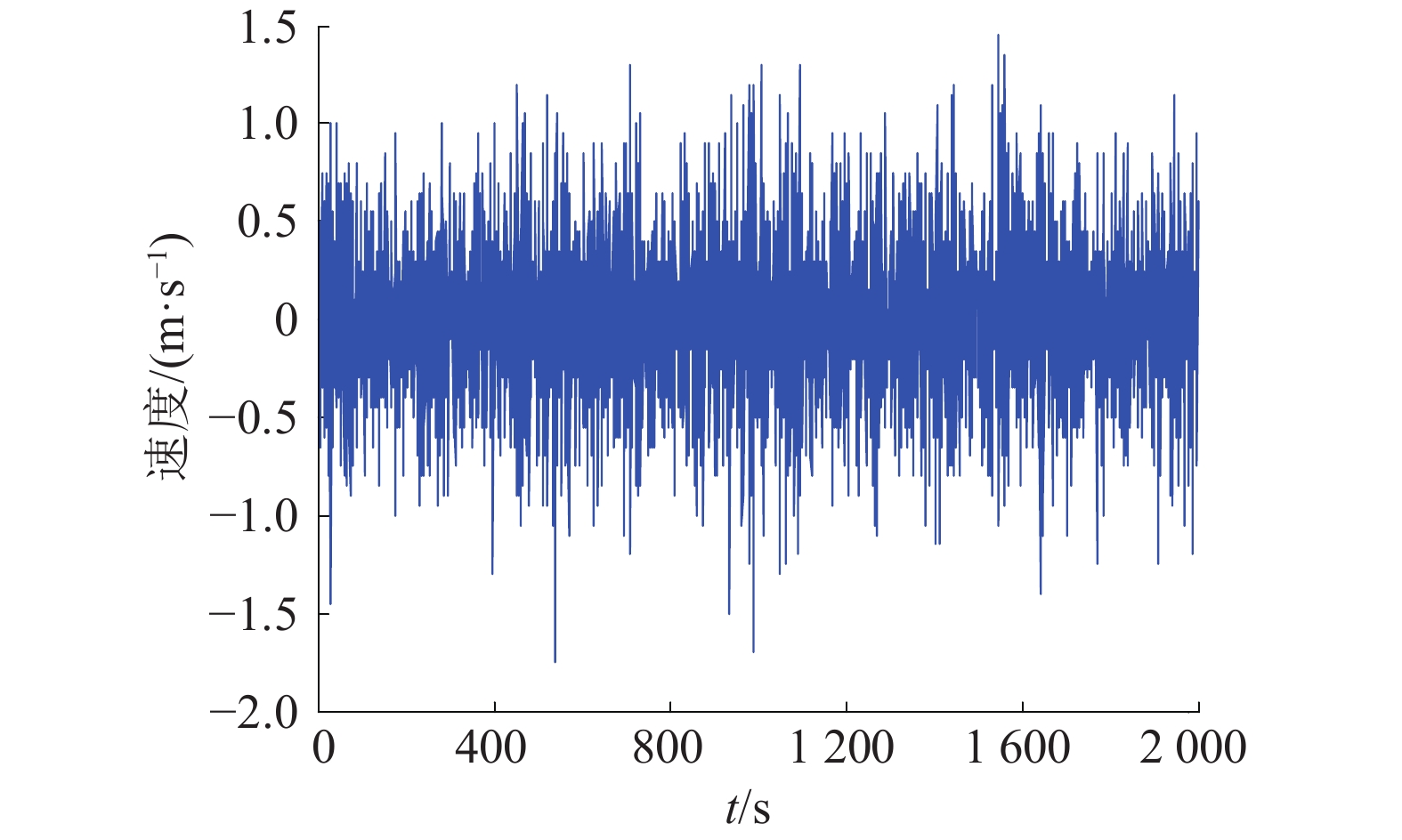
2 海洋实验2012年秋,在南海某一海域进行海洋环境噪声测量实验。将声学浮标电缆上的3个水听器分别布放在40、80、210 m深度;另一声学潜标布放在700 m深度。应用加拿大RBR公司的TD对水听器的深度进行实时测量,TD的采样时间间隔为2 s,量程为740 m。将深度数据对时间进行求导,得到各水听器的垂直速度。其中第一个水听器的垂直速度如图13所示。
|
Download:
|
| 图 13 TD记录的第一个水听器的垂直速度 | |
从图13可以看出,声学浮标的垂直速度是不断变化的,最高可以达到近1.5 m/s。取垂直速度相对均匀的时段进行计算,求得各水听器在相同时段内500、1 000、1 500、2 000 s的平均垂直速度分别如表1所示。
|
|
表 1 各水听器的平均垂直速度 |
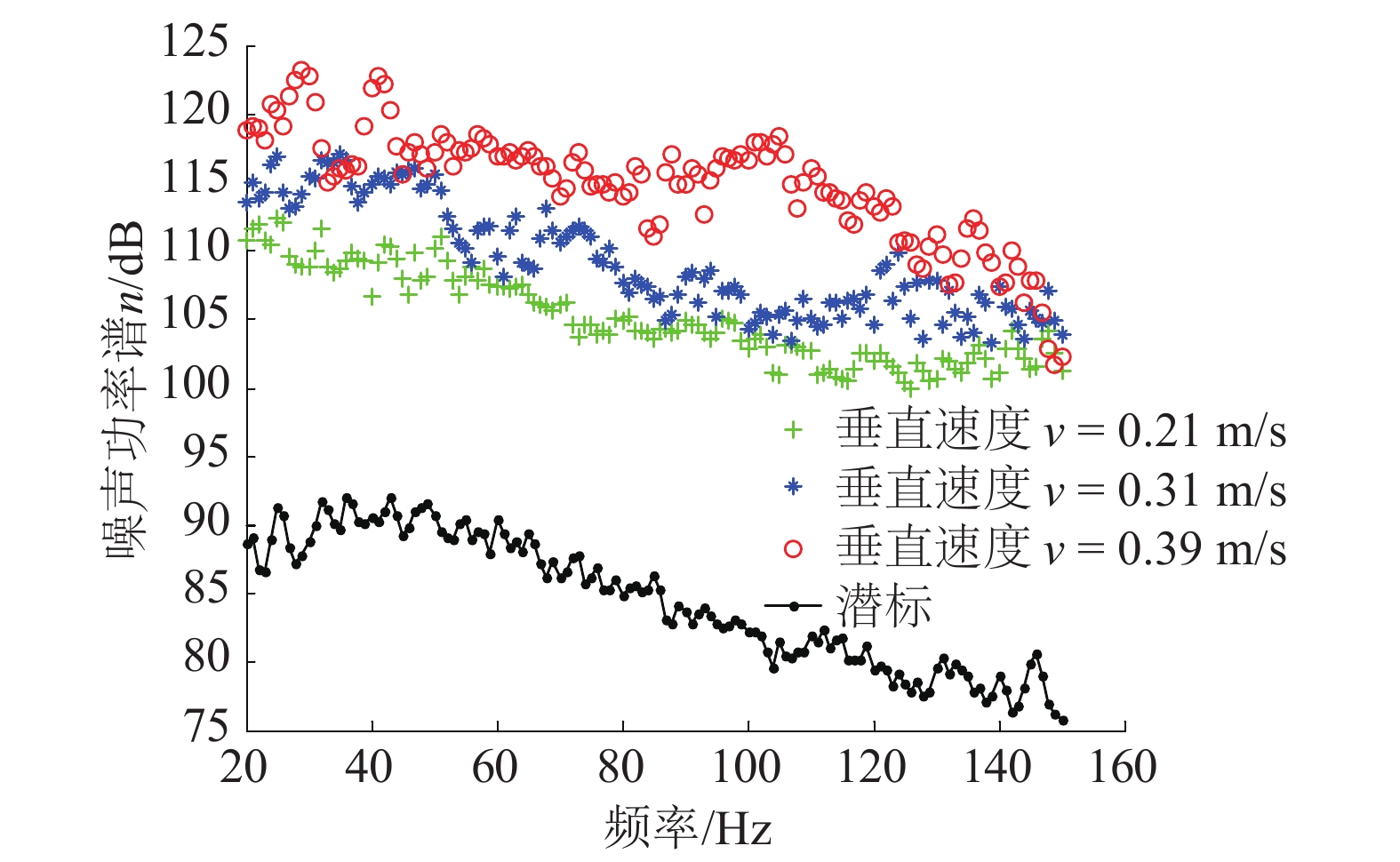
声学浮标和潜标采样率均为20 kHz,选取1 s数据,运用汉宁窗,数据重叠率50%,分段循环进行滑动FFT运算。得到声学浮标水听器平均垂直速度分别为0.21、0.31、0.39 m/s以及潜标的海洋环境噪声功率谱n的分贝值,如图14所示。
|
Download:
|
| 图 14 不同垂直速度下的流噪声功率谱 | |
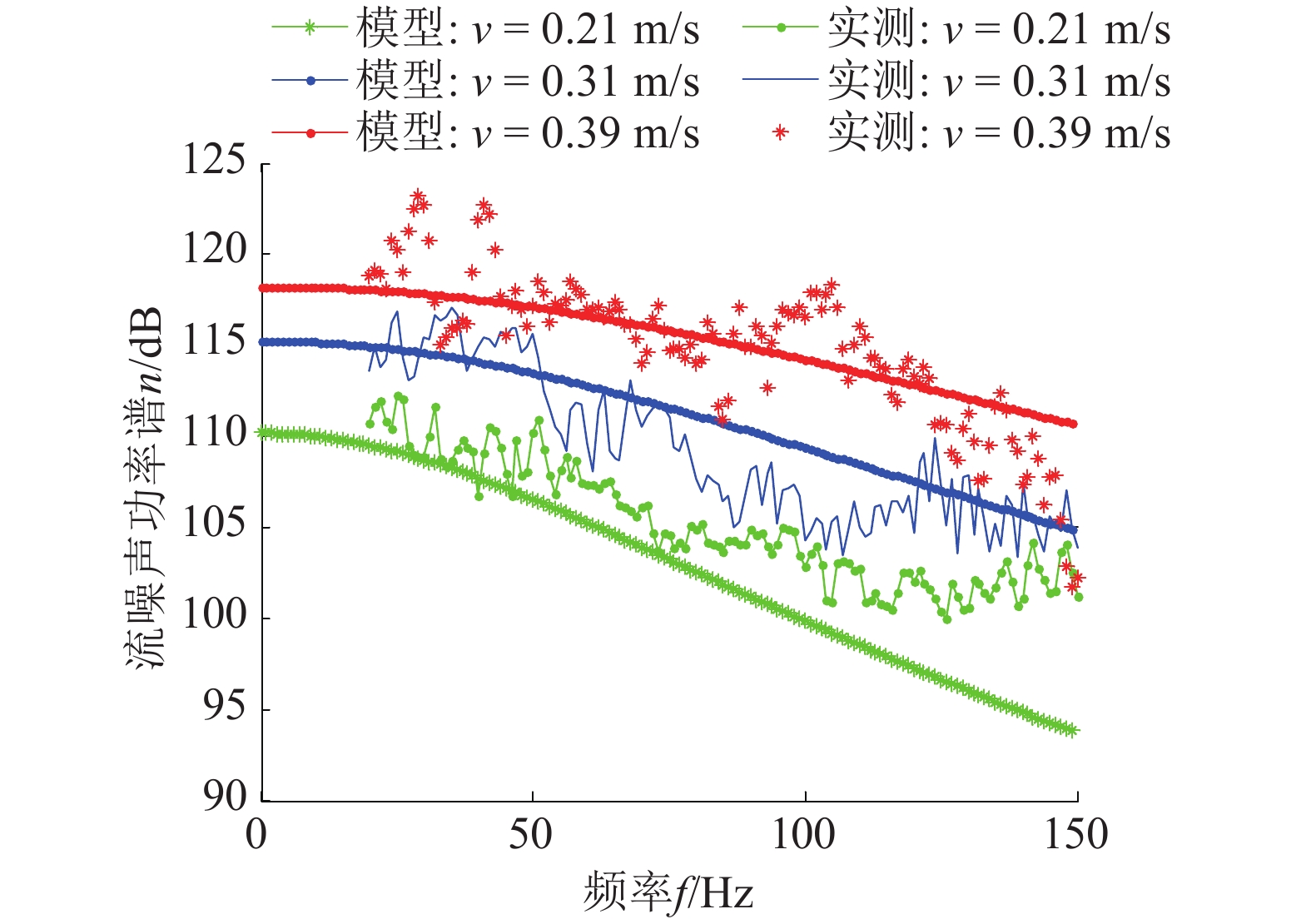
从图14可以看出,声学浮标水听器接收到的海洋环境噪声的功率谱级在150 Hz内,随着垂直速度的增加而增加;潜标接收到的海洋环境噪声功率谱级则相对较小。由于潜标不受海面波浪影响,观察到其TD测量的深度值变化很小,可以假设其没有流噪声干扰。因此我们可以运用声学浮标水听器接收的海洋环境噪声声压级减去潜标接收到的海洋环境噪声声压级,从而得到声学浮标水听器接收到的流噪声声压级。经计算,用实测数据得到的流噪声功率谱及运用模型得到的流噪声功率谱分别如图15所示。
|
Download:
|
| 图 15 实测不同深度水听器的功率谱 | |
从图15中可以看出,流噪声功率谱在150 Hz频段内,实测数据的大小与模型计算出的数值大小接近,稍大于模型的数值,这是因为实测的流噪声功率谱还包含一些其他的干扰,如声学浮标线缆机械噪声或海面的浪击噪声等。另外,一般情况下,实测的流噪声功率谱随着平均垂直速度的增大而增大;模型计算得到流噪声功率谱与实测的情况一样,在150 Hz频段内,也是随着平均垂直速度增大而增大。因此,总的来说,声学浮标流噪声谱模型与实测数据相符。
3 结论通过本文的分析,可以得到以下结论:
1)声学浮标流噪声谱模型,当水听器的垂直速度V>0.1 m/s时,可以直接将垂直速度带入计算得到流噪声大小。
2)流噪声与水听器的垂直速度有关,随着垂直速度的增大而增大。
3)通过噪声谱模型,我们还可以计算流噪声相关半径大小,相关半径大小与水听器的长度有关,水听器长度越长,流噪声的相关半径越大。
当然,海洋中还有其他不同方向的复杂的海流,对声学浮标水听器的外表面也会有一定的影响。因此,在实际使用时,水听器一般会戴上防流罩,以降低这些流噪声。
| [1] |
张民强, 林学清, 施性气, 等. 抗流激自噪声布设系统[J]. 海洋技术学报, 1983(2): 5-12. ( 0) 0)
|
| [2] |
HADDLE G P, SKUDRZYK E J. The physics of flow noise[J]. Journal of the acoustical society of America, 1969, 46(1B): 130-157. DOI:10.1121/1.1911663 ( 0) 0)
|
| [3] |
STRASBERG M. Nonacoustic noise interference in measurements of infrasonic ambient noise[J]. Journal of the acoustical society of America, 1979, 66(5): 1487-1493. DOI:10.1121/1.383543 ( 0) 0)
|
| [4] |
汪鸿振, 陈光冶. 水听器浮标系统噪声控制实验研究[J]. 噪声与振动控制, 2002(5): 11, 37. ( 0) 0)
|
| [5] |
马根卯, 张俊. 矢量拖曳线列阵流噪声自功率谱特性研究[J]. 声学与电子工程, 2014(2): 14-17. ( 0) 0)
|
| [6] |
时胜国, 于树华, 时洁, 等. 矢量拖线阵水听器流噪声响应特性[J]. 物理学报, 2015, 64(15): 305-314. ( 0) 0)
|
| [7] |
马根卯, 时胜国, 于树华. 矢量拖曳线列阵流噪声时-空相关特性研究[J]. 哈尔滨工程大学学报, 2015, 36(1): 57-61. ( 0) 0)
|
| [8] |
王晓林, 王茂法. 拖线阵水听器流噪声预报与实验研究[J]. 声学与电子工程, 2006(3): 6-11. ( 0) 0)
|
| [9] |
罗斌, 王茂法, 肖翔, 等. 流噪声背景下的细长线阵甚低频弱线谱检测算法[J]. 声学与电子工程, 2015(1): 15-19. ( 0) 0)
|
| [10] |
吴家喜, 李苹, 王健培. 水声测量浮标水面垂直振动分析[J]. 声学与电子工程, 2009(4): 44-45. ( 0) 0)
|
| [11] |
JASON I G. Reducing mechanical and flow-induced noise in the surface suspended acoustic receiver[D]. Cambridge: Massachusetts Institute of Technology, 1997: 48-49. https://www.researchgate.net/publication/44035605_Reducing_mechanical_and_flow-induced_noise_in_the_surface_suspended_acoustic_receiver?ev=auth_pub
( 0) 0)
|
| [12] |
ARAKERI V H, SATYANARAYANA S G, MANI S, et al. Studies on scaling of flow noise received at the stagnation point of an axisymmetric body[J]. Journal of sound and vibration, 1991, 146(3): 449-462. DOI:10.1016/0022-460X(91)90701-K ( 0) 0)
|
| [13] |
LAUCHLE G C. Flow noise scaling at the stagnation point of an axisymmetric body[J]. Journal of sound and vibration, 1992, 154(3): 568-572. DOI:10.1016/0022-460X(92)90788-Y ( 0) 0)
|
| [14] |
LEGENDRE R. High velocity acoustics[J]. Journal of sound and vibration, 1992, 157(2): 193-203. DOI:10.1016/0022-460X(92)90675-N ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


