视频中运动目标存在遮挡下的跟踪一直是计算机视觉研究的重点之一[1]。一直以来,大量的研究人员一直致力于目标在遮挡情况下的跟踪,如机器人视觉导航、人机交互、安防监控、太空视频会议等[2]。然而,遮挡对于目标跟踪是一个难点,特别是目标被严重遮挡且时间较长。视频图像序列运动目标遮挡下的跟踪总而言之分为以下几类:1)运动目标自遮挡下跟踪;2)运动目标被运动物体遮挡下的跟踪;3)背景场景结构遮挡下目标跟踪。
在遮挡目标跟踪中,遮挡的情况和对目标进行初始建模非常重要。对目标跟踪的预处理,主要是利用目标的形状、颜色、位置等特征作为先验知识[3-6]:对目标的形状轮廓进行建模时,需要图像确定、质量高且目标形状易提取,而现实中当环境存在噪声时,无法准确地提取;对目标的颜色建模需要目标颜色与背景区别大,在此基础上进行分割;对目标位置进行建模作为先验知识,需要利用位置信息和速度进行预测。现今各种各样的跟踪算法都是基于二维信息来实时跟踪运动目标,在实时跟踪过程中容易受到遮挡情况的影响,特别是当目标与背景图像灰度像素差别不大时,这种现象尤为明显。学者对于二维信息情况下的跟踪进行了研究,比如基于目标质心Mean Shift跟踪,但其只是对单个目标的跟踪效果良好[7];郭文强等[8]提出了基于卡尔曼滤波与云台的三维空间目标跟踪算法,通过及时调整云台角度获得目标方位角等信息,这是对于空间高速运动的运动目标跟踪,且计算量大;K. V sriharsha等[9-10]提出了加入动态场景分析并引入Kalman滤波的meanshift算法的目标跟踪算法,这些算法都是基于单个目标跟踪。当多目标时,对于2个外观特征不明显且相互遮挡下的目标跟踪,其跟踪效果不明显。现有的二维坐标跟踪算法效果不佳,而加入行为分析或者外观特征深度学习的算法又太复杂,针对这些问题,提出三维空间的跟踪算法。
1 基于背景差分的运动目标检测算法背景差分算法又叫做背景减差法[11],是目前场景固定情况下一种比较常用的检测目标的算法。在运动目标中,图像分为前景和背景。该方法是当前图像帧与前面已经准备好的背景图像帧作差分运算,在运算中通过灰度变化值变化来确定运动目标的区域。背景差分算法流程如图1所示。

|
Download:
|
| 图 1 背景差分算法流程 | |
图中
| ${D_{_k}} = |{f_k} - {f_{bk}}|$ |
| ${B_k} = \left\{ {\begin{array}{*{20}{c}} {1,D(k) > T} \\ {0,D(k) \leqslant T} \end{array}} \right.$ |
式中T为阈值,可以通过otsu自适应算法求得。二值化的图像再经过形态学滤波,对二值化图像的毛刺、断点连接、噪声点进行处理,仿真试验结果如图2、3所示。

|
Download:
|
| 图 2 90帧图像目标检测 | |

|
Download:
|
| 图 3 95帧图像目标检测 | |
从图2、3可以看出,背景差分算法检测效果良好,只是在背景中的灰度值与目标局部灰度值相似时会造成目标检测出现空洞的情况。
2 基本算法原理 2.1 sift算法原理sift算法是一种对两幅图像提取发生平移、旋转、变换等情况下的特征匹配[9]。sift算法由尺度不变性、关键点方向确定、特征向量生成、关键点位置等4部分组成。对于任何一副二维图像在不同尺度下可以用高斯卷积表示成
| $L(x,y,\sigma ) = G(x,y,\sigma ) * I(x,y)$ |
式中
| $G(x,y,\sigma ) = \frac{1}{{2\pi {\sigma ^2}}}{{{e}}^{ - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}}}$ |
式中
对于2个不同尺度的差分定义为高斯函数差分(Difference of Gaussian,DoG)算子,其定义如下:
| $D(x,y,\sigma ) = (G(x,y,k\sigma ) - G(x,y,\sigma ))I(x,y)$ |
关键点位置确定首先要剔除对比度低的点,对DoG算子进行泰勒级数展开:
| $D(x) = D + \frac{{\partial {D^T}}}{{\partial x}}\Delta x + \frac{1}{2}\Delta {x^T}\frac{{{\partial ^2}{D^T}}}{{\partial {x^2}}}\Delta x$ |
求对比度阈值
| $\left\{ {\begin{array}{*{20}{c}} {x \in X|D(\mathop x\limits^ \wedge )| \geqslant {T_c},x \in {X_0}} \\ {x \notin X|D(\mathop x\limits^ \wedge )| < {T_c},x \in {X_0}} \end{array}} \right.$ |
对边缘点进行剔除是由于边缘梯度方向上的曲率值较大,边缘上的曲率较小,算子DOG函数
| ${{H}} = \left[ {\begin{array}{*{20}{c}} {{D_{xx}}}&{{D_{xy}}} \\ {{D_{xy}}}&{{D_{yy}}} \end{array}} \right]$ |
由此矩阵H的迹和值为
| ${{Tr}}({{H}}) = {D_{xx}} + {D_{yy}} = \alpha + \beta $ |
| ${{Det}}({{H}}) = {D_{xx}}{D_{yy}} - {({D_{xy}})^2} = \alpha \beta $ |
H的迹和值比值为
| $\frac{{{{Tr}}{{({{H}})}^2}}}{{{{Det}}({{H}})}} = \frac{{{{(\alpha + \beta )}^2}}}{{\alpha \beta }} = \frac{{{{(\gamma + 1)}^2}}}{\gamma }$ |
由Hessian矩阵的迹和比值可以得出,Hessian矩阵只与两特征值之比有关,与特征值本身大小无关,设置一个合理的阈值
| $\theta \left( {x,y} \right) = {\tan ^{ - 1}}\frac{{L\left( {x,y + 1} \right) - L\left( {x,y - 1} \right)}}{{L\left( {x + 1,y} \right) - L\left( {x - 1,y} \right)}}$ |
| $\begin{aligned}& m\left( {x,y} \right) = \\& \sqrt {{{\left[ {L\left( {x + 1,y} \right) - L\left( {x - 1,y} \right)} \right]}^2} + {{\left[ {L\left( {x,y + 1} \right) - L\left( {x,y - 1} \right)} \right]}^2}} \end{aligned}$ |
对每个特征点的领域像素进行统计,找到统计直方图的峰值,用来确定关键点方向,至此特征点检测完毕,最后对生成的特征向量进行长度归一化,可以进一步消除光照对特征提取的影响。图4为sift算法提取的特征点仿真实验图。

|
Download:
|
| 图 4 sift算法仿真实验 | |
90帧图像和95帧图像提取的特征点都在运动目标区域上,2帧图像提取的特征点数分别为538和516,可以说明sift算法提取的特征点数很稳定。
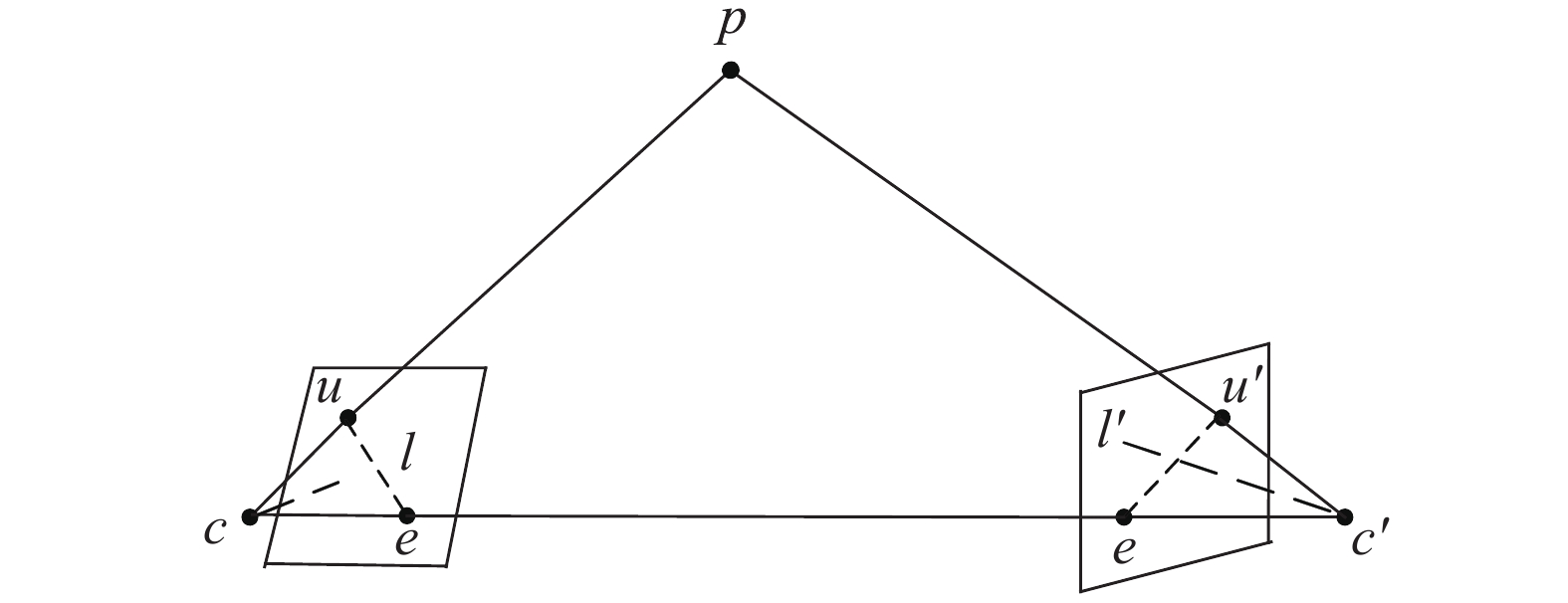
2.2 极线约束原理双目视觉的极线约束模型如图5所示。表示了空间点p经过摄像机的透视变换映射到左右摄像头u和u′。左右摄像机光心c和c′由基线连接起来,光心c和c′加上空间点p构成一个外极面,外极面与左右图像平面相交左右极线l和l′。极线约束是指空间中任何一点无论怎样运动,通过透视变换映射到左图像中点u在极线l,那么对应的点u′一定在右极线l′,而左右映射的点与基线相交点e和e′分别为左右极点。
|
Download:
|
| 图 5 双目极线约束原理 | |
FCM模糊聚类算法是将待聚类的数据分成多个模糊集,以各个样本到聚类中心的距离加权平均和最小作为判断的标准。FCM算法的隶属度矩阵U取值在[0, 1],uij相加的总和为1。其公式表示为
| $\sum\limits_{i = 1}^c {{u_{ij}} = 1} ,\;j = 1,\;2,\; \cdots ,\;n$ |
式中:c为聚类中心的数量,uij的j为属于第i类的数目隶属度关系数值。FCM目标函数公式为
| ${\lambda _m}\left( { u,\; v} \right) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {u_{ij}^md_{ij}^2} } $ |
式中:u和v分别为隶属度矩阵及中心矩阵,m为模糊参数,对于这个公式引入拉格朗日常数可得出隶属度uij和聚类中心vi:
| ${u_{ij}} = \frac{1}{{\displaystyle\sum\nolimits_{i = 1}^c {{{\left( {{d_{ij}}/{d_{rj}}} \right)}^{2/\left( {m - 1} \right)}}} }}$ |
| ${v_i} = \frac{{\displaystyle\sum\nolimits_{j = 1}^n {u_{ij}^m{x_j}} }}{{\displaystyle\sum\nolimits_{j = 1}^n {u_{ij}^m} }}$ |
Kalman滤波算法一种线性离散滤波算法,是一种离散最优化的回归数据处理方法[12],对于一种线性系统可以用一个随机过程运动方程来表示:
| ${{X}}(k) = {{AX}}(k - 1) + {{BU}}(k) + {{W}}(k)$ | (1) |
系统的观测方程为
| ${{Z}}(k) = {{HX}}(k) + {{V}}(k)$ | (2) |
一步预测方程为
| ${{X}}(k|k - {{1}}) = {{AX}}(k - {{1}}|k{{ - 1}}) + {{BU}}(k)$ |
一步协方差方程为
| ${{P}}(k|k{{ - 1}}) = {{AP}}(k{{ - 1}}|k{{ - 1}}){{{A}}^{ T}} + {{Q}}$ | (3) |
式中
| ${{X}}(k|k) = {{X}}(k|k - 1) + {{kg}}(k)(Z(k) - {{HX}}(k|k - 1))$ |
Kalman增益方程矩阵为
| ${{kg}}(k) = {{P}}(k|k - 1){{{H}}^{ T}}/{({{HP}}(k|k - 1){{{H}}^{ T}} + {{R}})^{ T}}$ | (4) |
协方差更新方程为
| ${ P}(k|k) = ({{I}} - { k{ g}}(k){{H}}){ P}(k|k - 1)$ |
式中I为单位矩阵。Kalman滤波要实现平滑、滤波、预测这3个步骤,在最小均方误差情况下并且自回归的更新下去。由Kalman滤波原理可知,只需要对当前的数据实时性处理,而不需要保存前面状态的数据,因此对运动目标跟踪必须先建立系统运动状态模型。
3 基于三维坐标的运动目标跟踪 3.1 三维坐标的提取传统的二维坐标结合Kalman滤波具有实时性高、算法复杂度低等特点。在追踪多目标情况下,目标运动相互之间存在遮挡,该算法无法识别目标运动状态,导致跟踪失败。
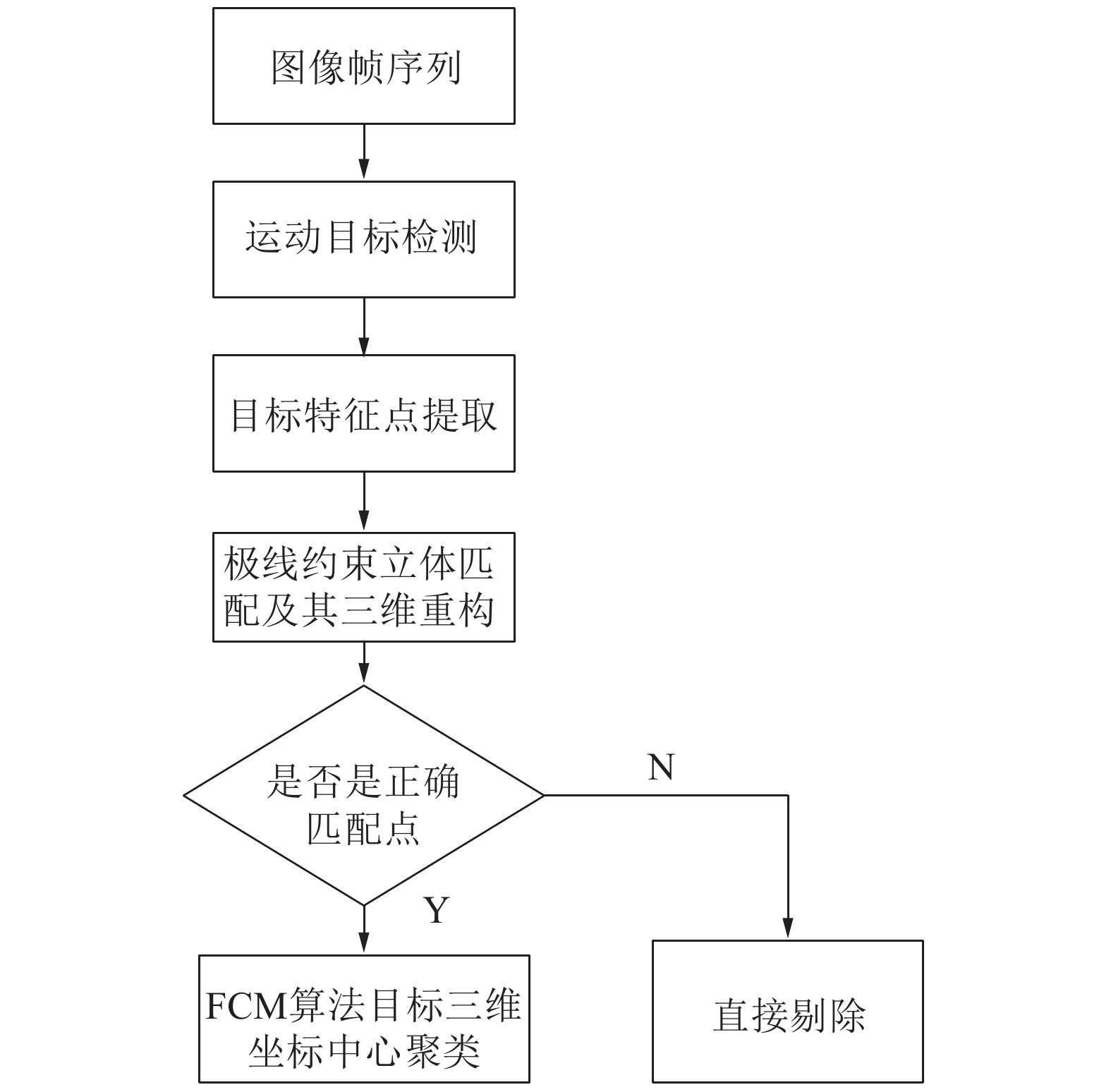
针对传统二维坐标跟踪算法的缺点,提出三维坐标运动目标跟踪算法。该算法基于目标的三维坐标结合Kalman滤波跟踪,三维坐标具有深度信息,利用目标坐标的瞬间不突变性,可以很好地适应目标遮挡下的追踪。该算法首先提取目标的特征点三维中心坐标,其算法流程如图6所示。
|
Download:
|
| 图 6 三维坐标提取流程 | |
其具体的实现步骤如下。
1) 运用背景差分算法对运动目标检测。
2) 对目标区域进行特征点提取,本文使用的sift算法提取目标特征。
3) 双目极限约束算法对左右图像提取的特征点进行立体匹配,获得目标的深度信息。
4) 对目标的特征点进行三维重构并对误匹配的特征点进行剔除,以免影响目标三维坐标中心聚类的准确性。
5) 运用FCM算法的C均值聚类求得各个目标的三维聚类中心点,为结合Kalman滤波目标跟踪作准备。
3.2 三维坐标与Kalman滤波结合图像序列之间的关系是一种马尔科夫链,因此当前帧图像必然与下一帧图像存在着必然的关系。对于视频图像中的运动目标大多处于低速运动目标的状态,为此我们可以采用一阶运动模型来描述目标的各个时刻的运动状态。Kalman滤波算法包含着滤波、平滑、预测3个阶段[2]。Kalman滤波算法适用多输入多输出,对于一般线性系统运动具有良好的平滑滤波效果。本系统使用的双目摄像头拍摄每秒20帧,为此假设目标当前的帧的坐标为
| $\left\{ {\begin{aligned}& {x\left( k \right) = x\left( {k - 1} \right) + {v_x}T} \\ & {y\left( k \right) = y\left( {k - 1} \right) + {v_y}T} \\ & {z\left( k \right) = z\left( {k - 1} \right) + {v_z}T} \end{aligned}} \right.$ |
式中:T为两帧之间的间隔,vx、vy、vz分别代表三维坐标各个坐标轴上的运动速度。由式(1)可得过程状态转移矩阵A:
| ${ A}{{ = }}\left[ {\begin{array}{*{20}{c}}1 & 0 & 0 & T & 0 & 0\\0 & 1 & 0 & 0 & T & 0\\0 & 0 & 1 & 0 & 0 & T\\0 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 1\end{array}} \right]$ | (5) |
由系统观测方程式(2)可得出观测矩阵H:
| ${ H}{{ = }}\left[ {\begin{array}{*{20}{c}}1 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0\end{array}} \right]$ | (6) |
由于没有外界的控制变量,为此对于式(1)中B取零,式(3)中Q和式(4)中R由系统的先验知识求得,Q越大表示预测值越接近于观测值,而R越大表示预测值越接近于过程值。由式(1)和(5)可得目标的具体信号运动模型为
| $\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{x(k)}\\[5pt]{y(k)}\\[5pt]{z(k)}\end{array}} \right]{{ = }}\left[ {\begin{array}{*{20}{c}}1 & 0 & 0 & T & 0 & 0\\[5pt]0 & 1 & 0 & 0 & T & 0\\[5pt]0 & 0 & 1 & 0 & 0 & T\\[5pt]0 & 0 & 0 & 1 & 0 & 0\\[5pt]0 & 0 & 0 & 0 & 1 & 0\\[5pt]0 & 0 & 0 & 0 & 0 & 1\end{array}} \right] \times \\\quad \quad \quad \quad \; \left[ {\begin{array}{*{20}{c}}{x(k - 1)}\\[5pt]{y(k - 1)}\\[5pt]{z(k - 1)}\\[5pt]{v{}_x}\\[5pt]{{v_y}}\\[5pt]{{v_z}}\end{array}} \right] + { W}(k)\end{array}$ |
同理由式(2)和(6)得到信号具体的观测模型为
| $\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{x\left( k \right)}\\[6pt]{y\left( k \right)}\\[6pt]{z\left( k \right)}\end{array}} \right]{{ = }}\left[ {\begin{array}{*{20}{c}}1 & 0 & 0 & 0 & 0 & 0\\[6pt]0 & 1 & 0 & 0 & 0 & 0\\[6pt]0 & 0 & 1 & 0 & 0 & 0\end{array}} \right] \times \\[8pt]\quad \quad \quad \quad \,\,\, \left[ {\begin{array}{*{20}{c}}{x\left( k \right)}\\[6pt]{y\left( k \right)}\\[6pt]{z\left( k \right)}\\[6pt]{{v_x}}\\[6pt]{{v_y}}\\[6pt]{{v_z}}\end{array}} \right] + { V}\left( k \right)\end{array}$ |
Kalman滤波通过观测模型k时刻的三维坐标观测值和k时刻的三维坐标修正值得到k时刻的Kalman滤波三维坐标值,再通过k时刻的三维坐标滤波值预测k+1时刻的三维坐标预测值,至此Kalman滤波在修正和预测两个过程不断进行下去。
4 仿真结果因为只需要运动目标的三维坐标,而没有使用到图像的彩色信息;因此采用了双目摄像头采集分辨率为1 200×1 600的灰度图像视频序列,仿真的处理器型号CPU为AMD-A10-5750M、主频为2.5 GHz,操作系统为Windows7,内存为4 GB,通过Matlab2013a实现。图7、8分别是传统二维坐标跟踪和三维坐标跟踪效果图,采用是的2个行人相向运动,遮挡后再返回,图7中星型点和圆圈点分别代表2个目标的二维中心像素坐标,而图8中星型点和圆圈点分别为追踪的三维坐标点映射变换到图像的二维像素坐标。

|
Download:
|
| 图 7 传统的二维坐标跟踪算法效果 | |

|
Download:
|
| 图 8 基于三维坐标的运动目标追踪效果图 | |
从图7可以看出,传统的二维质心跟踪算法中,两行人遮挡后返回时会发生跟踪目标丢失,而从第148帧图像可以看出,二维质心跟踪算法会误认为目标继续前行,则没有跟踪到目标返回,而导致跟踪目标错误;而基于三维坐标的运动目标跟踪遮挡后返回追踪目标效果良好。表1表示2种算法的运行时间对比结果。
|
|
表 1 2种算法运行时间对比 |
从表格中可以看出本文算法运行时间复杂度虽然比传统的复杂度高,但是差距不是特别大,在不考虑算法复杂度情况下本文算法能达到更好的跟踪效果。
5 结论本文在基于二维坐标的运动目标跟踪算法基础上,提出了基于三维目标跟踪算法的运动跟踪。该算法与传统二维跟踪算法不同的是,引入了目标的外观特征,对目标外观特征点进行三维重构后再进行聚类分析。其提出的算法具有以下优势:
1) 对于目标跟踪的场景大大提高,特别是对遮挡后跟踪的鲁棒性增加。
2) 加入了深度信息,分析推导了三维坐标与Kalman滤波结合对目标跟踪。
由于基于三维坐标的运动目标检测涉及到运动目标sift算法特征点的提取和三维重构,加大了计算量,从而导致实时性下降,下一步研究方向是对这些算法进行并行化运算研究,进一步提高其实时性。
| [1] |
谭艳, 王宇俊. 一种结合背景差分的改进CamShift目标跟踪方法[J]. 西南师范大学学报: 自然科学版, 2016, 41(9): 120-125. ( 0) 0)
|
| [2] |
翟明. 基于特征匹配与卡尔曼预测的多目标跟踪算法研究[D]. 沈阳: 东北大学, 2014: 1-55. http://cdmd.cnki.com.cn/Article/CDMD-10145-1016012179.htm
( 0) 0)
|
| [3] |
KRIEGER E, SIDIKE P, ASPIRAS T, et al. Directional ringlet intensity feature transform for tracking[C]//Proceedings of 2015 IEEE International Conference on Image Processing. Quebec, Canada: IEEE, 2015: 3871−3875.
( 0) 0)
|
| [4] |
BARBIERI T TDS, GOULARTE R. KS-SIFT: A keyframe extraction method based on local features[C]//Proceedings of 2014 IEEE International Symposium on Multimedia. Taichung, China: IEEE, 2014: 13−17.
( 0) 0)
|
| [5] |
JI Wenping, GUO Baolong, DING Guiguang. Detecting traffic volume statistics based on virtual coil with optical flow method[J]. Computer simulation, 2004, 21(1): 109-110, 117. ( 0) 0)
|
| [6] |
ASARI V K, ARIGELA S. Color image enhancement of low-resolution images captured in extreme lighting conditions[C]//Proceedings of SPIE 9120, Mobile Multimedia/Image Processing, Security, and Applications. Baltimore: SPIE, 2014: 91200Q.
( 0) 0)
|
| [7] |
姚放吾, 许辰铭. 基于目标质心的Meanshift跟踪算法[J]. 计算机技术与发展, 2012, 22(6): 104-106, 110. ( 0) 0)
|
| [8] |
郭文强, 高晓光, 侯勇严. 基于卡尔曼预测算法的云台三维空间目标跟踪[J]. 陕西科技大学学报, 2007, 25(3): 89-92. ( 0) 0)
|
| [9] |
余旺盛, 田孝华, 侯志强, 等. 基于关键区域特征匹配的视觉跟踪算法[J]. 电子学报, 2014, 42(11): 2150-2156. DOI:10.3969/j.issn.0372-2112.2014.11.004 ( 0) 0)
|
| [10] |
SRIHARSHA K V, RAO N V. Dynamic scene analysis using Kalman filter and mean shift tracking algorithms[C]//Proceedings of 2015 6th International Conference on Computing, Communication and Networking Technologies. Denton: IEEE, 2016: 1−8.
( 0) 0)
|
| [11] |
曲海琴. 一种改进型运动目标检测算法及其在视频监控系统中的应用研究[D]. 长春: 吉林大学, 2013: 1-47. http://cdmd.cnki.com.cn/Article/CDMD-10183-1013193516.htm
( 0) 0)
|
| [12] |
GIBSON J D, KOO B, GRAY S D. Filtering of colored noise for speech enhancement and coding[J]. IEEE transactions on signal processing, 1991, 39(8): 1732-1742. DOI:10.1109/78.91144 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


