空间电源系统作为航天飞行器的能量供应核心，它的可靠工作与否对于飞行任务能否有效执行以及航天飞行器能否安全运行等具有决定性作用^[1-4]。对于航天应用的锂离子电池系统，由于其工作条件复杂而恶劣，并且存在过充及过放现象、性能出现退化等具有挑战性的问题，因此，迫切需要建立一个专门针对锂离子电池系统的健康管理系统来对电池的状态进行在线监测和自主式管理^[2]。在这其中，最重要的部分就是对电池的实时寿命状态进行评估和预测。Saha等^[5]使用粒子滤波算法对电池电极阻抗和充电转移阻抗相应的指数增长进行参数估计，首先对阻抗进行预测，然后间接推断未来时刻容量退化趋势。然而由于实现电池的阻抗测量设备代价过大，同时阻抗测试条件过于苛刻，在实际应用条件下难以得到满足。He等^[6]利用EKF算法对锂离子电池容量的时间退化参数模型中的未知参数做出估计，得到电池剩余容量在未来阶段的退化趋势的预测结果。然而上述方法均没有考虑容量难以测量的现实。Chen Lu^[7]提出了一种利用锂电池几何特征估计容量的方法，但误差相对较大。Liu等^[8]提出了一种基于最小二乘支持向量回归（LSSVR）和HMM融合型算法来预测滚动轴承的健康状态，LSSVR用于预测特征信号，HMMs用于状态特征识别。本文提出的算法从在线可观测的电压、电流、时间等参数中提取能表征锂电池健康状况的特征向量，并鉴于HMM已经成功应用于机械故障诊断^[8-9]，本文尝试将HMMs用于锂电池状态监测中。

1 基本理论 1.1 HMM定义

HMM是一种描述双内嵌式随机过程的时间域统计分析模型，其中是一条描述状态间转移的马尔科夫链，另一随机过程描述状态与观测变量之间的映射关系^[10]。HMM可以简记成 $\lambda = \left( { \pi ,{A},{B}} \right)$ ，其中 $ \pi $ 表示初始概率分布向量； ${A} = {\left( {{a_{ij}}} \right)_{N \times N}}$ 是状态转移矩阵，其中 $a_{ij}$ 描述系统从状态 $S_{i}$ 转移到状态 $S_{j}$ 的概率， $N$ 表示模型所含的状态数；对于离散HMM，B是观测概率矩阵，对于连续HMM，B表示每一状态下的观测值概率密度函数。系统在状态 $S_{j}$ 下生成观测向量 ${o}_{t}$ 的概率可以使用高斯混合模型(Gaussian mixture model, GMM)来拟合，即

$\begin{aligned}{b_j}({{o}_t}) = & \sum\nolimits_{m = 1}^{{M_j}} {{w_{j,m}}{b_{j,m}}({{o}_t})} = \\[6pt]& \sum\nolimits_{m = 1}^{{M_j}} {{w_{j,m}}G({{o}_t},{{\mu }_{j,m}},{{\varSigma }_{j,m}})} \end{aligned}$

式中： ${M_j}$ 是状态 ${S_j}$ 的高斯分量数目； ${w_{j,m}}$ 是状态 ${S_j}$ 的第m个高斯分布的权值； ${{\mu }_{j,m}}$ 和 ${{\varSigma }_{j,m}}$ 分别是状态 ${S_j}$ 的第m个高斯分布的均值向量和协方差矩阵。假定观测向量 ${{o}_t}$ 的维数为D, ${b_{j,m}}({{o}_t})$ 的定义式如下：

$\begin{split}{b_{j,m}}({{o}_t}) = & N({{o}_t},{{\mu }_{j,m}},{{\varSigma }_{j,m}}){{ = }}\frac{1}{{\sqrt {{{\left( {2{\pi }} \right)}^D}{{|}}{{\varSigma }_{j,m}}{{|}}} }} \times {{ }}\\& \exp ( - \frac{1}{2}{({{o}_t} - {{\mu }_{j,m}})^{{T}}}{\varSigma }_{j,m}^{ - 1}({{o}_t} - {{\mu }_{j,m}}))\end{split}$

根据定义知，权重 ${w_{j,m}}$ 满足以下约束

$\left\{ \begin{aligned}& \sum\nolimits_{m = 1}^{{M_j}} {{w_{j,m}}} = 1\\[6pt]& {w_{j,m}} \geqslant 0\end{aligned} \right.(1 \leqslant j \leqslant N,1 \leqslant m \leqslant {M_j})$

经典HMM主要解决3个基本问题^[10-11]：

1）概率计算问题。即已知模型和观测序列，利用前向或后向算法计算该序列在模型下出现的概率。

2）学习问题。根据极大似然估计准则，利用Baum-Welch算法估计模型参数。

3）解码问题。即已知模型和观测序列，利用Viterbi算法求与观测序列最有可能的对应的状态序列。

1.2 参数初始化问题

针对Baum-Welch算法易陷入局部最优的问题，需要采用可靠的方法初始化HMM模型参数。文献[10]已经证明，HMM模型参数 ${ \pi}$ 和A的初始化选择对模型的最终收敛结果影响不大，而B的初始化越接近真实情况，HMM越能刻画系统的状态。因此，我们采用Viterbi算法结合k-means算法初始化B，具体步骤如下：

1）首先利用k-means算法将训练样本聚成N类，其中，第i类的样本被认为是在状态S_i下生成的，然后对每一状态下的观测向量再聚类成M类，最终，训练数据被分成N×M个簇。记状态S_j下的第m个高斯分量为X_j,m，则高斯分量X_j,m的权重w_j,m、均值向量μ_j,m和协方差矩阵 ${{\varSigma }_{j,m}}$ 的初始值可根据下式选取：

${\hat w_{j,m}} = \frac{{\text{分量}{X_{j,m}}\text{中的观测向量数目}}}{{\text{状态}{S_j}\text{下的观测向量数目}}}\quad \quad \quad \quad $

(1)

${\hat{ \mu }_{j,m}} = \text{分量}{X_{j,m}}\text{中的观测向量的均值向量}\quad $

(5)

${\hat{ \varSigma }_{j,m}} = \text{分量}{X_{j,m}}\text{中的观测向量的协方差矩阵}$

(6)

2）初始模型确定后，利用Viterbi算法求历史观测序列下的最优状态序列。

3）统计步骤2）每个状态下的观测向量，然后使用k-means聚类算法对每个状态下的观测向量聚成M类，根据式(1)~(3)更新模型参数。

4）重复步骤2）和3），直到模型收敛或大于设定的最大迭代次数，最终得到的模型参数 $\hat \lambda $ 即为初始模型参数。

1.3 算法流程

状态监测与识别的目的是从观测数据集中确定目前设备所处的状态，从而为健康管理提供依据。锂电池充放电实验监测的在线数据有电压、电流、时间及温度等参数，从这些可观测数据中提取能表征锂电池退化状态的特征向量，作为HMM模型的训练数据。从锂电池的衰退曲线分析，本文将锂电池衰退过程分为3个阶段：健康状态、退化状态1和退化状态2。如图1所示，基于HMM的退化状态识别主要分为训练过程和测试过程。我们针对不同的衰退状态分别建立HMM模型，并利用Baum-Welch算法训练模型，得到HMMs模型参数集 $\left\{ {{\lambda _1},{\lambda _2},{\lambda _3}} \right\}$ ；从系统当前的监测数据中提取特征序列O，根据极大相似准则判断其所属的退化状态^[12]，即

${ Class}\left( {O} \right) = \mathop {\arg \max }\limits_i P\left( {{O}|{\lambda _i}} \right)\;i \in \left\{ {1,2,3} \right\}$

2 数据来源与特征提取

实验采用的数据来源于马里兰大学CALCE的电池测试数据集中的常温正常退化数据^[13]。马里兰CALCE分别使用美国Arbin测试仪和CADEX测试仪进行锂电池性能退化实验。在实验中，对额定容量为1 100 mAh和1 350 mAh的2组电池进行测试，对应测试数据中的电池编号CS2与CX2。在本文的算法验证实验中，选择额定容量为1 100 mAh的CS2组中的CS2_35，CS2_37，CS2_38作为实验数据。本组数据以标准恒流0.5C充电至电池电压达到4.2 V，随后又以恒压充电直至电流衰减至0.05 A；放电循环以恒流1C放电，直至电压落至2.7 V，实验终止。

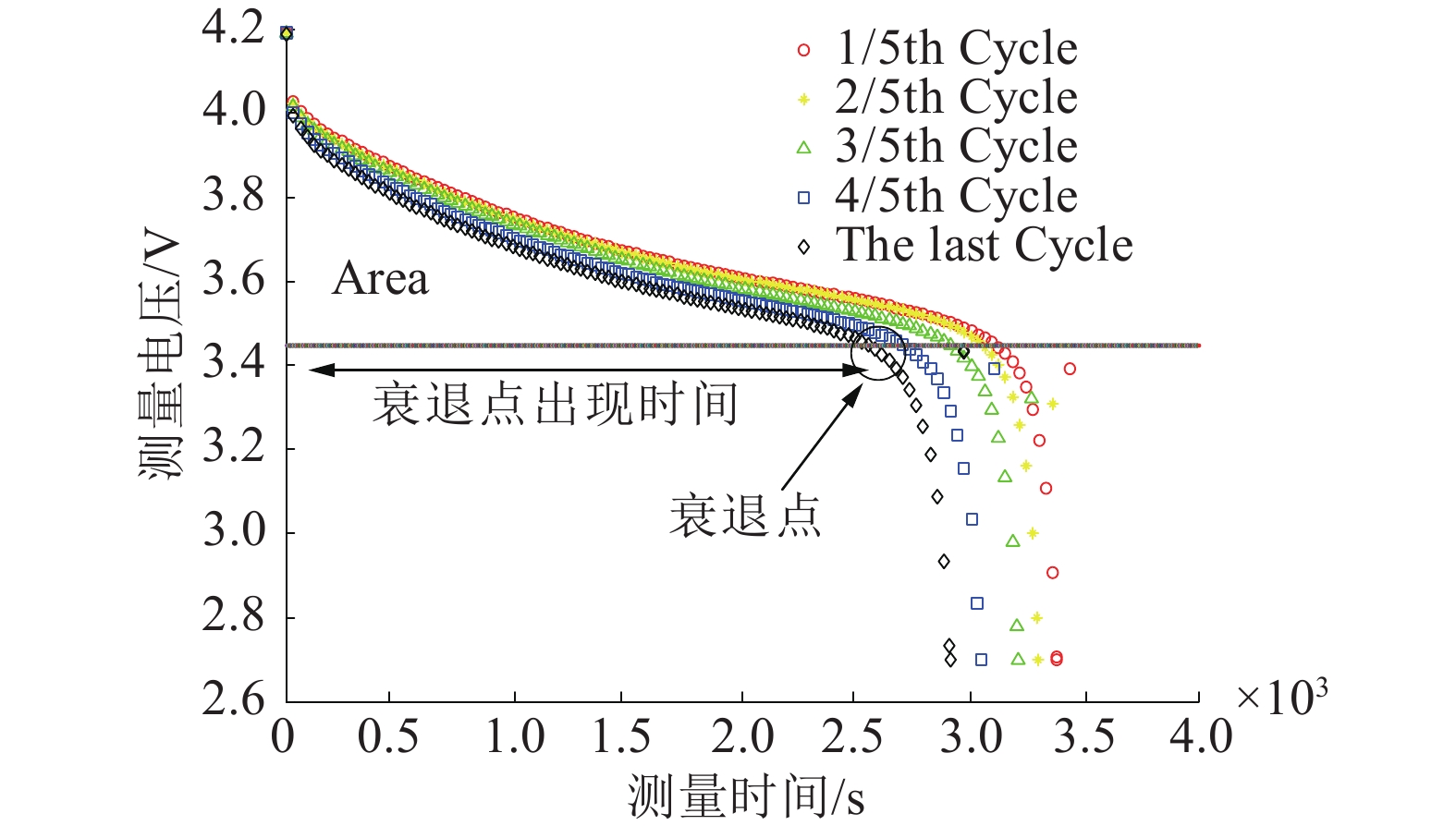
图2所示为CS2_35锂电池放电过程在不同循环周期下的电压变化曲线。在某一特定循环周期内，电压最初在极短的时间内快速下降，我们将这段时间称之为指数时期；然后电压平稳而缓慢的下降，这段时间电池能稳定正常供电，所以我们称这段时间为正常时期；当放电过程经过某一“拐点”，电压快速下降，电池再也不能维持系统的正常工作，我们称这段时间为衰退时期，“拐点”称之为衰退点。

我们发现衰退点出现时的电压与额定电压存在一定的线性关系^[14]：

$U = 0.82{U_0}$

式中：U表示衰退点出现电压，V；U₀表示额定电压，V。

我们还可以发现，在电池衰退过程中，电压曲线与衰退点出现电压U之间的面积不断缩小，也就是说，电池衰退的过程也是面积不断缩小的过程。Chen Lu^[7]表明充电过程的恒压充电时间与电池容量存在流形几何映射关系。因此，我们把衰退点出现的时间、电压曲线与衰退点出现电压之间的面积和恒压充电时间共同组成表征电池的寿命衰退程度的特征向量。图3所示为CS2_35锂电池提取出的特征。

3 实验仿真 3.1 退化状态识别

由于HMM模型是时间统计模型，因此我们将每5个循环周期作为一组观测序列。文献[6]证明电池的健康状态可由内阻和容量表征，因此，根据容量大小将全寿命周期分为3个退化状态：额定容量、电池容量退化到90%和82.5%分别对应健康状态、退化状态1和退化状态2。对不同退化状态均建立左右型结构的HMM，并设置状态数N为3，m每一隐状态下的混合高斯数目m=3。分别从不同退化状态下按照上文提取特征向量并组成观测序列，训练HMM，得到3个模型，记为{HMM₁,HMM₂,HMM₃}。本文设定的收敛误差为0.001，最大迭代次数为20。

图4所示为健康状态下经HMM模型初始化的相似概率的变化趋势图。可以看出，随着迭代次数的增加，相似概率先急剧增大然后趋于平稳，说明上述初始化方法可以明显改善模型参数初始化。

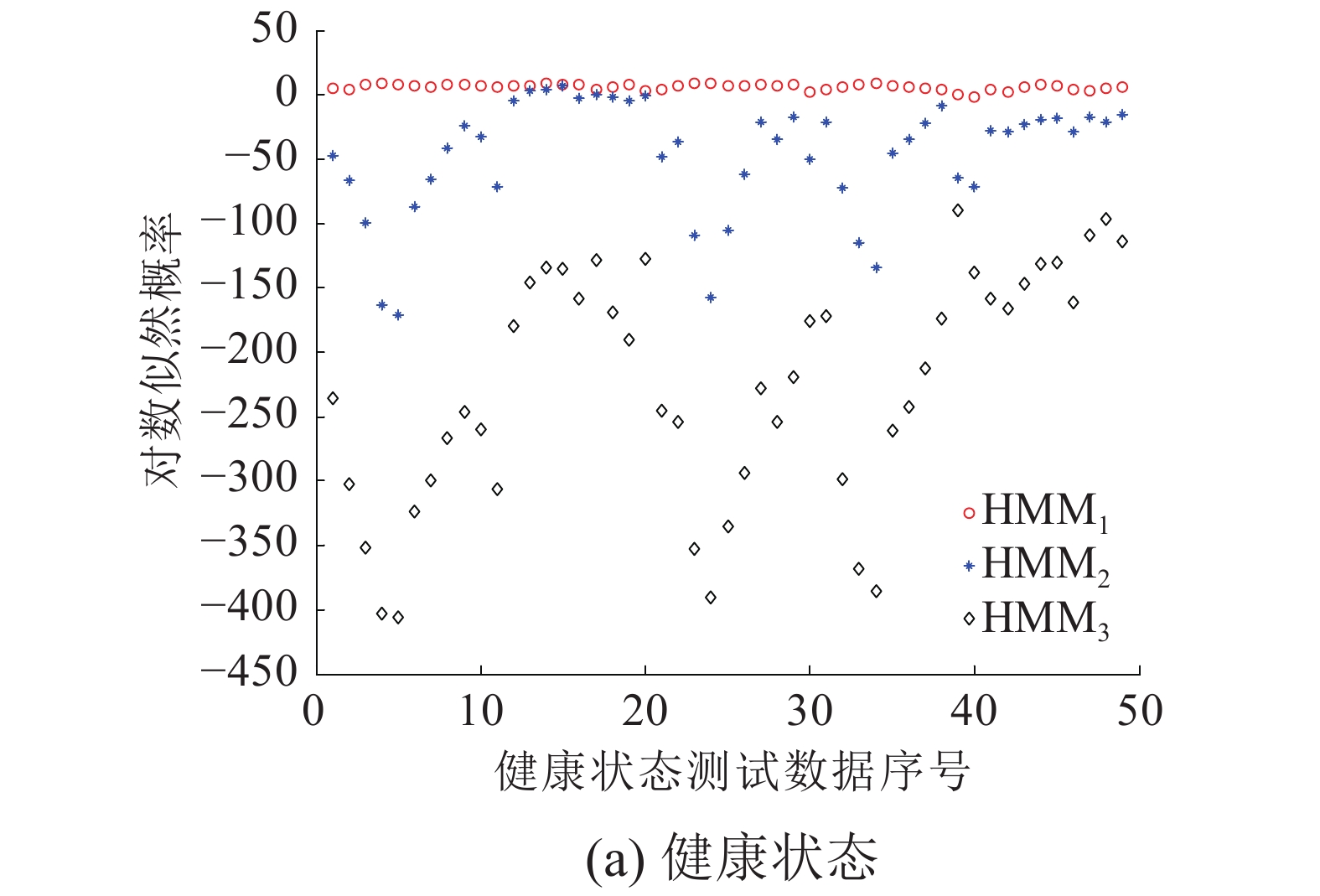
从锂电池CS2_35、CS2_37、CS2_38中选择出不同退化状态下的数据样本用于测试，识别率效果见图5和表1。结果表明HMM对退化状态的识别效果很好，正确分类率总体达到了95%以上。

3.2 对比实验

实验选择3层的BP神经网络作为对比算法。将观测向量o_t作为神经网络的输入，由于观测特征向量o_t的维数D=3，所以输入层神经元个数设置为3；神经网络的输出为观测向量o_t的类别标号，因此输出层神经元个数设置为3。本文神经网络的隐层神经元个数设置为5，正则化系数 $\lambda $ 为1。

由于神经网络是监督学习算法，将来自于健康状态下的测试样本贴标签1，退化状态1下的测试样本贴标签2，退化状态2下的测试样本贴标签3。表2为实验结果。结果表明，HMM相比于BP神经网络，对锂电池的退化识别率更高。这是因为神经网络虽然具有很强的非线性拟合能力，却无法解释自己的推理过程和推理依据；相反，HMM可以通过隐状态的转移刻画锂电池的退化过程。因此，HMM更适合对锂电池的老化过程建模。

4 结论

在各个应用工程领域，电池作为一种功能器件，其重要性都是不言而喻的，也正是因为如此，有关电池剩余寿命预测的技术研究也成为了电池研究中的十分重要的一部分。本文旨在对锂电池的退化状态进行监测。

1）从锂电池不同充放电循环周期下的充放电过程中提取到能表征锂电池老化程度的特征向量。

2）提出了一种基于HMM的锂电池退化状态识别算法。首先通过Baum-Welch算法分别对锂电池3种不同的退化状态（健康状态、退化状态1和退化状态2）。

3）建立HMM模型，然后将当前的观测信号通过前向−后向算法计算出不同模型下的相似概率，最后根据极大似然准则判断当前退化状态。实验结果表明，HMMs与BP神经网络相比，对锂电池的退化识别率更高，且更加稳定。

下一步工作将挖掘不同退化模型下的相似概率所包含的“退化程度”信息，并以此预测锂电池剩余寿命。