2. 海军驻426厂军事代表室,辽宁 大连 116005
2. Representative Office of Navy at Dalian 426 Factory, Dalian 116005, China
随着水下无人航行器(unmanned underwater vehicle,UUV)的应用越来越广泛,其对运动控制的要求越来越高[1-2]。当UUV执行大范围海底地形勘测、打捞作业以及海底管线检查等任务时,其水平面航迹跟踪能力是保障任务顺利完成的前提[3]。在实际工程中,海底管线、搜寻航路等可以被抽象为一系列线段顺次连接而成。基于成本、质量等方面的考虑,工程中的UUV通常被设定为欠驱动模式[4]。本文研究对象仅在其艉部配置了一组艉推进器、一对艉垂直舵和一对艉水平舵;也就是说,其水平运动缺少横向的控制输入。因而,该UUV在这个自由度上会受到加速度约束——二阶非完整型约束。此外,航行器在实际运行中还会受到水动力系数摄动以及海流的干扰。这些均使得欠驱动UUV的运动控制系统的设计具有挑战性[4-5]。
目前,欠驱动UUV航迹跟踪技术取得了大量的研究成果,其控制器设计方法主要有PID控制[6]、反步法[7-9]、滑模变结构控制[10]、模糊控制[11]以及神经网络控制[3, 11]等。李颀等[6]为了抵消不确定扰动对于UUV航迹跟踪的影响,提出了一种灰色预测PID航迹跟踪控制器。Lapierre等[7]利用虚拟向导法建立误差方程,从而获得系统状态与参考点动态之间的映射关系,进而利用李雅普诺夫稳定性理论和反步法设计了一个混合参数自适应鲁棒跟踪控制器。施淑伟等[8]建立了恒定海流干扰下的UUV运动模型,综合应用李雅普诺夫稳定性理论与反步法设计航迹跟踪控制器,可以保证跟踪误差在恒定海流干扰下的全局渐进收敛。苏玉民等[9]利用反步法针对鱼雷形UUV设计水平面航迹跟踪控制器。王璐等[10]利用Serret-Frenet坐标系建立误差方程;进而,采用迭代滑模控制理论,设计滑模增量反馈控制器,实现欠驱动UUV水平面航迹跟踪。夏国清等[11]提出了基于模糊神经网络欠驱动UUV的L2增益鲁棒航迹跟踪控制方法,用以实现未知海流干扰情况欠驱动UUV水平面航迹跟踪。周佳加等[3]针对欠驱动UUV在水动力参数变化和外界不确定干扰下的水平面航迹跟踪控制问题,提出了一种自适应神经网络控制方法;修改线段之间转向规则,进而降低拐点处的跟踪误差。
本文从实际工程需要出发,以基于离散航迹点所规划的直线航迹为期望航迹。从本质上来说,直线与曲线没有本质的区别,仅仅由所执行的任务需求的不同所决定。本文针对水平直线航迹跟踪控制任务,为了降低参数摄动以及未知恒定海流对于控制效果,提出一种基于非奇异终端滑模的全局有限时间收敛航迹跟踪控制方法。首先,通过引入局部Serret-Frenet坐标系,改进传统LOS指导方法,降低算法求解复杂度,并且可以避免当UUV距离期望航迹过远而无解的情况。进而,将航迹跟踪位置误差转化为航行器的艏向角误差。然后,利用非奇异终端滑模控制方法,设计动力学控制器,用以镇定艏向角误差。采用有限时间稳定性理论,分析所设计控制器的稳定性。最后,展示了一系列数值仿真结果。这些结果表明该控制方法可以有效地执行水平面航迹跟踪任务。
1 UUV航迹跟踪问题描述 1.1 欠驱动UUV运动模型欠驱动UUV的6自由度的空间运动是极其复杂的;通常,其基本力学关系利用动量定理和动量矩定理建立起来的[12]。在研究航行器空间运动时,航行器的水动力系数最多使用到二阶[12-13]。由于本文主要关注航行器的水平面运动,为了简化控制系统设计,因而仅仅考虑UUV的水平面运动模型。建立如下3自由度的二阶UUV的水平面动力学模型:
| $\left\{ {\begin{aligned}& {{m_{11}}\dot u = {m_{22}}vr - {d_{11}}u + {\tau _1}} \\ & {{m_{22}}\dot v = - {m_{11}}ur - {d_{22}}v} \\ & {{m_{33}}\dot r = ({m_{11}} - {m_{22}})uv - {d_{33}}r + {\tau _3}} \end{aligned}} \right.$ |
式中:
欠驱动UUV的水平面运动学方程为
| $\left\{ {\begin{aligned}& {\dot x = u\cos \; \psi - v\sin \; \psi } \\ & {\dot y = u\sin \; \psi + v\cos \; \psi } \\ & {\dot \psi = r} \end{aligned}} \right.$ |
式中:
当UUV航行于开阔水域时,其期望航迹可由一系列离散航迹点
| $\left\{ {\begin{aligned}& {x_i^{{d}}(\eta ) = k_i^x\eta + {x_i}} \\ & {y_i^{{d}}(\eta ) = k_i^y\eta + {y_i}} \end{aligned}} \right.$ |
式中:
| $\left\{ {\begin{aligned}& {k_i^x = {x_{i + 1}} - {x_i}} \\ & {k_i^y = {y_{i + 1}} - {y_i}} \end{aligned}} \right.$ |
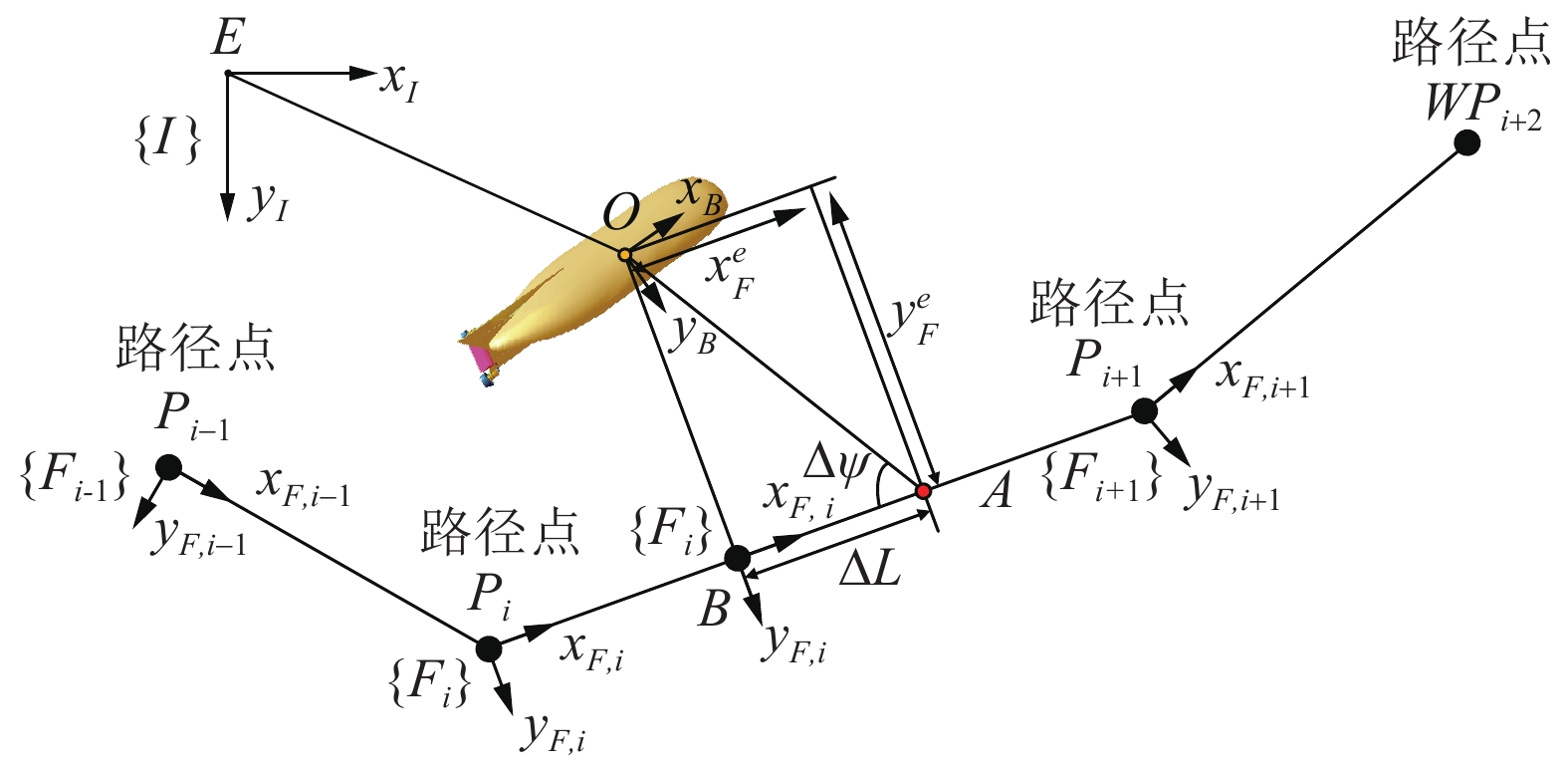
为了实现UUV水平面直线航迹跟踪任务,必须建立起航行器的当前位置与期望航迹之间的关系,即航迹跟踪误差方程。UUV水平面直线航迹跟踪示意图如图1所示。
|
Download:
|
| 图 1 基于离散航迹点的UUV水平航迹跟踪示意 | |
图中每个航迹点(除最后一个外)均引入一个局域Serret-Frenet坐标系{Fi},且坐标系{Fi}的
| ${\psi _{F,i}} = \arctan \frac{{{y_{i + 1}} - {y_i}}}{{{x_{i + 1}} - {x_i}}}$ |
当随体坐标系{B}的原点在期望航迹上投影点移动到第
| $OB = \frac{{\left| {k_i^y(x - {x_i}) + k_i^x({y_i} - y)} \right|}}{{\sqrt {k_i^{x2} + k{{_i^y}^2}} }}$ |
亦即
| $\Delta \psi = \arctan (\frac{{y_F^e}}{{x_F^e}})$ | (1) |
由式(1)可知,当
| ${\psi _{{d}}} = {\psi _{F,i}} + \Delta \psi $ |
那么,UUV的水平面航迹跟踪控制问题转化为航行器的艏向角跟踪期望角
为了简化UUV控制器的设计,航行器的水平面运动通常被分解为纵向速度控制子系统和转艏控制子系统2个子系统。为了实现控制目标,2个子系统分别引入非奇异终端滑模面[14-15];进而,设计出全局有限时间收敛的运动控制器。
2.1 纵向速度控制器设计根据实际工程需要,通常假定航行器的航行速度(即纵向速度)为恒定值。由于欠驱动UUV的横向缺少直接控制输入,因而航行器的纵向速度
| ${S_1}(t) = \int_0^t {{u_e}{{(}}\tau {{)d}}\tau } + {\mu _1}{\left| {{u_e}(t)} \right|^{{{{p_1}} / {{q_1}}}}}\operatorname{sgn} ({u_e}(t))$ |
式中:
| ${\dot S_1}(t) = {u_e}{{(}}t{{)}} + {\mu _1}\frac{{{p_1}}}{{{q_1}}}{\dot u_e}(t){\left| {{u_e}(t)} \right|^{{{{p_1}} / {{q_1}}} - 1}}\operatorname{sgn} ({u_e}(t))$ |
在不考虑航行器参数摄动的条件下,通过求取
| ${\tau _{1eq}} = {\hat X_u}u + {\hat X_{u\left| u \right|}}\left| u \right|u - {\hat m_{11}}\frac{{{q_1}}}{{{\mu _1}{p_1}}}{\left| {{u_e}} \right|^{2 - {p_1}/{q_1}}}$ | (2) |
式中“^”为UUV水动力系数的估计值,该估计值可以通过水池实验获得[12]。本文假设航行器的水动力系数的摄动存在上界,即
| $\left| {{m_{11}} - {{\hat m}_{11}}} \right| < {\tilde m_{11}},\;\left| {{X_u} - {{\hat X}_u}} \right| < {\tilde X_u},\;\left| {{X_{u\left| u \right|}} - {{\hat X}_{u\left| u \right|}}} \right| < {\tilde X_{u\left| u \right|}}$ |
由于参数摄动以及外界海流干扰的存在,等效控制律并不能保证航行器的控制效果;因此,必须引入趋近律。选取如下趋近律:
| ${\tau _{1r}} = - {K_1}\operatorname{sgn} ({S_1})$ | (3) |
式中
| ${K_1} = {\tilde X_u}\left| u \right| + {\tilde X_{u\left| u \right|}}{u^2} + {\tilde m_{11}}\frac{{{q_1}}}{{{\mu _1}{p_1}}}{\left| {{u_e}} \right|^{2 - {{{p_1}} / {{q_1}}}}} + {\sigma _1}$ |
式中
由式(2)和(3)可知,欠驱动UUV的纵向速度控制器为两式之和,可以得到
| ${\tau _1} = {\hat X_u}u + {\hat X_{u\left| u \right|}}\left| u \right|u - {\hat m_{11}}\frac{{{q_1}}}{{{\mu _1}{p_1}}}{\left| {{u_e}} \right|^{2 - {p_1}/{q_1}}} - {K_1}{\mathop{ sgn}} ({S_1})$ | (4) |
选取如下李雅普诺夫函数:
| ${V_1} = \frac{1}{2}{m_{11}}S_1^2$ | (5) |
那么,
| $\begin{aligned}& {{\dot V}_1} = {S_1}(({m_{11}} - {{\hat m}_{11}}){u_e} + {{\tilde m}_{11}}{u_e}{\mathop{ sgn}} ({S_1}) + \\& \;\;\; {\mu _1}\frac{{{p_1}}}{{{q_1}}}(({{\hat X}_u} - {X_u})u + ({{\hat X}_{u\left| u \right|}} - {X_{u\left| u \right|}})\left| u \right|u - \\& \;\;\; ({{\tilde X}_u}\left| u \right| + {{\tilde X}_{u\left| u \right|}}{u^2} + {\sigma _1}) \times {\mathop{ sgn}} ({S_1})){\left| {{u_e}} \right|^{{p_1}/{q_1} - 1}}{\mathop{ sgn}} ({u_e}))\; \leqslant \\& \;\;\; - {\mu _1}{\sigma _1}\frac{{{p_1}}}{{{q_1}}}\left| {{S_1}} \right| = - {\mu _1}{\sigma _1}\frac{{{p_1}}}{{{q_1}}}\sqrt {\frac{2}{{{m_{11}}}}} V_1^{{\textstyle{1 \over 2}}}\end{aligned}$ |
由式(5)可知,其为正定的、径向无界的。根据文献[16]中的定理2.2可知,控制器式(4)能够保证速度误差是全局有限时间收敛的。
2.2 转艏控制器设计由1.3节可知,UUV的水平面航迹跟踪控制问题已经转化为航行器的艏向角跟踪期望角
| ${V_2} = \frac{1}{2}\psi _e^2$ | (6) |
对式(6)求导,可以得到
| ${r_{{d}}} = {\dot \psi _{{d}}} - {\mu _2}\operatorname{sgn} ({\psi _e})$ |
从而,李雅普诺夫函数的导数满足
| ${\dot V_2} = - {\mu _2}\sqrt 2 V_2^{\tfrac{1}{2}}$ |
式中
下面的任务就是如何设计实际的控制输入镇定转艏角速度误差
| ${S_2}(t) = \int_0^t {{r_e}{{(}}\tau {{)d}}\tau } + {\mu _3}{\left| {{r_e}(t)} \right|^{{p_2}/{q_2}}}{\mathop{ sgn}} ({r_e}(t))$ |
式中:
| ${\dot S_2}(t) = {r_e}{{(}}t{{)}} + {\mu _3}\frac{{{p_2}}}{{{q_2}}}{\dot r_e}(t){\left| {{r_e}(t)} \right|^{{p_2}/{q_2} - 1}}{\mathop{ sgn}} ({r_e}(t))$ |
同理,可以到转艏控制的等效控制输入为
| $\begin{array}{l} {\tau _{3eq}} = ({{\hat m}_{22}} - {{\hat m}_{11}})uv + {{\hat N}_r}r + {{\hat N}_{r\left| r \right|}}\left| r \right|r - \\ {{\hat m}_{33}}\frac{{{q_2}}}{{{\mu _3}{p_2}}}{\left| {{r_e}} \right|^{2 - {p_2}/{q_2}}} + {{\hat m}_{33}}{{\dot r}_d} \end{array}$ | (7) |
且
转艏控制趋近律为
| ${\tau _{3r}} = - {K_2}\operatorname{sgn} ({S_2})$ | (8) |
式中
| $\begin{aligned}{K_2} = & ({{\tilde m}_{22}} + {{\tilde m}_{11}})\left| {uv} \right| + {{\tilde N}_r}\left| r \right| + {{\tilde N}_{r\left| r \right|}}{r^2}+\\& {{\tilde m}_{33}}\frac{{{q_2}}}{{{\mu _3}{p_2}}}{\left| {{r_e}} \right|^{2 - {p_2}/{q_2}}} + {\sigma _2}\end{aligned}$ |
式中
由式(7)和(8)可知,欠驱动UUV的转艏控制器为两式之和,可以得到
| $\begin{split}{\tau _3} = & ({{\hat m}_{22}} - {{\hat m}_{11}})uv + {{\hat N}_r}r + {{\hat N}_{r\left| r \right|}}\left| r \right|r - \\& {{\hat m}_{33}}\frac{{{q_2}}}{{{\mu _3}{p_2}}}{\left| {{r_e}} \right|^{2 - {p_2}/{q_2}}} - {K_2}{\mathop{ sgn}} ({S_2})\end{split}$ | (9) |
选取如下李雅普诺夫函数:
| ${V_3} = \frac{1}{2}{m_{33}}S_2^2$ |
那么,
| $\begin{aligned}{{\dot V}_3} = & {S_2}(({m_{33}} - {{\hat m}_{33}}){r_e} + {{\tilde m}_{33}}\left| {{r_e}} \right|{\mathop{ sgn}} ({S_2}) + {\mu _3}\frac{{{p_2}}}{{{q_2}}}(({{\hat m}_{22}} - {m_{22}} + \\& {m_{11}} - {{\hat m}_{11}})uv + ({{\hat N}_r} - {N_r})r + ({{\hat N}_{\left| r \right|r}} - {N_{\left| r \right|r}})\left| r \right|r - \\& (({{\tilde m}_{22}} + {{\tilde m}_{11}})\left| {uv} \right| + {{\tilde N}_r}\left| r \right| + {{\tilde N}_{\left| r \right|r}}{r^2} + {\sigma _2}){\mathop{ sgn}} ({S_2})) \times \\& {\left| {{r_e}} \right|^{{p_2}/{q_2} - 1}}{\mathop{ sgn}} ({r_e}))\; \leqslant - {\mu _3}{\sigma _2}\frac{{{p_2}}}{{{q_2}}}\left| {{S_2}} \right| = - {\mu _3}{\sigma _2}\frac{{{p_2}}}{{{q_2}}}\sqrt {\frac{2}{{{m_{33}}}}} V_3^{{\textstyle{1 \over 2}}}\end{aligned}$ |
根据文献[16]中的定理2.2可知,控制器式(9)能够保证转艏角速度误差是全局有限时间收敛。
2.3 控制系统稳定性分析为了分析欠驱动UUV水平航迹跟踪控制系统的稳定性,选取整体李雅普诺夫函数:
| ${V_{{{all}}}} = {V_1} + {V_2} + {V_3}$ | (11) |
由前述分析可知,式(10)为正定的、径向无界的。对式(10)求导,可得
| ${V_{{{all}}}} \leqslant - \min ({\mu _1}{\sigma _1}\frac{{{p_1}}}{{{q_1}}}\sqrt {\frac{2}{{{m_{11}}}}} ,{\mu _2}\sqrt 2 ,{\mu _3}{\sigma _2}\frac{{{p_2}}}{{{q_2}}}\sqrt {\frac{2}{{{m_{33}}}}} )V_{{{all}}}^{\tfrac{1}{2}}$ |
根据文献[16]中的定理2.2可知,欠驱动UUV的水平面直线航迹跟踪控制系统是全局有限时间稳定。
3 航迹跟踪控制仿真结果及分析本节基于欠驱动UUV的水平面3-DOF运动模型构建MATLAB仿真平台,用以验证本文所提出的非奇异终端滑模控制器的控制效果。该型欠驱动UUV的相关运动模型参数详见文献[17]。为了验证所提出控制方法的鲁棒性,在数值仿真中,航行器的水动力系数被引入
在数值仿真中,航行器的期望速度被设定为2 kn(大约为1 m/s);航行器的期望路径的期望航迹为(100, 100)→(100, 600)→(300, 600)→(300, 100)→(500, 100)→(500, 600)→(700, 600)→(1 000, 100),即梳子形搜索航迹。这样的航迹设定是航行器完成海底地形勘测、海上搜救和打捞作业、海洋调查等作业任务的首选参考航迹;因而,选择此种类型航迹进行仿真实验,具有很强的实际意义。
航行器的初始初始状态设定为x(0) = 200 m、y(0) = 50 m、ψ(0) = 90 m、u(0) = 0 m/s、v(0) = 0 m/s、r(0) = 0 rad/s。航行器的航迹跟踪控制器的控制增益参数被设定为:纵向速度控制器参数
|
Download:
|
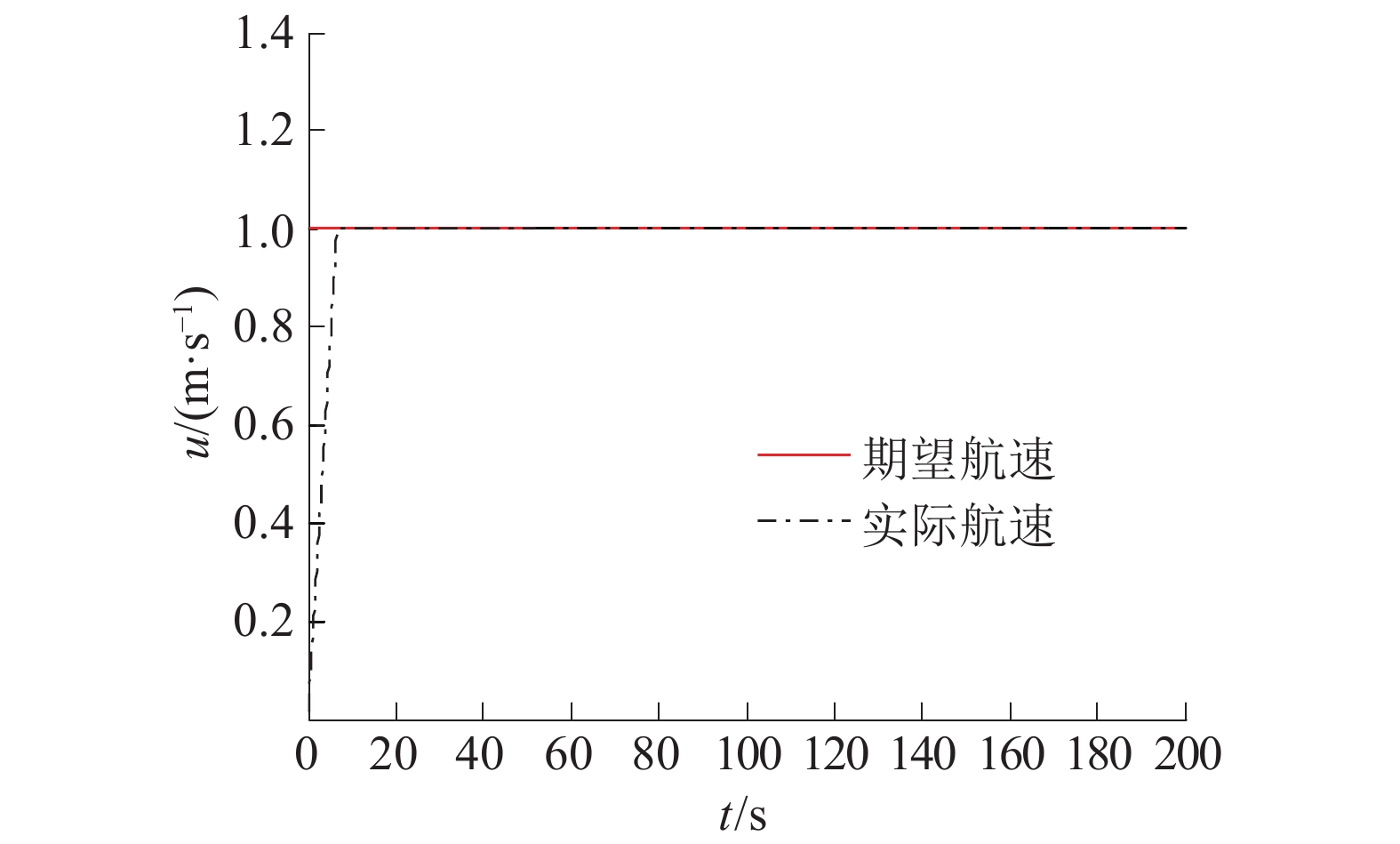
| 图 2 欠驱动UUV纵向速度响应曲线 | |
|
Download:
|
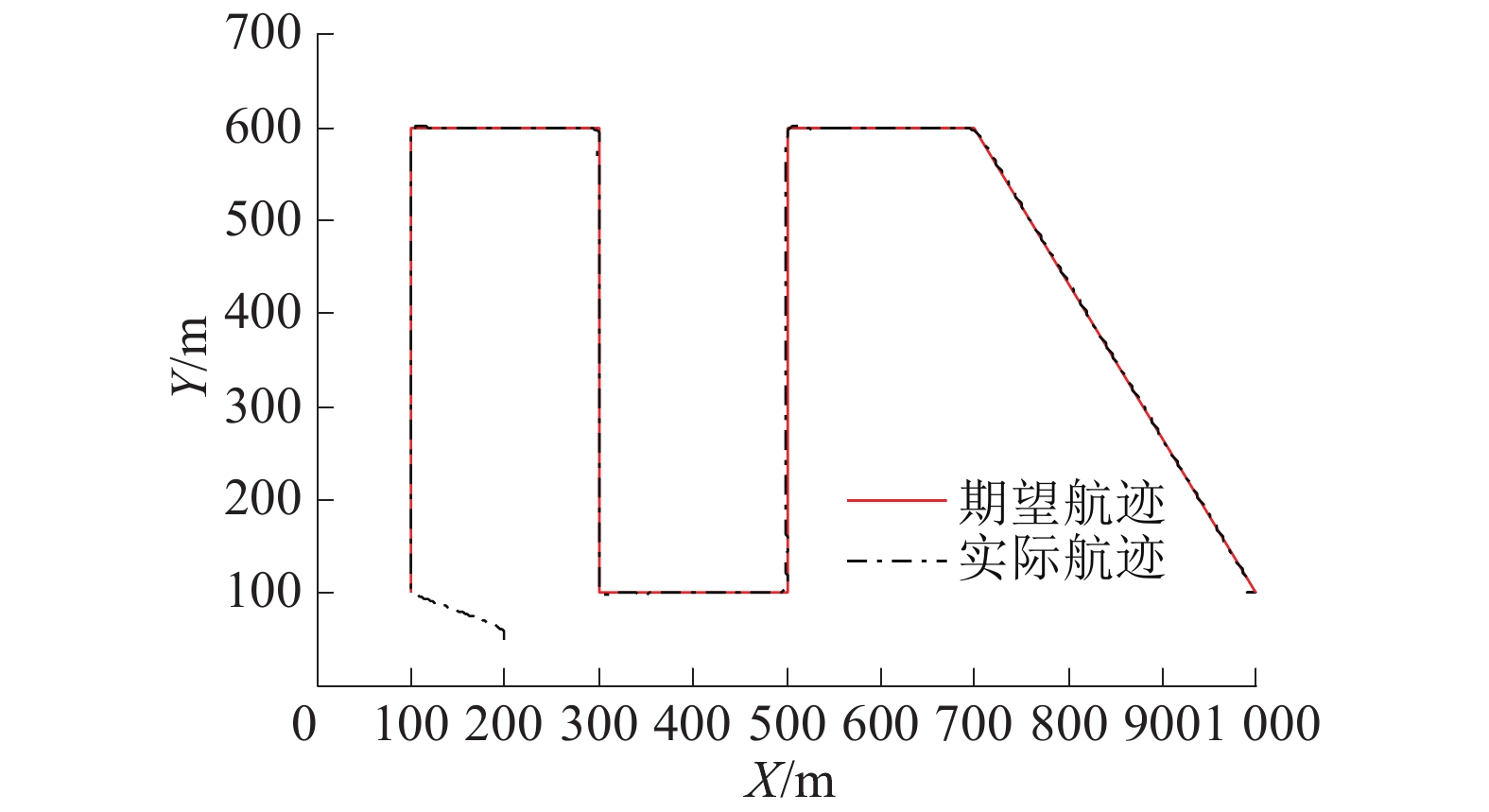
| 图 3 欠驱动UUV水平面航迹跟踪效果 | |
|
Download:
|
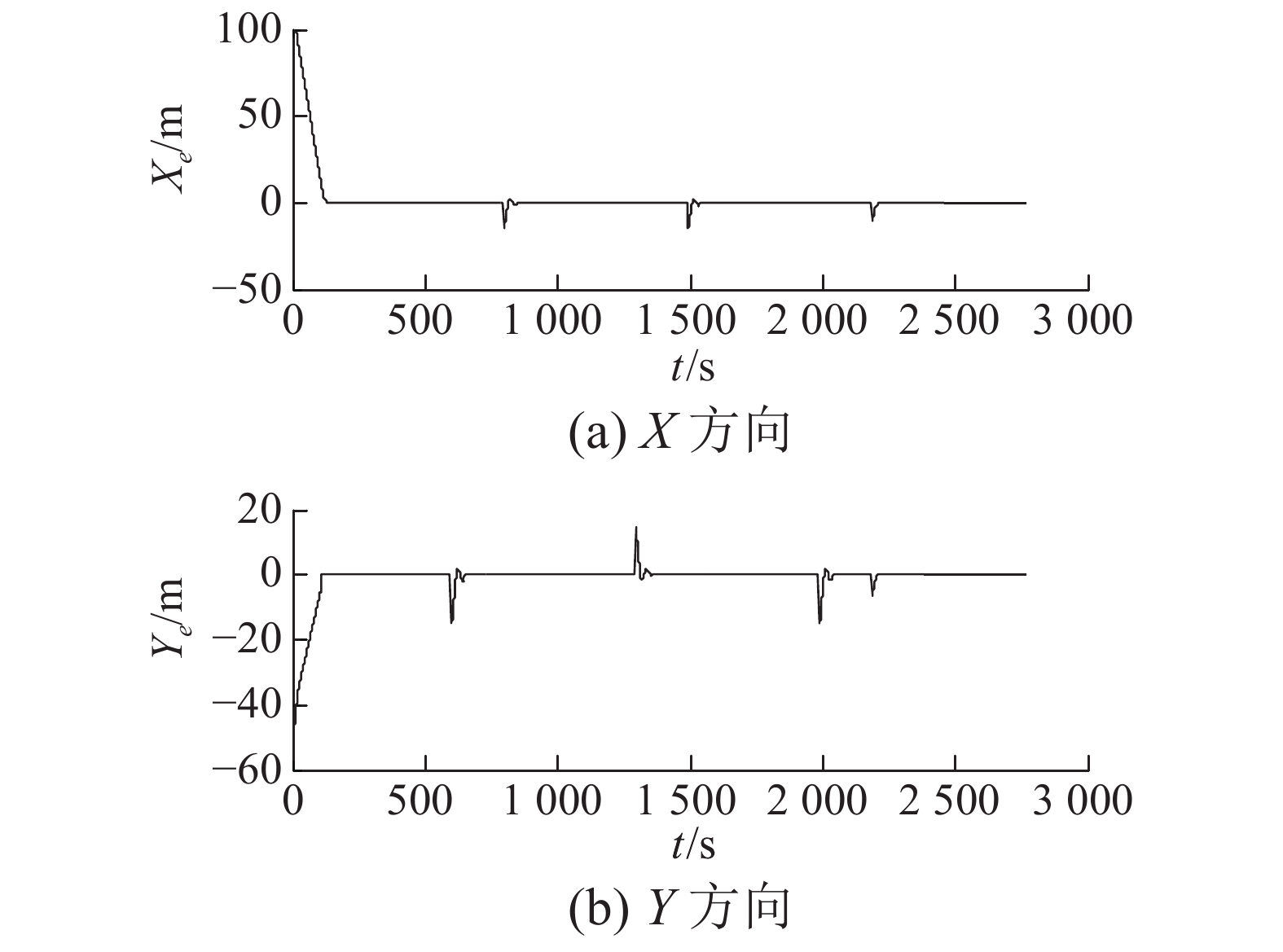
| 图 4 欠驱动UUV水平面航迹跟踪误差曲线 | |
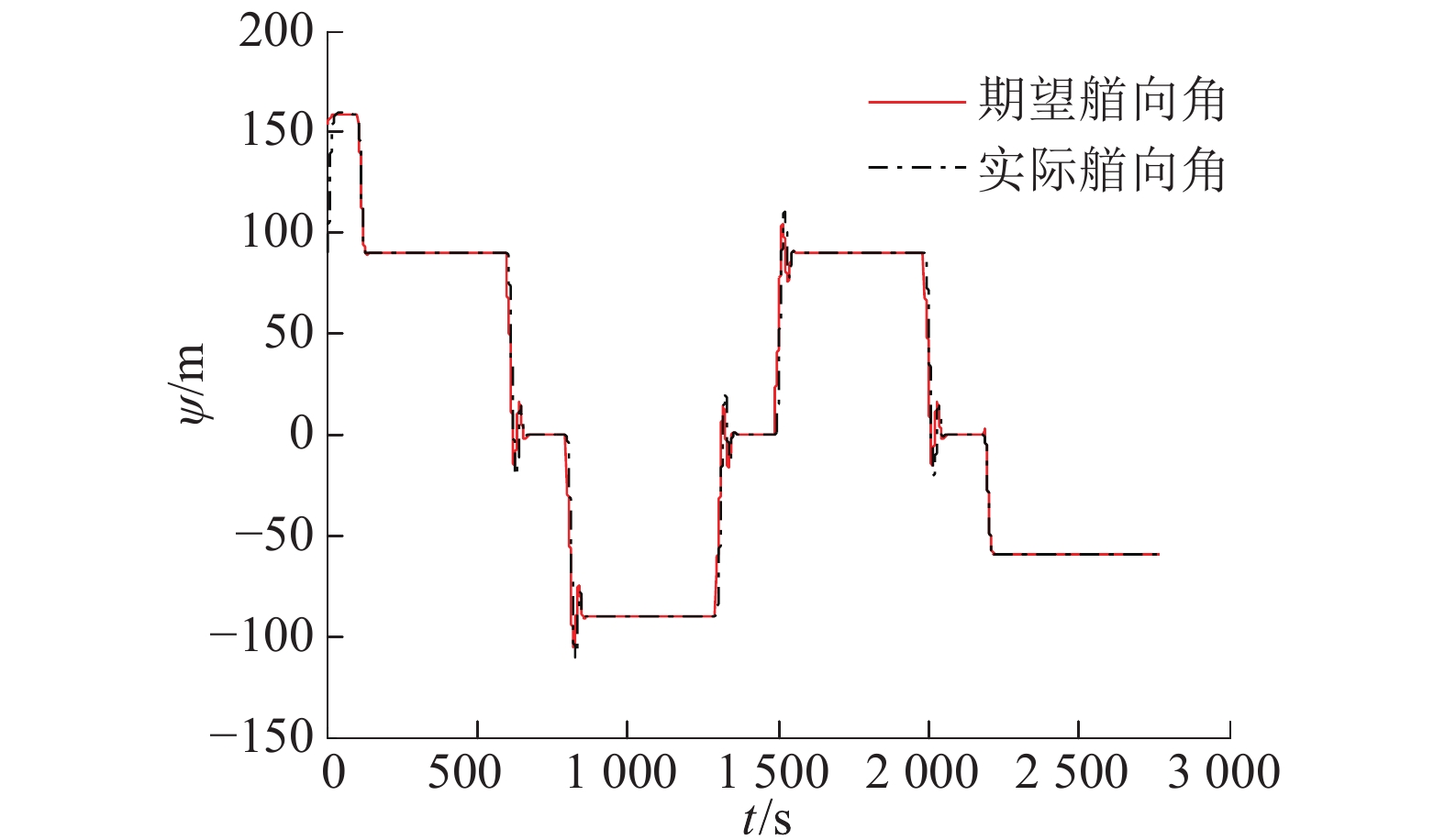
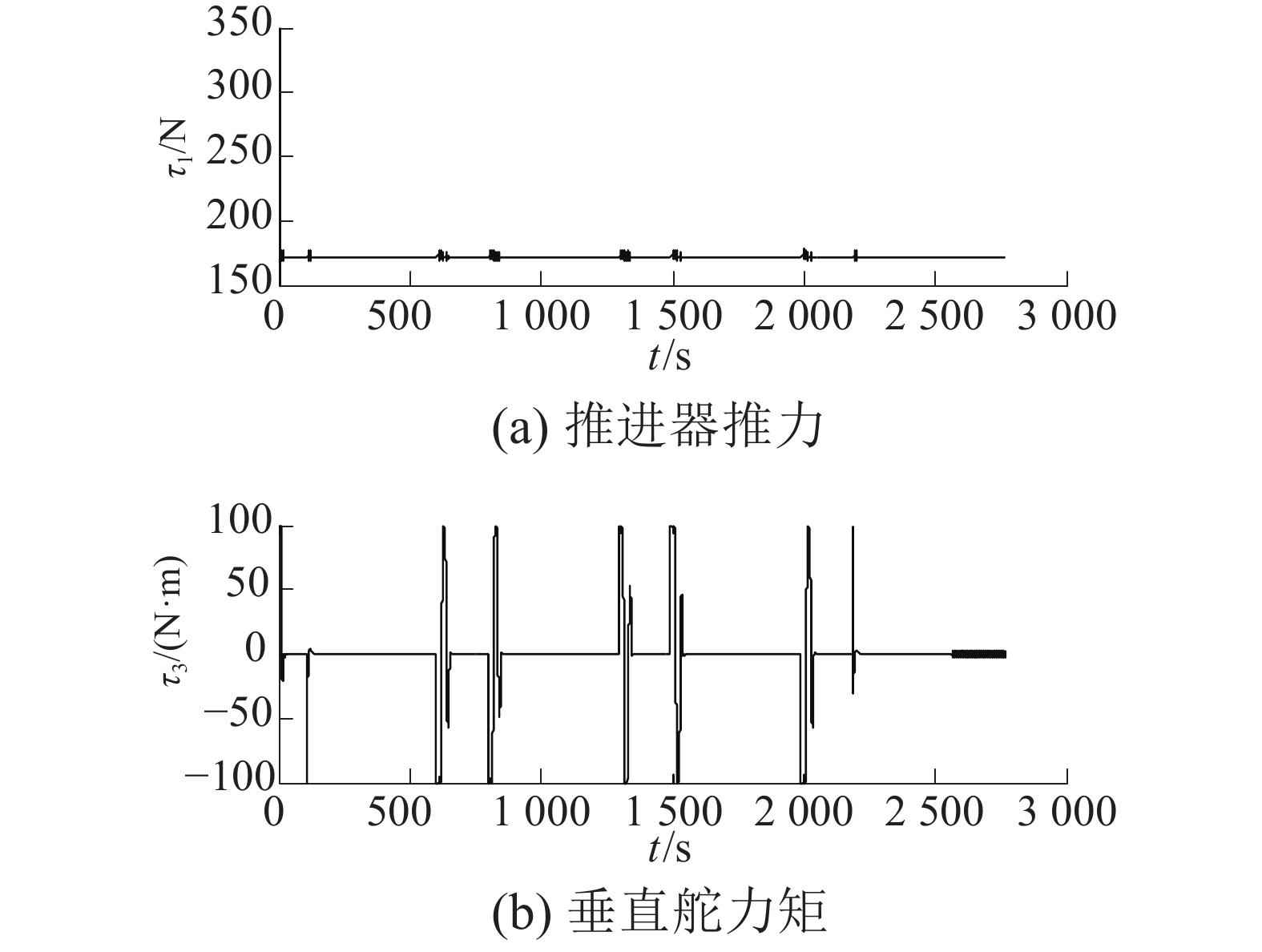
图2给出了欠驱动UUV的纵向速度响应曲线的前200 s。该控制器可以实现航行器的纵向速度无超调、快速地跟踪期望速度。图3给出了航行器的水平面直线航迹跟踪效果。图4展示了水平面直线航迹跟踪误差响应曲线。由图3、4可以看出,航行器在控制器式(9)作用下迅速接近期望航迹;在有限时间内,将跟踪误差镇定至零点。由于转弯时,出现航向角偏差较大的情况,因而航行器位置也响应的会出现一定偏差;但是,在控制器式(9)的作用下,位置偏差会很快趋近于零。图5展示了航行器的艏向角响应曲线,图6给出了航行器跟踪控制器的输出。
|
Download:
|
| 图 5 欠驱动UUV水平面航迹跟踪艏向角响应曲线 | |
|
Download:
|
| 图 6 欠驱动UUV水平面航迹跟踪控制器输出 | |
本文针对欠驱动UUV水平面直线航迹跟踪控制问题,基于非奇异终端滑模控制,提出了一种对于参数摄动以及恒定未知海流具有强鲁棒性的有限时间收敛的航迹跟踪控制器。本文研究成果具有如下优点:
1)通过改进LOS制导律和Serret-Frenet坐标系,解决了传统LOS存在无解情况,并且简化了算法复杂度。
2)任意航迹跟踪误差可以在有限时间内被镇定。
3)对于参数摄动和恒定未知海流具有强鲁棒性。
通过数值仿真,可以验证了所设计的航迹跟踪控制算法具有上述优点,实现欠驱动UUV对于分段连续航迹的精确跟踪控制。
| [1] |
陈强. 水下无人航行器[M]. 北京: 国防工业出版社, 2014: 1-43.
( 0) 0)
|
| [2] |
钱东, 唐献平, 赵江. UUV技术发展与系统设计综述[J]. 鱼雷技术, 2014, 22(6): 401-414, 419. ( 0) 0)
|
| [3] |
周佳加, 严浙平, 贾鹤鸣, 等. 改进规则下自适应神经网络的UUV水平面路径跟随控制[J]. 中南大学学报: 自然科学版, 2014, 45(9): 3021-3028. ( 0) 0)
|
| [4] |
王芳, 万磊, 李晔, 等. 欠驱动AUV的运动控制技术综述[J]. 中国造船, 2010, 51(2): 227-241. ( 0) 0)
|
| [5] |
王奎民. 主要海洋环境因素对水下航行器航行影响分析[J]. 智能系统学报, 2015, 10(2): 316-323. ( 0) 0)
|
| [6] |
李颀, 石秀华, 康智强. 基于灰色预测的AUV水平面轨迹跟踪控制研究[J]. 西安工业大学学报, 2012, 32(5): 384-387. ( 0) 0)
|
| [7] |
LAPIERRE L, JOUVENCEL B. Robust nonlinear path-following control of an AUV[J]. IEEE journal of oceanic engineering, 2008, 33(2): 89-102. DOI:10.1109/JOE.2008.923554 ( 0) 0)
|
| [8] |
施淑伟, 严卫生, 高剑, 等. 常值海流作用下的AUV水平面路径跟踪控制[J]. 兵工学报, 2010, 31(3): 375-379. ( 0) 0)
|
| [9] |
苏玉民, 曹建, 徐峰, 等. 鱼雷形水下机器人非线性航迹跟踪控制[J]. 上海交通大学学报, 2012, 46(6): 977-983. ( 0) 0)
|
| [10] |
王璐, 张利军, 王红滨, 等. 非线性迭代滑模的欠驱动AUV路径跟踪控制[J]. 计算机工程与应用, 2011, 47(27): 239-242. DOI:10.3778/j.issn.1002-8331.2011.27.065 ( 0) 0)
|
| [11] |
夏国清, 杨莹, 赵为光. 欠驱动AUV模糊神经网络L2增益鲁棒跟踪控制[J]. 控制与决策, 2013, 28(3): 351-356. ( 0) 0)
|
| [12] |
李殿璞. 船舶运动与建模[M]. 2版. 哈尔滨: 哈尔滨工程大学出版社, 2008: 154-190.
( 0) 0)
|
| [13] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. West Sussex, UK: John Wiley & Sons Ltd, 2011: 59−186, 221−225.
( 0) 0)
|
| [14] |
张袅娜. 终端滑模控制理论及应用[M]. 北京: 科学出版社, 2011: 1-18.
( 0) 0)
|
| [15] |
FENG Yong, YU Xinghuo, MAN Zhihong. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167. DOI:10.1016/S0005-1098(02)00147-4 ( 0) 0)
|
| [16] |
HUANG Xianqing, LIN Wei, YANG Bo. Global finite-time stabilization of a class of uncertain nonlinear systems[J]. Automatica, 2005, 41(5): 881-888. DOI:10.1016/j.automatica.2004.11.036 ( 0) 0)
|
| [17] |
PETTERSEN K Y, EGELAND O. Time-varying exponential stabilization of the position and attitude of an underactuated autonomous underwater vehicle[J]. IEEE transactions on automatic control, 1999, 44(1): 112-115. DOI:10.1109/9.739086 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


