在声呐工程中,为满足各种特定功能要求所用的材料成为水声材料,它们是声呐工程的物质基础。因为水声材料的性能对声呐的研究、设计、制造和试验来说是非常重要的,具有不同性能的水声材料适用于不同的场合,因此,必须准确把握被研究或准备使用的水声材料的性能参数[1]。
对于声隐身材料,人们最关注的是它的反射系数及吸声效果,常用的测量声反射系数的方法有声管法[2]、混响室法[3-4]和自由场测试法等,其中声管法主要有脉冲声法、驻波管法[5-6]、传递函数法[7-8]等。用脉冲声法即可以用宽带信号测量水声材料在宽频段的反射系数[9-10],又可以用单频信号测量水的在单频复反射系数,并可以通过复反射系数反演水声材料的纵波声速和衰减系数[10-11]。当用单频信号测量水声材料在多个频点上的复反射系数时因频点较多,处理数据后的反演工作则比较耗时耗力,而且结果不直观。针对该问题,本文开发了简单、易操作并且可以直观显示的计算反演软件,大大提高了工作效率。
1 脉冲声管测量水声材料声速和衰减系数原理当平面波垂直入射到两层半无限大介质分界面时,由分界面处声压连续、振速连续可得声压反射系数:
| $R = \frac{{{Z_2} - {Z_1}}}{{{Z_2} + {Z_1}}}$ | (1) |
式中:
图1为有中间层时平面波波垂直入射到分界面时声波入射、反射、透射示意图,由分界面处声压连续、振速连续可得声压反射系数:
| $R = \frac{{{Z_2}({Z_3} - {Z_1})\cos \left( {{k_2}l} \right) + { i}(Z_2^2 - {Z_1}{Z_3})\sin ({k_2}l)}}{{{Z_2}({Z_3} + {Z_1})\cos \left( {{k_2}l} \right) + { i}(Z_2^2 + {Z_1}{Z_3})\sin ({k_2}l)}}$ | (2) |
式中:

|
Download:
|
| 图 1 中间层的反射、透射示意图 | |
当样品末端为空气背衬(即“声软端”)时,式(2)可近似为
| ${Z_{in}} = {{j}}\frac{{\omega \rho }}{{\alpha + {{j}}\displaystyle\frac{\omega }{c}}}{{tanh}}\left( {\alpha d + {{j}}\beta d} \right)$ | (3) |
当样品末端为刚性背衬(即“声硬端”)时,式(2)可近似为
| ${Z_{in}} = {{j}}\frac{{\omega \rho }}{{\alpha + {{j}}\displaystyle\frac{\omega }{c}}}{{coth}}\left( {\alpha d + {{j}}\frac{{\omega d}}{c}} \right)$ | (4) |
同时也可以由式(1)求出材料样品的输入阻抗
| ${Z_{in}} = {\rho _w}{c_w}\frac{{1 + {{\operatorname{Re} }^{{{j}}\phi }}}}{{1 - {{\operatorname{Re} }^{{{j}}\phi }}}}$ | (5) |
式中:
从式(2)~(5)可以得出,对于声软末端:
| ${{j}}\frac{{\tanh \left( {\alpha d + {{j}}\displaystyle\frac{{\omega d}}{c}} \right)}}{{\alpha d + {{j}}\displaystyle\frac{{\omega d}}{c}}} = \frac{{{\rho _w}{c_w}}}{{\omega \rho d}}\frac{{1 + {{\operatorname{Re} }^{{{j}}\phi }}}}{{1 - {{\operatorname{Re} }^{{{j}}\phi }}}}$ | (6) |
对于声硬末端:
| ${{j}}\frac{{\coth \left( {\alpha d + {{j}}\displaystyle\frac{{\omega d}}{c}} \right)}}{{\alpha d + {{j}}\displaystyle\frac{{\omega d}}{c}}} = \frac{{{\rho _w}{c_w}}}{{\omega \rho d}}\frac{{1 + {{\operatorname{Re} }^{{{j}}\phi }}}}{{1 - {{\operatorname{Re} }^{{{j}}\phi }}}}$ | (7) |
由式(6)和(7)可知,只要测出样品反射系数的模值
下面先推导声软末端时反演纵波声速
式(6)左端可写成如下形式:
| ${{j}}\frac{{\tanh \left( {\alpha d + {{j}}\displaystyle\frac{{\omega d}}{c}} \right)}}{{\alpha d + {{j}}\displaystyle\frac{{\omega d}}{c}}} = {R_0} + {{i}}{X_0}$ | (8) |
式中:
由式(6)右端和式(8)右端可得:
| ${R_0} = \frac{{{\rho _w}{c_w}}}{{\omega \rho d}} \cdot \frac{{1 - {R^2}}}{{1 - 2R\cos \phi + {R^2}}}$ | (9) |
| ${X_0} = \frac{{{\rho _w}{c_w}}}{{\omega \rho d}} \cdot \frac{{2R\sin \phi }}{{1 - 2R\cos \phi + {R^2}}}$ | (10) |
对式(8)进行复数运算,可得输入阻
| ${R_0} \!=\! \frac{{\displaystyle\frac{{\omega d}}{c}\tanh (\alpha d)(1 \!+\! {{\tan }^2}(\displaystyle\frac{{\omega d}}{c})) \!-\! \alpha d\tan (\displaystyle\frac{{\omega d}}{c})(1 \!-\! {{\tanh }^2}(\alpha d))}}{{({{(\alpha d)}^2} \!+\! {{(\displaystyle\frac{{\omega d}}{c})}^2})(1 \!+\! {{\tanh }^2}(\alpha d){{\tan }^2}(\displaystyle\frac{{\omega d}}{c}))}}$ | (11) |
| ${X_0} \!=\! \frac{{\alpha d\tanh (\alpha d)(1 \!+\! {{\tan }^2}(\displaystyle\frac{{\omega d}}{c})) \!+\! \displaystyle\frac{{\omega d}}{c}\tan (\frac{{\omega d}}{c})(1 \!-\! {{\tanh }^2}(\alpha d))}}{{({{(\alpha d)}^2} \!+\! {{(\displaystyle\frac{{\omega d}}{c})}^2})(1 \!+\! {{\tanh }^2}(\alpha d){{\tan }^2}(\displaystyle\frac{{\omega d}}{c}))}}$ | (12) |
同理,声硬末端时可得输入阻
| ${R_0} \!=\! \frac{{\displaystyle\frac{{\omega d}}{c}\tanh (\displaystyle\frac{{\omega d}}{c})(1 \!+\! {{\tan }^2}(\displaystyle\frac{{\omega d}}{c})) \!+\! \alpha d\tan (\displaystyle\frac{{\omega d}}{c})(1 \!-\! {{\tanh }^2}(\displaystyle\frac{{\omega d}}{c}))}}{{({{(\alpha d)}^2} \!+\! {{(\displaystyle\frac{{\omega d}}{c})}^2})({{\tanh }^2}(\alpha d) \!+\! {{\tanh }^2}(\displaystyle\frac{{\omega d}}{c}))}}$ | (13) |
| ${X_0} = \frac{{\alpha d\tanh (\alpha d)(1 \!+\! {{\tan }^2}(\displaystyle\frac{{\omega d}}{c}))\! -\! \displaystyle\frac{{\omega d}}{c}\tan (\displaystyle\frac{{\omega d}}{c})(1 \!-\! {{\tanh }^2}(\alpha d))}}{{({{(\alpha d)}^2} \!+\! {{(\displaystyle\frac{{\omega d}}{c})}^2})({{\tanh }^2}(\alpha d) \!+\! {{\tan }^2}(\displaystyle\frac{{\omega d}}{c}))}}$ | (14) |
式(10)~(14)是非线性方程组,按迭代法,先假设一初值
图2所示为实验所需仪器有声管、信号源、功率放大器(B&K2713)、滤波器、测量放大器和采集器。其中声管是一根垂直放置的充水钢管,高4.05 m、内径5.64 cm、管厚3.30 cm、上限频率32.00 kHz、下限频率1.88 kHz。换能器是平面活塞型收发合置换能器,并且满足如下要求:与钢管间有声学隔离,以减弱换能器激发管壁振动;轴对称激发,以提高声管的上限频率;辐射面振幅均匀分布,以便减小轴对称的高阶波的幅度[10]。
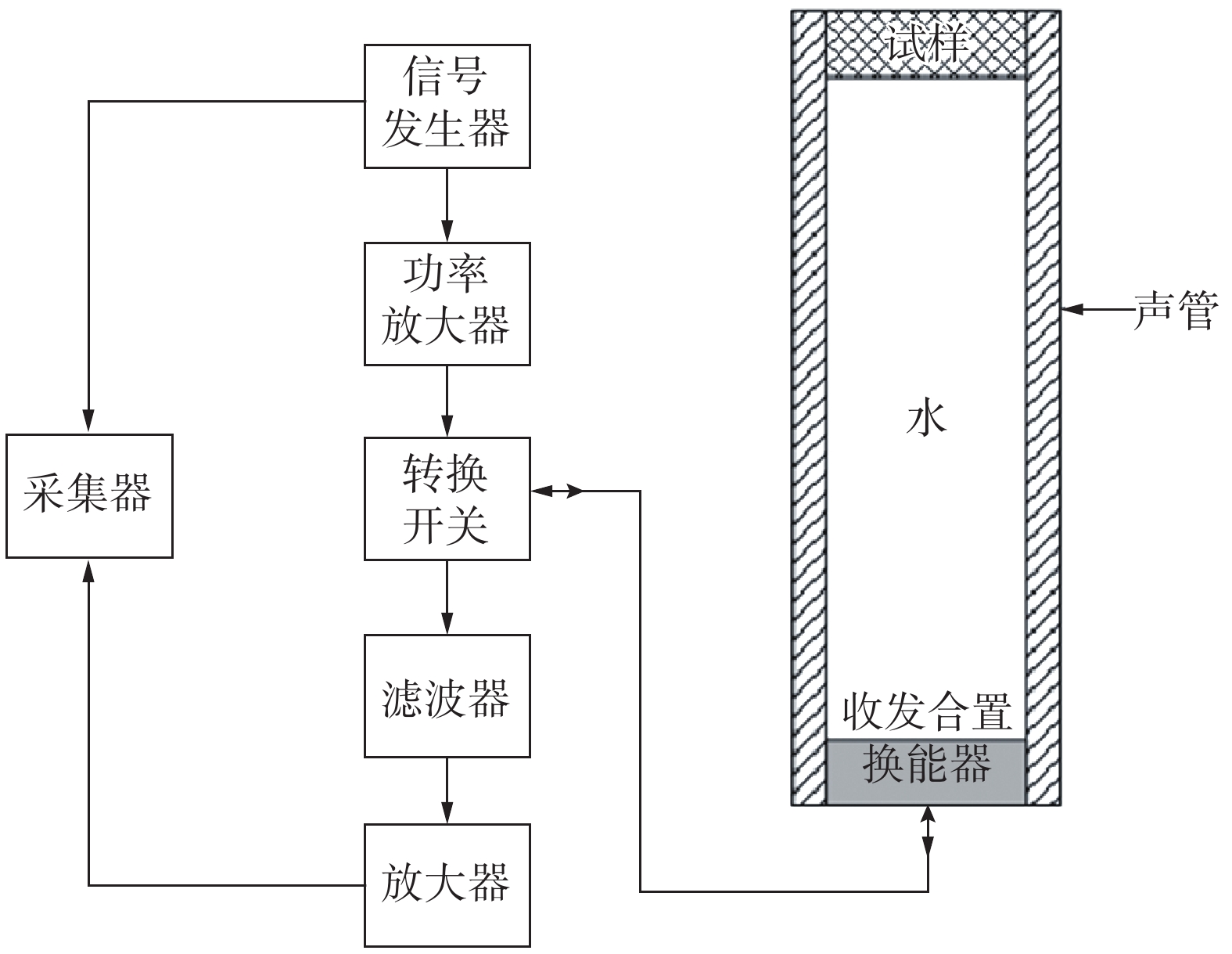
|
Download:
|
| 图 2 脉冲管法测量示意 | |
实验之前需要注意的是:首先将试样制作成圆柱形样品,厚度在0.3λ~0.6λ之间(λ为声波在样品中传播的波长),试样与声管内壁间应留有缝隙,但不大于0.2 mm;试样的表面必须平整,厚度要均匀;使用除气的蒸馏水,倒入声管后静置2~3 d去除气泡。
2.2 脉冲声管系统的工作过程试样在软末端条件下进行实验时需将试样用细绳悬挂在声管的上端。试样在准备正式测试前先在水中浸泡,以使试样表面充分浸润。试样从声管上端平行着滑入管口,而不是直接放到管口上,这样可以避免带入气泡。试样放入管口后等待数分钟后开始测量,以使试样与管内水之间达到温度平衡。试样放入管内后,需将试样上表面的水层吸干净。用采集器分别采集有试样时试样的反射信号和去掉试样后水面的反射信号,通过处理第一次反射波得到反射系数模值
| $\varphi = \nabla \phi \pm {{\pi }}。$ |
试样在硬末端条件下进行实验时需将试样均匀粘贴在刚性负载表面,刚性负载实际上是具有一定厚度的圆柱形钢块。用采集器分别采集有试样时试样的反射信号和去掉试样后钢块的反射信号,通过处理第一次反射波得到反射系数模值
| $\varphi = \nabla \phi \pm 4{{\pi }}fd/{c_w}。$ |
图形用户界面(graphic user interface, GUI)是指由窗口、菜单、图形、光标、按键、对话框和文本等各种图形对象组成的用户界面[12]。它让用户定制用户与MATLAB的交互方式,而命令窗口不是唯一与MATLAB的交互方式。用户通过鼠标或键盘选择、激活这些图标对象,使计算机产生某种动作或变化。MATLAB中设计图形用户界面的方法有使用可视化的界面环境和通过编写程序两种方法。本文中采用第一种方法,通过在空白GUI界面上添加图标对象,并在程序中输入命令后可实现计算功能的计算界面图3所示。
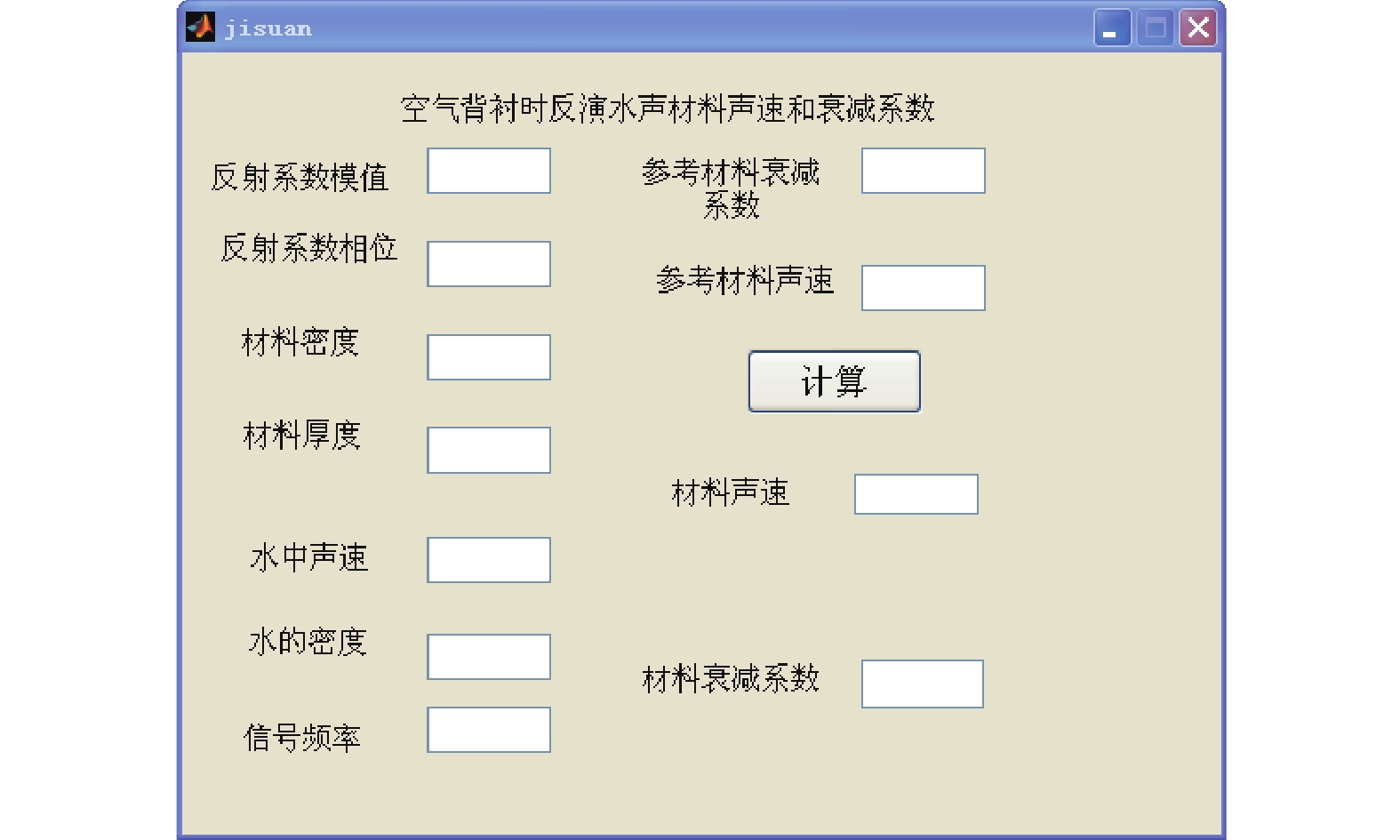
|
Download:
|
| 图 3 计算界面 | |
实验时先提前测量材料密度和厚度,然后通过采集器分别采集到水面反射信号和材料反射信号,处理数据后即可得到反射系数的模值和相角,然后将所有参数,如反射系数模值和相角、材料密度和厚度、水的密度和声速及发射信号频率输入到计算界面,并输入材料声速和衰减系数的估计值作为初始值,用MATLAB自带最小二乘法fsolve命令,逐步逼近,直到计算到满足所需的精度,即反演出材料的声速和衰减系数。需要注意的是,不同的初始值可能会反演出不同的结果,当初始值在真值附近时会迅速反演到真值;当初始值偏离真值太远时可能会反演不到真值或得到错误的结果。整个计算流程如图4所示。
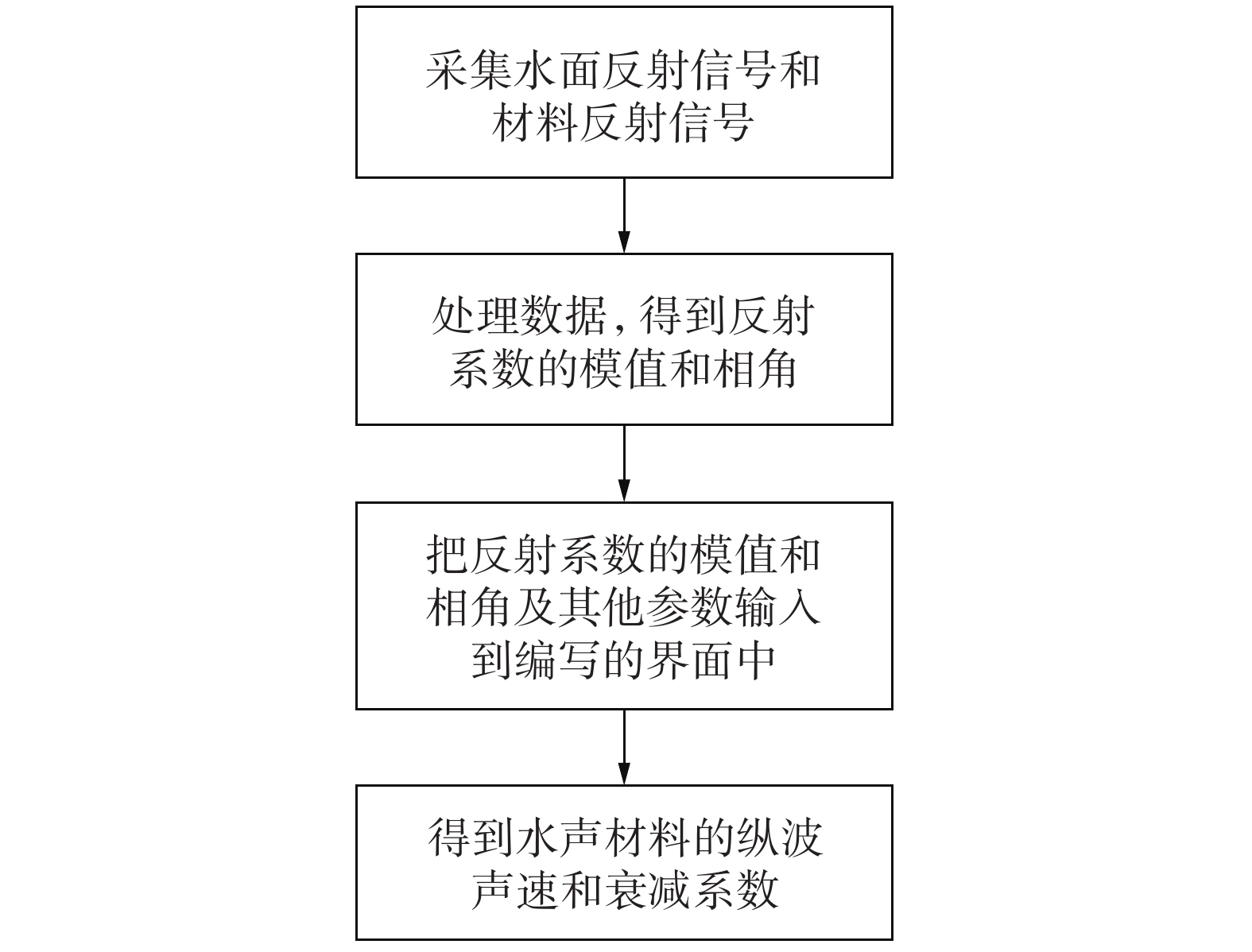
|
Download:
|
| 图 4 计算流程 | |
氯丁橡胶的密度ρ = 1 080.00 kg/m3,在频率f = 20.00 kHz、温度为13 ℃时纵波声速c = 1 510.00 m/s。衰减系数α = 5.00 dB/m,厚度d = 7.00 cm的氯丁橡胶在发射信号频率f = 20.00 kHz时经计算得反射系数模值R = 0.45,反射系数相角ϕ = −2.17,把数据输入界面反演计算得材料声速c = 1 509.44 m/s,衰减系数α = 4.92 dB/m,可认为与理论值一致,仿真计算界面如图5所示。
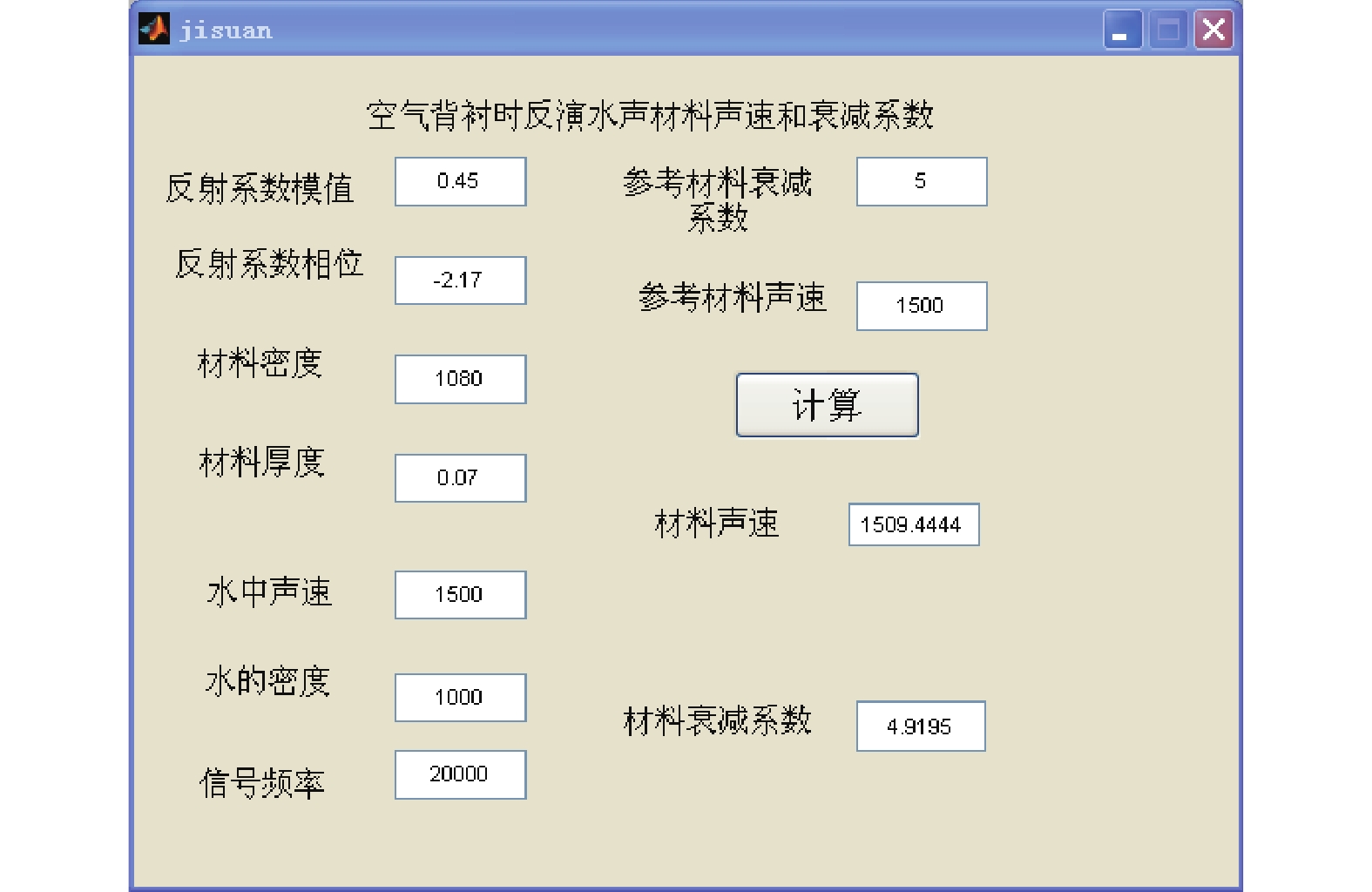
|
Download:
|
| 图 5 仿真计算界面 | |
由于在实际操作中存在测量误差,下面通过表1~3分析反射系数模值和相角测量存在误差时对反演结果的影响。
|
|
表 1 反射系数模值变化对反演的纵波声速和衰减系数的影响 |
|
|
表 2 反射系数相角变化对反演的纵波声速和衰减系数的影响 |
|
|
表 3 反射系数模值和相角同时变化对反演的纵波声速和衰减系数的影响 |
由表1可得,当反射系数相角不变时,衰减系数随反射系数模值的变小而增大;由表2可得,当反射系数模值不变时,声速随反射系数相角的变大而增大;表3也遵循上述两点,并且说明当模值和相角同时变化时引起的声速和衰减系数的改变要大于只有一个变量变化时引起改变。而且由表1、2可得,反射系数模值的改变对衰减系数的影响较大,反射系数相角的改变对声速的影响较小,而在实际测试中,反射系数模值的测量要比反射系数相角的测量要更容易精准,因此,在一定的测量误差内可以通过反演得到水声材料的声速和衰减系数。
4.2 实验研究实验于2016年8月在哈尔滨工程大学重点实验室进行,被测材料为浸水饱和后的松木,密度ρ = 870.70 g/m3,厚度d = 6.80 cm,在不同发射频率下测得的反射系数模值和相角及反演的声速和衰减系数如表4所示。
|
|
表 4 松木在不同频率时的反射系数模值、相角及反演的纵波声速和衰减系数 |
从表4中可知浸水松木声速与衰减系数与频率相关,可见浸水松木为频散介质。
在后期处理数据时只需把不同频率复反射系数输入到计算界面中即可得到声速和衰减系数,比分别在计算程序中修改数据提高了速度,缩短了后期处理时间。
5 结论本文在脉冲声管测量水声材料声速和衰减系数原理上,开发了计算水声材料声速与衰减系数的软件,完善了脉冲声管测量系数的后处理工作,通过仿真和实验验证了计算软件的可靠性与高效性,并通过反演存在测量误差时的结果,得到了以下结论:
1)材料的衰减系数主要由反射系数模值影响,材料的声速主要由反射系数相位影响;
2)通过实验测得的复反射系数反演得到的结果可知浸水松木为频散介质;
3)验证了脉冲声管法测水声材料的声速和声衰减系数,并且通过研制的软件缩短了后期处理数据的时间,提高了工作效率。
本文是先计算出复反射系数,再把复反射系数的模值和相位输入软件中反应材料的声速和声衰减系数,下一步工作计划是直接把测量数据导入到软件中计算复反射系数并反演材料的声速和声衰减系数,能进一步缩短处理数据的时间。
| [1] |
郑士杰, 缪荣兴. 水声计量测试技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 1995: 384-406.
( 0) 0)
|
| [2] |
陈建平, 何元安, 黄爱根. 水声材料声学参数及其声管测量方法[J]. 声学技术, 2015, 34(2): 109-114. ( 0) 0)
|
| [3] |
贺加添. 混响室法测量材料声吸收系数的有效性[J]. 烟台大学学报, 1995(3): 65-72. ( 0) 0)
|
| [4] |
温晓峰. 混响水箱测量水声材料吸声系数方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10217-1012265555.htm
( 0) 0)
|
| [5] |
俞悟周, 王坐民. 采用伪随机信号激励的驻波管三点测量法[J]. 声学学报, 1996, 21(4): 352-361. ( 0) 0)
|
| [6] |
ISO 10534-1: 1996 Acoustics-Determination of sound absorption coefficient and impedance in impedance tubes-PartⅠ: Method using standing wave ratio[S].
( 0) 0)
|
| [7] |
CHU W T. Transfer function technique for impedance and absorption measurement in an impedance tube using a single microphone[J]. J Acoustc Soc Am, 1986, 80(2): 550-560. ( 0) 0)
|
| [8] |
庞夜珍. 基于传递函数的吸声隔声测量方法与应用研究[D]. 大连: 大连理工大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10141-2006022031.htm
( 0) 0)
|
| [9] |
吕世金, 苗金林, 张晓伟. 水下材料声学性能宽频段测量方法[J]. 应用声学, 2011, 30(1): 37-45. DOI:10.11684/j.issn.1000-310X.2011.01.006 ( 0) 0)
|
| [10] |
赵渊博, 侯宏, 孙亮. 收发合置水声管中使用宽带脉冲的吸声测量方案[J]. 声学技术, 2014, 33(3): 213-217. ( 0) 0)
|
| [11] |
贾志富. 声学测量实验[M]. 北京: 国防工业出版社, 1989: 47-52.
( 0) 0)
|
| [12] |
缪荣兴, 王荣津. 水声材料纵波声速和衰减系数的脉冲管测量[J]. 声学与电子工程, 1986(2): 31-37. ( 0) 0)
|
| [13] |
焦勇, 周喻虹. 基于MATLAB的快速图形化数据处理软件设计[J]. 电子科技, 2005(7): 40-42. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


