2. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China
大数据无疑是当今信息时代里的热词,越来越多的学者开始关注大数据。中华人民共和国国民经济和社会发展第十三个五年规划纲要中提出“实施国家大数据战略,深化大数据在各行各业的创新应用,探索与传统产业协同发展新业态新模式。”如何将大数据应用于船舶行业也是许多学者不断探索的问题。到目前为止,对于船舶大数据技术的研究主要集中于海运方面。韩佳彤[1]基于大数据分析方法提出了一种船舶智能航线的设计方法;Zhang Liye[2]通过统计在新加坡港口的船舶安全距离,估算出了船舶安全距离的概率分布;Henttinen[3]指出classNK-NAPA GREEN系列系统利用船舶航行时的大数据进行分析,可以得到最佳的运营方案。目前还没有将大数据技术应用于船舶设计方面的研究。
船舶产品由于其结构复杂,产生的数据量极大,如果能够对每一艘船的详细数据进行采集、分类与储存,以便将来进行分析与应用,一定会对船舶的设计和生产有所帮助。以船舶主尺度统计公式为例,在船舶初步设计阶段需要根据统计公式初步估算主尺度,但是根据以往船型资料建立的统计公式已经不适合现代的新船型,本文旨在将大数据的思想应用于船舶主尺度确定,收集大量船型资料,从中拟合得到船舶新的主尺度统计公式。
1 大数据的特点与核心技术大数据的特点可以用4V来概括:Volume指数据容量巨大,Variety指数据种类繁多,Velocity指数据的产生和更新速度快,Value指数据的潜在价值巨大但是价值密度极低。由于大数据的这些特点,人们要在可接受的时间内处理大量的数据就必须要开发出相应的大数据技术。大数据领域的核心技术包括数据采集与预处理、数据存储与管理、数据分析与挖掘和数据展现与应用。具体的大数据技术包括数学技术、数据分析技术、可视化技术和云计算技术等[4]。数学技术是指在处理大数据时用到的统计和优化的数学思想;数据分析技术包括数据挖掘、机器学习、人工神经网络和信号处理等技术;可视化技术是指通过直观的显示方式来解释数据的技术;云计算是指将分析数据的解决方案托管在云端,用户以使用量计费的一种模式。
船舶在设计生产和运营过程中产生的数据符合大数据的特点,也需要有相应的大数据技术来将这些数据进行采集、分析和应用,使其创造出巨大价值。
2 数据采集大数据技术中,数据的采集是最基本也是最关键的步骤。本文以船舶主尺度确定为例子,从国际船级社的船舶录[5]中采集了大量船型资料,并进行大数据回归分析,回归出主尺度统计公式。目前,在主尺度建模方面已有许多学者进行了相关研究[6-11],但在小型游艇和高速双体船还没有相应研究,所以本文选择了双壳油船、小型游艇和高速双体船进行大数据的分析与研究。
2.1 双壳油船本文收集了433艘双壳油船的主尺度数据,均为2000年以后建造的,其中国内217艘,香港114艘,国外102艘。采集到的样本涵盖了从130载重吨至32万载重吨的双壳油船。表1统计了各载重吨分段内样本数量的分布情况。
|
|
表 1 双壳油船样本分布情况 |
本文收集了232艘小型游艇的主尺度数据,船舶建造时间为2004年至今,均为国内游艇。船舶总长最小的为7.98 m,最大的为33.53 m。由于统计的数据为小型游艇,所以主尺度总体变化不大,船舶数量相对船长分布较为均匀,取全部232艘小型游艇进行大数据回归分析。
2.3 高速双体船本文收集了54艘高速双体船的主尺度数据,船舶建造时间为1992年至今,均为国内游艇。其中51艘总吨位在182~610 t,3艘总吨位超过了2 000 t,为了保证拟合公式的可靠性,将这3艘船舶数据舍去,最后取51艘高速双体船进行大数据回归分析。
3 大数据回归分析在船舶初步设计阶段由于已知的数据较少,确定主尺度的传统方法主要是母型换算或者利用统计公式预估。统计公式必须以任务书中的已知量作为变量,不同的船舶在任务书中提供的已知量有所差别。
3.1 双壳油船对于双壳油船,在设计任务书中主要给出的是载重量和船速等数据,而且对于油船的研究已相对成熟,船型相对稳定,船舶主尺度基本随载重量变化而同向变化,所以本文以载重量为单一变量进行大数据回归分析。
1)垂线间长L(m)与载重量WD(t)的回归公式为
| $\begin{split}L = & 8.165 \times {10^{ - 13}}{W_{ D}}^3 - 1.102 \times {10^{ - 7}}{W_{ D}}^2 + \\& 5.664 \times {10^{ - 3}}{W_{ D}} + 70.861\;\;\;\;\left( {{R^2} = 0.967\;7} \right)\end{split}$ | (1) |
| $L = 8.568 7{W_{ D}}^{0.284 \,\,6}\;\;\;\left( {{R^2} = 0.945\;8} \right)$ | (2) |
式中R2为决定系数。分别利用式(1)和(2)预测样本的垂线间长,计算残差的平方,式(1)的残差平方和为4 780,式(2)的残差平方和为9 011,式(1)的预测值更接近真实值,取式(1)为垂线间长统计公式,关系曲线如图1所示。

|
Download:
|
| 图 1 L与WD关系曲线 | |
2)型宽B(m)与载重量WD(t)的回归公式为
| $\begin{split}B = & 4.004 \times {10^{ - 14}}{W_{ D}}^3 - 1.068 \times {10^{ - 8}}{W_{ D}}^2 + \\& 8.507 \times {10^{ - 4}}{W_{ D}} + 11.581\;\;\;\;\;\;\left( {{R^2} = 0.989\;1} \right)\end{split}$ | (3) |
| $B = 7.451 3\ln {W_{ D}} - 49.08\;\;\;\left( {{R^2} = 0.932\;5} \right)$ | (4) |
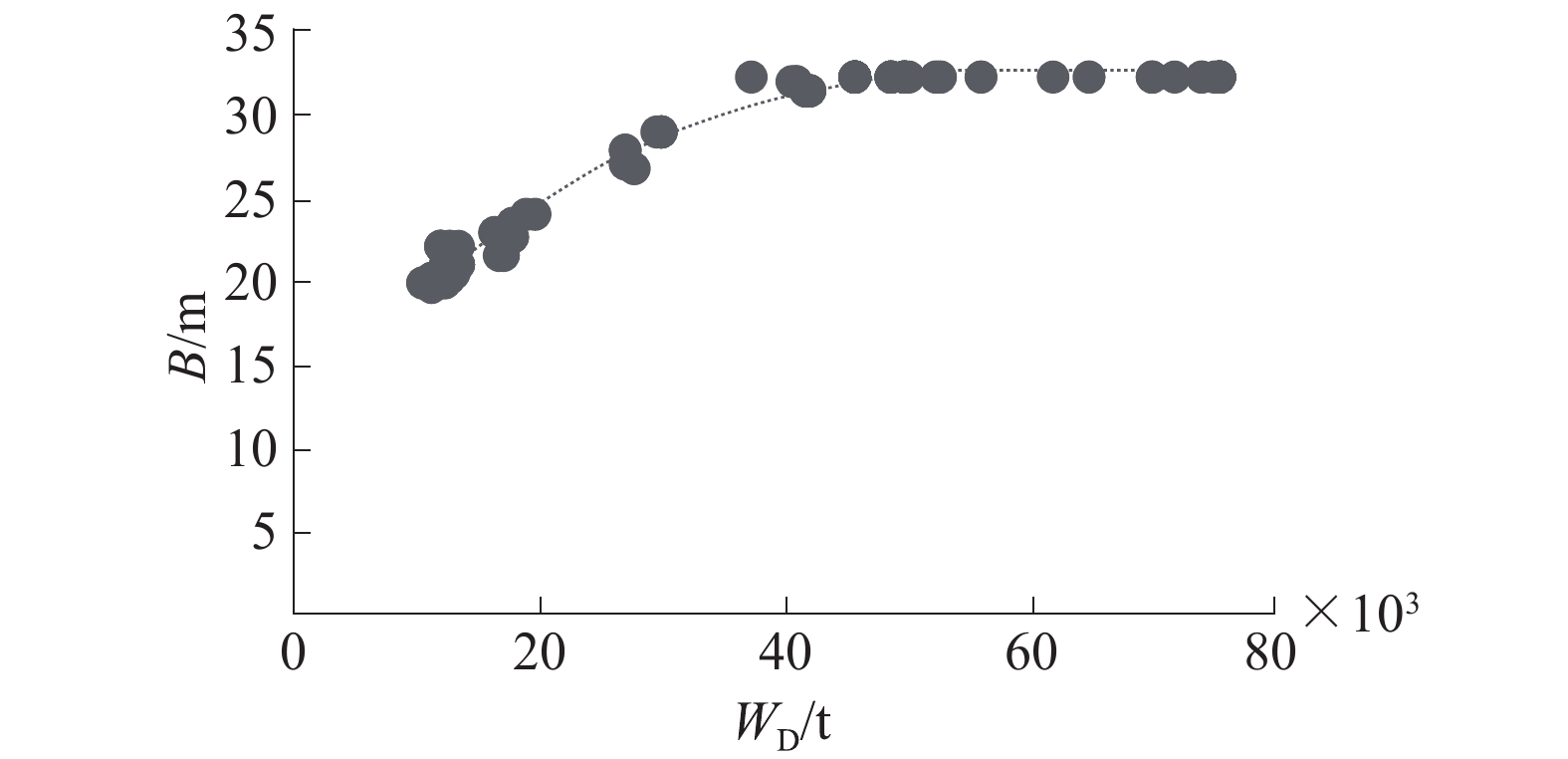
式(3)的残差平方和为42,式(4)的残差平方和为260,式(3)的预测值更接近真实值,取式(3)为型宽的统计公式,关系曲线如图2所示。
|
Download:
|
| 图 2 B与WD关系曲线 | |
3)型深D(m)与载重量WD(t)的回归公式为
| $\begin{split}D = & - 1.481 \times {10^{ - 14}}{W_{ D}}^3 - 3.855 \times {10^{ - 10}}{W_{ D}}^2 + \\& 2.278 \times {10^{ - 4}}{W_{ D}} + 8.028\;\;\;\;\;\;\;\left( {{R^2} = 0.978\;6} \right)\end{split}$ | (5) |
| $D = 0.308 \;2{W_{ D}}^{0.377 \;4}\;\;\;\left( {{R^2} = 0.977\;3} \right)$ | (6) |
式(5)的残差平方和为45,式(6)的残差平方和为51,式(5)的预测值更接近真实值,式(6)形式简单同时也较接近真实值,取式(5)为型深统计公式,关系曲线如图3所示。

|
Download:
|
| 图 3 D与WD关系曲线 | |
4)吃水d(m)与载重量WD(t)的回归公式为
| $d = 7.347{{ e}^{8.256 \times {{10}^{ - 6}}{W_{ D}}}}\;\;\;\left( {{R^2} = 0.889\;0} \right)$ | (7) |
| $d = 0.638 \;4{W_{ D}}^{0.266 \;1}\;\;\;\;\left( {{R^2} = 0.880\;5} \right)$ | (8) |
式(7)的残差平方和为73,式(8)的残差平方和为82,所以式(7)的预测值更接近真实值,取式(7)为吃水的统计公式,关系曲线如图4所示。

|
Download:
|
| 图 4 d与WD关系曲线 | |
对于小型游艇,在设计初期主要已知船舶总长和总吨位等参数,游艇总长基本随总吨变化而变化,本文对总长进行单变量回归,但是由于游艇的船型变化较大,型宽不仅与总吨和总长有关,与型深也有关系,型深亦如此,所以本文对游艇型宽与型深进行多变量的大数据回归分析。
1)总长L(m)与总吨GT(t)的回归公式为
| $\begin{split}L = & 3.901 \times {10^{ - 6}}{G_{{T}}}^3 - 1.414 \times {10^{ - 3}}{G_{{T}}}^2 + \\& 0.243\; 3{G_{{T}}} + 8.427 \;9\;\;\;\;\;\;\;\;\left( {{R^2} = 0.876\; 7} \right)\end{split}$ | (9) |
| $L = 4.476{G_{{T}}}^{0.349\; 8}\;\;\;\left( {{R^2} = 0.865\;8} \right)$ | (10) |
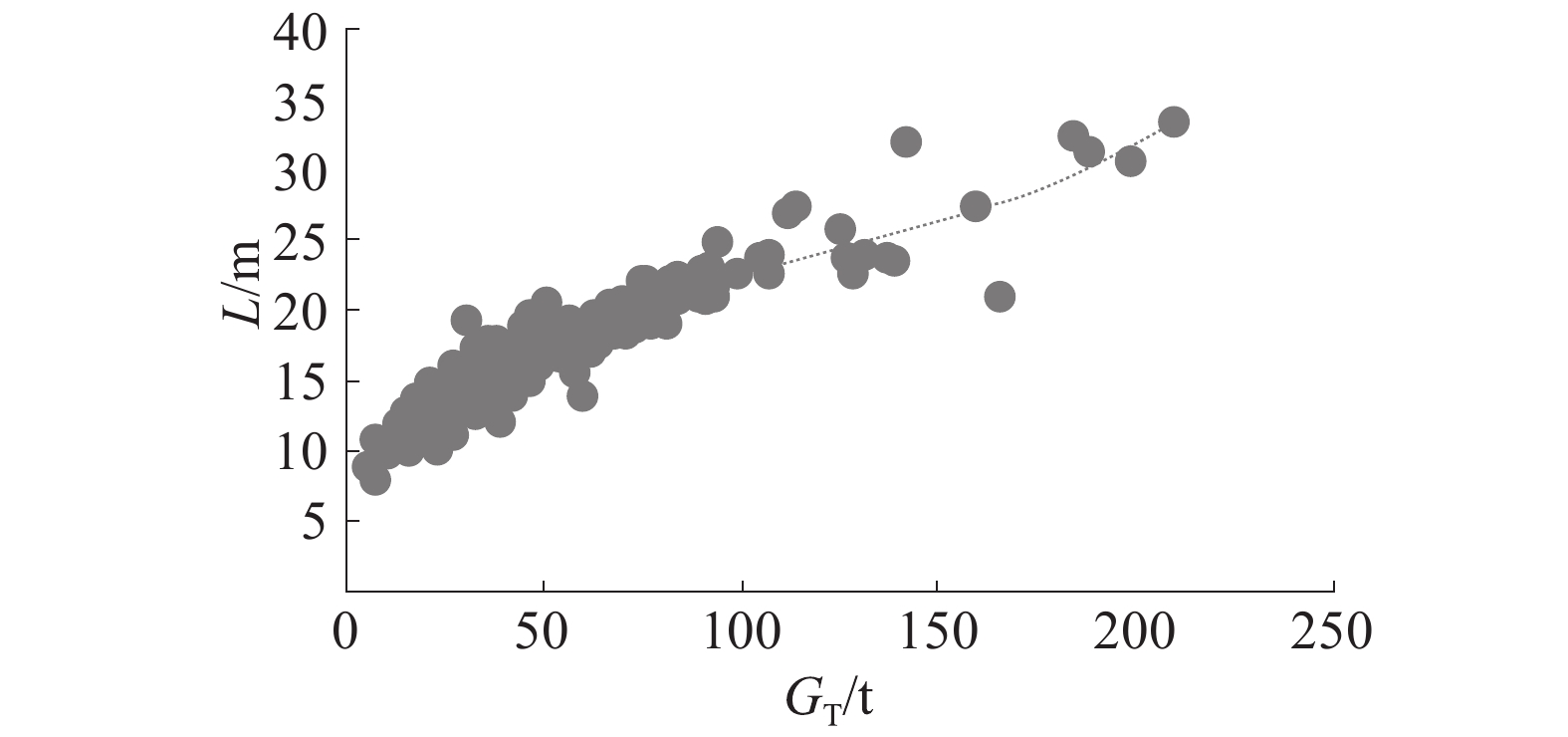
式(9)的残差平方和为570,式(10)的残差平方和为608,式(9)的预测值更接近真实值,式(10)较接近真实值且有较简单的形式,取式(9)为总长的统计公式,关系曲线如图5所示。
|
Download:
|
| 图 5 L与GT关系曲线 | |
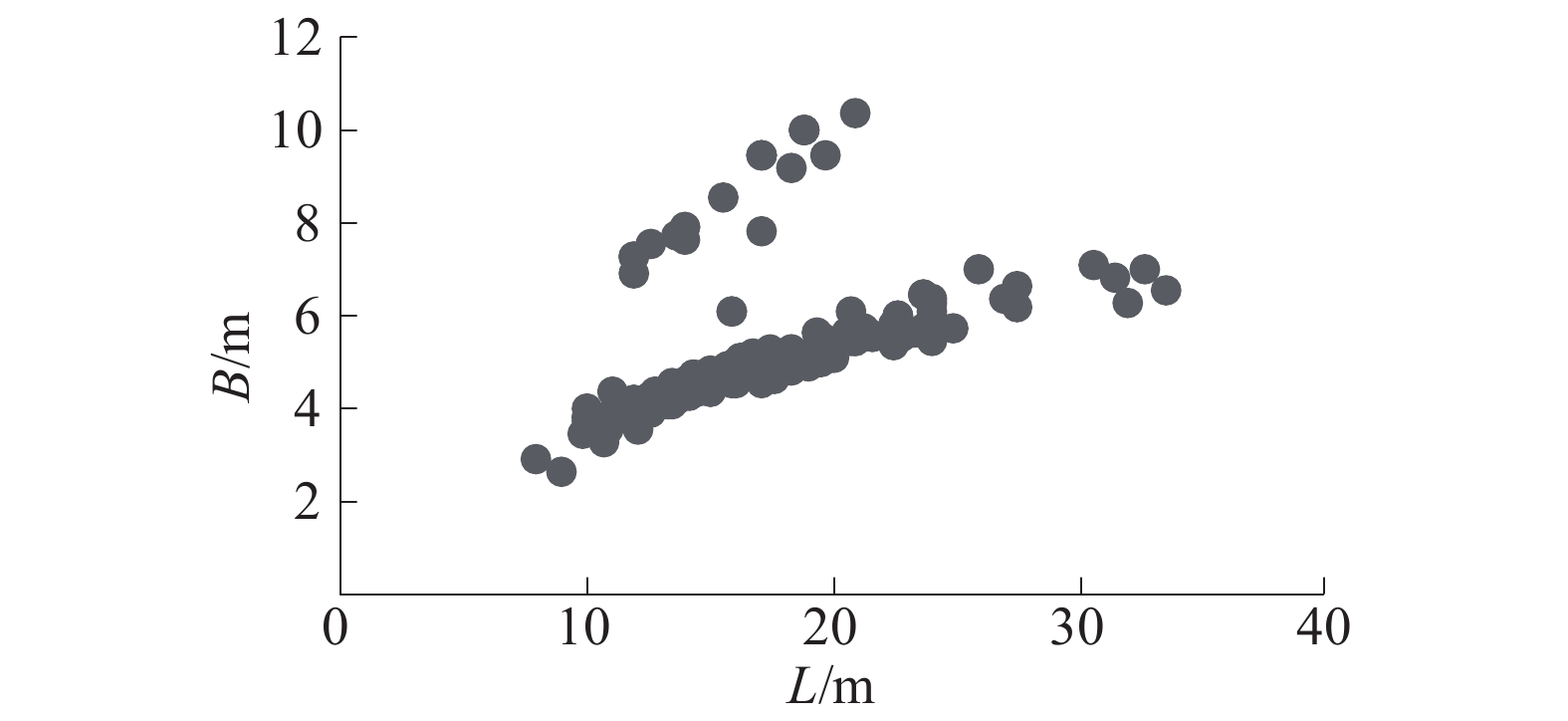
2)型宽B(m)与总长L(m)的大数据样本图如图6所示。
|
Download:
|
| 图 6 B与L大数据样本 | |
从样本图中注意到有一部分异常点偏离总体趋势,分析后发现样本这部分游艇的总吨较正常值大,但是总长没有发生变化,仅型宽增加。利用SPSS软件,以型宽B为因变量,总吨GT(t)、总长L(m)、型深D(m)为自变量进行多变量回归,回归公式为
| $\begin{split}& B = 2.651 \;6\sqrt[3]{{{G_{{T}}}}} - 0.208 \;2L - 0.846 \;3D + 1.273 \;2\\& \left( {{R^2} = 0.524} \right)\end{split}$ | (11) |
3)和型宽类似,以型深D(m)为因变量,总吨GT(t)、总长L(m)、型宽B(m)为自变量进行多变量回归,回归公式为
| $\begin{array}{l}D = 0.866 \;3\sqrt[3]{{{G_{{T}}}}} - 0.029 \;39L - 0.119 \;8B + 0.315 \;1\\\left( {{R^2} = 0.656} \right)\end{array}$ | (12) |
对于双体船,任务书中主要给出总吨位和船速等需求,本文以总吨GT为自变量,同时双体船的型深和吃水与片体的大小密切相关,由于缺少和双体船片体有关的数据,本文仅对垂线间长和型宽进行大数据回归分析。
1)垂线间长L(m)与总吨GT(t)的回归公式为
| $\begin{split}L = & 5.143 \times {10^{ - 7}}{G_{{T}}}^3 - 7.887 \times {10^{ - 4}}{G_{{T}}}^2 + \\& 0.401 \; 6{G_{{T}}} - 31.740\;\;\;\;\;\;\left( {{R^2} = 0.760\;5} \right)\end{split}$ | (13) |
| $L = 3.516 \;9{G_{{T}}}^{0.375 \;2}\;\;\;\left( {{R^2} = 0.585\;4} \right)$ | (14) |
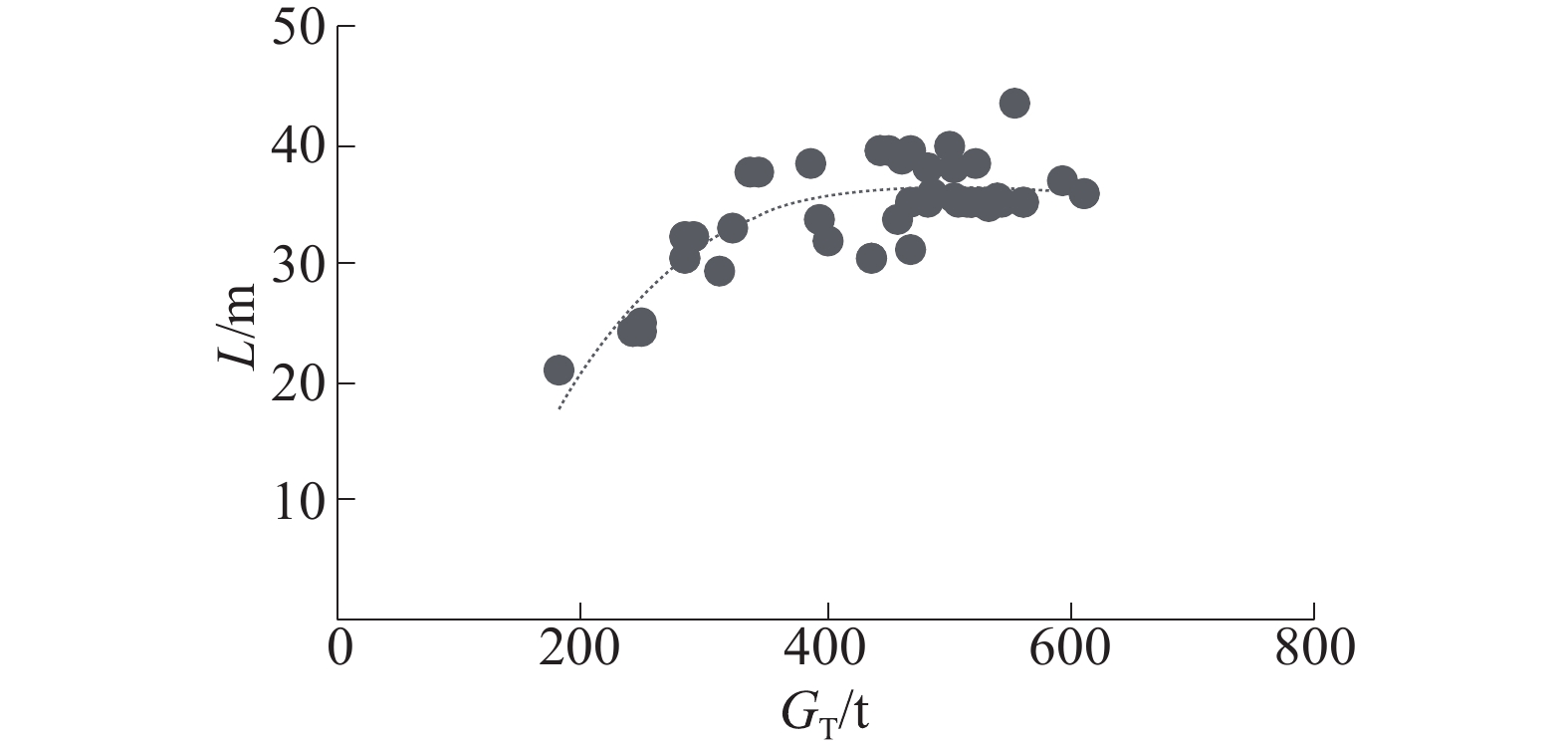
式(13)的残差平方和为350,式(14)的残差平方和为492,式(13)的预测值更接近真实值,取式(13)为垂线间长的统计公式,关系曲线如图7所示。
|
Download:
|
| 图 7 L与GT关系曲线 | |
2)型宽B(m)与总吨GT(t)的回归公式为
| $\begin{split}B = & - 1.094 \times {10^{ - 7}}{G_{{T}}}^3 + 1.520 \times {10^{ - 4}}{G_{{T}}}^2 - \\[4pt]& 0.056 \;13{G_{{T}}} + 14.974\;\;\;\;\;\;\left( {{R^2} = 0.760\;5} \right)\end{split}$ | (15) |
| $B = 6.665 \;6{{{e}}^{1.025 \times {{10}^{ - 3}}{G_{{T}}}}}\;\;\;\left( {{R^2} = 0.741\;8} \right)$ | (16) |
式(15)的残差平方和为23,式(16)的残差平方和为26,式(15)的预测值更接近真实值,但式(16)有较简单的形式,取式(15)为型宽统计公式,关系曲线如图8所示。

|
Download:
|
| 图 8 B与GT关系曲线 | |
为了检验回归效果,分别从双壳油船、小型游艇和高速双体船中随机选择5艘、5艘和3艘实船,对上述回归公式进行检验。这13艘船的主要尺度如表2~4所示。
|
|
表 2 双壳油船主要尺度 |
|
|
表 3 小型游艇主要尺度 |
|
|
表 4 高速双体船主要尺度 |
由表5可见各主尺度的回归公式的预测值与真实值的误差基本在10%的范围内,说明这些回归公式回归效果较好,具有一定的可靠性,可以作为初步设计的参考。
|
|
表 5 模型回归效果检验 |
本文以船舶主尺度确定为例子,为大数据技术应用于船舶设计提供了方法,通过对3种船型主尺度资料的收集和回归分析,得到了一套船舶主要尺度的数学模型,并且经过验证该数学模型是可靠的,可以反应船舶主尺度的变化规律,可用于船舶初步设计时的主尺度确定。以下是本文提出的3个建议:
1)本文收集的数据量还不够庞大,数据不够详细,今后应发展大数据相关技术,将船舶大数据进行采集分类,利用更大更详细的数据一定能拟合出更好的统计公式。
2)从本文研究来看,大数据技术应用于船舶主尺度确定是可行的,今后还可进一步尝试应用智能决策支持系统等智能系统进行船型数据的储存和建模分析。
3)应用上述回归公式时应注意适用的船型及主尺度范围,其中小型游艇的船型变化较大,设计者可不拘于回归公式的结果,自行设计。
| [1] |
韩佳彤. 基于大数据分析的海上智能航线设计[J]. 珠江水运, 2016(1): 78-79. ( 0) 0)
|
| [2] |
ZHANG Liye, WANG Hua, MENG Qiang. Big data-based estimation for ship safety distance distribution in port waters[J]. Transportation research record: journal of the transportation research board, 2014, 2479: 16-24. ( 0) 0)
|
| [3] |
HENTTINEN E. Big data: connecting and merging the dots from yard, to ship, to shore[J]. Marine log, 2015, 120(11): 43-44. ( 0) 0)
|
| [4] |
WANG Hai, XU Zeshui, FUJITA H, et al. Towards felicitous decision making: an overview on challenges and trends of big data[J]. Information sciences, 2016 (s367/368): 747−765.
( 0) 0)
|
| [5] |
中国船级社国际船舶录[EB/OL]. [2017-03-20]. http://psmis.ccs.org.cn/ship/list.do.
( 0) 0)
|
| [6] |
王运龙, 金朝光, 林焰, 等. 集装箱船船型要素数学建模研究[J]. 武汉理工大学学报: 交通科学与工程版, 2011, 35(5): 914-917. ( 0) 0)
|
| [7] |
刘飞, 林焰, 李纳, 等. 海监船与渔政船主尺度模型研究[J]. 舰船科学技术, 2012, 34(7): 49-54. ( 0) 0)
|
| [8] |
王运龙, 纪卓尚, 林焰. 自升式钻井平台方案设计智能决策支持系统[J]. 上海交通大学学报, 2009, 43(2): 182-186. ( 0) 0)
|
| [9] |
李纳, 陈明, 刘飞, 等. 基于广义回归神经网络与遗传算法的玻璃钢渔船船型要素优化研究[J]. 船舶工程, 2012, 34(4): 18-21. ( 0) 0)
|
| [10] |
杨蕖, 林焰, 刘飞, 等. 海监船与渔政船主尺度单变量回归分析[J]. 船舶工程, 2012, 34(2): 1-5. ( 0) 0)
|
| [11] |
WANG Yunlong, JI Zhuoshang, LIN Yan. Mathematically modeling the main dimensions of self-elevating drilling units[J]. Journal of marine science and application, 2009, 8(3): 211-215. DOI:10.1007/s11804-009-8045-9 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


