2. 哈尔滨工程大学 船舶与海洋工程学院, 黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
张力腿平台(TLP)是一种典型的顺应式平台,通过数条张力筋腱与海底相连[1]。TLP的六自由度运动可以简单分为两类,一类主要由系泊系统刚度控制,包括垂直面内的垂荡、横摇和纵摇;另外一类主要由结构的几何形式和系泊张力的水平分量决定,包括水平面内的纵荡、横荡和艏摇运动[2]。由于浮力和重力差筋腱产生了较大的刚度,使得TLP垂直面上运动的固有周期比较小,水平面上运动的固有周期一般比较大[3],其垂荡运动的固有周期一般为2~4 s内,水平方向的系统刚度只是预张力的小角度正选分量,纵横荡运动的固有周期一般在100~200 s内,其特有的结构形式较大程度地避免了波浪激励载荷共振的发生[4]。
张力腿平台在环境力作用下有着较大的位移,TLP系统的非线性恢复刚度在其动态运动中起着非常重要的作用。纵荡、横荡、垂荡相对于自身位移是一个非线性函数[5]。通常在进行TLP数值模拟时把平台被视为刚体,张力筋腱模拟为准静态弹簧[6],计算出的平台刚度矩阵便近似等效为时域分析中的系统刚度。但在实际结构中,系泊的张力筋腱是多成分的复合结构。平台在发生水平位移时导致平台垂向沉降发生,水平自由度和垂直向自由度耦合导致系统结构的刚度随空间位置产生非线性变化。而且,平台的水平运动导致吃水变化,系统环境回复刚度也发生了变化。其低频运动的相互耦合,结构在水平面上运动大变形导致了结构刚度矩阵和阻尼矩阵产生非线性变换[7-8],从而导致TLP在波浪中产生非线性运动。因而确保模型线性刚度矩阵的准确性是进行张力腿平台动态分析的首要工作,对平台刚度进行系统验证也成为确保计算分析准确的工作之一。
文中使用SESAM软件,对一座传统结构形式TLP的张力筋腱响应进行了研究。考虑平台的结构细节,使用Genie模块建立平台下浮体湿表面模型以及莫里森杆元模型,使用HydroD建模并计算了系统的质量矩阵、刚度矩阵和附加质量系数。考虑实际张力筋腱及立管结构分段,在DeepC中建立全耦合模型,进行静水刚度验证模拟和自由衰减模拟,并通过时域分析方法求解张力筋腱张力响应RAO。
1 平台结构及环境工况文中用于计算的传统张力腿平台由平台本体(平台上体、立柱和下体浮箱)、张力筋腱系泊系统以及立管系统三大部分组成,其主体结构由4根尺寸相同的圆柱形立柱与4个矩形浮箱连接构成,呈对称分布,主尺度见表 1。
|
|
表 1 张力腿平台主参数 |
TLP共8根张力筋,12根立管(1根钻井立管,11根生产立管),张力筋分段参数如表 2所示。在莫里森力的计算中,张力筋的拖曳力系数Cd和附加质量系数Ca规定如下:Cd=1.1(上部94.3 m长度部分),Cd=1.0(张力筋余下部分),Ca=1.0。立管拖曳力系数Cd取1.2,附加质量系数Ca取1。
|
|
表 2 张力筋分段参数 |
在HyDrod计算中,张力腿平台在体坐标系下的运动方程如下:
| $ \mathit{\boldsymbol{M\ddot X + B\dot X + KX = }}F\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\dot X}},\mathit{\boldsymbol{\ddot X}},t} \right) $ |
式中:M为浮体质量矩阵,K为其刚度矩阵,B为阻尼矩阵,
在TLP平台的线性刚度矩阵中,主要包含两部分贡献,一部分为张力筋的贡献,另一部分为浮体共有的静水刚度(静水恢复力)[10],张力筋的贡献在数量上起主导作用。具体刚度矩阵的各项系数中,起主要作用的仍然是对角阵上的各项,其他项主要是考虑到各自由度之间的相互耦合作用。实际上,刚度矩阵中的各项系数会随着平台位置的移动而发生变化,实质上是一个非线性项,只有平台运动幅度在一定范围内,可以近似认为是常数。本目标张力腿平台刚度矩阵中主要项的计算方法如下[11-12]:
对于纵荡自由度:
| $ \begin{array}{*{20}{c}} {{K_{11}} = \frac{{8{T_{0,{\rm{tendon}}}}}}{{{l_{{\rm{tendon}}}}}} + \frac{{11{T_{0,{\rm{priser}}}} + {T_{0,{\rm{driser}}}}}}{{{l_{{\rm{riser}}}}}}}\\ {{K_{31}} = 0\;\;\;{K_{51}} = - \bar h{K_{11}}} \end{array} $ |
式中:ltendon为张力筋原长,T0, tendon为初始预张力,T0, priser为生产立管顶部张紧式立管的初始预张力,T0, driser为钻井立管顶部张紧式立管的初始预张力,lriser为顶部张紧式立管的初始长度,h为重心到平台底部的距离。
横荡自由度:
| $ \begin{array}{*{20}{c}} {{K_{22}} = \frac{{8{T_{0,{\rm{tendon}}}}}}{{{l_{{\rm{tendon}}}}}} + \frac{{11{T_{0,{\rm{priser}}}} + {T_{0,{\rm{driser}}}}}}{{{l_{{\rm{riser}}}}}}{K_{11}}}\\ {{K_{32}} = 0}\\ {{K_{42}} = \bar h{K_{22}}} \end{array} $ |
垂荡自由度:
| $ {K_{33}} = \frac{{8{A_{{\rm{tendon}}}}{E_{{\rm{tendon}}}}}}{{{l_{{\rm{tendon}}}}}} + \frac{{8{A_{{\rm{priser}}}}{E_{{\rm{priser}}}} + {A_{{\rm{driser}}}}{E_{{\rm{driser}}}}}}{{{l_{{\rm{riser}}}}}} + 4{\rho _{\rm{W}}}gS $ |
式中:Atendon为张力筋横截面面积,Etendon为张力筋轴向刚度,Apriser为生产立管的横截面积,Epriser为生产立管的轴向刚度,Adriser为生产立管的横截面积,Edriser为生产立管的轴向刚度,ρW为海水的密度,g为重力加速度,S为浮筒横截面积。
横摇自由度:
| $ \begin{array}{*{20}{c}} {{K_{44}} = \frac{{4{A_{{\rm{tendon}}}}{E_{{\rm{tendon}}}}\left( {p_1^2 + p_2^2} \right)}}{{{l_{{\rm{tendon}}}}}} + }\\ {\frac{{11{A_{{\rm{priser}}}}{E_{{\rm{priser}}}}q_1^2 + {A_{{\rm{driser}}}}{E_{{\rm{driser}}}}q_2^2}}{{{l_{{\rm{riser}}}}}} + 4{\rho _{\rm{W}}}g{b^2}S}\\ {{K_{34}} = 0} \end{array} $ |
式中:p1、p2为张力腿y方向上的2个位置坐标,q1为生产立管y方向坐标,q2为钻井立管y方向坐标。b为浮筒中心y方向距离。
纵摇自由度:
| $ \begin{array}{*{20}{c}} {{K_{55}} = \frac{{4{A_{{\rm{tendon}}}}{E_{{\rm{tendon}}}}\left( {p_1^2 + p_2^2} \right)}}{{{l_{tendon}}}} + }\\ {\frac{{11{A_{{\rm{priser}}}}{E_{{\rm{priser}}}}q_1^2 + {A_{{\rm{driser}}}}{E_{{\rm{driser}}}}q_2^2}}{{{l_{{\rm{riser}}}}}} + {\rm{\pi }}{\rho _{\rm{W}}}g{b^2}{D^2}}\\ {{K_{35}} = 0} \end{array} $ |
式中D为浮筒直径。
艏摇自由度:
| $ \begin{array}{*{20}{c}} {{K_{66}} = \frac{{8{T_{0,{\rm{tendon}}}}\left( {p_1^2 + p_2^2} \right)}}{{{l_{{\rm{tendon}}}}}} + }\\ {\frac{{11{T_{0,{\rm{priser}}}}\left( {q_1^2 + q_2^2} \right) + {T_{0,{\rm{driser}}}}\left( {q_1^2 + q_2^2} \right)}}{{{l_{{\rm{riser}}}}}}}\\ {{K_{36}} = 0} \end{array} $ |
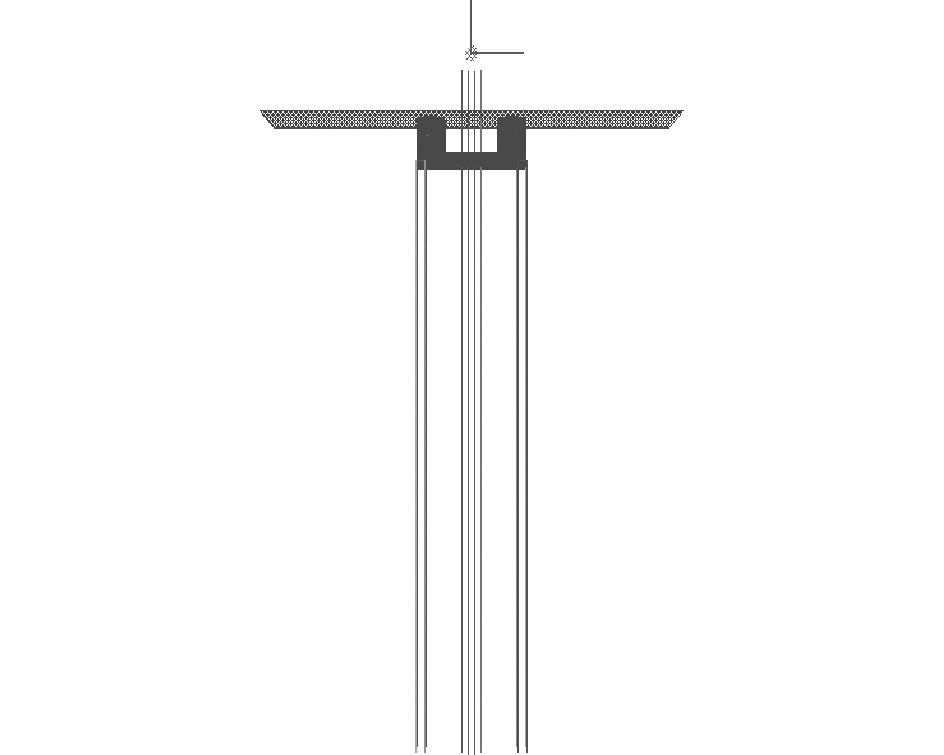
在本节中,使用SESAM软件中GeniE模块建立了湿表面模型以及莫里森杆元模型,网格划分尺度1 m,湿表面单元14 517个,如图 1所示。在HydroD模块中建立浮体-张力筋-TTR模型,如图 2所示,计算频域下TLP刚度矩阵。

|
图 1 湿表面模型 |
|
图 2 频域计算模型 |
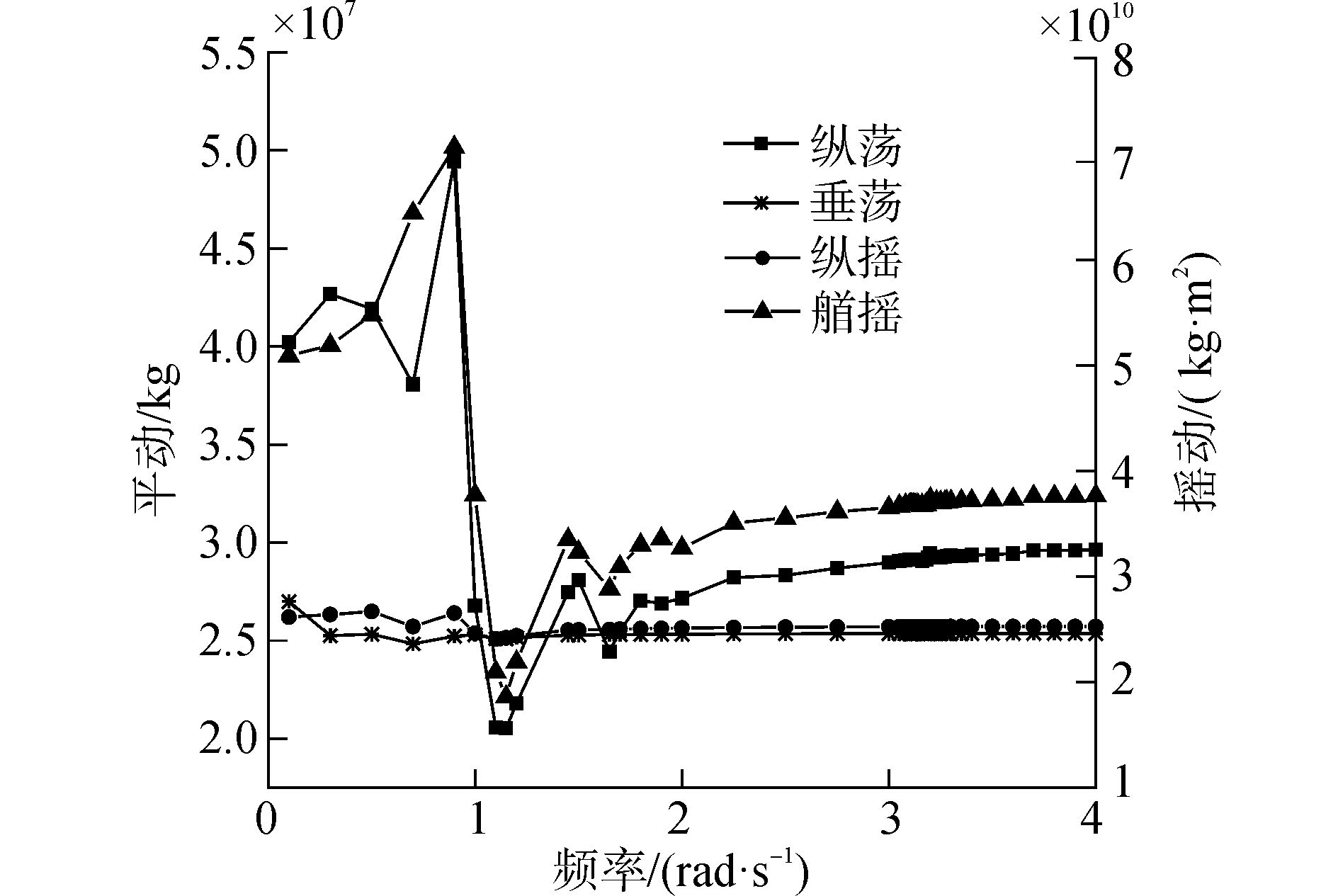
附加质量系数为一个6×6矩阵,文中分析对目标平台水动力性能起主要作用的主对角线上的4个值,横荡、纵摇、垂荡、艏摇附加质量如图 3所示。
|
图 3 附加质量系数 |
由附加质量图可以看出,由于平台的对称性,纵荡和横荡的附加质量是相同的,附加质量取值范围为2.20×107~5.52×107,垂荡方向附加质量范围为2.48×107~2.71×107。
在频域刚度计算的模型中加入了筋腱和立管模型,将其平台运动的影响等效为线性的刚度,通过考虑筋及立管刚度的影响计算得到平台的运动幅值响应。静水回复力矩阵K1以及张力筋及TTR刚度矩阵K2如下所示:
| $ {\mathit{\boldsymbol{K}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&{1.20 \times {{10}^7}}&{ - 5.07 \times {{10}^2}}&{8.80 \times {{10}^2}}&0\\ 0&0&{ - 5.07 \times {{10}^2}}&{ - 1.14 \times {{10}^{10}}}&{ - 1.70 \times {{10}^5}}&{ - 2.61 \times {{10}^4}}\\ 0&0&{8.80 \times {{10}^2}}&{ - 1.70 \times {{10}^5}}&{ - 1.14 \times {{10}^{10}}}&{ - 3.13 \times {{10}^6}}\\ 0&0&0&0&0&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{K}}_2} = \left[ {\begin{array}{*{20}{c}} {4.52 \times {{10}^5}}&0&0&0&{ - 1.03 \times {{10}^7}}&{ - 1.38 \times {{10}^3}}\\ 0&{4.52 \times {{10}^5}}&0&{1.03 \times {{10}^7}}&0&{1.02 \times {{10}^4}}\\ 0&0&{5.13 \times {{10}^8}}&{1.65 \times {{10}^5}}&{ - 1.24 \times {{10}^6}}&0\\ 0&{1.03 \times {{10}^7}}&{1.65 \times {{10}^5}}&{7.12 \times {{10}^{11}}}&{3.41 \times {{10}^6}}&{4.11 \times {{10}^6}}\\ { - 1.03 \times {{10}^7}}&0&{ - 1.24 \times {{10}^6}}&{3.41 \times {{10}^6}}&{7.12 \times {{10}^{11}}}&{5.56 \times {{10}^5}}\\ { - 1.03 \times {{10}^7}}&0&{ - 1.24 \times {{10}^6}}&{3.41 \times {{10}^6}}&{7.12 \times {{10}^{11}}}&{5.56 \times {{10}^5}} \end{array}} \right] $ |
使用DeepC模块建立全耦合模型,张力筋腱和TTR采用串联弹簧建模方式,每段有着不同的内径外径及刚度,如图 4所示。

|
图 4 时域计算模型 |
为了评估此方法建模的精确程度,以及TLP平台的水平方向刚度及水平偏移对垂荡的影响,通过施加水平方向为225°的力来得到平台的准静态偏移曲线。图 5为作用力施加在重心处时平台静态偏移曲线;图 6为T1、T5(迎浪和顺浪)两根张力筋顶部张力随水平运动变化曲线。

|
图 5 平台静态偏移及垂荡曲线 |

|
图 6 张力筋顶部张力曲线 |
从图 5中可以看出,随着作用在平台重心处水平力的增加,平台垂荡及水平刚度并非恒定值,平台整体刚度随着偏移/垂荡的增加而增大。当外力作用使平台产生较大偏移时,平台会产生绕重心的力矩。从图 6可以看出,由于力矩的产生,迎浪和背浪的2根张力筋出现了明显不同的张力值。张力筋T1和T5在水平位移为0时,张力筋顶部张力为初始预张力。
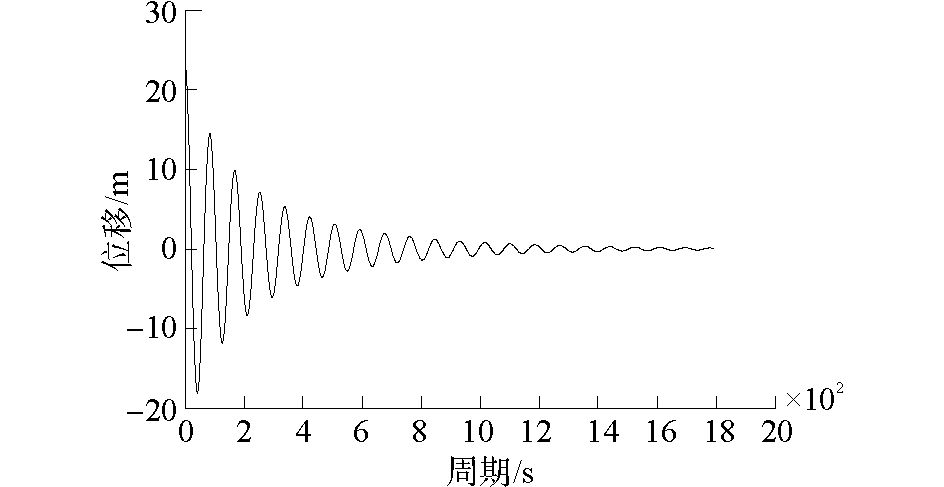
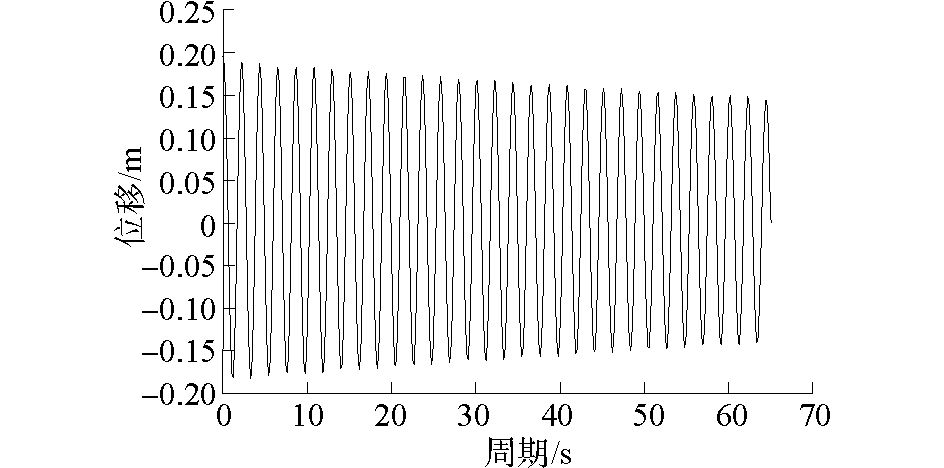
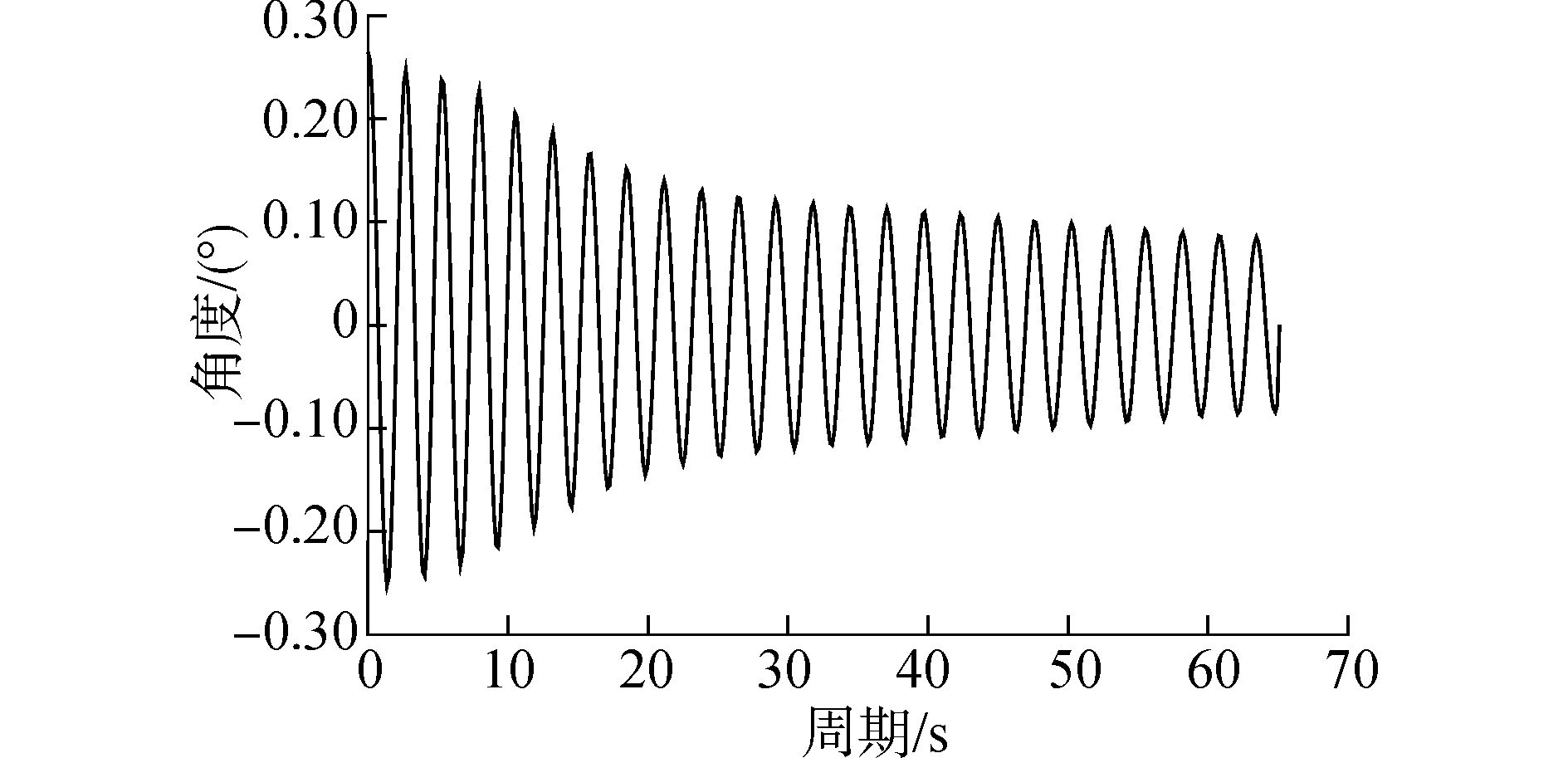
3 自由衰减模拟这里给出了模型纵荡、横荡、纵摇及艏摇4个自由度上的进行的自由衰减模拟,如图 7~10所示。通过后期数据处理,得到平台的运动的固有周期。
|
图 7 纵荡自由衰减 |
|
图 8 垂荡自由衰减 |
|
图 9 纵摇自由衰减 |
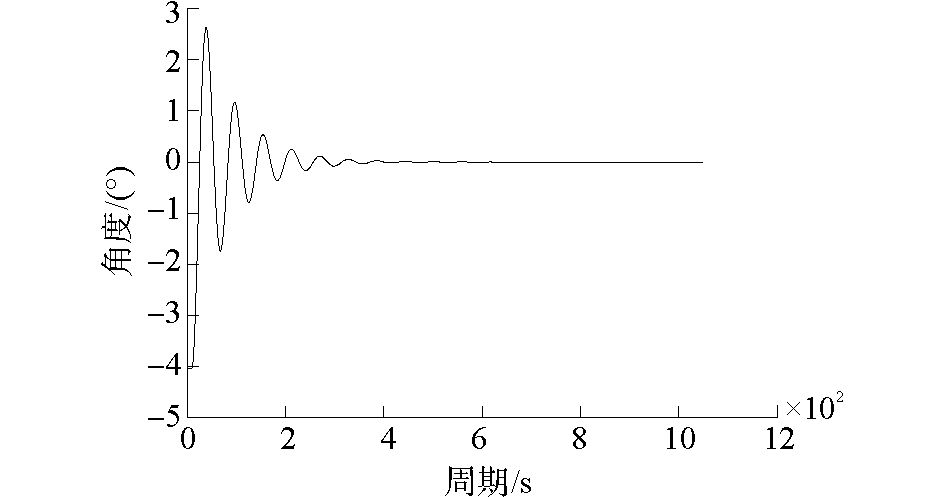
|
图 10 艏摇自由衰减 |
在随机海况下的二阶波浪力和频率ωi+ωj处振荡时,会与张力腿平台的垂荡、横摇纵摇产生共振。由于张力腿平台张力筋的刚度使张力腿平台的垂向运动(垂荡、横摇、纵摇)固有周期都相对较低,平台固有周期计算表达式为
| $ {T_i} = 2{\rm{\pi }}\sqrt {\frac{{L\left( {{M_{ii}} + {A_{ii}}} \right)}}{{EA}}} = 2{\rm{\pi }}\sqrt {\frac{{\left( {{M_{ii}} + {A_{ii}}} \right)}}{{{K_{ii}}}}} \left( {i = 1,2, \cdots 6} \right) $ |
式中:Kii是第i自由度上的系统刚度,Mii是i自由度上的结构质量/转动惯量,Aii是i自由度上的附加质量。结合前文求出的到的附加质量Aii及总刚度矩阵中的Kii,将结果与计算公式进行比较,如表 3所示。
|
|
表 3 软件模拟与公式计算对比表 |
从表 3中可以看出,模型进行自由衰减模拟后,纵荡、横荡和垂荡软件拟合结果和数值计算理论结果基本一致。
4 张力筋张力响应RAO本文采用时域分析方法计算规则波下所得的张力筋张力响应RAO。计算了在15个不同频率的规则波情况下,张力筋1、5两根张力筋张力响应。分别计算每种规则波(不同周期)情况下张力筋张力趋于稳定周期时的响应幅值,并通过单位化计算得到张力筋张力响应RAO。图 11、12分别为T1、T5两根张力筋张力响应的RAO。

|
图 11 T1张力筋张力响应RAOs |
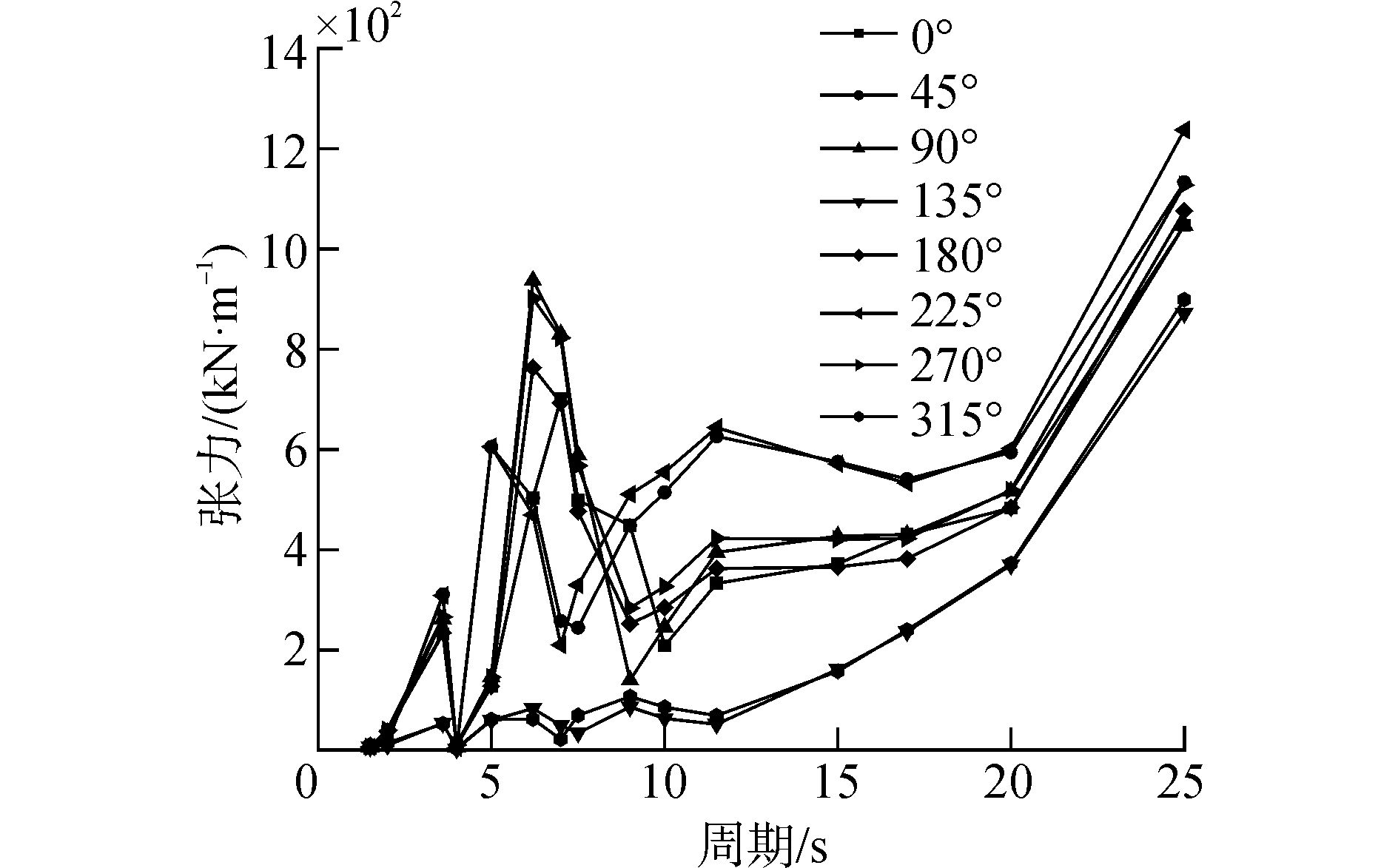
|
图 12 T5张力筋张力响应RAOs |
从图中可以看出,不同的来浪角度对不同的张力筋张力RAO有着不同的影响。张力筋张力的固有周期出现在6.5~7.5 s处,在90°和270°来浪时极致出现最大值。迎浪和背浪的张力筋RAO也有着不同的响应,T1的极值出现在270°来浪时,极值为934.5 kN/m;T5的极值出现在90°来浪时,极值为937.1 kN/m。
5 结论张力腿平台是深海油气开发中广泛应用的平台型式之一。在张力筋腱的有效约束下张力腿平台可以避开波浪能量集中的频率,使得平台在纵、横摇及垂荡性能上明显改善,大大提高了平台的适用范围、舒适度和安全性。文中通过对一座传统TLP张力筋腱进行研究,结果表明:
1) 筋腱及立管分段建模时,能更好地模拟实际工程中的TLP平台刚度,进行静水静力模拟测试,可以验证模型建模的准确性,为后续动力分析提供参考。
2) 提出一种模拟验证方法,通过筋腱及立管分段建模,求解平台线性刚度矩阵和附加质量系数矩阵,通过理论公式计算TLP运动的固有周期并与自由衰减模拟结果进行对比,视其结果拟合是否准确,可验证模型计算的准确性。
3) 提出在时域中计算张力筋张力响应RAO的方法,为后续TLP张力筋腱的相关研究提出一种可供参考的方法。
| [1] |
李军. 关于南海海洋平台选型及研究方向探讨[J]. 广东造船, 2010(1): 33-35. ( 0) 0)
|
| [2] |
ABOU-RAYAN A M, EL-GAMAL A R. Wave induced motion of a triangular tension leg platforms in deep waters[J]. Ocean systems engineering, 2013, 3(2): 149-165. DOI:10.12989/ose.2013.3.2.149 ( 0) 0)
|
| [3] |
任顺利, 陈建民, 梁艳霞. 张力腿刚度对平台运动响应影响分析[J]. 石油矿场机械, 2008, 37(5): 28-31. ( 0) 0)
|
| [4] |
SENJANOVIĆ I, TOMIĆ M, RUDAN S, et al. Investigation of nonlinear restoring stiffness in dynamic analysis of tension leg platforms[J]. Engineering structures, 2013, 56(6): 117-125. ( 0) 0)
|
| [5] |
SENJANOVIĆ I, TOMIĆ M, HADŽIĆN. Formulation of consistent nonlinear restoring stiffness for dynamic analysis of tension leg platform and its influence on response[J]. Marine structures, 2013, 30(1): 1-32. ( 0) 0)
|
| [6] |
SENJANOVIĆ I, HADŽIĆ N, TOMIĆ M. On the linear stiffness of tension leg platforms[EB/OL].[2016-12-20].https://www.researchgate.net/publication/265814615_On_the_linear_stiffness_of_tension_leg_platforms.
( 0) 0)
|
| [7] |
YANG C K, KIM M H. Transient effects of tendon disconnection of a TLP by hull-tendon-riser coupled dynamic analysis[J]. Ocean engineering, 2010, 37(8/9): 667-677. ( 0) 0)
|
| [8] |
EL-GAMAL A R, ESSA A, ISMAIL A. Effect of tethers tension force on the behavior of triangular tension leg platform[J]. American journal of civil engineering & architecture, 2014, 2(3): 107-114. ( 0) 0)
|
| [9] |
阎岩, 张崎, 黄一. 基于张力腿平台的顶张紧式立管碰撞分析[J]. 上海船舶运输科学研究所学报, 2012, 35(1): 1-6. ( 0) 0)
|
| [10] |
曾晓辉, 沈晓鹏, 刘洋, 等. 考虑多种非线性因素的张力腿平台动力响应[J]. 海洋工程, 2006, 24(2): 82-88. ( 0) 0)
|
| [11] |
杨慧. MOSES TLP在极端环境下的动力性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2015. http://d.g.wanfangdata.com.cn/Thesis_D750182.aspx
( 0) 0)
|
| [12] |
GU Jiayang, YANG Jianmin, LV Haining. Comprehensive study on tendon tension of TLP considering wind, wave and current[J]. Journal of ship mechanics, 2012, 16(9): 1041-1055. ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


