水翼双体船是结合了双体船和水翼船优点的一种复合型船舶,因具有良好的适航性和高速性而发展迅速,在军事与民用上都得到了广泛应用。水翼双体船在迎浪高速行驶时,水翼的升力作用可以降低航行兴波阻力和摩擦阻力,但同时船体相对于海平面的提升使得保持船体升沉/纵摇姿态的恢复力矩和力减小,使升沉/纵摇运动剧烈[1-2],因此针对水翼双体船升沉/纵摇运动控制的研究非常有必要。
三维的视景仿真相比传统的二维数字仿真,具有更加生动形象和画面直观的优点,能给人以身临其境的感受。以往在船舶运动控制方面使用视景仿真,一般都是事先在MATLAB中进行运动控制系统数字仿真,然后将仿真得到的数据导入视景仿真中,这样的方法中视景仿真只能起到“离线演示”的作用,而不能实现实时的在线交互式控制。文中搭建的水翼双体船升沉/纵摇鲁棒控制系统由视景仿真模块、算法模块和串口通信模块组成,算法模块中包含了离散的水翼双体船运动数学模型、海浪干扰模型、和鲁棒H2/H∞混合控制器的数学模型,本系统除了具有实时显示水翼双体船运动姿态变化曲线和数值的功能外,还能在线修改船体参数。
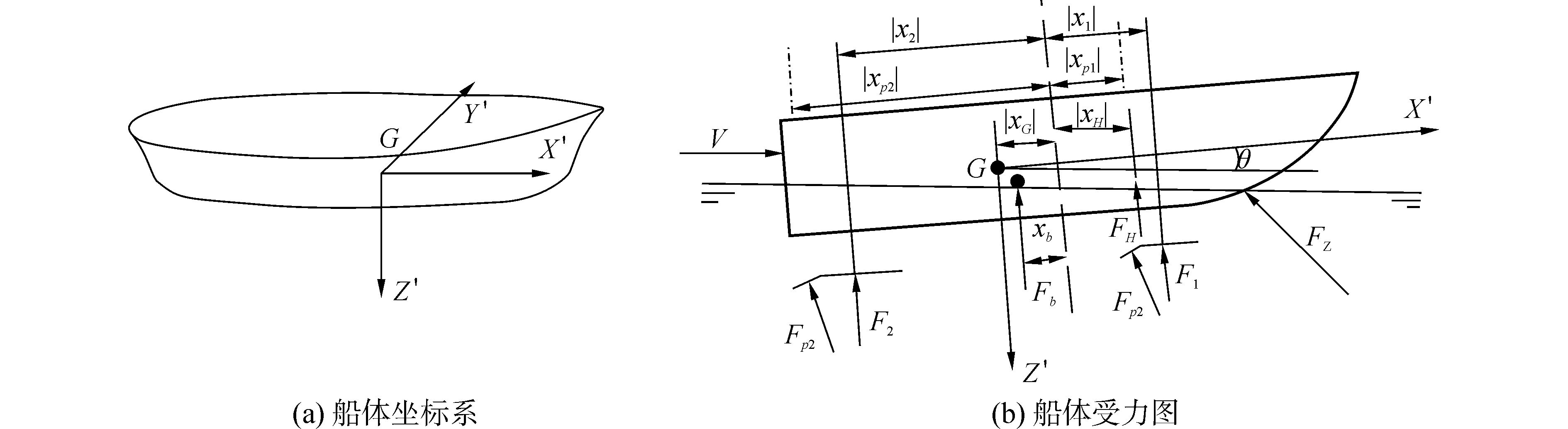
1 水翼双体船升沉/纵摇鲁棒H2/H∞控制 1.1 水翼双体船运动数学模型建立文中在建立水翼双体船运动数学模型时,参考的坐标系选用船体坐标系,如图 1(a)所示,在该坐标系下船体的受力图如图 1(b)所示。
|
图 1 水翼双体船运动数学模型 |
水翼双体船在随机海浪中航行时,其升沉/纵摇运动数学模型参考文献[2-5]如下,方程中各参量的量纲统一采用国际单位制:
| $ \begin{array}{l} \left( {m + \Delta m} \right)\left( {\ddot z + V\dot \theta } \right) = \sum\limits_{i = 1}^2 {\left( {{F_{fi}} + {F_{pi}}} \right) + } \\ 2{F_H}\cos \theta + {F_b}\cos \theta + \left( {m + \Delta m} \right)g\cos \theta + {F_z}\\ \left( {{I_{yy}} + \Delta {I_{yy}}} \right)\ddot \theta = - \sum\limits_{i = 1}^2 {\left( {{x_{fi}} + {x_G}} \right)\left( {{F_{fi}} + {F_{pi}}} \right) - } \\ 2\left( {{x_H} - {x_G}} \right){F_H}\cos \theta - \left( {{x_b} - {x_G}} \right){F_b}\cos \theta + {F_M} \end{array} $ |
式中:m为水翼双体船的质量,Δm为水翼双体船的附加质量,θ为纵摇角,z为升沉位移,V为沿x轴的前进速度,Iyy为水翼双体船相对于y轴的转动惯量,ΔIyy为相对于y轴的附加转动惯量,Ffi是水翼系统产生的力,Fpi为襟翼产生的力,FH是水翼双体船单个片体产生的升力,Fb是水翼双体船的浮力,Fz、FM分别为海浪产生的升沉干扰力和纵摇干扰力矩,g是重力加速度,|xi|、|xfi|、|xpi|、|xG|、|xH|、|xb|为水翼、襟翼、水翼双体船重心、水翼双体船的升力作用点和船体浮力作用点到船中的距离。力Fi、Fpi、FH和Fb的计算见参考文献[1]。
1.2 随机海浪模型建立常见的海浪是由风形成的不规则波,充分发展的海浪是一个动态平衡的随机过程,具有平稳的各态历经的性质。参考文献[1], 文中模拟的水翼双体船单个片体在z轴上的力和力矩分别为
| $ \begin{array}{*{20}{c}} {{Z_d} = - \rho g\sum\limits_{i = 1}^N {{E_i}k\left\{ {{A_i}\cos \left[ {\left( {{\omega _i} - kV\cos \chi } \right)t + {\varepsilon _i}} \right] + } \right.} }\\ {\left. {{B_i}\sin \left[ {\left( {{\omega _i} - kV\cos \chi } \right)t + {\varepsilon _i}} \right]} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{M_d} = - \rho g\sum\limits_{i = 1}^N {{E_i}k\left\{ {{C_i}\cos \left[ {\left( {{\omega _i} - kV\cos \chi } \right)t + {\varepsilon _i}} \right] + } \right.} }\\ {\left. {{D_i}\sin \left[ {\left( {{\omega _i} - kV\cos \chi } \right)t + {\varepsilon _i}} \right]} \right\}} \end{array} $ |
式中:
| $ {A_i} = \int_L {{F_i}\left( x \right)A\left( x \right)\cos \left( {kx\cos \chi } \right){\rm{d}}x} $ |
| $ {B_i} = \int_L {{F_i}\left( x \right)A\left( x \right)\sin \left( {kx\cos \chi } \right){\rm{d}}x} $ |
| $ {C_i} = \int_L {{F_i}\left( x \right)A\left( x \right)x\cos \left( {kx\cos \chi } \right){\rm{d}}x} $ |
| $ {D_i} = \int_L {{F_i}\left( x \right)A\left( x \right)x\sin \left( {kx\cos \chi } \right){\rm{d}}x} $ |
| $ {F_i}\left( x \right) = \frac{{\sin \left( {k\frac{{B\left( x \right)}}{2}\sin \chi } \right)}}{{k\frac{{B\left( x \right)}}{2}\sin \chi }}{{\rm{e}}^{ - kd\left( x \right)}} $ |
式中:
| $ {F_z} = 2{Z_d},{F_M} = 2{M_d} $ |
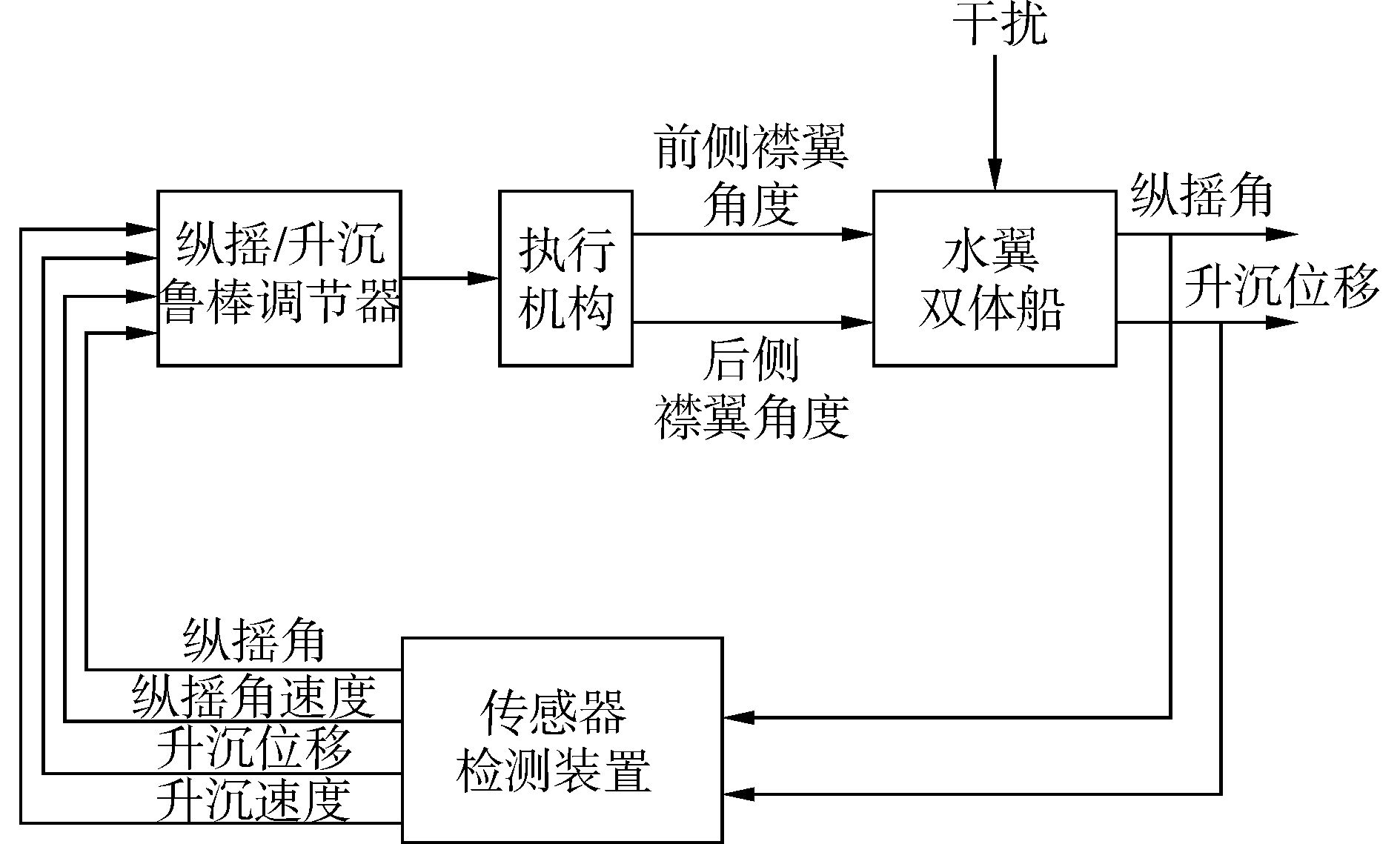
水翼双体船纵摇/升沉H2/H∞鲁棒控制结构框图如图 2所示。根据传感器检测装置得到实时的升沉位移、纵摇角、升沉速度及纵摇角速度4个状态量,鲁棒控制器就根据反馈回来的这4个变量计算得到减小纵摇/升沉运动需要的恢复力和力矩,然后设置前后襟翼的转动角度,使他们能够提供所需的力和力矩。
|
图 2 水翼双体船升沉/纵摇运动控制框图 |
设系统矩阵中含有参数摄动的离散系统为
| $ \begin{array}{*{20}{c}} {x\left( {k + 1} \right) = \left( {\mathit{\boldsymbol{A + }}\Delta \mathit{\boldsymbol{A}}} \right)x\left( k \right) + \left( {{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{ + }}\Delta {\mathit{\boldsymbol{B}}_1}} \right)u\left( k \right) + }\\ {{\mathit{\boldsymbol{B}}_2}\omega \left( k \right)} \end{array} $ |
| $ {z_\infty }\left( k \right) = {C_1}x\left( k \right) + {D_{11}}u\left( k \right) + {D_{12}}\omega \left( k \right) $ |
| $ {z_2}\left( k \right) = {C_2}x\left( k \right) + {D_{21}}u\left( k \right) + {D_{22}}\omega \left( k \right) $ |
| $ y\left( k \right) = \mathit{\boldsymbol{C}}x\left( k \right) + \mathit{\boldsymbol{D}}u\left( k \right) $ |
式中:x(k)为系统状态变量,u(k)为控制输入量,ω(k)为外界干扰,z∞为H∞控制性能的指标函数,z2为H2控制性能的指标函数,ΔA、ΔB1为反映参数摄动量的矩阵,且满足如下等式[8-10]
| $ \left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{A}}}&{\Delta {\mathit{\boldsymbol{B}}_1}} \end{array}} \right] = \mathit{\boldsymbol{HF}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{E}}_1}}&{{\mathit{\boldsymbol{E}}_2}} \end{array}} \right],{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{F}} \le \mathit{\boldsymbol{I}} $ |
式中:H、E1、E2是根据性能指标选取的常数矩阵。
为使不确定参数摄动在允许范围内,闭环系统都满足以下3个性能指标:
1) 闭环系统内部稳定。
2) 鲁棒H2性能指标:当干扰ω(t)为一个白噪声信号且具有单位谱密度,定义这样的一个性能指标,满足:
| $ \mathit{\Gamma }{{\kern 1pt} _2} = \left\| z \right\|_2^2 = \int_0^\infty {{\mathit{\boldsymbol{z}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{z}}\left( t \right){\rm{d}}t} \le {\gamma _2} $ |
3) 鲁棒H∞性能指标:当ω(t)为一个扰动信号且能量有界,从ω(t)到z∞(t)的闭环传递函数‖G‖∞2≤γ∞即
| $ \mathit{\Gamma }{{\kern 1pt} _\infty } = \int_0^\infty {\left( {\left\| {{z_\infty }} \right\|_2^2 - {\gamma _\infty }\left\| \omega \right\|_2^2} \right){\rm{d}}t} \le 0 $ |
基于上述指标设计鲁棒H2/H∞控制器, 利用Lyapunov稳定性定理进行设计,构造恰当的Lyapunov函数,使能同时满足以上3个性能指标,设计反馈控制规律u(t)=Kx(t),并采用以下3个定理完成鲁棒控制器的构造和推导。
定理1 对给定的对称矩阵
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{S}} < 0\\ {\mathit{\boldsymbol{S}}_{11}} < 0,{\mathit{\boldsymbol{S}}_{22}} - \mathit{\boldsymbol{SS}}_{12}^{\rm{T}}\mathit{\boldsymbol{S}}_{11}^{ - 1}{\mathit{\boldsymbol{S}}_{12}} < 0\\ {\mathit{\boldsymbol{S}}_{22}} < 0,{\mathit{\boldsymbol{S}}_{11}} - {\mathit{\boldsymbol{S}}_{12}}\mathit{\boldsymbol{S}}_{22}^{{\rm{ - 1}}}\mathit{\boldsymbol{S}}_{12}^{\rm{T}} < 0 \end{array} \right. $ |
定理2 定义变量x∈Rp,y∈Rq,存在这样的2个常数矩阵D和E,如果矩阵F满足FTF≤I,则有:
| $ 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{DFEy}} \le \varepsilon {\mathit{\boldsymbol{x}}^{\rm T}}\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{D}}^{\rm{T}}}\mathit{\boldsymbol{x + }}\frac{1}{\varepsilon }{\mathit{\boldsymbol{y}}^{\rm{T}}}{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{Ey}} $ |
成立,其中ε为任意正整数。
定理3 对于控制对象,存在一个鲁棒H2/H∞控制律的充分与必要条件,是存在常数γ>0,ε>0及一个对称正定矩阵R和任意合适维数的对称矩阵Q,使得下面的矩阵不等式
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{AR}} + {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{Q}} + {{\left( {\mathit{\boldsymbol{AR}} + {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{Q}}} \right)}^{\rm{T}}} + \varepsilon \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{H}}^{\rm{T}}}}&{{\mathit{\boldsymbol{B}}_2}}&{\mathit{\boldsymbol{RE}}_1^{\rm{T}} + {\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{E}}_2^{\rm{T}}}&{\mathit{\boldsymbol{RC}}_\infty ^{\rm{T}} + {\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{D}}_\infty ^{\rm{T}}}&{\mathit{\boldsymbol{RC}}_2^{\rm{T}} + {\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{D}}_2^{\rm{T}}}\\ * &{ - {\gamma ^2}}&0&0&0\\ * & * &{ - {\varepsilon ^{ - 1}}}&0&0\\ * & * & * &{ - \mathit{\boldsymbol{I}}}&0\\ * & * & * & * &{ - \mathit{\boldsymbol{I}}} \end{array}} \right] < 0 $ |
成立。则控制规律u(t)=QR-1x(t)是此系统的鲁棒控制器。
2 视景仿真系统设计与实现 2.1 三维模型建立水翼双体船三维模型建立是在MultiGen Creator中设计完成。前后水翼的三维模型图如图 3、4所示,图 5是经过上色与纹理映射后得到的最终的水翼双体船三维模型图。

|
图 3 前水翼 |
|
图 4 后水翼 |

|
图 5 水翼双体船最终效果图 |
利用LynX图形界面应用程序编辑器,进行水翼双体船纵摇/升沉运动的虚拟场景的模拟、特殊效果添加,将模型加载到场景中并驱动其运动起来,同时采用Vega的C语言应用程序接口和充足的库函数,极大地方便了后续程序代码的编写过程,在整个仿真系统的实现中起到了承上启下的作用[6]。图 6显示了在Vega中模拟加入了对象的海洋环境以及用通道显示的水翼模型。

|
图 6 Vega场景模拟 |
双体船升沉/纵摇运动控制交互式仿真就是采用了基于SDI(单文档)的MFC应用程序模板。在VC++6.0中建立基于Vega的MFC框架应用程序,能利用MFC自带的资源功能,使Vega应用程序的外观发生改变,最终得到更符合Windows操作系统使用习惯的程序界面,并且依仗MFC自身的优势,使得视景仿真功能的实现变得容易一些。
3 算法模块及通信端口设计 3.1 算法模块实现水翼双体船的运动数学模型相对比较复杂,海浪模型的建立也是一个工作量很大的过程,且VC++6.0中没有提供功能比较丰富的数学函数库,文中在算法模块手动设计数学模型中使用到的函数。
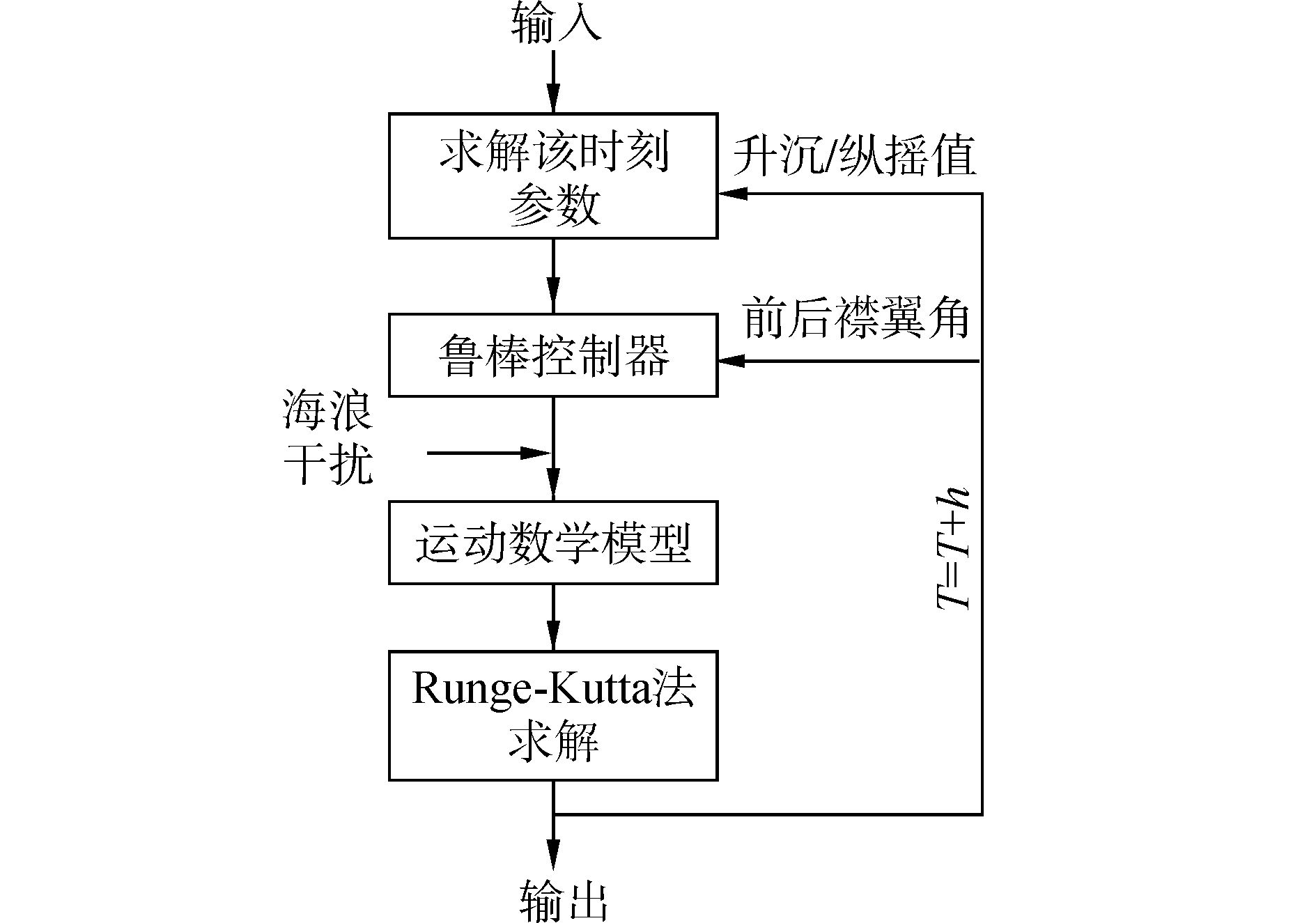
文中搭建的离散的运动控制数学模型,通过在MFC程序中设置一个定时器来实现,选取合适的时间步长,数学模型中的各个参数都是随时间变化的函数。水翼双体船的升沉/纵摇运动数学模型可以看作一个二元二阶微分方程组。通常在计算机中求解微分方程采用的是四阶经典Runge-Kutta法,文中的微分方程相对比较复杂,需要先将二阶的微分方程进行降阶处理,再采用经典的Runge-Kutta法来解算微分方程组。算法模块流程如图 7所示。
|
图 7 算法模块流程 |
基于RS232的串行通信方式所需线路少、成本低、操作简单,是PC机与单片机通信中较为常用的一种[7]。文中的物理通信采用的便是这种方式。算法模块中的输入输出就是利用串口通信技术使系统与上位机和下位机进行的实时数据交互。VC++6.0的开发环境专门针对串口通信提供的MSComm控件使用起来也很简便。在程序中加载了该控件后,再添加如下关键代码:
m_MSComm.Create(NULL, 0, CRect(0, 0, 0, 0), this, IDC_MSCOMM1);
m_MSComm.SetCommPort(3);
m_MSComm.SetInBufferSize(1024);m_MSComm.SetOutBufferSize(1024);m_MSComm.SetInputLen(0);m_MSComm.SetInputMode(1);
m_MSComm.SetRThreshold(1);m_MSComm.SetSettings(“9600, n, 8, 1”)。
4 仿真结果运行文中搭建的视景仿真程序,初始界面如图 8所示,图 9为截取的一个三维仿真画面。

|
图 8 水翼双体船视景仿真 |

|
图 9 三维仿真画面 |
文中采用的水翼双体船的主要参数参考文献[7], 仿真时船速设置为30 kn,海浪的有义波高设定为2.5 m,双体船的遭遇角是90°,计算得到参数矩阵为
| $ {\mathit{\boldsymbol{E}}_1} = {\left[ {\begin{array}{*{20}{c}} {0.07}&{0.01}&0&0&0&0&0&0&0&0&0&0\\ 0&0&{ - 32.20}&{ - 1.30}&0&0&0&0&0&0&0&0\\ 0&0&0&0&{ - 1.92}&{ - 0.07}&0&0&0&0&0&0\\ 0&0&0&0&0&0&{ - 4.78}&{ - 3.60}&0&0&0&0 \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{E}}_2} = {\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&0&{ - 3.94}&{0.51}&0&0\\ 0&0&0&0&0&0&0&0&0&0&{3.86}&{0.79} \end{array}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{A = }}\left[ {\begin{array}{*{20}{c}} 0&1&0&0\\ { - 0.1976}&{ - 7.7110}&{ - 185.5842}&{ - 80.0012}\\ 0&0&0&1\\ {0.01518}&{ - 0.2794}&{ - 6.8992}&{ - 4.6867} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0\\ { - 14.4925}&{ - 14.1929}\\ 0&0\\ {1.8577}&{ - 2.9225} \end{array}} \right] $ |
鲁棒H2/H∞控制器为
| $ {\mathit{\boldsymbol{K}}_{40}} = \left[ {\begin{array}{*{20}{c}} {0.7863}&{0.4925}&{ - 13.9359}&{ - 6.0893}\\ { - 0.2471}&{ - 0.1578}&{4.8166}&{2.2096} \end{array}} \right] $ |
设初始时刻水翼双体船的运动姿态值为
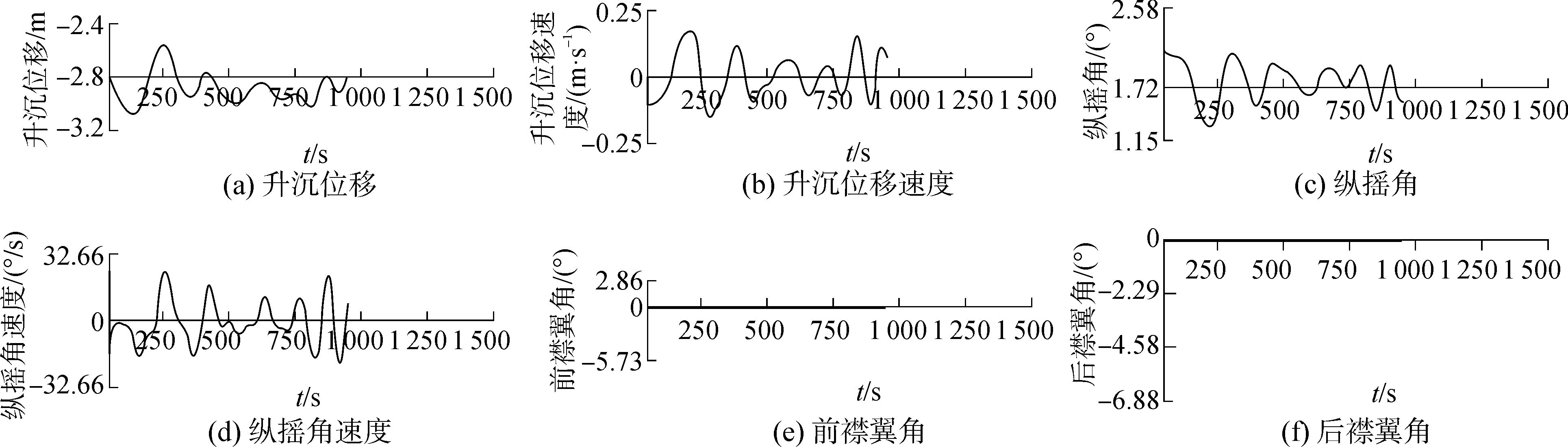
|
图 10 无控制规律作用下运动曲线 |
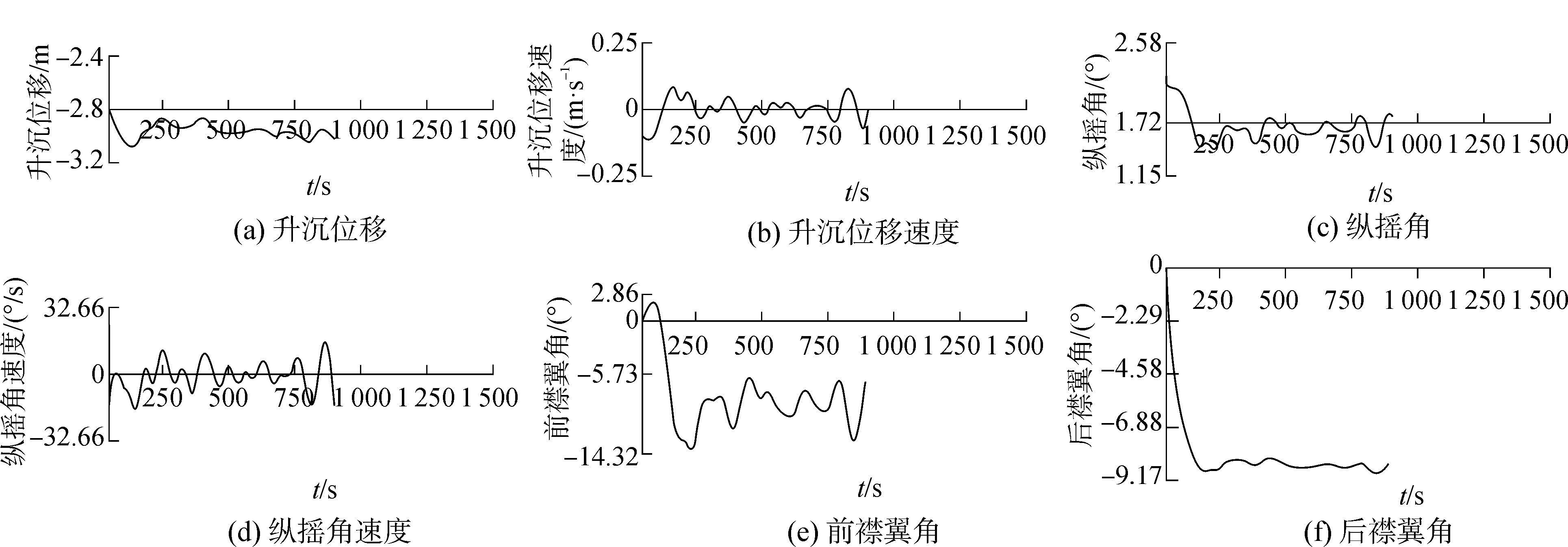
|
图 11 鲁棒控制作用下运动曲线 |
表 1给出了控制器作用前后仿真结果统计,并进行了数值分析。
|
|
表 1 鲁棒控制器作用前后仿真结果统计 |
从表 1中可以看出,在鲁棒控制器的作用下,升沉位移值跟纵摇角都降低了,升沉位移方差、纵摇角方差、升沉位移速度方差、纵摇角速度方差也大幅度降低,表明水翼双体船的升沉/纵摇运动性能有所提高。同时视景仿真系统具有沉浸感高、交互性好。
5 结论1) 文中在Creator、Vega和VC++6.0的开发环境中,搭建了一套离散的水翼双体船的运动姿态控制视景仿真系统,相比连续的控制系统更加贴合实际情况。
2) 采用鲁棒H2/H∞混合控制的方法控制附加襟翼,可以有效地稳定控制水翼双体船在随机海浪作用下的升沉/纵摇运动。
3) 采用三维视景仿真与二位数值曲线仿真相结合的方式能更加生动直观地展现船舶运动的过程,以及在控制规律作用下的效果,采用串口通信技术完成了实时的物理信息交互,而且便于下一步嵌入式控制器的设计与实现。
| [1] |
刘胜, 苏旭, 王宇超, 等. 水翼双体船纵摇/升沉鲁棒H2/H∞控制研究[C]//第三十二届中国控制会议. 西安, 中国, 2013.
( 0) 0)
|
| [2] |
王宇超, 刘胜, 苏旭. 水翼双体船纵向运动鲁棒增益调度控制研究[C]//第三十三届中国控制会议. 南京, 中国, 2014.
( 0) 0)
|
| [3] |
张显库, 关巍. 大惯性船舶航向保持的改进简捷鲁棒控制[J]. 中国航海, 2010, 33(3): 1-5. ( 0) 0)
|
| [4] |
任俊生. 高速水翼船非线性运动建模及控制的研究[D]. 大连: 大连海事大学, 2005: 19-38. http://cdmd.cnki.com.cn/Article/CDMD-10151-2005129711.htm
( 0) 0)
|
| [5] |
贾新乐, 杨盐生. 船舶运动数学模型——机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999: 306-336.
( 0) 0)
|
| [6] |
黄会营, 段晓明. 船舶运动视景仿真系统设计与实现[J]. 计算机仿真, 2012, 29(1): 369-373. ( 0) 0)
|
| [7] |
邓飙, 刘连伟. 基于Visual Studio的虚拟现实与半实物接口设计[J]. 兵器装备工程学报, 2015, 36(1): 114-117. ( 0) 0)
|
| [8] |
张显库, 吕晓菲, 郭晨, 等. 船舶航向保持的鲁棒神经网络控制[J]. 船舶力学, 2006(5): 54-58. ( 0) 0)
|
| [9] |
刘胜, 李高云, 方亮, 等. 船舶航向横摇/鲁棒控制研究[J]. 电机与控制学报, 2009, 13(1): 129-134. ( 0) 0)
|
| [10] |
ZhOU K, GLOVER K, BODENHEIMER B, et al. Mixed H2 and H∞ performance objectives:robust performance analysis[J]. IEEE transactions on automatic control, 1994, 39(8): 1564-1574. DOI:10.1109/9.310030 ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


