2. 中国电子科技集团公司 第五十四研究所, 河北 石家庄 050081
2. China Electronics Technology Group Corporation No. 54 th Research Institute, Shijiazhuang 050081, China
利用世界坐标系下空间3D点的坐标和图像坐标系下对应2D点坐标之间的几何关系求解相机位姿的问题称为透视n点投影(perspective-n-points, PnP)问题[1]。PnP问题是计算机视觉研究领域的经典问题之一,在许多领域都具有重要的应用价值,例如:移动机器人导航系统、实现机器人的实时定位与路径规划[2]、虚拟现实技术、实时的三维环境建模与渲染[3]等。
高精度快速位姿估计算法(efficient perspective n point, EPnP)由Lepetit和Moreno等[4]于2009年提出,其首次提出了基于虚拟控制点的求解方法,具有精度高、时间复杂度低等优点。杨森和吴福朝等[5]在EPnP算法基础上,提出了加权EPnP算法,相对于EPnP算法进一步提高了位姿的估计精度;Ferraz和Binefa于2014年提出基于EPnP的改进算法EPPnP[6]、CEPPnP[7]等。徐迟等[8]于2011年提出RPnP算法,该方法的创新性性表现在将对应点进行划分,然后利用三角约束构建代价函数,是一种非迭代的透视n点问题求解算法。针对PnP问题中存在的位姿计算结果精度不高、稳定性差、易受噪声干扰等问题,提出一种改进的PnP问题求解算法。
1 PnP问题PnP问题又称给定控制点的位姿估计问题,由Fishler和Bolles等[9]于1981年提出。PnP问题根据空间参考点数目n的大小,分成3≤n≤5和n≥6两类。第1类PnP问题在求解相机位置和姿态的过程中利用的参考点数较少,因此当图像受到噪声影响时,定位精度和角度较差[10]。第2类PnP问题,在求解相机位置和姿态的过程中利用的参考点数较多,因此这种PnP问题算法的研究主要集中在采用何种方式求解超定方程,如何在提高算法鲁棒性与抗噪能力的同时降低算法的运行时间。本文主要针对第2类PnP问题求解算法进行研究、分析和改进。
PnP问题求解方法大致分为两类:直接法和迭代法。直接法的优点是效率高,缺点是在噪声情况下不稳定。迭代法的优点是精度高、抗噪性较强,缺点是计算复杂、运行时间长、实时性差,能否收敛到最优点易受到初始值的影响[11]。
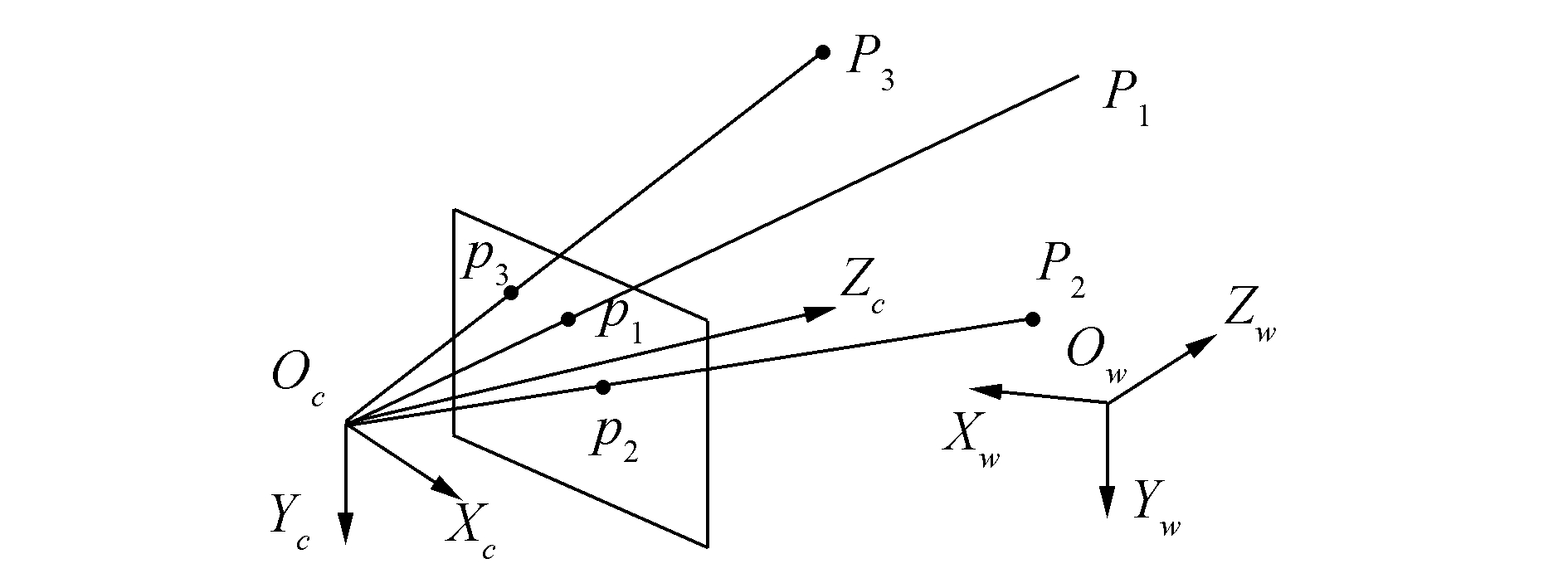
空间三维参考点Pi(i=1, 2, …, n)和对应投影点在图像坐标系下的位置pi(i=1, 2, …, n)之间的映射关系如图 1所示。
|
Download:
|
| 图 1 空间对应3D/2D点成像关系 | |
图 1中,XwYwZwOw表示世界坐标系,XcYcZcOc表示图像坐标系。
2 改进的PnP问题求解算法由经过标定的相机内部参数已知,世界坐标系下的空间3D参考点Pi(i=1, 2,…, n)对应参考点在相机坐标系下的2D点vi(i=1, 2,…, n),通过它们之间的对应关系得到两个坐标系之间的转换等式
| $ {\lambda _i}{\mathit{\boldsymbol{v}}_i} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_i} + \mathit{\boldsymbol{t}} $ |
式中:λi为vi点的深度,vi满足||vi||=1,R为旋转矩阵,t为平移向量。
世界坐标系下的空间3D点Pi在图像坐标系下的投影点为pi'=[x' y']T,对于投影点的位置的测量包含一定的不确定性,因此采用二维协方差矩阵来进行描述:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\mathit{\boldsymbol{p}}'\mathit{\boldsymbol{p}}'}} = \left[ {\begin{array}{*{20}{c}} {\sigma _{x'}^2}&{{\sigma _{x'y'}}}\\ {{\sigma _{y'x'}}}&{\sigma _{y'}^2} \end{array}} \right] $ |
通过坐标系变换矩阵A将图像坐标系下的点转换到相机坐标系下:
| $ \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{Ap}}' = \left[ \begin{array}{l} x\\ y\\ 1 \end{array} \right], {\mathit{\boldsymbol{J}}_\mathit{\boldsymbol{A}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\mathit{\boldsymbol{A}}_{x'}}}}{{\partial x'}}}&{\frac{{\partial {\mathit{\boldsymbol{A}}_{x'}}}}{{\partial x'}}}\\ {\frac{{\partial {\mathit{\boldsymbol{A}}_{y'}}}}{{\partial x'}}}&{\frac{{\partial {\mathit{\boldsymbol{A}}_{y'}}}}{{\partial y'}}}\\ 0&0 \end{array}} \right] $ |
式中JA为坐标系变换A的雅克比矩阵,所以根据式(1)计算相机坐标系下的点p的不确定性[12]。
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\mathit{\boldsymbol{pp}}}} = {\mathit{\boldsymbol{J}}_\mathit{\boldsymbol{A}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\mathit{\boldsymbol{p}}'\mathit{\boldsymbol{p}}'}}\mathit{\boldsymbol{J}}_\mathit{\boldsymbol{A}}^{\rm{T}} = \left[ {\begin{array}{*{20}{c}} {\sigma _x^2}&{{\sigma _{xy}}}&0\\ {{\sigma _{yx}}}&{\sigma _y^2}&0\\ 0&0&0 \end{array}} \right] $ | (1) |
式中协方差矩阵的秩为2,为奇异矩阵。将点p的坐标归一化得向量v。
| $ \begin{array}{l} \mathit{\boldsymbol{v}} = \left[ \begin{array}{l} {\mathit{\boldsymbol{v}}_x}\\ {\mathit{\boldsymbol{v}}_y}\\ {\mathit{\boldsymbol{v}}_z} \end{array} \right] = \frac{\mathit{\boldsymbol{p}}}{{||\mathit{\boldsymbol{p}}||}}, \\ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\mathit{\boldsymbol{vv}}}} = \left[ {\begin{array}{*{20}{c}} {\sigma _{{v_x}}^2}&{{\sigma _{{v_{xy}}}}}&{{\sigma _{{v_{xz}}}}}\\ {{\sigma _{{v_{yx}}}}}&{\sigma _{{v_y}}^2}&{{\sigma _{{v_{yz}}}}}\\ {{\sigma _{{v_{zx}}}}}&{{\sigma _{{v_{zy}}}}}&{\sigma _{{v_z}}^2} \end{array}} \right] \end{array} $ |
式中协方差矩阵由式(2)得出:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\mathit{\boldsymbol{vv}}}} = \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\mathit{\boldsymbol{pp}}}}{\mathit{\boldsymbol{J}}^{\rm{T}}}, \mathit{\boldsymbol{J}} = \frac{1}{{||\mathit{\boldsymbol{v||}}}}({\mathit{\boldsymbol{I}}_3} - \mathit{\boldsymbol{v}}{\mathit{\boldsymbol{v}}^{\rm{T}}}) $ | (2) |
由于协方差矩阵中各分量之间相关,不能采用最大似然求解法求解,因此引入零空间来表示向量v:
| $ {J_{{\mathit{\boldsymbol{v}}_r}}}\left( \mathit{\boldsymbol{v}} \right) = f({\mathit{\boldsymbol{v}}^{\rm{T}}}) = \left[ {r\;s} \right] = \left[ {\begin{array}{*{20}{c}} {{r_1}}&{{s_1}}\\ {{r_2}}&{{s_2}}\\ {{r_3}}&{{s_3}} \end{array}} \right] $ |
式中:函数f(·)为奇异值分解函数,Jvr(v)为向量v变换到向量vr的雅克比矩阵。
| $ {\mathit{\boldsymbol{v}}_r} = \left[ \begin{array}{l} {d_r}\\ {d_s} \end{array} \right] = \mathit{\boldsymbol{J}}_{{\mathit{\boldsymbol{v}}_r}}^{\rm{T}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} = 0 $ |
不确定性由向量v到向量vr的转换表示为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{r}}}{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{r}}}}} = \mathit{\boldsymbol{J}}_{{v_\mathit{\boldsymbol{r}}}}^{\rm{T}}\left( \mathit{\boldsymbol{v}} \right){\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\mathit{\boldsymbol{vv}}}}{J_{{\mathit{\boldsymbol{v}}_r}}}\left( \mathit{\boldsymbol{v}} \right) = \left[ {\begin{array}{*{20}{c}} {\sigma _{{v_{{r_x}}}}^2}&{{\sigma _{{v_{{r_{xy}}}}}}}\\ {{\sigma _{{v_{{r_{xy}}}}}}}&{\sigma _{{v_{{r_y}}}}^2} \end{array}} \right] $ |
通过式(3)得到相机的位姿:
| $ \left[ \begin{array}{l} {d_r}\\ {d_s} \end{array} \right] = \left[ \begin{array}{l} {\mathit{\boldsymbol{r}}^{\rm{T}}}\\ {\mathit{\boldsymbol{s}}^{\rm{T}}} \end{array} \right]\lambda _i^{ - 1}\left( {\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_i} + \mathit{\boldsymbol{t}}} \right) = 0 $ | (3) |
式中Pi=[px py pz]T,将式(3)展开得
| $ \begin{array}{l} 0 = {r_1}\left( {{{\hat r}_{11}}{p_x} + {{\hat r}_{12}}{p_y} + {{\hat r}_{13}}{p_z} + {t_1}} \right) + {{\hat r}_2}({{\hat r}_{21}}{p_x} + {{\hat r}_{22}}{p_y} \cdots + \\ \;\;\;\;\;\;\;\;\;{{\hat r}_{23}}{p_z} + {t_2}) + {{\hat r}_3}({{\hat r}_{31}}{p_x} + {{\hat r}_{32}}{p_y} + {{\hat r}_{33}}{p_z} + {t_3})\\ 0 = {s_1}({{\hat r}_{11}}{p_x} + {{\hat r}_{12}}{p_y} + {{\hat r}_{13}}{p_z} + {t_1}) + {s_2}({{\hat r}_{21}}{p_x} + {{\hat r}_{22}}{p_y} \cdots + \\ \;\;\;\;\;\;\;\;\;{{\hat r}_{23}}{p_z} + {t_2}) + {s_3}({{\hat r}_{31}}{p_x} + {{\hat r}_{32}}{p_y} + {{\hat r}_{33}}{p_z} + {t_3}) \end{array} $ | (4) |
将式(4)用齐次线性方程组表示为
| $ \mathit{\boldsymbol{Bu}} = 0 $ | (5) |
式中B为齐次方程组系数,u=
| $ \begin{array}{l} \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\Sigma }_{v_r^1v_r^1}^{ - 1}}& \cdots &0\\ \vdots&\vdots&\vdots \\ 0& \cdots &{\mathit{\Sigma }_{v_r^iv_r^i}^{ - 1}} \end{array}} \right]\\ {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{CBu}} = \mathit{\boldsymbol{Nu}} = 0 \end{array} $ |
式中u满足约束条件||u||=1。对系数矩阵N进行奇异值分解:
| $ \mathit{\boldsymbol{N}} = \mathit{\boldsymbol{UD}}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ |
式中旋转矩阵
| $ \begin{array}{l} \mathit{\boldsymbol{\hat R}} = \left[ {\begin{array}{*{20}{c}} {{{\hat r}_{11}}}&{{{\hat r}_{12}}}&{{{\hat r}_{13}}}\\ {{{\hat r}_{21}}}&{{{\hat r}_{22}}}&{{{\hat r}_{23}}}\\ {{{\hat r}_{31}}}&{{{\hat r}_{32}}}&{{{\hat r}_{33}}} \end{array}} \right]\\ \mathit{\boldsymbol{\hat t}} = \left[ {{{\hat t}_1}\;\;{{\hat t}_2}\;\;{{\hat t}_3}} \right] \end{array} $ |
式中平移向量
| $ \mathit{\boldsymbol{t}} = \underline {\sqrt[3]{{||{{\hat r}_1}||||{{\hat r}_2}||||{{\hat r}_3}||}}} $ |
旋转矩阵通过奇异值分解得到:
| $ \begin{array}{l} \mathit{\boldsymbol{\hat R}} = {\mathit{\boldsymbol{U}}_R}{\mathit{\boldsymbol{D}}_R}{\mathit{\boldsymbol{V}}_R}^{\rm{T}}\\ \;\mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{U}}_R}{\mathit{\boldsymbol{V}}_R}^{\rm{T}} \end{array} $ |
然后将旋转矩阵R和平移向量t作为初始值,采用高斯-牛顿法迭代寻找最优解。
3 实验结果与分析实验包含模拟数据实验和真实场景实验2个部分。实验平台为Inter Core i5-4460 CPU,主频为3.20 GHz,内存大小为8 GB;软件平台为MATLAB R2015b。
3.1 模拟数据实验及结果分析设定虚拟相机的分辨率为640像素×480像素,焦距800像素,相机光心坐标为[u0, v0]=[0, 0],空间参考点在相机坐标系中按照均匀分布规则生成,分布范围为[-2, 2]×[-2, 2]×[4, 8]的三维空间。为验证本文算法性能,采用RPnP算法、LHM算法[12]、DLS算法[13]、EPnP算法和CEPPnP算法进行对比分析。
旋转角度平均误差、平移向量平均误差和平均运行时间计算如式(6),分别为
| $ \begin{array}{l} {E_R} = {\frac{{\sum\limits_{i = 1}^N||f({{\mathit{\boldsymbol{\bar R}}}_i}) - f({\mathit{\boldsymbol{R}}_i})||}}{N}} \\ {E_t} = \frac{{\sum\limits_{i = 1}^N {||{\mathit{\boldsymbol{t}}_i} - {{\mathit{\boldsymbol{\bar t}}}_i}||} }}{{\sum\limits_{i = 1}^N {\mathit{\boldsymbol{||}}{\mathit{\boldsymbol{t}}_i}||} }} \times 100\% \\ \;\;\;\;S = \frac{{\sum\limits_{i = 1}^N {{s_i}} }}{N} \end{array} $ | (6) |
式中:N为实验次数、Ri为旋转矩阵、ti为平移向量、ER为旋转角度平均误差、Et为平移向量平均误差比例、S为算法平均运行时间、f(·)为旋转矩阵转换为旋转角度的变换函数。
1) 测试在不同对应点数目条件下,各个算法的位姿精度和运行时间。对应点n数目的变化范围为[0, 150],变化步长为10,每个对应点数目进行200次实验,实验结果如图 2所示。

|
Download:
|
| 图 2 对应点n数目与旋转角度、平移向量平均误差和算法时间复杂度之间的关系 | |
实验结果表明:a)在对应点数目n从10增加到150的过程中,本文算法求解的旋转角度平均误差和平移向量平均误差小于其他对比算法。b)本文算法时间复杂度低于LHM和DLS算法,高于RPnP、EPnP和CEPPnP算法,计算时间随对应点数增加而增大。
2) 测试在不同噪声强度条件下,各个算法的位姿计算精度。测试实验首先设定对应点n数目固定不变,然后向图像中的对应点添加均值为0,标准差为σ的高斯噪声,其中σ的范围为[0, 20],步长为1。对每级噪声进行200次实验,实验结果如图 3所示。

|
Download:
|
| 图 3 高斯噪声强度与旋转角度、平移向量平均误差的关系 | |
实验结果表明:a)在噪声强度从1增加到20的过程中,本文算法求解的旋转角度平均误差和平移向量平均误差小于其他对比算法。b) RPnP、LHM、DLS和EPnP算法求解的旋转角度平均误差和平移向量平均误差随着噪声增加而增大,而本文算法和CEPPnP算法结果没有随受噪声增加而显著增大,表明算法的稳定性高、抗噪能力强。
3.2 真实场景实验及结果分析实验环境:实验室;实验相机:Isight摄像头;测量工具:卷尺;实验对比算法:RPnP算法、EPnP算法和CEPPnP算法。实验步骤如下:首先在实验室中选择1点作为坐标系原点,建立世界坐标系;然后选取不同的4个场景,分别在室内的不同位置和角度采集图像,每个场景拍摄10幅,共计40幅,图像尺寸为320像素×240像素。其中对图像中的空间参考点进行标注,即参考点的世界坐标已知,拍摄时的相机位置采用卷尺进行测量。场景图像如图 4。

|
Download:
|
| 图 4 各场景采集图像 | |
|
Download:
|
| 图 5 平均误差 | |
|
Download:
|
| 图 6 平均协方差 | |
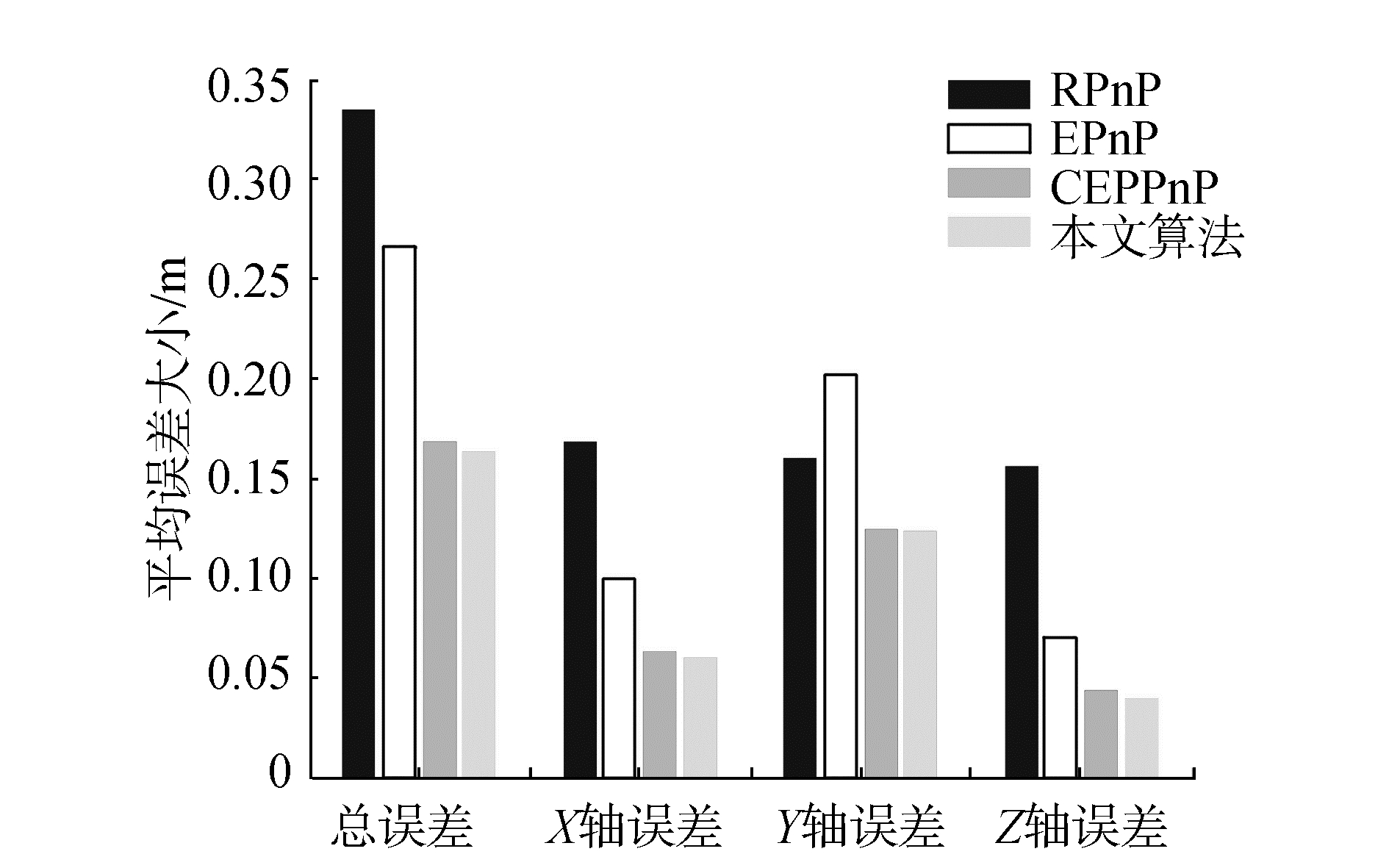
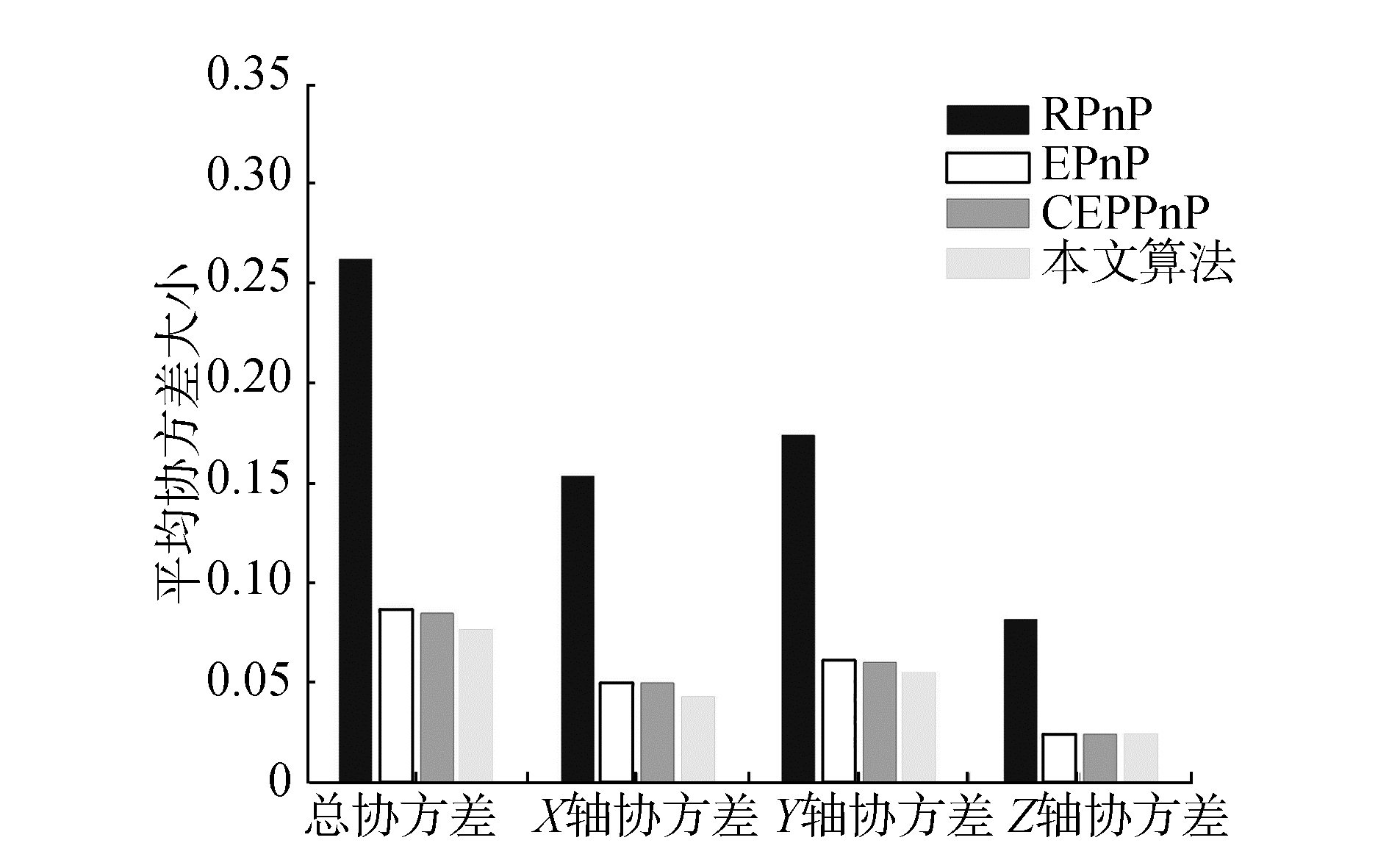
由图 5、6可得,RPnP、EPnP、CEPnP和本文算法平均定位误差分别为0.34、0.27、0.17、0.16 m;平均协方差分别为0.265、0.09、0.085和0.075,Y轴方向平均误差最大,Z轴方向平均误差最小。Y轴方向协方差最大,Z轴方向协方差最小。实验结果表明本文算法定位精度和稳定性高于其他对比算法。
4 结论1) 本文针对目前PnP算法中存在的位姿解算结果稳定性不高,容易受噪声干扰等问题,经过对多种PnP问题求解算法的分析,提出一种结合参考点不确定性的PnP问题求解算法。2)实验结果表明本文提出的算法旋转角度和平移误差均较小,且抗噪声能力强,鲁棒性好。该算法的缺点为算法的时间复杂度相对较高,接下来可以考虑采用GPU和多线程的处理方式,降低算法运行时间,以满足实际应用需求。
| [1] |
席志红, 李爽, 甘兴利. PnP算法在室内定位中的应用[J]. 无线电工程, 2017, 47(10): 39-44. ( 0) 0)
|
| [2] |
赵霞, 袁家政, 刘宏哲. 基于视觉的目标定位技术的研究进展[J]. 计算机科学, 2016, 43(6): 10-16, 43. ( 0) 0)
|
| [3] |
MVLLER M, RASSWEILER M C, KLEIN J, et al. Mobile augmented reality for computer-assisted percutaneous nephrolithotomy[J]. International journal of computer assisted radiology and surgery, 2013, 8(4): 663-675. DOI:10.1007/s11548-013-0828-4 ( 0) 0)
|
| [4] |
LEPETIT V, MORENO-NOGUER F, FUA P. EPnP:an accurate O(n) solution to the PnP problem[J]. International journal of computer vision, 2009, 81(2): 155-166. DOI:10.1007/s11263-008-0152-6 ( 0) 0)
|
| [5] |
YANG Sen, WU Fuchao. Weighted linear methods for camera pose estimation[J]. Journal of software, 2011, 22(10): 2476-2487. DOI:10.3724/SP.J.1001.2011.03916 ( 0) 0)
|
| [6] |
FÖRSTNER W. Minimal representations for uncertainty and estimation in projective spaces[C]//Proceedings of the 10th Asian Conference on Computer Vision. Queenstown, New Zealand, 2010: 619-632. http://dl.acm.org/citation.cfm?id=1966041
( 0) 0)
|
| [7] |
FERRAZ L, BINEFA X, MORENO-NOGUER F. Very fast solution to the PnP problem with algebraic outlier rejection[C]//IEEE Conference on Computer Vision and Pattern Recognition, Columbus, USA, 2014: 501-508. http://doi.ieeecomputersociety.org/10.1109/CVPR.2014.71
( 0) 0)
|
| [8] |
LI Shiqi, XU Chi, XIE Ming. A robust O(n) solution to the perspective-n-point problem[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(7): 1444-1450. DOI:10.1109/TPAMI.2012.41 ( 0) 0)
|
| [9] |
李书杰, 刘晓平. 摄像机位姿的高精度快速求解[J]. 中国图象图形学报, 2014, 19(1): 20-27. ( 0) 0)
|
| [10] |
TRIGGS B. Camera pose and calibration from 4 or 5 known 3D points[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision. Kerkyra, Greece, 1999: 278-284. http://doi.ieeecomputersociety.org/10.1109/ICCV.1999.791231
( 0) 0)
|
| [11] |
WU Yihong, HU Zhanyi. PnP problem revisited[J]. Journal of mathematical imaging and vision, 2006, 24(1): 131-141. DOI:10.1007/s10851-005-3617-z ( 0) 0)
|
| [12] |
LU C P, HAGER G D, MJOLSNESS E. Fast and globally convergent pose estimation from video images[J]. IEEE transactions on pattern analysis and machine intelligence, 2000, 22(6): 610-622. DOI:10.1109/34.862199 ( 0) 0)
|
| [13] |
HESCH J A, ROUMELIOTIS S I. A direct least-squares (DLS) method for PnP[C]//IEEE International Conference on Computer Vision. Barcelona, Spain, 2011: 383-390. http://doi.ieeecomputersociety.org/10.1109/ICCV.2011.6126266
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


