信号的调制类型识别在软件无线电、电子对抗、信号干扰方面有着广泛的应用[1]。雷达信号调制类型识别的主要任务是在完成雷达信号的预处理后,针对接收机接收到的感兴趣信号的观测数据,提取出相应的调制类型特征,并根据某种规则判定出该信号的调制类型,为后续的信息解调或威胁评估提供必要的信息,在机场安防及空中交通管制等任务中具有重要意义。
近年来,信号调制类型识别的研究在信号的分类特征提取以及分类器构造与算法方面均取得大量研究成果[2]。其中,在分类特征提取方面,循环谱具有良好的周期平稳性[3]和抗干扰性,可以在较低信噪比下实现信号的调制类型识别。在分类器构造方面,支持向量机具有结构简单、全局最优、推广能力强、学习和预测时间短等优点[4-5]。采用循环谱和支持向量机相结合的方法对信号的调制类型进行识别在低信噪比下具有较高的识别率[6], 但采用完整的循环谱存在计算量大的缺点。
本文对信号的循环谱采用距离判别的方法提取分类特征,并采用支持向量机对雷达信号的调制类型进行识别。仿真结果表明,利用基于距离判别的循环谱,减小了计算量,且提高了雷达信号调制类型的识别率。
1 循环谱理论设x(t)是循环平稳信号,则其均值和自相关函数为以T0为周期的周期信号。
| $ \begin{array}{l} \;m\left( t \right) = m(t + {T_0}){\rm{ }}\\ {R_x}\left( {t;\tau } \right) = {R_x}\left( {t + {T_0};\tau } \right) \end{array} $ | (1) |
式中自相关函数为
| $ {R_x}\left( {t;\tau } \right) = E\left\{ {x\left( {t + \frac{\tau }{2}} \right){x^*}\left( {t - \frac{\tau }{2}} \right)} \right\} $ | (2) |
将式(1)展开为傅里叶级数形式:
| $ {R_x}\left( {t;\tau } \right) = \sum\limits_{m = - \infty }^\infty {R_x^\alpha \left( \tau \right){{\rm{e}}^{j\frac{{2{\rm{ \mathsf{ π} }}}}{{{T_0}}}mt}}} $ | (3) |
令
| $ {R_x}\left( {t;\tau } \right) = \sum\limits_{m = - \infty }^\infty {R_x^\alpha \left( \tau \right){{\rm{e}}^{j2{\rm{ \mathsf{ π} }}\alpha t}}} $ |
式中的傅里叶系数为
| $ R_x^\alpha \left( \tau \right) = \frac{1}{{{T_0}}}\int\limits_{ - {T_0}/2}^{{T_0}/2} {{R_x}\left( {t;\tau } \right){{\rm e}^{j2{\rm{ \mathsf{ π} }}\alpha t}}{\rm{d}}t} $ | (4) |
Rxα(τ)的傅里叶变换Sxα(τ)称为循环谱密度函数
| $ S_x^\alpha \left( \tau \right) = \smallint _{ - \infty }^{ + \infty }R_x^\alpha \left( \tau \right){{\rm{e}}^{ - j2{\rm{ \mathsf{ π} }}f\tau }}{\rm{d}}\tau $ | (5) |
将式(2)和式(4)代入式(5)得循环谱密度估计为
| $ S_x^\alpha \left( \tau \right) = \mathop {\lim }\limits_{\Delta t \to \infty } \mathop {\lim }\limits_{T \to \infty } \frac{1}{{\Delta t}}\int\limits_{ - \frac{{\Delta t}}{2}}^{\frac{{\Delta t}}{2}} {S_{{X_T}}^\alpha \left( {t, f} \right){\rm{d}}t} $ |
式中SαXT(t, f)被称为循环周期图,即
| $ S_{{X_T}}^\alpha \left( {t, f} \right) = \frac{1}{T}{X_T}\left( {t, f + \frac{\alpha }{2}} \right)X_T^*\left( {t, f - \frac{\alpha }{2}} \right) $ |
式(6)为接收数据的短时傅里叶变换:
| $ {X_T}\left( {t, f + \frac{\alpha }{2}} \right) = \int\limits_{t - \frac{T}{2}}^{t + \frac{T}{2}} {x\left( u \right){{\rm{e}}^{j2{\rm{ \mathsf{ π} }}fu}}{\rm{d}}u} $ | (6) |
式中:Δt是接收数据的长度,T是短时傅里叶变换的窗长。实际仿真中通常采用时域平滑和频域平滑的循环谱周期图来估计信号的循环谱密度。本文采用时域平滑法来计算信号的循环谱密度,有
| $ \begin{array}{l} S_{xT}^{{\alpha _0} + q\Delta \alpha }{\left( {nL, {f_j}} \right)_{\Delta t}} = \mathop \sum \limits_r {X_T}\left( {rL, {f_k}} \right) \times \\ X_T^*\left( {rL, {f_l}} \right){g_c}\left( {n - r} \right){{\rm{e}}^{{\rm{j}}2{\rm{ \mathsf{ π} }}qr/p}}\\ {X_T}\left( {r, f} \right) = \sum\limits_{r = - N'/2}^{N'/2} {a\left( n \right)x\left( {r - n} \right){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}f\left( {r - n} \right){T_s}}}} \end{array} $ |
式中:XT(r, f)是复解调,又被称为循环周期图;a(n)为数据衰减窗;gc(n)为平滑窗;q=-P/2, …, P/2-1;L为抽取因子,满足L < N',当L=N'/4时效果最好;N为总的采样数,LP=N。
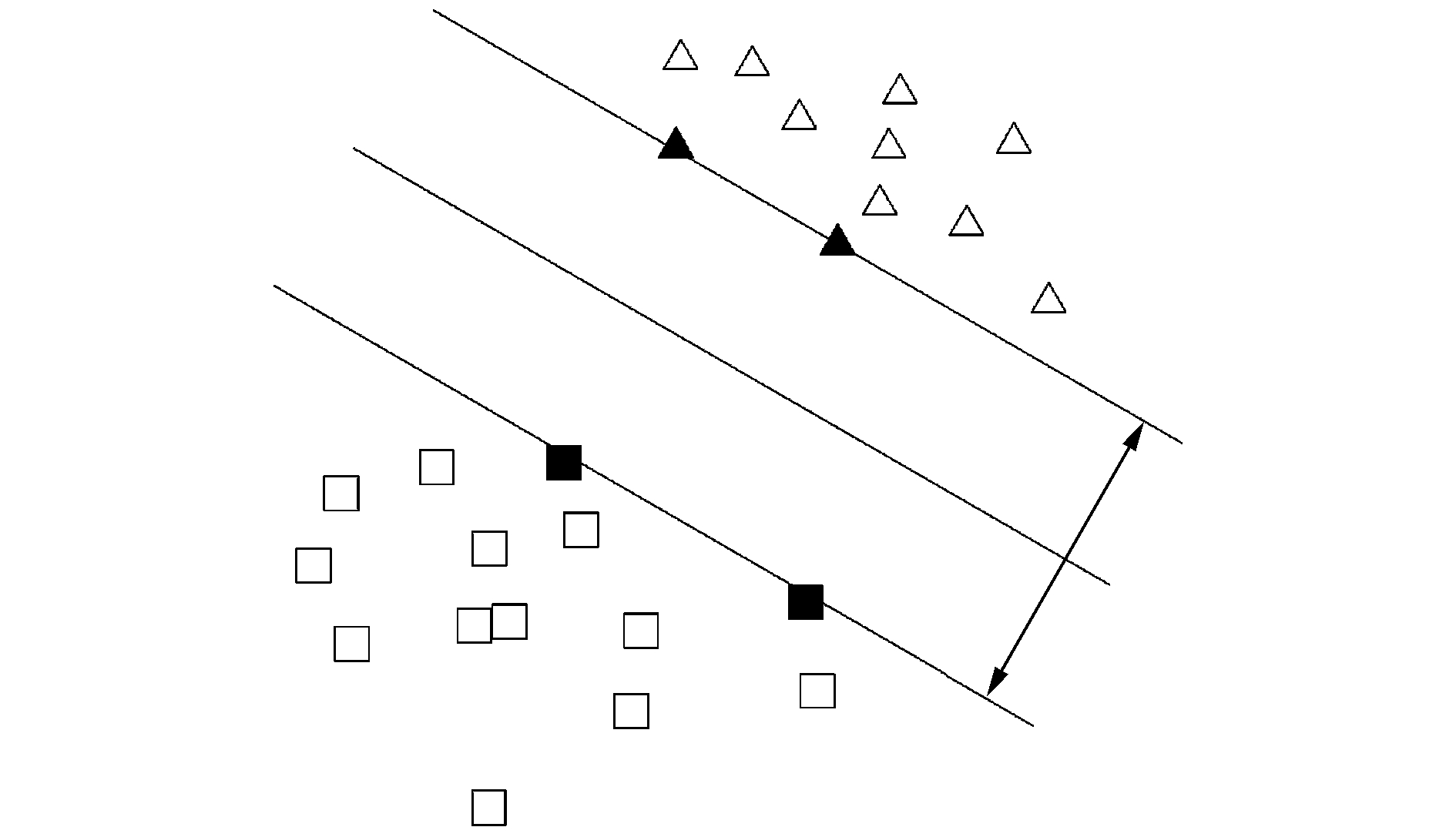
2 支持向量机支持向量机(SVM)[7-8]是建立在统计学习理论[9-10]VC维理论和结构风险最小化原理基础上的方法。图 1为支持向量机示意图。
|
Download:
|
| 图 1 支持向量机示意 | |
标准的支持向量机学习算法问题可以归结为求解一个受约束的二次型规划问题[11]。
设线性可分的样本集(xi, yi),其中满足x∈Rd,y∈{+1, -1},i=1, 2,…, N。d维空间中的线性判别函数为g(x)=wx+b,分类面方程为wx+b=0。
SVM的机理是寻找一个满足分类要求的最优分类超平面[12-14],使得该超平面在保证分类精度的同时, 能够使超平面两侧的空白区域最大化[15]。如果分类面归一化,则使得所有样本都满足g(x)≥1,这样分类间隔为2/‖w‖。当求分类间隔最大时,就是要求‖w‖最小,即满足
| $ {y_i}\left[ {w{x_i} + b} \right] - 1 \ge 0\left( {i = 1, 2, \cdots , N} \right) $ | (7) |
满足式(7)且使式(7)等号成立的样本称作支持向量,离分类面最近且平行于最优分类面的超平面H1和H2上的训练样本。
考虑线性不可分情况下增加的松弛项ζi,求最优分类面问题转换为如下约束问题:
| $ \begin{array}{*{20}{c}} {\min \frac{1}{2}{{\left\| w \right\|}^2} + C\sum\limits_{i = 1}^N {{\zeta _i}} }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}{y_i}\left[ {w{x_i} + b} \right] \ge 1 - {\zeta _i}\left( {i = 1, 2, \ldots , N} \right) \cdots {\zeta _i} \ge 0} \end{array} $ |
支持向量机的优势主要体现在解决线性不可分问题,通过引入核函数定义的非线性特征映射,将待分类数据映射到一个高维的特征空间中,从而很好地解决了非线性分类问题。
为了实现了在高维特征空间中样本的线性分类(相对原空间是非线性的分类),引入径向基核函数
| $ K\left( {x, {x_i}} \right) = \exp ( - \gamma {\left| {x - {x_i}} \right|^2}) $ |
核函数将原空间的数据隐含地表示在高维的特征空间中,并在其中训练了一个线性的分类器,训练过程并不需要知道具体的非线性映射。
3 算法原理及数字实现判别分析是多元统计中用于判别样品所属类型的一种统计分析方法。本文针对循环谱的多维矩阵,以距离判别方法提取一行最适合分类的信息,减小了计算量。由于循环谱是对称矩阵,后续计算量比较大,依行顺序从上到下选取循环谱矩阵的一半作为输入信号。将输入信号的循环谱密度按行求出所有类别的对应均值向量,并依次求出各类信号的行向量到相应的类别均值向量的欧式距离之和,最后将上述距离之和最大的一行循环谱信号作为分类特征,作为分类数据并训练支持向量机。
具体数字实现过程如下:
1) 分别求出K类信号的循环谱密度,并依照行顺序分别取循环谱密度矩阵的一半作为输入信号矩阵Mi(i=1, 2…, K);
2) 将K类信号各自得到的输入信号矩阵按行操作,分别求K类信号第j行的均值SijM(i=1, 2, …, K)以及K类信号总体的均值为
| $ {S^{jM}} = \frac{1}{K}\sum\limits_{i = 1}^K {} S_i^{jM}, j = 1, 2, \cdots $ |
3) 按距离判别的方式分别求取K类信号循环谱每行的欧式距离
| $ d_i^{jM} = \sum\limits_{i = 1}^K {{{(S_i^{jM} - {S^{jM}})}^2}} $ |
然后按照距离从大到小的顺序排列,选择距离最大的一行dijMmax作为分类的特征;
4) 将样本特征数据的40%作为训练集数据,用以训练支持向量机,得到最优的参数惩罚因子C和核函数参数γ;
5) 将样本特征数据剩余的60%作为测试集数据,用已经训练好的支持向量机模型得出样本数据的调制识别率。
4 实验仿真本文采用MATLAB对上述方法的有效性进行仿真验证。仿真参数设置如下:载波频率为400 kHz,数字采样频率为1 600 kHz,脉冲宽度为2 560 μs。本文利用MATLAB产生了简单脉冲调制(NS)、LFM、BPSK、QPSK、2FSK共5种雷达信号。并按功率比混合信号BPSK和QPSK,BPSK和2FSK,BPSK和LFM,QPSK和2FSK,QPSK和LFM,LFM和2FSK。
噪声环境为高斯白噪声,把高斯白噪声加入到调制信号中去,以1 dB为间隔在信噪比为-5~15 dB的条件下,每类信号分别生成500个样本数据。其中,每类信号用200个改进的循环谱特征数据训练支持向量机,用300个改进的循环谱特征数据做测试。
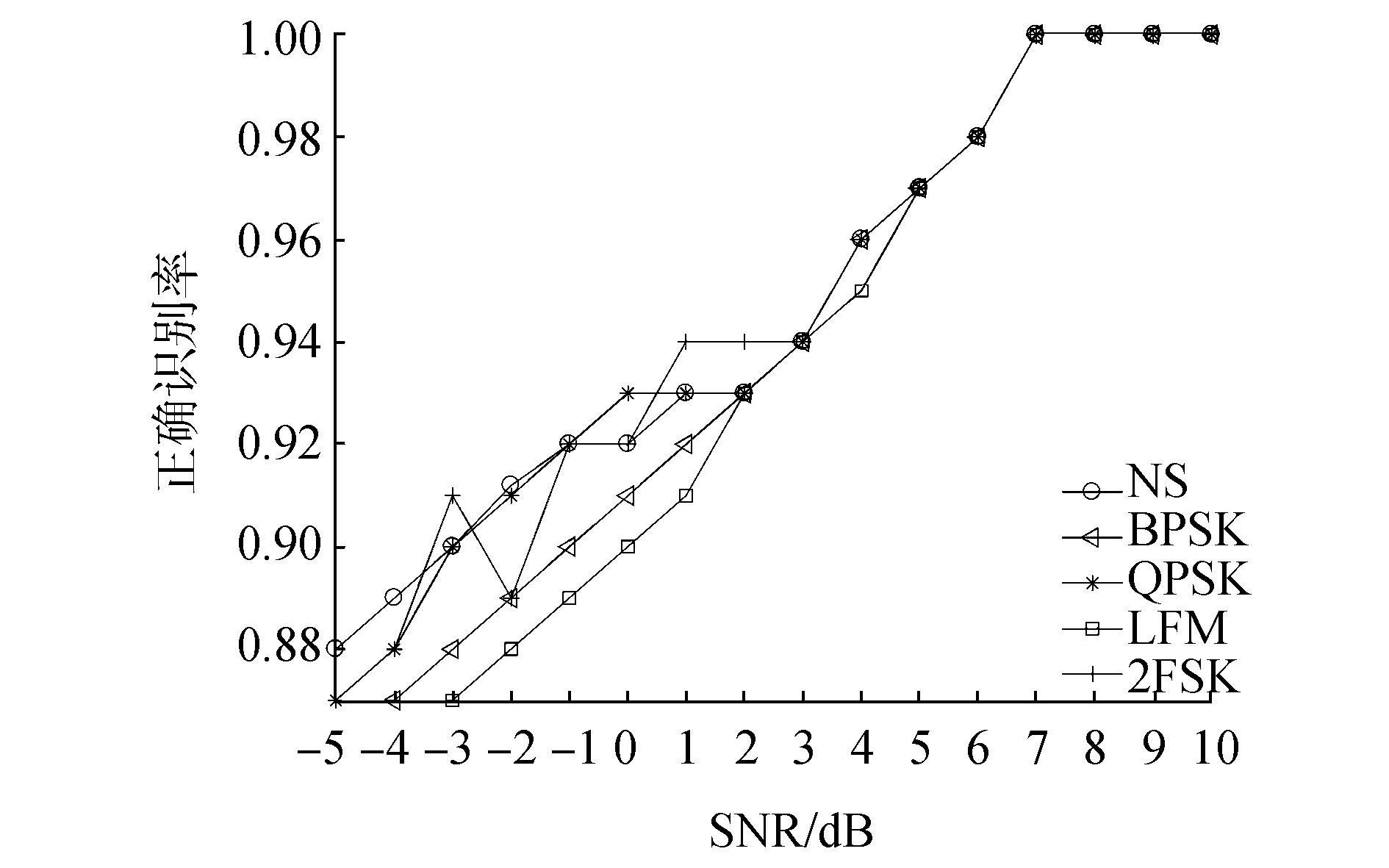
图 2给出了在不同信噪比环境下,本算法对5种雷达单信号的识别率。由图 2可以看出,本算法在较低信噪比环境下仍有较好的识别率。在信噪比为7 dB时,5种单信号的正确识别率为100%。
|
Download:
|
| 图 2 不同信噪比下单信号的正确识别率 | |
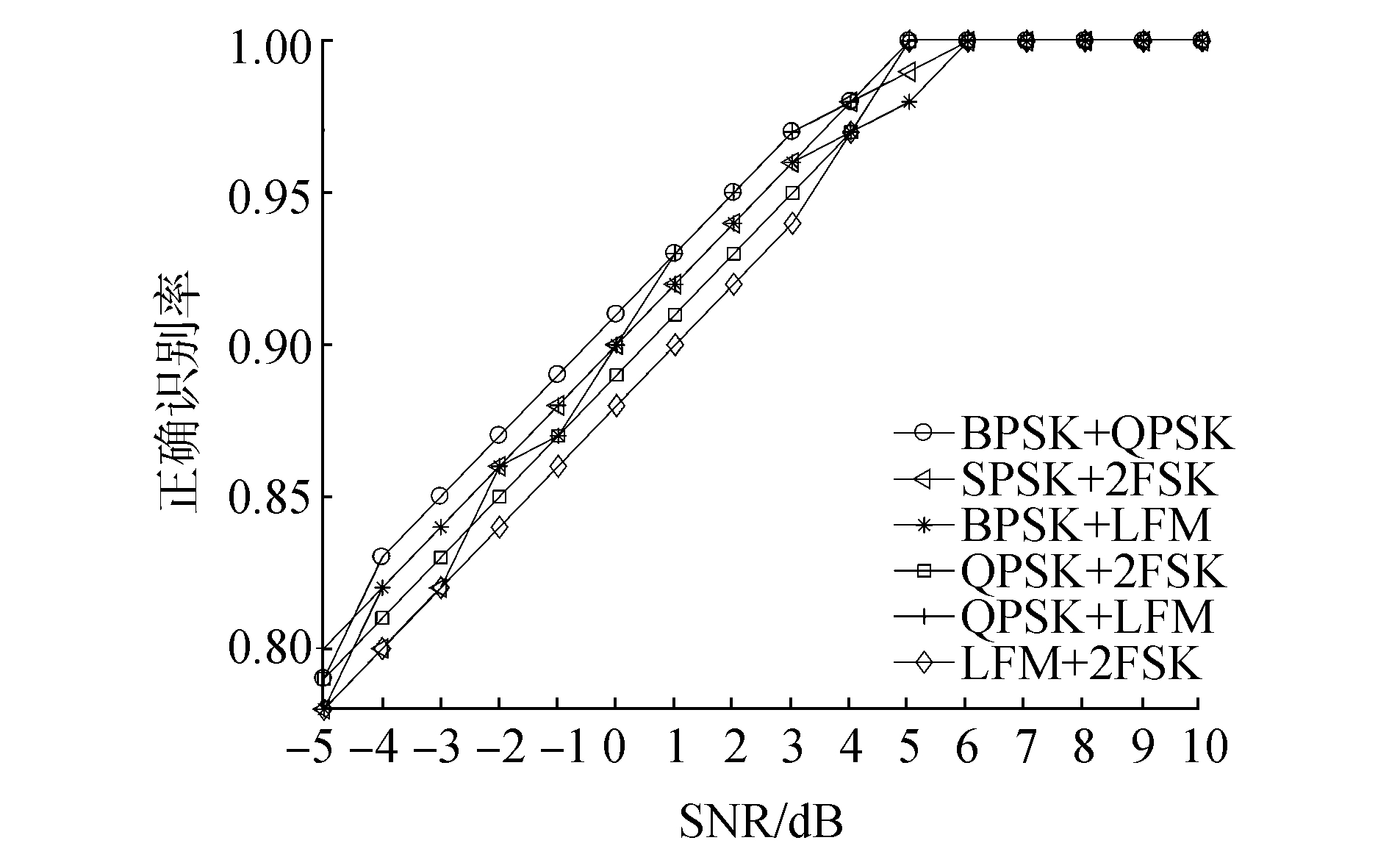
图 3、4给出了混合信号功率比为2:1和1:1时,在不同信噪比环境下,混合信号的正确识别率。从中可以看到,在较低信噪比环境下,混合信号功率差变大时混合信号的正确识别率会变低,而当混合信号功率相当时,其正确识别率会有所上升。这是由于两个信号中的一个功率较大时,另一个信号易被淹没或忽略为噪声。

|
Download:
|
| 图 3 功率比为2:1的混合信号的正确识别率 | |
|
Download:
|
| 图 4 功率比为1:1的混合信号的正确识别率 | |
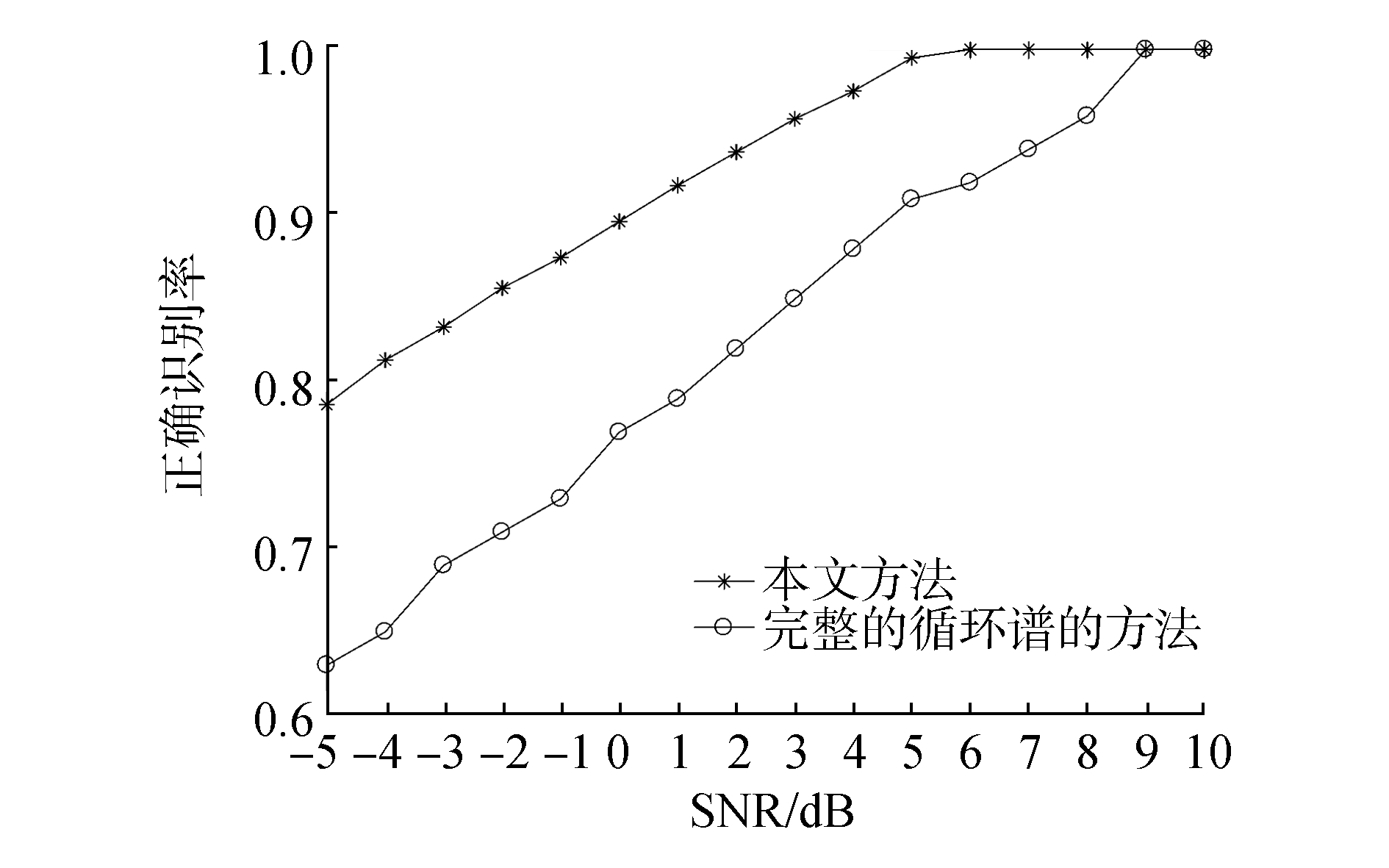
图 5、6对本文方法和循环谱结合支持向量机的方法的正确识别率进行了比较。从图中可以看出,本文的方法信号的识别率要高于完整的循环谱的方法。其中,在-5 dB时,本文方法对应的单信号和混合信号的识别率分别为88%和79%。而完整的循环谱方法所对应的单信号和混合信号的识别率为71%和63%。

|
Download:
|
| 图 5 不同方法的单信号的正确识别率 | |
|
Download:
|
| 图 6 不同方法的混合信号的正确识别率 | |
本文针对单个雷达调制信号和混合雷达调制信号的识别问题,提出了利用距离判别方法改进的雷达信号循环谱特征和支持向量机相结合的方法。该方法首先求出距离多类信号循环谱行均值最大的各行循环谱信号,然后训练支持向量机,并进行分类。MATLAB仿真表明该方法在较低信噪比下,对雷达调制信号具有良好的识别率。
| [1] |
李杨, 李国通, 杨根庆. 通信信号数字调制方式自动识别算法研究[J]. 电子与信息学报, 2005, 27(2): 197-201. ( 0) 0)
|
| [2] |
何继爱, 张文启. 通信信号调制识别技术及其发展[J]. 高技术通讯, 2016, 26(2): 157-165. DOI:10.3772/j.issn.1002-0470.2016.02.006 ( 0) 0)
|
| [3] |
PANAGIOTOU P, ANASTASOPOULOS A, POLYDOROS A. Likelihood ratio tests for modulation classification[C]//Proceedings of the 21st Century Military Communications. Los Angeles, USA, 2000: 670-674. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=904013
( 0) 0)
|
| [4] |
MAJI S, BERG A C, MALIK J. Classification using intersection kernel support vector machines is efficient[C]//Proceedings of 2008 IEEE Computer Vision and Pattern Recognition. Anchorage, USA, 2008: 1-8. http://www.mendeley.com/research/classification-using-intersection-kernel-support-vectormachines-efficien/
( 0) 0)
|
| [5] |
SCHÖLKOPF B, SUNG K K, BURGES C J C, et al. Comparing support vector machines with Gaussian kernels to radial basis function classifiers[J]. IEEE transactions on signal procesing, 1997, 45(11): 2758-2765. DOI:10.1109/78.650102 ( 0) 0)
|
| [6] |
王兰勋, 孟祥雅, 佟婧丽. 基于循环谱和稀疏表示的多信号调制识别[J]. 电视技术, 2015, 39(1): 92-95. ( 0) 0)
|
| [7] |
蔡艳宁, 汪洪桥, 叶雪梅. 复杂系统支持向量机建模与故障预报[M]. 北京: 国防工业出版社, 2015.
( 0) 0)
|
| [8] |
郎荣玲, 潘磊, 吕永乐, 等. 基于支持向量机的飞机故障诊断技术[M]. 北京: 国防工业出版社, 2016.
( 0) 0)
|
| [9] |
陈晓华, 刘大莲, 田英杰, 等. 可拓支持向量分类机[J]. 智能系统学报, 2018, 13(1): 147-151. ( 0) 0)
|
| [10] |
VAPNIK V N. 统计学习理论[M]. 许建华, 张学工, 译. 北京: 电子工业出版社, 2004.
( 0) 0)
|
| [11] |
刘高辉, 杨星. 一种混合核函数的支持向量机[J]. 微型机与应用, 2017, 36(11): 19-22. ( 0) 0)
|
| [12] |
龚成, 唐忠明. 整闭单项式理想作为乘子理想的实现性[J]. 中国科学:数学, 2017, 47(11): 1565-1570. ( 0) 0)
|
| [13] |
XIE Shangxin, LI Zhong, HU Hailong. Protein secondary structure prediction based on the fuzzy support vector machine with the hyperplane optimization[J]. Gene, 2018, 642: 74-83. DOI:10.1016/j.gene.2017.11.005 ( 0) 0)
|
| [14] |
BRUNER A, SHARIR M. Distinct distances between a collinear set and an arbitrary set of points[J]. Discrete mathematics, 2018, 341(1): 261-265. DOI:10.1016/j.disc.2017.08.037 ( 0) 0)
|
| [15] |
DAI Liuling, HUANG Heyan, CHEN Zhaoxiong. Ternary sequential analytic optimization algorithm for SVM classifier design[J]. Asian journal of information technology, 2005, 4(3): 2-8. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


