大规模MIMO技术是MIMO技术的演进,通过在基站配置大量的天线,获得更高的频谱效率。由于大规模MIMO系统可以有效地提高频谱利用率和系统容量,近几年来已经成为了学者们的研究热点[1-5]。另外,预编码技术可以在已知信道状态信息(channel state information,CSI)情况下,通过在发送端对发送的信号做一个预先的处理,以方便接收机进行信号检测,从而进一步提升系统性能。但是在FDD传输模式中,大规模多用户MIMO系统中大量的用户也会导致获取CSI困难的问题[6-8]。因此,如何设计一种预编码方案,使得在FDD传输模式下的大规模MIMO系统中获得准确的CSI,从而减小反馈开销,成为了需要去解决的问题[9-13]。
1 系统模型假定系统为FDD传输模式下单小区下行链路系统,其中有一个配置有M个垂直/水平极化分集天线单元的基站和N个配置有一个垂直或水平极化天线单元的活跃用户,且M和N均为偶数。由于人们的通常活动在建筑物这种小集群区域,因此将用户的位置视为空间集群,并划为G个群组。在平坦衰落信道下,第g个群组的接收信号如式(1):
| $ {\mathit{\boldsymbol{y}}_g} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}}_g^v}\\ {\mathit{\boldsymbol{y}}_g^h} \end{array}} \right] = \mathit{\boldsymbol{H}}_g^{\rm{H}}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{n}}_g} $ | (1) |
式中:ygv和ygh分别是用户垂直极化和水平极化的接收信号;ng=[ngv ngh]T是均值为0、方差为INg的复高斯噪声向量,即服从分布ng~CN(0, INg);第g个群组中的用户数量为Ng,为简单起见,假设N1=N2=…=NG=N,且N为偶数。ygv和ygh均为N/2×1的向量;Hg为第g个群组的信道矩阵,其中第k个用户的信道向量为hgk=[Hg]k。M×1的向量x为经过线性预编码后的发射信号,其表达式为
| $ \mathit{\boldsymbol{x}} = \sum\limits_{g = 1}^G {{\mathit{\boldsymbol{P}}_g}{\mathit{\boldsymbol{d}}_g}} $ |
式中:
利用Karhunen-Loeve变换和文献[1-2]中提出的部署有无穷小的天线单元的极化MIMO信道模型,第g个群组的下行链路信道Hg可表示为
| $ {\mathit{\boldsymbol{H}}_g} = \left( {\left[ {\begin{array}{*{20}{c}} 1&{{r_{xp}}}\\ {{r_{xp}}}&1 \end{array}} \right] \otimes \left( {{\mathit{\boldsymbol{U}}_g}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_g^{\frac{1}{2}}} \right)} \right)\left( {{\mathit{\boldsymbol{G}}_g} \odot \left( {\mathit{\boldsymbol{X}} \otimes {1_{r \times \frac{{\bar N}}{2}}}} \right)} \right) $ | (2) |
式中:rxp为垂直和水平极化天线单元之间的相关系数;Λg是由第g个群组中的空间协方差矩阵Rgs的非零特征值组成的rg×rg的对角矩阵,通常rg≤M;
| $ {\mathit{\boldsymbol{G}}_g} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{G}}_g^{vv}}&{\mathit{\boldsymbol{G}}_g^{hv}}\\ {\mathit{\boldsymbol{G}}_g^{vh}}&{\mathit{\boldsymbol{G}}_g^{hh}} \end{array}} \right] $ |
式中
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} 1&{\sqrt \chi }\\ {\sqrt \chi }&1 \end{array}} \right] $ | (3) |
式中:参数χ为XPD的倒数,且1≤XPD≤∞,即0≤χ≤1。根据文献[9-10],rxp≈0,因此式(2)可化简为
| $ {\mathit{\boldsymbol{H}}_g} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}}_g^{vv}}&{\mathit{\boldsymbol{H}}_g^{hv}}\\ {\mathit{\boldsymbol{H}}_g^{vh}}&{\mathit{\boldsymbol{H}}_g^{hh}} \end{array}} \right] $ |
Hg的协方差矩阵为
| $ {\mathit{\boldsymbol{R}}_g} = {\mathit{\boldsymbol{R}}_{gv}} + {\mathit{\boldsymbol{R}}_{gh}} $ |
式中Rgv和分Rgh为垂直和水平共极化用户子群组的协方差矩阵。长期参数Rgs和χ变化缓慢,因此本文假定它们均可在低反馈开销时准确地获得,而短期CSI参数Gg在短期相干时间内独立变化。基站获得反馈的CSI是非完美的,并且产生了巨大的开销。
3 预编码方案BD双重结构预编码由2部分组成,分别为利用空间相关性的块对角化(block diagonalization,BD)预处理和对每个解耦群组进行的正则化迫零(regularized zero force,RZF)预编码。
基于长期/短期CSIT的双重预编码方案可以有效降低运算复杂度和反馈开销,其预编码矩阵为
| $ {\mathit{\boldsymbol{V}}_g} = {\mathit{\boldsymbol{B}}_g} + {\mathit{\boldsymbol{P}}_g} $ |
式中
| $ {\mathit{\boldsymbol{y}}_g} = \mathit{\boldsymbol{H}}_g^{\rm{H}}{\mathit{\boldsymbol{B}}_g}{\mathit{\boldsymbol{P}}_g}{\mathit{\boldsymbol{d}}_g} + \sum\limits_{l = 1,l \ne g}^G {\mathit{\boldsymbol{H}}_g^{\rm{H}}{\mathit{\boldsymbol{B}}_l}{\mathit{\boldsymbol{P}}_l}{\mathit{\boldsymbol{d}}_l}} + {\mathit{\boldsymbol{n}}_g} $ | (4) |
为了消除对于其他群组的干扰,基于空间相关性的BD预处理矩阵Bg应满足条件:
| $ \mathit{\boldsymbol{H}}_l^{\rm{H}}{\mathit{\boldsymbol{B}}_g} \approx 0,l \ne g $ | (5) |
利用块对角化方法可以获得满足式(5)的预处理矩阵Bg。由式(3)的块对角化结构,首先定义
| $ {\mathit{\boldsymbol{U}}_{ - g}} = \left[ {U_1^a,U_2^a, \cdots ,U_{g - 1}^a,U_{g + 1}^a, \cdots ,U_G^a} \right] \in {C^{\frac{M}{2} \times \sum\nolimits_{l \ne g} {r_l^a} }} $ | (6) |
式中
式(6)中的矩阵U-g进行奇异值分解后的形式为
| $ {\mathit{\boldsymbol{U}}_{ - g}} = \left[ {\mathit{\boldsymbol{E}}_{ - g}^{\left( 1 \right)},\mathit{\boldsymbol{E}}_{ - g}^{\left( 0 \right)}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{ - g}^{\left( 1 \right)}}&{}\\ {}&{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{ - g}^{\left( 0 \right)}} \end{array}} \right]\mathit{\boldsymbol{V}}_{ - g}^{\rm{H}} $ |
| $ \mathit{\boldsymbol{E}}_{ - g}^{\left( 0 \right)} \in {C^{\frac{M}{2} \times \frac{M}{2} - \sum\nolimits_{l \ne g} {r_l^a} }} $ |
式中:
| $ {{\mathit{\boldsymbol{\tilde R}}}_g} = {\left( {{\mathit{\boldsymbol{I}}_2} \otimes \mathit{\boldsymbol{E}}_{ - g}^{\left( 0 \right)}} \right)^{\rm{H}}}{\mathit{\boldsymbol{R}}_g}\left( {{\mathit{\boldsymbol{I}}_2} \otimes \mathit{\boldsymbol{E}}_{ - g}^{\left( 0 \right)}} \right) $ |
定义
| $ \mathit{\boldsymbol{\tilde R}}_g^s = {\mathit{\boldsymbol{F}}_g}{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varLambda} }}}_g}\mathit{\boldsymbol{F}}_g^{\rm{H}} $ |
式中Fg为
| $ {\mathit{\boldsymbol{B}}_g} = {\mathit{\boldsymbol{I}}_2} \otimes \mathit{\boldsymbol{B}}_g^s,\mathit{\boldsymbol{B}}_g^s = \mathit{\boldsymbol{E}}_{ - g}^{\left( 0 \right)}\mathit{\boldsymbol{F}}_g^{\left( 1 \right)} $ |
通过预处理矩阵Bg可以将第g个群组的发送信号转换为维数为B的主导特征空间,从而与被其他群组信道跨越的子空间正交。B和rga的选取应满足条件
由式(4),第g个群组的有效信道为
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\bar R}}}_g} = \mathit{\boldsymbol{B}}_g^{\rm{H}}{\mathit{\boldsymbol{R}}_g}{\mathit{\boldsymbol{B}}_g} = \mathit{\boldsymbol{B}}_g^{\rm{H}}\left( {{\mathit{\boldsymbol{R}}_{gv}} + {\mathit{\boldsymbol{R}}_{gh}}} \right){\mathit{\boldsymbol{B}}_g} = }\\ {{{\mathit{\boldsymbol{\bar R}}}_{gv}} + {{\mathit{\boldsymbol{\bar R}}}_{gh}} = \left( {1 + \chi } \right)\left[ {\begin{array}{*{20}{c}} {{{\left( {\mathit{\boldsymbol{B}}_g^s} \right)}^{\rm{H}}}\mathit{\boldsymbol{R}}_g^s\mathit{\boldsymbol{B}}_g^s}&0\\ 0&{{{\left( {\mathit{\boldsymbol{B}}_g^s} \right)}^{\rm{H}}}\mathit{\boldsymbol{R}}_g^s\mathit{\boldsymbol{B}}_g^s} \end{array}} \right]} \end{array} $ |
通过前面的预处理,式(4)中来自其他群组的干扰几乎被完全消除。因此,接下来将对基于第g个群组短期CSIT的预编码矩阵Pg进行设计,以消除群组内的干扰。假设功率均等分配,具有非完美CSIT的RZF预编码矩阵公式为
| $ {\mathit{\boldsymbol{P}}_g} = {\xi _g}{{\mathit{\boldsymbol{\hat {\bar K}}}}_g}{{\mathit{\boldsymbol{\hat {\bar H}}}}_g} $ |
式中:
| $ {{\mathit{\boldsymbol{\hat {\bar K}}}}_g} = {\left( {{{\mathit{\boldsymbol{\hat {\bar H}}}}_g}\mathit{\boldsymbol{\hat {\bar H}}}_g^{\rm{H}} + \bar B\alpha I_B^ - } \right)^{ - 1}},{{\mathit{\boldsymbol{\hat {\bar H}}}}_g} = B_g^{\rm{H}}{{\mathit{\boldsymbol{\hat H}}}_g} $ |
式中:
| $ \begin{array}{*{20}{c}} {\xi _g^2 = \frac{{\bar N\frac{P}{N}}}{{\frac{P}{N}{\rm{tr}}\left( {\mathit{\boldsymbol{\hat {\bar H}}}_g^{\rm{H}}\mathit{\boldsymbol{\hat {\bar K}}}_g^{\rm{H}}\mathit{\boldsymbol{B}}_g^{\rm{H}}{\mathit{\boldsymbol{B}}_g}{{\mathit{\boldsymbol{\hat {\bar K}}}}_g}{{\mathit{\boldsymbol{\hat {\bar H}}}}_g}} \right)}} = }\\ {\frac{{\bar N}}{{{\rm{tr}}\left( {\mathit{\boldsymbol{\hat {\bar H}}}_g^{\rm{H}}\mathit{\boldsymbol{\hat {\bar K}}}_g^{\rm{H}}{{\mathit{\boldsymbol{\hat {\bar K}}}}_g}{{\mathit{\boldsymbol{\hat {\bar H}}}}_g}} \right)}}} \end{array} $ |
用
| $ \begin{array}{*{20}{c}} {\gamma _{gpk}^{BD} = \frac{{\frac{P}{N}\xi _g^2{{\left| {\mathit{\boldsymbol{h}}_{gk}^{\rm{H}}{\mathit{\boldsymbol{B}}_g}{{\mathit{\boldsymbol{\hat {\bar K}}}}_g}{{\mathit{\boldsymbol{\hat {\bar h}}}}_{gk}}} \right|}^2}}}{{\frac{P}{N}\Delta + \frac{P}{N}\sum\nolimits_{l \ne g} {\sum\nolimits_j {\xi _l^2{{\left| {\mathit{\boldsymbol{h}}_{gk}^{\rm{H}}{\mathit{\boldsymbol{B}}_l}{{\mathit{\boldsymbol{\hat {\bar K}}}}_l}{{\mathit{\boldsymbol{\hat {\bar h}}}}_{lj}}} \right|}^2}} } + 1}} = }\\ {\frac{{\frac{P}{N}\xi _g^2{{\left| {\mathit{\boldsymbol{h}}_{gk}^{\rm{H}}{\mathit{\boldsymbol{B}}_g}{{\mathit{\boldsymbol{\hat {\bar K}}}}_g}\mathit{\boldsymbol{B}}_g^{\rm{H}}{{\mathit{\boldsymbol{\hat {\bar h}}}}_{gk}}} \right|}^2}}}{{\frac{P}{N}\Delta + \frac{P}{N}\sum\nolimits_{l \ne g} {\sum\nolimits_j {\xi _l^2{{\left| {\mathit{\boldsymbol{h}}_{gk}^{\rm{H}}{\mathit{\boldsymbol{B}}_l}{{\mathit{\boldsymbol{\hat {\bar K}}}}_l}\mathit{\boldsymbol{B}}_l^{\rm{H}}{{\mathit{\boldsymbol{\hat {\bar h}}}}_{lj}}} \right|}^2}} } + 1}}} \end{array} $ |
式中
和速率表达式为
| $ {R_{BD}} = \sum\limits_{g = 1}^G {\sum\limits_{p \in \left\{ {v,h} \right\}} {\sum\limits_{k = 1}^{\underline 2 } {{{\log }_2}\left( {1 + \gamma _{gpk}^{BD}} \right)} } } $ |
为了评估BD双重结构预编码方案的性能,采用蒙特卡洛(monte-carlo,MC)方法进行仿真。同样将部署了双重极化线性阵列的基站天线个数设置为M=120,且N=32,G=4,N=8。对于预处理,设置B=min(2N, 2r),其中r为
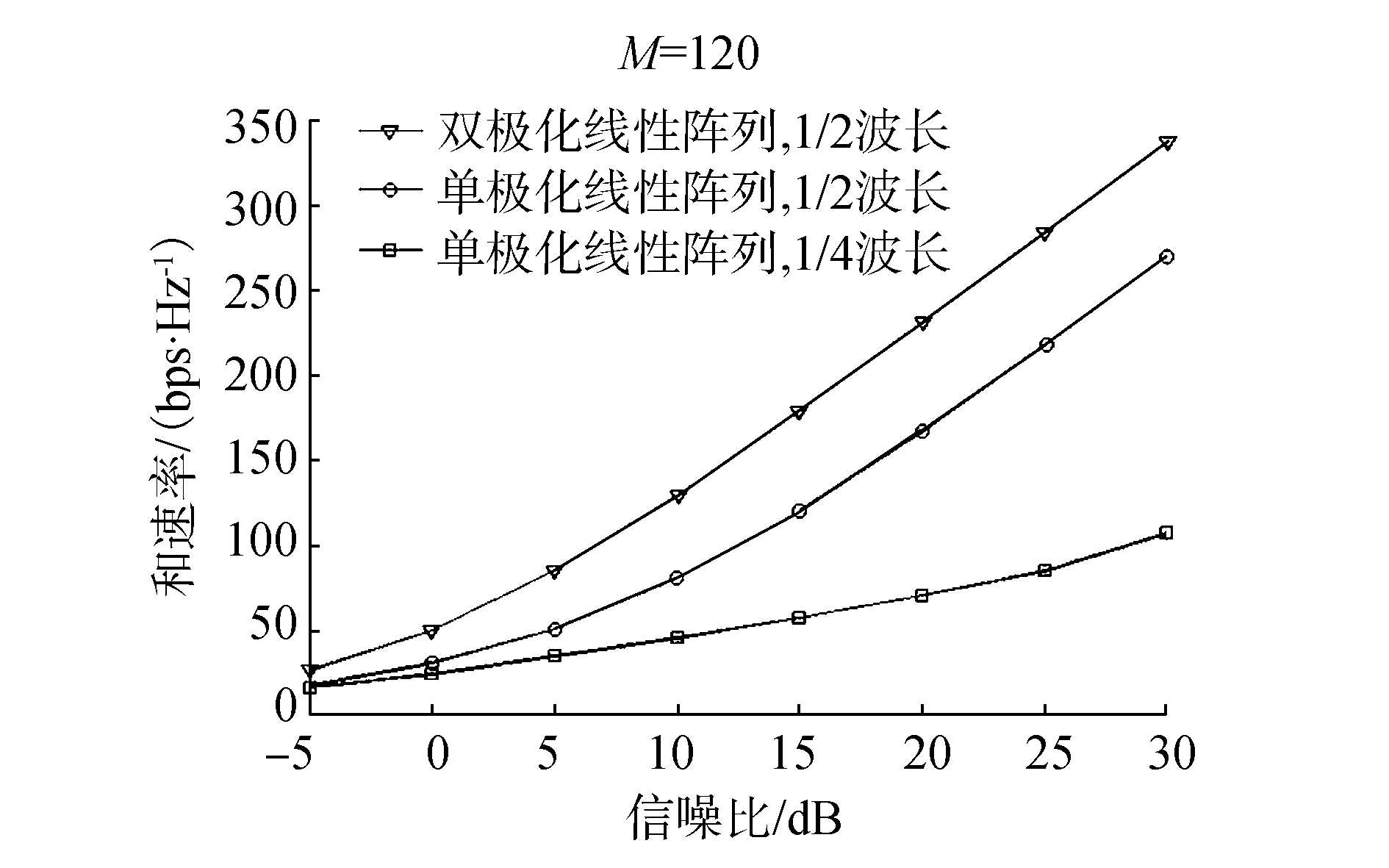
图 1给出了单极化和双极化线性阵列的双重预编码的和速率曲线。从图中可以看出,在ds=λ0/2的相同条件下,双极化阵列的性能优于单极化阵列。如果减小单极化阵列中天线的距离,即ds=λ0/4的情况下,单极化阵列的性能反而更差。因此多极化天线可以成为针对大规模MIMO系统空间限制问题的解决方案。
|
Download:
|
| 图 1 单极化与多极化预编码方案性能比较 | |
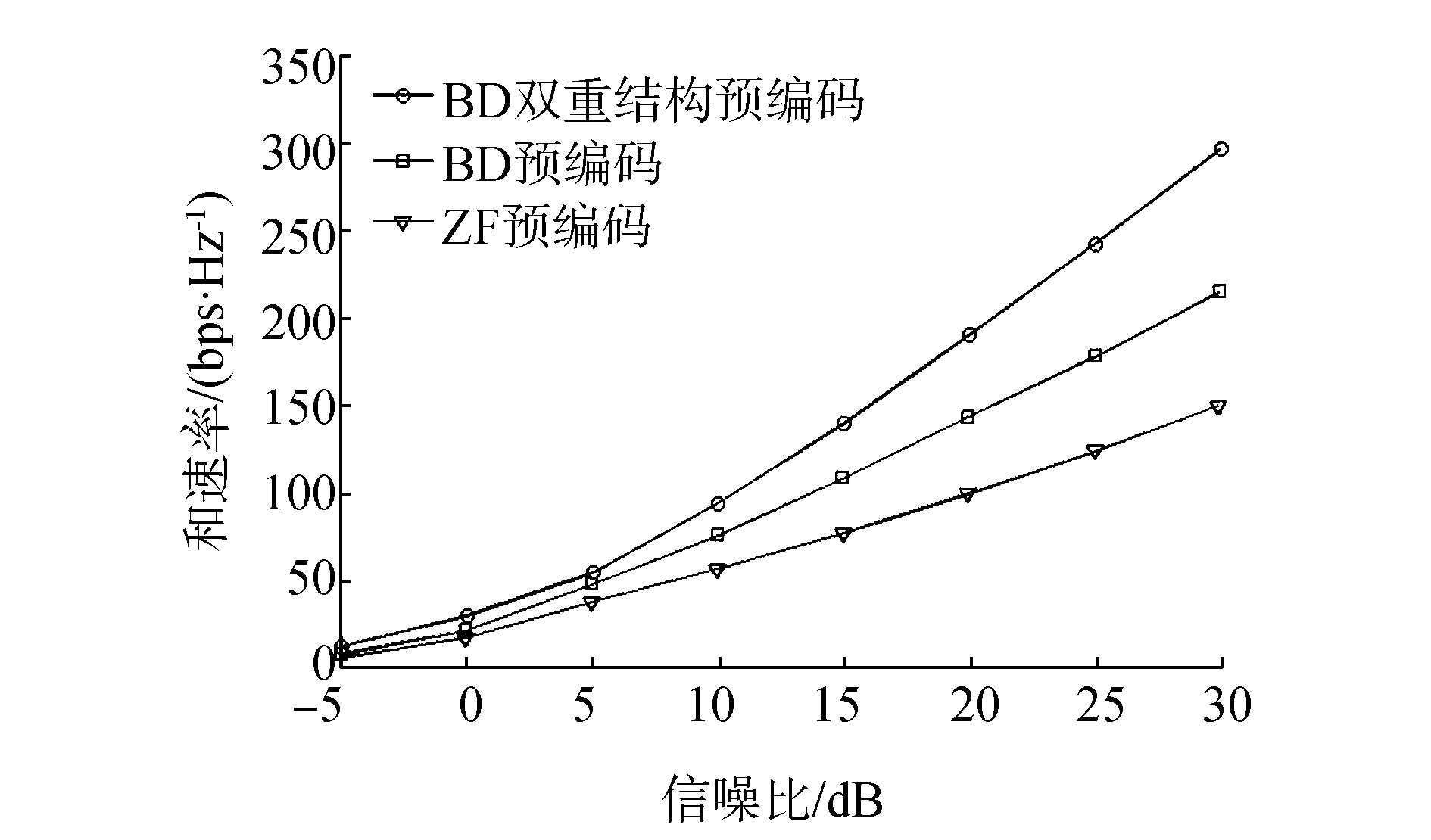
图 2给出了具有非完美CSIT,τ2=0.1的情况下,并且天线单元间不存在交叉极化现象,即χ=0的情况下,BD双重预编码与经典的ZF预编码、BD预编码随信噪比变化的和速率曲线。可以看出,BD是双重结构预编码方案可以获得更好的和速率性能,并且随着信噪比的增加,其展现的优势也越来越大。
|
Download:
|
| 图 2 BD双重结构预编码与经典预编码性能比较 | |
将基于空间相关的BD预处理与RZF预编码进行级联,设计了BD双重结构预编码方案,并对该方案的和速率进行推导。该预编码方案首先进行BD预处理,即利用波束成形,消除来自其他群组的干扰,然后利用RZF预编码技术,进一步消除群组内用户间的干扰。仿真结果表明,在FDD传输模式下,相比于经典的ZF预编码和MMSE预编码,BD双重结构预编码方案可以有效地减小反馈开销,获得更佳的和速率性能。
| [1] |
CLERCKX B, OESTGES C. MIMO wireless networks:channels, techniques and standards for multi-antenna, multi-user and multi-cell systems[M]. 2nd ed. Amsterdam: Academic Press, 2013.
( 0) 0)
|
| [2] |
KIM T, CLERCKX B, LOVE D J, et al. Limited feedback beamforming systems for dual-polarized MIMO channels[J]. IEEE transactions on wireless communications, 2010, 9(11): 3425-3439. DOI:10.1109/TWC.2010.09.090754 ( 0) 0)
|
| [3] |
WAGNER S, COUILLET R, SLOCK D T M, et al. Large system analysis of zero-forcing precoding in MISO broadcast channels with limited feedback[C]//Proceedings of 2010 IEEE Eleventh International Workshop Signal Processing Advances in Wireless Communications. Marrakech, Morocco: IEEE, 2010: 1-5. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5671035
( 0) 0)
|
| [4] |
ADHIKARY A, NAM J, AHN J Y, et al. Joint spatial division and multiplexing-the large-scale array regime[J]. IEEE transactions on information theory, 2013, 59(10): 6441-6463. DOI:10.1109/TIT.2013.2269476 ( 0) 0)
|
| [5] |
OESTGES C, CLERCKX B, GUILLAUD M, et al. Dual-polarized wireless communications:from propagation models to system performance evaluation[J]. IEEE transactions on wireless communications, 2008, 7(10): 4019-4031. DOI:10.1109/T-WC.2008.070540 ( 0) 0)
|
| [6] |
ZHANG Jun, WEN Chaokai, JIN Shi, et al. Large system analysis of cooperative multi-cell downlink transmission via regularized channel inversion with imperfect CSIT[J]. IEEE transactions on wireless communications, 2013, 12(10): 4801-4813. DOI:10.1109/TWC.2013.081413.120460 ( 0) 0)
|
| [7] |
DONG Liang, CHOO H, HEATH R W, et al. Simulation of MIMO channel capacity with antenna polarization diversity[J]. IEEE transactions on wireless communications, 2005, 4(4): 1869-1873. DOI:10.1109/TWC.2005.850318 ( 0) 0)
|
| [8] |
MARZETTA T L. Noncooperative cellular wireless with unlimited numbers of base station antennas[J]. IEEE transactions on wireless communications, 2010, 9(11): 3590-3600. DOI:10.1109/TWC.2010.092810.091092 ( 0) 0)
|
| [9] |
ASPLUND H, BERG J E, HARRYSSON F, et al. Propagation characteristics of polarized radio waves in cellular communications[C]//Proceedings of the 66th Vehicular Technology Conference. Baltimore, MD, USA: IEEE Xplore, 2007: 839-843. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4349833
( 0) 0)
|
| [10] |
COLDREY M. Modeling and capacity of polarized MIMO channels[C]//Proceedings of 2008 IEEE Vehicular Technology Conference. Singapore, Singapore: IEEE, 2008: 440-444. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4525659
( 0) 0)
|
| [11] |
HOYDIS J, TEN BRINK S, DEBBAH M. Massive MIMO in the UL/DL of cellular networks:how many antennas do we need?[J]. IEEE journal on selected areas in communications, 2013, 31(2): 160-171. DOI:10.1109/JSAC.2013.130205 ( 0) 0)
|
| [12] |
MURTI F W, ASTUTI R P, NUGROHO B S. Enhancing performance of block diagonalization precoding in multi user MIMO (MU-MIMO) downlink[C]//Proceedings of the 3rd International Conference on Information and Communication Technology (ICoICT). Nusa Dua, Bali: IEEE, 2015: 102-106. http://ieeexplore.ieee.org/document/7231405/
( 0) 0)
|
| [13] |
HERATH S P, NGUYEN D H N, LE-NGOC T. Vector perturbation precoding for multi-user CoMP downlink transmission[J]. IEEE access, 2015, 3: 1491-1502. DOI:10.1109/ACCESS.2015.2475237 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


