2. 沈阳新松机器人自动化股份有限公司, 辽宁 沈阳 110168;
3. 中国人民解放军94503部队, 山东 济南 250000
2. SIASUN Robot and Automation Company Limited, Shenyang 110168, China;
3. Unit 94503 of PLA, Jinan 250000, China
目标跟踪是计算机视觉中的一项重要课题,它具有广泛的应用,包括视频监控、机器人技术、医学诊断、气象分析等[1]。尽管在过去十年中目标跟踪技术已经取得了飞速进展,但是设计一个可以处理各种复杂情况,如光照变化、几何变形、快速移动、遮挡、背景杂波等[2]这样一个长期目标跟踪算法仍然非常具有挑战性。长时间目标跟踪的一个关键问题是当目标重新出现时的继续跟踪,使问题更棘手的是目标的外观可能会改变,导致与上一个跟踪视频帧无关。考虑到跟踪和检测算法都不能独立解决长期跟踪任务,Zdenek Kalal等[3-4]提出了一种新的目标跟踪算法(tracking-learning-detection, TLD)。TLD解决了被跟踪目标在被遮挡或在摄像机视野里消失后无法重新捕获的难题[5]。该算法在第一帧选定感兴趣的目标后,就可以自动进行鲁棒跟踪[6]。2012年Henriques[7]提出了核相关滤波器(kernelized correlation filters, KCF)目标跟踪算法,在相同的测试数据集上,相对于TLD的平均运行速度只有二十几帧每秒,而KCF的平均运行速度可达数百帧每秒,且具有较好的跟踪效果。但这两种算法只针对某些特定跟踪场景有效,对其他场景的目标跟踪性能较差或无法跟踪,缺少广泛适用性。故本文提出一种基于TLD框架的KCF目标跟踪算法,以提高算法的跟踪性能和适用性。
1 TLD及KCF跟踪算法 1.1 TLD基本原理TLD作为单目标长期跟踪算法,将跟踪任务分解为3部分。
1) 跟踪器。在连续帧之间目标的运动有限以及目标可见的前提下,通过LK(lucaks-kanade)光流法估计目标包围框中特征点的运动,此外使用具有跟踪故障检测功能的前后向误差检验和归一化互相关来提高跟踪准确率。
2) 检测器。通过对图像的全面扫描来定位目标。在该部分,单独测试每个子窗口以确定其是否包含跟踪目标,检测器采用了级联结构,包括图像块方差滤波器、集合分类器和最近邻分类器,旨在以较小的计算量筛选掉大量不相关的子窗口。
3) P-N学习[8]。通过学习不同的目标外观,评估检测器和跟踪器两者的性能,校正检测器的错误,并产生新的训练样本来重新训练检测器。通过P-N学习,检测器能够检测出更多的目标外观及目标周围的背景信息。
1.2 KCF基本原理KCF跟踪器主要是利用循环矩阵结构增强基于检测的跟踪方案的判别能力,使算法更高效。
1.2.1 循环矩阵分析假设对基样本的循环移位能够近似为对基样本的密集采样。设n×1向量
| $ \mathit{\boldsymbol{P=}}\left[\begin{matrix} 0 & 0 & \cdots & 0 & 1 \\ 1 & 0 & \cdots & 0 & 0 \\ 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0 \\ \end{matrix} \right] $ |
将x的所有循环移位{Pux|u=0, …, n-1}级联起来形成矩阵X:
| $ \mathit{\boldsymbol{X = }}C\left( x \right) = \left[{\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_{n-1}}}&{{x_n}}\\ {{x_n}}&{{x_1}}& \cdots &{{x_{n-2}}}&{{x_{n-1}}}\\ {{x_{n - 1}}}&{{x_n}}& \cdots &{{x_{n - 3}}}&{{x_{n - 2}}}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {{x_2}}&{{x_3}}& \cdots &{{x_n}}&{{x_1}} \end{array}} \right] $ |
由于矩阵X是由基样本x循环移位产生,因此它也被称为循环矩阵。任意循环矩阵都可以被傅里叶变换(DFT)矩阵对角化并可表示为
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{F}}{\rm{diag}}(\hat x){\mathit{\boldsymbol{F}}^{\rm{H}}} $ | (1) |
式中:F是不依赖于x的常数矩阵,
循环矩阵的特征分解可以用来简化线性回归的解。线性岭回归(即正则化最小二乘)的目标函数为
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{w}} \mathop \sum \limits_i {\left( {f({x_i})-{y_i}} \right)^2} + \lambda \left\| w \right\| $ |
式中λ是一个用来控制过度拟合的正则化参数,函数f可以写成基样本的线性组合,即f(x)=wTx。该岭回归的闭式解为
| $ \mathit{\boldsymbol{w}} = {({\mathit{\boldsymbol{X}}^{\rm{H}}}\mathit{\boldsymbol{X}} + \lambda \mathit{\boldsymbol{I}})^{-1}}{\mathit{\boldsymbol{X}}^{\rm{H}}}\mathit{\boldsymbol{y}} $ |
式中I为单位矩阵,也是一个循环矩阵,其生成向量为[1, 0, …, 0]。根据式(1)的性质,可以得到
| $ \mathit{\boldsymbol{\hat w = }}\frac{{\mathit{\boldsymbol{\hat x}} \odot \mathit{\boldsymbol{\hat y}}}}{{\mathit{\boldsymbol{\hat x}} \odot {{\mathit{\boldsymbol{\hat x}}}^*} + \lambda }} $ |
式中:
在非线性回归的情况下引入核函数。核函数的作用是把线性特征空间映射到一个更高维的非线性特征空间中,如果映射函数为φ(x),则
| $ f\left( z \right) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( z \right) $ | (2) |
式中w是训练样本的映射函数φ(xi)的线性组合:
| $ \mathit{\boldsymbol{w}} = \mathop \sum \limits_{i = 1}^n {\alpha _i}\mathit{\boldsymbol{\varphi }}({x_i}) $ | (3) |
将式(3)带入式(2)得
| $ f\left( z \right) = \mathop \sum \limits_{i = 1}^n {\alpha _i}\mathit{\boldsymbol{\kappa }}(z, {x_i}) $ |
式中κ(z, xi)=φT(z)φ(xi)。
基于核的岭回归的闭式解为
| $ \mathit{\boldsymbol{\alpha }} = {\left( {\mathit{\boldsymbol{K}} + \lambda \mathit{\boldsymbol{I}}} \right)^{-1}}y $ | (4) |
式中:K为所有训练样本之间的核相关矩阵,其元素Kij=κ(xi, xj)表示样本对(xi, xj)之间的点积;α是系数αi的向量。
K是循环矩阵,对式(4)对角化得
| $ \mathit{\boldsymbol{\hat \alpha }} = \frac{{{y^ \wedge }}}{{{{\hat {\boldsymbol{K}}}^{xx}} + \lambda }} $ | (5) |
式中kxx是核相关矩阵K=C(kxx)的第一行。
1.2.3 回归检测分析用Kz表示所有训练样本和所有候选图像块之间的核矩阵。样本和图像块分别是基样本x和基图像块z的循环移位。和1.2.2节类似,定义核矩阵:
| $ {\mathit{\boldsymbol{K}}^z} = C({k^{xz}}) $ |
式中kxz是x和z的核相关。根据式(4),可以计算出所有候选图像块的回归函数为
| $ f\left( z \right) = {\mathit{\boldsymbol{K}}^z}\alpha $ | (6) |
注意f(z)是一个矢量,包含所有z的循环移位的输出,即全检测响应。为了有效地计算式(6),将它对角化得
| $ \hat f\left( z \right) = {{\mathit{\boldsymbol{\hat k}}}^{xz}} \odot \hat \alpha $ |
式中系数
| $ {\mathit{\boldsymbol{k}}^{xx'}} = \exp \left( {\frac{{-1}}{{{\sigma ^2}}}\left( {{{\left\| \mathit{\boldsymbol{x}} \right\|}^2} + {{\left\| \mathit{\boldsymbol{x}} \right\|}^2}-2{F^{-1}}\left( {{{\mathit{\boldsymbol{\hat x}}}^*} \odot \mathit{\boldsymbol{\hat x'}}} \right)} \right)} \right) $ | (7) |
核相关函数只需计算点乘和向量范数,可以将单通道的KCF扩展到多通道,使用更多维特征代替原始图像的自然灰度像素。本文采用颜色[9]和方向梯度直方图(histogram of oriented gradients, HOG)特征,这两种特征相互补充。假设C+C1个通道的每一个向量连接构成向量x,即
| $ \begin{array}{c} \mathit{\boldsymbol{k}}_C^{^{xx'}} = \\ \exp \left( {\frac{{-1}}{{{\sigma ^2}}}\left( {{{\left\| \mathit{\boldsymbol{x}} \right\|}^2} + {{\left\| \mathit{\boldsymbol{x}} \right\|}^2}-2{F^{-1}}\left( {\sum\limits_C {\mathit{\boldsymbol{\hat x}}_C^{^*}} \odot \mathit{\boldsymbol{\hat x}}{\mathit{\boldsymbol{'}}_C}} \right)} \right)} \right) \end{array} $ |
KCF通过替换中值流跟踪器融入到TLD中,这有助于克服TLD中值流跟踪器的缺点和实现更稳定的目标跟踪。当目标在当前图像帧中消失后,KCF开始跟踪背景,把背景当作目标。而目标重新出现时,KCF依然跟踪背景;而改进算法包含TLD的学习部分,所以可以继续跟踪重新出现的目标。另外,在跟踪模块利用多特征融合,加入图像的颜色信息,这样能进一步提高算法的跟踪性能。虽然改进算法的思想很简单,但该改进算法非常有效,既提高了目标跟踪的成功率又增强了算法的适用性。改进算法的方案如图 1所示。
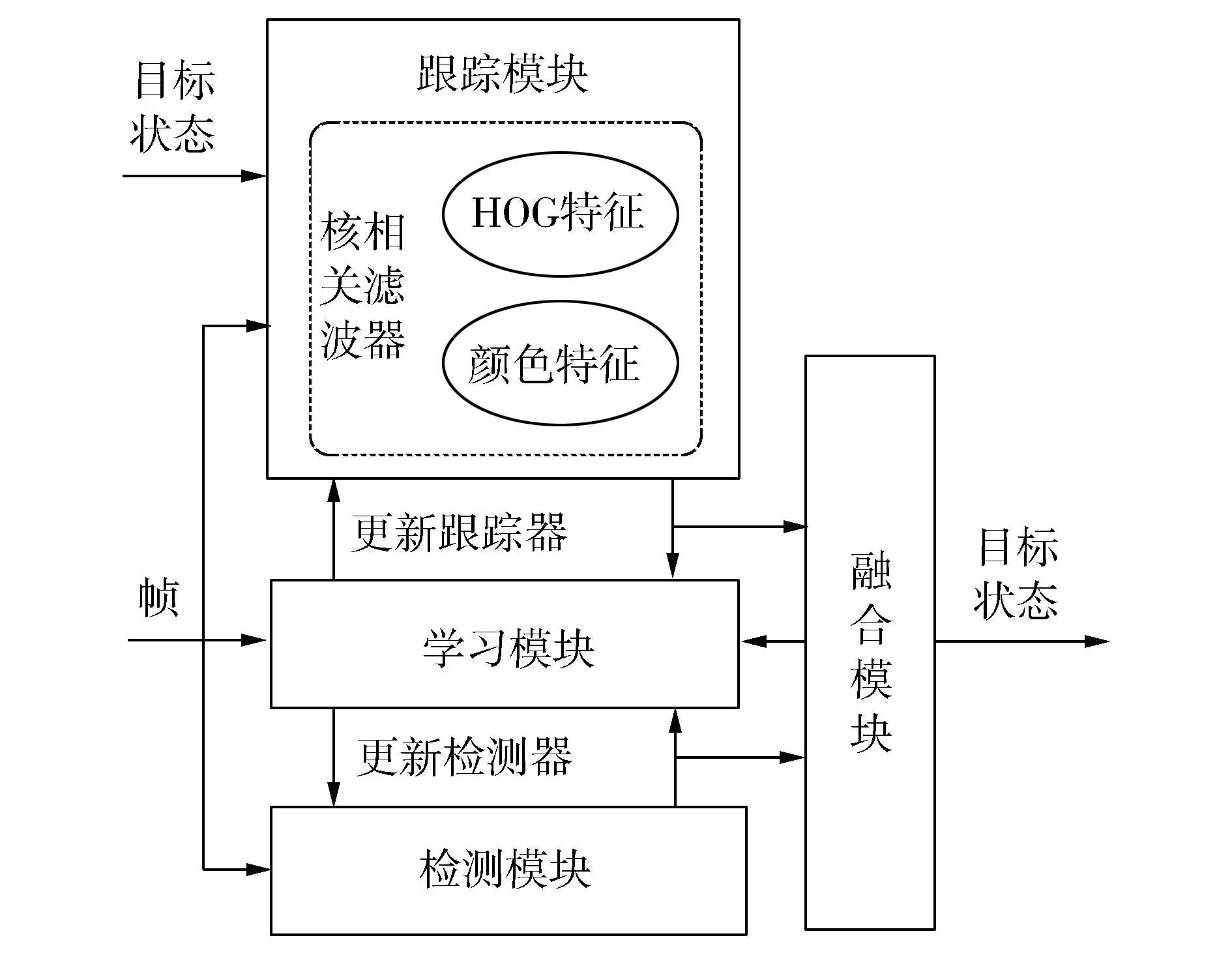
|
Download:
|
| 图 1 本文提出的方案 | |
在本文中,两个包围框bbox1和bbox2之间的重叠度用O(bbox1, bbox2)表示,其计算公式为
| $ O({\rm{bbo}}{{\rm{x}}_1}, {\rm{bbo}}{{\rm{x}}_2}) = \frac{{{\rm{area}}({\rm{bbo}}{{\rm{x}}_1} \cap {\rm{bbo}}{{\rm{x}}_2})}}{{{\rm{area}}({\rm{bbo}}{{\rm{x}}_1} \cup {\rm{bbo}}{{\rm{x}}_2})}} $ |
其中area(·)表示求面积。Sc和Sr分别表示保守相似度和相关相似度,文献[3]已给出详细的概念和计算表达式,本文在此不再详细叙述。
改进算法的实现过程如下:
1) 初始化跟踪框。
2) 输入当前视频帧。
3) 检测部分:由检测模块的级联分类器检测得到图像块并进行聚类,然后计算每个类的保守相似度
4) 跟踪部分:利用特征融合的KCF目标跟踪器输出一个目标图像块,并计算该图像块的保守相似度Skbbc。
5) 检测和跟踪融合:检测和跟踪融合过程如算法1所示。
算法1融合模块处理过程
| $ \begin{array}{l} \begin{array}{*{20}{l}} {1)\;{\rm{if}}\;S_{_{kbb}}^{^c} > 0.5}\\ {2)\;{\rm{if}}\;O(kbb, db{b_i}) > 0.7\& \& S_{_{db{b_i}}}^{^r} > 0.6\;{\rm{then}}}\\ {3)\;dbb = {\rm{sum}}(db{b_i})}\\ {4)\;fbb = {\rm{mean}}\left( {10*kbb, dbb} \right)}\\ {5)\;{\rm{end}}\;{\rm{if}}}\\ {6)\;{\rm{else}}\;{\rm{if}}\;O(kbb, db{b_i}) < 0.4\& \& S_{_{dbb}}^{^c} > 0.65\;{\rm{then}}} \end{array}\\ \begin{array}{*{20}{l}} {7)\;fbb = dbb}\\ {8)\;{\rm{else}}}\\ {9)\;{\rm{object}}\;{\rm{is}}\;{\rm{lost}}}\\ {10)\;{\rm{end}}\;{\rm{if}}} \end{array} \end{array} $ |
① 算法1中的(1)至(5)行:如果KCF的输出包围框的保守相似度Skbbc大于0.5,认为跟踪器有效,对满足条件O(kbb, dbbi)>0.7和Srdbbi>0.6的检测器的输出包围框dbbi进行累加得到dbb,然后对kbb和dbb求加权平均得到最终的输出包围框fbb;②算法1中的(6)至(7)行:认为跟踪器无效,从检测器输出的图像块中找到距离跟踪器最远(O(kbb, dbbi 较小)的一个,同时它的保守相似度大于给定阈值,则选择该图像块作为最终的输出;③算法1中的(8)至(9)行:目标丢失。
6) 学习和更新。TLD的学习模块通过正负样本进行在线学习;TLD的检测器通过在线训练分类器进行更新;KCF跟踪模块通过检测器对其进行初始化来更新目标位置,并由循环移位生成正负样本,利用核相关滤波器预测下一帧目标的位置。该步骤中,学习模块在线学习、检测器更新以及跟踪器重新初始化的具体过程如图 2所示。
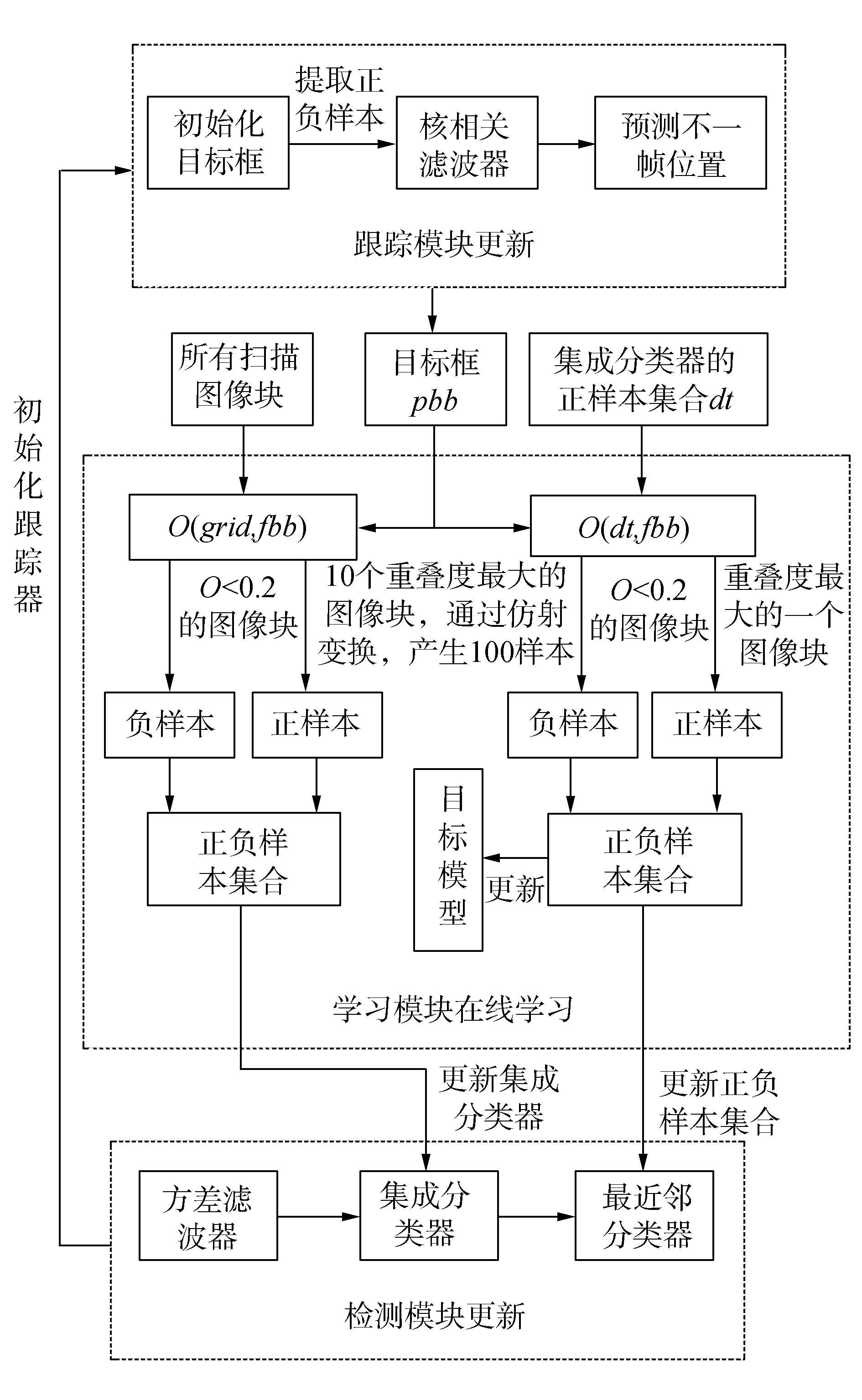
|
Download:
|
| 图 2 学习和更新过程 | |
7) 跟踪下一帧,返回步骤2)。
3 实验结果与性能分析改进算法与TLD跟踪算法和KCF跟踪算法在基准数据集[10]上进行对比实验,这些试验序列包括目标快速运动、遮挡、非刚性形变和旋转等挑战条件,如表 1所示。跟踪算法在MATLAB2015b上实现,实验环境是:处理器为Intel-i3,主频为2.53 GHz,内存为4 GB,操作系统为Windows 7。
|
|
表 1 实验测试序列描述 |
在本文中,采用精度和成功率来评估跟踪算法的鲁棒性[11-12]。
1) 精度图
跟踪精度的一个广泛使用的评价指标是中心位置误差(center location error, CLE),即跟踪目标框中心位置与实际(ground truth)目标框中心位置之间的像素距离。精度图用来评估跟踪算法的整体性能,其被定义为所有跟踪帧的CEL小于给定CEL阈值的帧数占总帧数的百分比,CEL阈值的变化范围是0~50。
2) 成功率图
另一种评估标准为包围框重叠度O(BG, BT),简记为O,其中BG是目标的实际包围框,BT是跟踪包围框。用成功率图来测量视频序列的跟踪性能,即统计所有跟踪帧的包围框重叠度O大于给定的阈值O0的帧数Nsuccess占总帧数Ntotal的比率,计算公式为
| $ p(O > {O_0}) = \frac{{{N_{{\rm{success}}}}}}{{{N_{{\rm{total}}}}}}, {O_0} \in \left[{0, 1} \right] $ |
3种跟踪算法的精度图和成功率图如图 3所示,本文采用CLE阈值为20像素时的精度值(图例里的数值)对跟踪算法进行排序。根据每种算法的成功率图曲线下的面积(area under curve, AUC)大小(图例里的数值)对跟踪算法进行排序。本文也给出了平均包围框重叠度(average bounding box overlap score, AOS),如表 2所示,通过对不同挑战条件的4个视频序列的跟踪,从表中可以看出,改进算法的AOS明显高于TLD和KCF。
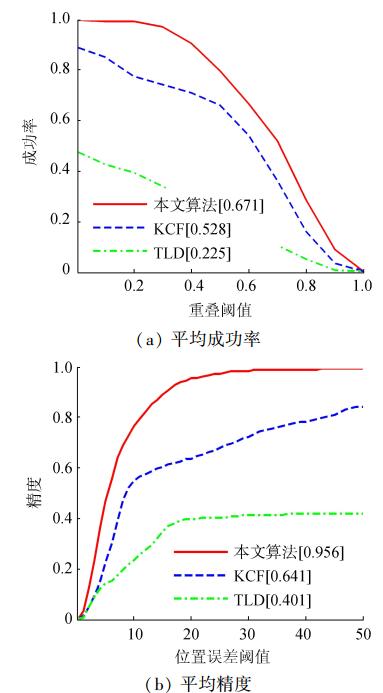
|
Download:
|
| 图 3 所有测试视频的平均成功率图和平均精度图 | |
|
|
表 2 平均包围框重叠度 |
为了分析不同跟踪挑战条件对算法的影响,图 4~7给出了具有代表性帧的跟踪结果截图。在图 4中,序列包含大量的遮挡和因快速移动而引起的模糊。TLD中的中值流跟踪器和级联检测器将会失效,导致跟踪失败。而改进算法会持续跟踪,直到跟踪结束。如图 5所示,要跟踪的目标是一个非刚性运动的人,大量的肢体运动影响了TLD的学习能力,导致跟踪失败。改进算法融合了KCF,而KCF对于非刚性形变的目标跟踪效果良好。所以改进算法的跟踪效果明显好于TLD。图 7展示了目标全旋转的跟踪情景,在该情景中,TLD的中值光流跟踪器会发生漂移,只有当目标重新出现且学习模块保留着先前目标的正负样本集合时才可能重新初始化,继续跟踪目标。学习模块保留的正负样本集合如图 8所示。而改进算法在旋转的过程中一直保持跟踪。在图 7中,当目标消失后重新出现时,KCF开始跟踪背景,目标重新跟踪失败。而改进算法继续跟踪,因为改进算法包含TLD的学习模块。

|
Download:
|
| 图 4 快速移动跟踪情景(测试序列1) | |

|
Download:
|
| 图 5 非刚性目标跟踪情景(测试序列2) | |

|
Download:
|
| 图 6 全旋转情景(测试序列3) | |

|
Download:
|
| 图 7 重新跟踪情景(测试序列4) | |

|
Download:
|
| 图 8 学习模块保留的正负样本集合 | |
表 3是文中3种算法在不同视频序列中的平均帧率。从表中可以看出,改进算法的速度不及原始TLD算法,但以较少的帧率为代价,达到了跟踪性能的极大提升。
|
|
表 3 平均帧率 |
通过在不同视频序列上对跟踪算法进行测试,实验结果证明了本文算法具有较高的目标跟踪成功率。本文的主要改进如下:
1) 有效地对TLD和KCF进行融合,提出一种基于核相关滤波器的TLD目标跟踪算法。在该算法中,TLD的学习模块解决了改进算法对目标消失又重现后的继续跟踪问题;而KCF增强了全旋转、快速移动和非刚性目标跟踪的鲁棒性。
2) 利用特征融合改进跟踪模块,进一步增强改进算法的整体跟踪性能。
目前提出的大部分跟踪算法只适合特定目标跟踪场景,对于一些其他场景的跟踪效果较差,而改进算法适合大部分现实场景的目标跟踪。但改进算法引入的特征融合增加了一部分计算成本,因此下一步的研究方向是在保证算法的跟踪成功率和适用性的同时降低算法的复杂度。
| [1] |
LI Yang, ZHU Jianke, HOI S C H. Reliable patch trackers: robust visual tracking by exploiting reliable patches[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA: IEEE, 2015: 353-361. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7298632
( 0) 0)
|
| [2] |
SMEULDERS A W M, CHU D M, CUCCHIARA R, et al. Visual tracking:an experimental survey[J]. IEEE transactions on pattern analysis and machine intelligence, 2014, 36(7): 1442-1468. DOI:10.1109/TPAMI.2013.230 ( 0) 0)
|
| [3] |
KALAL Z, MIKOLAJCZYK K, MATAS J. Tracking-learning-detection[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(7): 1409-1422. DOI:10.1109/TPAMI.2011.239 ( 0) 0)
|
| [4] |
KALAL Z, MATAS J, MIKOLAJCZYK K. Online learning of robust object detectors during unstable tracking[C]//Proceedings of the IEEE 12th International Conference on Computer Vision Workshops. Kyoto, Japan: IEEE, 2009: 1417-1424. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5457446
( 0) 0)
|
| [5] |
金哲, 刘传才. 加速的TLD算法及其在多目标跟踪中的应用[J]. 计算机系统应用, 2016, 25(6): 196-201. ( 0) 0)
|
| [6] |
邢藏菊, 温兰兰, 何苏勤. TLD视频目标跟踪器快速匹配的研究[J]. 小型微型计算机系统, 2015, 36(5): 1113-1116. ( 0) 0)
|
| [7] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 ( 0) 0)
|
| [8] |
KALAL Z, MATAS J, MIKOLAJCZYK K. P-N learning: bootstrapping binary classifiers by structural constraints[C]//Proceedings of 2010 IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, USA: IEEE, 2010: 49-56. https://www.computer.org/csdl/proceedings/cvpr/2010/6984/00/05540231-abs.html
( 0) 0)
|
| [9] |
VAN DE WEIJER J, SCHMID C, VERBEEK J, et al. Learning color names for real-world applications[J]. IEEE transactions on image processing, 2009, 18(7): 1512-1523. DOI:10.1109/TIP.2009.2019809 ( 0) 0)
|
| [10] |
WU Yi, LIM J, YANG M H. Online object tracking: a benchmark[C]//Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, USA: IEEE, 2013: 2411-2418. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6619156
( 0) 0)
|
| [11] |
EVERINGHAM M, VAN GOOL L, WILLIAMS C K I, et al. The Pascal visual object classes (VOC) challenge[J]. International journal of computer vision, 2010, 88(2): 303-338. DOI:10.1007/s11263-009-0275-4 ( 0) 0)
|
| [12] |
WU Yunxia, JIA Ni, SUN Jiping. Real-time multi-scale tracking based on compressive sensing[J]. The visual computer, 2015, 31(4): 471-484. DOI:10.1007/s00371-014-0942-5 ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


