能量回收技术是无线传感网络自供能和微型化发展的关键技术之一,压电能量回收技术因其具有低成本、高能量密度、无电磁干扰和易系统集成等特点而发展迅速。近年来有许多学者研究了利用悬臂梁式压电振动能量回收装置最大限度地获取电能的问题[1-2],研究成果表明回收能量的大小与悬臂梁和压电片的厚度比[3]、悬臂梁的结构尺寸[4-5]、压电材料的性能[6]等有关,确定了回收装置的机械结构和压电片材料后的压电片粘贴位置和尺寸显得尤为重要。刘树林等[7]通过测试开路电压、短路电流和LED功率等实现了基于Euler-Bernoulli梁模型的压电振动发电机前二阶振型状态下压电片位置优化;LI Hua等[8]通过对锥形壳压电能量回收装置的开路电压方程、能量方程求导实现了压电片尺寸优化。针对振动主动控制研究领域中的压电片位置与尺寸优化问题,有学者提出采用遗传算法[9-11]和粒子群算法[12-14]来解决。
从目前所查阅的文献看,针对悬臂梁式压电振动能量回收装置上压电片位置和尺寸同时优化的问题还鲜见报道。
文中研究运用标准粒子群算法实现悬臂梁式压电振动能量回收装置(以下简称压电悬臂梁)上压电片粘贴位置和尺寸的优化问题。首先推导出压电悬臂梁的能量方程;然后以能量方程为目标函数,运用标准粒子群算法优化压电片位置和尺寸,通过算例得到一阶、二阶、三阶模态下压电片最优位置和尺寸;再者运用Abaqus软件进行仿真分析。
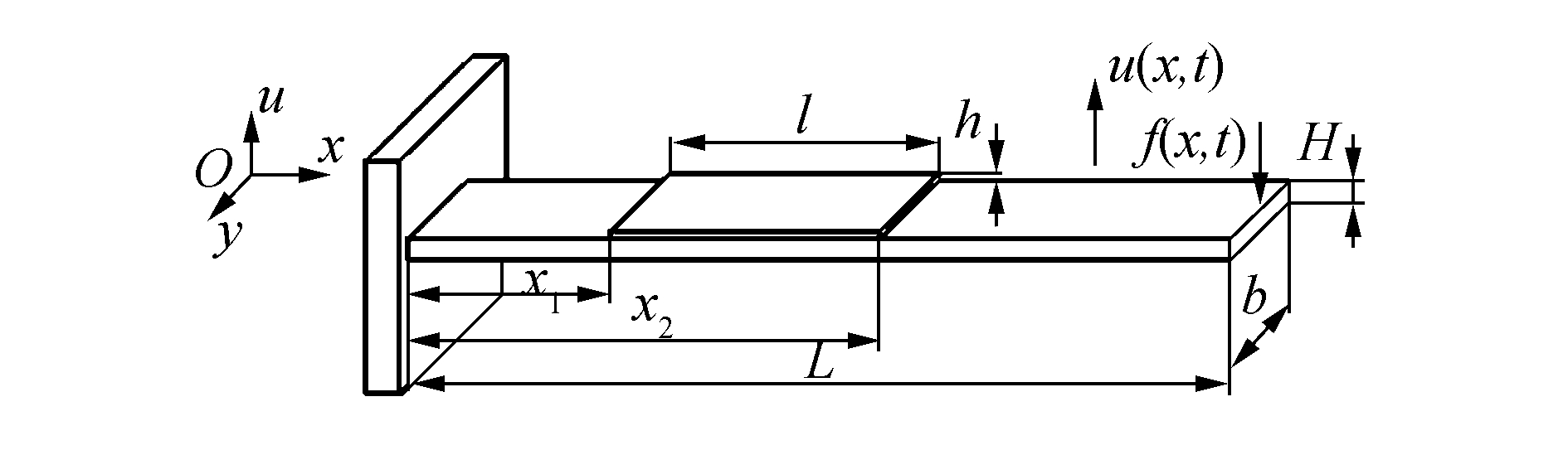
1 能量方程压电悬臂梁的结构主要有悬臂梁、压电片和支座,如图 1所示。设悬臂梁长为L,宽为b,厚为H;在悬臂梁上粘贴压电片,压电片左端距悬臂梁固定端为x1,右端距悬臂梁固定端距离为x2,压电片长为l,宽与梁宽b相同,厚为h,h≤H,可以认为粘贴压电片后的悬臂梁是均匀的。
|
图 1 压电悬臂梁的结构示意 |
悬臂梁自由端受激励时的主要变形为弯曲变形,基于Euler-Bernoulli假设,压电悬臂梁的振动形式由式(1)的微分方程描述[12]:
| $ \begin{array}{*{20}{c}} {\rho A\frac{{{\partial ^2}u\left( {x,t} \right)}}{{\partial {t^2}}} + c\frac{{{\partial ^5}u\left( {x,t} \right)}}{{\partial {x^4}\partial t}} + EI\frac{{{\partial ^4}u\left( {x,t} \right)}}{{\partial {x^4}}} = }\\ {f\left( {x,t} \right)\delta \left( {x - L} \right)} \end{array} $ | (1) |
式中:ρ、A、E、I分别为悬臂梁的密度、横截面积、弹性模量、惯性矩、材料阻尼系数;x为梁的位置坐标;u(x, t)为梁的横向振动位移;f(x, t)为梁自由端所受激励;
当悬臂梁在xou平面里做弯曲振动时,梁的横向振动位移可以表达为
| $ u\left( {x,t} \right) = \sum\nolimits_{k = 1}^\infty {{\eta _k}\left( t \right){U_k}\left( x \right)} $ | (2) |
式中:ηk(t)为相对于k阶固有频率ωk的模态坐标函数;Uk(x)为相对于固有频率x1的固有振型函数。
Uk(x)具有如下表达式:
| $ {U_k}\left( x \right) = \cosh \left( {{s_k}x} \right) - \cos \left( {{s_k}x} \right) + {v_k}\left( {\sinh \left( {{s_k}x} \right) - \sin \left( {{s_k}x} \right)} \right) $ | (3) |
式中:
| $ {v_k} = - \frac{{\sinh \left( {{s_k}L} \right) - \sin \left( {{s_k}L} \right)}}{{\cosh \left( {{s_k}L} \right) - \cos \left( {{s_k}L} \right)}} $ | (4) |
sk可以通过悬臂梁频率方程得到:
| $ \cos \left( {{s_k}L} \right)\cosh \left( {{s_k}L} \right) = - 1 $ | (5) |
假设压电悬臂梁在自由端受正弦激励,即f(x, t)=f0sin(ωt),f0为激励幅值,ω为激励频率。将式(5)和式(2)代入式(1)有:
| $ \begin{array}{*{20}{c}} {\rho A\sum\limits_{k = 1}^\infty {{{\ddot \eta }_k}\left( t \right){U_k}\left( x \right)} + c\sum\limits_{k = 1}^\infty {{{\dot \eta }_k}\left( t \right)U_k^{\left( 4 \right)}\left( x \right)} + }\\ {EI\sum\limits_{k = 1}^\infty {{\eta _k}\left( t \right)U_k^{\left( 4 \right)}\left( x \right)} = {f_0}\sin \left( {\omega t} \right)\delta \left( {x - L} \right)} \end{array} $ | (6) |
式中:
由式(3)可以推导得Uk(4)(x)=sk(4)(x),将之代入式(6),得如下方程:
| $ \begin{array}{*{20}{c}} {\rho A\sum\limits_{k = 1}^\infty {{{\ddot \eta }_k}\left( t \right){U_k}\left( x \right)} + c\sum\limits_{k = 1}^\infty {{{\dot \eta }_k}\left( t \right)s_k^4{U_k}\left( x \right)} + }\\ {EI\sum\limits_{k = 1}^\infty {{\eta _k}\left( t \right)s_k^4{U_k}\left( x \right)} = {f_0}\sin \left( {\omega t} \right)\delta \left( {x - L} \right)} \end{array} $ | (7) |
在式(7)两端同时乘以Un(x),Un(x)为相对于固有频率ωn的固有振型函数,并进行如下积分运算:
| $ \begin{array}{l} \int_0^L {\rho A\sum\limits_{k = 1}^\infty {{{\ddot \eta }_k}\left( t \right){U_k}\left( x \right){U_n}\left( x \right){\rm{d}}x} } + \\ \int_0^L {c\sum\limits_{k = 1}^\infty {{{\dot \eta }_k}\left( t \right)s_k^4{U_k}\left( x \right){U_n}\left( x \right){\rm{d}}x} } + \\ \int_0^L {EI\sum\limits_{k = 1}^\infty {{\eta _k}\left( t \right)s_k^4{U_k}\left( x \right){U_n}\left( x \right){\rm{d}}x} } = \\ \int_0^L {{f_0}\sin \left( {\omega t} \right)\delta \left( {x - L} \right){U_n}\left( x \right){\rm{d}}x} \end{array} $ | (8) |
式(8)中
| $ \begin{array}{*{20}{c}} {\int_0^L {\rho A\sum\limits_{k = 1}^\infty {{{\ddot \eta }_k}\left( t \right){U_k}\left( x \right){U_n}\left( x \right){\rm{d}}x} } = }\\ {\rho A{{\ddot \eta }_k}\left( t \right)\left[ {\int_0^L {{U_1}\left( x \right){U_n}\left( x \right){\rm{d}}x} + \int_0^L {{U_2}\left( x \right){U_n}\left( x \right){\rm{d}}x} + } \right.}\\ { \cdots + \int_0^L {{U_{k - 1}}\left( x \right){U_n}\left( x \right){\rm{d}}x} + \int_0^L {{U_k}\left( x \right){U_n}\left( x \right){\rm{d}}x} + }\\ {\left. {\int_0^L {{U_{k + 1}}\left( x \right){U_n}\left( x \right){\rm{d}}x} + \cdots } \right]} \end{array} $ | (9) |
因为Uk(x)和Un(x)满足如下正交条件[15]:
| $ \left\{ \begin{array}{l} \int_0^L {{U_k}\left( x \right){U_n}\left( x \right) = 0} ,n \ne k\\ \int_0^L {{U_k}\left( x \right){U_n}\left( x \right) \ne 0} ,n = k \end{array} \right.\left( {n = 1,2,3, \cdots ,k, \cdots } \right) $ | (10) |
所以对式(9)方括号中的各项,当n=k时,只有
| $ \int_0^L {\rho A\sum\limits_{k = 1}^\infty {{{\ddot \eta }_k}\left( t \right){U_k}\left( x \right){U_n}\left( x \right){\rm{d}}x} } = \rho A{{\ddot \eta }_k}\left( t \right)\int_0^L {U_k^2\left( x \right){\rm{d}}x} $ | (11) |
同理可将式(8)等号左边的第2项和第3项做类似简化,对式(8)等号右边项进行积分计算,这样式(8)可以表达为如下形式:
| $ \begin{array}{*{20}{c}} {\rho A{{\ddot \eta }_k}\left( t \right)\int_0^L {U_k^2\left( x \right){\rm{d}}x} + cs_k^4{{\dot \eta }_k}\left( t \right)\int_0^L {U_k^2\left( x \right){\rm{d}}x} + }\\ {EIs_k^4{\eta _k}\left( t \right)\int_0^L {U_k^2\left( x \right){\rm{d}}x} = {f_0}\sin \left( {\omega t} \right){U_k}\left( L \right)} \end{array} $ | (12) |
即
| $ {{\ddot \eta }_k}\left( t \right) + 2{\xi _k}{\omega _k}{{\dot \eta }_k}\left( t \right) + \omega _k^2{\eta _k}\left( t \right) = {F_k}\sin \left( {\omega t} \right) $ | (13) |
式中:ξk为梁的k阶阻尼比,
对于正弦激励,ηk(t)稳态响应也是正弦形式,即ηk(t)=ηk*sin(ωt+φk)。ηk*为模态坐标的幅值,φk为模态坐标的相位,由式(13)可以得到ηk*、φk为
| $ \eta _k^ * = \frac{{{F_k}}}{{\omega _k^2\sqrt {{{\left( {1 - {{\left( {\frac{\omega }{{{\omega _k}}}} \right)}^2}} \right)}^2} + 4\zeta _k^2{{\left( {\frac{\omega }{{{\omega _k}}}} \right)}^2}} }} $ | (14) |
| $ {\varphi _k} = \arctan \left( {\frac{{2{\xi _k}\left( {\frac{\omega }{{{\omega _k}}}} \right)}}{{1 - {{\left( {\frac{\omega }{{{\omega _k}}}} \right)}^2}}}} \right) $ | (15) |
将式(14)、(15)代入式(2)可得压电悬臂梁横向振动位移表达式为
| $ \begin{array}{*{20}{c}} {u\left( {x,t} \right) = \sum\limits_{k = 1}^\infty {\frac{{{F_k}}}{{\omega _k^2\sqrt {{{\left( {1 - {{\left( {\frac{\omega }{{{\omega _k}}}} \right)}^2}} \right)}^2} + 4\xi _k^2{{\left( {\frac{\omega }{{{\omega _k}}}} \right)}^2}} }}} \cdot }\\ {\sin \left( {\omega t + \arctan \left( {\frac{{2{\xi _k}\left( {\frac{\omega }{{{\omega _k}}}} \right)}}{{1 - {{\left( {\frac{\omega }{{{\omega _k}}}} \right)}^2}}}} \right)} \right){U_k}\left( x \right)} \end{array} $ | (16) |
当ω=ωk时,梁体产生共振,此时压电悬臂梁吸收外界的振动能、产生较高的电能。梁体此时的变形主要为该阶固有频率所对应的主振型,其他各阶振型的影响可忽略不计。因此,压电悬臂梁的横向振动位移即为压电片的应变,由式(2)可知,压电片的应变近似表达式为
| $ u\left( {x,t} \right) \approx {\eta _k}\left( t \right){U_k}\left( x \right) $ | (17) |
根据Maxwell方程和压电理论,压电悬臂梁的开路电压为[16]
| $ \varphi = - \frac{{bh}}{S}\int_x {\left( {{h_{31}}r\frac{{{\partial ^2}u\left( {x,t} \right)}}{{\partial {x^2}}}} \right){\rm{d}}x} $ | (18) |
式中:h31为压电常量;S为压电片有效面积;r为梁的中性面到压电片中性面的距离,
当ω=ωk时,将式(17)、式(3)代入式(18),得开路电压表达式为
| $ \varphi = - \frac{{bh}}{S}\int_x {\left( {{h_{31}}r\frac{{{\partial ^2}\left( {{\eta _k}\left( t \right){U_k}\left( x \right)} \right)}}{{\partial {x^2}}}} \right){\rm{d}}x} = \\ - \frac{{bh{h_{31}}rs_k^2{\eta _k}\left( t \right)}}{S}\int_x {\left[ {\cosh \left( {{s_k}x} \right) + \cos \left( {{s_k}x} \right) + {v_k}\left( {\sinh \left( {{s_k}x} \right) + \sin \left( {{s_k}x} \right)} \right)} \right]{\rm{d}}x} $ | (19) |
当不考虑时域时,式(19)中ηk(t)可取为ηk*,这样可得开路电压幅值,表达为如下形式:
| $ {\varphi ^ * } = \frac{{bh{h_{31}}rs_k^2\eta _k^ * }}{S}\int_x {\left[ {\cosh \left( {{s_k}x} \right) + \cos \left( {{s_k}x} \right) + {v_k}\left( {\sinh \left( {{s_k}x} \right) + \sin \left( {{s_k}x} \right)} \right)} \right]{\rm{d}}x} $ | (20) |
求得了压电片的开路电压方程后,可以推导出压电片的能量方程。考虑电能从振动中转化而来并存于压电片中,不考虑能量回收电路的影响,即压电片的能量为开路形式,则能量方程表达为[17]
| $ Q = \frac{1}{2}C{\varphi ^2} $ | (21) |
式中:C为压电片电容,
将式(20)代入式(21),且压电片在梁长方向上是从x1到x2,这样能量方程可以表达为
| $ {Q^ * } = \frac{1}{2}{C^{\left( {\varphi * } \right)}}2 = \frac{1}{2}\frac{{{\varepsilon _{33}}bhh_{31}^2{r^2}s_k^4{{\left( {\eta _k^ * } \right)}^2}}}{{{x_2} - {x_1}}} \cdot\\ {\left[ {\int_{{x_1}}^{{x_2}} {\left( {\cosh \left( {{s_k}x} \right) + \cos \left( {{s_k}x} \right) + {v_k}\left( {\sinh \left( {{s_k}x} \right) + \sin \left( {{s_k}x} \right)} \right)} \right){\rm{d}}x} } \right]^2} $ | (22) |
要使回收的能量Q*尽可能的大,就要取得最优的压电片左端位置坐标x1和右端位置坐标x2,0≤x1≤x2≤L。取得了x1和x2,也就得到了最优贴片位置即压电片中心位置点
| $ {q_k}\left( {{x_1},{x_2}} \right) = \frac{1}{{{x_2} - {x_1}}}{\left[ {\int_{{x_1}}^{{x_2}} {\left( {\cosh \left( {{s_k}x} \right) + \cos \left( {{s_k}x} \right) + {v_k}\left( {\sinh \left( {{s_k}x} \right) + \sin \left( {{s_k}x} \right)} \right)} \right){\rm{d}}x} } \right]^2} $ | (23) |
比较式(22)、(23),qk(x1, x2)取得最大值时Q*取得最大值。qk(x1, x2)大小与x1和x2取值有关,可采用对于连续取值的全局寻优问题寻优性能较好的标准粒子群优化算法(particle swarm optimization, PSO)求得使qk(x1, x2)取最大值的x1和x2。
2.1 标准粒子群优化算法考虑形如
| $ \begin{array}{*{20}{c}} {{V_{i,j}}\left( {t + 1} \right) = w \cdot {V_{i,j}}\left( t \right) + {c_1} \cdot {r_{1,i,j}}\left( t \right) \cdot }\\ {\left( {{P_{i,j}}\left( t \right) - {X_{i,j}}\left( t \right)} \right) + {c_2} \cdot {r_{2,i,j}}\left( t \right) \cdot \left( {{G_{i,j}}\left( t \right) - {X_{i,j}}\left( t \right)} \right)} \end{array} $ | (24) |
| $ {X_{i,j}}\left( {t + 1} \right) = {V_{i,j}}\left( {t + 1} \right) + {X_{i,j}}\left( t \right) $ | (25) |
式中:1≤i≤M,1≤j≤N;t表示迭代次数;c1、c2统称为学习因子,通常取值均为2,r1, i, j(t)、r2, i, j(t)为[0, 1]区间内相互独立生成的均匀分布的随机数;每个粒子的飞行速度范围满足Vi, j(t)∈[-Vmax, Vmax],同时粒子们相应的位置范围也满足一定的条件,即Xi, j(t)∈[-Xmax, Xmax]。式(24)中w为惯性权重:
| $ w\left( t \right) = \frac{{\left( {{w_{\max }} - {w_{\min }}} \right) \cdot \left( {{t_{\max }} - t} \right)}}{{{t_{\max }}}} + {w_{\min }} $ |
式中:tmax为最大迭代次数;wmax为最大惯性权重;wmin为最小惯性权重。
标准PSO算法的进化过程可概括为以下几个步骤:
1) 参数初始化:设定粒子群规模M,粒子空间维数N;选取最大迭代次数tmax;学习因子为2;粒子飞行最大速度,粒子位置变化范围;设定t=0,在N维空间中随机选择粒子的位置与速度;选取最大惯性权重和最小惯性权重。
2) 计算种群中每个粒子当前位置Xi(t)处的适应度函数值,将适应度函数依然定义为式(23)。针对每个粒子,比较当前位置Xi(t)对应的适应度函数值和其个体历史最优位置Pi(t)对应的适应度函数值,优则替换Pi(t)的适应度函数值,并有Pi(t)=Xi(t),反之则保持不变。
3) 针对各个粒子,分析个体历史最优位置Pi(t)和群体历史最优位置G(t),并比较两者所对应的适应度函数值,优则替换G(t)的适应度函数值,并有G(t)=Pi(t),反之则保持不变。
4) 根据进化方程(24)、(25)分别对所有粒子的位置与速度进行更新。
5) 若未达到最大进化代数tmax,则置t=t+1,返回步骤2)继续执行,若达到最大进化代数,则以得到的具有最大适应度的个体作为最优解输出。
2.2 算例运用2.1节提出的基于标准PSO算法的压电片位置和尺寸优化方法,给出压电片的最优贴片位置和最优尺寸的算例,计算前三阶模态下压电片的最优贴片位置和最优尺寸。
取悬臂梁长L=0.1 m,由式(4)、(5)可算得vk、sk(k=1, 2, 3),再由式(23)可得一阶、二阶、三阶模态下的目标函数分别为
| $ {q_1}\left( {{x_1},{x_2}} \right) = \\ \frac{1}{{\left( {{x_2} - {x_1}} \right)}}{\left[ {\int_{{x_1}}^{{x_2}} {\left( {\cosh \left( {18.751x} \right) + \cos \left( {18.751x} \right) + 0.7341\left( {\sinh \left( {18.751x} \right) + \sin \left( {18.751x} \right)} \right)} \right){\rm{d}}x} } \right]^2} $ | (26) |
| $ {q_2}\left( {{x_1},{x_2}} \right) =\\ \frac{1}{{\left( {{x_2} - {x_1}} \right)}}{\left[ {\int_{{x_1}}^{{x_2}} {\left( {\cosh \left( {46.941x} \right) + \cos \left( {46.941x} \right) + 1.0185\left( {\sinh \left( {46.941x} \right) + \sin \left( {46.941x} \right)} \right)} \right){\rm{d}}x} } \right]^2} $ | (27) |
| $ {q_3}\left( {{x_1},{x_2}} \right) = \\ \frac{1}{{\left( {{x_2} - {x_1}} \right)}}{\left[ {\int_{{x_1}}^{{x_2}} {\left( {\cosh \left( {78.548x} \right) + \cos \left( {78.548x} \right) + 0.9992\left( {\sinh \left( {78.548x} \right) + \sin \left( {78.548x} \right)} \right)} \right){\rm{d}}x} } \right]^2} $ | (28) |
标准PSO优化算法各参数取值如下:目标函数依然分别为q1(x1, x2)、q2(x1, x2)、q3(x1, x2),粒子维数为2,粒子飞行最大速度为0.1,粒子位置变化范围为[0, 0.1],最大迭代次数取100,粒子群规模取40,学习因子取2,最大惯性权重取0.9,最小惯性权重取0.4。运用MATLAB软件运行了标准PSO优化程序,获得了0.1 m梁的前三阶模态下压电片的左端最优位置x1和右端最优位置x2,结果如表 1所示。
|
|
表 1 标准PSO算法0.1 m梁前三阶模态下压电片最优贴片位置与最优尺寸 |
为更好地与标准PSO优化算法结果进行比较,运用MATLAB软件运行了遗传算法优化程序,程序控制参数取值如下:设计变量x1和x2的取值范围为[0,0.1]。取编码精度δ =0.000 1,x1和x2的编码长度可由式
|
|
表 2 遗传算法0.1 m梁前三阶模态下压电片最优贴片位置与最优尺寸 |
观察表 1、2可知,分别运用标准PSO和遗传算法得到的0.1 m梁前三阶模态下压电片最优位置的结果非常接近。压电片最优位置和最优尺寸具有如下结论:一阶模态下压电片的最优贴片位置在梁根部,最优尺寸为梁长一半;二阶模态下压电片的最优贴片位置在梁中部,最优尺寸为梁长一半;三阶模态下压电片的最优贴片位置在距梁根部三分之二处,最优尺寸为梁长的三分之一。
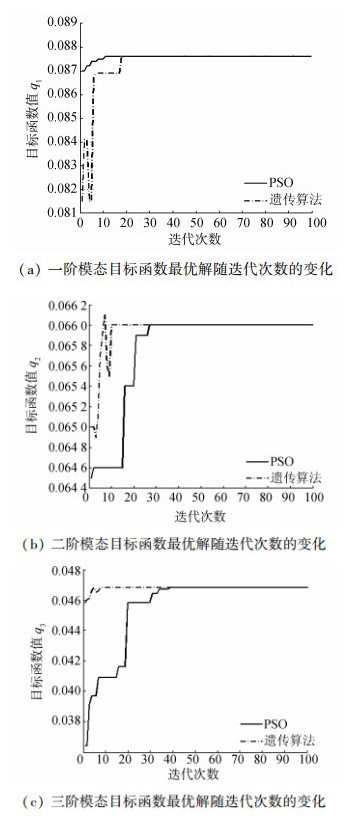
进一步分别给出一阶、二阶、三阶模态下,运用标准PSO和遗传算法得到目标函数值最优解随迭代次数的变化曲线如图 2所示, 可知运用标准PSO和遗传算法得到最优解的收敛速度也是很接近的。
|
图 2 目标函数最优解随迭代次数的变化 |
采用abaqus对压电悬臂梁进行仿真分析。模型为在悬臂梁基板上贴一层相对很薄的压电片,梁基板和压电片的材料属性参数见表 3;压电片材料PZT-4的属性见表 4。悬臂梁基板采用8节点六面体线性减缩积分的三维实体单元C3D8R,压电片采用8节点六面体线性压电单元C3D8E。
|
|
表 3 悬臂梁和压电片的材料参数 |
|
|
表 4 PZT-4材料属性 |
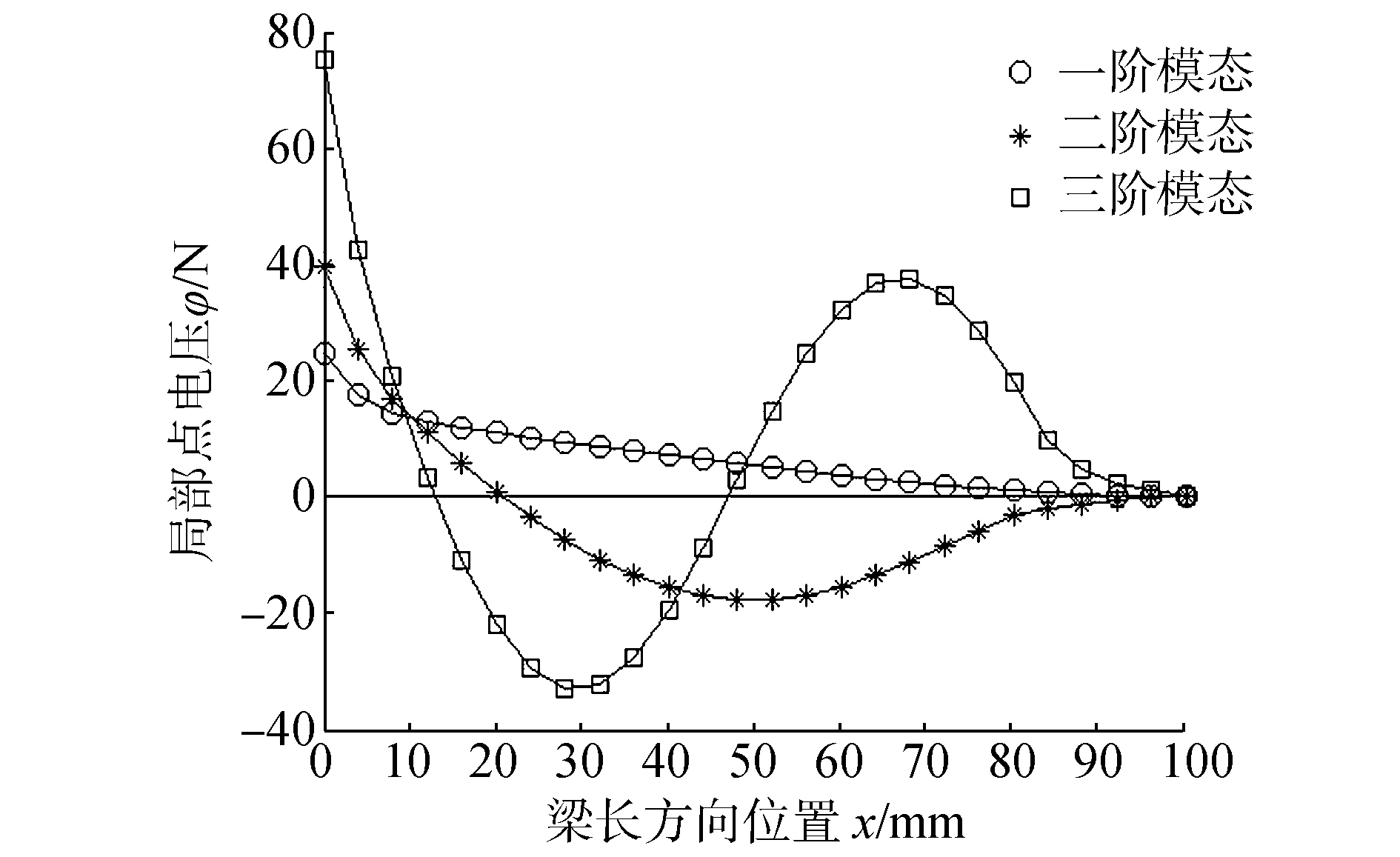
对100 mm长压电悬臂梁进行仿真分析。悬臂梁基板尺寸为:长L=100 mm,宽B=10 mm,厚H=1 mm;压电片尺寸为:长l=100 mm,宽b=10 mm,厚h=0.1 mm。对该模型进行模态分析,得到一阶、二阶、三阶固有频率分别为f1=57.72 Hz,f2=361.42 Hz,f3=1 012.5 Hz。在悬臂梁自由端分别施加频率为一阶固有频率f1、二阶固有频率f2和三阶固有频率f3的正弦激励,幅值分别为1、0.3、0.1 mm,通过仿真分析分别得到一阶、二阶和三阶模态下沿梁长方向均匀分布的26个点的点电压,仿真结果如图 3所示。
|
图 3 100 mm梁前三阶模态下局部点电压 |
由图 3可知,一阶模态下压电片最优贴片位置在梁根部;二阶模态下压电片可能最优贴片位置在梁根部或梁中部;三阶模态下压电片可能最优贴片位置在梁根部、梁长的三分之一处或梁长的三分之二处。
1) 仿真分析并计算一阶模态下的能量,将长分别为5、10、20、30、40、50、60、70、80、90 mm,宽与厚为10 mm与0.1 mm的压电片从悬臂梁根部开始分别贴于10个相同规格的梁上,在梁自由端施加幅值1 mm、频率f1的正弦激励,通过仿真分析得到这10个压电片在激振力作用下各自产生的开路电压,再由式(22)计算得到各压电能量值,结果如图 4所示。

|
图 4 100 mm梁一阶模态下的压电能量 |
2) 仿真计算二阶模态下的能量,按压电片贴于梁根部与梁中部两种情况讨论。当压电片贴于悬臂梁根部时,将长分别为5、10、20、30、40、50、60、70、80、90 mm的压电片从梁根部开始贴于10个梁上,在梁自由端施加幅值1 mm、频率f2的正弦激励,通过仿真分析与计算得到模态二下这10种长度压电片贴于梁根部时的压电能量,结果如图 5中Q21所示;当压电片贴于梁中部时,即压电片中心置于悬臂梁中部,将这10种长度的压电片分别贴于10个悬臂梁上,在梁自由端施加幅值为1 mm、频率为f2的正弦激励,通过仿真分析与计算得到模态二下这10种长度压电片贴于梁中部时的压电能量,结果如图 5中Q22所示。

|
图 5 100 mm梁二阶模态下的压电能量 |
3) 仿真计算三阶模态下的能量,分压电片贴于悬臂梁根部、梁长的三分之一和梁长的三分之二处3种情况讨论。当压电片贴于梁根部时,将长分别为5、10、20、30、40、50、60 mm的压电片从梁根部开始贴于7个规格相同的梁上,在梁自由端施加幅值1 mm、频率f3的正弦激励,通过仿真分析与计算得到模态三下这7种长度压电片贴于梁根部时的压电能量,结果如图 6中Q31所示;当压电片贴于梁长的三分之一处时,即压电片中心置于距梁固定端35 mm处,将这7种长度的压电片贴于7个梁上,在梁自由端施加幅值1 mm、频率f3的正弦激励,通过仿真分析与计算得到模态三下这7种长度压电片贴于梁长三分之一处时的压电能量,结果如图 6中Q32所示;当压电片贴于梁长的三分之二处时,即压电片中心置于距梁固定端70 mm处,将这7种长度的压电片贴于7个梁上,在梁自由端施加幅值1 mm、频率f3的正弦激励,通过仿真分析与计算得到模态三下这7种长度压电片贴于梁长三分之二处时的压电能量,结果如图 6中Q33所示。

|
图 6 100 mm梁三阶模态下的压电能量 |
观察图 3~6,通过100 mm长的压电悬臂梁的仿真分析结果可知,前三阶模态下压电片最优位置和最优尺寸基本一致:一阶模态下压电片的最优贴片位置在悬臂梁根部,最优尺寸约为梁长的一半;二阶模态下,压电片最优贴片位置在梁中部,最优尺寸约为梁长一半;三阶模态下,压电片最优贴片位置在梁的三分之二处,最优尺寸约为梁长的三分之一。该仿真结果与2.2节标准PSO算法取得的结果一致,说明标准PSO算法是实现振动能量回收装置压电片贴片位置和尺寸优化行之有效的方法之一。分析以上对比结果可知,文中运用标准PSO算法获得压电片最优位置和最优尺寸的方法是行之有效的。
4 结论文中实现了基于标准PSO算法的压电悬臂梁上压电片贴片位置和尺寸的优化。首先推导出了压电悬臂梁的能量方程;然后提出了一种基于标准PSO算法的压电悬臂梁上压电片贴片位置和尺寸的优化方法,运用MATLAB软件编制了标准PSO算法优化程序,并通过算例得出了一阶、二阶和三阶模态下压电片左端位置坐标和右端位置坐标,进而计算得到了最优贴片位置与最优尺寸;最后运用Abaqus软件仿真分析得到了前三阶模态下的最优贴片位置与最优尺寸。
比较算例结果与仿真结果可知:
1) 标准PSO算法与Abaqus软件仿真的结果基本吻合:一阶模态下,压电片最优贴片位置位于悬臂梁根部,最优尺寸约为梁长一半;二阶模态下,压电片最优贴片位置位于梁中部,最优尺寸约为梁长一半;三阶模态下,压电片最优贴片位置位于梁的三分之二处,最优尺寸约为梁长的三分之一;
2) 结果验证了运用标准PSO算法实现压电振动能量回收系统中压电片位置和尺寸优化方法的有效性。
| [1] |
文晟, 张铁明, 刘旭, 等. 基于压电效应的振动能量回收装置的研究进展[J]. 机械科学与技术, 2010, 29(11): 1515-1520. ( 0) 0)
|
| [2] |
边义祥, 杨成华. 基于压电材料的振动能量回收技术现状综述[J]. 压电与声光, 2011, 33(4): 611-622. ( 0) 0)
|
| [3] |
阚君武, 唐可洪, 王淑云, 等. 压电悬臂梁发电装置的建模与仿真分析[J]. 光学精密工程, 2008, 16(1): 71-75. ( 0) 0)
|
| [4] |
袁江波, 谢涛, 陈维山, 等. 悬臂梁压电发电装置的实验研究[J]. 振动与冲击, 2009, 28(7): 69-72. ( 0) 0)
|
| [5] |
LIANG Zhu, XU Chundong, REN Bo, et al. Optimization of cantilevered piezoelectric energy harvester with a fixed resonance frequency[J]. Technological sciences, 2014, 57(6): 1093-1100. DOI:10.1007/s11431-014-5556-7 ( 0) 0)
|
| [6] |
SODANO H A, INMAN D J, PARK G. Comparison of piezoelectric energy harvesting devices for recharging batteries[J]. Journal of intelligent material systems and structures, 2005, 16(10): 799-807. DOI:10.1177/1045389X05056681 ( 0) 0)
|
| [7] |
刘树林, 许小勇, 翟宇毅, 等. 振动模态对压电发电机陶瓷片粘贴位置的影响[J]. 光学精密工程, 2011, 19(8): 1801-1809. ( 0) 0)
|
| [8] |
LI Hua, HU Shundi, TZOU H S. Size optimization of conical piezoelectric energy harvester[C]//Proceedings of 2011 Symposium on Piezoelectricity, Acoustic Waves and Device Applications (SPAWDA). Shenzhen, China, 2011:485-488.
( 0) 0)
|
| [9] |
高瑞贞, 张京军, 郑骥, 等. 基于改进遗传算法主动柔性结构压电元件位置优化[J]. 计算力学学报, 2008, 25(4): 542-546. ( 0) 0)
|
| [10] |
DHURI K D, SESHU P. Multi-objective optimization of piezo actuator placement and sizing using genetic algorithm[J]. Journal of sound and vibration, 2009, 323(3/4/5): 495-514. ( 0) 0)
|
| [11] |
HADAS Z, KURFURST J, ONDRUSEK C, et al. Artificial intelligence based optimization for vibration energy harvesting applications[J]. Microsystem technologies, 2012, 18(7/8): 1003-1014. ( 0) 0)
|
| [12] |
潘继, 蔡国平. 桁架结构作动器优化配置的粒子群算法[J]. 工程力学, 2009, 26(12): 35-39. ( 0) 0)
|
| [13] |
潘继, 陈龙祥, 蔡国平. 柔性板压电作动器的优化位置与主动控制实验研究[J]. 振动与冲击, 2010, 29(2): 117-120. ( 0) 0)
|
| [14] |
马天兵, 裘进浩, 季宏丽, 等. 基于粒子群的压电结构多目标同步优化控制[J]. 沈阳工业大学学报, 2012, 34(5): 569-575. ( 0) 0)
|
| [15] |
胡海岩. 机械振动基础[M]. 北京: 北京航空航天大学出版社, 2005: 38-1188.
( 0) 0)
|
| [16] |
TZOU H S. Piezoelectric shells:distributed sensing and control of continua[M]. London: Kluwer Academic Publishers, 1993: 146.
( 0) 0)
|
| [17] |
HU Shundi, CHUANG K C, TZOU H S. PVDF energy harvester on flexible rings[C]//Proceedings of 2010 Symposium on Piezoelectricity, Acoustic Waves and Device Applications (SPAWDA). Xiamen, China, 2010:100-105.
( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


