2. 陕西科技大学 机电工程学院, 陕西 西安 710021
2. Electromechanical Engineering School, Shanxi University of Science & Technology, Xi'an 710021, China
控制式差动无级变速器是由基本型无级变速器对差动轮系进行封闭而成的一种组合式无级变速传动装置。通过选取装置内各不同的传动参数,可以实现精密调速并扩大基本型无级变速器承载能力,或者扩大基本型无级变速器的调速范围,甚至实现过零调速,因而具有广泛的应用前景。
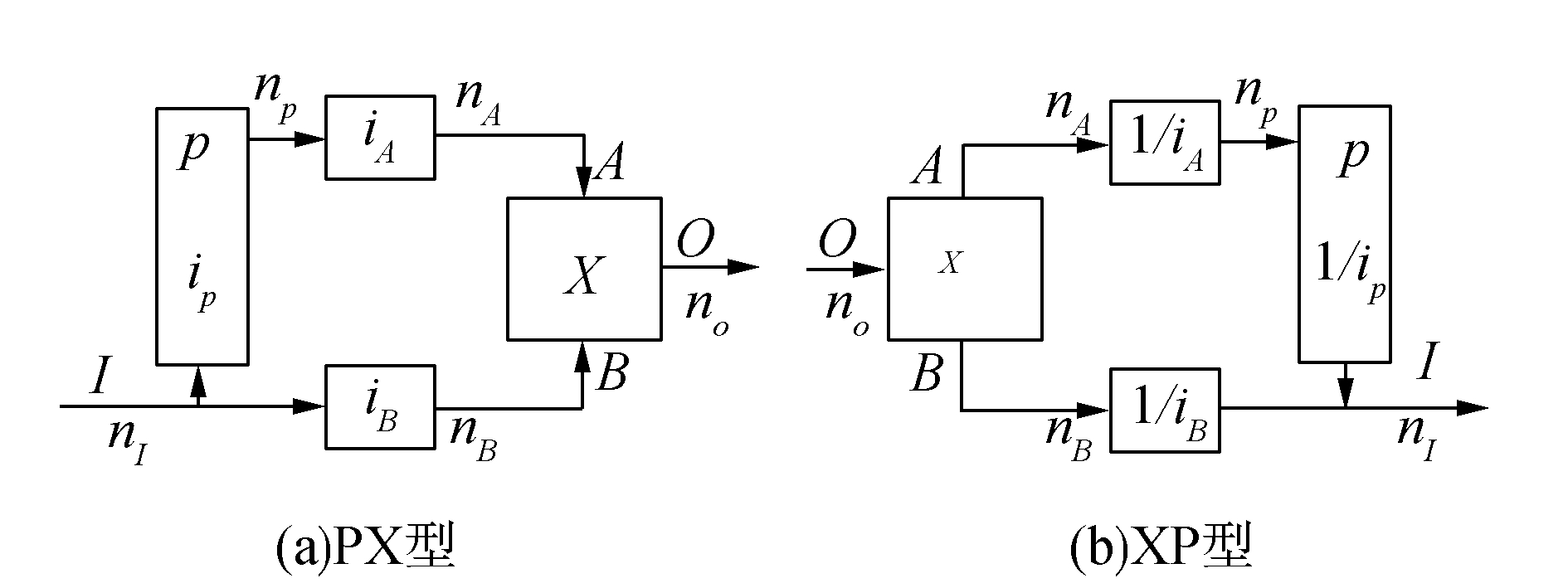
1 控制式差动无级变速装置结构分析控制式差动无级变速装置从结构上可分为PX型和XP型[1],如图 1所示。
|
图 1 控制式差动无级调速装置原理图 |
图中:P为机械式无级变速器;X为行星差动齿轮机构;A、B、O为分别为行星差动轮系的3个基本构件。对于PX型装置,O为输出端;对于XP型装置,O为输入端;I、P为无级变速器的两个伸出端,对于PX型装置,I为输入端;对于XP型装置,I为输出端;nA、nB、nO、nI、np分别为A、B、O、I、P各轴的转速;
通过对控制式差动无级变速器的各轴的转速以及基本型带式无级变速器调速范围的分析,计算并推导出整个装置的输出转速和各参数的关系式。
分析传动装置输出轴的2个输出极限速度的关系,计算出装置的调速范围R。通过分析带式无级变速器的传动比、行星差动齿轮的传动比及定轴轮系的传动比之间的关系来确定差动无级变速器在不同参数条件下的调速情况及功率流的流向[2]。
|
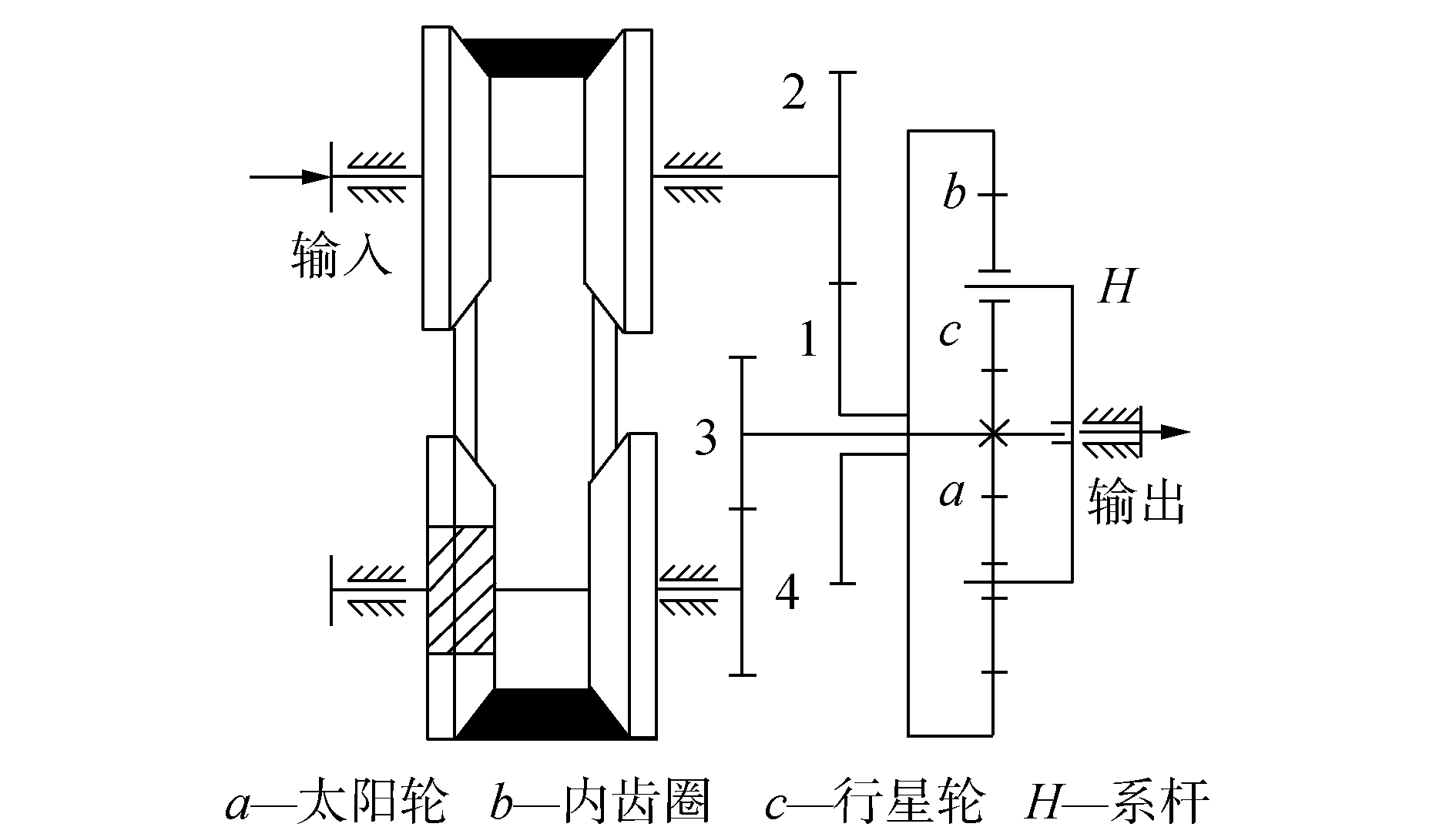
图 2 PX型控制式差动无级变速器结构简图 |
控制式差动无级变速器在传递动力和转矩的过程中,由于装置由无级变速器和差动轮系并联而成,两者的组合使其内部形成了一个封闭的空间,要实现扩大调速范围,精密调速甚至实现过零调速时,装置内部多数情况会出现功率回流的现象,这就使其内部的运动学分析变得十分复杂。
在实现扩大调速范围出现的回流功率会加大装置所承受的功率,而这与扩大调速范围则成相对的。所以实现扩大变速装置的调速范围时(或其他工况的情况时),都有必要对装置进行功率流的分析,并推导出在不同情况下装置内部的循环功率的情况。
图 2为PX型控制式差动无级变速器结构简图,下面的运动学分析则以图 2为例。
2.1 装置调速范围的计算如图 2所示,分别以na、nb和nH表示差动轮系的中心轮a、内齿圈b和系杆H,由文献[3]可知装置的输出转速公式为
| $ {n_H} = \frac{{{i_B} - i_{ab}^H{i_A}{i_P}}}{{\left( {1 - i_{ab}^H} \right){i_A}{i_B}{i_P}}}{n_D} $ |
式中:iabH是差动轮系转化机构的传动比;ip、iA和iB分别为V带无级变速器和两定轴齿轮副传动的传动比;nD为电机的输入转速。
当iP=iPmax和iP=iPmin时的两个输出极限转速分别为
| $ \begin{array}{l} {n_{{H_1}}} = \frac{{{i_B} - i_{ab}^H{i_A}{i_{P\max }}}}{{\left( {1 - i_{ab}^H} \right){i_A}{i_B}{i_{P\max }}}}{n_D}\\ {n_{{H_2}}} = \frac{{{i_B} - i_{ab}^H{i_A}{i_{P\min }}}}{{\left( {1 - i_{ab}^H} \right){i_A}{i_B}{i_{P\min }}}}{n_D} \end{array} $ | (1) |
所以当两极限转速有nH1>nH2时,装置的调速范围为
| $ R = {R_1} = \frac{{q/{i_{{P_{\max }}}} - i_{ab}^H}}{{q/{i_{{P_{\min }}}} - i_{ab}^H}} = \frac{{q - i_{ab}^H \cdot {i_{{P_{\max }}}}}}{{q{R_p} - i_{ab}^H \cdot {i_{{P_{\min }}}}}} $ | (2) |
而当两极限转速有nH1<nH2时,同理可得装置的调速范围为
| $ R = {R_2} = \frac{{q/{i_{{P_{\min }}}} - i_{ab}^H}}{{q/{i_{{P_{\max }}}} - i_{ab}^H}} = \frac{{q - i_{ab}^H \cdot {i_{{P_{\min }}}}}}{{q - i_{ab}^H \cdot {i_{{P_{\max }}}}}}{R_p} $ |
式中:
如图 2所示的传动装置中,影响装置输出变化及类型的主要参数有q、iabH、ip等,一般情况下行星差动轮系采用负号传动机构,其传动比iabH取负值;带式无级变速器的传动比ip为正,而参数q则主要有两定轴齿轮副的传动比iA、iB来确定[3-4]。
文献[4]可知装置类型主要有下列几种情况:
1) 在q·iabH·ip<0情况下,控制式差动无级调速装置属精密调速型(A型)。
2) 在q·iabH·ip>0情况下,
a) 当
b) 当
3) 在
a) 当
b) 当
为了更加清楚地判定装置的类型,故将其判定结果用表 1表示。
|
|
表 1 装置类型的判定 |
根据差动轮系个基本构件间的转速关系[5],可得XP型控制式差动无级调速装置的输出转速为
| $ {n_0} = \frac{{{i_B}/i_{Hb}^a}}{{1 - q/\left( {i_{ab}^H \cdot {i_p}} \right)}}{n_I} $ |
式中:n0表示装置的输出转速;nI表示装置的输入转速。
从上文可以得出XP装置与PX装置相一致的结论。但对于XP型装置,无论各传动参数怎样变动,输出转速n0都不可能为零,因此这时XP型传动装置不能用于过零调速,即不会有过零调速型(B0型)。
2.4 功率流分析 2.4.1 不考虑功率损失时的功率流判定由于控制式差动无级调速装置是基本型无级调速装置和差动轮系并联组合而成的,所以装置内部的功率情况比较复杂,它受到装置内各传动参数的影响。下面为暂不考虑功率损失的情况下功率流的流向及其量的判定。
设PI和PO分别表示装置中的输入构件I和输出构件O传动的功率,在不考虑功率损失的情况下[6],有
| $ {P_I} = - {P_O} = {P_A} + {P_B} $ |
式中:PA、PB是差动轮系的基本构件A和B流过的功率,其正值表示功率流入差动轮系,负值表示功率流出差动轮系;PH是装置的输出功率。
| $ {P_A} = - {P_H} \cdot \frac{q}{{q - {i_p}i_{AB}^H}} = {P_I} \cdot \frac{q}{{q - {i_p}i_{AB}^H}} $ |
| $ {P_B} = - {P_H} \cdot \frac{{ - {i_p}i_{AB}^H}}{{q - {i_p}i_{AB}^H}} = {P_I} \cdot \frac{{ - {i_p}i_{AB}^H}}{{q - {i_p}i_{AB}^H}} $ |
1) 在qipiABH>0的情况下
a)当
b) 当
2) 在qipiABH<0情况下,此时在装置中没有封闭循环功率。
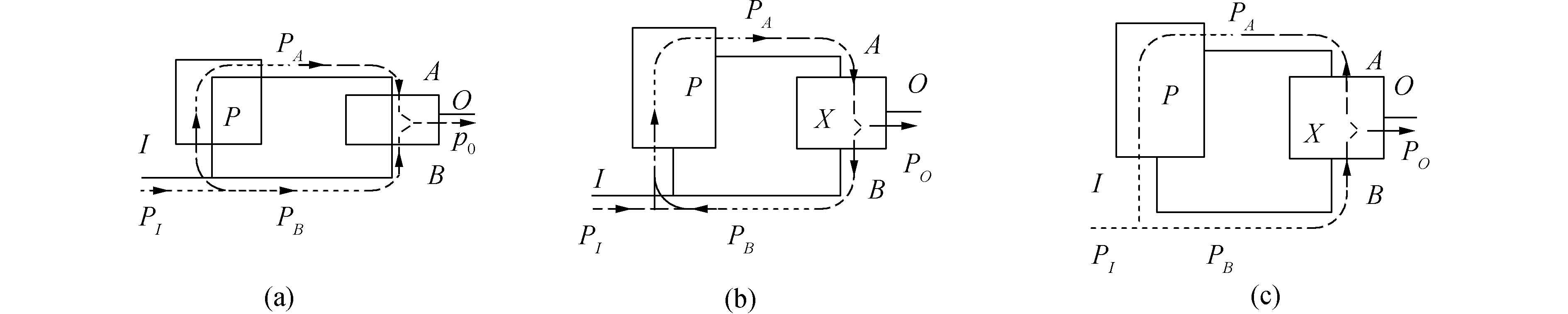
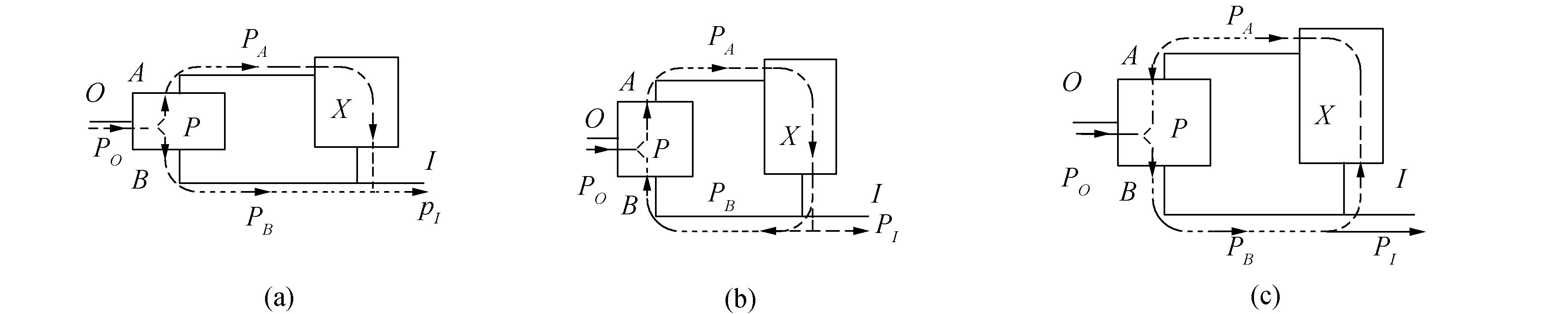
为了方便直观起见,将以上装置内功率流的分析结果用表 2表示。图 3为PX型图,图 4为XP型图。
|
|
表 2 控制式差动无级变速传动装置功率流向情况 |
|
图 3 PX型图 |
|
图 4 XP型图 |
由上我们可知,精密调速型(A型)装置可不存在循环功率,而扩大调速范围型(B型)和过零调速型(B0型)装置中必然会存在循环功率。因此要想得到较大的调速范围,必然会有封闭循环功率存在。
2.4.2 考虑功率损失时功率流的判定上文对在不考虑功率损失的情况下,详细分析了调速传动装置内功率流的流向及其量的关系。但是由于在传动的过程中,装置内必然会存在各种功率的损失,因此实际上并非完全如上文所分析的情况。现在在考虑功率损失时情况下来对装置内的功率流情况进行说明[9]。
在一般的差动轮系中常采用2K-H机构,若将差动轮系中的系杆H作为PX型装置的输出端O(或XP型装置的输入端I),差动轮系X为隔离体,此时则有输出功率PA、PB、PH之间的关系为:
| $ {P_A} = \frac{{{n_A}}}{{{n_H}}} \cdot \frac{1}{{i_{AB}^H\eta _o^x - 1}}{P_H} $ | (3) |
| $ {P_B} = \frac{{{n_B}}}{{{n_H}}} \cdot \frac{{\eta _o^x}}{{i_{AB}^H\eta _o^x - 1}}{P_H} $ | (4) |
当转化机构中功率从A流向B时,x=1;当转化机构中功率从B流向A时,x=-1。
对于PX型传动装置,PH为输出功率(而对于XP型装置,PH则为输入功率)。在这两种情况下PH均为已知量,所以通过式(3)、(4)就可以求出A、B两构件的实际传动功率。
如果O端不是差动轮系的系杆H,而是轮系的其他基本构件,则需要对一些参数进行适当的变换,同样的方法仍然可以求出输出功率PA、PB、PO三者之间的关系。
3 传动装置的效率分析控制式差动无级变速器是由基本型无级变速器和差动轮系并联组合而成的装置。这种装置在调速时能获得极细微的输出转速变化,通过选择合适的参数,可以使输入的一大部分功率从差动轮系流入,一小部分功率从基本型无级变速器流入,从而克服了基本型无级变速器传递功率较小的缺点,使传递功率成倍增加,同时也提高了装置的使用寿命;或使调速范围大幅度扩大,甚至实现过零(反向)调速。控制式差动无级变速器在传动参数选择合适的情况下,其效率比基本型无级变速器高,因而具有更为广泛的应用前景[10]。
控制式差动无级调速装置结构复杂,在扩大调速型和过零调速型时内部必定有封闭循环功率流的存在,且效率分析相当复杂[11],效率的计算方法有很多,如М.А.Крейнес提出的传动比法(克莱依涅斯法)、啮合传动功率法[12-13]。文中选择用啮合传动功率法来分析计算传动装置的传动效率。以图 1装置为例,电机用于齿轮1、4的功率分别为
| $ {P_A} = {P_4}{\eta _A}{\eta _P} = \frac{{{T_H} \cdot {n_D}}}{{9\ 459{i_A}{i_P}}} \cdot \frac{1}{{i_{AB}^H\eta _o^x - 1}}{\eta _A}{\eta _P} $ |
| $ {P_B} = {P_7}{\eta _B} = \frac{{i_{AB}^H\eta _o^x}}{{9\ 459\left( {1 - i_{AB}^H\eta _o^x} \right){i_B}}}{T_H}{\eta _D}{\eta _B} $ |
装置的输入功率为
| $ {P_O} = {P_A} + {P_B} = \frac{{{T_H}{\eta _D}}}{{9\ 459\left( {1 - i_{AB}^H\eta _o^x} \right)}}\left( {\frac{{i_{AB}^H\eta _o^x}}{{{i_B}}}{\eta _B} - \frac{{{\eta _A}{\eta _B}}}{{{i_A}{i_P}}}} \right) $ |
装置的输出功率为
| $ {P_H} = \frac{{{T_H}{n_H}}}{{9549}} = \frac{{{T_H}{\eta _D}}}{{9\ 459\left( {1 - i_{AB}^H} \right){i_A}{i_B}{i_P}}}\left( {{i_B} - i_{AB}^H{i_A}{i_P}} \right) $ |
求得装置的效率为
| $ \eta = \frac{{{P_H}}}{{{P_D}}} = \frac{{\left( {{i_B} - i_{AB}^H{i_A}{i_P}} \right)\left( {1 - i_{AB}^H\eta _O^x} \right)}}{{\left( {\frac{{i_{AB}^H\eta _O^x}}{{{i_B}}}{\eta _B} - \frac{{{\eta _A}{\eta _P}}}{{{i_A}{i_P}}}} \right)\left( {i - i_{AB}^H} \right){i_A}{i_B}{i_P}}} $ | (5) |
式中:ηp为宽V带无级变速器的传动效率;η0为行星差动轮系的传动效率;ηA、ηB为定轴齿轮副的传动效率。
当转化机构中功率从A流向B时,x=1,当转化机构中功率从B流向A时,x=-1。
3.1 装置的效率计算控制式差动无级变速器效率的计算公式为式(5),结合上文分析及初选数据可得到:iA=-1.294;iB=2.582;iabH=-4,设:ηB=0.940 9;η0=0.940 9。将所求得数据带入效率计算式(5)中则:
| $ \begin{array}{*{20}{c}} {\eta = \frac{{\left( {{i_B} - i_{ab}^H{i_A}{i_P}} \right)\left( {1 - i_{ab}^H\eta _0^x} \right)}}{{ - \left( {\frac{{i_{ab}^H\eta _0^x}}{{{i_B}}}{\eta _B} - \frac{{{\eta _A}{\eta _p}}}{{{i_A}{i_p}}}} \right)\left( {1 - i_{ab}^H} \right){i_A}{i_B}{i_p}}} = }\\ {\frac{{\left( {2.582 - 4 \times 1.294{i_p}} \right)\left( {1 + 4 \times {{0.9409}^{ - 1}}} \right)}}{{\left( {\frac{4}{{2.582}} + \frac{{0.85}}{{1.294{i_p}}}} \right) \times 6.47 \times 2.582{i_p}}}} \end{array} $ | (6) |
由式(6)可知传动装置效率的高低与无级变速器的传动比有关系。当取不同的ip值时即:ip=0.5,1.0,1.5,2.0时,将其分别带入式(6),得效率分别为0.001 3,0.379,0.778 3,0.826 2。即当ip=ipmax=2时,整个传动的装置效率最大;当ip=ipmin=0.5时,整个传动的装置效率最小。
3.2 装置的功率流分析及计算 3.2.1 功率流的分析根据上文中对功率流的分析,当

|
图 5 装置内部功率流向图 |
当宽V带无级变速器传动比取最小ip=ipmin=0.5时,传动装置效率最小,循环功率最大,所以取效率η=0.007 3,计算其最大功率PAmax;根据对循环功率的分析,由式(1)、(2)可得:
| $ \begin{array}{*{20}{c}} {{n_H} = \frac{{{i_B} - i_{ab}^H{i_A}{i_{P\min }}}}{{\left( {1 - i_{ab}^H} \right){i_A}{i_B}{i_{P\min }}}}{n_1} = }\\ {\frac{{2.582 - 5.167 \times 0.5}}{{ - 1.294 \times 2.582 \times \left( {1 + 4} \right) \times 0.5}} \times 1390 = 0.499\ 2\;{\rm{r/min}}} \end{array} $ |
| $ {n_A} = \frac{{{P_I}}}{{{i_A}{i_P}}} = \frac{{1390}}{{ - 1.294 \times 0.5}} \times 1390 = - 2\ 148.377\;{\rm{r/min}} $ |
| $ {P_H} = \eta {P_I} = 0.0073 \times 0.75 = 0.005475\;{\rm{kW}} $ |
| $ {P_A} = \frac{{{n_A}}}{{{n_H}}} \cdot \frac{{{P_H}}}{{i_{ab}^H\eta _o^x - 1}} = \frac{{ - 214\ 8.377}}{{0.499\ 2}} \cdot \frac{{0.005\ 475}}{{ - 4\eta _o^x - 1}} = 4.567\ 5\;{\rm{kW}} $ |
计算后可知最大循环功率为4.567 5 kW。
4 结论1) 文章给出了控制式差动无级变速器在不同装置不同传动条件下功率流的流向的判定情况。
2) 装置属于精密调速型时不会出现循环功率,装置属于扩大调速和过零调速型的时候,装置内部必有循环功率存在。
3) 最后应用啮合功率法对装置的传动效率进行了分析,给出传动效率的计算公式。
| [1] |
姜艳姝, 魏世娟. 模拟测头在齿轮测量中心上的应用研究[J]. 哈尔滨理工大学学报, 2009, 14(4): 121-125. ( 0) 0)
|
| [2] |
黄爱文. 一种新型船用无级变速系统设计与分析[J]. 机械传动, 2015, 39(6): 148-151. ( 0) 0)
|
| [3] |
BIRCH S. Audi takes CVT from 15th century to 21st century[Z]. Automotive Engineering International, 2000:1.
( 0) 0)
|
| [4] |
张淳, 周令华. 控制式差动无级调速装置的传动特性(续)[J]. 齿轮, 1990, 14(2): 9-14, 38. ( 0) 0)
|
| [5] |
张淳, 李志愿, 吉涛. 控制式差动无级变速器调速控制方案的研究[J]. 制造业自动化, 2012, 34(2): 128-129, 153. ( 0) 0)
|
| [6] |
杨利红, 璩瑶瑶, 张淳. 控制式差动无级变速器的优化设计[J]. 机械制造与自动化, 2013, 42(1): 171-173. ( 0) 0)
|
| [7] |
杨端光. 封闭式周转轮系的传动效率计算[J]. 机械设计与制造, 2008(5): 23-25. ( 0) 0)
|
| [8] |
李志愿, 张淳. 基于MATLAB的控制式差动无级变速器优化设计[J]. 煤矿机械, 2011, 32(10): 43-45. DOI:10.3969/j.issn.1003-0794.2011.10.020 ( 0) 0)
|
| [9] |
王乃信, 张锁怀, 孙怀禄, 等. 控制式自动稳速变速器的研制[J]. 西北轻工业学院学报, 1991, 9(4): 15-23, 108. ( 0) 0)
|
| [10] |
张淳, 赵越. 用于印字模切机的控制式差动无级变速器的结构研究及虚拟装配[J]. 机械传动, 2014, 38(1): 154-155. ( 0) 0)
|
| [11] |
濮良贵, 纪名刚. 机械设计[M]. 8版. 北京: 高等教育出版社, 2006.
( 0) 0)
|
| [12] |
张淳, 赵越. 过零调速型控制式差动无级变速器中回流功率的优化分配研究[J]. 机械传动, 2014, 38(2): 123-125. ( 0) 0)
|
| [13] |
饶振刚. 行星齿轮传动设计[M]. 北京: 化学工业出版社, 2003.
( 0) 0)
|
| [14] |
周有强. 机械无级变速器[M]. 北京: 化学工业出版社, 2001.
( 0) 0)
|
| [15] |
阮忠唐. 机械无级变速器设计与选用指南[M]. 北京: 化学工业出版社, 1999: 9.
( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


