随着船舶与海洋技术的发展,水翼也广泛地应用于各类船舶上,一个典型的应用即水翼艇。水翼一般安装在靠近自由液面的位置,需要考虑自由液面的影响,因此其水动力性能与无限水域中的翼型不同,其中水翼的浸深对其升力和阻力具有较大的影响。
早期对浅浸水翼的研究大多数是基于势流理论,Vladimirov[1]研究了水翼的升力和阻力特性,薄翼理论和线性化的自由液面条件被广泛运用于水翼绕流的研究;Hess和Smith[2]提出了边界元法后即广泛用于水翼绕流的计算,显然,使用势流理论对水翼绕流进行研究时忽略了流体的黏性,随着高性能计算机技术的发展,使有限体积法得以解决黏性流动的问题;Kunz等[3]对全浸物体的空化流场进行了多相流计算流体力学(CFD)分析;Li等[4]采用k-ω湍流模型对水翼的非定常空化绕流进行了研究;Münch等[5]通过实验和CFD方法对振动水翼进行了对比研究;Ducoin和Young[6]使用层流和湍流模型研究了黏流中复杂水翼的水弹性响应和稳定;Esfahanian和Akbarzadeh[7]对不可压、无黏性、稳态、非空化或空化条件下的二维NACA0012水翼的绕流进行了数值模拟。以上大部分都是在敞水条件下进行的研究,而对自由液面影响的研究也逐渐引起了广泛的关注,Kramer等[8]研究了不同傅汝德数和攻角下二维板的兴波;Djavareshkian等[9]采用基于压力的隐式有限体积法研究水翼绕流及自由液面的影响。
文中对水翼近自由面的运动进行了数值模拟研究,主要关注兴波等现象。首先对NACA 0012翼型的兴波和NACA 4412翼型的压力分布进行了研究验证。随后研究了自由液面对NACA 4412翼型水动力性能的影响,主要研究浸深对升力和阻力变化的影响,针对翻卷波现象也进行了讨论。
1 数值理论 1.1 控制方程流体动力学的基本控制方程包括连续性方程、动量和能量守恒方程。在文中的计算中,一般认为水介质为不可压缩流体,而空气介质对计算结果影响较小,也可简化为理想气体。因此在数值分析参数设置中,需要重点考虑连续性方程和动量守恒方程。
| $\begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho \mathit{\boldsymbol{u}}} \right) + \nabla \cdot \left( {\rho \mathit{\boldsymbol{u}} \otimes \mathit{\boldsymbol{u}}} \right) = \nabla \cdot \left( {\mu \nabla \otimes \mathit{\boldsymbol{u}}} \right) - \nabla \rho + \rho \mathit{\boldsymbol{g}}\\ \quad \quad \quad \quad \quad \quad \quad \nabla \cdot \mathit{\boldsymbol{u}} = 0 \end{array}$ |
式中:u=(u, v, w)为速度矢量,ρ为流体密度,P为压强,g为重力加速度。
1.2 湍流模型k-ε双方程模型是目前黏性流场使用最为广泛的模型。该模型又分为标准k-ε模型、RNG k-ε模型和Realizable k-ε模型3种。
标准k-ε模型是在原始的单方程模型的基础上,新引入一个关于湍流耗散率ε的方程后形成。k-ε模型需要将流场假定为完全的湍流场,因此k-ε模型的应用需是完全的湍流场。
湍流动能方程引申为
| $\begin{array}{l} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ \quad \quad \quad {G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k} \end{array}$ |
湍流耗散方程为
| $\begin{array}{l} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ \quad \quad {G_{1\varepsilon }}\frac{\varepsilon }{k} + \left( {{G_k} + {C_{3\varepsilon }}{C_b}} \right){C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_k} \end{array}$ |
式中:Gk为平均速度梯度引起的湍流动能,Gb为浮力作用引起的湍流动能,σk、σε分别是与k和ε对应的湍流普朗特数(Prandtl),Sk、Sε由用户自行给定,C1ε、C2ε、C3ε为经验常数。
1.3 自由界面追踪方法在VOF法提出之前,针对自由界面追踪问题,研究者基本束手无策。Hirt和Nichols在解决此类问题时突破地引入一个流体体积函数方程,从而使流场的数学模型能够很好地与数值计算的特性相结合,开创了二项流计算的新时代。经过几十年来科研工作者的不断改进与完善,VOF方法已经成为了流体力学研究与解决实际工程领域问题时最常用的方法之一。
1.3.1 流体体积分数求解和运动界面捕捉流体体积分数变量F在每个时间步长上保持符合控制方程。然后求解控制方程组,求出网格中变量F的分布,这是VOF方法解决的问题。但是这只是知道了界面的大致位置所在,每个网格内的交界面形状、方向仍然是不确定的。怎么通过相邻的网格F的值精确地得到两相流体交界面的形状仍是难点,如果得到的交界面不够精确,在接下来的迭代过程中同样会影响流场求解的精度。同时,由于相函数F的阶梯性质,在求解该变量时也需要进行一定的处理,才能使迭代继续。目前常用的处理方法总结起来主要包括液面重构技术和液面追踪技术两种。这两种方法的本质区别是,一个为几何方法,一个则是数学差分方法。
1.3.2 CICSAM格式运动界面重构在通过VOF法对存在运动界面的二相流计算时,经过多次的迭代运算,数值结果必然会出现耗散,使得运动界面的宽度大幅度变宽,有时甚至包含数个网格尺度。为了使得运动界面保持锐利,从而维持计算的连续性和精确度,在VOF方法中需要通过几何方法对运动界面进行特殊重构。
Ubbink和Issa[10]的Compressive Interface Capturing Scheme for Arbitrary Meshes(CICSAM)格式是利用了精细的网格内界面的迁移方法得到的。通过设置法向量为网格内运动界面法向的直线对界面位置进行逼近,若设的界面法向量为n=(n1, n2),则新构成的界面是n1x+n2y=α的形式。然后通过几何关系可以补充求解α需要的额外方程,然后求解联立方程就可确定出界面的位置了。
通过和NVD思想结合,CICSAM-VOF通过引入高阶耗散格式、色散模式并在两者之间灵活切换,从而在保持有界相函数的同时,得到或光顺或锐利的运动界面,从而大幅提高了该方法的精度和应用范围。CICSAM方法在离散的输运方程中,通过面库朗数Cf和体库朗数CD确定了流体在主体网格D和受体网格A中的对流效率,其中面库朗数Cf的确定基于线性插值:
| $\begin{array}{l} \quad \quad \quad {C_f} = (1 - {\beta _f}){C_D} + {\beta _f}{C_A}\\ (C_p^{t + \delta t} - C_p^t){V_p} = - \sum\limits_{f = 1}^n {\frac{1}{2}} ({({C_f}{F_f})^t} + {C_f}F_f^{t + \delta t})\delta t \end{array}$ |
式中:下标p和f分别代表了主、受体网格的中心和边界,下标D、A分别代表了主体、受体网格,n是网格数量,Vp是网格体积,Ff是主、受体网格之间的对流量。βf则是CICSAM权重因子,定义为
| ${\beta _f} = \frac{{{{\tilde F}_f} - {{\tilde F}_D}}}{{1 - {{\tilde F}_D}}}$ |
式中
在计算βf的过程中会引起体积分数不守恒,导致对流场的模拟失真。在改进的CICSAM方法中,通过对过渡区域网格内流体在网格边界上输运量进行修正,从而确定界面与格子边线的交点坐标。从而保证了在保持体积函数的守恒性的同时,又维持了体积分数函数满足有界性条件。
2 水面下水翼航行兴波模拟 2.1 模型及网格建立为了更好地与已有的试验结果做对比,参考试验文献[11]使用了NACA0012和NACA4412翼型作为实验翼型。模型布置参考实验水槽的设置,如图 1所示。将弦长20.3 cm的NACA0012翼型放置在距离底边界17.5 cm的水域中,来流方向设置为5倍弦长,尾流方向设置为9倍弦长。在水槽试验中,由于实验设备的原因,水槽的上部并不封闭。在模型设置时,将空气区域的高度设置为5倍弦长,较高的空气区域可以使水翼的浸深高度可以在较大范围内变化,且当兴波较大时,可以防止出现飞溅现象导致计算域内的质量不守恒,有利于计算的稳定性。
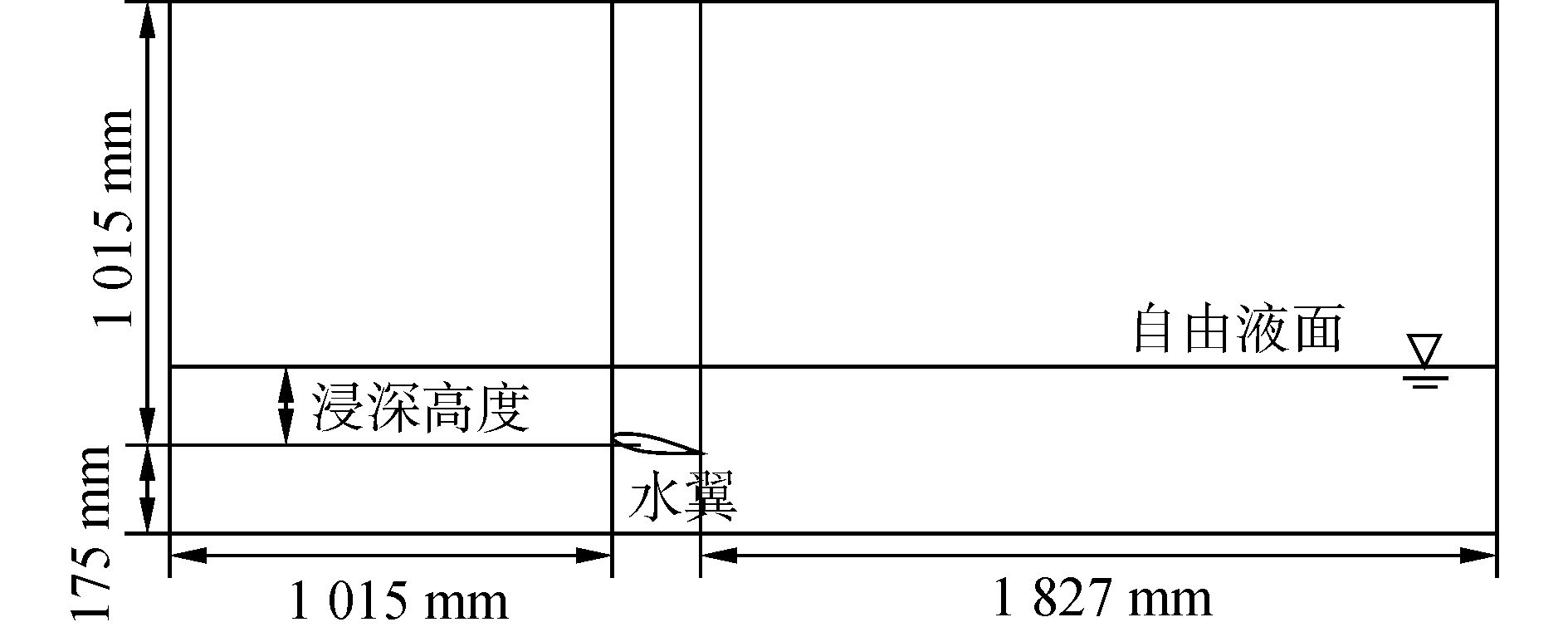
|
图 1 计算域模型 |
在CFD数值计算分析中,良好的网格划分是至关重要的环节,网格的质量直接决定着计算结果的收敛性、计算效率和计算精度。在该模型中,将水域流场分割成尺寸为δx=δy=0.02 m的均匀结构网格,如图 2所示,对水翼的划分采用通过O型网格,有利于在控制全局网格数量的同时,对水翼表面进行加密。设置距水翼最近处边界层厚度为0.001 m。同样,对自由液面处的网格也进行加密处理,厚度0.005 m。

|
图 2 翼型网格拓扑结构 |
通过此种方式对近自由液面水翼计算域建立模型,最后生成的全局网格数为100 000,壁面y+控制在50以内,能够满足湍流计算的精度要求且保证计算效率。
2.2 NACA0012兴波对比分析在FLUENT中进行数值计算。边界条件采用速度入口和压力出口,水翼上下表面和底面边界设置为壁面,上方空气边界设置为Symmetry对称面。
参考相关文献,使用的空气介质密度ρA=1.225 kg/m3,设置空气的动力黏性系数μA=1.789 4×10-5 N·S/m2,对于计算域参考压力,设置参考压力取值点位于空气域内的,绝对值为0 Pa。水域中水介质的密度ρW=998.2 kg/m3,水的动力黏性系数μW=1.003×10-3 N·S/m2,来流速度设为0.8 m/s,模型分别采用了层流、RNG k-ε湍流模型进行对比计算,压力速度耦合采用SIMPLE算法,通过有限体积法离散,中心差分格式运算扩散相。分别通过定常运算获得稳定流场,每次迭代过程中通过CICSAM对新产生的自由液面兴波形状进行精确重构,最后提取稳定后的波形曲线与实验值进行对比。
图 3为分析NACA0012翼型在h/c=0.91、攻角为5°时的兴波现象。Froude数为Fr=0.571 1,雷诺数Re=1.592×106,层流和湍流结果分别和试验值、Karim数值结果[11]进行对比。
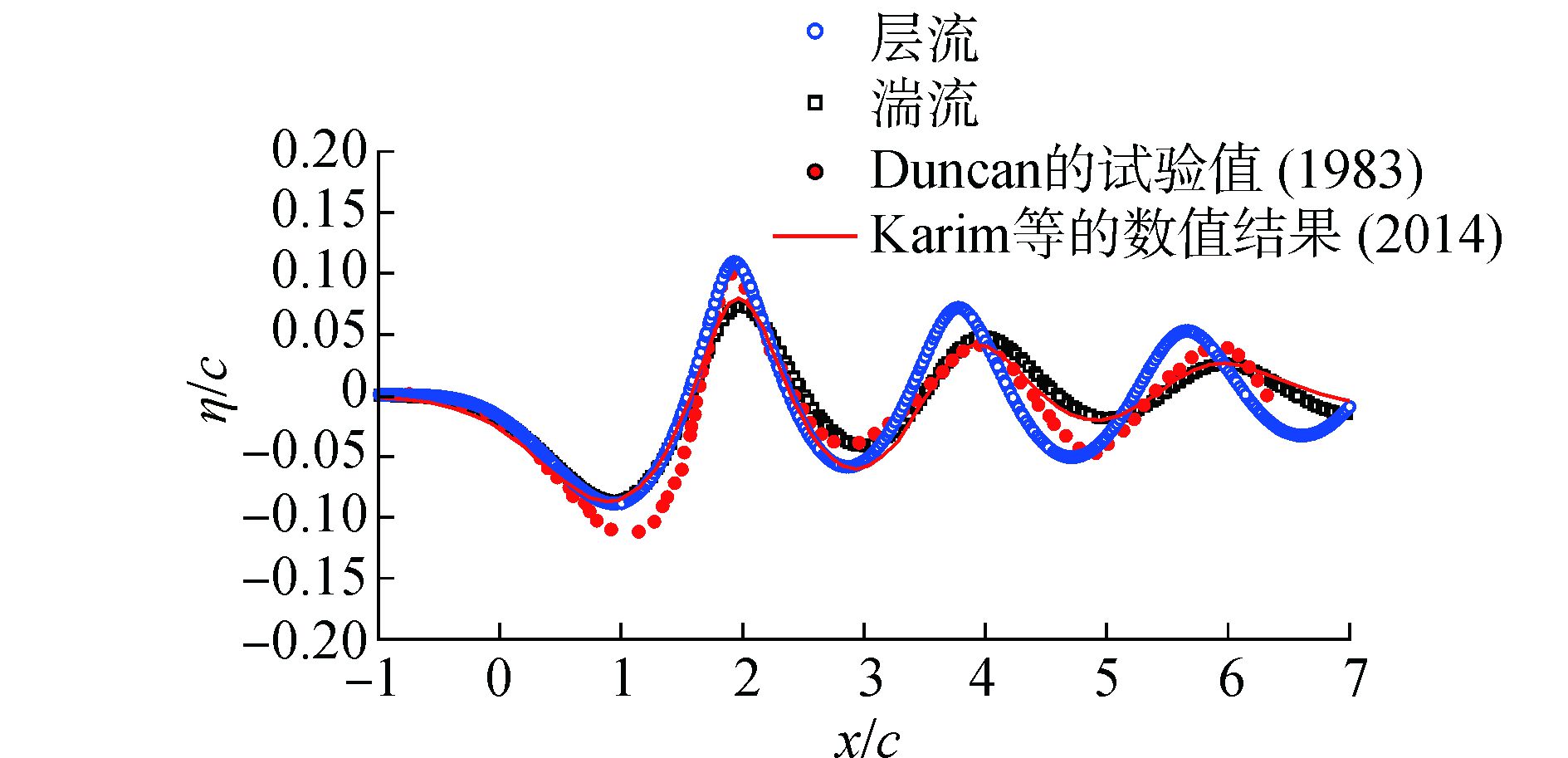
|
图 3 层流、湍流兴波对比 |
可以看到,层流模型和实验值在第1个波峰处拟合较好。由于湍流模型的能量耗散稍大,所以第1个波峰则稍低于实验值,这是比较合理的。而在波长方面,湍流模型的波峰位置与实验值基本相同,而层流模型则稍短。
总体而言,在较为简单的兴波模拟中,2种计算结果与实验值吻合都较好。由于在数值模拟中采用的是二维模型,所以可以较好地避免实验中的一些产生误差的因素,如三维尺度效应等。而且可以看到,实验数据中第2个波峰与第3个波峰基本等高,且与第1个波峰相差极大,这样不规则的波浪衰减也是很难在数值仿真中模拟得到的。无论层流还是湍流模型,得到的3个波峰高度衰减规律都相当的规则。综合考虑接下来的计算需求,文中在接下来的近自由液面水翼航行模拟上选用RNG k-ε湍流模型。其产生的流场如图 4所示。

|
图 4 RNG k-ε湍流模型自由液面结果 |
在计算域的速度云图(图 5)可以发现,水翼上表面流速大于下表面,在尾迹区域存在极长的尾流区域。在波浪表面处,波峰处的水域流速和波谷处的空气流速小于平均速度(0.8 m/s),而波谷处的水域流速和波峰处的空气流速则大于平均流速。而从速度矢量图(图 6)可以看到,翼前缘和后缘的速度小于翼型其他部位。
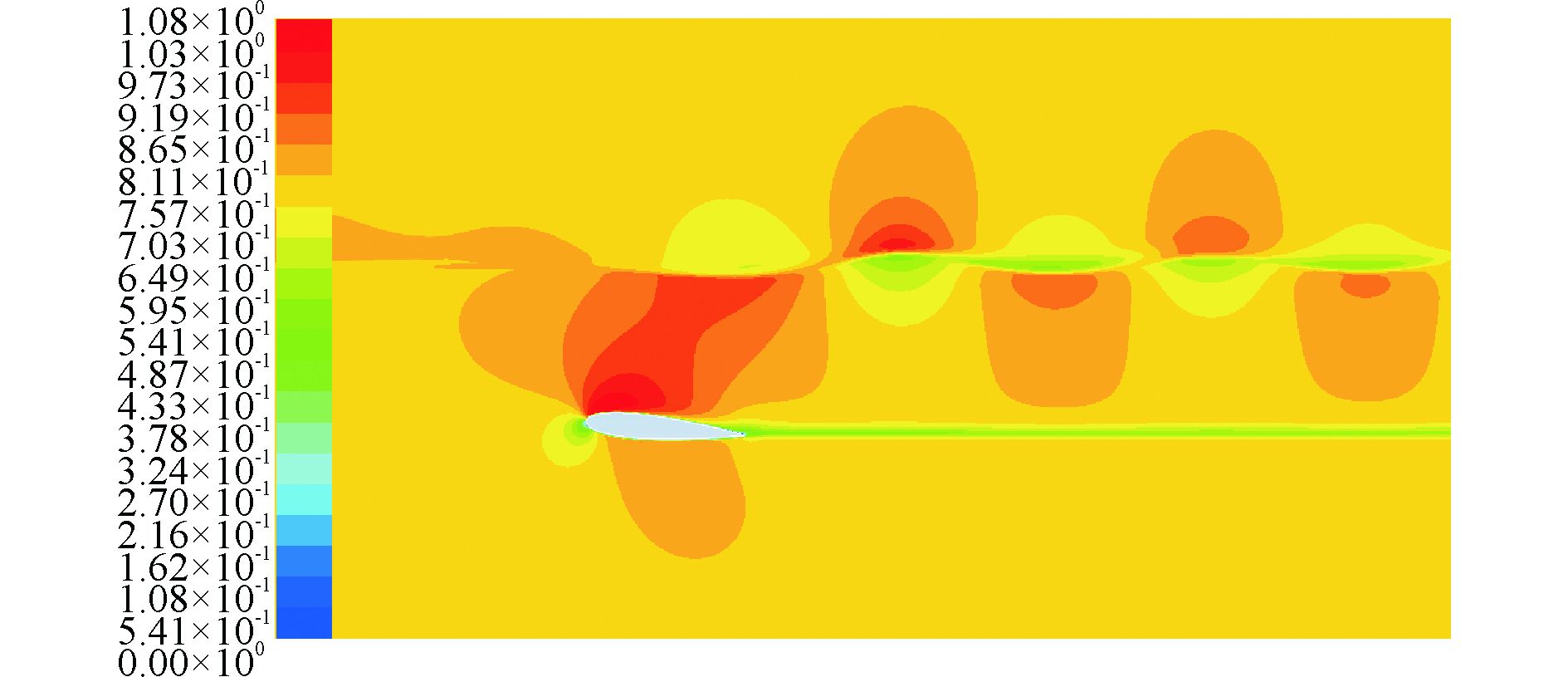
|
图 5 计算域速度云图 |
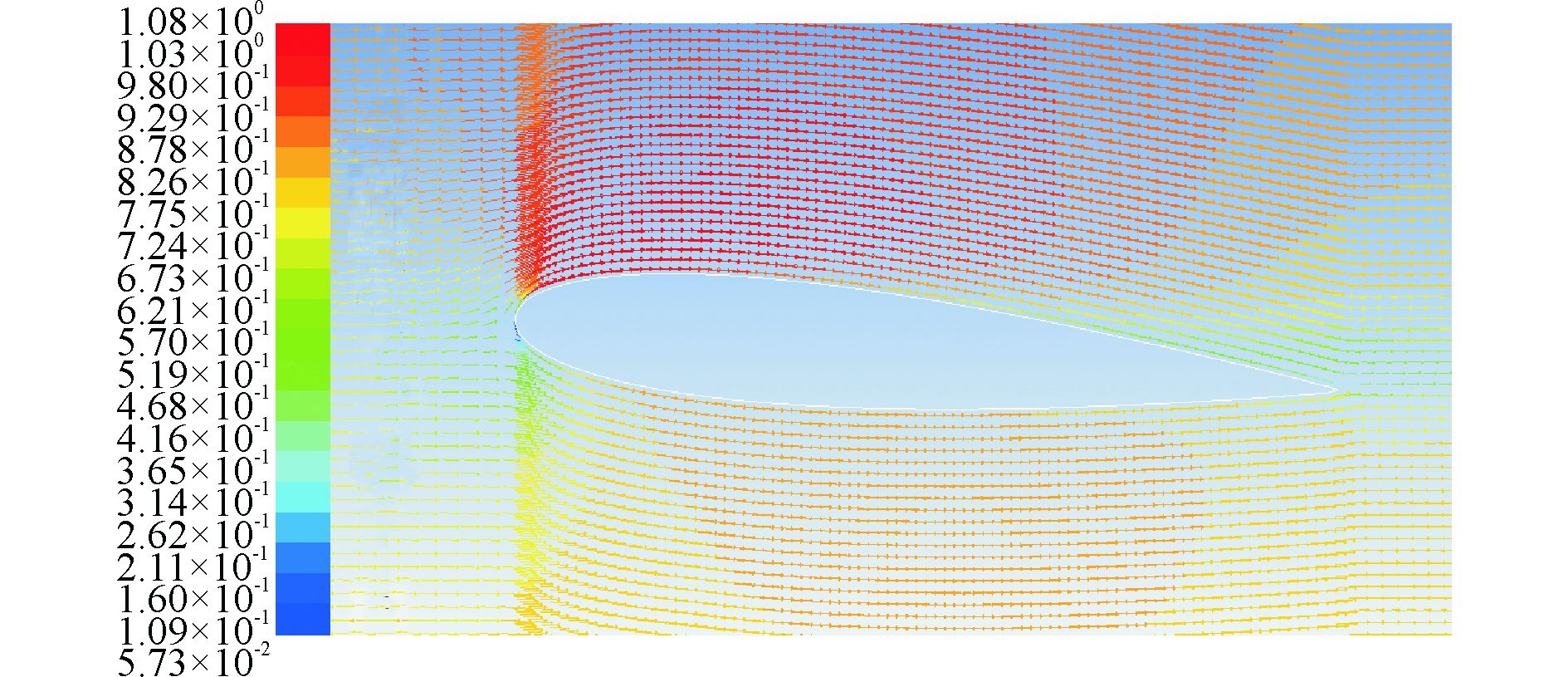
|
图 6 翼型表面速度矢量图 |
均匀来流中的翼型中,来流速度V与翼型弦线之间的夹角为机翼的夹角。对于非对称翼型或者有攻角翼型时,绕翼型流动的流场是上下不对称的。翼型上面流速增加、压力减小,下面流速减小、压力增大。翼型表面的压力系数定义为
| ${C_p} = \frac{p}{{\frac{1}{2}\rho {V^2}}}$ |
表面压力及摩擦力的总和,在垂直与翼型来流速度方向向上的分量称为机翼的升力L,平行于翼型来流方向的分量则称为机翼的阻力D。由于摩擦力远远小于阻力,因此一般忽略不计。常常采用无因次量的升力系数和阻力系数来表示翼型的升力和阻力,如
| $\begin{array}{l} {C_L} = \frac{L}{{\frac{1}{2}\rho {V^2}b}}\\ {C_D} = \frac{D}{{\frac{1}{2}\rho {V^2}b}} \end{array}$ |
为了进一步分析水翼兴波的现象,在探究不同工况下水翼兴波变化时,采用了非对称翼型NACA4412作为实验对象。作为一个经典的非对称翼型(如图 7),NACA4412的中弧线是一条向上弯曲的曲线。其升阻比比对称翼型NACA0012大得多,产生的兴波同样大得多,并且在攻角和来流达到一定值后,会在最高波峰出现波浪破碎现象,这是自由液面捕捉中的难点。

|
图 7 NACA4412模型结构 |
计算模型与Duncan试验模型保持一致,设置攻角α=5°,Froude数Fr=1.03。通过首先分析h/c=0.94、h/c=0.6两种浸深工况下翼型表面的压力分布Cp。通过图 8可以看出可以看到,翼型表面压力系数拟合较好。
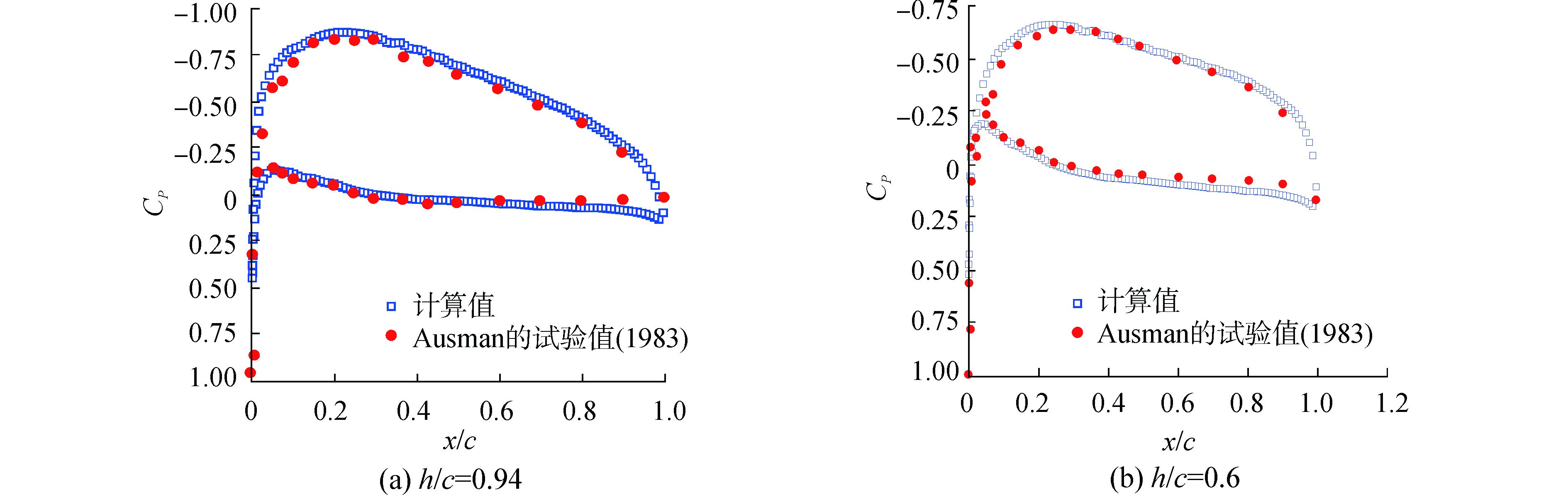
|
图 8 Fr=1.03, α=5°时NACA4412表面压力分布 |
分析NACA4412翼型在Froude数Fr=1时的升力、阻力性能。图 9分别给出了不同浸深下自由液面对升力、阻力性能影响的结果图。从图 9(a)中可以看出,h/c在0~2时,CFD的计算结果比势流计算结果稍大;图 9(b)中可以明显看出CFD的计算结果比势流计算结果大很多。

|
图 9 不同浸深下升力曲线、阻力曲线与升阻比的变化 |
从图 9可以看出,h/c在0~2时,水翼的升力不断增大,而阻力则先增大再减少。当浸深h/c大于2的情况,水翼的升力系数基本保持不变,但一直到浸深约为5倍弦长后,水翼的阻力系数才趋于平稳。可以从升阻比曲线上看到,升阻比在h/c为1~2时迅速增加,在h/c增加到5后,自由表面效应几乎消失了。
保持攻角5°不变,改变浸深。着重分析h/c在1~2时的兴波情况,如图 10所示。可以看到在h/c从1.2增加到1.8的过程中,最大的波高度比η/c变化极大,从0.175下降到约0.05。
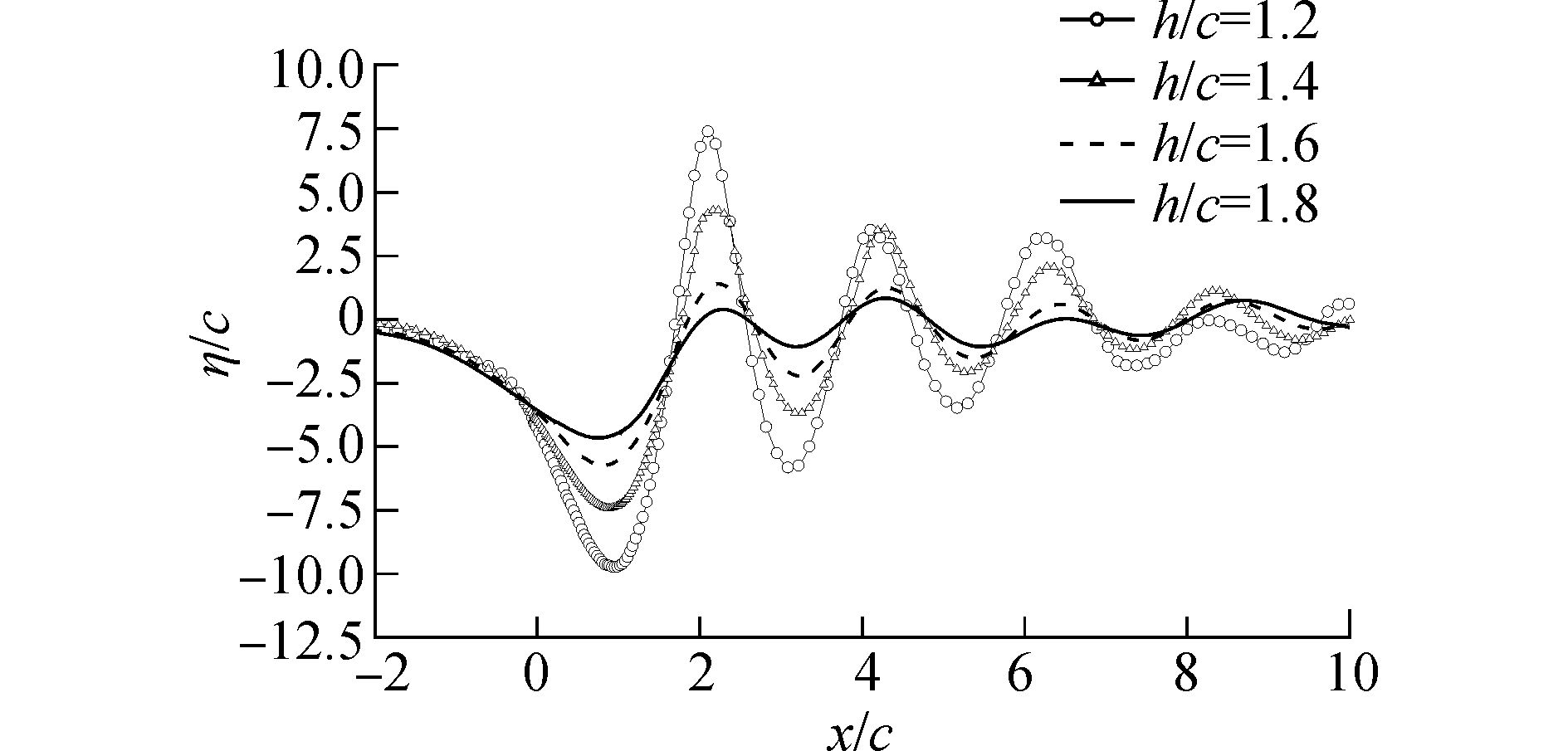
|
图 10 不同浸深下的兴波图形 |
图 11为h/c为1.4时,改变水翼攻角得到的兴波随攻角变化的波形图。可以看到,在0°攻角下,由于高升力水翼的原因,自由界面已经受到了影响。随着攻角不断增大,最大的波高度比η/c不断增大。
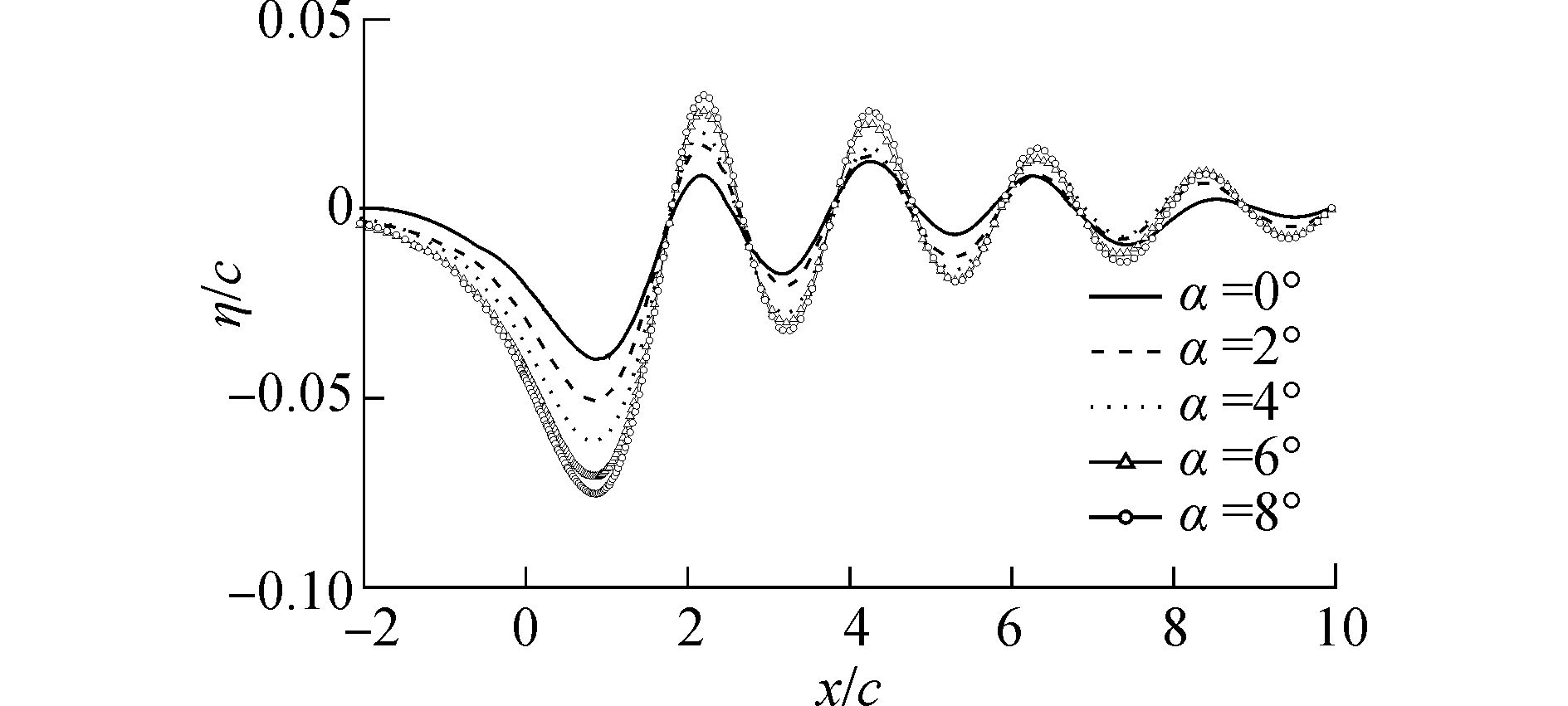
|
图 11 不同攻角下的兴波图形 |
从不同攻角、浸深的对比中,可以看到兴波的波长不受浸深改变或者翼型攻角变化而变化,但波幅宽度受到的影响较为明显。而在浸深比h/c大于4后,水翼航行基本可以等效为深水,自由表面效应可以忽略。
2.4 破碎波模拟近自由液面运动下波浪破碎波的出现是较为常见但难以捕捉的现象。高Froude数、较小的浸深以及较大攻角都会引起破碎波的现象。无论是实验模拟还是数值仿真,波浪的破碎都是研究难点。在实验模拟中,由于三维水翼的尺度效应,破碎波往往难以在整个展长上出现,且破碎波存在的时间较短,所以难以观测,或者只能观测到一个大概的破碎区域,难以对细节进行深入观测。而在数值仿真的研究中,由于CICSAM重构方法的出现,使得对波浪产生破碎瞬间自由液面的演变过程仿真成为可能。
文中仍采用NACA4412模型进行仿真,实验工况为Fr=0.571 1,α=10°且h/c=0.6。采用RNG k-ε湍流模型, 进行非定常运算,时间步长为0.01 s。
通过图 12可以看到,当t=0.6 s时,水翼后波峰开始向左侧运动;当t=0.65 s时,射流变得更加明显,并开始向左侧下落;t=0.7 s后,射流触碰下液面边界,并于t=0.75 s时形成了第1个空腔;而随着时间发展,第2个射流再次向左侧发展并于t=0.8 s回落与下界面形成第2个空腔。多次弹射后水头返回下自由界面并与来流合并,产生的多个空腔也不断被压扁减小,最终形成稳定的波形。
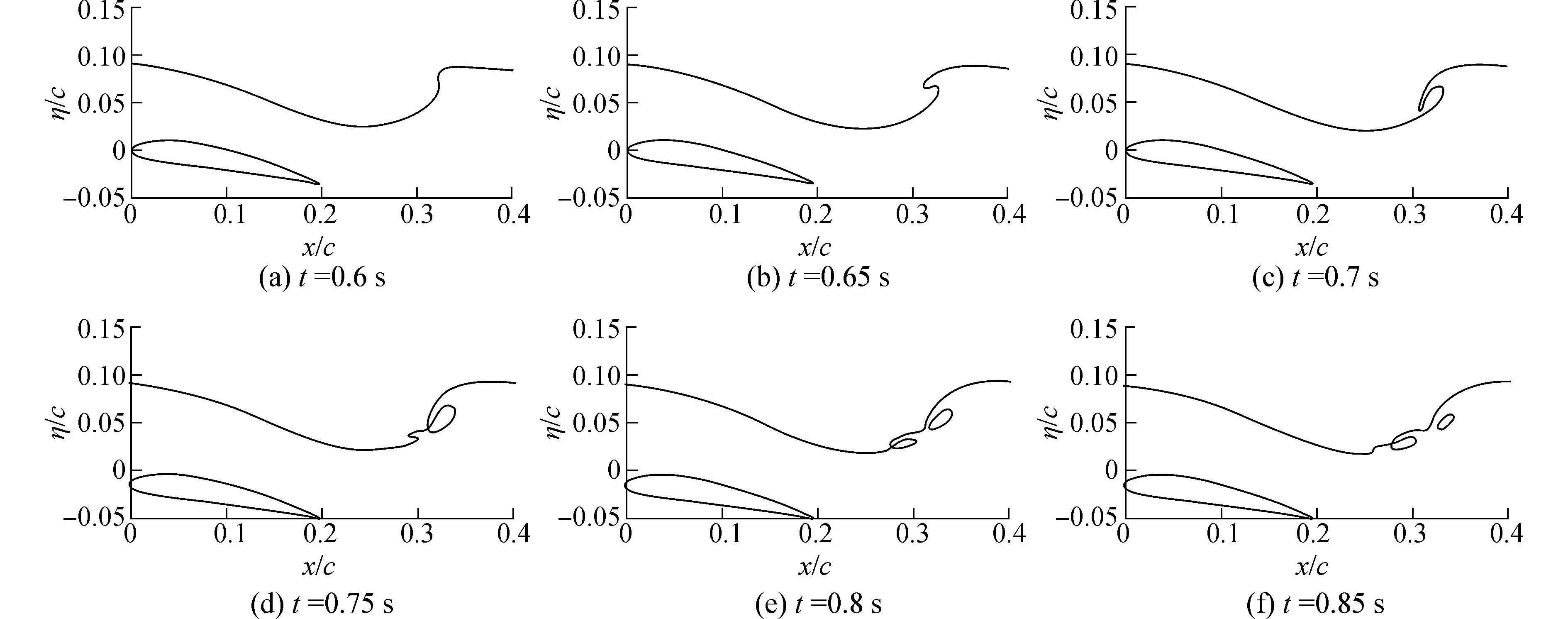
|
图 12 Fr=0.571 1, α=10°, h/c=0.6时的波浪翻卷 |
但同时需要注意到,实际情况中破碎波的产生同时伴随着表面大片水花。如果想要模拟出精确的水滴分离运动,对网格精细程度和计算机性能有极高要求。因此文中在破碎波模拟时并未加入离散水滴相,所以得到的现象中无法展现精细的水滴运动现象。
对应t=0.6 s、t=0.8 s时域内的压力云图如图 13所示,上面第1层区域为空气所在的低压区,而在第2层区域压力随着自由液面形状的变化而变化。第3层区域的压力则基本不受液面破碎波影响,而主要受水翼影响。而在最下面深水区域,压力基本不受影响。
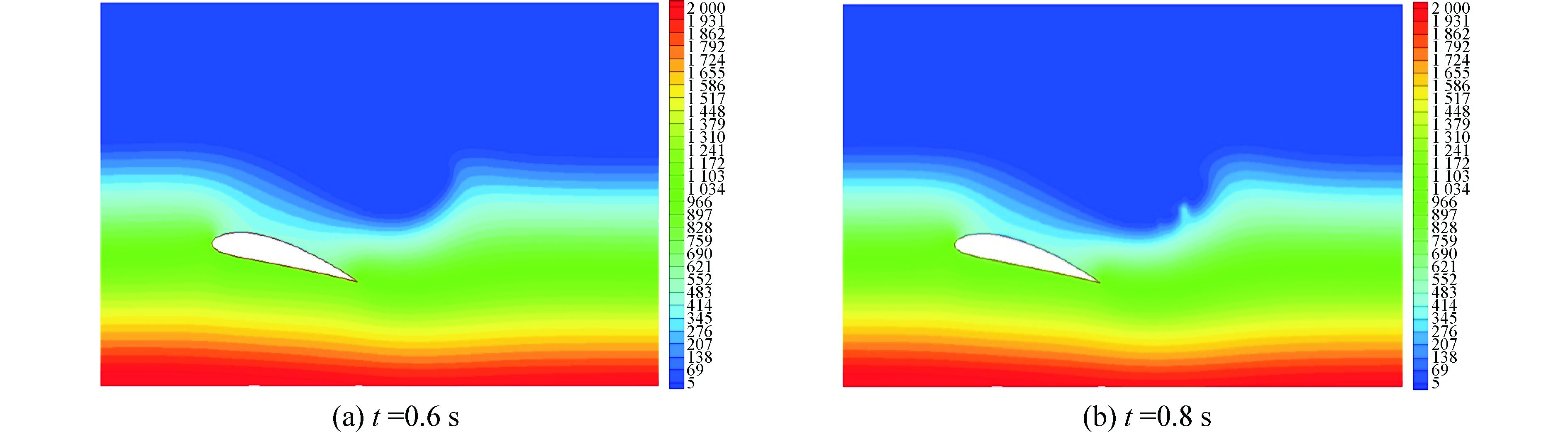
|
图 13 翼型表面压力云图 |
流体的流线图如图 14,同样与自由表面演变相符。t=0.6 s时,流线十分光顺规则;而在t=0.8 s时,2个空腔附近都形成了小的漩涡,而第3个漩涡则出现在正上方的空气中。
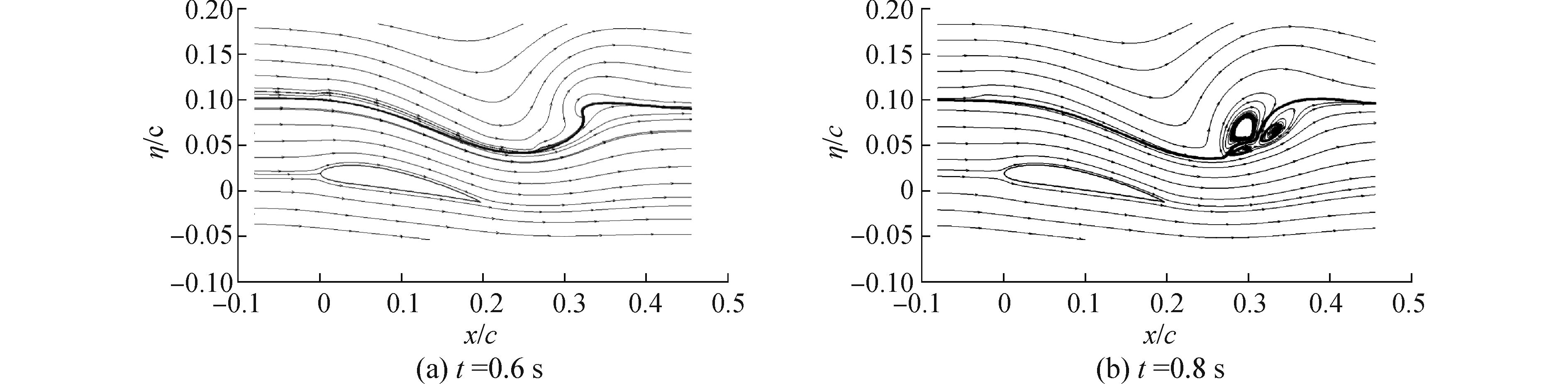
|
图 14 翼型表面和自由液面附近的流线图 |
文中根据有限体积法求解雷诺时均N-S方程,对近自由液面的水翼进行了计算和分析,得出了如下结论:
1) 在较为简单的兴波模拟中,层流模型和湍流模型的计算结果同试验结果均吻合较好。其中,层流模型在第1个波峰处拟合较好,而湍流模型由于能量耗散稍大,所以第1个波峰则稍低于实验值,这也是比较合理的,这验证了数值模拟方法的可行性。
2) 通过对非对称翼型NACA4412的计算,根据不同攻角、浸深的对比,从中可以知道兴波的波长不受浸深改变或者翼型攻角变化而变化,但波幅宽度受到的影响较为明显。而在浸深比h/c大于4后,水翼航行基本可以等效为深水,自由表面效应可以忽略。
3) 对NACA4412模型进行数值仿真,很好地模拟了波浪产生破碎瞬间自由液面的演变过程。
| [1] |
VLADIMIROV A N. Approximate hydrodynamic design of a finite span hydrofoil. NACA-TM-1341[R]. Washington:NACA, 1955.
( 0) 0)
|
| [2] |
HESS J L, SMITH A M O. Calculation of potential flow about arbitrary bodies[J]. Progress in aerospace sciences, 1967, 8(8): 1-138. ( 0) 0)
|
| [3] |
KUNZ R F, BOGER D A, CHYCZEWSKI T S, et al. Multi-phase CFD analysis of natural and ventilated cavitation about submerged bodies[C]//3rd ASME/JSME Joint Fluids Engineering Conference. San Francisco, USA. 1999:1.
( 0) 0)
|
| [4] |
LI D, GREKULA M, LINDELL P. Towards numerical prediction of unsteady sheet cavitation on hydrofoils[J]. Journal of hydrodynamics:ser B, 2010, 22(5): 741-746. DOI:10.1016/S1001-6058(10)60024-8 ( 0) 0)
|
| [5] |
MVNCH C, AUSONI P, BRAUN O, et al. Fluid-structure coupling for an oscillating hydrofoil[J]. Journal of fluids and structures, 2010, 26(6): 1018-1033. DOI:10.1016/j.jfluidstructs.2010.07.002 ( 0) 0)
|
| [6] |
DUCOIN A, YOUNG Y L. Hydroelastic response and stability of a hydrofoil in viscous flow[J]. Journal of fluids and structures, 2013, 38(3): 40-57. ( 0) 0)
|
| [7] |
ESFAHANIAN V, AKBARZADEH P. Numerical investigation on a new local preconditioning method for solving the incompressible inviscid, non-cavitating and cavitating flows[J]. Journal of the franklin institute, 2011, 348(7): 1208-1230. DOI:10.1016/j.jfranklin.2010.01.008 ( 0) 0)
|
| [8] |
KRAMER M R, MAKI K J, YOUNG Y L. Numerical prediction of the flow past a 2-D planing plate at low Froude number[J]. Ocean engineering, 2013, 70(6): 110-117. ( 0) 0)
|
| [9] |
DJAVARESHKIAN M H, ESMAEILI A, PARSANIA A. Numerical simulation of smart hydrofoil in marine system[J]. Ocean engineering, 2013, 73(6): 16-24. ( 0) 0)
|
| [10] |
UBBINK O. Numerical prediction of two fluid systems with sharp interfaces[D]. London:University of London, 1997.
( 0) 0)
|
| [11] |
KARIM M M, PRASAD B, RAHMAN N. Numerical simulation of free surface water wave for the flow around NACA 0015 hydrofoil using the volume of fluid (VOF) method[J]. Ocean engineering, 2014, 78(3): 89-94. ( 0) 0)
|
| [12] |
GIESING J P, SMITH A M O. Potential flow about two-dimensional hydrofoils[J]. Journal of fluid mechanics, 1967, 28(1): 113-129. DOI:10.1017/S0022112067001934 ( 0) 0)
|
| [13] |
CHEN C K, LIU H. Submerged vortex lattice method for calculation of the flow around a three-dimension hydrofoil[J]. Journal of ship mechanics, 2005, 9(2): 41-45. ( 0) 0)
|
| [14] |
CHEN Z M. A vortex based panel method for potential flow simulation around a hydrofoil[J]. Journal of fluids and structures, 2012, 28(1): 378-391. ( 0) 0)
|
| [15] |
XU G D, WU G X. Hydrodynamics of a submerged hydrofoil advancing in waves[J]. Applied ocean research, 2013, 42(42): 70-78. ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


