在大风条件下能够生存的柱状仙人掌,其不规则的截面形状可能对柱体绕流效果有一定的影响。海上结构物无疑会面对着极高的雷诺数,其量级一般在105~106,掌握这种高雷诺数流场的绕流特性有利于更好地了解海洋柱状结构物的绕流特征。目前的科研结果一般是将圆柱作为考察的目标。詹昊等[1]对于各种雷诺数下的圆柱绕流进行了分析求解;何鸿涛[2]对圆柱绕流和它的操纵方法进行了分析计算研究;韩韶英[3]对带轴向板条的圆柱绕流进行了求解;龚细斌[4]对波浪形圆柱的涡激振动机理进行了数值模拟研究;Kai Zhang等[5]对圆柱的形状改变对于绕流产生的影响进行了数值模拟研究;许媛欣[6]对方柱绕流的涡激振动及控制方式实行了考察;陈禹等[7]对不同雷诺数下的圆柱绕流进行了数值模拟研究;林琳[8]对绕圆柱湍流场的发展及立管涡激振动进行了研究。为改变柱体的绕流情况,科研人员采取了增添分流平板、肩部吸气和尾部吹气、改变横截面以及改变展向分布等方法,然而这些研究大多是集中在中低雷诺数的条件下的圆柱体上进行的。而且上述研究成果大多是在风洞试验模型下测得的,仅有少数研究是以水为介质的。在实际的工程应用中,特别是随着海洋的逐渐开发,水对柱体绕流的影响变得越发重要。
1 柱体模型的设计 1.1 柱体模型设计的理论基础在一定条件下,当无穷远处的均匀来流流经圆柱时,圆柱两边的边界层接二连三地脱离,产生周期性地反向的旋涡,不断往后发展,称作卡门涡街。不管是处于低雷诺数还是高雷诺数的情况下,卡门涡街的形成总是表现柱体绕流流场特点的关键要素[9]。所有处于一定流速的自由来流其中的不良绕流体,其尾部总会形成尾涡,尾涡的生成和脱离会形成作用在绕流体上的沿流动方向和与流动方向成直角的周期性作用力。形成的周期性作用力在一定条件下能够引发绕流体的振荡:反之,振荡的绕流体又能够对流场形成一定程度的干扰,即涡激振动[10-12]。
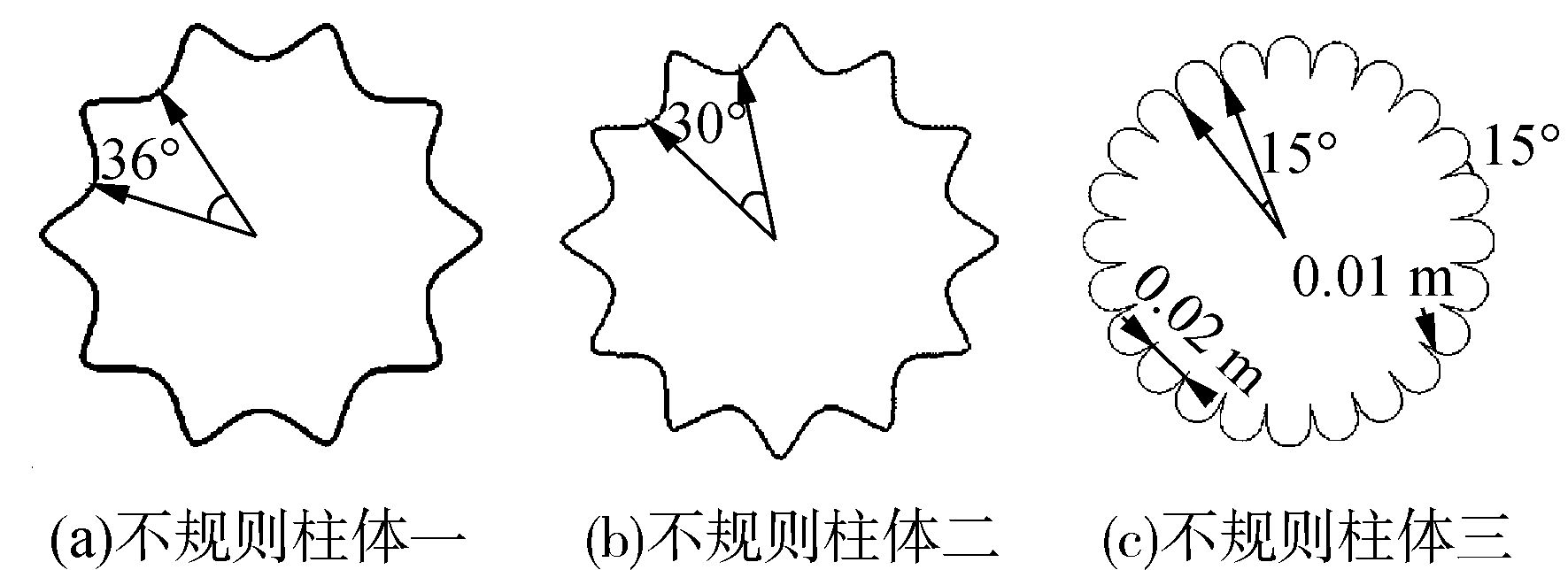
1.2 模型建立通过观察柱状仙人掌的截面形状,用STAR-CCM+内自带的建模软件设计了3个不规则柱体,如图 1所示不规则柱体的外径D=0.2 m,内径d=0.16 m。不规则柱体一均匀分布着10个突起,每个突起占整个圆周的度数的1/10,即36°,突起是由外圆上等分的10个点与内圆上相对应等分的10个点用样条曲线连接而成的。不规则柱体二均匀分布着12个突起,每个突起占整个圆周的度数的1/12,即30°,突起是由外圆上等分的12个点与内圆上相对应等分的12个点用样条曲线连接而成的。不规则柱体三均匀分布着24个突起,每个突起占整个圆周的度数的1/15,即15°,突起是由夹角为15°且长度为0.01 m的线段与直径为0.02 m的半圆交替连接而成的。
|
图 1 不规则柱体模型局部效果 |
不可压缩牛顿流体的运动满足连续性方程和动量守恒方程:
| $\begin{array}{l} \quad \quad \quad \quad \quad \quad \quad \quad \quad \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}}\\ \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial \rho }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {u_i^\prime u_j^\prime } } \right) + {S_j} \end{array}$ |
式中:ui和uj是速度分量的时均值(i、j=1, 2, 3),p是压力的时均值,ρ为流体密度,μ为动力黏性系数,
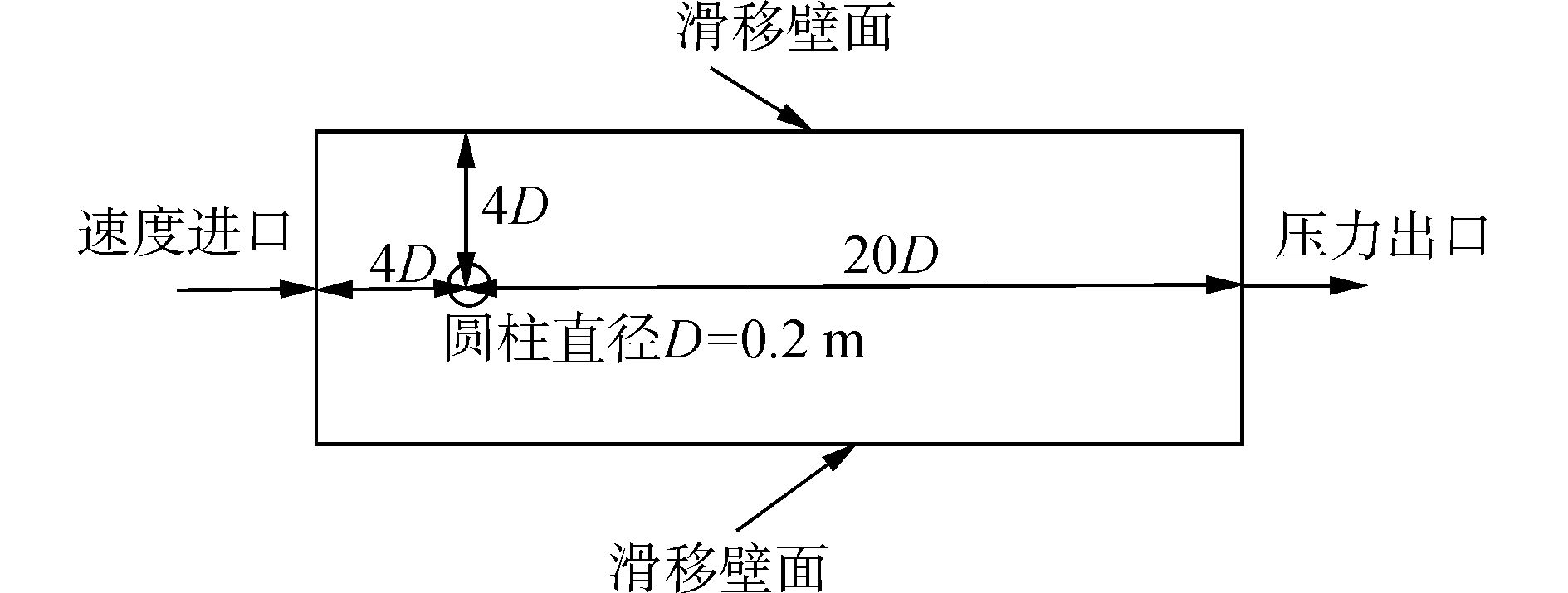
如图 2所示圆柱直径D=0.2 m,模型流场的长度是24D,宽度是8D,圆柱的圆心与流域速率进口的间距为4D,与流域压力出口的间距为20D,与上下边界的间距为4D。流域的参照压力强度是一个标准大气压101 325 Pa。不规则柱体的流域和圆柱的相同。选择物理模型有二维、隐式不定常、液体、分离流、恒密度、湍流、K-Omega湍流、湍流抑制等。
|
图 2 圆柱绕流模拟范围图 |
文中采用数值模拟软件STAR-CCM+来进行网格划分。选择网格化模型:表层重构、多面体网格生成器和棱柱层网格生成器。设置基础尺寸大小为0.01 m,设置棱柱层数大小为5,设置棱柱层厚度基数百分比大小为15%,生成体网格后再进行细化,得到的柱体附近网格如图 3所示。

|
图 3 圆柱网格 |
文中所采用的流体材料为水,其密度ρ=997.561 kg/m3;流体动力黏性系数μ为0.001 003 kg/(ms);柱体绕流的参考面积A设为0.2 m2。因为入口边界与圆柱的距离相对柱体的尺寸足够大,因而入口处采用“速度进口”边界条件,速度大小随着雷诺数的改变而改变,从而可以经由改变来流速度的方法达成改变雷诺数的要求。当Re=8×105时,速度大小为4 m/s;当Re=3.6×106时,速度大小为18 m/s。设置湍流强度数值大小为0.5,柱体绕流所需的边界包括速度进口、压力出口、对称平面以及壁面。
3 数值模拟结果运用STAR-CCM+进行模拟,得到了雷诺数Re=8×105和3.6×106两种情况下的涡量云图,并进行了比较分析。
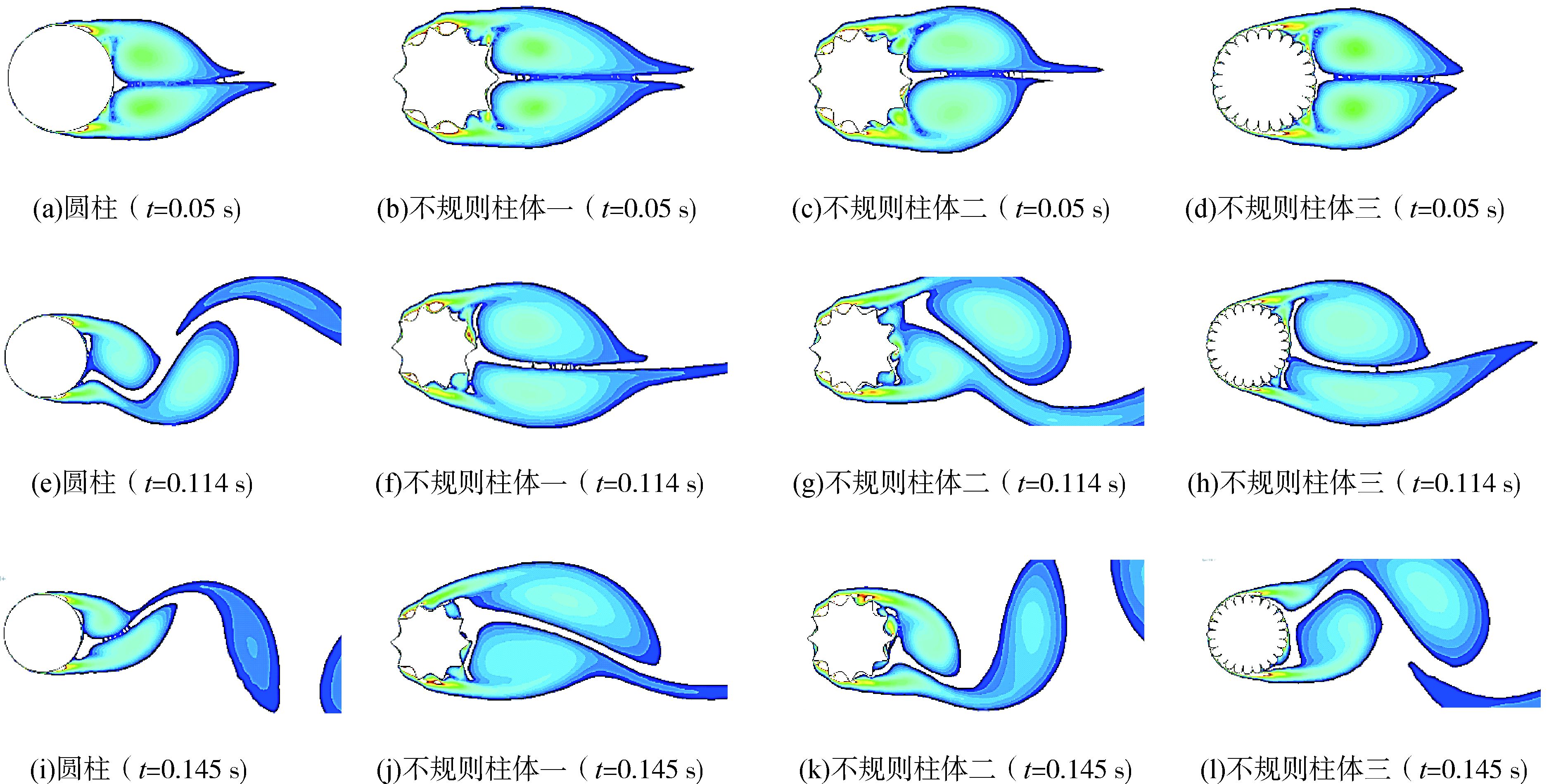
3.1 Re=3.6×106时的模拟结果对Re=3.6×106的情况,即能够重新出现准脉动性发出的比较规律的紊流涡街的雷诺数,进行模拟分析,得到尾涡脱落初期的涡量云图,如图 4所示。
|
图 4 尾涡脱落初期涡量云图(Re=3.6×106) |
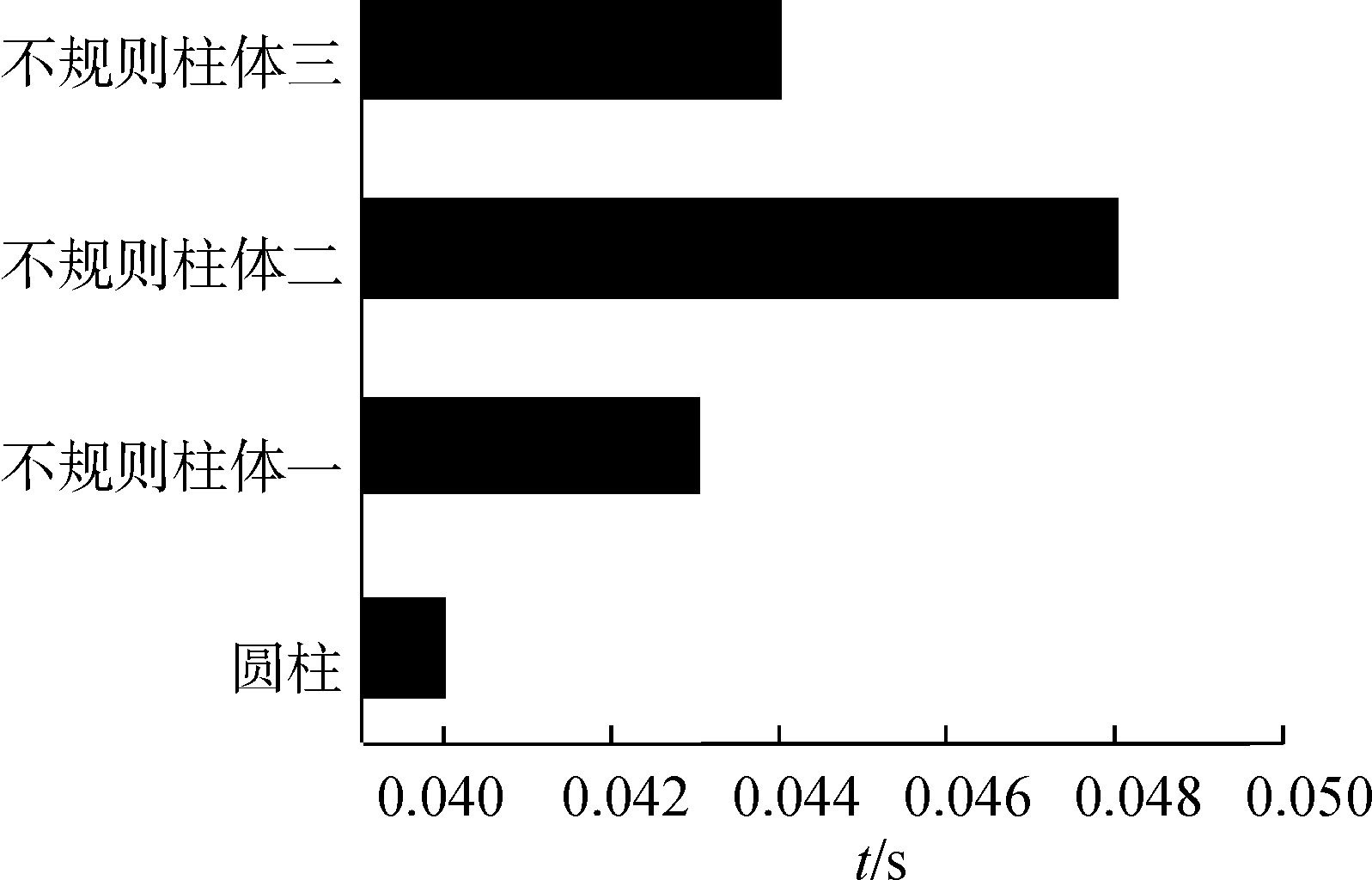
通过比较4个模型的尾涡脱落初期的过程发现,不规则柱体模型能够影响尾涡的脱落。4个模型的尾涡脱落周期柱状图如图 5所示。
|
图 5 尾涡脱落周期柱状图(Re=3.6×106) |
通过对比尾涡稳定脱离后的脱落周期发现,不规则柱体尾涡脱落的周期都比圆柱的大,即不规则柱体延缓了尾涡的脱落。
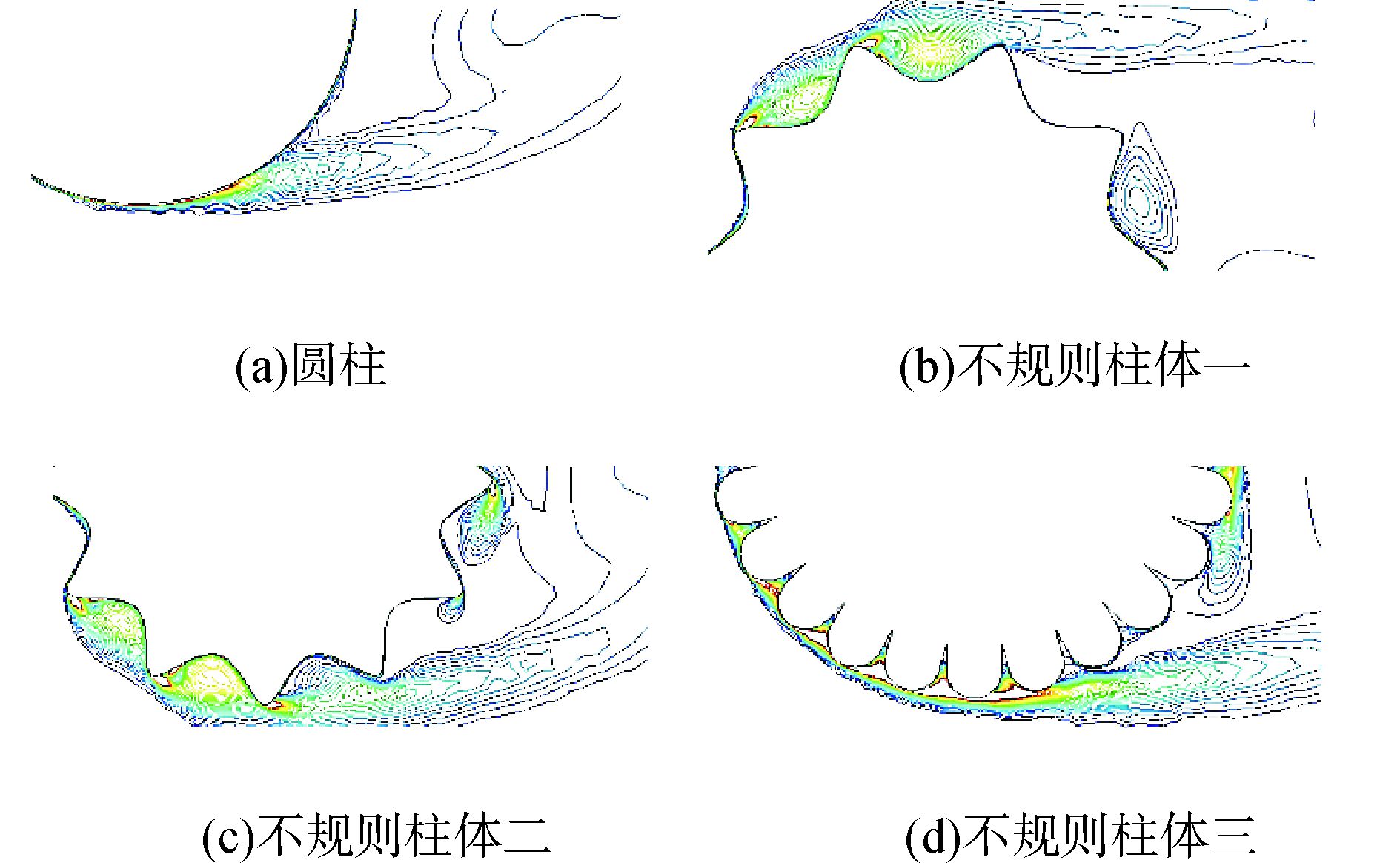
4个模型的局部涡量图,如图 6所示。
|
图 6 局部涡量图(Re=3.6×106) |
通过观察尾涡稳定脱落后的绕流状态发现,在不规则柱体的凹槽内会产生小旋涡。不规则柱体两侧的小旋涡会使本将脱离的绕流吸附在柱体表面上,从而延缓绕流的脱离;不规则柱体尾部的小旋涡会在尾部上下移动,相继吸引两侧即将脱落的尾涡,从而达到延缓尾涡脱落的目的。
3.2 Re=8×105时的模拟结果对于Re=8×105的情况,即超临界区,进行数值模拟分析。以不规则柱体一为例,得到尾涡脱落初期的涡量云图,如图 7所示。

|
图 7 尾涡脱落初期涡量云图(Re=8×105) |
通过比较2个模型的尾涡脱落初期的过程发现,在超临界区,不规则柱体模型也能够影响尾涡的脱落。
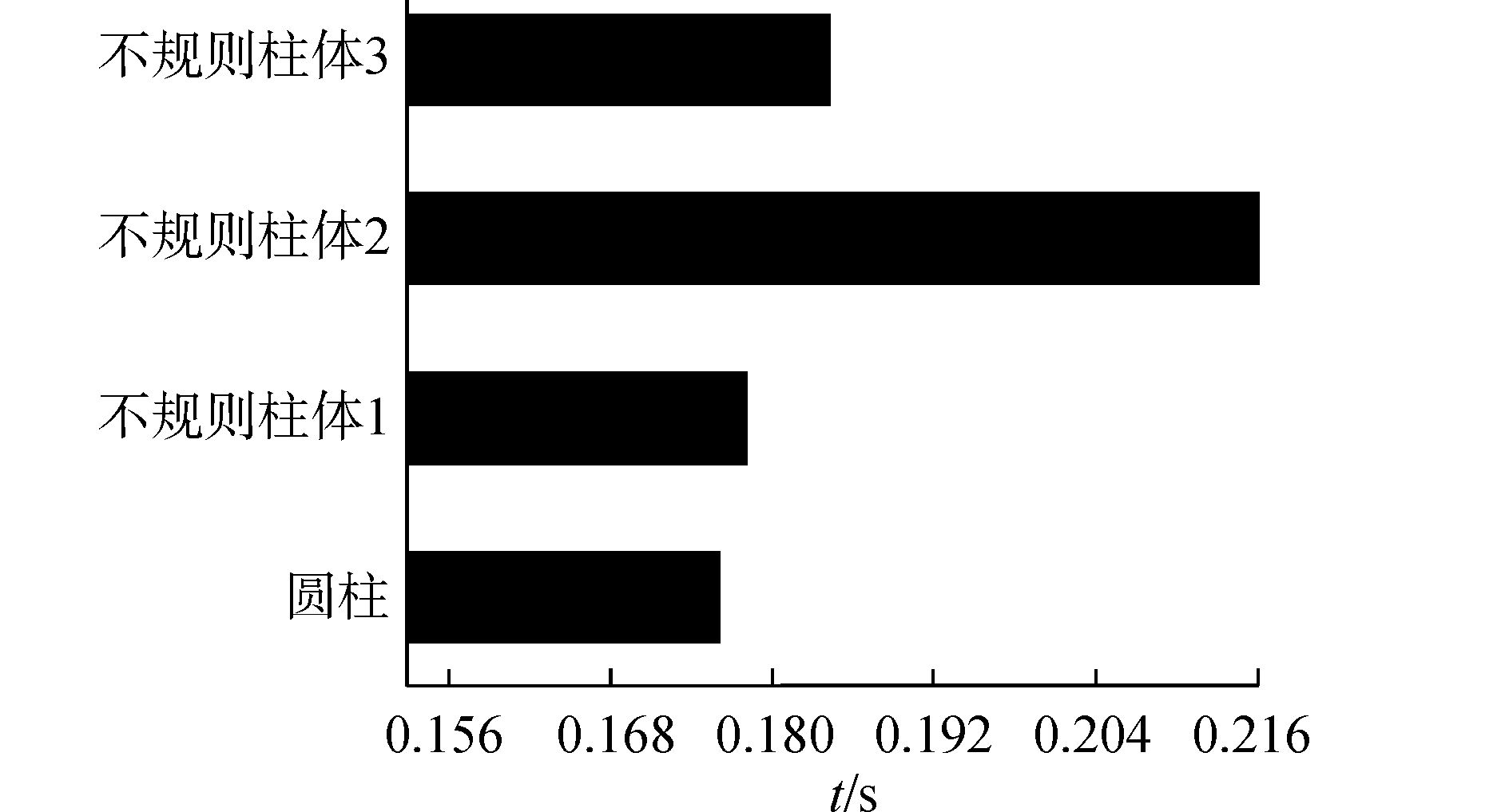
4个模型的尾涡脱落周期柱状图,如图 8所示。
|
图 8 尾涡脱落周期柱状图(Re=8×105) |
通过对比尾涡稳定脱离后的脱落周期发现,在超临界区,不规则柱体尾涡脱落的周期都比圆柱的大,即不规则柱体延缓了尾涡的脱落,且比Re=3.6×106时的周期大很多。综合比较,不规则柱体二对尾涡脱落周期的影响最大。
4个模型的局部涡量图,如图 9所示。

|
图 9 局部涡量图(Re=8×105) |
通过观察尾涡稳定脱落后的绕流状态发现,在超临界区,不规则柱体对绕流的影响机理与Re=3.6×106时的相同,产生的小旋涡处的涡量值比附近的绕流大,且小旋涡处的速度较大、压力较小,使其能够吸引绕流,最终起到延缓尾涡脱落的目的。
4 结论文中通过对柱状仙人掌的生存环境及截面形状的研究,考虑柱状仙人掌凹凸结构的形状分布特点,设计出了带有凹凸结构的不规则柱体。然后通过数值模拟得出了4个模型在不同雷诺数下的涡量云图。
1) 通过对比普通圆柱体绕流和改变截面形状后的绕流效果,发现不规则柱体会使绕流在凹槽内形成小旋涡,能够吸引绕流,从而延缓尾涡的脱落。
2) 在2种雷诺数情况下,3个不规则柱体均能起到效果,其中不规则柱体二在Re=8×105时的效果最明显。
3) 文中对柱体截面形状进行了设计,并对超临界区和极超临界区进行了数值模拟,为处在大风大浪工况下的海洋平台、海底运输管道等的应用提供了理论基础。
4) 本课题可以经由设计更好的不规则柱体模型、更好的划分网格以及计算柱体受力等以进一步深入研究。
| [1] |
詹昊, 李万平, 方秦汉, 等. 不同雷诺数下圆柱绕流仿真计算[J]. 武汉理工大学学报, 2008, 30(12): 129-132. ( 0) 0)
|
| [2] |
何鸿涛. 圆柱绕流及其控制的数值模拟研究[D]. 北京: 北京交通大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10004-2010142484.htm
( 0) 0)
|
| [3] |
韩韶英. 带轴向板条圆柱绕流数值模拟研究[D]. 青岛: 中国海洋大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10423-1011229571.htm
( 0) 0)
|
| [4] |
龚细斌. 波浪型圆柱涡激振动机理的数值研究[D]. 武汉: 武汉理工大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10497-1015000558.htm
( 0) 0)
|
| [5] |
ZHANG K, KATSUCHI H, ZHOU D, et al. Numerical study on the effect of shape modification to the flow around circular cylinders[J]. Journal of wind engineering & industrial aerodynamics, 2016, 152: 23-40. ( 0) 0)
|
| [6] |
许媛欣. 方柱绕流涡激振动及控制方法的数值研究[D]. 天津: 天津大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10056-1015017530.htm
( 0) 0)
|
| [7] |
陈禹, 李强, 郭廷凯. 不同雷诺数下的圆柱绕流数值模拟研究[J]. 中国水运月刊, 2015, 15(7): 88-90. ( 0) 0)
|
| [8] |
林琳. 绕圆柱湍流场发展及立管涡激振动的研究[D]. 大连: 大连理工大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1014154616.htm
( 0) 0)
|
| [9] |
李文春, 金晗辉, 任安禄, 等. 气固两相三维圆柱绕流的直接数值模拟[J]. 工程热物理学报, 2006, 27(5): 808-810. ( 0) 0)
|
| [10] |
陈伟. 涡激振动的离散涡数值模拟[D]. 大连: 大连理工大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10141-2010021489.htm
( 0) 0)
|
| [11] |
王丽丽. 两层黏性流中水平圆柱体的涡激振动特性研究[D]. 上海: 上海交通大学, 2007. http://d.wanfangdata.com.cn/Thesis/D029516
( 0) 0)
|
| [12] |
及春宁, 李非凡, 陈威霖, 等. 圆柱涡激振动研究进展与展望[J]. 海洋技术学报, 2015, 34(1): 106-118. ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


