近年来,许多已建和正在建设的混凝土大坝都处于强震高发区,进行大坝的地震响应规律研究对此类地区的大坝抗震设计和安全性评估具有重要意义。在地震研究方面,震害记录与调查、现场大比例尺模型试验和原位观测等方面的实测资料得到不断积累[1],但在数值模拟方面,如何设置合理的边界条件以模拟土体无限性,更为真实地反映结构的动力特性,仍需继续努力。无限单元在模拟土体无限性方面具有高效准确的特点,故文中利用通用结构力学分析软件ABAQUS,将无限元法应用在重力坝地震动力分析中,为重力坝抗震设计提供一定的参考。
1 无限元法在无限区域或半无限空间问题的有限元分析中,比如坝体与地基的相互作用问题分析时,通常的研究方法是根据规范选取一定范围的地基区域,在边界上施加人工边界条件。这种方法对计算精度的影响以及地基范围的选取目前没有明确的答案。若采用无限元单元,只要截取有限范围的地基,就能满足计算精度要求,并且符合无穷远处位移为零的边界条件,物理概念更加明确[2]。
在本质上,无限单元与普通有限元并没有什么不同,只是基于其远域的特点在形函数的处理上有所不同,在静力计算时加一个衰减函数,在动力计算时,还要加一个波传播函数,一方面考虑波动幅值的衰减,另一方面考虑波动的振动性质[3-4]。
1.1 无限元边界理论1973年,R.Ungless最早提出无限元的概念[5],后经过Bettess、Beer、Zienkiewicz等人的改进和发展。20世纪80年代,张楚汉[6-7]、葛修润[8]等对无限元的研究使其应用范围更为广泛。90年代及以后,燕柳斌等[9]利用无限元方法模拟半空间弹性地基和重力坝地基;向前、孙萍[10-11]采用有限元-无限远耦合方法,研究了波在无限远介质中的能量弥散现象,在研究过程中采用有限元-无限元耦合方法,模拟拱坝的无限域地基,从而反映出波在无限域中逐渐消散的现象。
ABAQUS里面提供的无限元单元实质上为有限元的一部分,与边界元、半解析法相比,无限元无需涉及解析解表达式。概括起来无限元具有如下特点:从局部坐标系中的有限域映射到整体坐标系中的无限域,实现计算区域半无限大的特点;在静、动力分析时它不仅可以实现远场位移为零的效果,而且在动力分析时还可以吸收外行反射到边界的反射波,很好地模拟了半无限域地基的辐射阻尼效应,实现了结构地基的相互作用[3-4];网格数量少,计算效率高,结果精确。
1.2 二维单向无限元坐标变换和位移函数图 1表示9结点二维无限单元,其中1、3、5号结点与8结点平面有限元耦合,2、4、6号结点为无限元的中间结点,7、8、9号结点在无穷远处。

|
图 1 二维单向映射 |
单元内任意点在局部和整体两种坐标系中的坐标变换式为[12]:
| $\begin{array}{l} x = {N_1}\left[ \eta \right]\left[ {{M_1}\left[ \xi \right]{x_1} + {M_2}\left[ \xi \right]{x_2}} \right] + \\ \quad {N_3}\left[ \eta \right]\left[ {{M_1}\left[ \xi \right]{x_3} + {M_2}\left[ \xi \right]{x_4}} \right] + \\ \quad \;{N_5}\left[ \eta \right]\left[ {{M_1}\left[ \xi \right]{x_5} + {M_2}\left[ \xi \right]{x_6}} \right]\\ y = {N_1}\left[ \eta \right]\left[ {{M_1}\left[ \xi \right]{y_1} + {M_2}\left[ \xi \right]{y_2}} \right] + \\ \quad {N_3}\left[ \eta \right]\left[ {{M_1}\left[ \xi \right]{y_3} + {M_2}\left[ \xi \right]{y_4}} \right] + \\ \quad \;{N_5}\left[ \eta \right]\left[ {{M_1}\left[ \xi \right]{y_5} + {M_2}\left[ \xi \right]{y_6}} \right] \end{array}$ |
式中:Mi为映射函数,M1=-2ξ/[1-ξ],M2=[1+ξ]/[1-ξ];Ni为形函数,N1[η]=η[η-1]/2, N3[η]=[1+η][1-η],N5[η]=[1+η]/2。
| $\begin{array}{l} u = {N_1}\left[ \eta \right]\left[ {{N_1}\left[ \xi \right]{u_1} + {N_2}\left[ \xi \right]{u_2}} \right] + \\ \quad {N_3}\left[ \eta \right]\left[ {{N_1}\left[ \xi \right]{u_3} + {N_2}\left[ \xi \right]{u_4}} \right] + \\ \quad \;{N_5}\left[ \eta \right]\left[ {{N_1}\left[ \xi \right]{u_5} + {N_2}\left[ \xi \right]{u_6}} \right]\\ v = {N_1}\left[ \eta \right]\left[ {{N_1}\left[ \xi \right]{v_1} + {N_2}\left[ \xi \right]{v_2}} \right] + \\ \quad {N_3}\left[ \eta \right]\left[ {{N_1}\left[ \xi \right]{v_3} + {N_2}\left[ \xi \right]{v_4}} \right] + \\ \quad \;{N_5}\left[ \eta \right]\left[ {{N_1}\left[ \xi \right]{v_5} + {N_2}\left[ \xi \right]{v_6}} \right] \end{array}$ |
式中:ui、vi(i=1~6) 为i结点在x、y方向的位移分量。
2 无限元边界精度验证以二维均匀弹性半空间的动力响应问题来验证无限元边界的精确性。为简化计算,介质的弹性模量和密度分别取E=1和ρ=1,波源为沿y方向作用于弹性半空间表面的暂态分布荷载F(x, t)=T(t)S(x),T(t)和S(t)的表达式如下:
| $\begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {T\left( t \right) = t,0 < t \le 1}\\ {T\left( t \right) = 2 - t,1 < t \le 3}\\ {T\left( t \right) = t - 4,3 < t \le 4}\\ {T\left( t \right) = 0,t > 4} \end{array}} \right.\\ \left\{ {\begin{array}{*{20}{l}} {S\left( x \right) = 1, - 1 \le x \le 1}\\ {S\left( x \right) = 0,其他} \end{array}} \right. \end{array}$ |
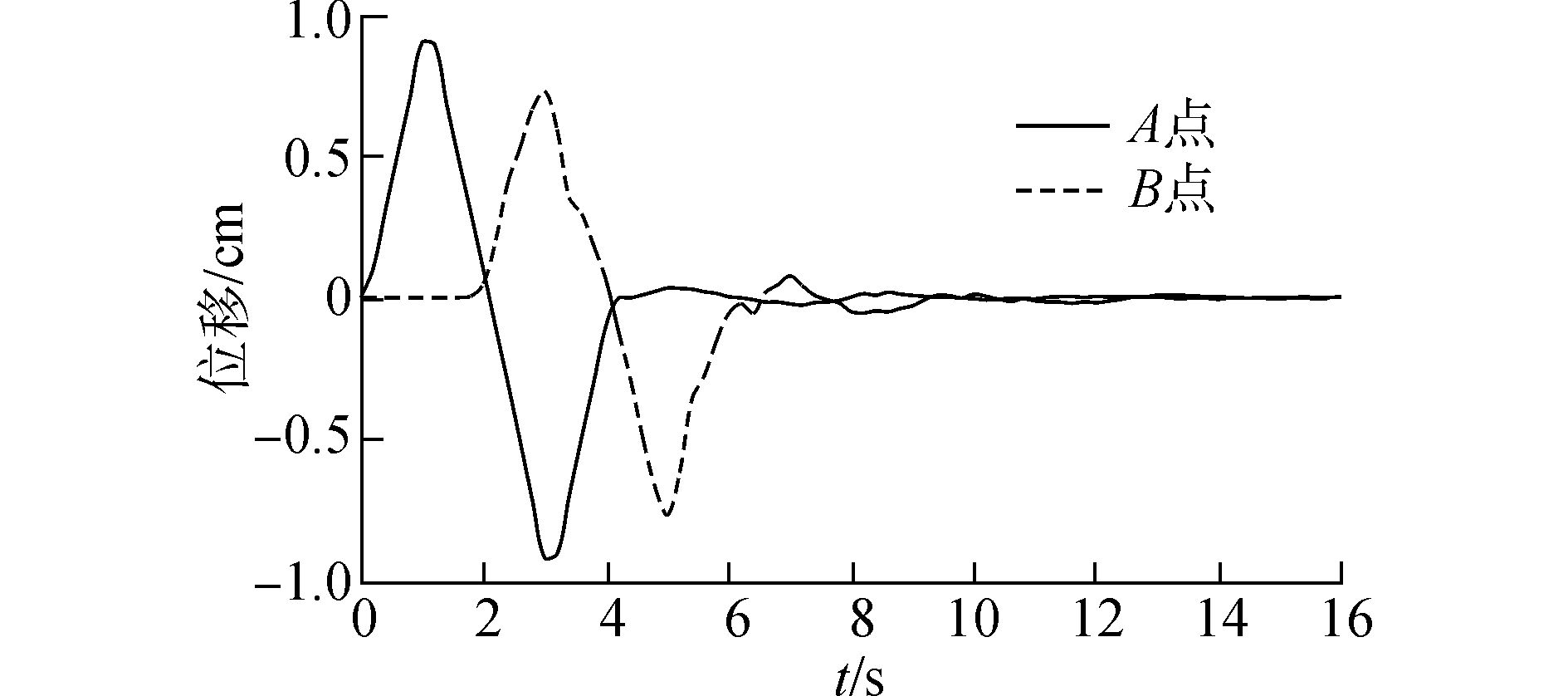
利用有限元软件ABAQUS建模,计算区域为-2≤x≤2,-2≤y≤0,有限元部分单元类型为CPS4R,网格大小为0.1,无限元边界单元类型为CINPS4,时间间隔为0.02 s,总计算时长为16 s,取上表面中点A(0, 0) 和下表面中点B(0,-2) 为观测点。同时,计算此模型在刚性边界条件(底面全约束,侧面约束水平位移)下的动力响应,与无限元边界的位移进行比较。计算结果如图 2、3所示。
|
图 2 无限元边界条件的计算结果 |
|
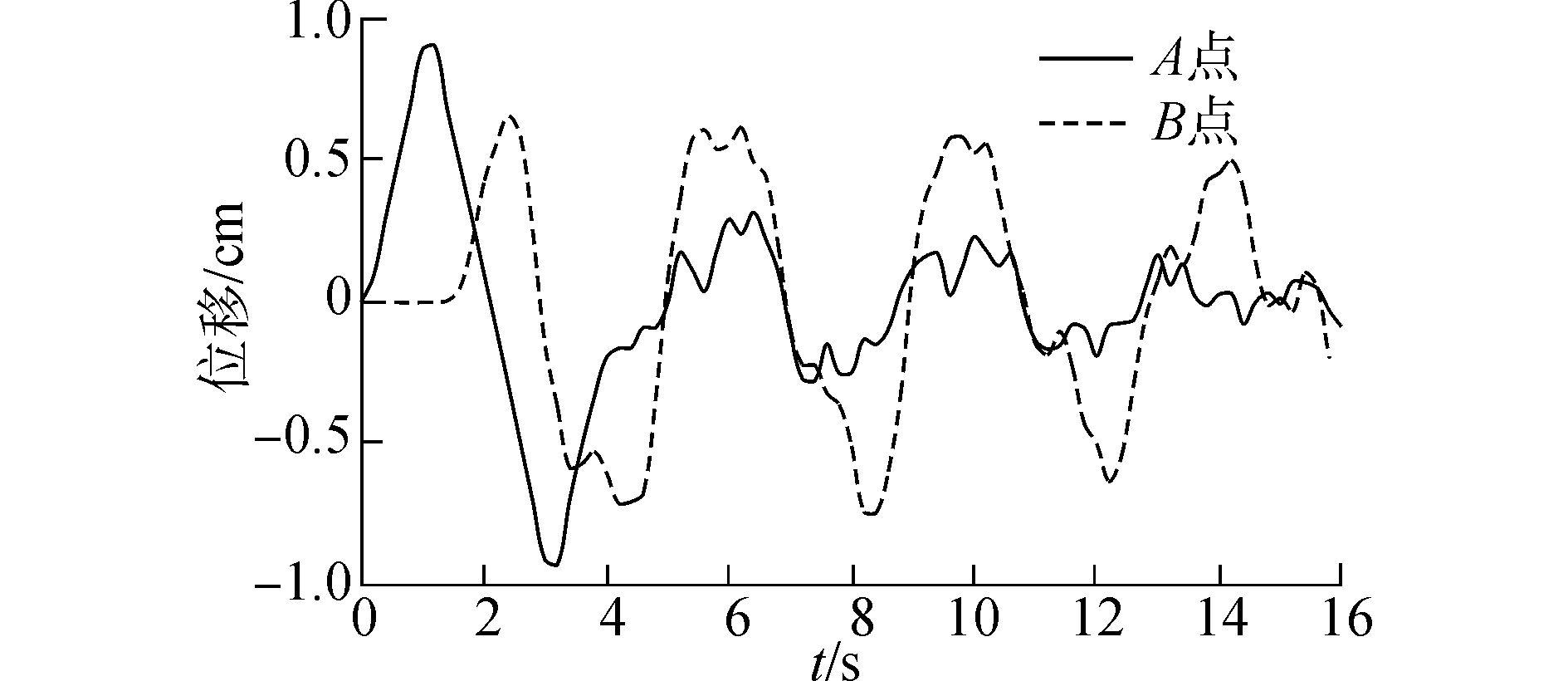
图 3 刚性边界条件的计算结果 |
由图 2可以看出,无限元边界对波的吸收十分明显。在表面施加近似简谐荷载的作用下,观测点A和B的位移时程曲线均呈现出简谐波型,由于表面波传递到底面需要一定时间,故观测点B的位移响应较A点有一定的延时;两测点在荷载停止后的短暂时间内,有一些微小的滞后位移,之后位移趋向于零,计算结果符合实际。
由图 3可以看出,在采用刚性边界时,观测点的位移时程曲线与实际结果有较大差异,在荷载停止作用后,介质内的波动依然没有停止,甚至十分剧烈,一直持续到计算时间结束。这是由于刚性边界具有反射性,当波动荷载传播到截断边界处不能有效地向无限远处传播消散,反而反射形成附加的惯性力作用在介质上,导致计算结果不断波动。
3 重力坝地震响应分析 3.1 计算参数某一混凝土重力坝,坝高为100 m,上游坝面整体为铅垂方向,下游铅垂方向长度为10 m,坝顶宽10 m,坡面系数为0.6。上游正常蓄水位80 m,下游水位20 m。坝体材料为采用同一混凝土,弹性模量为3×1010 Pa,泊松比为0.167,密度为2 400 kg/m3,抗拉强度为1.96×106 Pa,抗压强度为22×106 Pa;坝基视为同一材料,弹性模量为6×108 Pa,泊松比为0.2,密度为2 040 kg/m3。
3.2 模型概况重力坝长度比宽度大很多,将其简化视为平面问题考虑。坝体考虑弹塑性作用,材料选用混凝土损伤塑性模型,坝基为弹性材料。材料阻尼选用Rayleigh阻尼,参数根据Rayleigh阻尼相关公式进行计算,α坝=0.14,β坝=0.017;α土=0.276,β土=0.034。
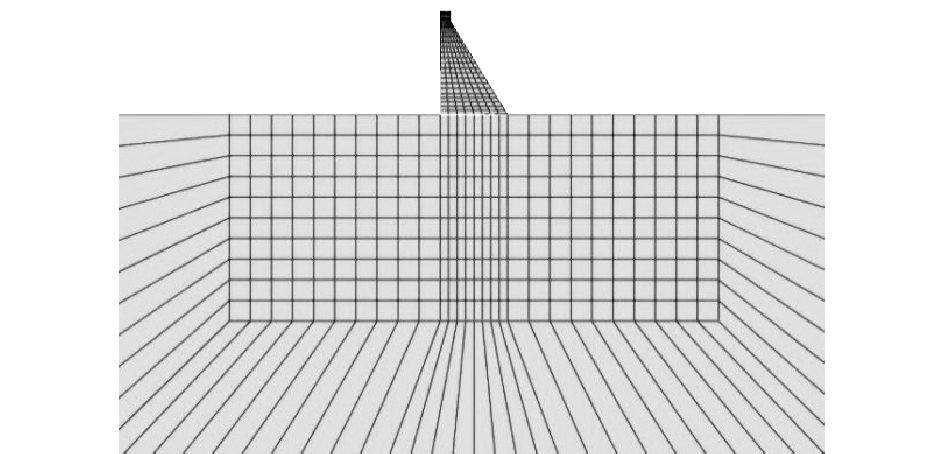
在模型坝基有限元范围的确定过程或者能够中:坝基部分上、下游分别取1~5倍坝高,坝基深度也分别取1~5倍坝高,计算模型及网格划分见图 4,模型施加重力和静水压力后,不同计算模型下的坝体应力如表 1所示。可以得出,坝体应力随着有限元区域和网格数量的增加而增大,但当计算区域坝基上、下游及深度均为3倍坝高以上时,应力不再增大而是逐渐趋于稳定。经分析最终确定计算区域,有限元部分坝基上、下游均取300 m,坝基深度取300 m,边界设置无限单元。有限元单元类型为CPS4R,无限单元类型为CINPS4,模型网格总个数为1 216,其中无限单元个数为88。
|
图 4 重力坝模型 |
|
|
表 1 不同计算模型下的坝体应力MPa |
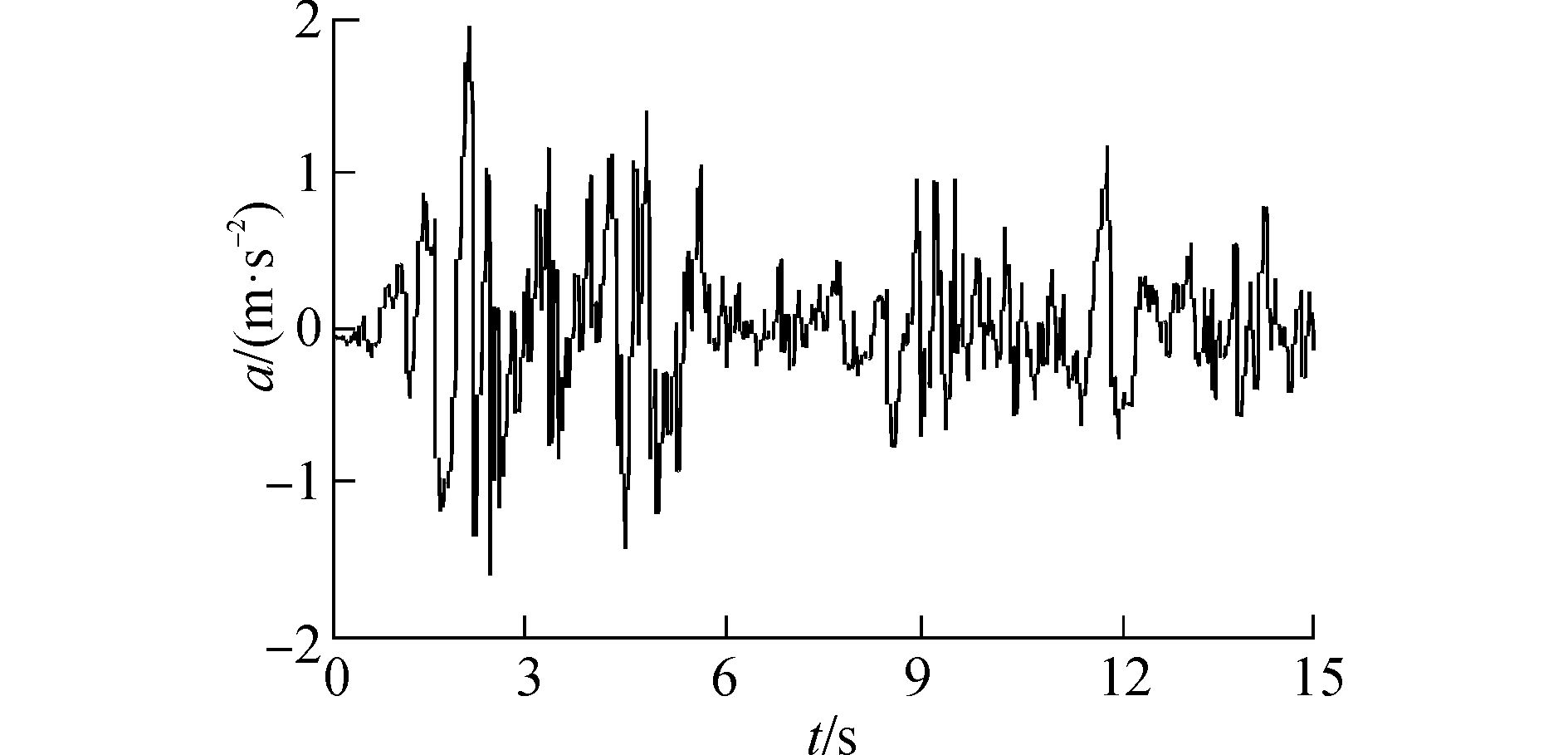
地震波采用1940年EI-Centro N-S方向地震波,此地震波广泛应用于结构的抗震试验及数值模拟分析。仅考虑水平向地震作用,保持频谱特性不变,将加速度峰值调整为0.2 g,即对应于文献[14]规定的8度地震烈度,持续时间取前15 s,此时主要地震活动已结束,时间间隔为0.02 s,图 5为调整后地震波时程加速度曲线图。
|
图 5 EI-Centro时程加速度曲线 |
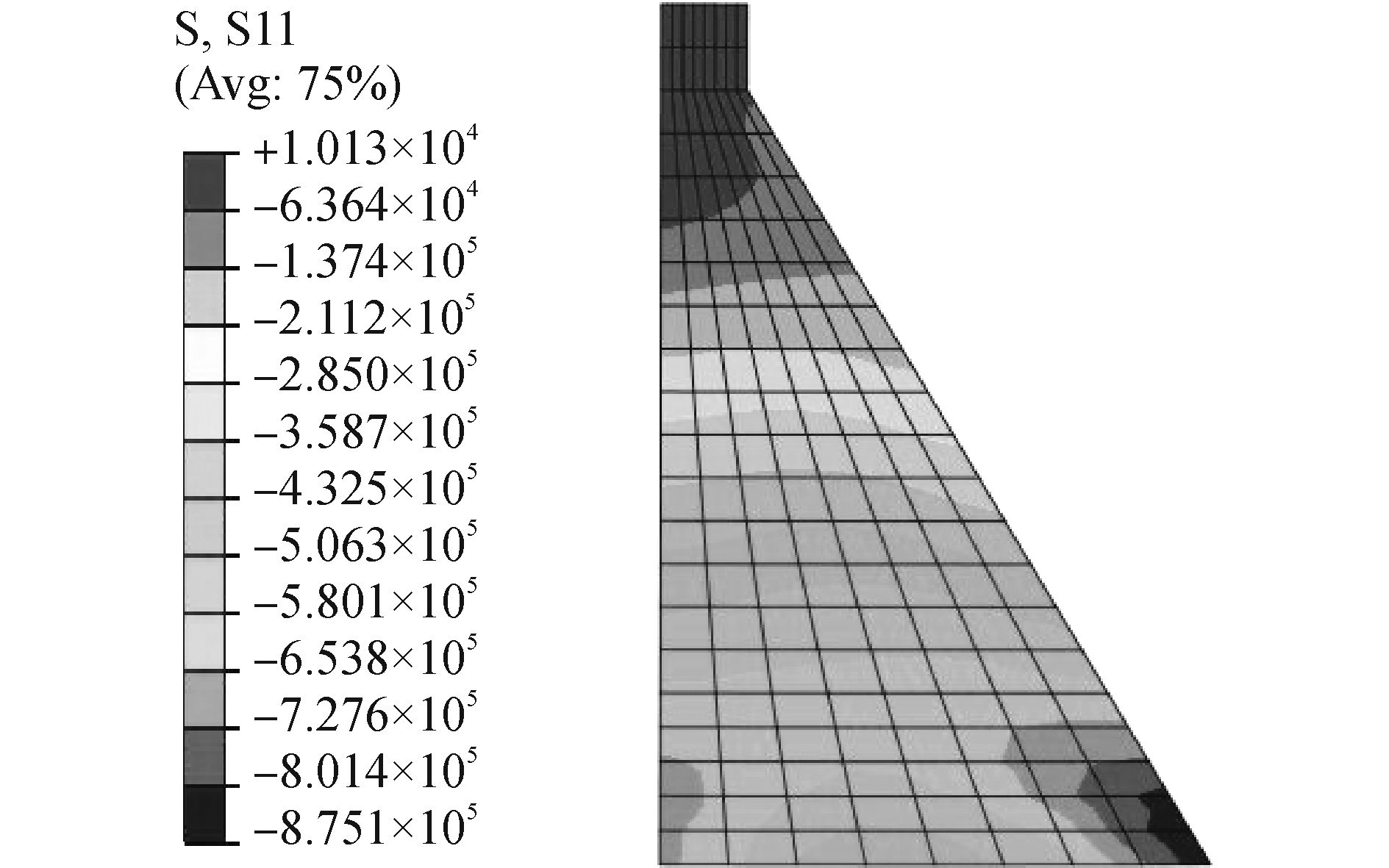
图 6为重力坝在静力作用时水平应力分布云图,图 7为重力坝在静力及地震波同时作用下的最大水平应力分布云图。可以看出,两种情况下坝趾和坝踵处均存在压应力集中现象,坝顶水平应力较小,有小部分区域受到拉应力作用。地震作用导致结构整体所受的水平应力有了显著增长,最大水平应力满足材料强度要求,由666.9 kPa增长至875.1 kPa,增幅达到31.2%,最大受压位置也有所改变,在静力状态靠近上游坝趾处应力最大,在动力状态下则为坝踵处应力最大。大坝底部应力分布呈现抛物线形状,即“中间小、两头大”的分布形式,由此可见坝趾和坝踵处为大坝的抗震薄弱位置,在进行混凝土坝的材料强度选择时,应提高坝趾和坝踵处的抗压性。

|
图 6 水平静应力分布 |
|
图 7 最大水平动应力分布 |
综合分析重力坝动应力分布规律,坝体上部总体应力分布小于坝体下部,因此在设计和施工允许的情况下,可以对大坝上下部采用不同强度的混凝土,上部使用强度较低的混凝土即可满足受力要求,下部采用强度较高的混凝土以提供较高的抗压强度,并在坝踵和坝址位置加密配筋,确保结构具有较高的安全系数,满足抗震规范要求。
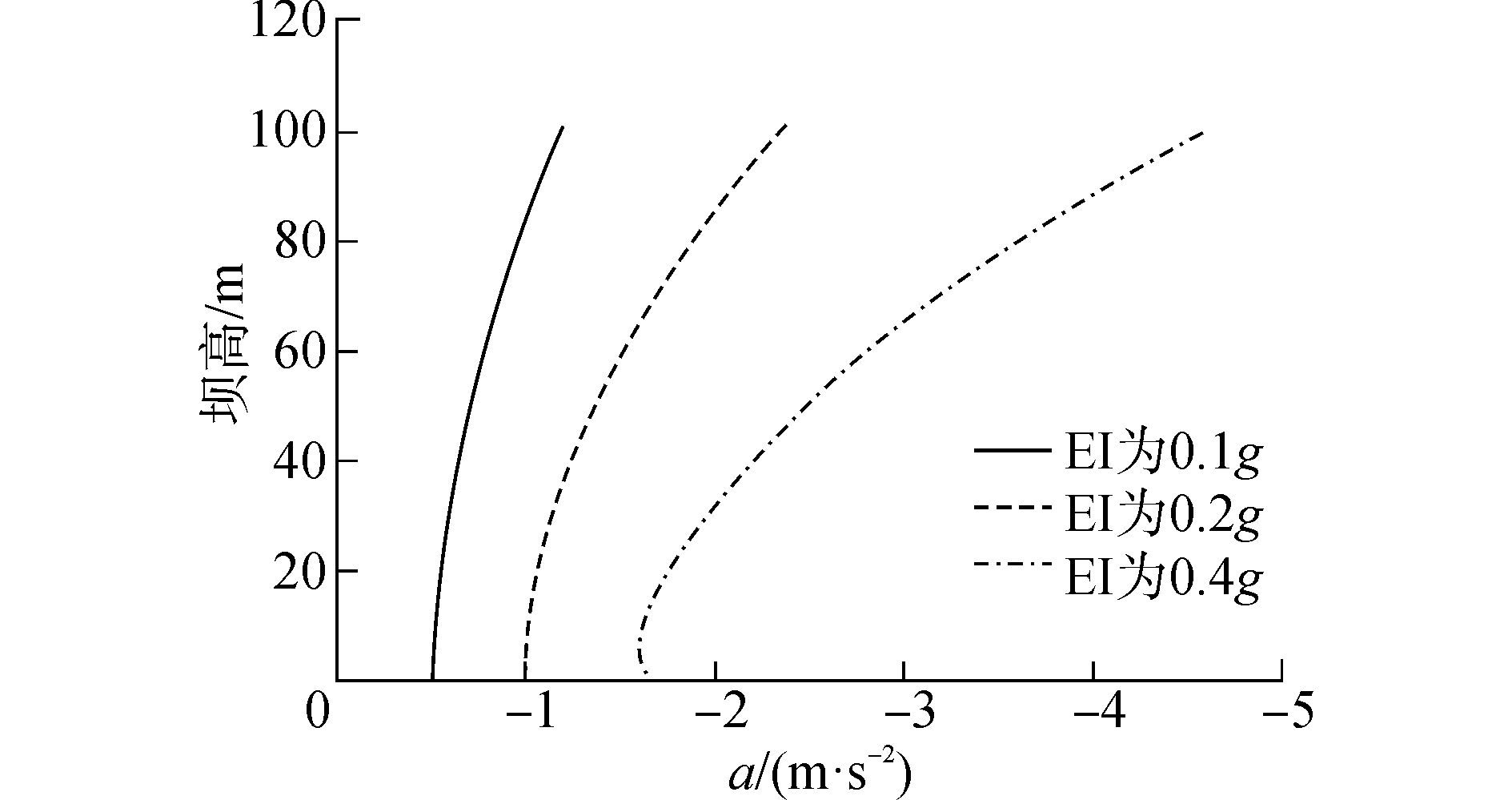
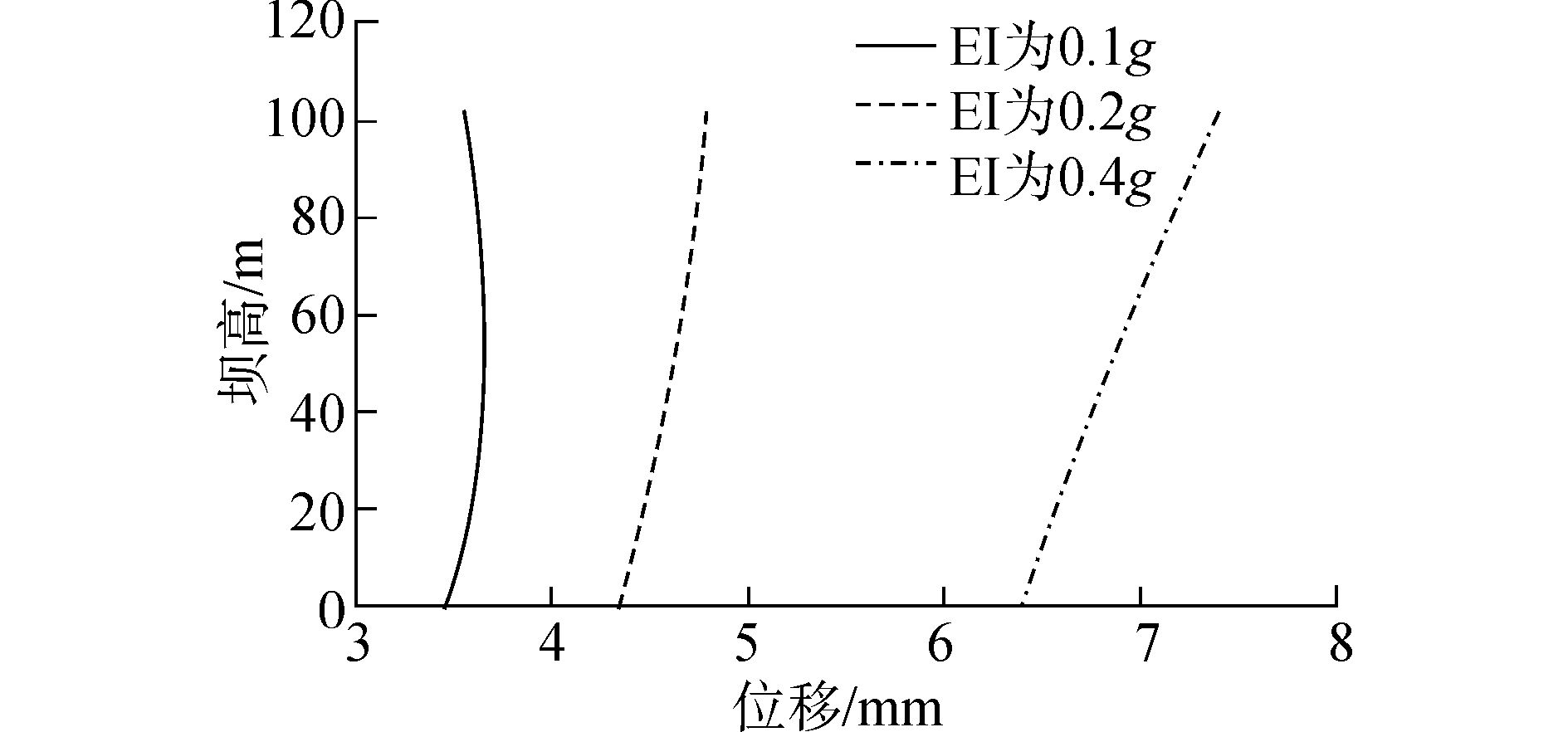
3.3.2 地震强度对重力坝地震响应的影响仅考虑水平向地震作用,将EI-Centro地震波的峰值加速度分别调整为0.1g、0.2g和0.4g输入地基底部,即对应于文献[14]规定的7、8、9度地震烈度,研究地震强度对重力坝的影响。由图 8、9可知,在EI-Centro地震波作用下,大坝峰值加速度方向指向大坝上游,大坝的水平峰值加速度和水平峰值位移随着地震强度的增大而增大,且强度越大,沿坝高的响应增大速率越大。大坝顶端基本为峰值响应的最大处,峰值加速度分别为1.17、2.55和4.57 m/s2,比值接近于1:2:4,与输入的加速度比值相同,说明了由于地基土体的放大作用,重力坝的加速度反应大于输入的加速度。峰值水平位移为3.58、4.81和7.38 cm,比值与地震波加速度峰值的比值不同。
|
图 8 不同地震强度下沿坝高的峰值加速度曲线 |
|
图 9 不同地震强度下沿坝高的峰值水平位移曲线 |
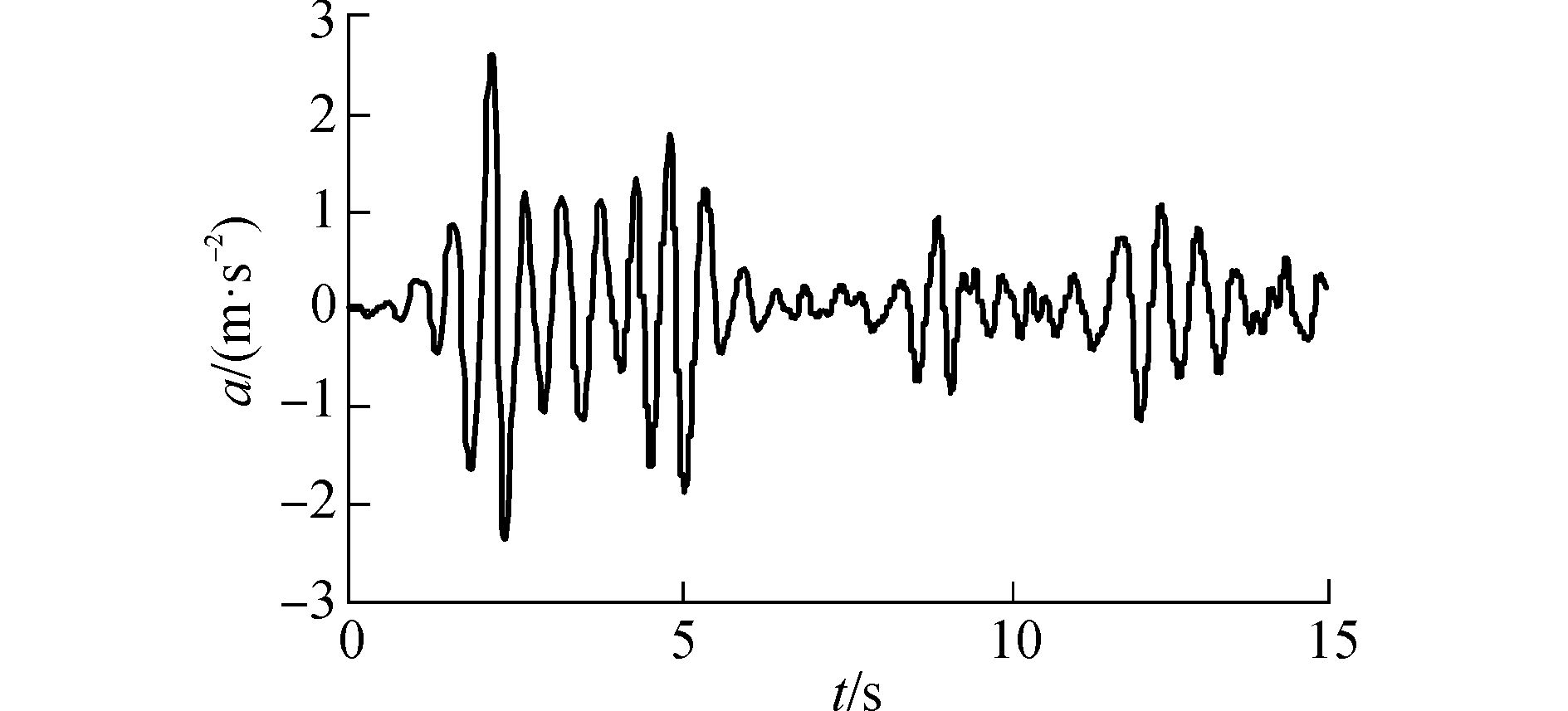
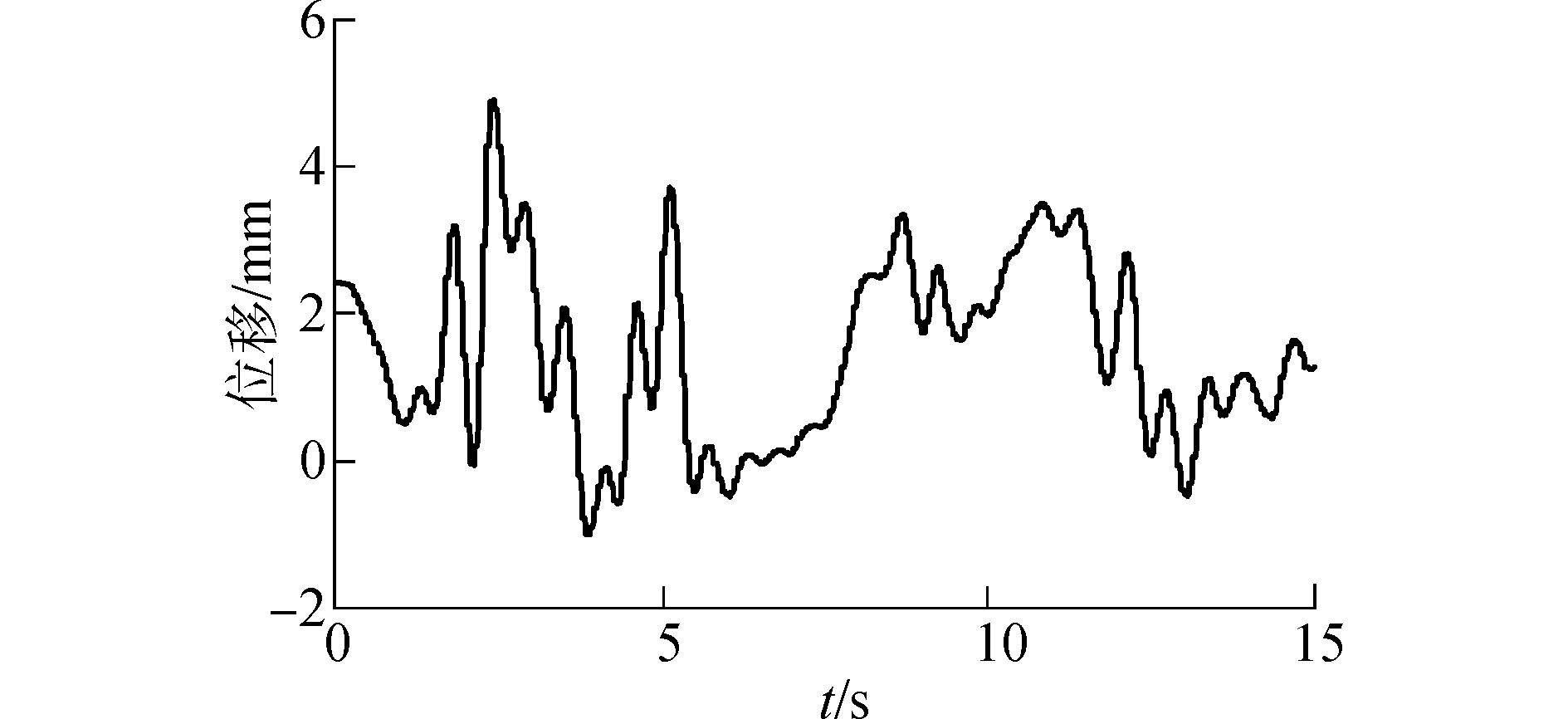
图 10、11为地震波峰值为0.2g时,大坝顶端上游处加速度和水平位移变化的时程曲线,可以看出大坝顶端加速度和位移在地震波的作用下不断波动,主要产生向下游方向的位移,加速度到达峰值的时刻为2.22 s,位移到达峰值的时刻为2.48 s,加速度和位移到达峰值的时间较地震波的峰值出现时间2.14 s均稍有延迟,说明结构的动力响应相对于外部激励具有滞后性。
|
图 10 地震波峰值为0.2g时大坝顶部加速度时程曲线 |
|
图 11 地震波峰值为0.2g时大坝顶部水平位移时程曲线 |
仅考虑水平方向的地震作用,研究EI-Centro、Taft、Northridge地震波对重力坝地震响应的影响,持续时间均取前15 s,此时3种地震波的主要地震活动均已结束。这3种波的频谱成分均以低频为主,但具有各自的特点,其余2种波的加速度时程曲线如图 12、13所示。将3种地震波的峰值加速度调整为0.2g后分别输入到基底中进行地震响应分析。

|
图 12 Taft波 |

|
图 13 Northridge波 |
1) 不同地震波对重力坝水平加速度的影响。对比不同地震波作用下的重力坝地震峰值水平加速度响应,由图 14可以看出,加速度幅值沿坝高均逐渐增大,但并不是线性增大,最大值分别为-2.36、1.51、1.86 m/s2,均大于输入的地震波加速度峰值,EI-Centro波引起的响应幅值最大。地震波频谱特性对加速度沿坝高的增大速率和加速度方向有影响,在EI-Centro波作用下加速度沿坝高的增大效果最为显著,在EI-Centro波作用下最大峰值加速度方向指向大坝上游,其余地震波作用下最大峰值加速度方向指向大坝下游。

|
图 14 沿坝高峰值水平加速度曲线 |
2) 不同地震波对重力坝水平位移的影响。图 15为峰值水平位移沿坝高的分布曲线,对比分析可以得出以下结论:由于重力坝整体刚度大,在不同地震波作用下,重力坝沿高度峰值水平位移均差值不大,最大差值仅为0.51 cm,顶部位移最大,分别为7.38、7.45、5.29 cm,重力坝在Taft地震波作用时,最大峰值水平位移幅值最大,说明Taft地震波的频率与结构的自振频率最接近。

|
图 15 沿坝高峰值水平位移曲线 |
在重力坝地震响应分析中,选取无限元作为模型的边界条件,在提高模型计算效率的同时,消除刚性边界反射地震波对结构响应的影响,得到更为精确的钢筋混凝土重力坝地震响应规律,符合结构的动力学原理,为重力坝抗震设计提供一定的参考。
1) 经过研究发现,重力坝的动应力较静力状态有了显著增大,坝踵、坝址附近容易出现压应力集中现象,在大坝的抗震设计中应特别注意此处是否满足材料强度的要求。
2) 结构峰值水平加速度和峰值水平位移随着地震强度、幅值的增大呈非线性增大,大坝顶端为响应最大处。
3) 峰值出现的时间较地震加速度峰值到达时间有所延后,体现了结构动力响应的滞后性。
本文对于地震波的模拟,采用最常见的加速度时程分析法,在后续的研究中可以采用更加精确的方法来模拟地震波对结构的作用,有待进一步研究和探讨。
| [1] |
毛海涛, 王晓菊, 付亚男, 等. 无限元法在无限深透水坝基渗流计算中的应用[J]. 人民黄河, 2014, 36(2): 90-92. ( 0) 0)
|
| [2] |
王刚. 碾压混凝土重力坝动力稳定非线性分析[D]. 大连: 大连理工大学, 2014: 13-17. http://cdmd.cnki.com.cn/Article/CDMD-10141-1015572215.htm
( 0) 0)
|
| [3] |
何益斌. 三维水平成层地下介质有限元网格划分研究[D]. 长沙: 湖南大学, 2013: 41-50. http://cdmd.cnki.com.cn/Article/CDMD-10532-1014121555.htm
( 0) 0)
|
| [4] |
赵宝友. 大型岩体洞室地震响应及减震措施研究[D]. 大连: 大连理工大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10141-2010021861.htm
( 0) 0)
|
| [5] |
UNGLESS R F. An infinite finite element[D]. M. A. Sc:University of British Columbia, 1973:1-10.
( 0) 0)
|
| [6] |
ZHANG Chuhan, ZHAO Chongbin. Coupling method of finite and infinite elements for strip foundation wave problems[J]. Earthquake engineering and structural dynamics, 1987, 15: 839-851. DOI:10.1002/(ISSN)1096-9845 ( 0) 0)
|
| [7] |
代凌辉, 唐新军, 徐千军. 无限元应用于土石坝坝基远场探讨[J]. 人民黄河, 2012, 34(2): 103-105. ( 0) 0)
|
| [8] |
葛修润, 谷先荣, 丰定祥. 三维无限元和节理无界元[J]. 岩土工程学报, 1986, 8(5): 9-20. ( 0) 0)
|
| [9] |
孙正华. 碾压混凝土重力坝抗震安全评价及坝基稳定分析研究[D]. 宜昌: 三峡大学, 2013: 15-17. http://d.wanfangdata.com.cn/Thesis/D471020
( 0) 0)
|
| [10] |
向前. 无限元参与地基基础-坝体动力相互作用分析[D]. 南宁: 广西大学, 2004: 28-35. http://www.cnki.com.cn/Article/CJFDTOTAL-GDTM200509007.htm
( 0) 0)
|
| [11] |
赵丙华. 基于有限元-无限元耦合法的半无限土动力响应分析[D]. 北京: 北京交通大学, 2012: 21-23. http://cdmd.cnki.com.cn/Article/CDMD-10004-1012355909.htm
( 0) 0)
|
| [12] |
何力, 彭刚, 胡婷, 等. 无限元在地基基础-坝体体系数值分析中的应用[J]. 红水河, 2011, 3: 29-32. DOI:10.3969/j.issn.1001-408X.2011.05.007 ( 0) 0)
|
| [13] |
吴鸿庆, 任侠. 结构有限元分析[M]. 北京: 中国铁道出版社, 2000.
( 0) 0)
|
| [14] |
NB35047-2015, 水电工程水工建筑物抗震设计规范[S]. 北京: 水电水利规划设计总院, 2015.
( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


