目标跟踪技术一直是计算机视觉领域研究的热点问题,其在视频检索、人机交互以及无人驾驶汽车等领域都有良好的应用前景[1]。目标跟踪算法可以分为生成式方法和判别式方法[2]。得益于近几年机器学习的长足发展,判别式目标跟踪算法成为跟踪算法的主要研究方向。判别式目标跟踪算法引入机器学习的方法,将目标跟踪看作是一个二分类问题,即从背景区域提取出目标区域。因此判别式跟踪算法又被称作是基于检测的目标跟踪算法。目前比较流行的基于检测的跟踪算法有基于核化的结构化输出(structured output tracking with kernel, Struck)算法[3]、跟踪-学习-检测(tracking-learning-detection, TLD)算法[4]和压缩感知(compressive tracking, CT)算法[5]等。这些算法都存在一个问题:为了能够满足跟踪过程的实时性,这些算法只是选取所有样本中的部分训练样本和候选样本,从而减少训练分类器的计算量。但是训练出来的分类器不能够充分利用跟踪目标及其周围的背景信息,这直接影响了跟踪算法的跟踪性能。为了解决这个问题,Henriques等[6]提出了基于循环结构的跟踪(circulant structure of tracking-by-detection with kernel, CSK)算法,将训练样本进行循环位移得到大量的训练样本,达到了密集采样的效果。同时产生的训练样本具有循环结构,通过构造循环矩阵以及傅里叶变换的方法能够将训练的计算量下降几个等级,极大地提升了训练的速度。之后,Henriques等[7]在CSK的基础上,利用核相关滤波器(high speed tracking with kernelized correlation filters, KCF)将其扩展到多通道特征上,极大地提高了跟踪结果的精度。
传统的KCF算法在目标发生刚性形变、出平面旋转等条件下跟踪效果不佳,为此本文将KCF算法分成运动模型、特征提取、检测模型和模型更新方法4个模块进行分析。根据实验分析的结果,对KCF算法的特征提取方式和模型更新方案上进行改进。
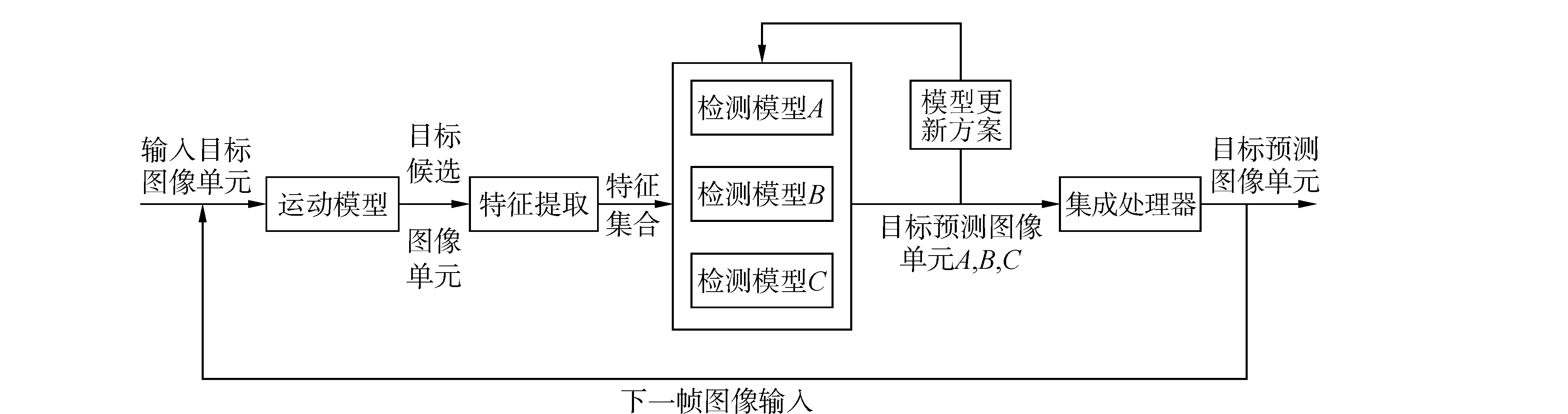
1 基于检测的目标跟踪系统基于检测的目标跟踪系统可以分成运动模型、特征提取、检测模型、模型更新方案和集成处理器5个模块[8], 系统框架如图 1所示。
|
图 1 基于检测的目标跟踪系统框架 |
跟踪系统通常在视频序列的第一帧图像中人工标注出目标区域,然后以第一帧图像对检测模型进行初始化。在后续图像序列中,运动模型产生目标候选图像单元。通过对图像单元进行特征提取,将图像单元转换成特征集合输入到检测模型。检测模型对输入的每个图像单元进行计算并给出一个输出响应,将输出响应最大的图像单元作为当前目标图像单元。根据检测模型的输出结果,按照设定的模型更新方案对检测模型进行更新。如果一个跟踪系统存在多个检测模型,那么集成处理单元会将每个检测模型的预测结果进行集成处理,从而得到更好的预测结果。最后输出预测的当前帧目标图像单元,同时将当前帧图像作为后续视频序列的输入。
2 核相关滤波器算法分析由于KCF跟踪算法只有一个检测模型,因此不存在集成处理模块。根据上文提出的基于检测的目标跟踪系统框架,将核相关滤波器算法分成运动模型、特征转换、检测模型和模型更新方法4个部分进行分析。
2.1 运动模型对于每一帧图像,运动模型根据前一帧图像预测的目标区域来产生训练样本和目标候选区域集合。常用的运动模型有粒子滤波、滑动窗等。以下给出一种构造循环样本矩阵的运动模型。
将通过人工标注或者检测模型检测出来的目标区域图像作为正样本,用n×1的向量x=(x1, x2, …, xn-1, xn)表示。那么可以通过置换矩阵P将向量x进行循环移位, 从而产生大量的负样本。
| $ \mathit{\boldsymbol{P}}{\rm{ = }}\left[\begin{array}{l} 0\;\;\;0\;\;\;0\;\; \cdots \;\;\;1\\ 1\;\;\;0\;\;\;0\;\;\; \cdots \;\;\;0\\ 0\;\;\;1\;\;\;0\;\;\; \cdots \;\;\;0\\ \vdots \;\;\;\; \vdots \;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\; \vdots \\ 0\;\;\;0\;\;\; \cdots \;\;\;1\;\;\;0 \end{array} \right] $ | (1) |
置换矩阵P与向量x的乘积Px=(xn, x1, x2, …, xn-1)将向量x向右移位一次,将其转换为一个新的负样本。利用这种循环特性,可以对目标图像单元x进行n次循环移位{Pμx|μ=0, …, n-1},从而构造一个循环样本矩阵:
| $ \mathit{\boldsymbol{X}} = C\left( x \right) = \left[\begin{array}{l} {x_1}\;\;\;{x_2}\;\;\;{x_3}\;\;\; \cdots \;\;\;{x_n}\\ {x_n}\;\;\;{x_1}\;\;\;{x_2}\;\;\; \cdots \;\;\;{x_{n-1}}\\ {x_{n-1}}\;\;{x_n}\;\;\;{x_1}\;\; \cdots \;\;\;{x_{n-2}}\\ \vdots \;\;\;\;\;\;\; \vdots \;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {x_2}\;\;\;\;{x_3}\;\;\;\;{x_4}\;\; \cdots \;\;\;{x_1} \end{array} \right] $ | (2) |
对于循环移位得到的训练样本xi,根据训练样本离正样本的距离按照高斯分布赋予一个标注yi。
2.2 特征提取特征提取从图像中提取相应的特征,从而得到更加有效的图像信息。本文使用了3种常用的特征描述子,分别是原始像素(raw pixel)、方向梯度直方图(histogram of oriented gradient, HOG)特征以及颜色名称空间(color name,CN)特征[9]。
1) 原始像素特征:通过将图像转换到一定的尺寸,然后将其转换成灰度图像,以每个像素的灰度值作为图像的特征。
2) HOG特征:HOG特征首次由Dalal等[10]提出,用于进行行人检测。HOG特征通过计算和统计图像局部区域的梯度方向直方图来提取图像特征。
3) CN特征:CN特征首先由Danelljan等[11]引入到目标跟踪算法当中,这种特征将RGB空间的图像信息转换到11维空间的颜色描述特征中。同时,将颜色名称空间映射到10维的标准正交子空间。这种映射在减少CN特征维度的同时,也将CN特征进行了聚集。
2.3 检测模型通过上述两步得到的目标样本集合对检测模型进行训练,得到了跟踪的检测模型。检测模型通过对目标候选图像单元进行计算,返回一个输出响应。从目标候选图像单元中选取输出响应最大的图像单元作为目标区域。
在KCF算法中,对检测模型训练的目的是得到一个目标函数f(x)= < w, φ(x)>,使得训练样本xi与它们的回归目标yi之间的正则化二次损失函数最小。
| $ \mathop {\min }\limits_w {\sum\limits_i {{{\left( {f\left( {{x_i}} \right)-{y_i}} \right)}^2} + \lambda \left\| \mathit{\boldsymbol{w}} \right\|} ^2} $ | (3) |
式中:φ表示将输入空间映射到希尔伯特空间,使用的核函数κ(x, x′)=φ(x)·φ(x′),λ为用于防止过拟合的正则化系数。
通过核技巧可以将w的解转换为输入样本的线性组合[6]:
| $ \mathit{\boldsymbol{w}} = \sum\limits_i {{\alpha _i}\varphi \left( {{x_i}} \right)} $ | (4) |
这样就将对系数向量w的求解转换为对于系数向量α的求解。根据文献[12], α的解为
| $ \mathit{\boldsymbol{\alpha = }}{\left( {\mathit{\boldsymbol{K}} + \lambda \mathit{\boldsymbol{I}}} \right)^{-1}}\mathit{\boldsymbol{y}} $ | (5) |
式中:K为核矩阵,其中的元素Ki, j=κ(xi, xj)。I为单位矩阵,y中的元素为yi。
对于核矩阵K,如果其中的核函数是酋不变的,那么这个核矩阵是循环矩阵。因此式(5) 可以利用循环矩阵的特性,将其进行傅里叶转换到频域,有
| $ \mathit{\boldsymbol{\hat \alpha = }}\frac{{\mathit{\boldsymbol{\hat y}}}}{{\mathit{\boldsymbol{\hat k + \lambda }}}} $ | (6) |
式中:
对于新的一帧图像中的目标候选图像单元z,那么检测模块对其的输出响应为
| $ f\left( z \right) = \left\langle {\mathit{\boldsymbol{w}}, \varphi \left( z \right)} \right\rangle = \sum\limits_i {{\alpha _i}k\left( {z, {x_i}} \right)} $ | (7) |
可以看出,对候选目标图像单元的检测也只需要计算其中的一个向量,而不需要计算所有的候选目标,因此也极大地提升了检测速度。将得到最大响应的目标候选图像单元作为新的目标区域位置,从而完成对目标位置的预测。
2.4 模型更新方案模型更新方案决定对目标外观模型以及检测模型更新的策略和频率。以下给出2种模型更新方案。
1) 传统KCF算法中给出以下模型更新方案。
| $ {\mathit{\boldsymbol{x}}_t} = \left( {1-\eta } \right){\mathit{\boldsymbol{x}}_{t-1}} + \eta {\mathit{\boldsymbol{x}}_t} $ | (8) |
| $ {\mathit{\boldsymbol{\alpha }}_t} = \left( {1-\eta } \right){\mathit{\boldsymbol{\alpha }}_{t-1}} + \eta {\mathit{\boldsymbol{\alpha }}_t} $ | (9) |
式中:η为学习因子,x为目标特征向量,α为检测模型系数。
这种模型更新方案只用到了当前帧和上一帧图像的信息,当目标出现形变、遮挡和旋转时,很容易导致跟踪过程中出现漂移的现象。
文献[11]给出了一种利用从第一帧图像提取的模型到当前帧模型的更新方案,取得很好的跟踪效果。本文采取类似的模型更新方法,将其转化到核相关滤波器跟踪算法当中。由于考虑了之前所有帧图像的信息,那么式(1) 中的损失函数可表示为
| $ \varepsilon = \sum\limits_{j = 1}^{\rm{t}} {\left( {\sum\limits_i {{{\left| {\left\langle {{\mathit{\boldsymbol{w}}^j}, \varphi \left( {x_i^j} \right)} \right\rangle-y_i^j} \right|}^2} + \lambda {{\left\| {{\mathit{\boldsymbol{w}}^j}} \right\|}^2}} } \right)} $ | (10) |
在第t帧图像中,模型系数为
| $ {\mathit{\boldsymbol{\hat \alpha }}^t} = \frac{{\sum\limits_{j = 1}^t {{{\hat y}^j}{{\mathit{\boldsymbol{\hat K}}}^j}} }}{{\sum\limits_{j = 1}^t {{{\mathit{\boldsymbol{\hat K}}}^j}\left( {{{\mathit{\boldsymbol{\hat K}}}^j} + \lambda } \right)} }} $ | (11) |
式中Kj的元素kij=κ(xj, xij)。此时对于模型系数的更新可以通过对模型系数的分子和分母分别进行更新。我们将其作为本文的第2种模型更新方法。
2) 改进后的模型更新方法
| $ \mathit{\boldsymbol{\hat \alpha }}_{{\rm{num}}}^t = \left( {1-\eta } \right)\mathit{\boldsymbol{\hat \alpha }}_{{\rm{num}}}^{t-1} + \eta {\hat y^t}{\mathit{\boldsymbol{\hat K}}^t} $ | (12) |
| $ \mathit{\boldsymbol{\hat \alpha }}_{{\rm{den}}}^t = \left( {1-\eta } \right)\mathit{\boldsymbol{\hat \alpha }}_{{\rm{den}}}^{t-1} + \eta {\mathit{\boldsymbol{\hat K}}^t}\left( {{{\mathit{\boldsymbol{\hat K}}}^t} + \lambda } \right) $ | (13) |
| $ {\mathit{\boldsymbol{x}}^t} = \left( {1-\eta } \right){\mathit{\boldsymbol{x}}^{t-1}} + \eta {\mathit{\boldsymbol{x}}^t} $ | (14) |
式中η是学习因子。需要注意的是对目标模型特征向量的更新方法与式(8) 相同。
3 实验分析文献[13]提出的目标跟踪系统评估方法已经成为目标跟踪领域的主流评估方式,本文使用其中的2种评估方法对跟踪算法进行分析。第一种是重叠率(overlap rate)曲线的线下面积(area under curve, AUC)方法,重叠率指的是跟踪算法预测的目标外形框与真实人工标注的目标外形框之间的交集和并集之比。对于给定的阈值,可以通过重叠率来计算整个视频序列跟踪成功率。AUC越大,代表这个跟踪算法的精确度越高。另外一种评估方法是中心像素误差(central pixel error)曲线在阈值20处的精确度。中心像素误差指的是跟踪算法预测的目标外形框与真实人工标注的目标外形框中心像素之间的距离。本文采用了文献[12]中的38个彩色图像视频序列作为实验算法验证数据集。
实验环境配置如下:MATLAB 2013a,2.5 GHz CPU处理器以及4 GB内存。
3.1 模型更新方案比较本节针对2.4中提出的2种模型更新方案,在保持其余模块相同的情况下,比较2种更新方法对跟踪算法的影响。其中特征提取方式选择CN特征。令式(8)~(9) 模型更新方案为方案一,式(12)~(14) 模型更新方案为方案二,基于2种模型更新方案的跟踪算法在38个视频序列的跟踪结果如图 2所示。

|
图 2 不同模型更新方案下跟踪算法的结果 |
由图 2可以看出改进后的模型更新方案极大地提升了跟踪算法的性能。其中精确度高了14.6%,跟踪成功率高了7.8%。可以看出基于所有帧图像提取的模型更新方法具有更强的鲁棒性,在相同的运动模型、特征提取和检测模型下具有更好的效果。
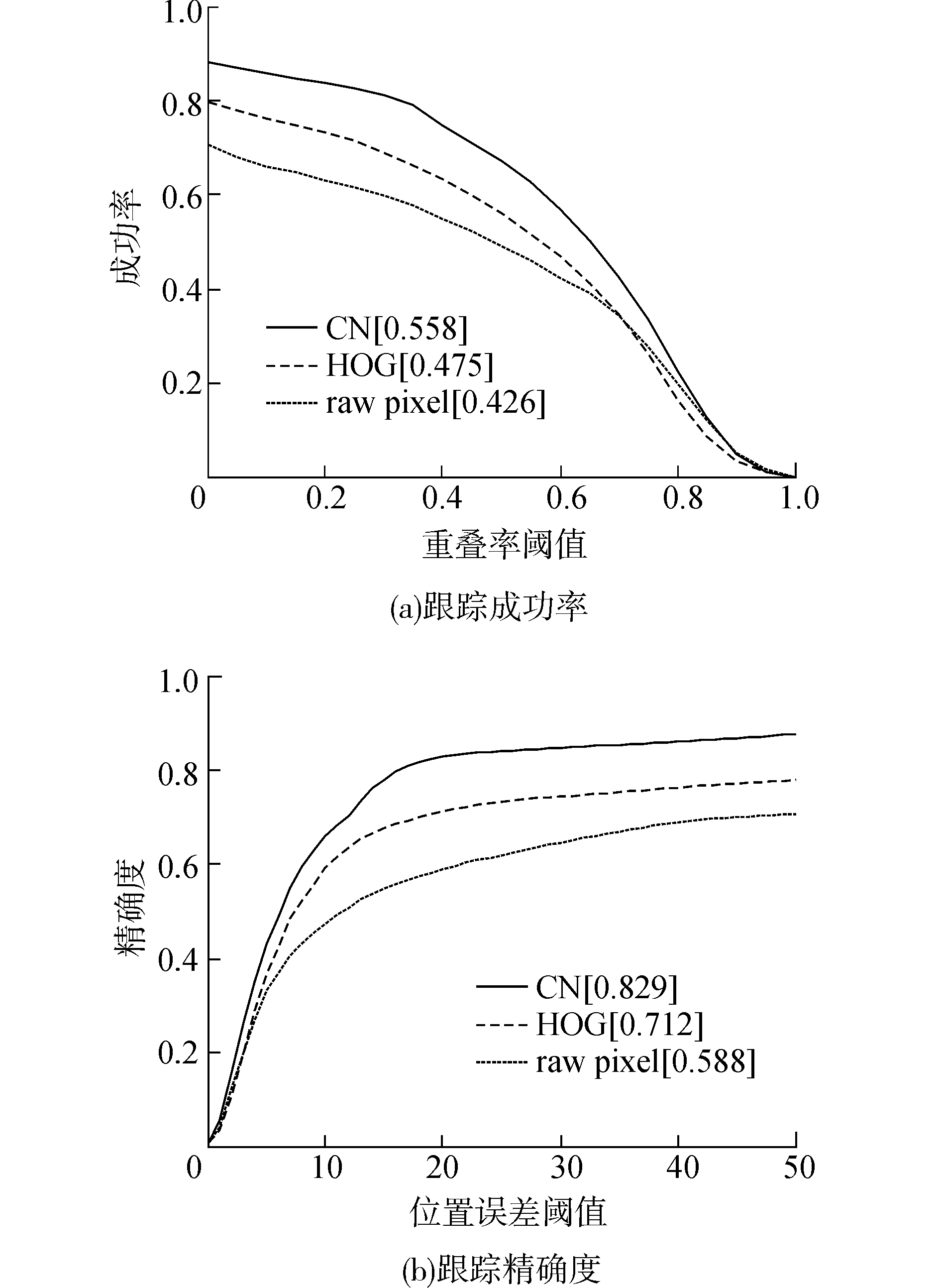
3.2 特征提取比较在2.2节中给出了3种特征描述子,本节在保持其余模块相同的情况下,比较基于3种特征提取方法下的目标跟踪效果。其中模型更新方案选取模型更新方案二。3种跟踪算法在38个视频序列的结果如图 3所示。
|
图 3 不同特征提取下的跟踪算法的结果 |
根据跟踪结果图可以看出,基于CN特征的跟踪算法取得最好的跟踪效果。相对于HOG特征,基于CN特征的跟踪结果精确度高出了11.7%,跟踪成功率高出了8.3%。相对于像素值特征,精确度高出了24.1%,成功率高出了13.2%。由此可以确定,选取良好的特征描述子对于目标跟踪算法的跟踪效果具有极大的作用。
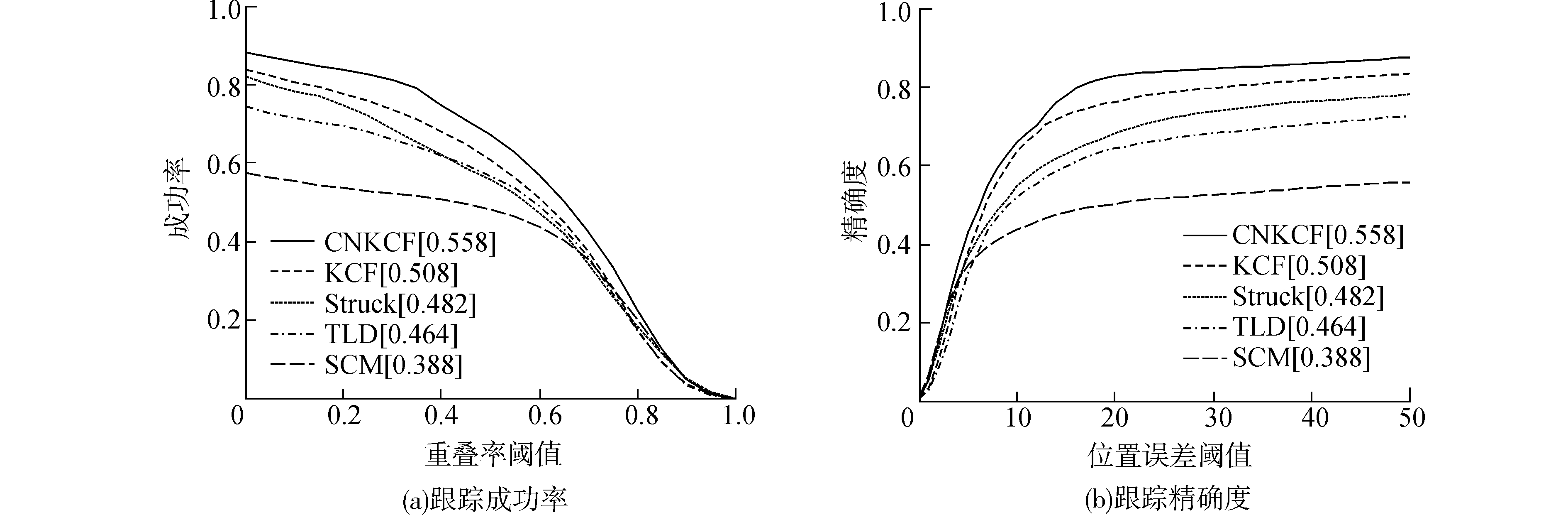
3.3 改进的核相关滤波跟踪算法根据上述2个实验的分析结果,本文采用第二节中的运动模型和检测模型,特征提取方式选择CN特征,模型更新方案选择方案二,提出基于CN特征的KCF跟踪算法(CNKCF)。为了验证CNKCF的性能,本文将其与KCF以及文献[12]中性能最好的3个跟踪算法(Stuck,TLD以及SCM[14])进行比较。5种跟踪算法在38个视频序列的跟踪效果如图 4所示。由图 4可以看出,改进后的KCF算法相对于传统的KCF算法性能具有很大的提升。其中跟踪成功率提高了5%,精确度提高了6.6%。
|
图 4 不同跟踪算法的跟踪结果 |
此外,为了分析新算法在不同干扰条件下的适应性,本文比较了5种算法在文献[12]中提出的除出视角干扰之外的10个干扰条件下跟踪算法的效果。实验结果显示,相对于传统的KCF跟踪算法,CNKCF算法在10种干扰条件下性能都有不同程度的提升。其中对目标形变、遮挡和出平面旋转干扰跟踪性能的提升最大。受于篇幅限制,本文只列出目标形变,遮挡和出平面旋转3种干扰条件下的实验结果,如图 5所示。其中15个视频出现目标形变,20个视频出现目标遮挡,24个视频出现出平面旋转。

|
图 5 不同跟踪算法在干扰条件下的跟踪结果 |
本文对核相关滤波器算法分成运动模型、特征提取、检测模型和模型更新方案进行分析,比较了基于不同特征和不同模型更新方案下的算法跟踪结果。通过实验分析得出以下结论:
1) 选取合适的特征描述子和模型更新方案能够极大地提高跟踪算法的性能;
2) 不同特征对各种干扰条件的抗干扰能力不同。
因此,在未来的工作中可以通过以下两点提高跟踪算法的性能。一是构造更加丰富的图像特征,如深度卷积神经网络提取到的图像特征,可以对干扰条件有更好的适应性。二是将现有的特征进行特征融合,在丰富特征的同时,也能够提高跟踪算法的抗干扰能力。
| [1] |
钟必能, 陈雁, 沈映菊, 等. 在线机器学习跟踪算法的研究进展[J]. 华侨大学学报:自然科学版, 2014, 35(1): 41-46. ( 0) 0)
|
| [2] |
LIU Qi, ZHAO Xiaoguang, HOU Zengguang. Survey of single-target visual tracking methods based on online learning[J]. IET computer vision, 2014, 8(5): 419-428. DOI:10.1049/iet-cvi.2013.0134 ( 0) 0)
|
| [3] |
HARE S, SAFFARI A, TORR P H S. Structured output tracking with kernels[C]//Proceedings of the 2011 IEEE International Conference on Computer Vision. Barcelona:IEEE, 2011:263-270.
( 0) 0)
|
| [4] |
KALAL Z, MIKOLAJCZYK K, MATAS J. Tracking-learning-detection[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(7): 1409-1422. DOI:10.1109/TPAMI.2011.239 ( 0) 0)
|
| [5] |
ZHANG Kaihua, ZHANG Lei, YANG M H. Real-time compressive tracking[C]//ECCV 2012:Proceedings of the 12th European Conference on Computer Vision. Berlin:Springer, 2012:864-877.
( 0) 0)
|
| [6] |
HENRIQUES J F, CASEIRO R, MARTINS P, el al. Exploiting the circulant structure of tracking-by-detection with kernels[C]//ECCV 2012:Proceedings of the 12th European Conference on Computer Vision. Berlin:Springer, 2012:702-715.
( 0) 0)
|
| [7] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 ( 0) 0)
|
| [8] |
WANG Naiyan, SHI Jianping, YEUNG D Y, et al. Understanding and diagnosing visual tracking systems[C]//2015 IEEE International Conference on Computer Vision. Santiago:IEEE, 2015:3101-3109.
( 0) 0)
|
| [9] |
VAN DE WEIJER J, SCHMID C, VERBEEK J, et al. Learning color names for real-world applications[J]. IEEE transactions on image processing, 2009, 18(7): 1512-1523. DOI:10.1109/TIP.2009.2019809 ( 0) 0)
|
| [10] |
DALAL N, TRIGGS B. Histograms of oriented gradients for human detection[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Santiago:IEEE, 2005:886-893.
( 0) 0)
|
| [11] |
DANELLJAN M, KHAN F S, FELSBERG M, et al. Adaptive color attributes for real-time visual tracking[C]//Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern recognition. Columbus, OH:IEEE, 2014:1090-1097.
( 0) 0)
|
| [12] |
RIFKIN R, YEO G, POGGIO T. Regularized least-squares classification[J]. Nato Science Series Sub Series Ⅲ Computer and Systems Science, 2003: 131-154. ( 0) 0)
|
| [13] |
YANG M H, LIM J, WU Yi. Online object tracking:a benchmark[C]//Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, OR:IEEE, 2013:2411-2418.
( 0) 0)
|
| [14] |
ZHONG Wei, LU Huchuan, YANG M H. Robust object tracking via sparsity-based collaborative model[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI:IEEE, 2012:1838-1845.
( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


