逆变器的控制技术主要有无差拍控制、重复控制、滞环电流控制、准比例谐振控制和比例积分控制等。而文献[1]提出的PI控制策略原理简单、容易实现、控制参数容易整定,然而在静止坐标系下的PI控制器并不能实现对正弦量的无静差跟踪。同步参考坐标系下的PI控制在三相逆变器的控制已经是个很成熟的问题,然而对单相逆变器的应用很少[2]。本文将提出单相逆变器电压环在同步参考系下的控制策略,由于这种转换至少需要两个正交信号,所以虚拟一相才能形成两相[3]。而在旋转坐标系下的PI控制并不能判定整个系统的稳定性,因此需要将其转换到静止坐标系下来调整控制参数判定系统的稳定性[4]。转换后将dq坐标系下的PI控制变为静止坐标系下的比例谐振控制,在基波频率处获得很高的电压增益,这样可以对基波很好地控制,减小稳态误差,获得正弦度更好的正弦波。对单相逆变器进行小信号建模画出系统控制框图进行电压反馈解耦,简化电流环的设计,并提高整个系统的鲁棒性[5]。并针对电压环在dq坐标系下存在的耦合进行解耦,最终实现直流给定信号的无静差控制。
1 单相逆变器的参数设计与建模在双极性SPWM调制逆变器中,输出滤波器主要用来滤除在开关频率及其附近频率的谐波以改善输出电压波形[6-7]。已知系统的输出功率,由电路理论可知:
| $ R = \frac{{\bar U_o^2}}{P} = \frac{{{{\left( {311/\sqrt 2 } \right)}^2}}}{{1000}} \approx 50\Omega $ | (1) |
式中
| $ f \ll {f_0} \ll {f_k} $ | (2) |
式中:f为逆变器输出电压基波频率,f0为逆变器输出滤波器转折频率,fk为输出电压最低次谐波的频率。取f0为10倍的基波频率,值为500 Hz。
| $ \left\{ \begin{array}{l} \sqrt {{L_0}{C_0}} = \frac{1}{{2\pi {f_0}}}\\ \sqrt {{L_0}/{C_0}} = \left( {0.5 \sim 0.8} \right)R \end{array} \right. $ | (3) |
由式(3) 得到L=2 mH,C=60 μF,此时最大电流脉动符合式(4) 要求:
| $ \left\{ \begin{array}{l} \Delta {I_{{L_{\max }}}} = \frac{E}{{2L{f_s}}} = 5.25\;{\rm{A}}\\ {f_s} = 1/2\pi \sqrt {{L_0}{C_0}} = 459\;{\rm{Hz}} \end{array} \right. $ | (4) |
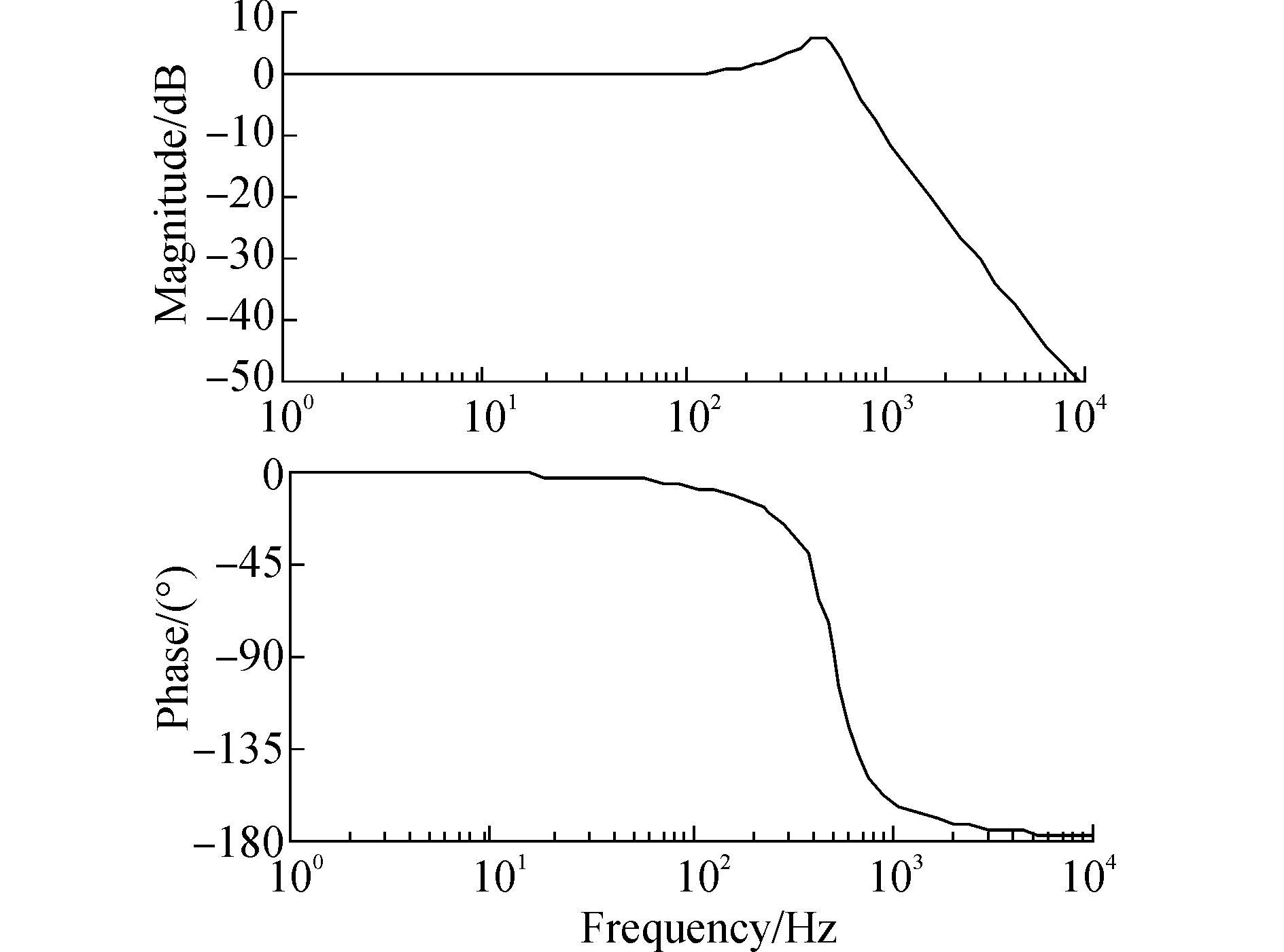
当考虑电感的内阻时,取电感内阻为0.01 Ω,单相全桥逆变器的输出滤波器频域表达式如式(5),伯德图如图 1所示。
| $ G\left( s \right) = \frac{1}{{LC{s^2} + \left( {\frac{L}{R} + rC} \right)s + 1 + \frac{r}{R}}} $ | (5) |
|
图 1 LC滤波器伯德图 |
对于电感L和电容C的选择要考虑以下因素:
1) 电感上的基波电压将使负载上的基波电压产生变化;输出电容的基波电流与负载电流之和将改变逆变器输出电流。
2) 在逆变器带纯电阻负载时,电容中的基波电流将使逆变器桥臂输出电流增大;感性负载时由于电容电流与负载电流方向相反,会使逆变器桥臂输出电流减小[10]。
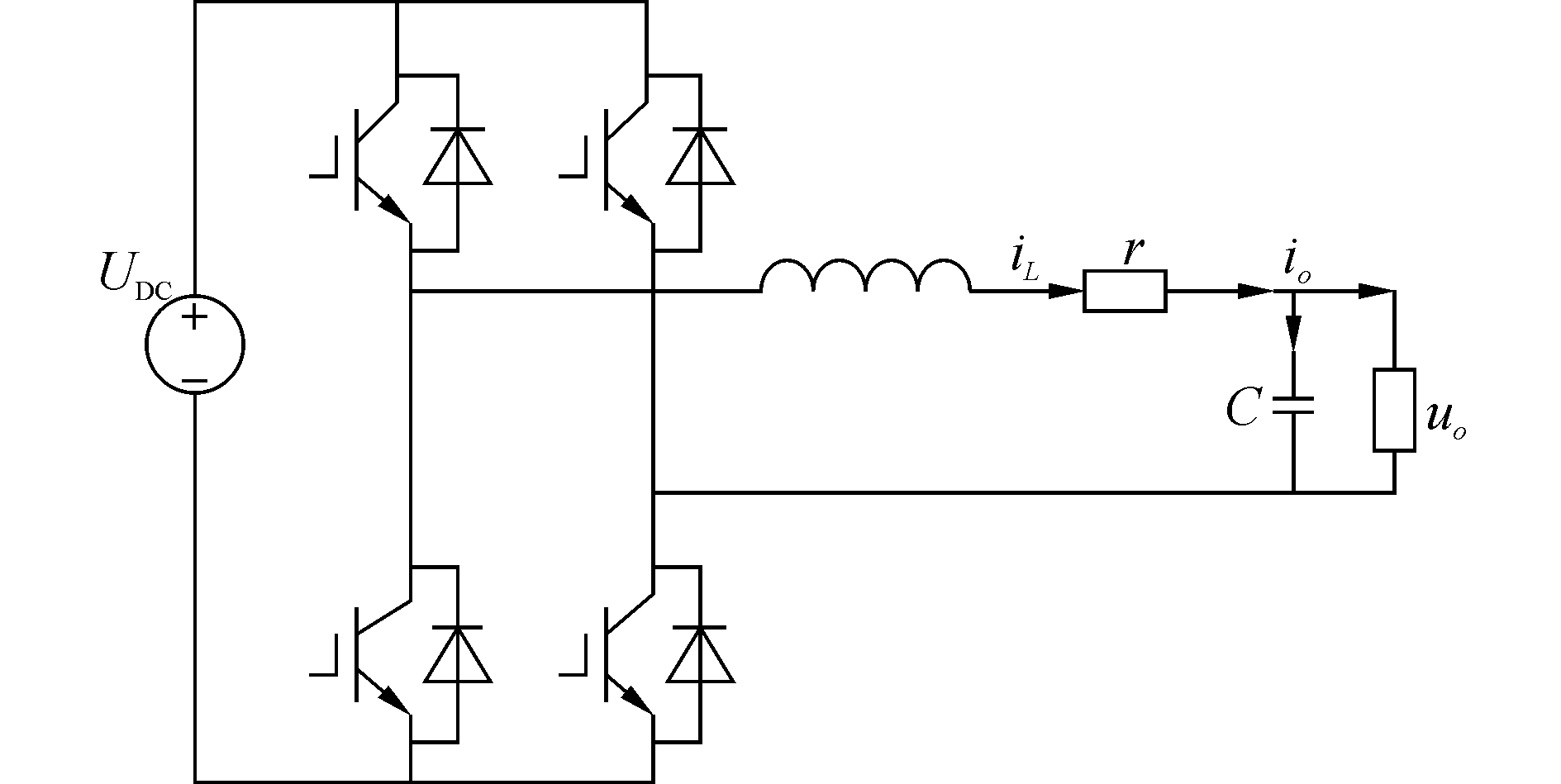
图 2为单相逆变器拓扑结构图。该系统主要由直流电源、逆变电路、LC滤波器以及4个绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)组成[11-12]。根据图 2的拓扑结构可以得到式(6),KPWM为调制器输入到逆变器的传递函数。KPWM=UDC/Vm,根据实际情况和具体要求Vm取2 000。
|
图 2 单相逆变器拓扑结构图 |
| $ \left\{ \begin{array}{l} L\frac{{{\rm{d}}{i_L}}}{{{\rm{d}}t}} = {K_{{\rm{PWM}}}}{U_{{\rm{DC}}}}-{u_o}-r{i_L}\\ C\frac{{{\rm{d}}{u_o}}}{{{\rm{d}}t}} = {i_C} = {i_L}-{i_o} \end{array} \right. $ | (6) |
根据式(6) 以及小信号模型可以得到系统的控制框图,如图 3所示。图中Gv为电压环控制器,Gc为电流环控制器,其中G1=1/(Ls+r), G2=1/Cs,系统参数见表 1。

|
图 3 单相逆变器系统控制框图 |
|
|
表 1 单相逆变器控制系统参数 |
电流环的设计可以改善系统的瞬态响应和稳态性能。穿越频率较低,低频段的增益较小,将会影响系统的快速跟随能力;若穿越频率较高会改善系统的快速跟随能力,但是会影响系统的稳定性,且电流环穿越频率的设置也会限制电压环的带宽。折中考虑,电流环的穿越频率为开关频率的1/5~1/10[15]。基于这个选择的标准,电流环的穿越频率设定为4 kHz。根据电流开环的传递函数,通过一个比例环节将电流环的穿越频率校正在4 kHz左右。
电流内环传递函数和电容电压存在耦合,为了简化系统建模和控制器的设计,提高系统的鲁棒性,进行电压反馈解耦,如图 4所示。

|
图 4 单相逆变器解耦系统控制框图 |
解耦后将简化电流环的设计,解耦后系统的控制框图如图 5所示。

|
图 5 单相逆变器解耦后系统控制框图 |
此时电流环的开环传递函数为
| $ {G_{zc}} = \frac{{{K_{{\rm{PWM}}}}}}{{Ls + r}} $ | (7) |
电流环控制器为一个简单的比例环节,通过校正,电流环控制器为比例控制,电流环控制器伯德图如图 6所示。

|
图 6 电流环控制器伯德图 |
比例积分控制器(PI)的传递函数为
| $ {G_{{\rm{PI}}}} = {K_{\rm{P}}} + \frac{{{K_{\rm{I}}}}}{s} $ | (8) |
式中:KP为比例积分控制器的比例系数,KI为积分系数,其在电网基波频率ωf处的增益为
| $ \left| {{G_{{\rm{PI}}}}\left( {{\rm{j}}{\omega _f}} \right)} \right| = \sqrt {K_{\rm{P}}^2 + {{\left( {\frac{{{K_{\rm{I}}}}}{{{\omega _f}}}} \right)}^2}} $ | (9) |
PI环节在s域的表达式可以简化为
| $ {G_{{\rm{PI}}}} = {K_{\rm{P}}}\left( {1 + \frac{1}{{{T_{\rm{I}}}s}}} \right) $ | (10) |
则通过PI环节滞后的角度为
| $ \theta = \arctan \left( {\frac{1}{{{T_{\rm{I}}}\omega }}} \right) $ | (11) |
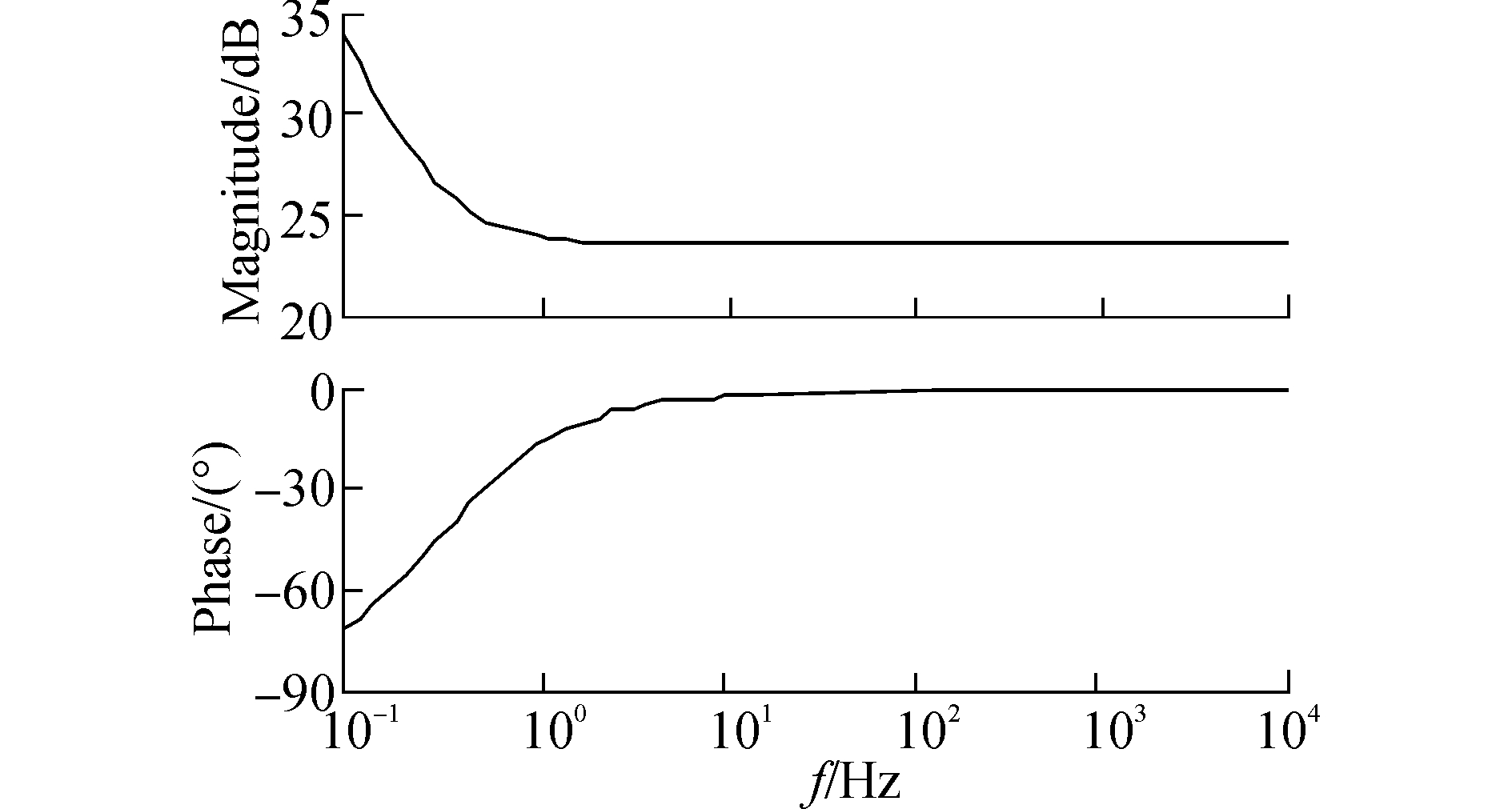
式(11) 中TI=KP/KI,图 7为PI控制器的伯德图。
|
图 7 PI控制器伯德图 |
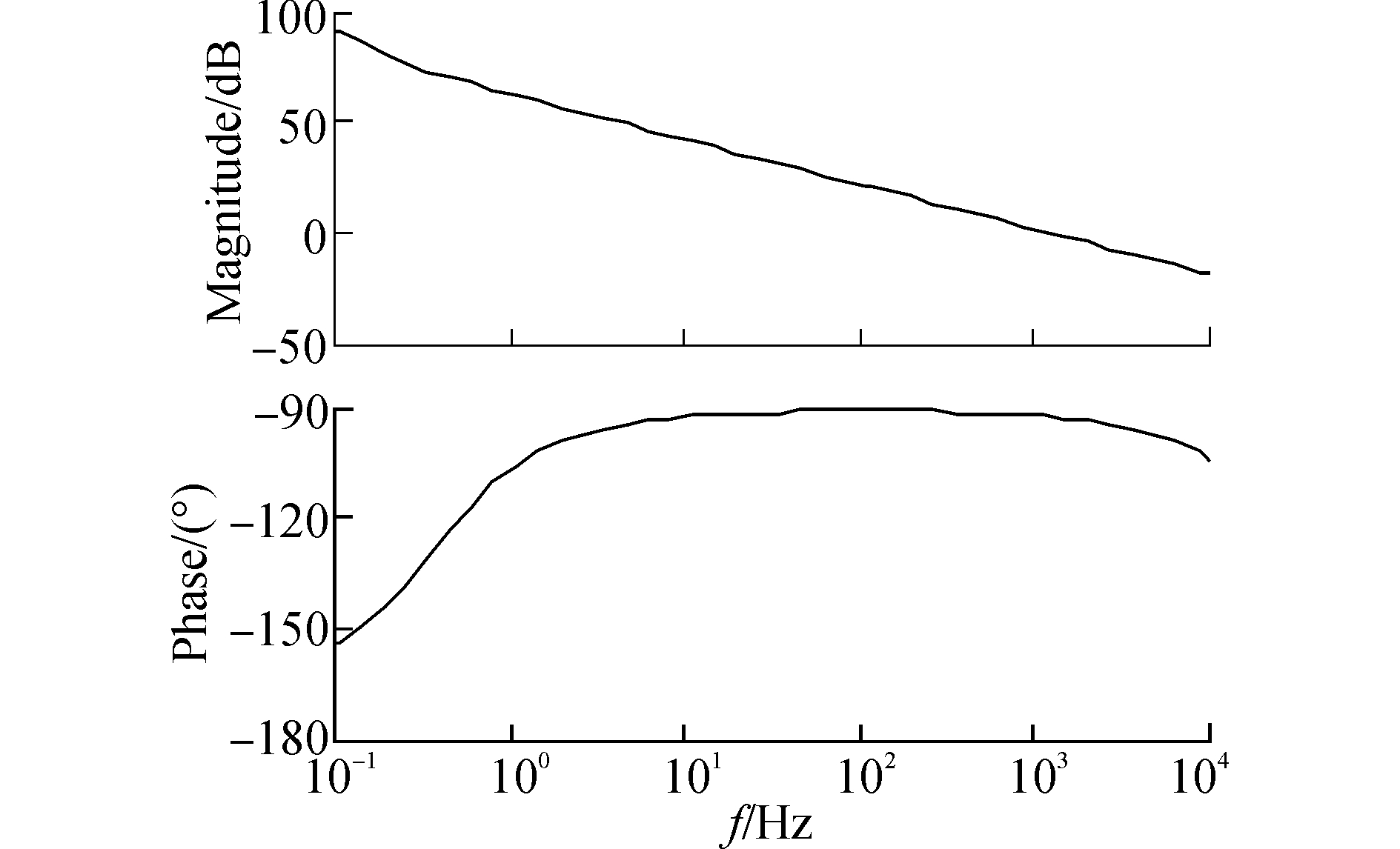
在PI控制中,KP越大系统超调量越大越不稳定,但是调整时间越短;TI越大系统超调量越小,但是调整时间越长。电压环的带宽一般选定在10倍的基波频率和1/10的开关频率之间, 可以得到快速的动态响应和抗噪声干扰的能力。因此将电压环的带宽设定在1 kHz左右[16]。通过调节PI参数使电压环的被控系统稳定。图 8为电压环在静止坐标系下的控制器的伯德图。
|
图 8 静止坐标系下电压环控制器伯德图 |
由图 7、8可以看出,PI控制器为一阶控制器,在电网的基波频率(50 Hz)处的增益约为30 dB,因此在跟踪正弦信号时可能会出现稳态误差。根据式(11) 可知静止坐标系下的PI控制会表现为明显的相位滞后,即跟踪电流给定值时会出现相位误差,其在基波频率处的增益可通过增加比例放大系数来增大,即减小稳态静差,但不可能消除。因此幅值误差表现并不明显,主要表现为相位误差。
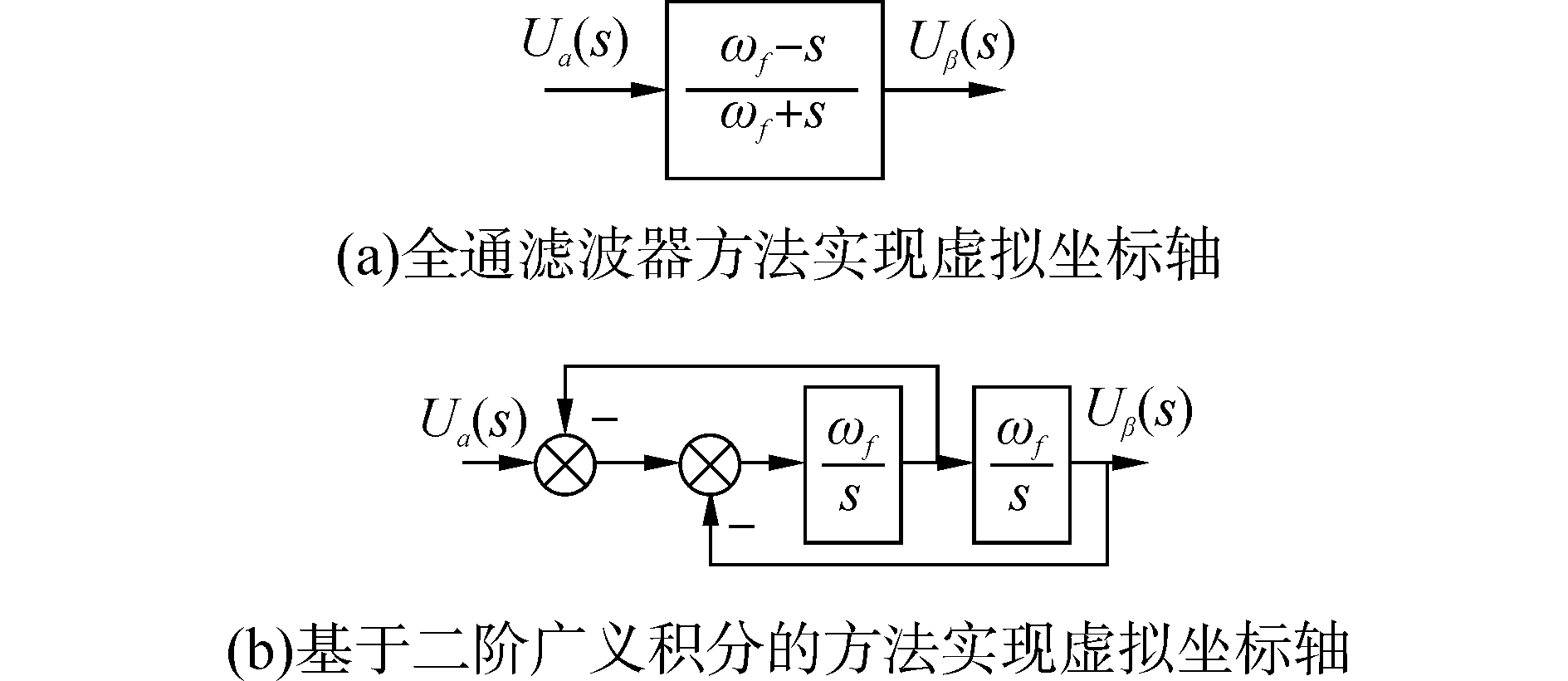
3.2 同步旋转坐标系下的电压环控制策略电压环在同步旋转坐标系下做比例积分制器设计,然而这种转换至少需要2个正交信号,所以需要虚拟一相才能形成正交的两相,考虑到在进行dq坐标变换时,对于单相系统需要虚拟β轴坐标。文献[7]介绍了一种在工作频率范围内相当于全通滤波器方法实现虚拟β坐标轴的方法。文献[9]介绍了一种基于二阶广义积分的方法实现虚拟β坐标轴的方法,如图 9所示。这里将分别简要介绍分析2种方法,以决定文中采取何种方法实现虚拟β坐标。令输出电压为Uα,经过如图 9(a)、(b)控制器虚拟得到Uβ。
|
图 9 2种不同移相方式框图 |
图 9中ωf为正弦指令信号角频率。通过图 10可以很方便地得到虚拟坐标的传递函数,利用MATLAB可以很方便地绘制2种方法的频率特性。

|
图 10 虚拟坐标轴传递函数频率特性 |
图 10中实线在工作频率范围内相当于全通滤波器方法实现虚拟坐标轴频率特性,对角频率为ωf的指令信号实现90°相移,可见该方法对所有频率无衰减,容易引入高频干扰。虚线为二阶广义积分方法的频率特性,由于其频率特性为低通滤波器特性,对角频率为ωf的指令信号无衰减,实现90°相移,且对高频干扰具有抑制作用。对比来看,二阶广义积分方法具有更优越的性质,因此论文拟采用二阶广义积分方法实现移相。于是根据式(12) 得到Uβ:
| $ \frac{{{U_\beta }\left( s \right)}}{{{U_\alpha }\left( s \right)}} = \frac{{\omega _f^2}}{{{s^2} + {\omega _f}s + \omega _f^2}} $ | (12) |
将单相逆变器的输出电压通过坐标变换从静止坐标系变换到旋转坐标系,分别在dq轴进行PI控制,再进行坐标反变换变换到静止坐标系下,iα*(t)即为电流环的给定值。

|
图 11 SRFPI控制结构框图 |
然而采用平均模型的方法建立实际电路与正交虚拟电路的模型。依据式(13) 和单相逆变器的平均状态方程,得出系统在dq坐标系下的状态方程(14):
| $ \left[\begin{array}{l} {U_d}\\ {U_q} \end{array} \right] = \left[\begin{array}{l} \cos \;\theta \;\;\;\;\;\sin \;\theta \\ -\sin \;\theta \;\;\;\cos \;\theta \end{array} \right]\left[\begin{array}{l} {U_\alpha }\\ {U_\beta } \end{array} \right] $ | (13) |
| $ \begin{array}{l} \frac{{\rm{d}}}{{{{\rm{d}}_t}}}\left[\begin{array}{l} {U_d}\\ {U_q} \end{array} \right] = \frac{1}{C}\left[\begin{array}{l} {I_d}\\ {I_q} \end{array} \right] - \frac{1}{{RC}}\left[\begin{array}{l} {U_d}\\ {U_q} \end{array} \right] + \left[\begin{array}{l} 0\;\;\;\;\;\omega \\ -\omega \;\;0 \end{array} \right]\left[\begin{array}{l} {U_d}\\ {U_q} \end{array} \right]\\ \frac{{\rm{d}}}{{{{\rm{d}}_t}}}\left[\begin{array}{l} {I_d}\\ {I_q} \end{array} \right] = \frac{{{U_{{C_f}}}}}{L}\left[\begin{array}{l} {D_d}\\ {D_q} \end{array} \right] - \frac{1}{L}\left[\begin{array}{l} {U_d}\\ {U_q} \end{array} \right] + \left[\begin{array}{l} 0\;\;\;\;\;\omega \\ -\omega \;\;0 \end{array} \right]\left[\begin{array}{l} {U_d}\\ {U_q} \end{array} \right] \end{array} $ | (14) |
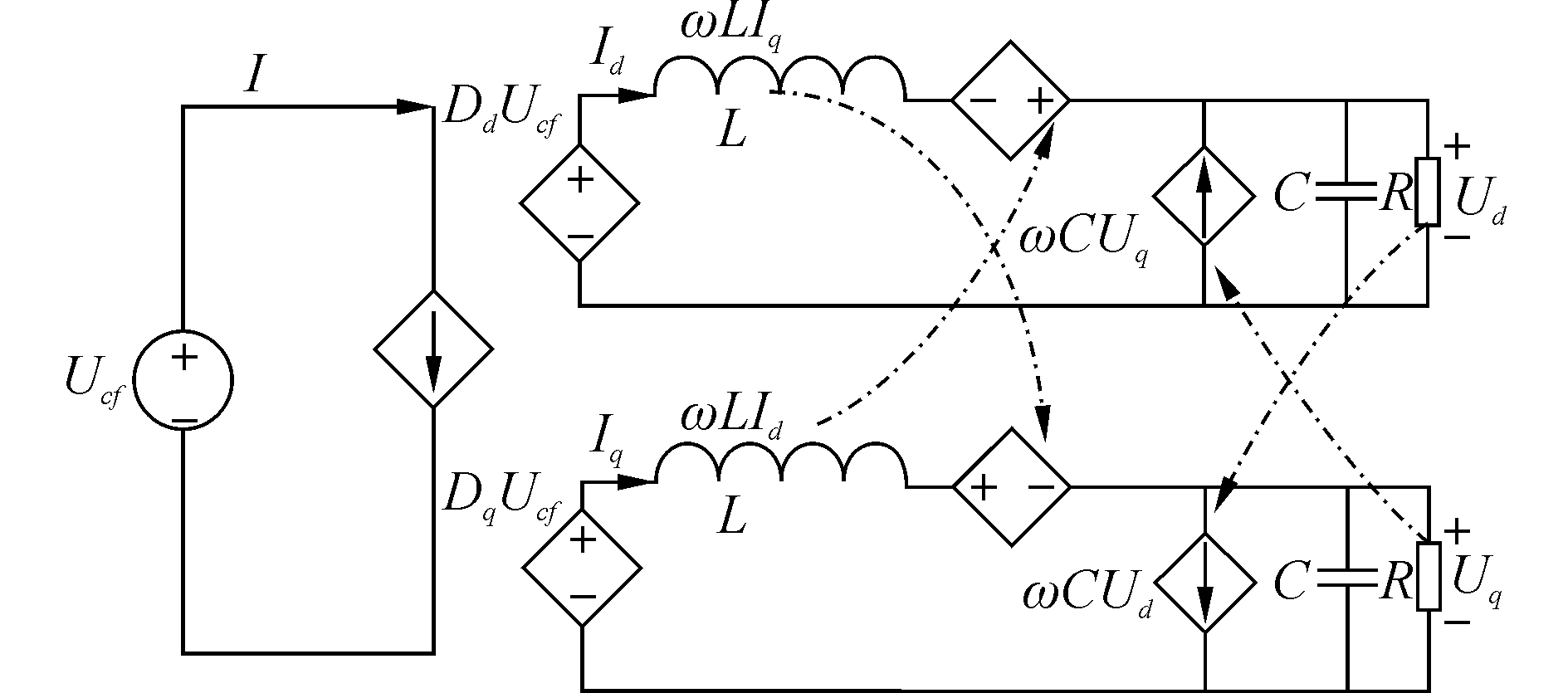
从式(14) 可以看出,在dq坐标系下,系统输出电流Id和Iq除受控制量DdUCf和DqUCf的影响外,还受耦合电压ωfLId和ωfLIq扰动以及输出电压Ud和Uq扰动的影响。同理,系统输出电压Ud和Uq除受逆变器输出电流Id和Iq控制外,还受耦合电流ωfCUq和ωfCUd以及输出负载电流IdR和IqR的扰动影响,如图 12所示。
|
图 12 单相逆变器dq解耦控制框图 |
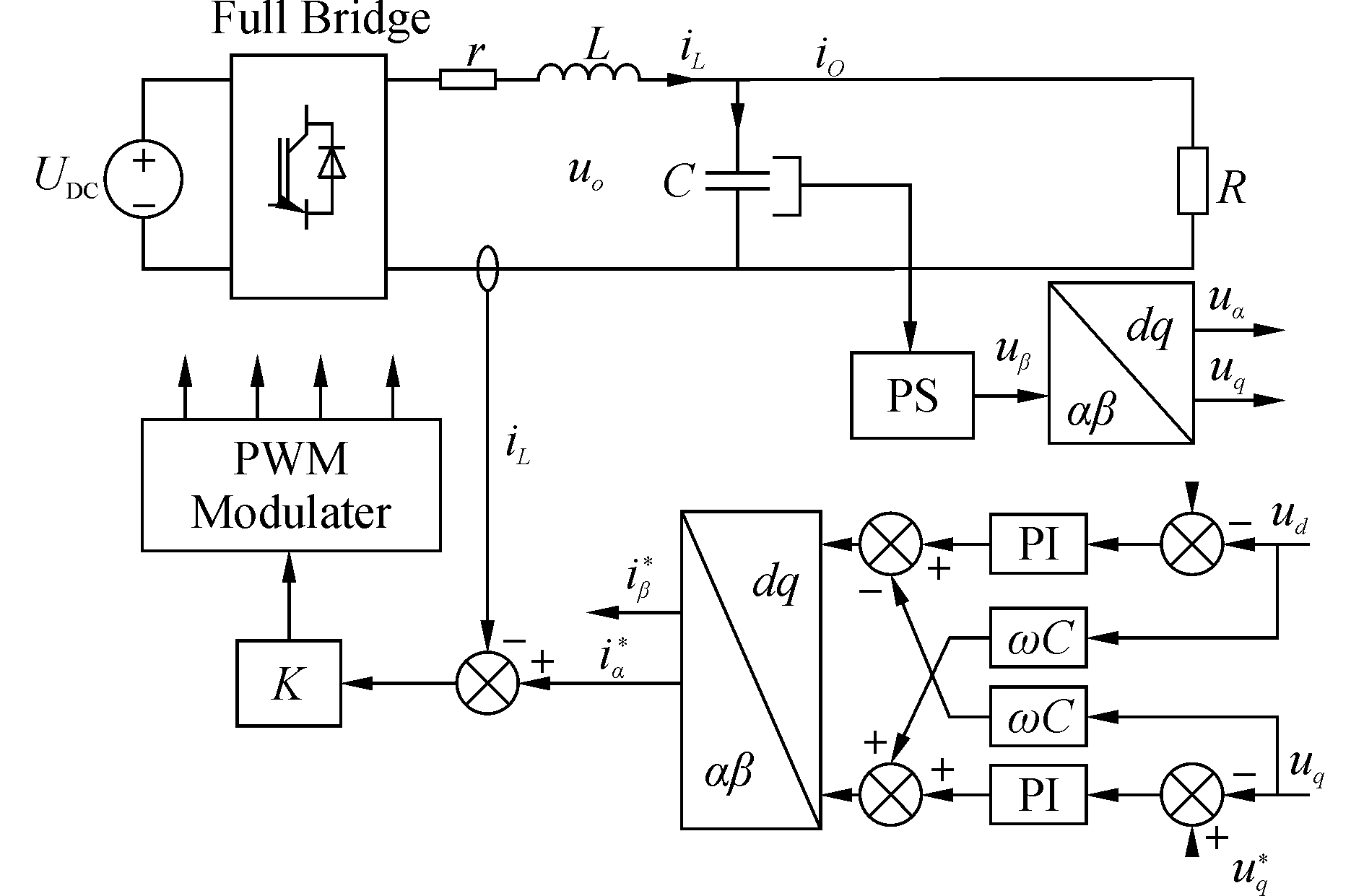
由于在文中只有电压环在dq坐标系下进行控制,电流环在静止坐标系下进行比例控制,只需要对电压环进行解耦,解耦控制框图如13所示。
|
图 13 单相逆变器双闭环dq电压反馈解耦控制框图 |
解耦后,由于电压环工作在同步旋转坐标系下,并不能简单地调整控制器参数来评估整个系统的稳定性,因此需要将同步参考坐标系下的PI控制转换到静止坐标系下。式(15) 表示通过坐标变换变换到dq坐标系下,分别在dq轴上进行PI控制,随后通过反变换变换到αβ坐标系下。其中*代表卷积。
| $ \begin{array}{l} \left[\begin{array}{l} i_\alpha ^*\left( t \right)\\ i_\beta ^*\left( t \right) \end{array} \right] = \left[\begin{array}{l} \cos \left( {\omega t} \right)\;\;\;\;-\sin \left( {\omega t} \right)\\ \sin \left( {\omega t} \right)\;\;\;\;\;\;\cos \left( {\omega t} \right) \end{array} \right]\\ \left\{ {\left[\begin{array}{l} {G_{{\rm{PI}}}}\left( t \right)\;\;\;\;0\\ \;\;\;0\;\;\;\;\;\;{G_{{\rm{PI}}}}\left( t \right) \end{array} \right]\left\{ {\left[\begin{array}{l} \cos \left( {\omega t} \right)\;\;\;\sin \left( {\omega t} \right)\\ -\sin \left( {\omega t} \right)\;\;\;\cos \left( {\omega t} \right) \end{array} \right]\left[\begin{array}{l} {U_\alpha }\left( t \right)\\ {U_\beta }\left( t \right) \end{array} \right]} \right\}} \right\} \end{array} $ | (15) |
将式(15) 两边同时进行拉普拉斯变换得到式(16):
| $ \left[\begin{array}{l} {i_\alpha }\left( s \right)\\ {i_\beta }\left( s \right) \end{array} \right] = \frac{1}{2}\left[\begin{array}{l} {G_{{\rm{PI}}}}\left( {s + {\rm{j}}\omega } \right)-{\rm{j}}{G_{{\rm{PI}}}}\left( {s + {\rm{j}}\omega } \right)\\ + {G_{{\rm{PI}}}}\left( {s-{\rm{j}}\omega } \right) + {\rm{j}}{G_{{\rm{PI}}}}\left( {s-{\rm{j}}\omega } \right)\\ + {\rm{j}}{G_{{\rm{PI}}}}\left( {s + {\rm{j}}\omega } \right){G_{{\rm{PI}}}}\left( {s + {\rm{j}}\omega } \right)\\ - {\rm{j}}{G_{{\rm{PI}}}}\left( {s - {\rm{j}}\omega } \right) + {G_{{\rm{PI}}}}\left( {s - {\rm{j}}\omega } \right) \end{array} \right]\left[\begin{array}{l} {U_\alpha }\left( s \right)\\ {U_\beta }\left( s \right) \end{array} \right] $ | (16) |
把GPI(s)=KP+KI/s代入式(16) 化简得到
| $ \left[\begin{array}{l} i_\alpha ^*\left( s \right)\\ i_\beta ^*\left( s \right) \end{array} \right] = \left[\begin{array}{l} {K_{\rm{P}}} + \frac{{{K_{\rm{I}}}s}}{{{s^2} + \omega _0^2}}-\frac{{{K_{\rm{I}}}{\omega _0}}}{{{s^2} + \omega _0^2}}\\ \;\;\;\;\frac{{{K_{\rm{I}}}{\omega _0}}}{{{s^2} + \omega _0^2}}\;\;\;{K_{\rm{P}}} + \frac{{{K_{\rm{I}}}s}}{{{s^2} + \omega _0^2}} \end{array} \right]\left[\begin{array}{l} {u_\alpha }\left( s \right)\\ {u_\beta }\left( s \right) \end{array} \right] $ | (17) |
根据式(12) 和(17) 可以得到:
| $ {G_v} = \frac{{{a_4}{s^4} + {a_3}{s^3} + {a_2}{s^2} + {a_1}s + {a_0}}}{{{s^4} + {\omega _f}{s^3} + 2\omega _f^2{s^2} + \omega _f^3s + \omega _f^4}} $ | (18) |
式中:a4=KP, a3=KPωf, a2=2KPωf2+KI, a1=KPωf3 +KIωf, a0=KPωf4-KIωf3+KIωf2。
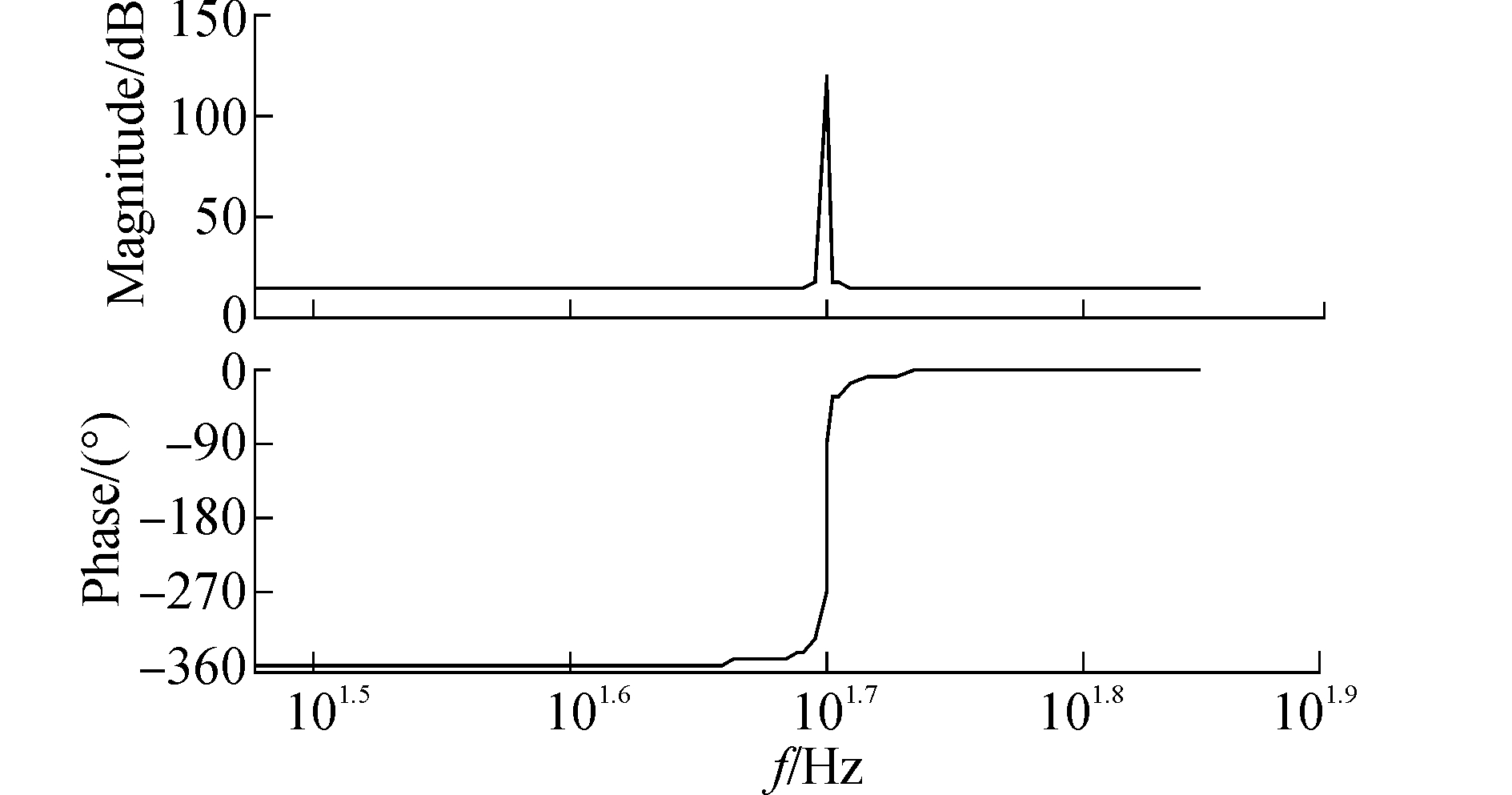
图 14为KP=5,KI=10转换函数Gv伯德图。由伯德图分析可知,旋转坐标系下的PI调节器能够准确跟踪正弦指令,在于旋转坐标系下的PI调节器等效为静止坐标下的比例谐振控制器,由内模原理可知,比例谐振控制器能够跟踪正弦信号的原因在于控制器本身具有正弦信号的内模,当误差信号为零时仍然能够输出正弦信号[17]。
|
图 14 转换函数Gv伯德图 |
此时电压环的被控对象如图 15所示,表达式如式(19) 所示。

|
图 15 电压环被控对象 |
| $ {G_{zv}} = \frac{{{K_{{\rm{PWM}}}}{G_c}{G_1}{G_2}}}{{1 + {K_{{\rm{PWM}}}}{G_c}{G_1} + {G_2}/R}} $ | (19) |
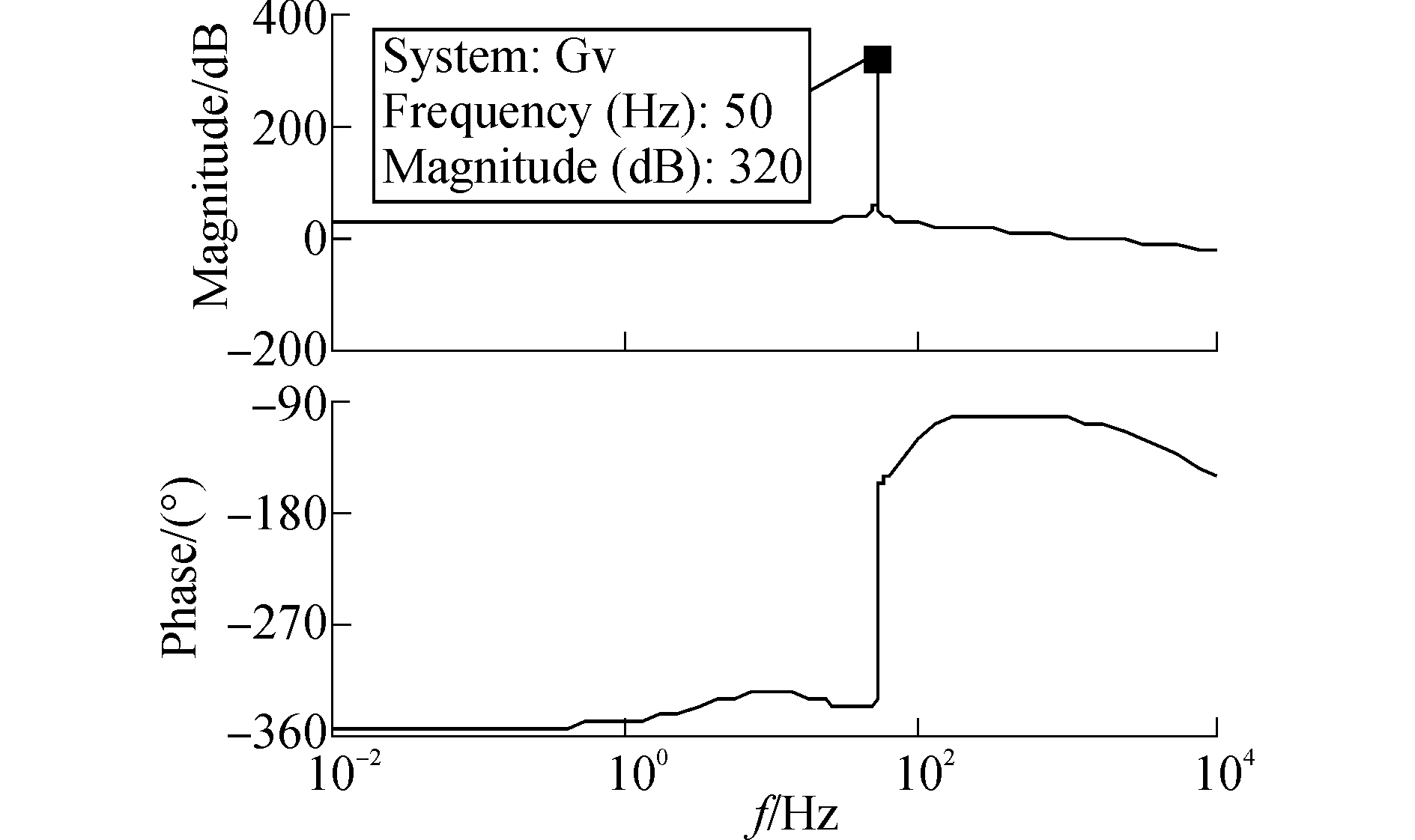
通过调节PI参数校正KP=0.022,KI=5。将电压环的带宽设定在1 kHz。电压环控制器伯德如图 16所示,SRFPI控制在基波频率50 Hz处获得一个很高的电压增益,大约为320 dB,可以很好地跟踪正弦信号,以便对基波进行更好的控制。而静止坐标系下的PI控制,在基波频率处的增益不到30 dB,在跟踪正弦信号时可能会出现稳态误差,即跟踪电流给定值时会出现相位误差。
|
图 16 电压环控制器伯德图 |
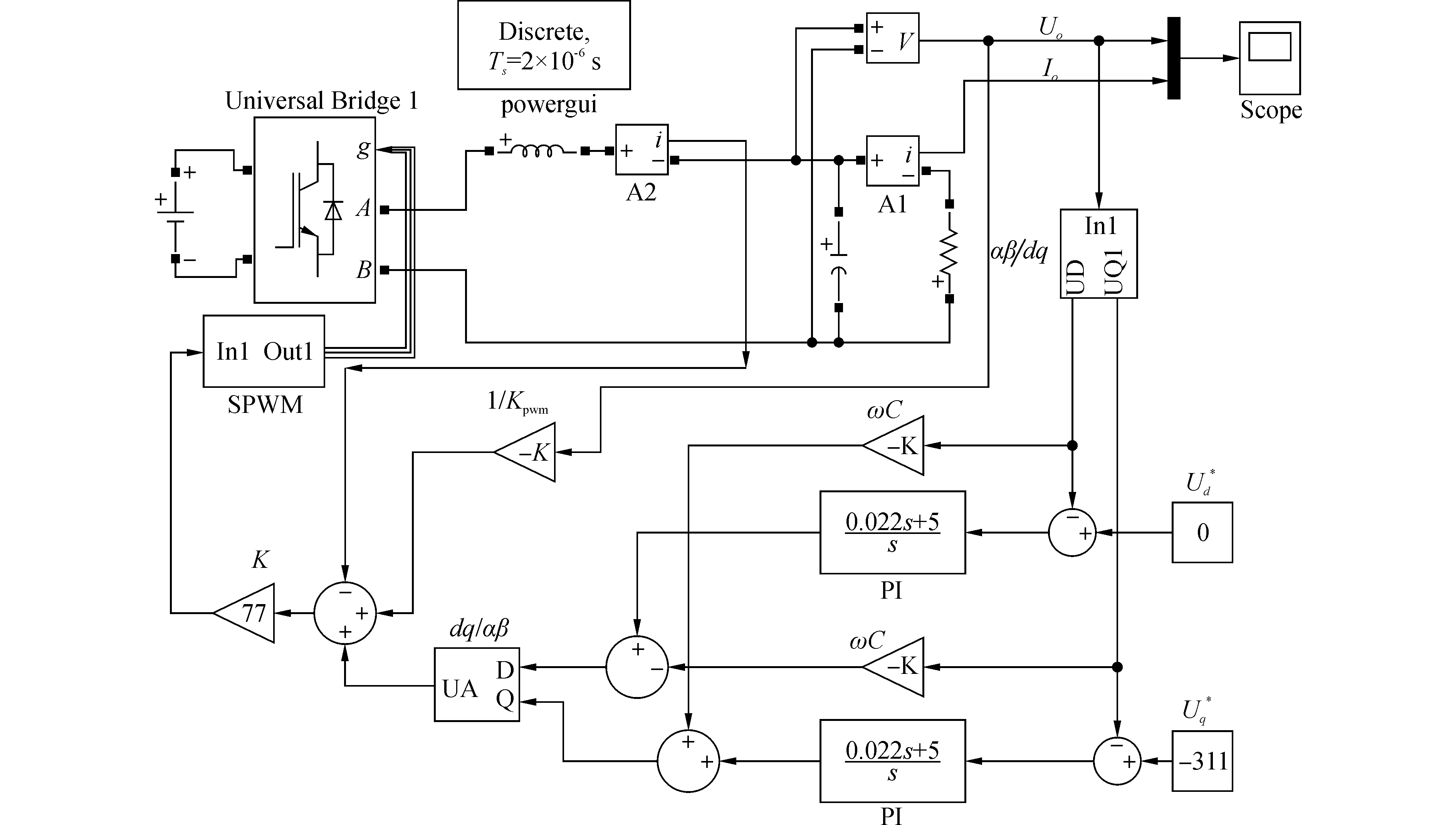
根据上述的理论分析进行SIMULINK仿真实验,图 17为SRFPI双闭环仿真图,通过总谐波失真(total harmonic distortion,THD)分析验证SRFPI控制与静止坐标系下的双环控制相比,前者得到的正弦波的正弦度会更好。图 18为2种情况下的输出电压波形的THD分析。
|
图 17 SRFPI控制双环仿真 |

|
图 18 2种情况的THD分析 |
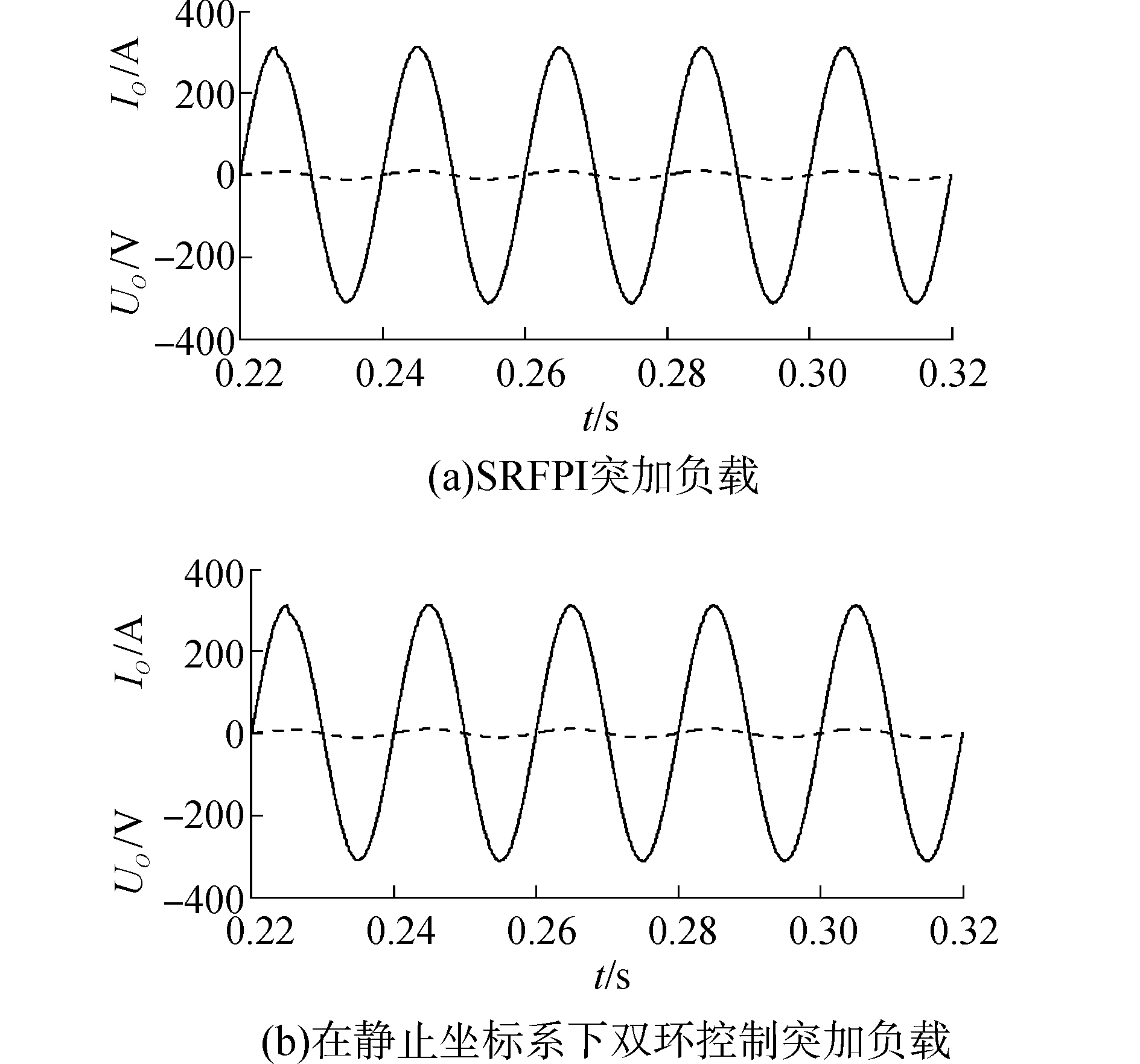
图 19为在0.225 s突加负载时2种不同情况的电压电流波形。由二者的仿真结果可知单相逆变器在dq坐标变换控制方式下,系统受到扰动时,具有强的稳定性及抗干扰性。
|
图 19 突加负载两种情况的输出电压波形 |
1) 本文利用电压反馈解耦简化了控制系统的设计,提高了系统的鲁棒性。
2) 提出电压环在dq坐标系下的PI控制电流环在静止坐标系下的比例控制的双闭环控制策略。通过计算将旋转坐标系下的PI控制可以转换为静止坐标系下的比例谐振控制,在基波频率处获得较大的幅值增益,对正弦波进行更好的跟踪的能力。
3) SIMULINK仿真验证了SRFPI双环控制相比于传统在静止坐标系下的双环控制具有抗扰动性好以及能实现无静差跟踪等优点。
| [1] |
刘邓, 刘军, 陶忠正, 等. 比例积分与比例谐振对单相逆变器控制的研究与仿真[J]. 电气工程学报, 2015, 10(10): 64-68. ( 0) 0)
|
| [2] |
RYAN M J, LORENZ R D. A synchronous-frame controller for a single-phase sine wave inverter[C]//Applied Power Electronics Conference and Exposition. Atlanta, USA, 1997:813-819.
( 0) 0)
|
| [3] |
GRASSI G. Generalized synchronization between different chaotic maps via dead-beat control[J]. Chinese physics B, 2012, 21(5): 104-110. ( 0) 0)
|
| [4] |
ZMOOD D N, HOLMES D G. Stationary frame current regulation of PWM inverters with zero steady state error[C]//Power Electronics Specialists Conference. Charleston, USA, 1999:1185-1190.
( 0) 0)
|
| [5] |
郭小强. 光伏并网逆变器通用比例复数积分控制策略[J]. 中国电机工程学报, 2015, 35(13): 3393-3399. ( 0) 0)
|
| [6] |
王亚威. 基于双闭环准比例谐振控制的逆变器研究[D]. 大连: 大连理工大学, 2014.
( 0) 0)
|
| [7] |
侯凌云. 基于无延时坐标变换的单相逆变器并网控制技术研究[D]. 秦皇岛: 燕山大学, 2011.
( 0) 0)
|
| [8] |
胡文平, 周云飞. 基于准比例谐振控制器的高性能逆变器研究[J]. 武汉理工大学学报, 2010, 32(23): 85-88. DOI:10.3963/j.issn.1671-4431.2010.23.022 ( 0) 0)
|
| [9] |
孟强, 牟龙华, 许旭锋. 基于单相dq变换控制的光伏系统仿真[J]. 电网与清洁能源, 2013, 29(11): 65-69. DOI:10.3969/j.issn.1674-3814.2013.11.015 ( 0) 0)
|
| [10] |
王颢雄, 马伟明, 肖飞, 等. 双dq变换软件锁相环的数学模型研究[J]. 电工技术学报, 2011, 26(7): 237-241. ( 0) 0)
|
| [11] |
XU Shungang, WANG Jinping, XU Jianping. A current decoupling parallel control strategy of single-phase inverter with voltage and current dual closed-loop feedback[J]. IEEE transactions on industrial electronics, 2013, 60(4): 1306-1313. DOI:10.1109/TIE.2011.2161660 ( 0) 0)
|
| [12] |
ROWE C N, SUMMERS T J, BETZ R E, et al. Implementing the virtual output impedance concept in a three phase system utilising cascaded pi controllers in the dq rotating reference frame for microgrid inverter control[C]//15th European Conference on Power Electronics and Applications (EPE). Lille, France, 2013:1-10.
( 0) 0)
|
| [13] |
CROWHURST B, EL-SAADANY E F, EL C L, et al. Single-phase grid-tie inverter control using dq transform for active and reactive load power compensation[C]//International Conference on Power and Energy (PECon). Kuala Lumpur:Malaysia, 2010:489-494.
( 0) 0)
|
| [14] |
胡寿松. 自动控制原理[M]. 5版. 北京: 科学出版社, 2007: 258-260.
( 0) 0)
|
| [15] |
徐德鸿. 电力电子系统建模及控制[M]. 北京: 机械工业出版社, 2006: 10-17.
( 0) 0)
|
| [16] |
林渭勋. 现代电力电子技术[M]. 北京: 机械工业出版社, 2006: 112-113.
( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


