|
收稿日期: 2017-12-26; 预印本: 2018-04-08
基金项目: 国家自然科学基金 (编号:61673234,U1636124)
第一作者简介: 袁静,1981年生,女,博士研究生,研究方向为高光谱解混。E-mail:yuanjing20110824@sina.com
|
摘要
丰度估计(AE)是从高光谱图像中识别地物的关键预处理技术。由于线性模型的可解释性以及数学上的可操作性,基于该模型的线性回归技术CLR(Constrained Linear Regression)在丰度估计中受到了广泛关注。目前,该方法仅仅考虑到了估计数据与被估计数据之间的能量相似性,没有考虑数据内部的变化信息之间的相似性,比如一阶梯度之间的相似性以及二阶梯度之间的相似性。为了提高丰度估计精度,本文提出了融合数据内部变化信息的稀疏低秩丰度估计算法。首先通过增加一阶梯度和二阶梯度的约束项改进传统的丰度估计的数学模型。其次,通过采用范数不等式和优化理论证明了在约束条件下,该模型的有效性及该模型在相关领域的可拓展性。接着,采用辅助变量将改进的数学模型变为增强拉格朗日函数。最后,采用交替双向乘子技术ADMM(Alternating Direction Method of Multipliers)求解该模型并估计高光谱图像的丰度。经仿真实验和实际高光谱图像的实验证明该方法能够改善仿真数据和实际高光谱数据的丰度估计的效果,特别是当端元的丰度存在丰富的变化细节时,丰度估计的精度和抗噪性能均优于当前较流行的丰度估计算法。
关键词
丰度估计, CLR, 变化信息, 稀疏低秩, ADMM
Abstract
Abundance estimation (AE) plays an important role in the processing and analysis of hyperspectral images. Constrained linear regression is usually developed to estimate abundance matrix due to its simplicity and mathematical tractability. However, this approach only focuses on the fitness between the estimated and ground-truth data without considering the internal variability such as the similarity among the first-order gradients and among the second-order gradients. To improve the accuracy of the AE, a novel method of adding internal variability to sparse low-rank AE was proposed. First, first- and second-order gradient constraint terms were used to modify the traditional mathematical model of sparse and low-rank AE. Second, norm inequality and optimization theory were applied to demonstrate the validity of the novel model. The model has been proven applicable to other related fields under constraint conditions. Third, auxiliary variables were utilized to transform the mathematic model to the enhanced Lagrange function (ELF). Finally, the ELF was solved by the alternating direction method of multipliers to estimate the abundance of hyperspectral images. In general, the traditional method of sparse and low-rank AE is the alternating direction sparse and low-rank unmixing (ADSpLRU). In this study, ADSpLRU-FOG refers to the method that adds the first-order gradient to the sparse and low-rank AE, whereas ADSpLRU-FSOG refers to the method that adds first- and second-order gradients to the sparse and low-rank AE. Experiment carried on the USUG library showed that, (1) in the convergent experiment, ADSpLRU-FOG and ADSpLRU-FSOG algorithms converged to a slightly lower NMSE than ADSpLRU. ADSpLRU-FSOG algorithm converged to the lowest NMSE among the three methods. (2) In the robust experiment, ADSpLRU-FOG and ADSpLRU-FSOG algorithms reached higher estimation accuracy than ADSpLRU in terms of SRE under white and colored noises. Among them, ADSpLRU-FSOG achieved remarkably higher SRE value than the other methods. (3) In the visual experiment, ADSpLRU-FOG algorithm could maintain the first-order gradient structure of the data more than ADSpLRU. Meanwhile, the ADSpLRU-FSOG algorithm could preserve the second-order gradient structure of the data better than ADSpLRU-FOG and ADSpLRU algorithms. Experiment based on the Urban and Jasper actual hyperspectral database showed that the accuracy of abundance matrix estimation from ADSpLRU-FSOG was better than those from ADSpLRU and ADSpLRU-FOG. Experimental results suggest that the novel method of adding the internal variability to the abundance matrix estimation can improve convergent behavior, maintain the structure of information of first-order and second-order gradients, obtain comparable estimation accuracy, and enhance robust performance for AE.
Key words
abundance estimation, CLR, internal variability, sparse and low-rank, ADMM
1 引 言
高光谱遥感因其在行星探测,精准农业,军事目标识别,森林研究,目标探测等方面的广泛应用而倍受关注Rosin(2001)。近年来,它被广泛应用于环境监测。但由于其空间分辨率较低,可能导致高光谱图像中的每个像元同时包含了多个地面微小物质的光谱信息,该像元被称为混合像元,该物质被称为端元。大量的混合像元阻碍了高光谱的应用(Bioucas-Dias 等,2012)。如何从混合像元中区分存在哪些端元(端元提取)和每种端元在混合像元中所占的比例(丰度估计)是高效地完成地物识别和分类的关键技术,称之为光谱解混技术(Bioucas-Dias 等,2012)。地面的多样性和复杂性增加了端元提取的难度。为了避免不准确地端元提取给丰度估计带来不可靠的估计效果,随着地物波谱库(端元谱库)的不断丰富,稀疏解混方法越来越受到业界的关注(Feng 等,2016;Iordache 等,2011)。稀疏解混的目标是在已知端元谱库的基础上估计各个端元的丰度,也叫丰度估计。其前提假设是混合光谱可以表示为多个纯端元光谱的线性组合(Iordache 等,2011;Candès 等,2006)。一般情况下已知的端元谱库含有大量纯端元光谱信息,从中选择若干个端元的光谱谱逼近混合像元的光谱,将导致丰度稀疏性,所以该方法被称为稀疏解混或稀疏丰度估计。丰度估计的目的是确定混合像元中存在哪些端元以及每个端元所占的比例(丰度)。Candès等(2006)通过为丰度矩阵施加
上述研究工作均是以光谱域的先验知识为基础,下面将介绍以空间域的先验知识为基础的研究工作:Qu等(2014)和Iordache等(2014)认为同质区域的混合像元的光谱具有很高的相似性, 其相应的丰度矢量具有很高的相关性。Qu等(2014)认为处于局部邻域的混合像元一般是由相同的地物构成。该性质表明丰度矩阵的列具有线性相关性,可由低秩矩阵做近似估计。另外,Iordache等(2014)认为丰度矩阵列的相关性可由行的稀疏性进行表示, 通过为丰度矩阵的行施加
Yang等(2016)利用稀疏编码的去噪功能提出了融合去噪过程和稀疏解混的丰度估计算法CHyDU(Coupled HSI Denoising and Unmixing)。提高了丰度估计的鲁棒性, 其代价是需要大量的计算时间。Yi等(2017)将超分辨重建技术的优势和光谱解混的优势进行融合提出联合高分辨重建与稀疏解混的新算法JHSr-Un(Joint Hyperspectral Superres-olution and Unmixing)。该算法同时提高了超分辨重建和光谱解混的鲁棒性。
此外,根据信号处理和机器学习文献(Richard等, 2012;Oymak等, 2015;Golbabaee和Vandergheynst, 2012;Richard等, 2014;Chen和Huang, 2012)和低秩矩阵估计技术(Bach,2008;Bioucas-Dias等, 2012;Negahban和Wainwright,2011; Babacan等,2012)的逆理论, 交替方向乘法ADMM(Alternating Direction Method of Multipliers)技术在丰度估计的求解中具有方便快捷的优点(Boyd等,2011)。
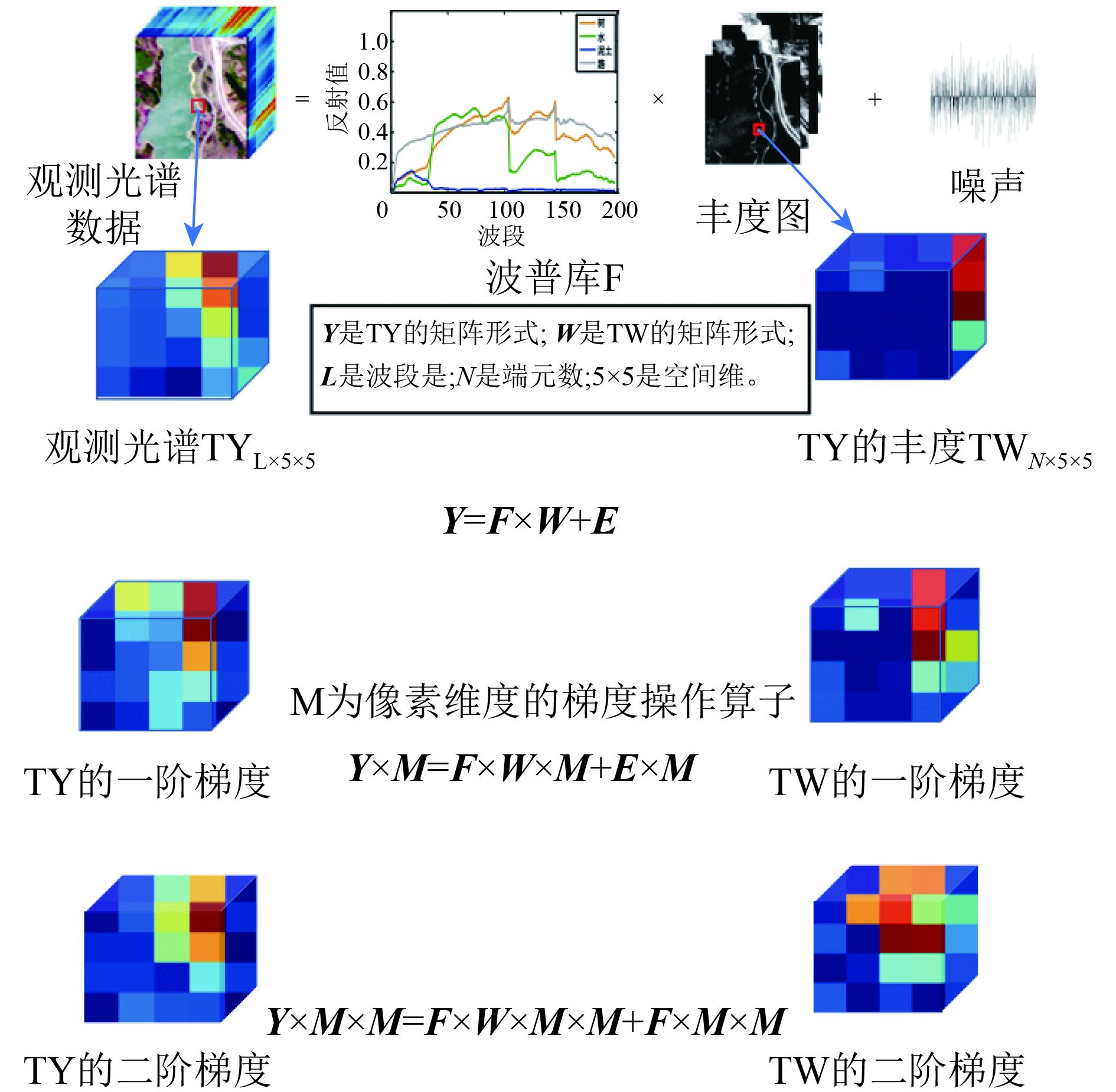
上述方法存在的问题是:数学模型中考虑了估计数据与被估计数据之间的能量相似性,没有考虑数据内部的变化信息之间的相似性;比如一阶梯度之间的相似性以及二阶梯度之间的相似性。观察图1所示的线性混合过程。通过截取光谱数据中
本文的创新性体现在以下几个方面:
(1)通过利用一阶梯度和二阶梯度改进了(袁静,2017b) (Giampouras 等,2016)的数学模型。提出同时融合一阶梯度和二阶梯度的带约束的线性回归方法,称为二阶增强的带约束的回归算法FSOECLR(The First and Second Order Enhanced Constrained Linear Regression algorithm)。
(2)通过相关数学理论证明FSOECLR的有效性以及在相关领域的可拓展性。将改进的线性回归模型应用于高光谱的丰度矩阵估计领域, 并推导出采用ADMM技术求解改进模型的方法。
2 融入变化信息的有效性证明
设已知观测数据矩阵
| $ {{Y}} = {{\textit{Θ}}} {{W}} + {{E}} $ | (1) |
在已知数据矩阵
从
| $ {P_1}:\mathop {\arg \min }\limits_{{w}} ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + f({{W}}) $ | (2) |
融入一阶梯度差异信息后数学模型
| ${P_2}:\mathop {\arg \min }\limits_{{w}} ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \beta ||{{YM}} - {{\textit{Θ}}} {{WM}}||_F^2 + f({{W}})$ | (3) |
式中,
采用二阶梯度改进数学模型
| $\begin{array}{l} {P_3}:\mathop {\arg \min }\limits_{{w}} ||{{Y}} - \Theta {{W}}||_F^2 + \beta ||{{YM}} - {{\textit{Θ}}} {{WM}}||_F^2+ \\ \eta ||{{YO}} - {{\textit{Θ}}} {{WO}}||_F^2 + f({{W}}) \end{array}$ | (4) |
式中, 参数
| $ \begin{split} &{J_{p1}}({{W}}) = ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + f({{W}})\\ &{J_{p2}}({{W}}) = ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \beta ||{{YW}} -{{\textit{Θ}}} {{WM}}||_F^2 + f({{W}}) \end{split} $ |
| $ \begin{split} {J_{p3}}({{W}}) = & ||{{Y}} -{{\textit{Θ}}} {{W}}||_F^2 + \beta ||{{YM}} - {{\textit{Θ}}}{{WM}}||_F^2 + \\ & ||{{YO}} - {{\textit{Θ}}} {{WO}}||_F^2 + f({{W}}) \end{split}$ | (5) |
证明过程如下:
(1) 观察数学模型P1和数学模型P2。根据
| $\beta ||{{YM}} -{{\textit{Θ}}} {{WM}}||_F^2 \leqslant \beta ||{{M}}||_F^2||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2$ | (6) |
不等式(6)的两边同时加上
| $\begin{split} & ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + f({{W}}) + \beta ||{{YM}} -{{\textit{Θ}}} {{WM}}||_F^2 \leqslant \\ & ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + f({{W}}) + \beta ||{{M}}||_F^2 ||{{Y}} -{{\textit{Θ}}} {{W}}||_F^2 \end{split} $ | (7) |
式(7)的左边是目标函数
将式(7)的右边重新整理可得
| $(1 + \beta ||{{M}}||_F^2)||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + f({{W}})$ | (8) |
令
则有模型
| ${P_{12}}:\mathop {\arg \min }\limits_{{w}} (1 + \beta ||{{M}}||_F^2)||{{Y}} -{{\textit{Θ}}} {{W}}||_F^2 + f({{W}})$ | (9) |
根据不等式(7), 可得
| $ {J_{{P_2}}} \leqslant {J_{{P_{12}}}} $ | (10) |
式(9)
| ${P_{13}}:\mathop {\arg \min }\limits_{{w}} ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \frac{1}{{1 + \beta ||{{M}}||_F^2}}f({{W}})$ | (11) |
其目标函数
| ${J_{{P_{13}}}}({{W}}) = ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \frac{1}{{1 + \beta ||{{M}}||_F^2}}f({{W}})$ |
观察
| $ {J_{{P_{13}}}}({{W}}) \leqslant {J_{{P_1}}}({{W}}) $ | (12) |
根据不等式(10), (12)以及模型P12与模型P13等价, 有
结论1 数学模型P2优于数学模型P1。
(2)观察数学模型P2和数学模型P3: 其中
| $\begin{split} & \eta ||{{YO}} - {{\textit{Θ}}}{{WO}}||_F^2 = \eta ||{{YMM}} - {{\textit{Θ}}} {{WMM}}||_F^2 \leqslant \\ & \eta ||{{M}}||_F^2||{{YM}} - {{\textit{Θ}}} {{WM}}||_F^2 \leqslant \\ & \eta ||{{M}}||_F^2||{{M}}||_F^2||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 \end{split}$ | (13) |
即
| $\eta ||{{YO}} - {{\textit{Θ}}} {{WO}}||_F^2 \leqslant \eta ||{{M}}||_F^2||{{M}}||_F^2||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2$ | (14) |
不等式(14)两边同时加上
| $||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \beta ||{{YM}} -{{\textit{Θ}}} {{WM}}||_F^2 + f({{W}})$ |
得
| $ \begin{split} & ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \beta ||{{YM}} - {{\textit{Θ}}} {{WM}}||_F^2 + f({{W}}) + \\ & \eta ||{{YO}} - {{\textit{Θ}}} {{WO}}||_F^2 \leqslant \\ & ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \beta ||{{YM}} - {{\textit{Θ}}} {{WM}}||_F^2 + f({{W}}) + \\ & \eta ||{{M}}||_F^2||{{M}}||_F^2||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 \end{split}$ | (15) |
则重新整理不等式(15)的右边项
| $ \begin{split} & ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \beta ||{{YM }}- {{\textit{Θ}}} {{WM}}||_F^2 + f({{W}}) + \\ & \eta ||{{YO}} - {{\textit{Θ}}} {{WO}}||_F^2 \leqslant \\ & (1 + \eta ||{{M}}||_F^2||{{M}}||_F^2)||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \\ & \beta ||{{YM}} - {{\textit{Θ}}} {{WM}}||_F^2 + f({{W}}) \end{split} $ | (16) |
观察式(16)小于号左边的表达式, 是数学模型P3的目标函数
观察式(16)小于号右边的表达式, 是下列数学模型P22的目标函数
| $ \begin{split} & {P_{22}}:\mathop {\arg \min }\limits_w (1 + \eta ||{{M}}||_F^2||{{M}}||_F^2)||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2+ \\ & \beta ||{{YM}} - {{\textit{Θ}}} {{WM}}||_F^2 + f({{W}}) \end{split} $ | (17) |
根据不等式(16)得出
| $ {J_{{P_3}}}({{W}}) \leqslant {J_{{P_{22}}}}({{W}}) $ | (18) |
式(17)
| $ \begin{split} & {P_{23}}:\mathop {\arg \min }\limits_{{w}} ||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \frac{1}{{1 + \eta ||{{M}}||_F^2||{{M}}||_F^2}}||{{YM}} \\ & {{\textit{Θ}}}{{WM}}||_F^2 + \frac{1}{{1 + \eta ||{{M}}||_F^2||{{M}}||_F^2}}f({{W}}) \end{split} $ | (19) |
由于
观察
根据不等式(18), (20)以及模型P23与模型P22等价, 有
结论2 数学模型P3优于数学模型P2。
综合结论1与结论2, 有
结论3 数学模型P3优于数学模型P2, 数学模型P1。
(3) 观察W的变化。由
| ${{W}} = {{{\textit{Θ}}} ^{ - 1}}{{Y}} + {({{{\textit{Θ}}} ^{\rm{T}}}{{\textit{Θ}}})^{ - 1}}{f'}({{W}})$ | (20) |
由
| ${{W}} = {{{\textit{Θ}}} ^{ - 1}}{{Y}} + {({{{\textit{Θ}}} ^{\rm{T}}}{{\textit{Θ}}})^{ - 1}}{f'}({{W}})(1 + {{M}}{{{M}}^{\rm{T}}})$ | (21) |
由
| ${{W}} = {{{\textit{Θ}}} ^{ - 1}}{{Y}} + {({{{\textit{Θ}}} ^{\rm{T}}}{{\textit{Θ}}})^{ - 1}}{f'}({{W}})(1 + {{M}}{{{M}}^{\rm{T}}} + {{O}}{{{O}}^{\rm{T}}})$ | (22) |
由式(20)、(21)、(22)可知3个不同的目标函数中的W的变化是不同的。同时可得到当
结论4 P3模型的估计值优于P2模型的估计值, P2模型的估计值优于P1模型的估计值。因此, 融合一阶梯度的线性回归算法(P2)的精度优于传统的线性回归算法(P1);而融入一阶梯度和二阶梯度的线性回归算法(P3)精度优于传统线性回归算法(P1)和仅含有一阶梯度的线性回归算法(P2)。当
3 基于滑动窗的稀疏低秩的丰度矩阵估计算法
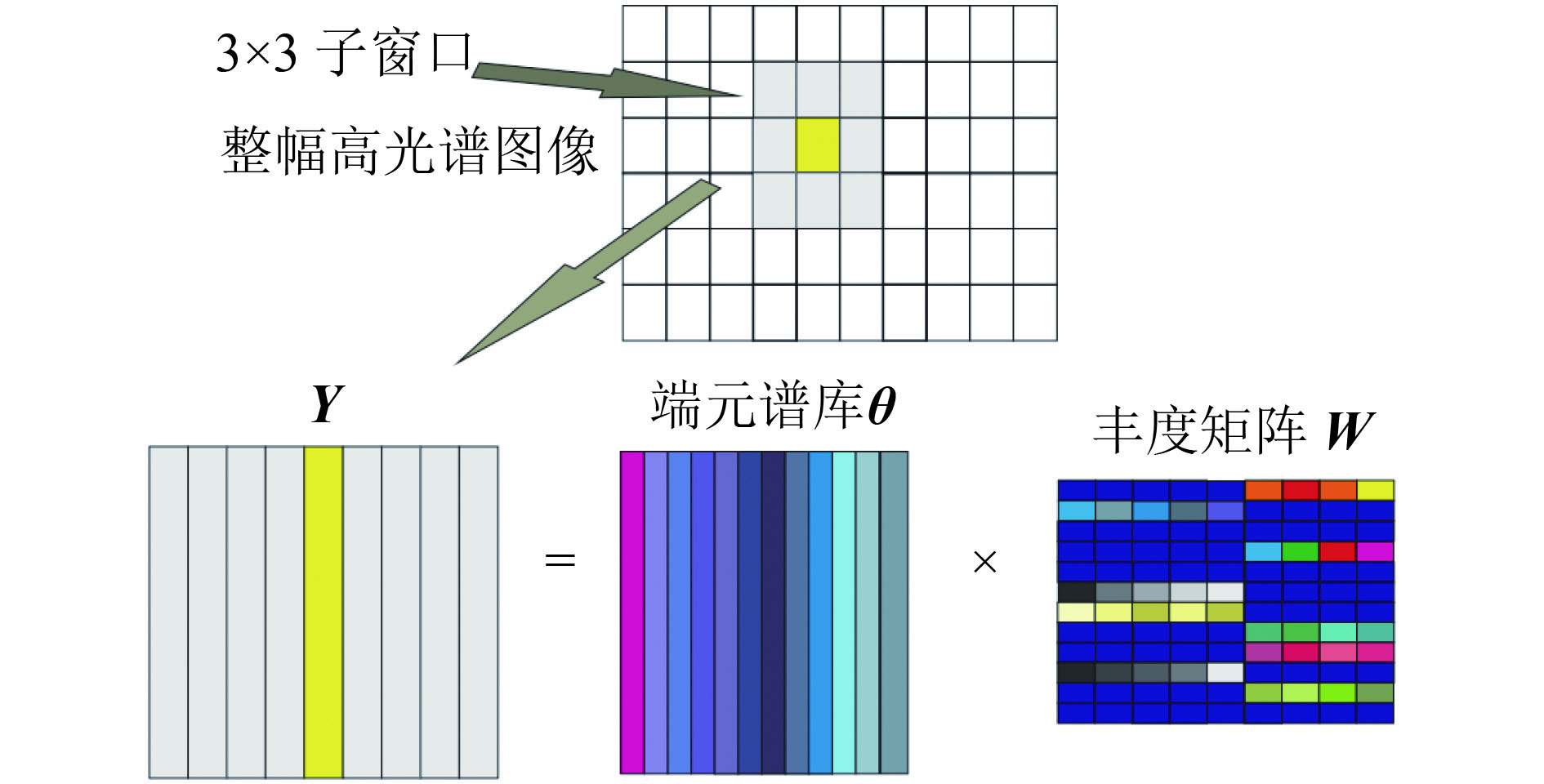
Giampouras等(2016)提出基于滑动窗的丰度矩阵估计问题, 并阐述稀疏低秩丰度估计的算法原理。假设有L波段的高光谱图像, 图像中的每个像元由N个端元组成。用
| $ {{Z}}_6^{t + 1} = {{Z}}_6^t - ({{\textit{Θ}}} {{{W}}^{t + 1}}{{W}} + {{\textit{γ}}} _6^{t + 1}) $ | (24) |
式中, W和E分别表示丰度和噪声。根据物理涵义, 丰度矩阵具有非负性以及归一性(丰度矩阵每列数据的和为1)(Bioucas-Dias 等, 2012)。其数学描述为
| ${{W}} > {0.1^{\rm{T}}}{{W}} = {{{\textit{1}}}^{\rm{T}}}$ | (25) |
根据Giampouras等(2016)的结论:在稀疏性和低秩性的前提假设下, 丰度矩阵归一性约束条件可以忽略。估计丰度矩阵W的问题由稀疏低秩线性回归方法实现, 其数学模型表示如下
| $ \widehat {{W}} = \mathop {\arg \min }\limits_{{{w}} \in R_ + ^{N \times {k^2}}} (\frac{1}{2}||{{Y}} -{{\textit{Θ}}} {{W}}||_F^2 + \gamma ||{{W}}|{|_1} + \\ \tau ||{{W}}|{|_*} + {I_R} + ({{W}})) $ | (26) |
式中,γ、τ是丰度矩阵稀疏性和低秩性的正则化参数。
4 融合数据内部变化信息的稀疏低秩丰度估计算法
4.1 数学模型
Giampouras等(2016)提出的稀疏低秩丰度矩阵估计算法的数学模型没有考虑数据内部的变化信息, 而袁静等(2018)仅仅考虑了一阶差分的信息。根据图1以及第二节的证明, 本文对式(26)所表达的数学模型做如下改进。
(1)本文用一阶梯度代替文献(袁静 等, 2018)中的一阶差分, 为融入一阶梯度信息的丰度矩阵估计重建数学模型PFG。
| $ \begin{split} (PFG)\widehat {{W}} = & \mathop {\arg \min }\limits_{{{w}} \in R_ + ^{N \times {k^2}}} (\frac{1}{2}||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \\ & \gamma ||{{W}}|{|_1} + \tau ||{{W}}|{|_*} + \\ & \frac{1}{2}\beta ||{{YM}} - \Theta {{WM}}||_F^2 + {I_R} + ({{W}})) \end{split}$ | (27) |
式中,M表示一阶梯度算子。本文采用滑动窗的稀疏低秩丰度估计策略(Giampouras等,2016),其窗口大小为
| ${{M}} = \left[ {\begin{array}{*{20}{c}} 2&0&0&0&0&0&0&0&0 \\ { - 1}&2&0&0&0&0&0&0&0 \\ 0&{ - 1}&2&0&0&0&0&0&0 \\ { - 1}&0&{ - 1}&2&0&0&0&0&0 \\ 0&{ - 1}&0&{ - 1}&2&0&0&0&0 \\ 0&0&{ - 1}&0&{ - 1}&2&0&0&{ - 1} \\ 0&0&0&{ - 1}&0&{ - 1}&2&{ - 1}&0 \\ 0&0&0&0&{ - 1}&0&{ - 2}&2&{ - 1} \\ 0&0&0&0&0&{ - 1}&0&{ - 1}&2 \end{array}} \right]$ |
本文用ADMM技术求解融入一阶梯度信息后的数学模型, 并称之为融合像素维的一阶梯度结构的交替方向稀疏低秩解混算法ADSpLRU-FOG(Alternating Direction Sparse and Low-Rank Unmixing With First-Order Gradient)。
(2)采用二阶梯度进一步改进上述数学模型。并重建数学模型PFSG。
| $\begin{split} & (PFSG)\widehat {{W}} = \mathop {\arg \min }\limits_{{{w}} \in R_ + ^{N \times {k^2}}} (\frac{1}{2}||{{Y}} - {{\textit{Θ}}} {{W}}||_F^2 + \gamma ||{{W}}|{|_1} + \tau ||{{W}}|{|_*} + \\ & \frac{1}{2}\beta ||{{YM}} - {{\textit{Θ}}} {{WM}}||_F^2 + \frac{1}{2}\beta ||{{YO}} - \Theta {{WO}}||_F^2 + {I_R} + ({{W}})) \end{split} $ | (28) |
式中,O表示二阶梯度算子。O=M×M 采用ADMM求解该模型, 称之为融合像素维的一阶和二阶梯度结构的交替方向稀疏低秩解混算法ADSpLRU-FSOG(Alternating Direction Sparse and Low-Rank Unmixing With First-Order and Second-Order Gradient)。
4.2 求解改进的数学模型PFSG
用ADMM算法求解数学模型PFSG的过程是。首先通过引入辅助矩阵变量, 将数学模型PFSG重新描述为
| $\begin{split} & (PFSG2):\mathop {{{{\textit{γ}}} _1}, {{{\textit{γ}}} _2}, {{{\textit{γ}}} _3}, {{{\textit{γ}}}_4}, {{{\textit{γ}}}_5}, {{{\textit{γ}}} _6}}\limits^{\min } \{ \frac{1}{2}||{{{\textit{γ}}} _1} - {{Y}}||_F^2 + \gamma ||{{{\textit{γ}}}_2}|{|_1} + \\ & \tau ||{{{\textit{γ}}}_3}|{|_*} + {I_R} + \left({{{{\textit{γ}}} _4}} \right) + \beta \frac{1}{2}||{{{\textit{γ}}} _5} - {{YM}}||_F^2 + \\ & \eta \frac{1}{2}||{{{\textit{γ}}} _6} - {{YO}}||_F^2\} \\ & {{\rm { s.t. }} {{\textit{γ}}}_{1}-{{{\textit{Θ}}}} {{W}}=0, {{\textit{γ}}}_{2}}-{{{W}}=0, {{\textit{γ}}}_{3}}-{{W}}=0 \\ & {{{\textit{γ}}}_{4}-{{W}}=0, \quad {{\textit{γ}}}_{5}-{{\textit{Θ}}} {{WM}}=0}, \\ & {{{\textit{γ}}}_{6}-{{\textit{Θ}}} {{WO}}=0} \end{split}$ |
构造模型PFSG的增强拉格朗日函数
| $ \begin{split} & {L_2}({{W}}, {{{\textit{γ}}} _1}, {{{\textit{γ}}}_2}, {{{\textit{γ}}} _3}, {{{\textit{γ}}}_4}, {{{\textit{γ}}}_5}, {{{\textit{γ}}}_6}) = \\ & \frac{1}{2}||{{{\textit{γ}}}_1} - {{Y}}||_F^2 + \gamma ||{{{\textit{γ}}}_2}|{|_1} + \\ & \tau ||{{{\textit{γ}}}_3}|{|_*} + {I_R} + ({{{\textit{γ}}}_4}) + \beta \frac{1}{2}||{{{\textit{γ}}}_5} - {{YM}}||_F^2 + \\ & \eta \frac{1}{2}||{{{\textit{γ}}}_6} - {{YO}}||_F^2 + tr[{{Z}}_1^{\rm{T}}({{{\textit{γ}}}_1} - {{\textit{Θ}}} {{W}})] + tr[{{Z}}_2^{\rm{T}}({{{\textit{γ}}} _2} - {{W}})] + \\ & tr[{{Z}}_3^{\rm{T}}({{{\textit{γ}}} _3} - {{W}})] + tr[{{Z}}_4^{\rm{T}}({{{\textit{γ}}} _4} - {{W}})] + \\ & tr[{{Z}}_5^{\rm{T}}({{{\textit{γ}}}_5} - {{\textit{Θ}}} {{WM}})] + tr[{{Z}}_6^{\rm{T}}({{{\textit{γ}}}_6} - {{\textit{Θ}}} {{WO}})] + \\ & \frac{\mu }{2}(||{{\textit{Θ}}} {{W}} - {{{\textit{γ}}}_1}||_F^2 + ||{{W}} - {{{\textit{γ}}}_2}||_F^2 + ||{{W}} - {{{\textit{γ}}}_3}||_F^2 +\\ & ||{{W}} - {{{\textit{γ}}}_4}||_F^2 + ||{{\textit{Θ}}} {{WM}} - {{{\textit{γ}}}_5}||_F^2 + ||{{\textit{Θ}}} {{WO}} - {{{\textit{γ}}} _5}||_F^2) \end{split} $ | (30) |
采用ADMM算法求解模型PFSG, 由于增加了O的表达式, 使得求解W的过程发生变化, 总结如下
| $ \begin{split} &{{{J}}^t} = {{{\textit{Θ}}}^{\rm{T}}}{{\textit{γ}}}_1^t + {{\textit{γ}}}_2^t + {{\textit{γ}}}_4^t + {{{\textit{Θ}}}^{\rm{T}}}{{\textit{γ}}}_5^t{{\rm{M}}^{\rm{T}}} + {{{\textit{Θ}}}^{\rm{T}}}{{\textit{γ}}}_6^t{O^{\rm{T}}} \\ & {H^t} = {{{\textit{Θ}}}^{\rm{T}}}{{Z}}_1^t + {{Z}}_2^t + {{Z}}_3^t + {{Z}}_4^t + {{{\textit{Θ}}}^{\rm{T}}}{{Z}}_5^t{{\rm{M}}^{\rm{T}}} + {{{\textit{Θ}}}^{\rm{T}}}{{Z}}_6^t{{{O}}^{\rm{T}}} \\ & Finv = {({{{\textit{Θ}}}^{\rm{T}}}{{\textit{Θ}}} + 3{{{I}}_N})^{ - 1}} \\ & {{A}} = - Finv({{{\textit{Θ}}}^{\rm{T}}}{{\textit{Θ}}});{{B}} = {{{M}}^{\rm{T}}}{{M}} + {{{O}}^{\rm{T}}}{{O}} \\ & {{C}} = Finv \times ({{{H}}^t} + {{{J}}^t}) \\ & {{{W}}^{t + 1}} = dlyap({{A}}, {{B}}, {{{C}}^t}) \end{split} $ | (31) |
式中,t表示第t次的迭代;
AXB-X+C=0(Lu,1986)辅助变量
| $ \begin{split} {{\textit{γ}}}_6^{t + 1} = & \mathop {\arg \min }\limits_{{{\textit{γ}}}_5^t} \left( {L_2}({{{W}}^{t + 1}}, \Upsilon _1^{t + 1},{{\textit{γ}}}_2^t, {{\textit{γ}}}_3^t, {{\textit{γ}}}_4^t, {{\textit{γ}}}_5^t, {{\textit{γ}}} _6^t)\right) = \\ & \frac{1}{{\mu + 2\beta }}(2\beta {{YO}} + \mu {{\textit{Θ}}} {{{W}}^{t + 1}}{{O}} - {{Z}}_6^t) \end{split} $ | (32) |
在
| ${{Z}}_6^{t + 1} ={{Z}}_6^t - ({{\textit{Θ}}} {{{W}}^{t + 1}}{{O}} + {{\textit{γ}}} _6^{t + 1})$ | (33) |
其收敛条件与Giampouras等(2016)和袁静等(2018)一致。其他变量的迭代计算方法和迭代终止条件与上类似。现将两个改进模型的算法统一整理如算法1所示。
算法1
输入 Y, Θ
设置:
初始化:
Repeat
直到: 收敛。
输出
式中,SHR(·)表示软阈值操作函数, 是稀疏约束的数值计算方法(Iordache 等, 2012)。SVT(·)是用于优化低秩约束的数值计算方法(Giampouras 等, 2016)。
5 实验与分析
为了评价本文提出的融合变化信息的稀疏低秩丰度估计算法(ADSpLRU-FSOG), 分别针对1个仿真数据和两个真实高光谱遥感数据开展相关实验。并与CHyDU算法(Yang 等, 2016), ADSpLRU算法(Giampouras 等, 2016)算法和ADSpLRU-FOG算法(袁静 等, 2018)进行比较。其中ADSpLRU算法, ADSpLRU-FOG算法和ADSpLRU-FSOG算法均为基于3×3的滑动窗的局部算法。CHyDU算法属于同时考察整幅光谱图像的全局算法。
(1)高光谱仿真数据库1。首先确定空间维的混合像元的数量是
(2)实际高光谱数据1-Urban。高光谱图像数据Urban,307×307个像元,每个像元对应的是2 m的地表区域。每个像元的光谱波段是210个,谱分辨率是10 nm。由于水蒸气和空气的影响,删除了波段1—4,6,87,101—111,136—373,198—210的数据。Zhu等(2014b)对原始的Urban数据进行处理后,得到含有162个波段的高光谱数据,该数据中含有6种不同的地物:“#泥土”,“#金属”,“#房屋”,“#树木”,“#草地”和“#柏油马路”。其端元光谱库含有该六种地物在162个波段下的光谱数据。该数据通过人工解译和基本的解混算法提供了参考丰度。为了验证本文算法,本文截取30×30的空间长方形区域。起始坐标(150, 150)。数据维度198×900(“900”表示的是观测光谱数据的空间维度是30×30)。
(3)实际高光谱数据2-JasperRidge库。高光谱图像数据JasperRidge是流行高光谱数据 (Zhu 等,2014b)。有512×614像素。有224个波段。光谱分辨率高达9.46 nm。由于图像太复杂,Zhu 等,(2014b)截取100×100像素的子图像。由于水蒸气和大气效应密集,保留了198个通道。数据中含有4个端元成分:“#路”,“#土壤”,“#水”和“#树”。该数据通过手工选取端元和基本的解混算法提供了参考丰度。为了验证本文算法,本文截取了30×30的子图像。坐标始于(10, 10)。数据维度是
首先给出CHyDU算法(Yang 等,2016),ADSpLRU算法(Giampouras 等,2016),ADSpLRU-FOG算法(袁静 等,2018),ADSpLRU-FSOG算法的时间消耗实验和评价指标说明。然后从实验参数设置,实验步骤等方面阐述实验过程,并针对实验结果进行分析和讨论。
5.1 时间消耗实验
本实验的运行平台环境如下:CPU配置:8个CPU;型号为Intel Coe i4;内存:16 G。
仿照Giampouras等(2016)和袁静(2017b)的局部解混思想。针对仿真库1中的数据, 采用9×224的滑动窗(“9”意味着3×3的滑动窗的大小)对81×224的混合像元(“81”指的是仿真观测光谱数据的空间维度是9×9)进行丰度估计并统计所消耗的时间,其中,最大迭代次数是9000次(共需要9个滑动窗口,每个滑动窗口的最大迭代次数1000次),计算每迭代一次的平均消耗的时间(表1)。该表格说明ADSpLRU算法的计算速度最快,大约为0.488 ms;ADSpLRU-FOG算法的计算速度为4.6 ms,比ADSpLRU算法的计算时间长,其原因是计算ADSpLRU-FOG模型的过程中增加了一阶梯度信息的优化过程。ADSpLRU-FSOG算法的计算速度是5.3 ms,其原因是求解ADSpLRU-FSOG模型的过程中增加了一阶梯度和二阶梯度信息的约束项。
表 1 计算时间比较
Table 1 Running time comparison
| 算法 | CHyDU | ADSpLRU | ADSpLRU-
FOG |
ADSpLRU-
FSOG |
| 时间/s | 531.3769 | 3.7116 | 33.8919 | 38.8363 |
| 迭代次数 | 5528 | 7608 | 7326 | 7209 |
| 时间/每次/ms | 96.1 | 0.488 | 4.6 | 5.3 |
与局部解混思想不同的是,CHyDU算法是全局解混算法。其时间消耗高达96.1 ms。该算法需要进行字典学习以达到去噪目的,因此,其时间消耗最大。
总之,融入变化信息的丰度估计算法比ADSpLRU算法的时间消耗更多,但比CHyDU算法更节省时间。
5.2 评价指标
关于丰度估计的评价指标,文献(Iordache M D,2012)指出信号重建误差SRE(Signal Reconstruction Error)更能准确地评估丰度估计的性能,建议采用SRE代替均方根误差RMSE(Root Mean Square Error)。因此,本文采用SRE评价整体丰度估计效果;用SREs评价每个基本端元的丰度估计效果。SRE是丰度真值的能量与估计的丰度误差能量之比(Iordache等,2011),其定义如下
| $SRE = 10{\log _{10}}\left(\frac{{||{{W}}|{|_F}}}{{||{{W}} - {{{W}}'}|{|_F}}}\right)$ | (34) |
式中,W是丰度真值,
| $SRE = 10{\log _{10}}\left(\frac{{||{{W}}|{|_F}}}{{||{{{W}}'} - {{W}}_i'|{|_F}}}\right)$ |
式中,
5.3 仿真实验
本节主要介绍融合信息变化差异的丰度矩阵估计算法的各项性能。基于仿真库1开展收敛性、抗噪性、参数影响3个方面的实验。
5.3.1 收敛性实验
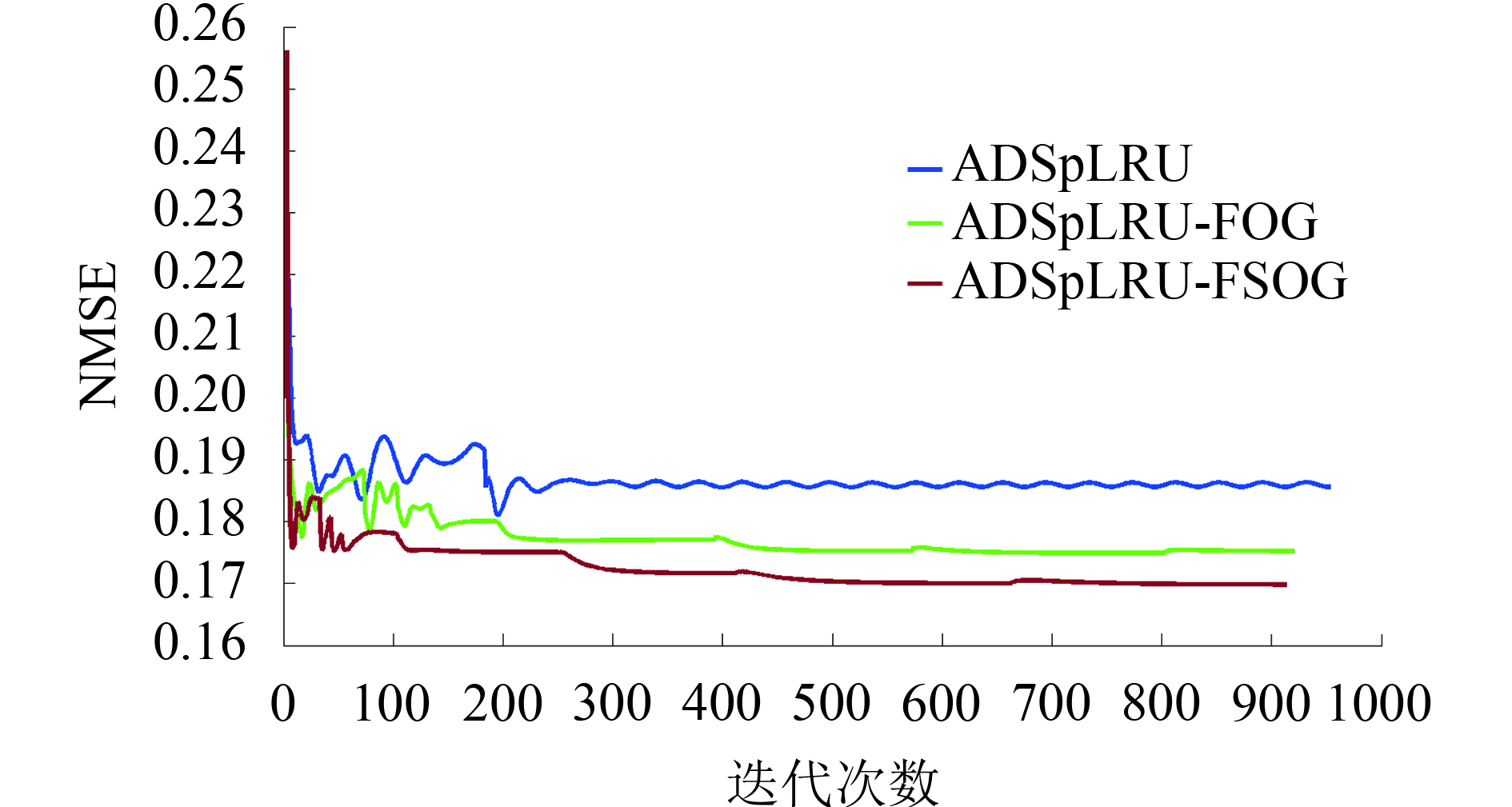
本次实验旨在探索改进算法在迭代过程中的收敛性。由于ADSpLRU-FSOG算法属于滑动窗的局部算法,则仅比较其与ADSpLRU算法(Giampouras 等,2016)和ADSpLRU-FOG算法(袁静 等,2018)的收敛性能。实验数据采用的是仿真库1中被30dB的高斯白噪声污染的仿真数据,运行10次,采用归一化的均方误差 NMSE(Normalized Mean Square Error)作为度量收敛性能的指标。该指标定义如下:
实验结果(图3)说明含梯度信息的丰度估计算法较好地改进了ADSpLRU算法的收敛性。ADSpLRU-FSOG算法比ADSpLRU-FOG增加了二阶梯度信息,所以其收敛性能最佳。
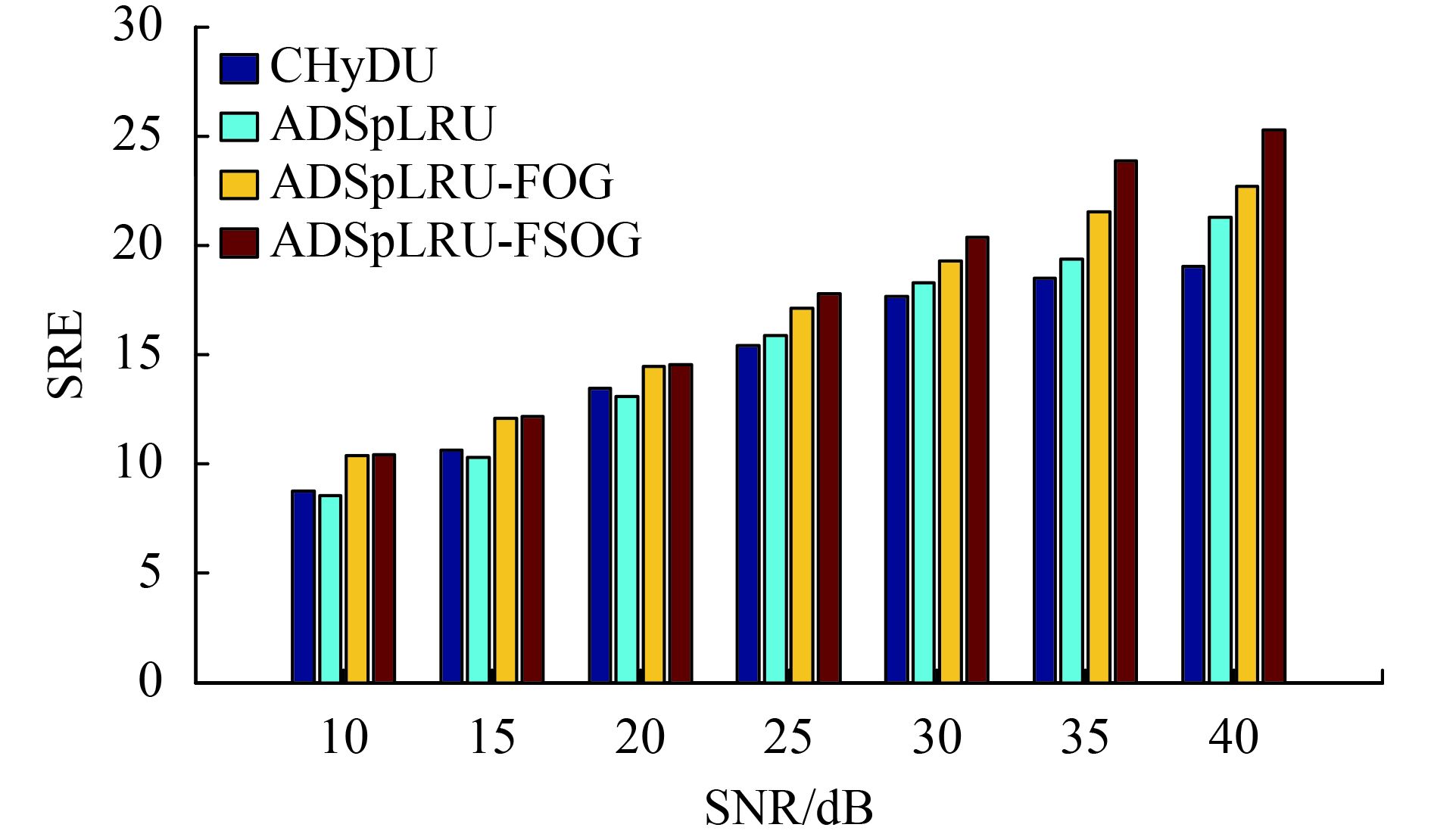
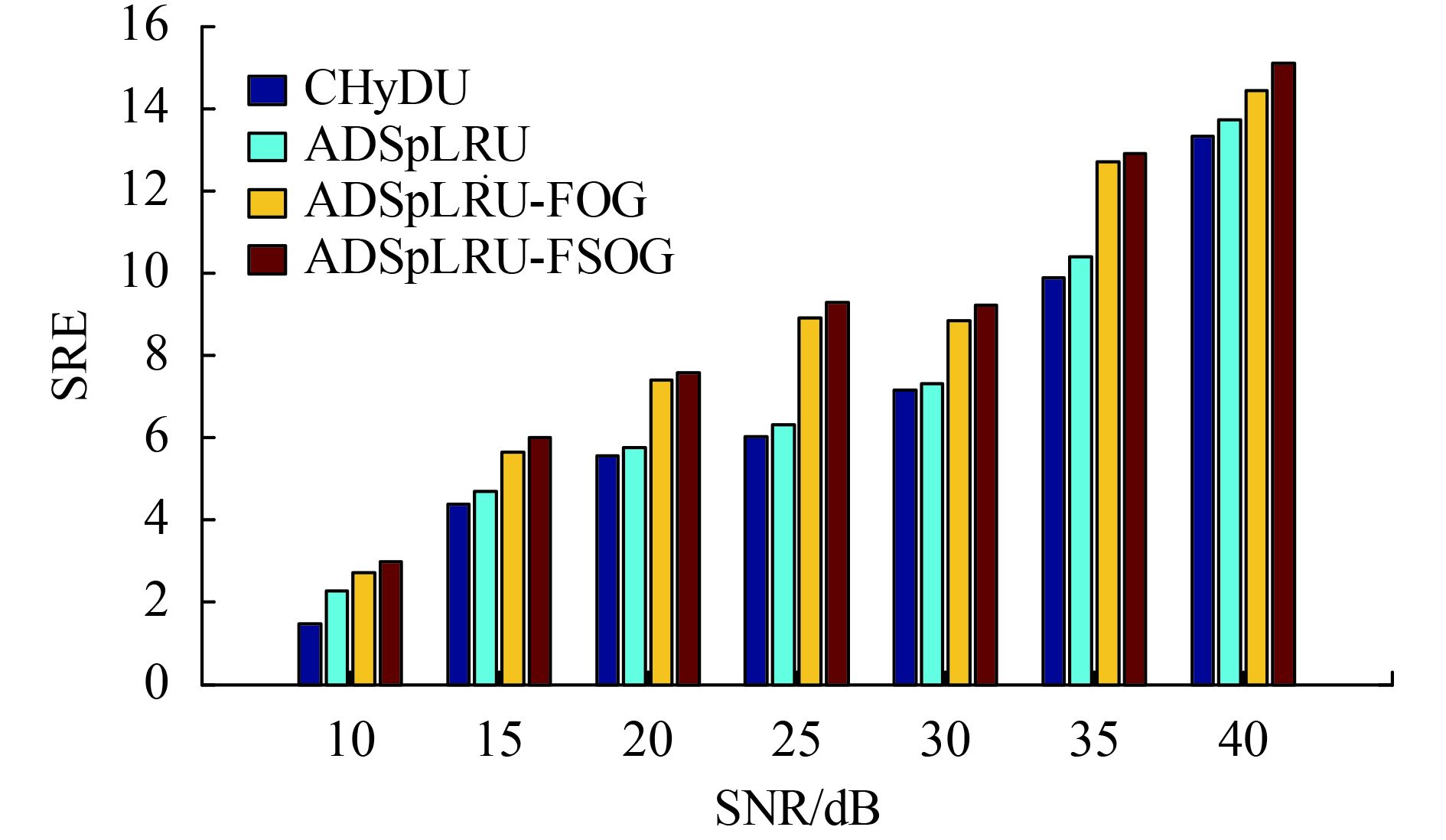
5.3.2 抗噪实验
本次实验探索改进算法在噪声干扰下的抗噪能力。针对仿真库1中高斯白噪声污染的观测光谱数据,分别采用4种不同的丰度估计算法进行估计,计算其平均SRE值。同理,针对由彩色噪声污染的光谱数据,采用相同的实验过程和实验方法。实验过程中涉及到参数如表2所示。由于对不同的光谱图像进行稀疏低秩丰度估计时,使得估计效果最佳的稀疏参数是不同的。稀疏参数的大小会直接影响到估计丰度的梯度。因此,为了更好地利用梯度信息,本实验采取的策略是让稀疏参数
表 2 参数设定
Table 2 Parameters setting
| 算法 | γ | τ | µ | β | η | τ0 | η0 | µ0 | τ1 |
| ADSpLRU |
|
|
0.01 | — | — | — | — | — | — |
| ADSpLRU-FOG |
|
0.00001 | 0.01 |
|
— | — | — | — | — |
| ADSpLRU-FSOG |
|
|
0.01 |
|
|
— | — | — | — |
| CHyDU |
|
— | 0.01 | — | — |
|
1.15
|
1 | 20 |
| 注:δ是观测光谱图像中高斯噪声的标准差。μ是算法模型的增强拉格朗日方程中的惩罚参数。该参数未出现在数学模型中。 | |||||||||
为了说明表2与
| $ \begin{split} \left\{ {\widehat {{{W}}, }\widehat {{X}}, \widehat {{D}}, \{ \widehat {{{{\alpha}} _i}}\} } \right\} = & \mathop {\arg \min }\limits_{W \in R_ + ^{N \times PQ}} ({\tau _0}||{{X}} - {{Y}}||_F^2 + \\ & \sum\limits_{i = 1}^I {(||{{{R}}_i}{{X}} - {{D}}{\alpha _i}||_F^2 + {\eta _0}||{{{\alpha}} _i}|{|_1}}) + {\mu _0}||{{X}}|{|_*} + \\ & {\tau _1}||{{X}}- {{\textit{Θ}}} {{W}}||_F^2 + \gamma ||{{W}}|{|_1} + {I_R} + ({{W}})) \end{split} $ | (36) |
(1)高斯白噪声:该实验旨在比较ADSpLRU-FOG算法、ADSpLRU-FSOG算法、ADSpLRU算法和CHyDU算法在高斯白噪声环境下的抗噪性能(图4)。经观察发现:ADSpLRU-FSOG算法优于其他算法。分析原因如下:4种算法均具有去噪能力,在稀疏解混过程中,CHyDU算法在稀疏性重视程度上是一样的 (用相同稀疏参数),而局部算法的对整幅图的稀疏性重视程度是不同的(用不同的稀疏参数)。所以局部算法优于CHyDU的全局算法。此外,由于增加了一阶梯度信息,ADSpLRU-FOG的丰度估计效果优于ADSpLRU。ADSpLRU-FSOG算法强化一阶梯度和二阶梯度信息使得丰度估计效果较优于其他算法。此外,发现在10dB的时候,ADSpLRU-FSOG算法比ADSpLRU-FOG算法稍微差些分析其原因是:此次实验中存在稀疏性约束参数为0.01的情况,此时,改进算法与原始算法效果几乎一致或较差;分析其原因:当稀疏参数大时,稀疏性弱,为零的项应该较多,该情况意味着其一阶梯度和二阶梯度减少,易受噪声信息影响,使得改进算法的效果不够明显且容易变差。
(2)有色噪声:在真实的高光谱图像中,破坏数据的噪声往往比白噪声更加复杂。因此,为了评估所提出的方法在实际条件下的抗噪性能,为线性混合像元添加模拟的有色噪声(Giampouras 等,2016)。图5说明了对于不同的SNR值,改进算法在SRE指标下的有效性。观察到ADSpLRU-FOG算法和ADSpLRU-FSOG在整个信噪比范围内比其他算法获得更好的结果。此外,与ADSpLRU-FOG相比,ADSpLRU-FSOG的性能更好。该实验结果说明了融合变化信息的丰度矩阵估计算法在彩色噪声的干扰下具有较强的鲁棒性。且随着信噪比的增加其抗噪能力更加明显。
5.3.3 参数η的实验
Giampouras等(2016)讨论了参数
当
总之,二阶梯度越大其有效参数η区域越容易获得。
5.4 效果可视化实验
5.4.1 基于仿真库1的可视化实验
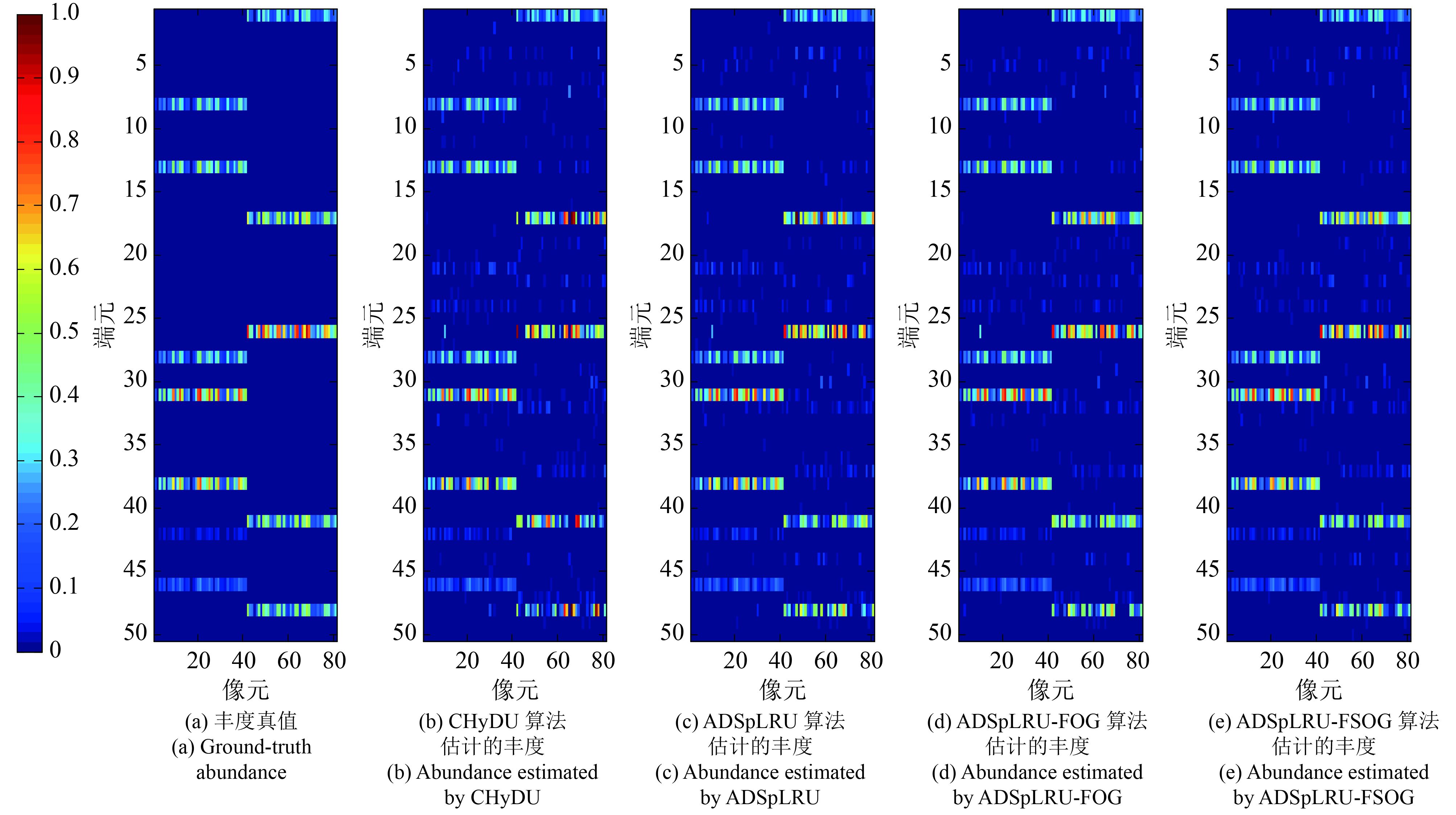
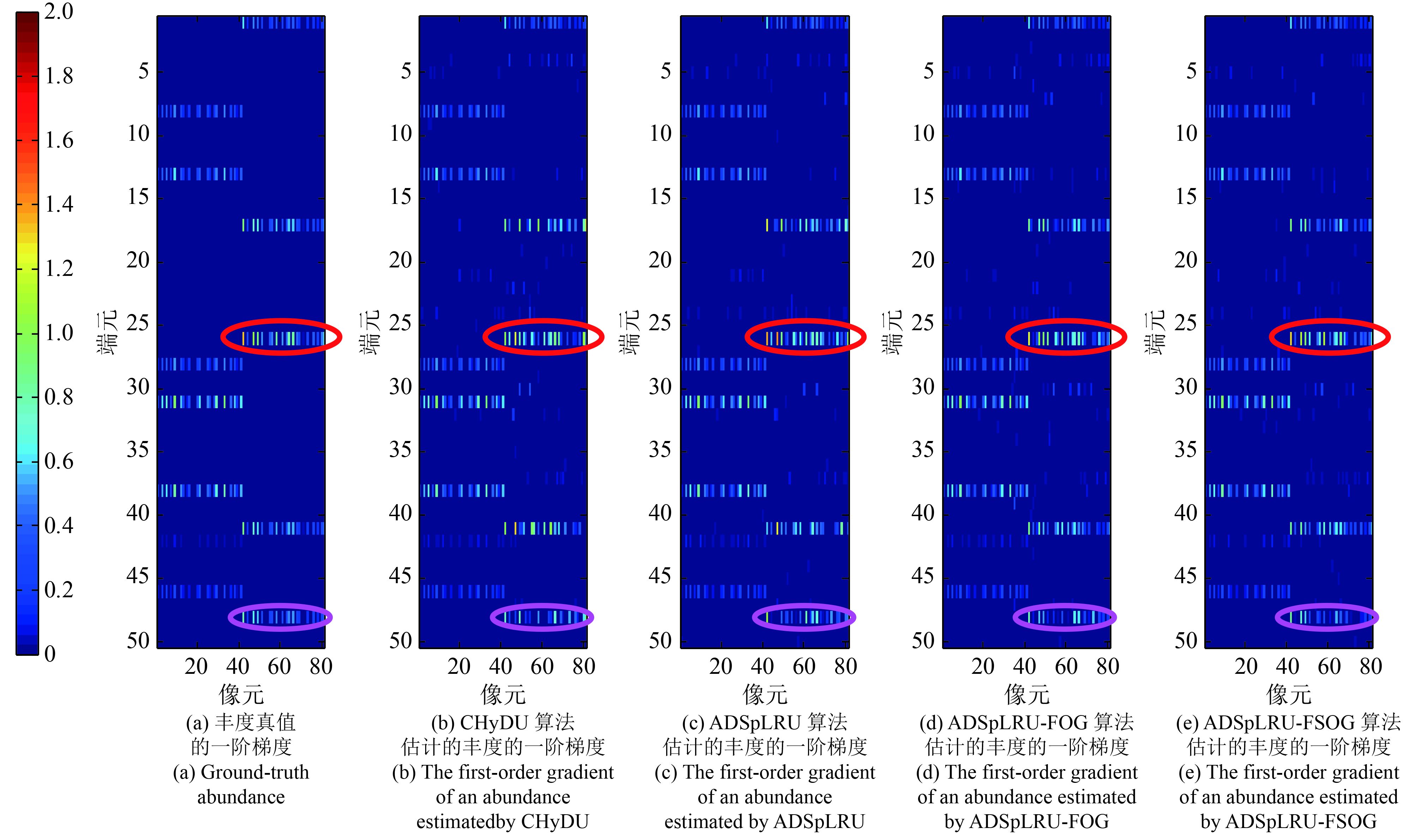
本次实验通过可视化的方法检验改进算法在丰度矩阵估计中的有效性。对仿真库1中由35dB的高斯白噪声干扰的仿真数据进行丰度估计的结果如图7所示。图8是图7的各个子图的一阶梯度。图9是图7的各个子图的二阶梯度。各子图与相应的真值图的相似性结果如表3所示。例如:行“图7”,列“SREs(子图(a),子图(b))”的值18.4922, 表示度量图7(a)与图7(b)相似度的SREs值是18.4922。颜色栏反映了颜色与丰度值之间的对应关系。值得注意的是:在本实验中,有的丰度梯度图最大值是2,有的丰度梯度的最大值是1.5。在显示过程中,前者数值为2的区域与后者数值为1.5的区域的可视化效果相同。为了更好的与真值进行可视化地比较并凸出视觉差异,将所有的丰度的一阶梯度数据(含真值数据)统一进行归一化处理,处理后的数据范围是[0, 2],并得到图8所示的效果。按照同样的方法处理所有丰度的二阶梯度得到如图9所示的效果。此外, 为了凸显差异, 采用椭圆形在图7、图8、图9中的部分差异区域进行了标记。图7、图8、图9和表3表明:ADSpLRU-FOG算法能保持一阶梯度信息并改善传统稀疏低秩的丰度矩阵估计的效果;ADSpLRU-FSOG算法能进一步地较好地保持数据的一阶梯度和二阶梯度信息,改善丰度矩阵的估计效果。此外,对比图7(c),图7(d)和图7(e)的标记区域发现:图7(e)的细节信息比图7(d)的细节信息丰富;图7(d)的细节信息比图7(c)的细节信息丰富。由此说明ADSpLRU-FSOG算法比ADSpLRU-FOG算法提供更多的细节信息;ADSpLRU-FOG算法比ADSpLRU算法提供更多的细节信息。
5.4.2 基于实际光谱库(Urban)的可视化实验
本实验在实际光谱库1-Urban开展的可视化实验。根据5.5.1节介绍的实验方法采用四种不同的算法估计地物“草地”的丰度并进一步提取其一阶梯度和二阶梯度(图10)。图10(b)是图10(a)的各子图的一阶梯度。图10(c)是图10(a)的各子图的二阶梯度。各子图与可视作真值的参考图进行比较得到如表4所示结果。该图与表4表明:DSpLRU-FOG算法能保持一阶梯度信息,改善传统稀疏低秩的丰度矩阵估计的效果;ADSpLRU-FSOG算法能保持较多的一阶梯度和二阶梯度信息,提高丰度估计精度。
总之,上述两个可视化实验说明:在梯度信息较丰富的情况下,ADSpLRU-FSOG算法能够保持数据的一阶梯度和二阶梯度结构,改善丰度的估计效果。分析其原因是:CHyDU算法通过字典学习实现去噪,ADSpLRU通过稀疏低秩实现去噪,这种去噪过程都会模糊图像边缘,而ADSpLRU-FOG算法和ADSpLRU-FSOG算法通过增加梯度约束的方法,在去噪的同时尽量减弱去噪给图像边缘模糊带来的影响。使得丰度估计效果较好。
5.5 实际高光谱图像的实验
本节对实际高光谱数据1(Urban库)和实际高光谱数据2(Jasper Ridge库)开展丰度估计实验。比较ADSpLRU-FSOG算法与ADSpLRU算法(Giampouras 等,2016),ADSpLRU-FOG算法(袁静 等,2018)和CHyDU算法(Yang J,2016)的丰度估计效果。同时,为了评价ADSpLRU-FSOG算法,在实际光谱实验中增加了融合二阶梯度的交替方向稀疏低秩解混算法ADSpLRU-SOG(Alternating Direction Sparse and Low-Rank UnMixi-ng With Second-Order Gradient)。该算法是ADSpLRU-FSOG算法的特例,仅考虑了二阶梯度信息,未关注一阶梯度信息。
5.5.1 实际光谱数据1- Urban
针对实际光谱数据1的实验过程如下:将其划分为若干个3×3
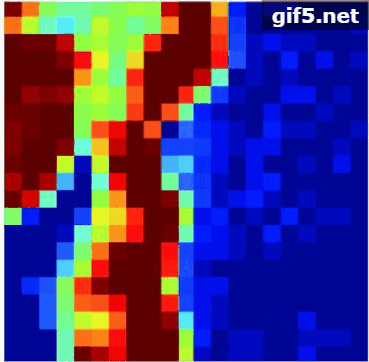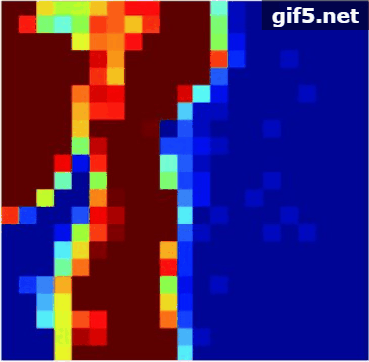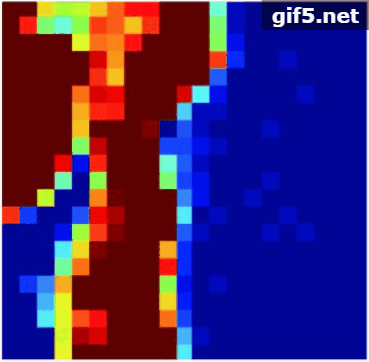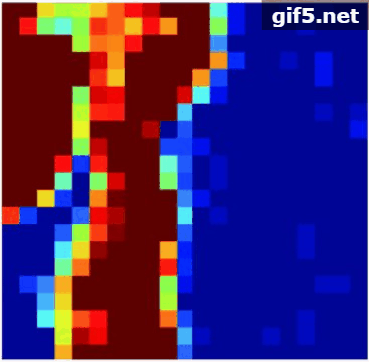
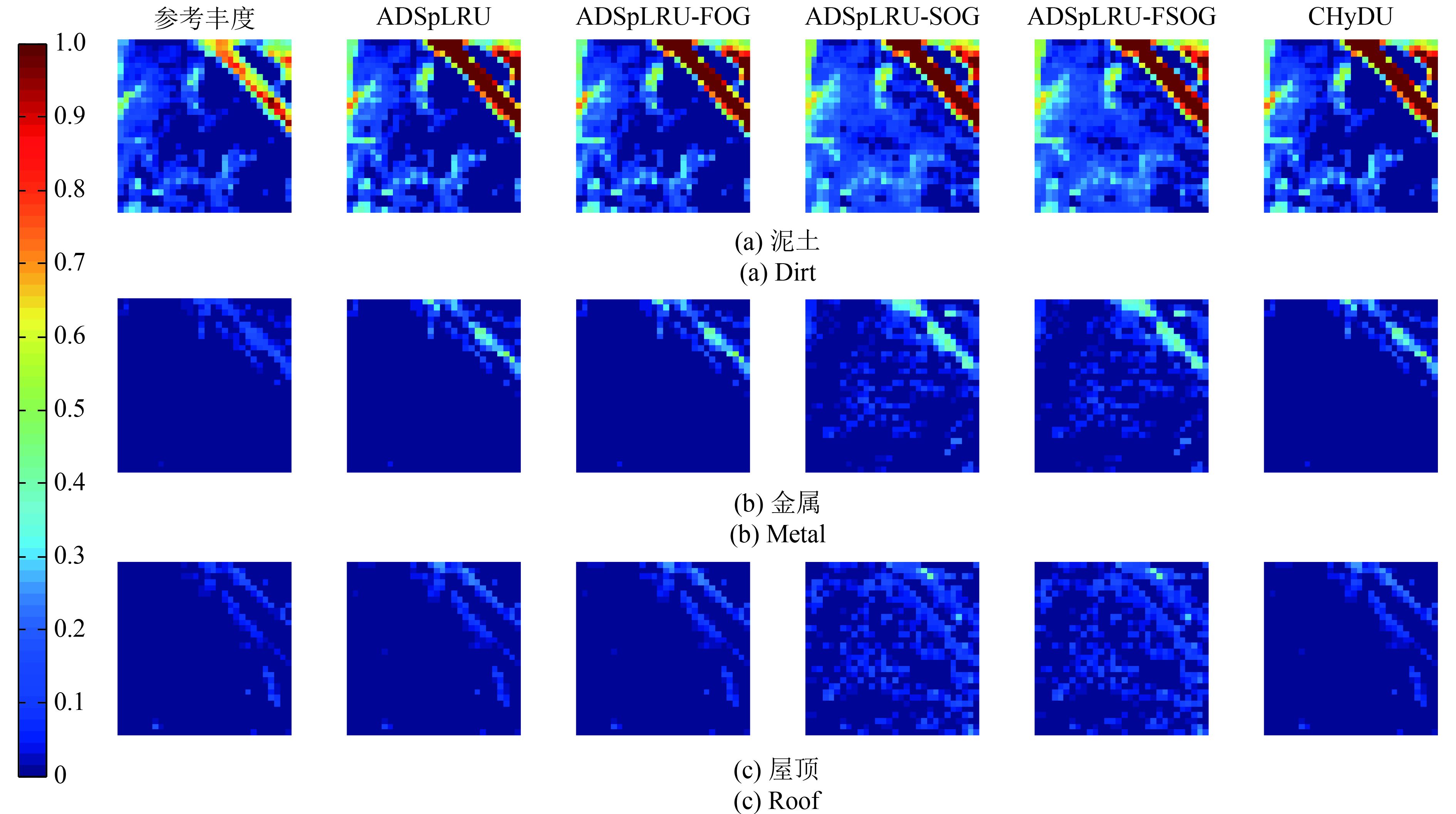
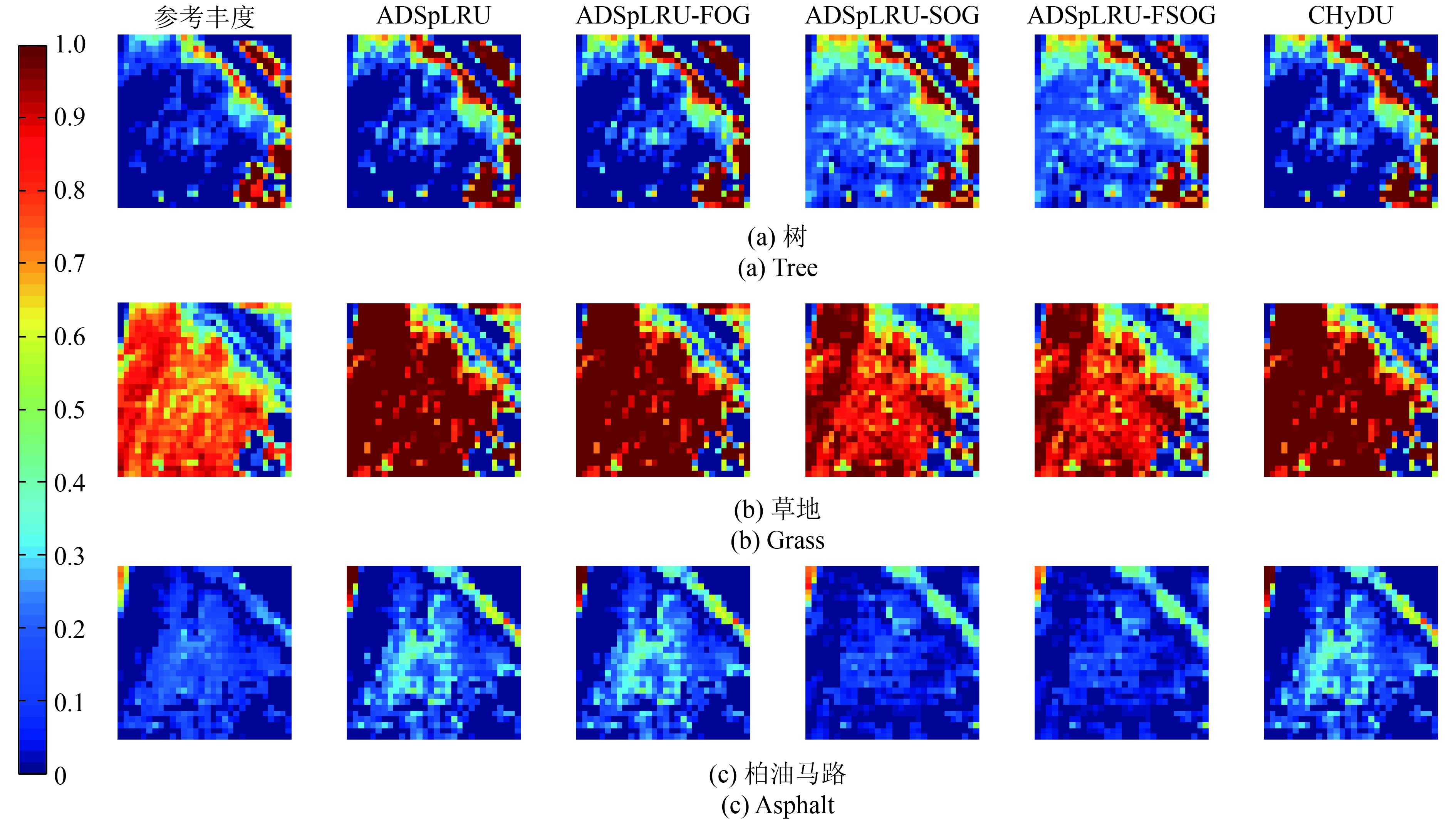
 的子区域,分别采用ADSpLRU-FSOG算法、ADSpLRU-FOG算法和ADSpLRU-SOG算法估计每个子区域的丰度;而CHyDU算法,是全局算法,通过对整个光谱数据1进行估计得到其丰度。最后,与Zhu(2014)提供的参考丰度进行对比。其参数设置如表2所示。丰度估计结果如表5所示。表中的总SRE直接通过式(34)计算得到。丰度估计效果如图11,图12所示。每行的第1列是(Zhu等,2014b)提供的Urban数据的参考丰度。
的子区域,分别采用ADSpLRU-FSOG算法、ADSpLRU-FOG算法和ADSpLRU-SOG算法估计每个子区域的丰度;而CHyDU算法,是全局算法,通过对整个光谱数据1进行估计得到其丰度。最后,与Zhu(2014)提供的参考丰度进行对比。其参数设置如表2所示。丰度估计结果如表5所示。表中的总SRE直接通过式(34)计算得到。丰度估计效果如图11,图12所示。每行的第1列是(Zhu等,2014b)提供的Urban数据的参考丰度。
表 5 基于Urban光谱图像库的丰度矩阵估计效果
Table 5 SRE for different estimated Abundance on Urban
| 端元 | 算法 | ||||
| ADSpLRU | ADSpLRU-FOG | ADSpLRU-SOG | ADSpLRU-FSOG | CHyDU | |
| SREs-泥土 | 12.3550 | 12.3630 | 12.1184 | 12.1484 | 12.2927 |
| SREs-金属 | 8.5381 | 8.5206 | 2.7131 | 2.7431 | 8.6976 |
| SREs-屋顶 | 13.7000 | 13.6967 | 3.2755 | 3.2755 | 13.6693 |
| SREs-树 | 14.4755 | 14.4853 | 13.7234 | 13.8234 | 14.4735 |
| SREs-草地 | 15.9218 | 15.9232 | 22.6132 | 22.6432 | 15.9148 |
| SREs-柏油马路 | 13.4621 | 13.5224 | 13.1193 | 13.1493 | 13.8140 |
| SRE | 15.1106 | 15.1214 | 16.2549 | 17.1970 | 15.1152 |
| 注: 斜体表示丰度估计效果最佳的数据。 | |||||
通过表5和图12(b)可见:ADSpLRU-FSOG算法估计地物“草地”的丰度的精度优于其他算法。从图12(b)可见该图内部含有丰富的梯度信息。从图11(b), 图11(c)中发现该区域的地物“金属”和“屋顶”的丰度较少,且梯度变化极小。因此,ADSpLRU-FSOG算法对这种地物的估计效果与其他算法相比较差,究其原因是这些地物的梯度变化信息较少,容易将噪声视作梯度信息保留下来。总之,在该实验数据上ADSpLRU-FSOG算法对丰度存在明显梯度变化的地物进行丰度估计,效果较好。
5.5.2 实际光谱数据2- Jasper Ridge
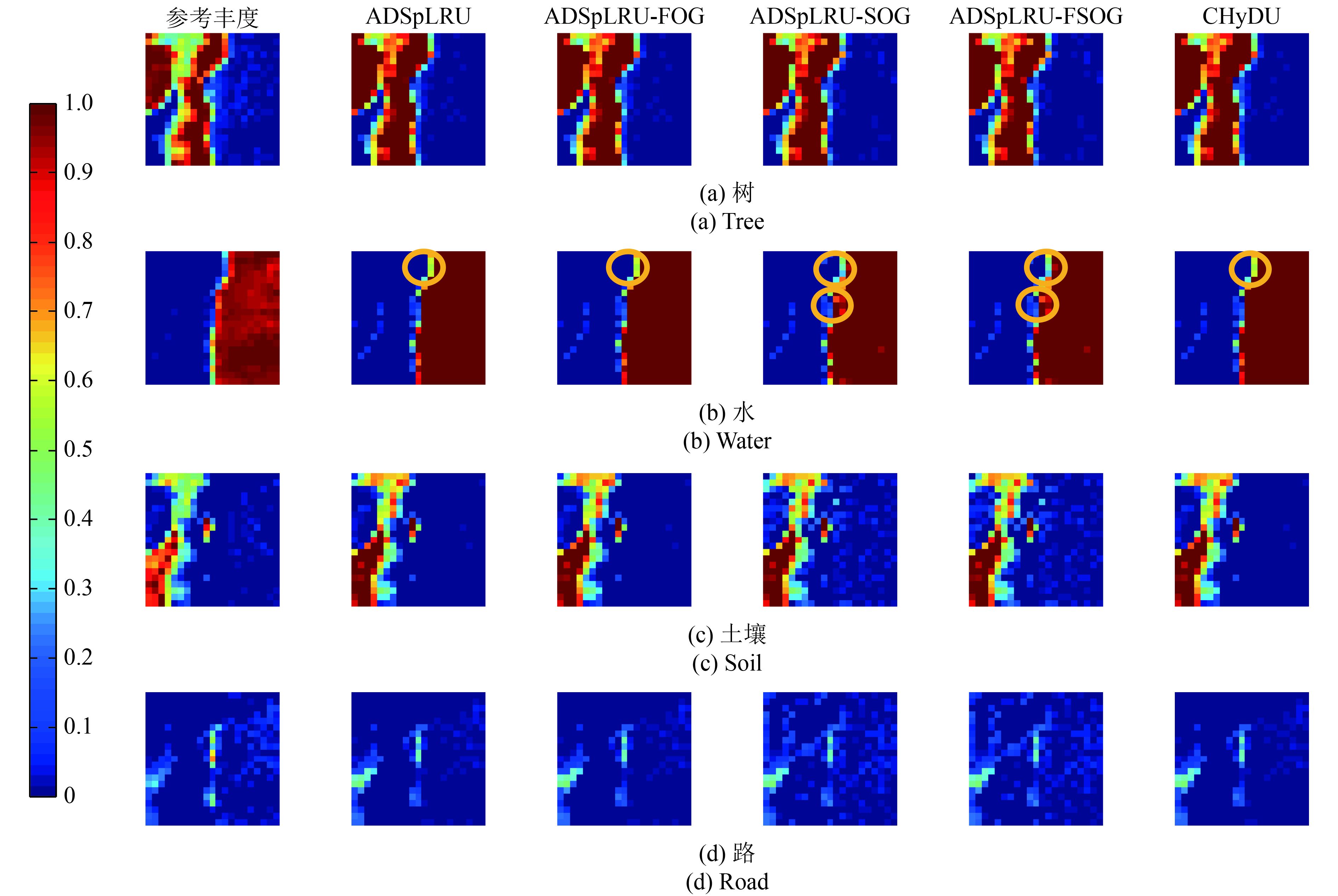
针对实际光谱数据2,采用5.5.1节的实验方法进行丰度估计实验(表6)。图13给出四种不同地物丰度的可视化估计结果。ADSpLRU-FSOG算法与ADSpLRU-FOG算法的丰度估计效果可视化效果不够明显,为了突出差异,部分差异用椭圆形已经圈出。通过表6和图13可见:ADSpLRU-FSOG算法在地物“树木”和“水”的丰度估计较好。ADSpLRU-FOG算法在地物“土壤”和“道路”的丰度估计效果该库上的丰度估计的总体效果较好于其他算法。其中ADSpLRU-FSOG算法估计土壤和道路的丰度中叠加了若干噪声。分析其原因:CHyDU(Yang等,2016)算法和ADSpLRU算法(Giampouras 等,2016)均存在去噪能力,容易滤除其内部梯度信息,易模糊该端元丰度图的边缘。ADSpLRU-FOG算法(袁静 等,2018),ADSpLRU-SOG算法,ADSpLRU-FSOG算法通过梯度信息弱化了去噪带来的边缘模糊的情况。ADSpLRU-FSOG算法通过增加一阶梯度约束和二阶梯度约束进一步强化局部细节,能够提高丰度估计精度,但容易带来额外的噪声。
表 6 基于Jasper Ridge光谱图像库的丰度矩阵估计效果
Table 6 SRE For different estimated abundance on Jasper Ridge
| 端元 | 算法 | ||||
| ADSpLRU | ADSpLRU-FOG | ADSpLRU-SOG | ADSpLRU-FSOG | CHyDU | |
| SREs-树 | 18.5032 | 18.5062 | 19.1972 | 19.1981 | 18.5046 |
| SREs-水 | 18.3662 | 18.3720 | 20.9012 | 20.9021 | 18.3771 |
| SREs-土壤 | 20.6450 | 20.6481 | 19.9209 | 19.9198 | 20.6457 |
| SREs-路 | 17.2642 | 17.2723 | 15.4373 | 16.4385 | 17.2207 |
| SRE | 18.6509 | 18.6602 | 20.2815 | 20.2983 | 18.6699 |
| 注: 黑斜体表示丰度估计效果最佳的数据。 | |||||
6 结 论
本文首先从数学理论上证明了将一阶梯度差异和二阶梯度差异项添加到带约束的线性回归模型中是有效的。其次利用该信息改进稀疏低秩丰度估计算法模型,推导出采用sylvester方程求解新模型的方法。通过实验证明了当光谱数据空间维的梯度信息较丰富时,融合数据内部变化信息差异的丰度估计能够改进收敛效果,保持一阶梯度和二阶梯度信息,较好地提高丰度估计的精度,改善抗噪性能。但当梯度信息太少时,容易受到噪声干扰。如何改善该情况将是下一步研究的主要内容。同时,按照同样的思路,三阶梯度以及更高阶梯度信息的加入给稀疏低秩丰度矩阵估计带来的影响将是未来研究的主要方向之一。
志 谢 本研究部分实验和数据得到希腊国家天文台的空间应用与遥感研究所(IAASARS)的Paris V.Giampouras的帮助和指导。
参考文献(References)
-
Babacan S D, Luessi M, Molina R and Katsaggelos A K. 2012. Sparse Bayesian methods for low-rank matrix estimation. IEEE Transactions on Signal Processing, 60 (8): 3964–3977. [DOI: 10.1109/TSP.2012.2197748]
-
Bach F R. 2008. Consistency of trace norm minimization. The Journal of Machine Learning Research, 9 : 1019–1048.
-
Bioucas-Dias J M, Plaza A, Dobigeon N, Parente M, Du Q, Gader P and Chanussot J. 2012. Hyperspectral unmixing overview: geometrical, statistical, and sparse regression-based approaches. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 5 (2): 354–379. [DOI: 10.1109/JSTARS.2012.2194696]
-
Boyd S, Parikh N, Chu E, Peleato B and Eckstein J. 2011. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine Learning, 3 (1): 1–122. [DOI: 10.1561/2200000016]
-
Candès E J, Romberg J and Tao T. 2006. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 52 (2): 489–509. [DOI: 10.1109/TIT.2005.862083]
-
Chen F and Zhang Y. 2013. Sparse hyperspectral unmixing based on constrained Lp-L2 optimization . IEEE Geoscience and Remote Sensing Letters, 10 (5): 1142–1146. [DOI: 10.1109/LGRS.2012.2232901]
-
Chen L S and Huang J Z. 2012. Sparse reduced-rank regression for simultaneous dimension reduction and variable selection. Journal of the American Statistical Association, 107 (500): 1533–1545. [DOI: 10.1080/01621459.2012.734178]
-
Clark R N, Swayze G A, Wise R, Livo E, Hoefen T, Kokaly R F and Sutley S J. 2007. USGS digital spectral library splib06a. Reston, VA: U. S. Geological Survey
-
Feng R Y, Zhong Y F and Zhang L P. 2016. Adaptive spatial regularization sparse unmixing strategy based on joint MAP for hyperspectral remote sensing imagery. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 9 (12): 5791–5805. [DOI: 10.1109/JSTARS.2016.2570947]
-
Giampouras P V, Themelis K E, Rontogiannis A A and Koutroumbas K D. 2016. Simultaneously sparse and low-rank abundance matrix estimation for hyperspectral image unmixing. IEEE Transactions on Geoscience and Remote Sensing, 54 (8): 4775–4789. [DOI: 10.1109/TGRS.2016.2551327]
-
Golbabaee M and Vandergheynst P. 2012. Compressed sensing of simultaneous low-rank and joint-sparse matrices. eprint arXiv: 1211. 5058
-
Iordache M D, Bioucas-Dias J M and Plaza A. 2011. Sparse unmixing of hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing, 49 (6): 2014–2039. [DOI: 10.1109/TGRS.2010.2098413]
-
Iordache M D, Bioucas-Dias J M and Plaza A. 2012. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 50 (11): 4484–4502. [DOI: 10.1109/TGRS.2012.2191590]
-
Iordache M D, Bioucas-Dias J M and Plaza A. 2014. Collaborative sparse regression for hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 52 (1): 341–354. [DOI: 10.1109/TGRS.2013.2240001]
-
Lu T X. 1986. Solution of the matrix equation AX-XB = C. Computing, 37 (4): 351–355. [DOI: 10.1007/BF02251092]
-
Negahban S and Wainwright M J. 2011. Estimation of (near) low-rank matrices with noise and high-dimensional scaling. The Annals of Statistics, 39 (2): 1069–1097. [DOI: 10.1214/10-AOS850]
-
Oymak S, Jalali A, Fazel M, Eldar Y C and Hassibi B. 2015. Simultaneously structured models with application to sparse and low-rank matrices. IEEE Transactions on Information Theory, 61 (5): 2886–2908. [DOI: 10.1109/TIT.2015.2401574]
-
Qian Y T, Jia S, Zhou J and Robles-Kelly A. 2011. Hyperspectral unmixing via L1/2 sparsity-constrained nonnegative matrix factorization . IEEE Transactions on Geoscience and Remote Sensing, 49 (11): 4282–4297. [DOI: 10.1109/TGRS.2011.2144605]
-
Qu Q, Nasrabadi N M and Tran T D. 2014. Abundance estimation for bilinear mixture models via joint sparse and low-rank representation. IEEE Transactions on Geoscience and Remote Sensing, 52 (7): 4404–4423. [DOI: 10.1109/TGRS.2013.2281981]
-
Richard E, Obozinski G and Vert J P. 2014. Tight convex relaxations for sparse matrix factorization//Advances in Neural Information Processing Systems 27. Montreal, Canada: Curran Associates, Inc.: 3284-3292
-
Richard E, Savalle P A and Vayatis N. 2012. Estimation of simultaneously sparse and low rank matrices//Proceedings of the 29th International Conference on International Conference on Machine Learning. Edinburgh, Scotland: ACM: 51-58
-
Rontogiannis A A, Themelis K, Sykioti O and Koutroumbas K. 2013. A fast variational Bayes algorithm for sparse semi-supervised unmixing of OMEGA/Mars Express data//2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing. Gainesville, FL, USA: IEEE: 1-4 [DOI: 10.1109/WHISPERS.2013.8080749]
-
Rosin P L. 2001. Robust pixel unmixing. IEEE Transactions on Geoscience and Remote Sensing, 39 (9): 1978–1983. [DOI: 10.1109/36.951088]
-
Sigurdsson J, Ulfarsson M O and Sveinsson J R. 2014. Hyperspectral unmixing with Lq regularization . IEEE Transactions on Geoscience and Remote Sensing, 52 (11): 6793–6806. [DOI: 10.1109/TGRS.2014.2303155]
-
Sun L, Jeon B, Zheng Y H and Chen Y J. 2016. Hyperspectral unmixing based on L1-L2 sparsity and total variation//2016 IEEE International Conference on Image Processing. Phoenix, AZ, USA: IEEE: 4349-4353 [DOI: 10.1109/lelP.2016.7533181]
-
Tang W, Shi Z W and Duren Z. 2014. Sparse hyperspectral unmixing using an approximate L0 norm . Optik, 125 (1): 31–38. [DOI: 10.1016/j.ijleo.2013.06.073]
-
Themelis K E, Rontogiannis A A and Koutroumbas K. 2010. Semi-supervised hyperspectral unmixing via the weighted lasso//IEEE International Conference on Acoustics, Speech, and Signal Processing. Dallas, Texas, USA: IEEE : 1194–1197. [DOI: 10.1109/ICASSP.2010.5495385]
-
Themelis K E, Rontogiannis A A and Koutroumbas K D. 2012. A novel hierarchical Bayesian approach for sparse semisupervised hyperspectral unmixing. IEEE Transactions on Signal Processing, 60 (2): 585–599. [DOI: 10.1109/TSP.2011.2174052]
-
Yang J X, Zhao Y Q, Chan J C W and Kong S G. 2016. Coupled sparse denoising and unmixing with low-rank constraint for hyperspectral image. IEEE Transactions on Geoscience and Remote Sensing, 54 (3): 1818–1833. [DOI: 10.1109/TGRS.2015.2489218]
-
Yi C, Zhao Y Q, Yang J X, Chan J C W and Kong S G. 2017. Joint hyperspectral superresolution and unmixing with interactive feedback. IEEE Transactions on Geoscience and Remote Sensing, 55 (7): 3823–3834. [DOI: 10.1109/TGRS.2017.2681721]
-
Yuan J and Zhang Y J. 2017. Application of sparse denoising auto encoder network with gradient difference information for abnormal action detection. Acta Automatica Sinica, 43 (4): 604–610. [DOI: 10.16383/j.aas.2017.c150667] ( 袁静, 章毓晋. 2017. 融合梯度差信息的稀疏去噪自编码网络在异常行为检测中的应用. 自动化学报, 43 (4): 604–610. [DOI: 10.16383/j.aas.2017.c150667] )
-
Yuan J, Zhang Y J and Yang D H. 2018. Sparse and low-rank abundance estimation with structural information. Journal of Infrared and Millimeter Waves, 37 (2): 144–153. ( 袁静, 章毓晋, 杨德贺. 2018. 融入结构信息的稀疏低秩丰度估计在光谱解混中的应用. 红外与毫米波学报, 37 (2): 144–153. )
-
Zhang X D. 2013. Matrix Analysis and Applications. 2nd ed. Beijing: Tsinghua University Press: 44 (张贤达. 2013. 矩阵分析与应用. 2版. 北京: 清华大学出版社: 44)
-
Zhu F Y, Wang Y, Fan B, Xiang S M, Meng G F and Pan C H. 2014a. Spectral unmixing via data-guided sparsity. IEEE Transactions on Image Processing, 23 (12): 5412–5427. [DOI: 10.1109/TIP.2014.2363423]
-
Zhu F Y, Wang Y, Fan B, Meng G F and Pan C H. 2014b. Effective spectral unmixing via robust representation and learning-based sparsity. eprint arXiv: 1409. 0685