出版日期: 2019-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20197446
2019 | Volumn23 | Number 4
上一篇 | 下一篇

技术方法

机载WIDAS地表观测的BRDF原型反演算法验证

何丹丹¹ , 焦子锑^1,2 , 董亚冬¹ , 张小宁¹ , 张虎³ , 丁安心¹

1. 北京师范大学地理科学学部遥感科学与工程研究院，北京 100875

2. 遥感科学国家重点实验室北京师范大学，北京 100875

3. 天津师范大学城市与环境学院，天津 300387

收稿日期: 2017-11-16; 预印本: 2018-04-11

基金项目: 国家重点研发计划(编号：2016YFB0501404)；国家自然科学基金(编号：41571326)

第一作者简介: 何丹丹，1992年生，女，硕士研究生，研究方向为定量遥感、地表二向性反射和植被结构参数反演等。E-mail：yimirs@126.com

通信作者简介: 焦子锑，1970年生，男，副教授，研究方向为多角度定量遥感的理论与应用，包括多角度光学遥感的建模、信息提取与应用。E-mail：jiaozt@bnu.edu.cn

摘要

地表反照率表征地面对太阳辐射的反射能力，在地表能量平衡中起着重要的作用。2008年黑河的WATER实验中，针对机载红外广角双模式成像仪(WIDAS)观测角度小的特点，发展了一种基于MODIS二向性反射分布函数(BRDF)原型估算WIDAS反照率的算法。然而，在2012年黑河HiWATER实验中，WIDAS的观测角度范围由早期30°观测天顶角升级为最大观测天顶角52°，这一改造对数据预处理(辐射定标、大气校正和多角度配准)产生影响，使WIDAS数据出现明显的噪声，为WIDAS地表反照率的反演带来新挑战。针对新问题，采用新的地表观测数据，进一步验证了BRDF原型算法反演机载WIDAS反照率的能力。为了获取准实时BRDF先验知识，基于核驱动模型和各向异性平整指数(AFX)首先准实时提取了实验区5种MODIS的BRDF原型；然后，将其作为先验知识应用到黑河WIDAS机载数据的反照率反演中；最后，利用实验区的反照率实测数据进行算法验证。本研究比较了3个算法处理该问题的能力：(1)基于BRDF原型作为先验知识的算法；(2)完全基于核驱动的全反演算法；(3)基于朗伯假设的方法，通过算法对比分析，可更好地分析验证算法(1)的性能。结果表明：(1)BRDF原型算法反演精度最高且稳定，尤其是当观测数据位于垂直主平面时，全反演算法由于缺少大角度观测数据的约束，更容易出现异常值；BRDF原型算法的最大绝对误差为0.034，相对于全反演算法和朗伯假设方法精度分别提高了约18%和71%；(2)针对2012年黑河机载WIDAS观测噪声较大的新问题，BRDF原型反演算法表现出了良好的抗噪声性能。通过对WIDAS反照率反演和验证进一步表明，在多角度观测数据信息量不足以进行全反演，且观测受噪声影响较大时，BRDF原型作为先验知识，提供了一种有效解决该问题的手段，对提高反照率反演的精度、增强反演的稳定性有重要作用。

关键词

遥感, 黑河, MODIS, 机载WIDAS, 核驱动模型, AFX, BRDF原型, 地表反照率

Verification of BRDF archetype inversion algorithm from surface observations of airborne WIDAS

HE Dandan¹ , JIAO Ziti^1,2 , DONG Yadong¹ , ZHANG Xiaoning¹ , ZHANG Hu³ , DING Anxin¹

1.College of Remote Sensing and Engineering, Faculty of Geographical Science, Beijing Normal University, Beijing 100875, China

2.State Key Laboratory of Remote Sensing Science, Beijing Normal University, Beijing 100875, China

3.College of Urban and Environmental Sciences, Tianjin Normal University, Tianjin 300387, China

Abstract

Surface albedo qualifies the proportion of incoming light reflected by the land surface and plays an important role in the earth’s energy budget. In the WATER experiment of Heihe in 2008, we developed an algorithm for estimating the albedo of Wide-angle Infrared Dual-mode line/area Array Scanner (WIDAS) based on the MODIS Bidirectional Reflection Distribution Function (BRDF) archetype-based algorithm for the narrow-angle observations of the airborne WIDAS. However, in the HiWATER experiment in 2012, the WIDAS observation angle range was upgraded from the early 30° to the maximum observation zenith angle of 52°, which impacted the data preprocessing (radiation scaling, atmospheric correction, and multi-angle registration). This condition caused significant noise and created new challenges for the surface albedo inversion of WIDAS. In the current study, we addressed new problems and adopted new surface observation data to verify the ability of the BRDF archetype-based algorithm to retrieve the albedo of WIDAS. To obtain quasi-real-time BRDF prior knowledge, we first extracted five BRDF archetypes as a priori information from 500 m MODIS BRDF parameter product (MCD43A1) within the Heihe experimental region. Then, we applied these BRDF archetypes to airborne WIDAS multi-angular observations for albedo estimates based on the hotspot-corrected linear kernel-driven BRDF model, that is, RossThickChen-LiSparseReciprocal model. Finally, field albedo measurements were conducted to validate the broadband albedo estimates. We compared three commonly used albedo estimate methods, namely, the BRDF archetype-based algorithm that was developed in our previous paper; full-inversion BRDF/albedo algorithm that has been adopted as the operational MODIS BRDF/albedo algorithm; and Lambertian assumption method that is commonly used to estimate surface albedo, especially when only nadir observations are available. The performance of the BRDF archetype-based algorithm was verified by comparison and analysis of the algorithms. Unsurprisingly, the accuracy of the albedo retrievals by using the BRDF archetype-based algorithm was obtained at 0.034, which was 18% and 71% higher than those of the full inversion algorithm and the Lambertian assumption method, respectively. The inversion and verification of the WIDAS demonstrated that the BRDF archetype-based method was noise resistant and obtained stable albedo estimates. Therefore, our previous conclusions were confirmed by using new WIDAS observations. Given the merit of the proposed archetype-based algorithm, we strongly recommend it to the user community, especially for narrow-angle observations that need a priori information for stable retrievals of surface albedo.

Key words

remote sensing, Heihe, MODIS, Wide-angle Infrared Dual-mode line/area Array Scanner (WIDAS), kernel-driven BRDF model, AFX, BRDF archetype, surface albedo

1 引　言

地表反照率是影响地球能量收支平衡的重要参数，被广泛应用于数值天气预报和大气环流模型中(Dickinson，1983)。目前已经有大量的研究将多种区域和全球尺度的地表反照率产品应用于地表能量平衡及全球变化(Lucht等，2000；Schaaf 等，2002；Bacour和Bréon，2005)。因此，获取较高精度的地表反照率对气候的时空变化研究具有重要意义。

目前，反照率的反演中，比较常用的一种方法是通过核驱动模型对多角度数据进行拟合，然后通过核的外推和积分来计算(李小文，1989；Lucht和Lewis，2000；Schaaf 等，2002)。核驱动模型反演地表反照率算法对观测的数量及观测角度分布都有一定的要求(Jin 等，2003)，高分辨数据一般仅能通过某一特定方向获取，并且很难在短时间获取大区域范围的多角度数据，所以这些因素都影响了核驱动模型的反演精度(张虎等，2013)。WOD (Weight Of Determination)表征多角度观测数据在处理过程中对噪声的放大程度，可用来评价多角度数据的空间分布情况，尤其在MODIS质量评价体系得到很好的应用。WOD>2即表明数据质量较差(Jin 等，2003)，而部分WIDAS观测数据的WOD取值甚至可以大于100，关于数据的详细介绍参见2.1。BRDF原型为有效地解决这一问题提供了新途径(Li 等，2001；Jiao 等，2014；Dong 等，2016)。本研究主要目的在于应用2012年新的机载WIDAS飞行和反照率实测数据进行BRDF原型算法的验证，包括其精度、抗噪性和稳定性等。区别于2008年黑河反照率反演工作的主要方面包括数据和方法上的改进(Jiao 等，2015)：(1)2012年机载WIDAS传感器设计为52°视场角，实际飞行观测的有效视场角度为45°，比2008年黑河机载WIDAS传感器的30°视场角有较大的改进，因此，研究这一角度下先验知识应用有其必要性；(2)2012年机载WIDAS多角度数据的预处理过程中(辐射定标、大气校正、大角度数据配准)噪声明显，因此，探索BRDF先验知识的应用对反照率反演的稳定性和精度有重要意义；(3)针对黑河区域在飞行期间的地表各向异性的变化特点，提取该区域的BRDF原型，而不是应用全球尺度全年的BRDF原型。因此，BRDF先验知识更有针对性；(4)采用最新改进的核驱动模型RTCLSR(Ross Thick Chen-Li Sparse Reciprocal)，新模型对某些BRDF特征的拟合能力进一步加强(Bréon 等，2002；Jiao 等，2016)。

针对这些新数据和出现的新问题，本研究对比了3种反照率反演算法，但主要关注和分析基于BRDF原型的反演结果。然后基于地面测量的反照率数据，对反演结果进行了对比与验证。

2 数据与方法

2.1 黑河WIDAS数据

“黑河流域生态—水文过程综合遥感观测联合试验”(HiWATER)是以黑河流域已建立的观测系统以及2007年—2009年开展的“黑河综合遥感联合试验”(WATER)成果为基础，联合多学科、多机构、多项目的科研人员，于2012年—2015年在黑河流域开展的一次卫星和航空遥感及地面观测互相配合的多尺度综合观测试验。

2012年8月1日在黑河上游，利用运12飞机，搭载WIDAS传感器，开展了可见光/近红外、热红外的多角度航空遥感试验。WIDAS系统集成了高分辨率相机一台、可见光/近红外5波段多光谱相机两台(最大视场角50°)和热像仪一台(最大视场角80°)。具体的仪器参数见表1，本研究中仅使用了WIDAS的面阵成像的CCD数据。WIDAS的传感器为广角镜头成像，经过数据的预处理后，可从相邻图像的重叠区域提取同一地物的多角度信息。机载WIDAS能够获取5个可见光波段的7个观测角度的反射率数据，但是，由于缺少大角度下的观测，从而影响了WIDAS多角度数据所包含的信息量。最大设计观测天顶角约为52°，但在大气校正过程中并没有考虑地表各向异性反射特征的影响作用。同时，观测角度的增大，增加了图像配准的难度，这些因素对多角度数据噪声产生较大影响。

表 1 黑河WIDAS主要性能参数
Table 1 Parameters of the Heihe WIDAS data

下载CSV

参数	CCD相机	热红外相机
像元数	1360×1024	320×240
波段设置	460 nm、555 nm、620 nm、685 nm、760 nm	8—12 μm
视场角/°	50°	80°
分辨率/m	0.5 m	5 m
可提取的观测角度	前向52°到后向52°之间的7个角度	前向46°到后向46°之间的7个角度

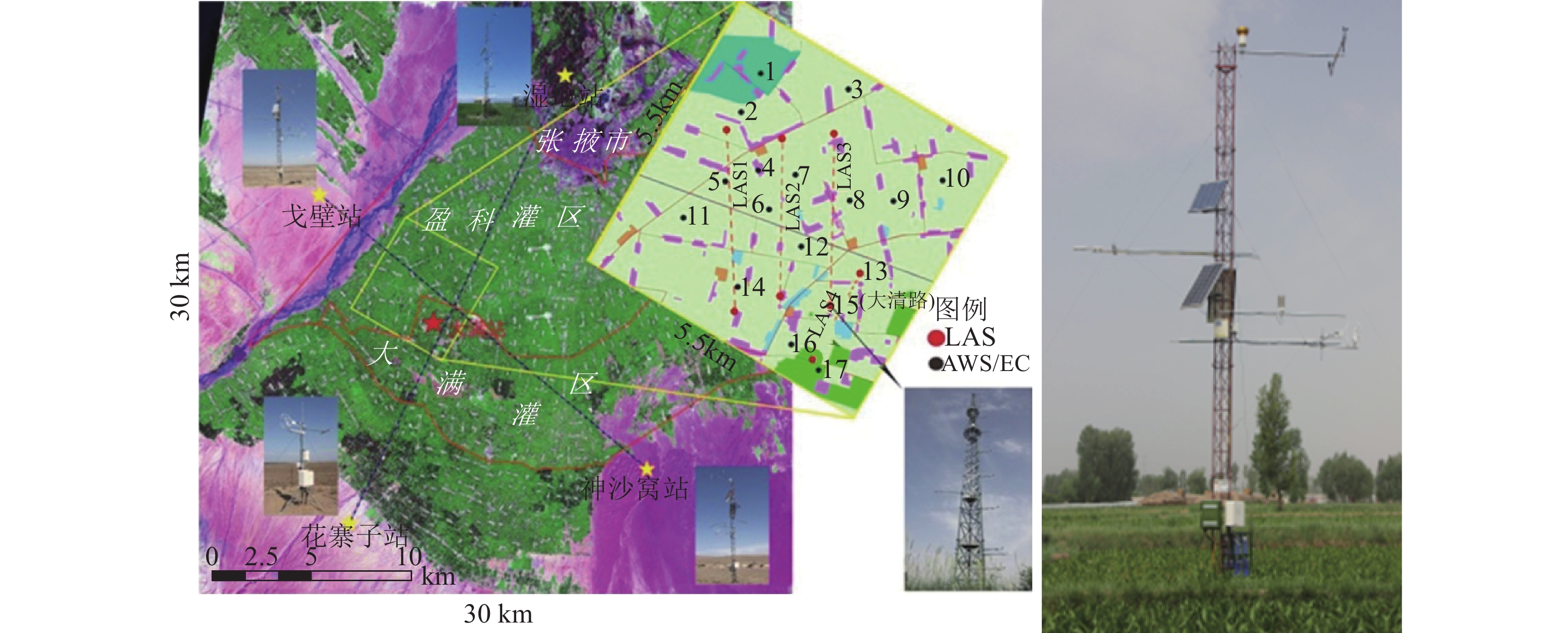
研究区航空遥感试验飞行区域分布图如图1(李新等，2012)，该流域位于97.1°E—102.0°E和37.7°N—42.7°N。关于研究区的飞行数据的具体信息可以参考寒区旱区科学数据中心网站(http://westdc.westgis.ac.cn/hiwater[2017-11-16])。同时，地面观测实验还提供了一些与飞行同步的地表反照率表测量的数据。这些数据可用于WIDAS地表反照率的验证。

图 1 航空遥感试验飞行区域分布图(李新等，2012)

Fig. 1 Map of the aerial remote sensing experimental flight area over the Heihe River Basin(Li et al.，2012)

2.2 核驱动模型

核驱动模型常用来从多角度观测数据反演地表反照率，它是用一定物理意义的核的线性组合来表述地表的二向性反射特征。对于地表的一个非朗伯像元，其表面散射可以表示为各向同性散射，体散射和几何光学散射3种组分的加权和的形式(Nicodemus 等，1977；Li 等，1999；Lucht 等，2000；Liu 等，2013)

$\begin{gathered} R\left({{\theta _i}, {\theta _v}, \varphi,{\textit{λ}} } \right) = {f_{{\rm{iso}}}}\left({\textit{λ}} \right) + {f_{{\rm{vol}}}}\left({\textit{λ}} \right){K_{{\rm{vol}}}}\left({{\theta _i}, {\theta _v}, \varphi } \right) + \\ {f_{{\rm{geo}}}}\left({\textit{λ}} \right){K_{{\rm{geo}}}}\left({{\theta _i}, {\theta _v}, \varphi } \right) \\ \end{gathered} $

(1)

式中，R为太阳天顶角θ_i、观测天顶角θ_v和相对方位角φ处的方向反射率；K_vol为体散射核，K_geo为几何光学核，它们都是入射角和观测角的函数，在R中所占的比例通过f_geo和f_vol来控制，f_iso用来表示各向同性散射在R中的贡献。本文使用的全反演算法就是核驱动模型，首先利用线性回归的方法，反演出拟合观测数据最优的f_iso，f_vol和f_geo等3个权重，然后通过核的积分与3个参数的权重，求出黑天空和白天空的反照率，也可以通过内插或外推求任意光线入射角和观测角的二向反射。

选用的体散射核和几何光学核为热点改进的罗斯厚核(RossThickChen)(Chen和Cihlar，1997；董亚冬等，2014)和李氏稀疏互易核(LiSparseR)(Wanner 等，1995)。因为这些核只是作为观测与太阳角度的函数，计算反照率时，核的积分可以预先求出。

2.3 反演算法

AFX(Anisotropic Flat Index)是基于核驱动模型构造的角度指数，定义为白天空反照率和地表各向同性参数f_iso的比，结合式(1)化简为(焦子锑等，2011；Jiao 等，2012, 2014)

${\rm{AFX}} = 1 + \frac{{{f_{{\rm{vol}}}}\left({\textit{λ}} \right)}}{{{f_{{\rm{iso}}}}\left(\lambda \right)}}{H_{\ker \_{\rm{vol}}}} + \frac{{{f_{{\rm{geo}}}}\left({\textit{λ}}\right)}}{{{f_{{\rm{iso}}}}\left({\textit{λ}} \right)}}{H_{\ker \_{\rm{geo}}}}$

(2)

式中，H_{ker_vol}，H_{ker_geo}为体散射核和几何光学核的双半球积分值，分别为0.189184和－1.377622。从式(2)可以看出，AFX是被各向同性参数标准化的几何光学权重参数和体散射权重参数与两个核的积分的线性表达式。

AFX<1表示几何光学散射类型主导，指示着一个屋顶状的BRDF形状；AFX>1表示体散射类型主导，指示着一个碗状的BRDF形状；否则，AFX≈1，指示一个较平的BRDF形状(Jiao 等，2014)。研究表明AFX较好地表征地表基本散射类型的变化，可由模型3个参数直接求得AFX，并以此作为分类指标建立BRDF原型，用来表征地表BRDF形状的变化。

参考Jiao等(2014)提出的BRDF原型的建立方法，针对黑河区域的地表各向异性变化特点，采用MODIS的BRDF参数(MCD43A1)数据，首先提取了相应的BRDF原型，具体参数信息如表2所示，其中 $F_{{\rm{iso}}}'$ 、 $F_{{\rm{vol}}}'$ 和 $F_{{\rm{geo}}}'$ 为标准化的模型参数。由表2可以看出，相对于全球BRDF原型的变化，针对黑河地区的某些BRDF原型变化范围较为集中，因此，这些BRDF原型用作针对黑河区域的机载WIDAS数据的先验知识，相对于全球BRDF原型的变化，期待会有更好的约束效果。因此，将基于这些原型，采用原型反演算法对WIDAS的反照率数据进行反演，这是针对新的WIDAS机载数据，应用新的BRDF原型作为先验知识，对原型算法的进一步检验(Jiao 等，2015)。

表 2 红和近红外波段5种BRDF原型参数
Table 2 The AFX and the five BRDF archetypal parameters for the red and NIR bands

下载CSV

波段	类别	AFX_mean	ƒ_iso	ƒ_vol	ƒ_geo	F_isoˊ	F_volˊ	F_geoˊ
红波段	R1	0.5611	0.1343	0.0211	0.0454	0.5	0.0785	0.1690
	R2	0.6754	0.1667	0.0532	0.0465	0.5	0.1595	0.1395
	R3	0.7736	0.1671	0.0717	0.0373	0.5	0.2146	0.1116
	R4	0.9076	0.1389	0.0819	0.0214	0.5	0.2947	0.0769
	R5	1.1918	0.0875	0.1097	0.0038	0.5	0.6267	0.0218
近红外波段	N1	0.7680	0.3076	0.1662	0.0750	0.5	0.2701	0.1219
	N2	0.9012	0.3100	0.1816	0.0471	0.5	0.2929	0.0760
	N3	0.9942	0.3202	0.2010	0.0289	0.5	0.3139	0.0451
	N4	1.0923	0.3411	0.2583	0.0126	0.5	0.3787	0.0184
	N5	1.1862	0.3276	0.3217	0.0011	0.5	0.4909	0.0017

作为比较，采用3种算法：(1)是基于核驱动模型的全反演算法，详见2.2节；(2)是基于朗伯假设算法，即以天顶方向的反射率代替反照率，该方法尤其是对于缺少多角度观测数据时，常常被直接采用；(3)是基于核驱动模型，采用BRDF原型作为先验知识的反演算法。反演过程如下：假定一组有n个观测的多角度观测数据B， ${{B}} = {\rho _0}\left( {\varOmega _{i, 0}, \varOmega _{r, 0}} \right),$ $ {\rho _1}\left( {\varOmega _{i, 1}, \varOmega _{r, 1}} \right), \cdots , {\rho _{n-1}}(\varOmega _{i, n-1}, \varOmega _{r, n-1})$ ，假设已知与其对应的BRDF原型为BRDF′，它在数据B的观测位置对应的原型反射率数据为 $B'$ , $B'\!\! =\! \!{\rho _0'}\left( {\varOmega _{i, 0}, \varOmega _{r, 0}} \right), {\rho _1'}\left( {\varOmega _{i, 1}, \varOmega _{r, 1}}\! \right), \cdots\! , \rho _{n - 1}'(\varOmega _{i, n-1} , \varOmega _{r, n-1} \!)$

求调整系数a，通过平移BRDF原型，使得B和aB′的差异最小。采用最小二乘拟合法，最小化拟合误差e²可表示为

${e^2} = {\sum\limits_{i = 0}^{n - 1} {\left({{\rho _i} - a{\rho _i}} \right)} ^2}$

(3)

从而得到调整系数a

$a = \frac{{\sum\limits_{j = 0}^{n - 1} {{\rho _j}\cdot{\rho _j}'} }}{{\sum\limits_{j = 0}^{n - 1} {{{\left({{\rho _j}'} \right)}^2}} }}$

(4)

这样，数据B的BRDF就可以表示为

${\rm{BRDF}} = a \cdot {\rm{BRDF}}'$

(5)

拟合误差RMSE可以表示为

${\rm{RMSE}} = \sqrt {\frac{1}{{n - 1}}\sum\limits_{k = 0}^{n - 1} {{{\left({{\rho _k} - a{\rho _k}'} \right)}^2}} } $

(6)

得到RMSE最小的BRDF原型作为数据的先验BRDF；然后，通过式(4)确定调整系数a；最后，黑天空BSA和白天空WSA反照率与选定的最优原型的黑天空BSA′和白天空WSA′反照率之间的关系可以表示为

${\rm{BSA}}\left({\theta, {\textit{λ}} } \right) = a \cdot {\rm{BSA}}'\left({\theta,{\textit{λ}}} \right) = a\sum\limits_k {{F_k}} {h_k}\left(\theta \right)$

(7)

${\rm{WSA}}\left({\textit{λ}} \right) = a\cdot{\rm{WSA}}'\left({\theta,{\textit{λ}} } \right) = a\sum\limits_k {\left({{F_k}\left({\textit{λ}}\right){H_k}} \right)} $

(8)

式中， ${h_k}\left( \theta \right)$ 是相应的核在观测半球的积分值，它们是太阳天顶角的函数；H_k是核在入射和观测半球的积分值。RossThickChen和LiSparseR对应的在双半球空间的积分值分别是0.189184和−1.377622。

将每个波段的5种BRDF原型分别拟合WIDAS相应波段的多角度数据，将拟合误差RMSE最小的BRDF原型作为先验知识，最后得到WIDAS多角度数据的地表反照率。上述方法得到的地表照率为波谱反照率，为得到真实地表宽波段反照率，利用了黑河综合遥感联合实验采集的103条典型地物连续波谱，根据MODTRAN模拟的下行辐射计算，然后，生成这些波段数据的统计信息并建立线性的波段转换系数(Liang，2001；Li 等，2009)，转换公式如式(9)

${\alpha _{{\rm{short}}}} = - 0.6678{\alpha _1} + 0.7649{\alpha _2} + 0.2691{\alpha _3} + 0.4667{\alpha _4}$

(9)

式中，α₁、α₂、α₃和α₄分别为蓝、绿、红和近红外波段的波谱反照率。

3 结果与分析

3.1 WIDAS反照率对比分析

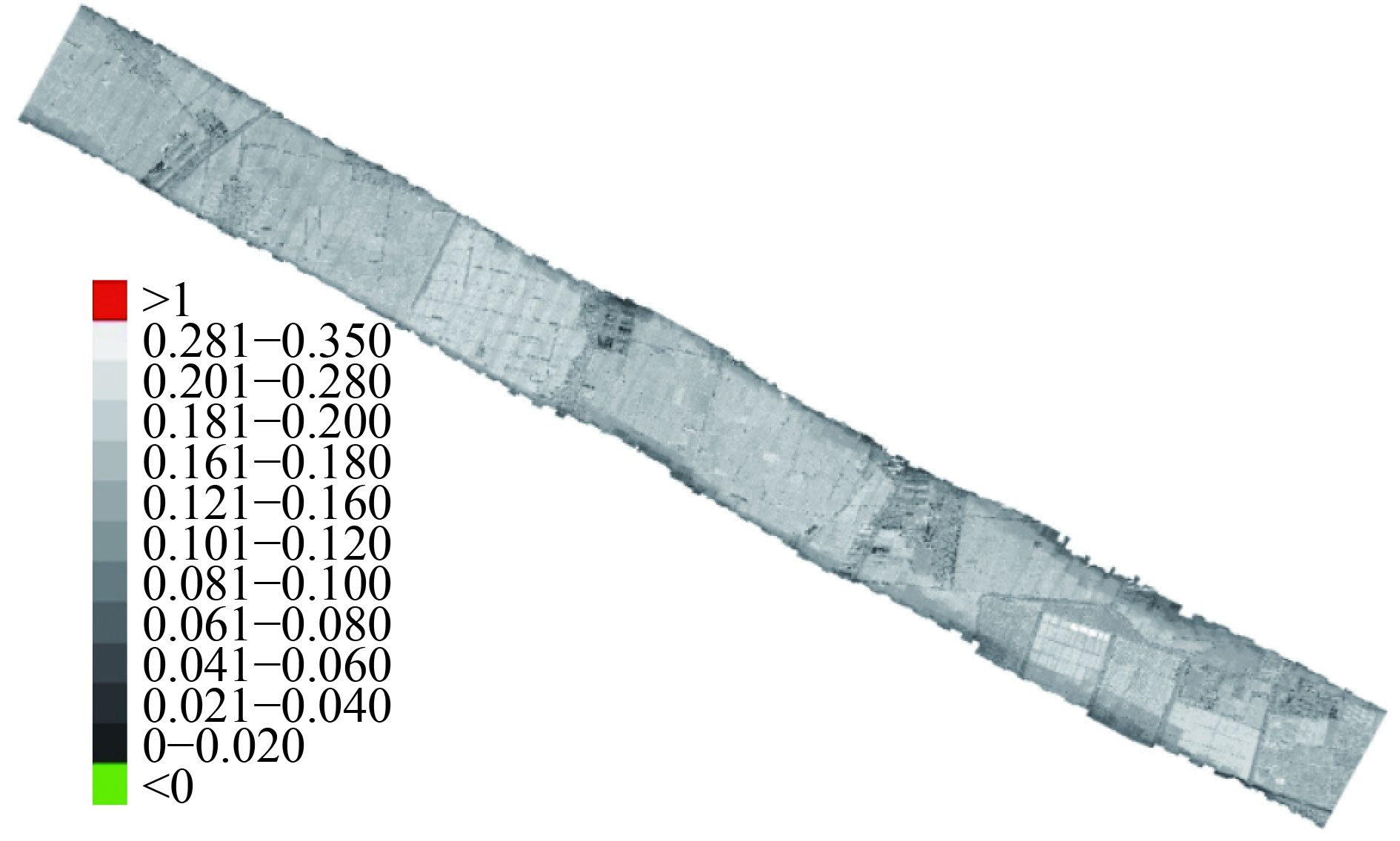
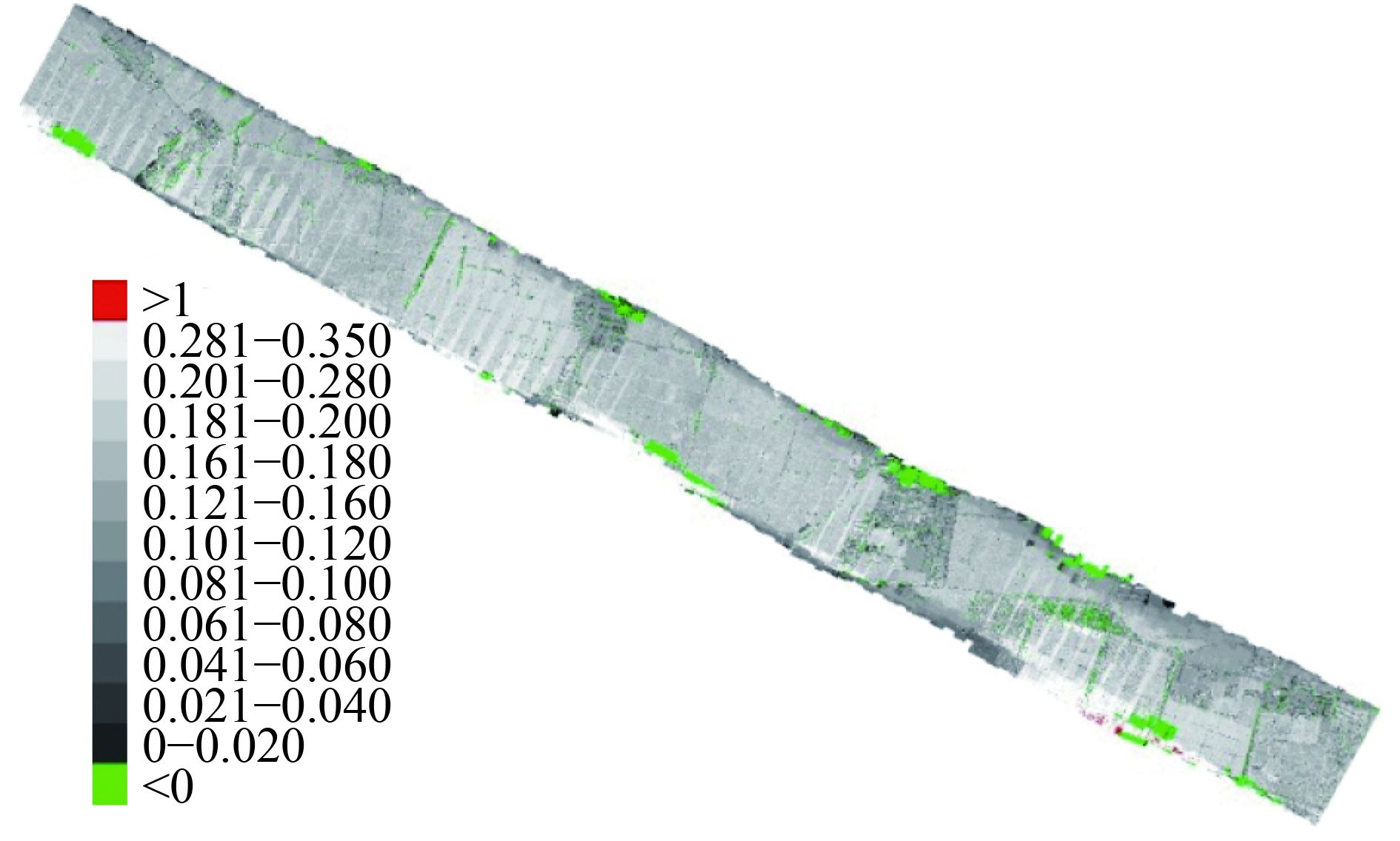
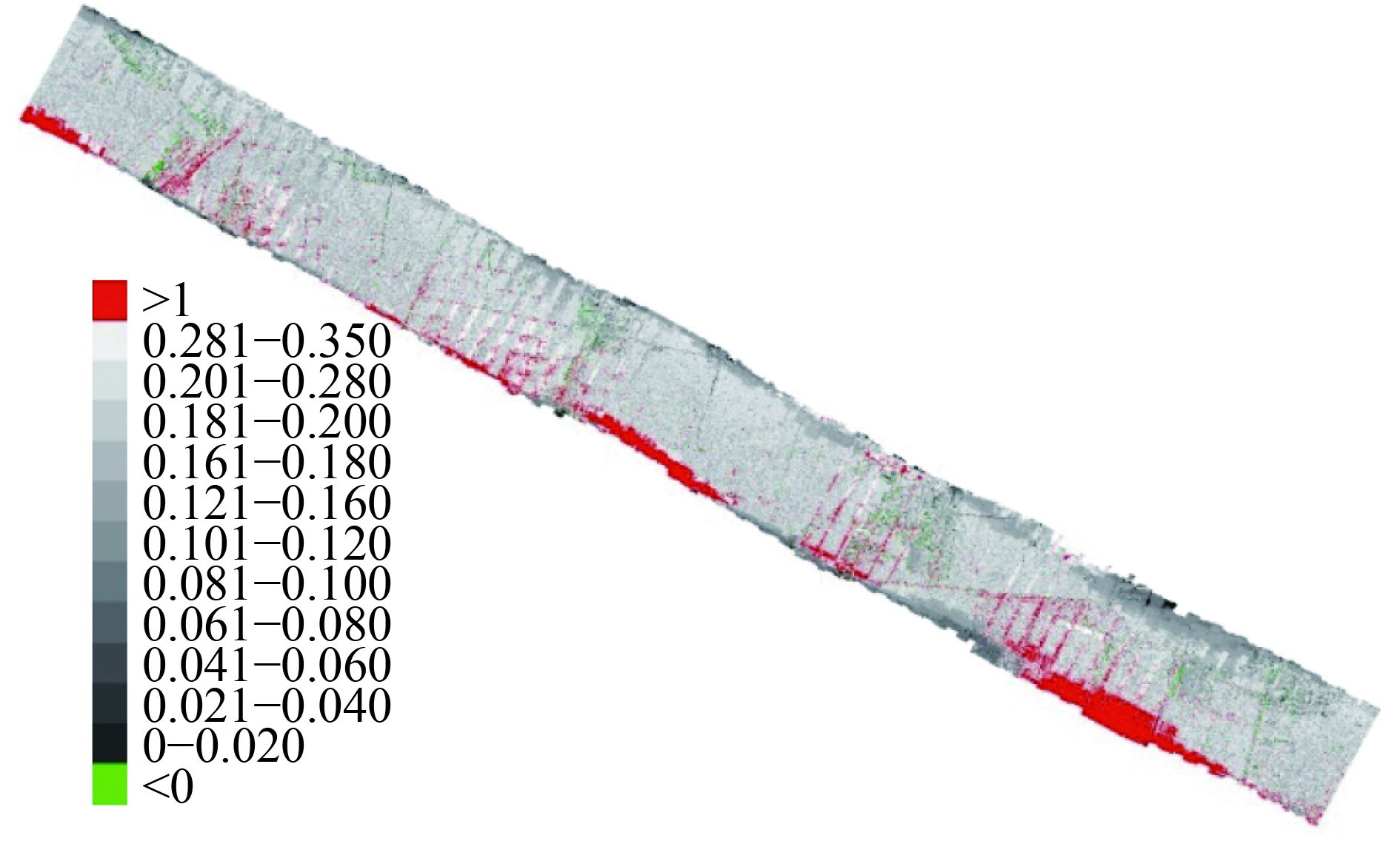
对于黑河机载WIDAS多角度数据，采用原型反演算法得到的地表反照率，全反演得到的反照率，以及朗伯假设得到的地表反照率如图2—图4所示。结果显示，受地表各向异性及观测噪声的影响，朗伯算法得到的反照率(图4)空间上变化剧烈，表现出明显的不连续，不确定性最大，显著地表现为其反照率大于1的异常值占2%左右，并且存在反照率小于0的异常值。这显然已超出了反照率的物理硬边界[0, 1]。图3是全反演得到的反照率，航带边缘观测角度少且大角度下没有约束，所以也同样出现一定比例小于0或大于1的反照率值，但总体反照率值在空间上的变化不确定性减小，这表明，多角度数据的积分对噪声有一定的平滑效果。这两种结果表明先验知识约束的必要性。基于BRDF原型的算法(图2)由于能够对地表各向异性进行约束和纠正，同时，对观测的多角度数据进行角度积分，有效考虑了半球空间的反射模式变化，反演结果在正常变化范围内，比朗伯假设得到的结果表现的更加稳定，但总体上小于朗伯假设的反照率结果。

图 2 根据最小拟合误差选择的BRDF原型作为先验知识得到的地表反照率

Fig. 2 Broadband blue-sky albedo derived using the proposed method

图 3 全反演算法得到的反照率

Fig. 3 Broadband blue-sky albedo derived using the full inversion

图 4 根据朗伯假设得到的地表反照率

Fig. 4 Broadband blue-sky albedo derived using the Lambertian assumption method

在图中反照率小于0或大于1结果，主要原因是传感器在辐射定标和大角度图像配准时产生的噪声的影响，同时，由于广角传感器的边缘效应，使图像交界处产生一些条带状噪声。由于观测角度仅为45°，且大部分情况下不在主平面上，直接通过全反演算法得到的反照率也会出现极端的情况(大于1或小于0)，这主要是由于缺少大角度观测所造成的。

该分析表明，根据最小拟合误差所选择的BRDF原型，能够有效地约束BRDF的变化，尤其在观测角度较少且主要集中在天顶方向时，对大角度的约束更为显著和必要。相对而言，全反演和朗伯假设，会有较明显的高估，这与获取观测时的太阳天顶角有关，且由于噪声的影响，更易产生异常值。因此，基于BRDF原型的算法具有良好的抗噪性能，噪声适应能力强。

3.2 WIDAS反照率验证

黑河2012年地面实测数据中，可用的数据包括3，7，8，10，14号站点在8月1日的数据(图5)。在这段时间内，玉米还没有完全封垄。这些反照率表提供了实验区域时间上较为连续的反照率观测，反照率表架设高度为1.5—2.5 m，每隔10 min采样一次(10 min内的观测均值)。本研究采用飞机过境时间为中心，将前后各10 min内的观测数据的平均值作为地面观测的真值。为了消除噪声的影响以及与地面站点的尺度进行匹配，反照率表的观测范围可以通过下式进行估算

$f = 2H\tan \left({{\rm{HFOV}}} \right)$

(10)

式中，H为反照率表的高度，HFOV为半视场角。采用的反照率表CNR1(Kipp&Zonen/NR01, Hukseflux)的半视场角为80°，通过式(10)计算得到的反照率表的视场范围约为22 m。

图 5 地面验证站点分布示意图及14号自动气象站

Fig. 5 Distribution of flux towers in the Yingke Oasis and the #14 automatic meteorological station

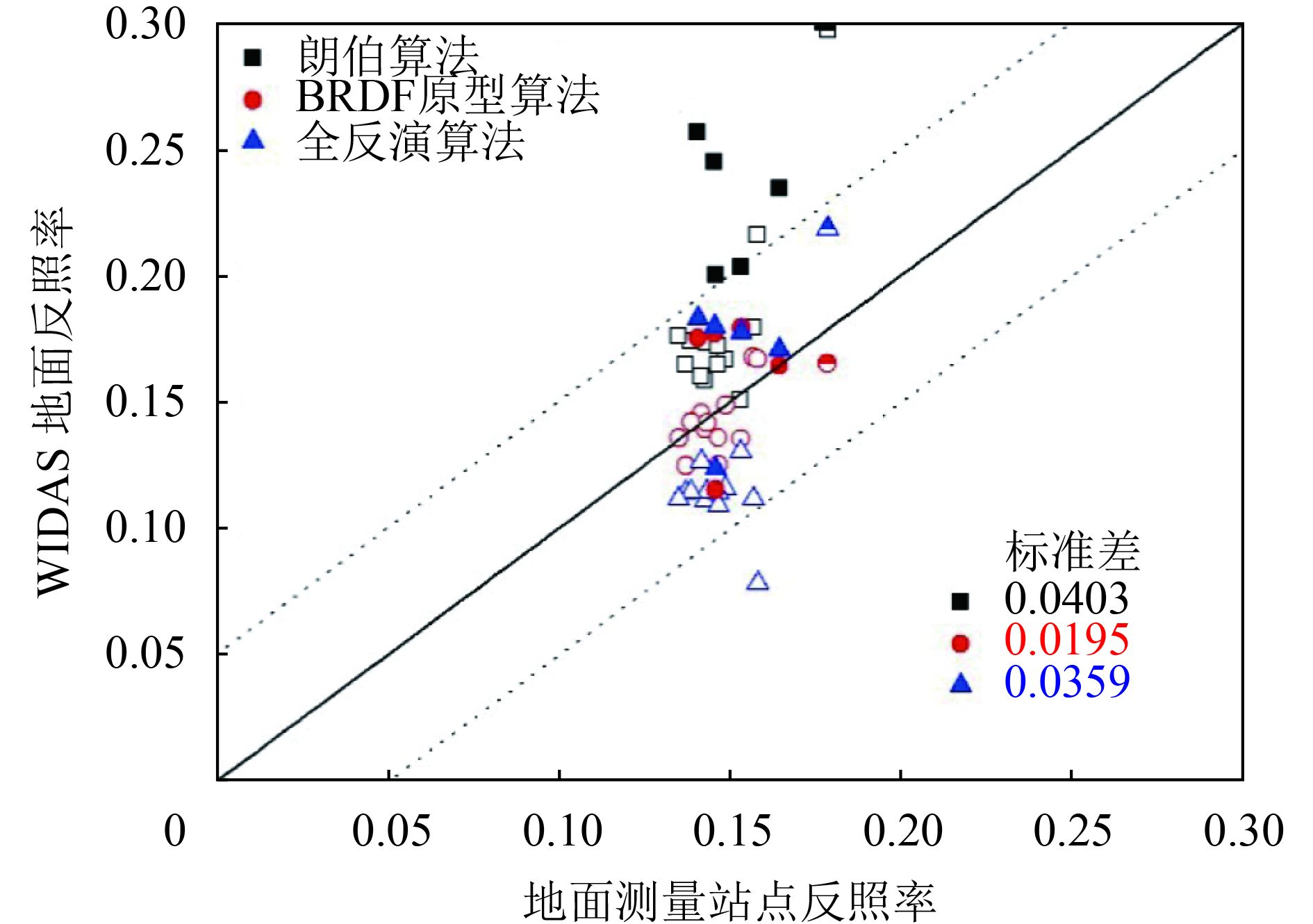
为了保证验证数据在观测视角一致，将WIDAS反照率结果在地面站点附近60×60窗口内的反照率的均值与地表实测数据进行比较(图6实心状数据)。同时，在比较2008年和2011年同一时间的黑河区域和验证站点Landsat计算出的归一化植被指数(NDVI)变化不大之后，作为辅助对比数据，加入黑河2008年的地面观测的反照率表数据(Jiao 等，2015)(图6空心状数据)和黑河2011年盈科飞行区域的一个地面验证点(You 等，2014)(图6半空心状数据)，但这两年验证数据的可信度低于2012年的验证数据。

图 6 根据最小拟合误差反演的BRDF原型(圆点)，朗伯算法(方框)以及全反演算法(三角点)得到WIDAS地表反照率与地面实测数据的对比

Fig. 6 Scatter plot of field-measured albedos compared with the inversion albedo of using the BRDF archetype-based algorithm(dots), Lambertian algorithm (squares) and the full inversion algorithm (triangles) from airborne WIDAS data

图6列出了3种算法反演的地表反照率的值，即根据最小RMSE对应的BRDF原型的方法(图6中圆点)、全反演算法(图6中三角点)以及朗伯假定算法(图6中正方形点)用于进一步分析不同算法反演的差异性。

很明显，基于朗伯假设的方法，将最小观测天顶角的方向反射率直接作为反照率，总体上明显高估了地面反照率表观测的结果，反演结果变化剧烈，标准差为0.0403。进一步验证了早期很多文献的结论，即在反演地表反照率时，朗伯假定的方法常常会引入较大的误差，且不稳定，精确反演地表反照率需要考虑地表的各向异性特征。不稳定的主要原因是由于朗伯假设算法抗噪性能差，这取决于天顶方向反射率的噪声水平。

根据最小拟合误差选择的BRDF原型算法反演结果都在0.05以内，且反演结果稳定，标准差为0.0195。全反演算法结果较为离散，标准差为0.0359，虽然小于朗伯假设的结果，但明显高于BRDF原型的反演结果，这主要是由于WIDAS的45°天顶角范围仍然不足以进行稳定的全反演。因此，BRDF先验知识的应用仍然必要。

4 结　论

算法验证是定量遥感研究中的关键环节，尤其当因传感器升级改造，致使观测数据特点发生变化的情况下，此时原算法能否适应新数据的特点，达到预先的设计精度目标需要深入和广泛的评估验证，这对进一步了解算法的鲁棒性和对数据的适当能力有重要意义。

机载多角度观测数据是获取实验区高分辨率数据的主要手段，也是星载数据进行地表参数反演的主要验证数据源。由于各种原因，多年来，机载多角度数据获取面临的一个主要的问题是多角度范围较小，不能很好地满足多角度应用的需求。因此，如何利用先验知识，从有限角度信息的机载多角度数据中，进行高精度稳定地地表参数反演，是遥感界面临的一个主要问题。本文主要对黑河实验区2012年机载WIDAS多角度观测数据进行反照率的估算以及对BRDF原型算法的验证。针对2012年机载WIDAS多角度数据噪声较大的特点，对比了3种算法并将结果与相应的地面验证点进行分析比较。

创新性主要体现在以下几个方面：(1)有效利用2012年的WIDAS多角度数据和地面实测反照率数据，对BRDF原型算法进行了验证，尤其在多角度观测不足和数据噪声大的情况下。(2)针对黑河区域地表各向异性的变化特点，提取了与之对应的MODIS BRDF原型作为先验知识，因此在先验知识的应用上，比2008年黑河机载WIDAS数据的反演更有针对性。(3)采用了热点校正的RTCLSR模型，虽然该模型已成功用于地表结构参数的反演，但应用于反照率的反演尚属首次。(4)对比分析了3种反演方法，再一次验证了BRDF原型的方法在小角度反照率反演的可行性，稳定性及抗噪性。BRDF原型算法对噪声的平滑能力是本次研究针对现有黑河数据一个新发现。将上述3种方法得到的反照率结果与地面验证数据进行比较，BRDF原型反演绝对精度达0.034，相对于全反演算法提高18%，相对朗伯假设方法提高71%。虽然基于这些单调地表类型(玉米)的验证点数据，BRDF原型反演精度提高并不显著，但从所给出的整个飞行区域的反照率结果分析，BRDF原型反演的优势非常明显。

验证结果表明，BRDF原型作为先验知识确实能够在不同条件下，较好地约束BRDF的形状，在观测角度较小时尤为显著；全反演算法和朗伯假定方法，总体上高估了地表反照率，同时，抗噪声能力差。由于本次实验WIDAS机载数据噪声大，这两种方法的反照率反演结果出现了一些异常值，以至于使反照率的硬边界超出了反照率的物理限制[0, 1]。这表明，BRDF原型作为先验知识，除了能对反演有效地约束，同时，也能有效地克服噪声的影响，产生高精度、稳定反演。

由于目前只有少量的地面验证点可用，在与不同年份的验证点比较时，反照率还与当时的气候条件等(如土壤水分等)有关，并且这些验证点主要为农作物(玉米)，在今后的工作中需要收集地面验证点的更多信息如气候和不同地表类型的验证点数据，以便更好地验证BRDF原型算法的反演精度。对于MODIS的BRDF原型，其空间分辨率为500 m，如何考虑像元尺度效应的影响，将其更好地用于高分辨率的数据，也是一个有待解决的科学问题。同时，黑河数据获取是在8月份植被茂盛时期的数据，在未来的研究中，希望能够进一步研究植被不同生长期反演结果的精度。

参考文献(References)

Bacour C and Bréon F M. 2005. Variability of biome reflectance directional signatures as seen by polder. Remote Sensing of Environment, 98 (1): 80–95. [DOI: 10.1016/j.rse.2005.06.008]

Bréon F M, Maignan F, Leroy M and Grant I. 2002. Analysis of hot spot directional signatures measured from space. Journal of Geophysical Research: Atmospheres, 107 (D16): 4282 [DOI: 10.1029/2001JD001094]

Chen J M and Cihlar J. 1997. A hotspot function in a simple bidirectional reflectance model for satellite applications. Journal of Geophysical Research: Atmospheres, 102 (D22): 25907–25913. [DOI: 10.1029/97JD02010]

Dickinson R E. 1983. Land surface processes and climate—surface albedos and energy balance. Advances in Geophysics, 25 : 305–353. [DOI: 10.1016/S0065-2687(08)60176-4]

Dong Y D, Jiao Z T, Zhang H, Li J Y, Jiao G P and Shi H Y. 2014. Efficient algorithm for improving the hotspot effect of the operational MODIS BRDF product. Journal of Remote Sensing, 18 (4): 804–825. [DOI: 10.11834/jrs.20143229] ( 董亚冬, 焦子锑, 张虎, 李佳悦, 焦广平, 石涵予. 2014. 改善MODIS BRDF产品热点效应的方法研究. 遥感学报, 18 (4): 804–825. [DOI: 10.11834/jrs.20143229] )

Dong Y D, Jiao Z T, Zhang H, Bai D N, Zhang X N, Li Y and He D D. 2016. A visualization tool for the kernel-driven model with improved ability in data analysis and kernel assessment. Computers and Geosciences, 95 : 1–10. [DOI: 10.1016/j.cageo.2016.06.010]

Jiao Z T, Hill M J, Schaaf C B, Zhang H, Wang Z S and Li X W. 2014. An anisotropic flat index (AFX) to derive BRDF archetypes from MODIS. Remote Sensing of Environment, 141 : 168–187. [DOI: 10.1016/j.rse.2013.10.017]

Jiao Z T, Li X W, Wang J D and Zhang H. 2011. Assessment of MODIS BRDF shape indicators. Journal of Remote Sensing, 15 (3): 432–456. [DOI: 10.11834/jrs.20110073] ( 焦子锑, 李小文, 王锦地, 张虎. 2011. 评估MODIS的BRDF角度指数产品. 遥感学报, 15 (3): 432–456. [DOI: 10.11834/jrs.20110073] )

Jiao Z T, Schaaf C B, Dong Y D, Román M, Hill M J, Chen J M, Wang Z S, Zhang H, Saenz E, Poudyal R, Gatebe C, Bréon F M, Li X W and Strahler A. 2016. A method for improving hotspot directional signatures in BRDF models used for MODIS. Remote Sensing of Environment, 186 : 135–151. [DOI: 10.1016/j.rse.2016.08.007]

Jiao Z T, Zhang H, Dong Y D, Liu Q, Xiao Q and Li X W. 2015. An algorithm for retrieval of surface albedo from small view-angle airborne observations through the use of BRDF archetypes as prior knowledge. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 8 (7): 3279–3293. [DOI: 10.1109/JSTARS.2015.2414925]

Jiao Z T, Zhang H and Li X W. 2012. To derive a prior database of archetypal BRDF shapes from ground measurements using anisotropic flat index (AFX)//Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium. Munich, Germany: IEEE: 6753-6756 [DOI: 10.1109/IGARSS.2012.6352555]

Jin Y F, Schaaf C B, Gao F, Li X W, Strahler A H, Lucht W and Liang S L. 2003. Consistency of MODIS surface bidirectional reflectance distribution function and albedo retrievals: 1. Algorithm performance. Journal of Geophysical Research: Atmospheres, 108 (D5): 4158 [DOI: 10.1029/2002JD002803]

Li X, Li X W, Li Z Y, Ma M G, Wang J, Xiao Q, Liu Q, Che T, Chen E X, Yan G J, Hu Z Y, Zhang L X, Chu R Z, Su P X, Liu Q H, Liu S M, Wang J D, Niu Z, Chen Y, Jin R, Wang W Z, Ran Y H, Xin X Z and Ren H Z. 2009. Watershed allied telemetry experimental research. Journal of Geophysical Research: Atmospheres, 114 (D22): D22103 [DOI: 10.1029/2008JD011590]

Li X W. 1989. Bidirectional reflectance and angular signature of objects. Remote Sensing of Environment China, 4 (1): 67–72. ( 李小文. 1989. 地物的二向性反射和方向谱特征. 环境遥感, 4 (1): 67–72. )

Li X W, Gao F, Chen L Z and Strahler A H. 1999. Derivation and validation of a new kernel for kernel-driven BRDF models//Proceedings of the Remote Sensing for Earth Science, Ocean, and Sea Ice Applications. Florence, Italy: SPIE: 368-379 [DOI: 10.1117/12.373123]

Li X W, Gao F, Wang J D and Strahler A. 2001. A priori knowledge accumulation and its application to linear BRDF model inversion. Journal of Geophysical Research: Atmospheres, 106 (D11): 11925–11935. [DOI: 10.1029/2000JD900639]

Li Xin, Liu Shaomin, Ma Mingguo, et al. 2012. HiWATER: An integrated remote sensing experiment on hydrological and ecological processes in the Heihe River Basin. Advances in Earth Science, 27 (5): 481–498. ( 李新, 刘绍民, 马明国, 等. 2012. 黑河流域生态—水文过程综合遥感观测联合试验总体设计. 地球科学进展, 27 (5): 481–498. )

Liang S L. 2001. Narrowband to broadband conversions of land surface albedo I: algorithms. Remote Sensing of Environment, 76 (2): 213–238. [DOI: 10.1016/S0034-4257(00)00205-4]

Liu Q, Wang L Z, Qu Y, Liu N F, Liu S H, Tang H R and Liang S L. 2013. Preliminary evaluation of the long-term glass albedo product. International Journal of Digital Earth, 6 (S1): 69–95. [DOI: 10.1080/17538947.2013.804601]

Lucht W and Lewis P. 2000. Theoretical noise sensitivity of BRDF and albedo retrieval from the EOS-MODIS and MISR sensors with respect to angular sampling. International Journal of Remote Sensing, 21 (1): 81–98. [DOI: 10.1080/014311600211000]

Lucht W, Schaaf C B and Strahler A H. 2000. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Transactions on Geoscience and Remote Sensing, 38 (2): 977–998. [DOI: 10.1109/36.841980]

Nicodemus F E, Richmond J C, Hsia J J, Ginsberg I W and Limperis T. 1977. Geometrical Considerations and Nomenclature for Reflectance. Monograph Number 160. US Department of Commerce

Schaaf C B, Gao F, Strahler A H, Lucht W, Li X W, Tsang T, Strugnell N C, Zhang X Y, Jin Y F, Muller J P, Lewis P, Barnsley M, Hobson P, Disney M, Roberts G, Dunderdale M, Doll C, D’Entremont R P, Hu B X, Liang S L, Privette J L and Roy D. 2002. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sensing of Environment, 83 (1/2): 135–148. [DOI: 10.1016/S0034-4257(02)00091-3]

Wanner W, Li X and Strahler A H. 1995. On the derivation of kernels for kernel-driven models of bidirectional reflectance. Journal of Geophysical Research: Atmospheres, 100 (D10): 21077–21089. [DOI: 10.1029/95JD02371]

You D Q, Wen J G, Liu Q, Liu Q H and Tang Y. 2014. The angular and spectral kernel-driven model: assessment and application. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (4): 1331–1345. [DOI: 10.1109/JSTARS.2013.2271502]

Zhang H, Jiao Z T, Dong Y D, Huang X Y, Li J Y and Li X W. 2013. An algorithm for retrieval albedo from BRDF archetype. Journal of Remote Sensing, 17 (6): 1475–1491. [DOI: 10.11834/jrs.20133022] ( 张虎, 焦子锑, 董亚冬, 黄兴英, 李佳悦, 李小文. 2013. 基于BRDF原型反演地表反照率. 遥感学报, 17 (6): 1475–1491. [DOI: 10.11834/jrs.20133022] )

摘要

关键词