多通道合成孔径雷达SAR(Synthetic Aperture Radar)的发展和运用使得成像雷达的信息获取能力和抗干扰能力获得了极大提升，已成为成像雷达的重要发展方向(Sjögren 等，2014；常玉林 等，2009)。与常规SAR相比，多通道SAR可从雷达回波信号相位中获取更多的有用信息，并具有更高的系统自由度，充分吸引了各国在民用与军事领域的重点关注和发展，机载与星载多通道SAR的应用已较为广泛。现阶段较为成熟的多通道SAR技术包括相位干涉技术(Krieger 等，2009)、地面动目标检测(Dawidowicz 等，2012)、高分辨率宽测绘带成像(Zhang 等，2015)和多通道对消技术等。其中SAR多通道对消技术可利用各通道接收的干扰信号之间的相位关系实现干扰对消，是一种直接有效的抗干扰方法。

天线沿航迹或垂直航迹分布的多通道SAR系统可利用多通道对消技术抑制有源干扰信号。甘荣兵等人(2005a, 2005b)讨论了散射波干扰信号的双通道对消原理，验证了对消效果并指出该技术会造成真实回波的周期性损失，同时为了解决对消过程中的补偿相位估计问题，依据两路对消后能量最小准则提出了自动相位搜索算法。马晓岩等人(2007)提出抑制压制性干扰的三通道对消方法，通道数的增多扩大了真实回波的损失周期，从而减少了对消成像中对消暗条纹的数量。李晨和朱岱寅(2007)和张双喜等人(2011)分别研究了利用多天线检测和抑制SAR欺骗式干扰的方法。Lin等人(2014)提出一种新的双通道数据采集方式，利用该方式对干扰站进行定位，从而获取较为准确的补偿相位来完成干扰对消。可见，多通道对消能够适应包括散射波在内的多种干扰类型，而且运算量较小，具有较好的抗干扰性能。当前对抗多通道对消技术的方法研究很少，黄龙等人(2015)研究了多天线干扰机对干涉SAR双通道对消系统的干扰效果，采用多天线模拟干扰机的运动，从而改变对消时补偿相位的分布，形成了密集的对消暗条纹遮蔽效果，但该文献只针对噪声压制性干扰进行研究，干扰类型单一。现有文献虽然对SAR散射波干扰进行了深入探究和改进(刘业民 等，2011；杨伟宏 等，2012；Huang 等，2015)，但针对多通道SAR系统对抗效果的分析相对较为匮乏。

基于上述背景，本文针对多通道对消技术提出方位向余弦调相散射波干扰方法。首先讨论了双通道对消原理，并构建了余弦调相散射波干扰的信号模型，结合余弦调相信号的频谱搬移特性对干扰信号的SAR成像特性进行分析。然后以双通道对消系统为例，着重分析了该方法对补偿相位估计结果(自动相位搜索结果)和对消输出结果的影响。本文干扰方法可在常规SAR成像中形成多个沿方位向分布的虚假散射场景，在双通道对消成像结果中可使得真实场景被多次复制搬移，同时产生密集的明暗条纹，严重降低干扰对消后的场景成像质量，对多通道SAR系统的工作特点和抗干扰性能具有较强的针对性。

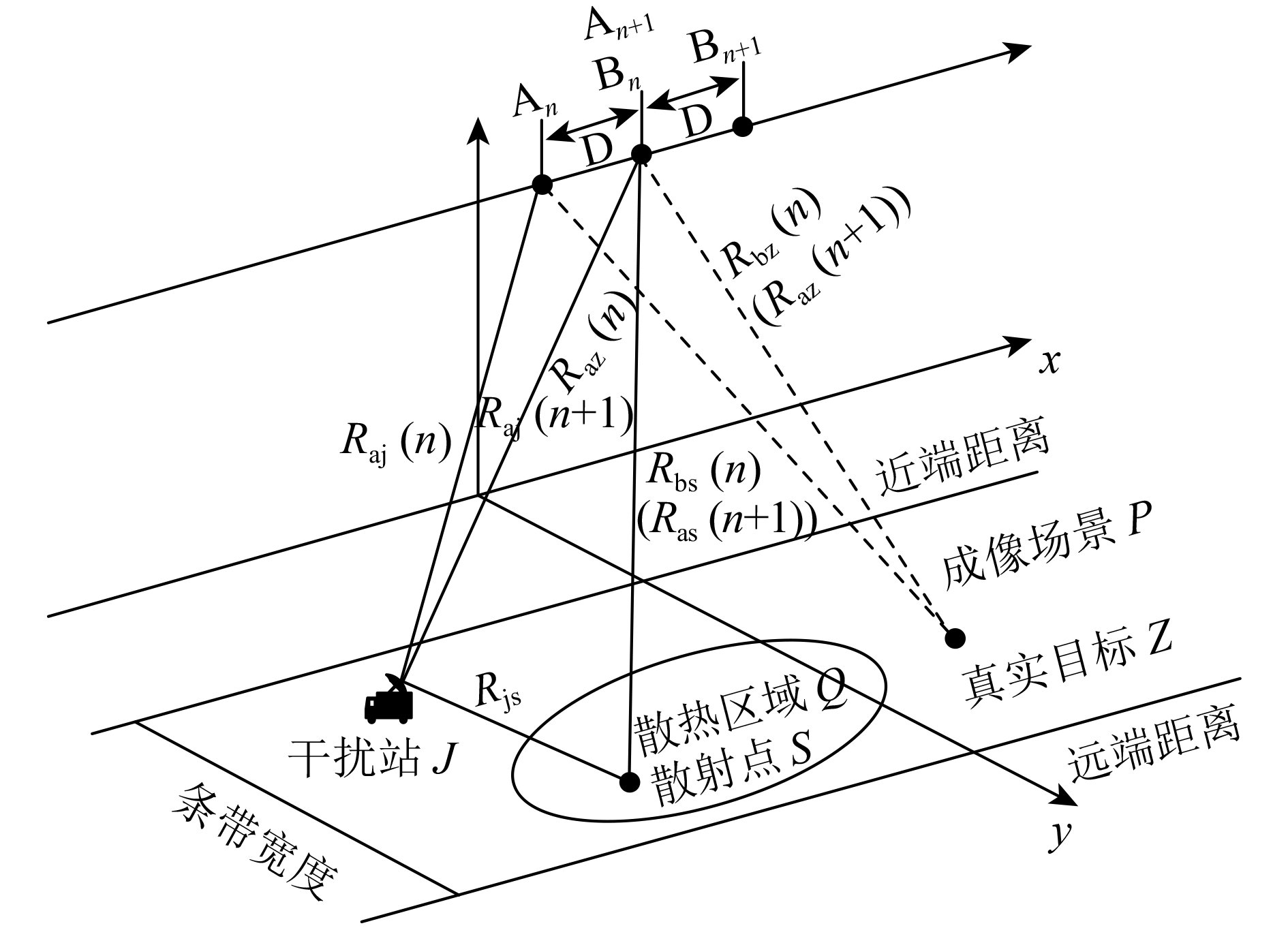
本节主要以传统散射波干扰的双通道对消为例展开分析，散射波干扰的原理：当干扰站接收到SAR发射的脉冲信号后放大并转发至特定散射区域，信号经过该区域散射后与原始回波信号混合并被SAR接收。在干扰过程中，整个散射区域都相当于干扰源，干扰信号便会携带真实目标的散射信息，因此在频域、时域和极化域都很难被识别，可形成较好的2维相干干扰效果。并且干扰信号从多个连续方向进入雷达主瓣，传统的旁瓣抑制和空域滤波方法很难抑制散射波干扰(甘荣兵 等，2005b；Bucciarelli 等，2008)。

散射波干扰和SAR双通道对消原理如图1所示，两通道子孔径天线沿航迹排列，A天线发射信号，A、B两天线同时接收信号。设两天线间距满足对消条件 $D = kTv$ ，其中 $T$ 为SAR信号脉冲重复周期， $v$ 为SAR平台运行速度， $k$ 为正整数。A_n、B_n分别表示A、B两天线在第 $n$ 慢时刻(慢时间采样时刻)的位置，在经历了 $k$ 个脉冲重复周期 $T$ 后，A天线到达B天线的 $n$ 时刻位置，此时两天线在第 $n + 1$ 慢时刻的位置分别为A_n+1和B_n+1。设成像测绘带P中任意点目标Z和散射区域Q内的任意散射点S，根据散射波干扰原理，A天线在 $n + 1$ 时刻和B天线在 $n$ 时刻所接收到的真实回波信号与干扰信号的传播路径分别为

$\left\{ {\begin{aligned} & {{Y_{{\rm{az}}}}(n + 1) = 2 \cdot {R_{{\rm{bz}}}}(n) = 2 \cdot {R_{{\rm{az}}}}(n + 1)}\\ & {{Y_{{\rm{aj}}}}(n + 1) = {R_{{\rm{aj}}}}(n + 1) + {R_{{\rm{js}}}} + {R_{{\rm{bs}}}}(n)}\\ & {{Y_{{\rm{bz}}}}(n) = {R_{{\rm{az}}}}(n) + {R_{{\rm{bz}}}}(n)}\\ & {{Y_{{\rm{bj}}}}(n) = {R_{{\rm{aj}}}}(n) + {R_{{\rm{js}}}} + {R_{{\rm{bs}}}}(n)} \end{aligned}} \right.$

(1)

式中， ${R_{{\rm{az}}}}(n)$ 、 ${R_{{\rm{bz}}}}(n)$ (或 ${R_{{\rm{az}}}}(n + 1)$ )分别为 $n$ 时刻两天线到真实点目标Z的距离； ${R_{{\rm{aj}}}}(n)$ 、 ${R_{{\rm{aj}}}}(n + 1)$ 分别为A天线在 $n$ 与 $n + 1$ 时刻与干扰站J的距离； ${R_{{\rm{bs}}}}(n)$ (或 ${R_{{\rm{as}}}}(n + 1)$ )为 $n$ 时刻B天线到散射点S的距离； ${R_{{\rm{js}}}}$ 为干扰站J到散射点S的距离。则A天线 $n + 1$ 时刻和B天线 $n$ 时刻的真实目标回波信号和散射波干扰信号的相位差为

$\left\{ {\begin{aligned} & \begin{aligned} \Delta {\varphi _{\rm{z}}}\left(n \right) = & {{2{\text{π}}\left({{Y_{{\rm{az}}}}(n + 1) - {Y_{{\rm{bz}}}}(n)} \right)}/{\textit{λ}}} = \\ & {{2{\text{π}}\left({{R_{{\rm{bz}}}}(n) - {R_{{\rm{az}}}}(n)} \right)}/{\textit{λ}}} \\ \end{aligned} \\ & \begin{aligned} \Delta {\varphi _{\rm{j}}}\left(n \right) = & {{2{\text{π}}\left({{Y_{{\rm{aj}}}}(n + 1) - {Y_{{\rm{bj}}}}(n)} \right)}/{\textit{λ}}} = \\ & {{2{\text{π}}\left({{R_{{\rm{aj}}}}(n + 1) - {R_{{\rm{aj}}}}(n)} \right)}/{\textit{λ}}} \\ \end{aligned} \end{aligned}} \right.$

(2)

记A天线 $n + 1$ 时刻接收的点Z回波信号和点S散射波干扰信号分别为 ${s_{{\rm{az}}}}(n + 1)$ 、 ${s_{{\rm{aj}}}}(n + 1)$ ，B天线n时刻接收的点Z回波信号和干扰信号分别为 ${s_{{\rm{bz}}}}(n)$ 、 ${s_{{\rm{bj}}}}(n)$ ，两天线接收的干扰信号满足关系

${s_{{\rm{bj}}}}(n) = {s_{{\rm{aj}}}}(n + 1) \cdot \exp \left({{\rm{j}}\Delta {\varphi _{\rm{j}}}(n)} \right)$

(3)

设两天线分别在 $n + 1$ 和n时刻接收的总信号为

$\left\{ \begin{aligned} & {s_{\rm{a}}}(n + 1) = {s_{{\rm{az}}}}(n + 1) + {s_{{\rm{aj}}}}(n + 1) \\ & {s_{\rm{b}}}(n) = {s_{{\rm{bz}}}}(n) + {s_{{\rm{bj}}}}(n) \end{aligned} \right.$

(4)

分析式(2)可知相邻慢时刻两通道接收的干扰信号间的相位差 $\Delta {\varphi _{\rm{j}}}(n)$ 与散射点位置无关，只与干扰站位置有关，即对于每个n时刻 $\Delta {\varphi _{\rm{j}}}(n)$ 可进行量化，这是实现对消散射波干扰的关键条件。因此只需要对A通道 $n + 1$ 时刻信号进行相位补偿 $\Delta {\varphi _{\rm{j}}}(n)$ ，再与B通道 $n$ 时刻信号相减即可消除散射波干扰信号，结合式(2)—(4)并进行 ${\rm{Fresnel}}$ 近似处理可得对消输出结果为

$\begin{aligned} \Delta s(n) = & {s_{\rm{b}}}(n) - {s_{\rm{a}}}(n + 1) \cdot \exp \left({{\rm{j}}\Delta {\varphi _{\rm{j}}}(n)} \right){\kern 1pt} = \\ & {s_{{\rm{bz}}}}(n) \cdot \left( {1 - \exp \left( {{\rm{j}}\left({\Delta {\varphi _{\rm{j}}}(n) - \Delta {\varphi _{\rm{z}}}(n)} \right)} \right)} \right) \approx \\ & {s_{{\rm{bz}}}}(n) \cdot \left( {1 - \exp \left({{\rm{j}}{{2{\text{π}}D({x_{\rm{z}}} - {x_{\rm{j}}})}/{({\textit{λ}} {R_{{\rm{j}}0}})}}} \right)} \right) \end{aligned} $

(5)

式中， ${x_{\rm{z}}}$ 、 ${x_{\rm{j}}}$ 分别为真实目标Z和干扰站J的方位向坐标； ${R_{{\rm{j}}0}}$ 为干扰站到SAR系统的最短斜距。可见，散射波干扰信号被有效抑制，但场景真实目标回波信号 ${s_{{\rm{bz}}}}(n)$ 受到 $[1 - \exp ({\rm{j}}2{\text{π}}D({x_{\rm{z}}} - {x_{\rm{j}}})/({\textit{λ}} {R_{{\rm{j}}0}}))]$ 调制：当 $2{\text{π}}D({x_{\rm{z}}} - {x_{\rm{j}}})/({\textit{λ}} {R_{{\rm{j}}0}})$ $ \approx 2k{\text{π}}$ $(k \in {\rm{Z}})$ 时，调制项接近于0，方位向坐标接近 ${x_{\rm{z}}}$ 的真实点回波信号被削弱，最终导致场景成像中出现周期性暗条纹。如当 ${x_{\rm{z}}} = {x_{\rm{j}}}$ 时 $\Delta s = 0$ ，即干扰站所在方位向的场景回波被完全抑制，相近的区域成像变暗。在实际运用中，可增加通道数量来增大成像场景的对消损失周期，从而改善成像效果(马晓岩 等，2007)。

准确估计干扰信号的补偿相位 $\Delta {\varphi _{\rm{j}}}(n)$ 是实现双通道干扰对消的关键，若能够利用侦察技术获取干扰站准确位置，便可以计算较为准确的补偿相位。但对散射波干扰站进行定位的难度较大，且干扰对消无需实时处理，所以一般直接利用自动相位搜索法从接收信号中估计补偿相位 $\Delta {\varphi _{\rm{j}}}(n)$ (甘荣兵 等，2005b)。相位搜索法实现有效估计的条件是两通道在 $n$ 和 $n + 1$ 时刻所收信号中都含有干扰信号且存在相位关系，其基本流程是：对于合成孔径时间内的每个 $n$ 时刻，在 $[ - {\text{π}}, {\text{π }}]$ 内按一定规则搜索估计相位 $\Delta {\varphi _{\rm{j}}}^\prime (n)$ ，使用 $\Delta {\varphi _{\rm{j}}}^\prime (n)$ 对A通道 $n + 1$ 时刻信号相位进行补偿，再和B通道 $n$ 时刻信号相减，当差信号能量能够取得最小值时，就以该 $\Delta {\varphi _{\rm{j}}}^\prime (n)$ 作为 $n$ 时刻补偿相位 $\Delta {\varphi _{\rm{j}}}(n)$ 的最终估计值。现有研究表明干信比越大，估计相位越接近于准确相位(黄龙 等，2015)。

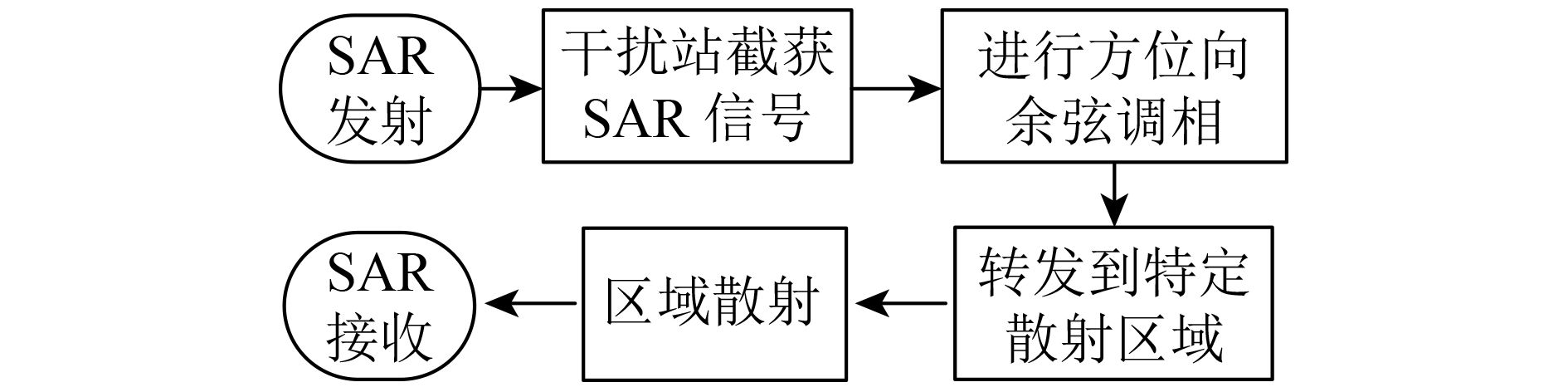
双通道对消技术对传统散射波干扰具有较好的抑制性能，因此需要对散射波干扰进行改进。方位向余弦调相可实现干扰信号的方位向扩展(房明星 等，2016)，并改变相邻慢时刻干扰信号之间的相位关系，对传统散射波干扰信号进行方位向余弦调相，干扰实施的基本流程如图2所示。

首先对余弦调相散射波干扰的成像特性展开分析。余弦调相信号一般形式为

${p_m}\left(t \right) = \cos \left({2{\text{π}}{f_{\rm{c}}}t + {\beta _m}\cos (2{\text{π}}{f_m}t)} \right)$

(6)

式中， ${f_m}$ 为调制频率； ${\beta _m}$ 为调制指数。式(6)级数展开可得

${p_m}\left(t \right) = \sum\limits_{n = - \infty }^{ + \infty } {{J_n}({\beta _m})} \cos \left({2{\text{π}}({f_{\rm{c}}} + n{f_m})t + \frac{{n{\text{π}}}}{2}} \right)$

(7)

式中， ${J_n}({\beta _m})$ 为第一类 $n$ 阶贝塞尔函数。则式(7)频谱可表示为

$\begin{aligned} {P_m}\left( f \right) = & {\text{π}}\sum\limits_{n = - \infty }^{ + \infty } {{J_n}({\beta _m})} \left( {{e^{ - {\rm{j}}\frac{{n{\text{π}}}}{2}}}\delta \left( {2{\text{π}} (f + {f_{\rm{c}}} + n{f_m})} \right) + } \right.\\ & \left. {{e^{{\rm{j}}\frac{{n{\text{π}}}}{2}}}\delta \left( {2{\text{π}} (f - {f_{\rm{c}}} - n{f_m})} \right)} \right) \end{aligned} $

(8)

忽略干扰机转发延时，设未经调制的传统散射波信号形式为

$\begin{aligned} {s_{\rm{j}}}\left({{t_{\rm{r}}}, {t_{\rm{a}}}} \right) = & \sigma \cdot {\rm{rect}}\left({\frac{{{t_{\rm{r}}} - {{{Y_{\rm{j}}}({t_{\rm{a}}})}/c}}}{{{T_{\rm{p}}}}}} \right){\rm{rect}}\left({\frac{{{t_{\rm{a}}}}}{{{T_{\rm{L}}}}}} \right)\; \cdot \\ & \exp \left( {{\rm{j{\text{π}} }}{\mu _{\rm{r}}}{{\left({{t_{\rm{r}}} - \frac{{{Y_{\rm{j}}}({t_{\rm{a}}})}}{c}} \right)}^2}} \right)\exp \left({ - {\rm{j}}2{\text{π}}{f_{\rm{c}}}\frac{{{Y_{\rm{j}}}({t_{\rm{a}}})}}{c}} \right) \end{aligned} $

(9)

式中， ${t_{\rm{r}}}$ 为距离向快时间； ${t_{\rm{a}}}$ 为方位向慢时间； $\sigma $ 为散射点的后向散射系数； ${f_{\rm{c}}}$ 为载频； $\,{\mu _{\rm{r}}}$ 为距离向调频斜率； $v$ 为SAR平台行进速度； ${T_{\rm{L}}}$ 为合成孔径时间； ${Y_{\rm{j}}}({t_{\rm{a}}}) = {R_{{\rm{aj}}}}({t_{\rm{a}}}) + {R_{{\rm{js}}}} + {R_{{\rm{as}}}}({t_{\rm{a}}})$ 为 ${t_{\rm{a}}}$ 时刻散射波干扰信号的传播距离。设方位向余弦调相信号的复数形式为

${p_m}\left({{t_{\rm{a}}}} \right) = \exp \left({{\rm{j}}{\beta _m}\cos (2{\text{π}}{f_m}{t_{\rm{a}}})} \right)$

(10)

则经过余弦调相后的散射波干扰信号为

${s_{{\rm{j}}m}}({t_{\rm{r}}}, {t_{\rm{a}}}) = {s_{\rm{j}}}({t_{\rm{r}}}, {t_{\rm{a}}}) \cdot {p_m}({t_{\rm{a}}})$

(11)

结合式(8)和式(11)可得干扰信号的二维频谱为

${S_{{\rm{j}}m}}({f_{\rm{r}}}, {f_{\rm{a}}}) = \sum\limits_{n = - \infty }^{ + \infty } {{J_n}({\beta _m}){S_{\rm{j}}}({f_{\rm{r}}}, {f_{\rm{a}}} - n{f_m})} $

(12)

式中， ${S_{\rm{j}}}({f_{\rm{r}}}, {f_{\rm{a}}})$ 为传统散射波干扰信号 ${s_{\rm{j}}}({t_{\rm{r}}}, {t_{\rm{a}}})$ 的2维频谱。由式(12)可知方位向余弦调相实际上完成了对散射波信号多普勒频谱的周期性搬移，且第 $n$ 阶搬移量幅度受到第一类 $n$ 阶贝塞尔函数调制。结合式(9)—式(11)，可得干扰信号经过2维匹配滤波的输出结果为

$\begin{gathered} {y_{{\rm{j}}m}}({t_{\rm{r}}}, {t_{\rm{a}}}) = \left({1 - \frac{{\left| {t_{\rm{r}}^*} \right|}}{{{T_{\rm{p}}}}}} \right){\rm{sinc}}\left({{\mu _{\rm{r}}}t_{\rm{r}}^*({T_{\rm{p}}} - \left| {t_{\rm{r}}^*} \right|)} \right) \cdot {\kern 1pt} \\ \sum\limits_{n = - \infty }^{ + \infty } {{J_n}({\beta _m})} \left({1 - \frac{{\left| {t_{\rm{a}}^ * } \right|}}{{{T_{\rm{L}}}}}} \right){\rm{sinc}}\left({{u_{\rm{a}}}(t_{\rm{a}}^ * + \frac{{n{f_m}}}{{{u_{\rm{a}}}}})({T_{\rm{L}}} - \left| {t_{\rm{a}}^ * } \right|)} \right) \\ \end{gathered} $

(13)

式中， $t_{\rm{r}}^* = {t_{\rm{r}}} - ({R_{{\rm{j}}0}} + {R_{{\rm{js}}}} + {R_{{\rm{s}}0}})/c$ 为经过距离徙动校正后与慢时间无关的干扰信号到达时间； ${R_{{\rm{s}}0}}$ 为散射点到SAR的最短斜距； ${t_{\rm{a}}}^ * $ 为散射波方位向到达时间。分析式(13)可知，余弦调相散射波干扰信号可在方位向形成多个虚假散射目标，第 $n$ 阶假目标的距离向和方位向峰值时刻分别为 ${t_{\rm{r}}}^ * = 0$ 和 ${t_{\rm{a}}}^ * = - n{f_m}/$ ${\mu _{\rm{a}}}$ ，其中 ${u_{\rm{a}}} = - 2{v^2}/\lambda {R_{{\rm{s}}0}}$ 。由于散射区域内所有点目标都等效于干扰源，所以最终干扰效果为多个沿方位向分布的虚假散射场景，且相邻场景中心间距为 $\Delta x = |v{f_m}/{\mu _{\rm{a}}}|$ 。

通过上述分析可知，干扰改进后同时具备余弦调相和散射波的干扰效应和优势，在实现散射波2维相干干扰效果的同时，将虚假散射场景在方位向进行了拓展，进一步提升了干扰性能。但对于双通道系统而言，干扰关键在于方位向调制能够改变干扰信号在相邻慢时刻到达两通道的相位差，从而改变自动相位搜索法对补偿相位的估计结果。现把测绘带内所有点目标纳入分析，记第 $n$ 时刻的慢时间表示为 ${t_a} = nT$ ，结合式(10)和式(11)可得 $A$ 通道 $n + 1$ 时刻和 $B$ 通道 $n$ 时刻接收到的余弦调相散射波干扰信号为

$\left\{ \begin{aligned} & \sum\limits_{q = 1}^Q {{s_{a{\rm{j}}m, q}}(n + 1)} = \sum\limits_{q = 1}^Q {{s_{a{\rm{j}}, q}}(n + 1)} \cdot {p_m}(n + 1) = \\ & \sum\limits_{q = 1}^Q {{s_{a{\rm{j}}, q}}(n + 1)} \cdot \exp \left( {{\rm{j}}{\beta _m}\cos \left({2{\text{π}}{f_m}(n + 1)T} \right)} \right) \\ & \sum\limits_{q = 1}^Q {{s_{b{\rm{j}}m, q}}(n)} = \sum\limits_{q = 1}^Q {{s_{b{\rm{j}}, q}}(n)} \cdot {p_m}(n) = \\ & \sum\limits_{q = 1}^Q {{s_{b{\rm{j}}, q}}(n)} \cdot \exp \left({{\rm{j}}{\beta _m}\cos (2{\text{π}}{f_m}nT)} \right) \end{aligned} \right.$

(14)

式中， ${s_{a{\rm{j}}, q}}(n + 1)$ 、 ${s_{b{\rm{j}}, q}}(n)$ 分别表示 $A$ 、 $B$ 通道接收的散射区域 $Q$ 中第 $q$ 散射点所散射的传统散射波干扰信号，且对于任意第 $q$ 点都满足式(3)关系，即有

${s_{b{\rm{j}}, q}}(n) = {s_{a{\rm{j}}, q}}(n + 1) \cdot \exp \left({{\rm{j}}\Delta {\varphi _{\rm{j}}}(n)} \right)$

(15)

结合式(4)得 $A$ 通道 $n + 1$ 时刻和 $B$ 通道 $n$ 时刻接收到的总信号为

$ \left\{ \begin{aligned} & \sum {{s_a}(n + 1)} = \sum\limits_{p = 1}^P {{s_{az, p}}(n + 1)} + \sum\limits_{q = 1}^Q {{s_{a{\rm{j}}m, q}}(n + 1)} \\ & \sum {{s_b}(n)} = \sum\limits_{p = 1}^P {{s_{bz, p}}(n)} + \sum\limits_{q = 1}^Q {{s_{b{\rm{j}}m, q}}(n)} \end{aligned} \right. $

(16)

式中， ${s_{az, p}}(n + 1)$ 、 ${s_{bz, p}}(n)$ 分别表示A通道n+1时刻和B通道n时刻接收的成像测绘带 $P$ 中第 $p$ 真实点所反射的SAR信号。记自动相位搜索过程中的搜索相位 $\Delta {\varphi _j}^\prime (n)$ ，结合式(14)—式(16)对 $A$ 通道相位补偿后与 $B$ 通道相消可得差信号为

$ \begin{aligned} \Delta s\left( n \right) = & \sum {{s_b}\left( n \right)} - \sum {{s_a}(n + 1)} \cdot \exp \left( {{\rm{j}}\Delta {\varphi _j}^\prime (n)} \right) = \\ & \sum\limits_{p = 1}^P {\left( {{s_{b{\textit{z}},p}}(n) - {s_{a{\textit{z}},p}}(n + 1) \cdot \exp \left( {{\rm{j}}\Delta {\varphi _j}^\prime (n)} \right)} \right)} \;\; + \\ & \sum\limits_{q = 1}^Q {{s_{b{\rm{j}},q}}(n)} \cdot \exp \left( {{\rm{j}}{\beta _m}\cos (2{\text{π}} {f_m}nT)} \right) \cdot \\ & \left( {1 - \exp \left( {{\rm{j}}\Delta {\varphi _j}^\prime (n) - {\rm{j}}\Delta {\varphi _j}(n) + } \right.} \right.\\ & \left. {\left. {{\rm{j}}{\beta _m}\cos \left( {2{\text{π}}{f_m}(n + 1)T} \right) - {\rm{j}}{\beta _m}\cos (2{\text{π}} {f_m}nT)} \right)} \right) = \\ & \sum\limits_{p = 1}^P {\left( {{s_{b{\textit{z}},p}}(n)\left( {1 - \exp \left( {{\rm{j}}\Delta {\varphi _j}^\prime (n) - {\rm{j}}\Delta {\varphi _{{\textit{z}},p}}(n)} \right)} \right)} \right)} \; + \\ & \sum\limits_{q = 1}^Q {{s_{bjm,q}}(n)} \left( {1 - \exp \left( {{\rm{j}}\Delta {\varphi _j}^\prime (n) - {\rm{j}}\Delta {\varphi _j}(n) - } \right.} \right.\\ & \left. {\left. {{\rm{j}}2{\beta _m}\sin ({\text{π}}{f_m}T)\sin ({\text{π}}{f_m}nT + {\text{π}}{f_m}T)} \right)} \right) \end{aligned} $

(17)

式中， $\Delta {\varphi _{{\textit{z}}, p}}(n)$ 表示两通道接收的第 $p$ 点反射的真实回波信号相位差。分析式(17)可知差信号 $\Delta s(n)$ 由两部分组成，第1个求和项为真实目标回波分量，第2个求和项为干扰分量。观察干扰分量，可在 $[ - {\text{π}}, {\text{π}}]$ 范围内搜索到相位

$\Delta {\varphi _{\rm{j}}}^\prime (n) \!=\! \Delta {\varphi _{\rm{j}}}(n) \!+\! 2{\beta _m}\sin ({\text{π}}{f_m}T)\sin (2{\text{π}}{f_m}Tn \!+\! {\text{π}}{f_m}T) \!+\! 2k{\text{π}}$

(18)

当搜索相位 $\Delta {\varphi _j}^\prime (n)$ 满足式(18)时，差信号 $\Delta s(n)$ 中的干扰分量可被完全抑制为0，从而差信号能量获得了最大程度的降低，符合自动相位搜索法的能量最小原则，故此时的 $\Delta {\varphi _j}^\prime (n)$ 即为 $n$ 时刻补偿相位最终估计结果。可以看出估计的补偿相位在原补偿相位 $\Delta {\varphi _j}(n)$ 的基础上进一步受到关于慢时间 ${t_{\rm{a}}}$ ( ${t_{\rm{a}}} = nT$ )的正弦函数调制，调制指数和调制频率分别为

$\left\{ \begin{aligned} &{\beta _m}^\prime = 2{\beta _m}\sin ({\text{π}}{f_m}T) \\ & {f_m}^\prime = {f_m} \end{aligned} \right.$

(19)

因此方位向间歇采样虽然能够大幅改变相位差的分布，却并不影响双通道对消系统抑制干扰分量。但当采用式(18)所示的补偿相位代入式(17)进行补偿时，结合 ${\rm{Fresnel}}$ 近似处理可得此时差信号形式为

$ \Delta s\left(n \right) = \sum\limits_{p = 1}^P {\left( {{s_{b{\textit{z}}, p}}(n)\left( {1 - \exp \left(\begin{gathered} {\rm{j}}2{\beta _m}\sin ({\text{π}}{f_m}T)\sin (2{\text{π}}{f_m}Tn + {\text{π}}{f_m}T) + {\rm{j}}{{2{\text{π}}D({x_{{\rm{z}}, p}} - {x_{\rm{j}}})}/{({\textit{λ}} {R_{j0}})}} \end{gathered} \right)} \right)} \right)} $

(20)

式中， ${x_{{\rm{z}}, p}}$ 为成像测绘带 $P$ 内第 $p$ 点的真实方位向坐标。分析式(19)可知，此时差信号中已无干扰分量，但与式(5)所示的传统散射波对消结果相比，真实目标回波分量中新增了关于慢时间 ${t_{\rm{a}}}$ 的正弦调制项 $\exp (2{\beta _m}\sin ({\text{π}}{f_m}T)\sin (2{\text{π}}{f_m}{t_{\rm{a}}} +{\text{π}}{f_m}T))$ ，其调制指数和调制频率与式(19)相同。

由于该调制项是关于慢时间 ${t_{\rm{a}}}$ 的正弦函数，在与真实目标回波信号 ${s_{bz, p}}(n)$ 相乘时，实际上是完成了对真实回波信号 ${s_{bz, p}}(n)$ 的方位向正弦调相。因此在经过方位向匹配滤波后，该正弦调相带来的结果应当与第2节余弦调相分析方法相同，即真实目标(场景)将在方位向上呈现周期性的重复搬移，且搬移后的场景间隔为

$\Delta x' = \left| {v{f_m}^\prime /{\mu _a}} \right|$

(21)

而且第 $n$ 阶搬移目标(场景)的幅度与贝塞尔函数 ${J_n}({\beta _m}^\prime)$ 相关。同时大量真实目标的回波信号仍能被削弱、抑制或增强，最终对真实场景的对消成像结果造成严重破坏。

需要指出的是，由于多通道SAR干扰抑制技术的本质与SAR双通道对消相同，都是通过提取和利用多个通道所接收信号的相位关系来实现对干扰信号的区分和消除，因此方位向相位调制干扰的技术应用及其相关结论同样可以拓展到对抗多通道SAR干扰抑制技术。下面以SAR双通道对消系统为例对本文干扰方法的影响效果进行验证分析。

设置SAR双通道对消系统工作于正侧视，实验参数设置如表1所示，系统平台高度为6000 m。成像方位向范围为 $[ - 110\;{\rm{m}}, 110\;{\rm{m}}{\kern 1pt} ]$ ，距离向范围为 $[9900\;{\rm{m}}, 10100{\kern 1pt} \;{\rm{m}}{\kern 1pt} {\kern 1pt} ]$ 。图3为无干扰时真实场景的SAR成像，图中长方形标记区域为特定散射区域，三角形标记为干扰站 $J$ 位置，坐标为 $(9910\;, 0{\kern 1pt} {\kern 1pt})$ ，实验过程中干扰站位置与散射区域不变。

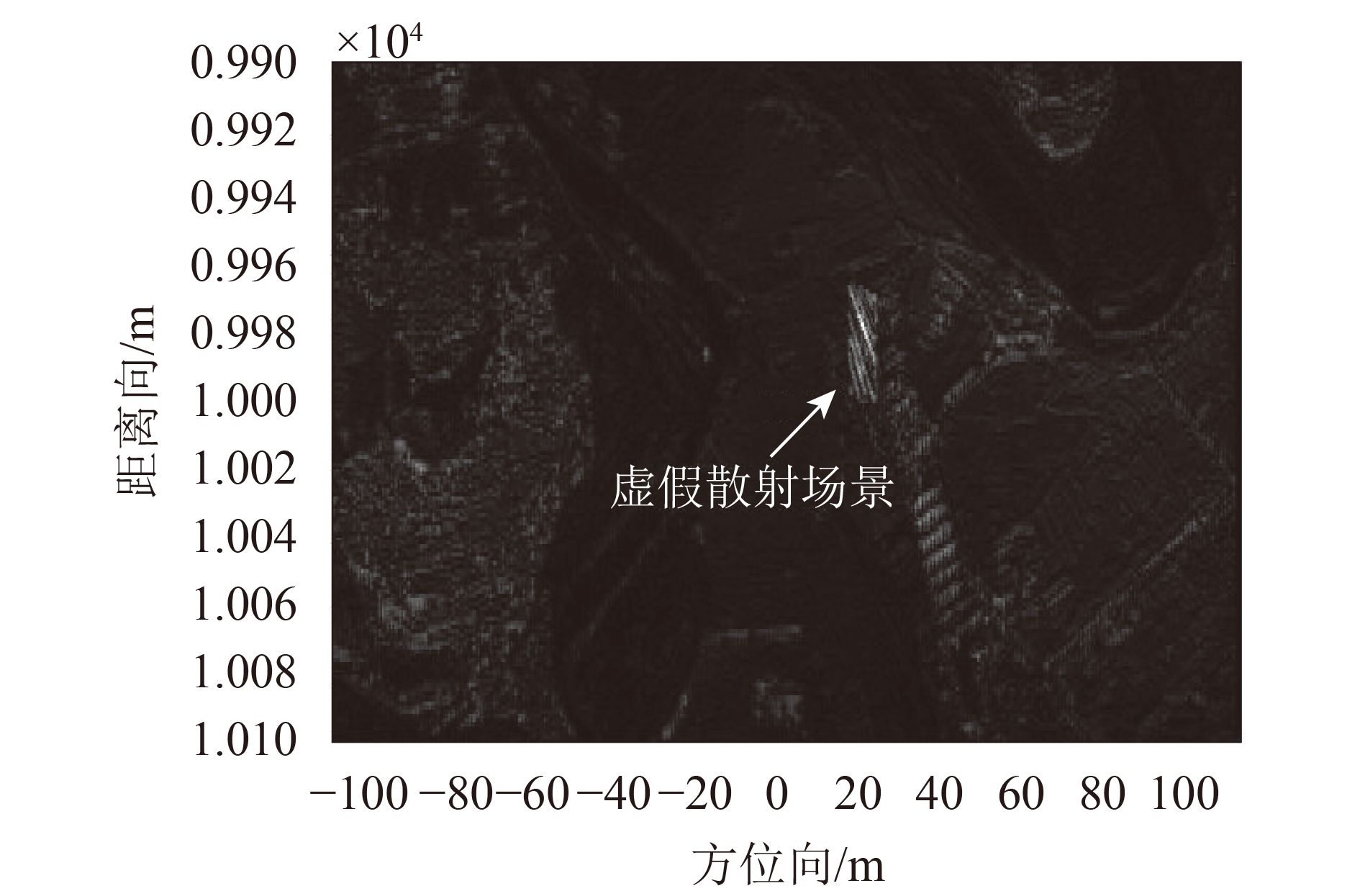
当干扰机对散射区域实施传统的散射波干扰时，SAR成像(未进行双通道对消)结果如图4所示，在原散射区域的左下方形成虚假的面状散射场景。这是因为SAR接收到的散射波干扰信号来自于散射区域的所有点目标，并且携有地物目标的散射信息。并且散射波信号传播路径的变化使得干扰成像中各散射点的相对位置发生了改变，最终形成对散射区域的复制搬移和畸变(刘业民 等，2011；Huang 等，2015)，具有较好的欺骗和遮蔽干扰效果。

传统散射波干扰的双通道对消结果如图5所示，比较图4可以看出虚假散射场景已经被完全抑制，散射波干扰失效。同时依据式(5)可知对消后真实目标回波信号受到调制，使得在方位向上接近干扰站的真实目标呈现出幅度的低谷，场景成像沿方位向形成对消暗条纹。仿真结果与理论分析一致，有效验证了系统对散射波干扰的对消性能。

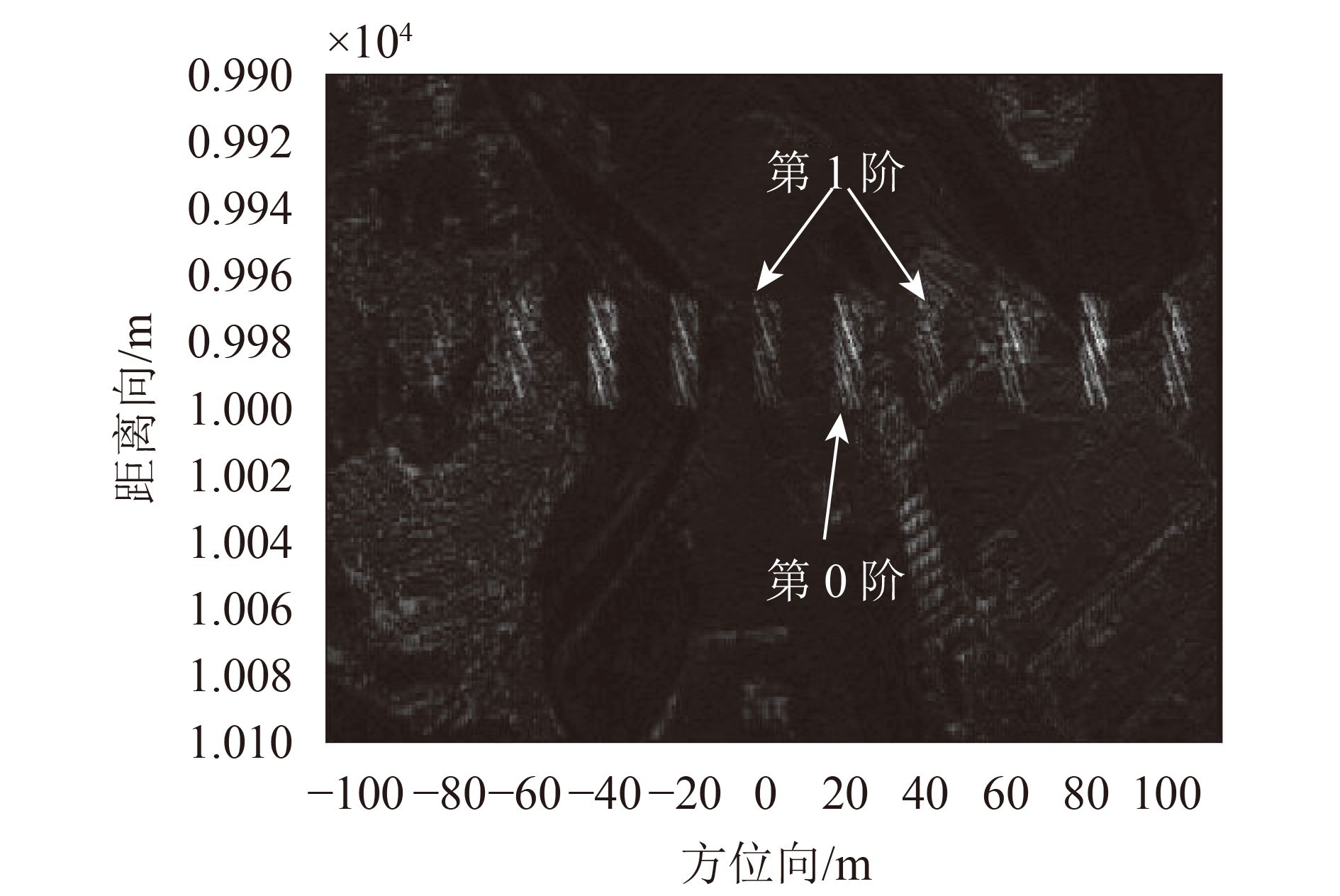
对传统散射波干扰进行方位向余弦调相，设置调制参数为 $\,\,{\beta _m} = 4.3$ ， ${f_m} = 27\;{\rm{Hz}}$ ，此时SAR成像结果(未进行双通道对消)如图6所示，余弦调相散射波干扰在方位向上形成多个虚假散射场景。其中第0阶虚假散射场景的位置与图4相同，相邻场景中心的间隔约为20.2 m，且高阶虚假场景幅度由于和 ${J_n}(\,{\beta _m})$ 相关而逐渐减弱，最终“淹没”在两侧的场景成像中，干扰效果与式(13)分析计算结果基本相同。

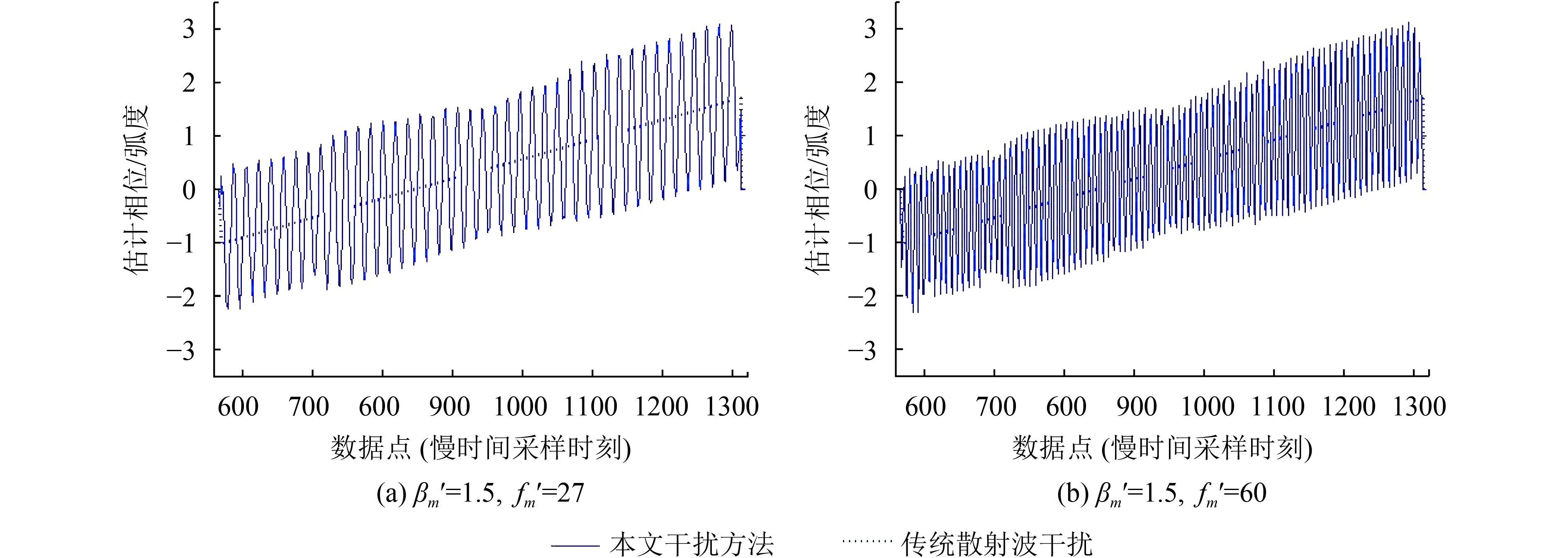
下面针对本文干扰方法对SAR双通道对消系统的影响进行仿真分析，结合式(19)设置干扰参数：正弦调制指数均为 $\,\,{\beta _m}^\prime = 1.5$ ，调制频率分别为27 Hz和60 Hz。此时系统通过自动相位搜索法所估计的补偿相位如图7中实线所示，虚线为传统散射波干扰下的补偿相位 $\Delta {\varphi _j}(n)$ 。从图8中可以看出，估计相位呈现出以 $\Delta {\varphi _j}(n)$ 中心的正弦状态变化，波幅约为1.5，即与 $\,\,{\beta _m}^\prime $ 相近；变化频率分别约为27 Hz和60 Hz，即与 ${f_m}^\prime $ 设相近。可见本文干扰方法能够适应相位搜索过程中的能量最小原则，从而大幅改变补偿相位的估计结果，所达到的影响效果与式(18)的理论分析一致，下面进一步对相位估计后的对消结果进行验证。

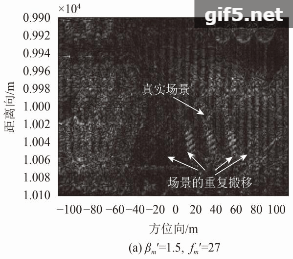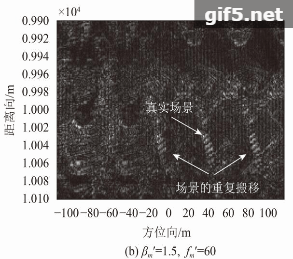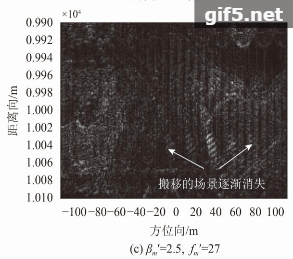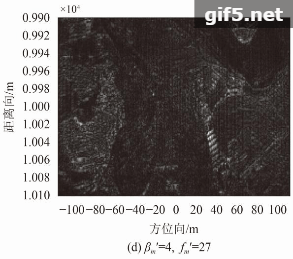
图8为多种干扰参数下余弦调相散射波干扰的双通道对消成像。从多个图中可以看出，干扰形成的虚假散射场景经过对消处理后被完全抑制，但同时真实场景成像受到了严重破坏。以图8(a)为例分析可知，真实场景在方位向上呈现出多次重复和搬移，移位的重叠影像遮挡了原有地物信息，同时在图像方位向上显现出较为密集的明暗条纹，这些结果均与式(20)理论分析一致。显然，以真实场景信息损失来换取干扰分量抑制是得不偿失的。对比图8(a)和图8(b)，由于箭头所指的地物场景特征较为明显，以其为参照物可以充分明确真实场景搬移后的间隔和调制频率 ${f_m}^\prime $ 的正比关系。根据式(21)计算可得在27 Hz和60 Hz的调制频率下，场景搬移间隔 $\Delta x'$ 分别为20.33 m和45.18 m，与图8(a)、图8(b)所示的间隔基本一致。

进一步分析调制指数 $\,\,{\beta _m}^\prime $ 对成像结果的影响， ${f_m}^\prime $ 均设置为27 Hz， $\,\,{\beta _m}^\prime $ 依次设为1.5、2.5和4，对消成像依次如图8(a)、图8(c)和图8(d)所示。通过观察可得，在调制频率不变的情况下，随着调制指数 $\,\,{\beta _m}^\prime $ 逐渐增大，搬移的场景幅度逐渐减小，在 $\,\,{\beta _m}^\prime = 4$ 时已无法看到场景的重叠影像，此时干扰效果大幅下降。这是由于第 $n$ 阶搬移场景的幅度与 ${J_n}(\,{\beta _m}^\prime)$ 成正相关，而贝塞尔函数幅值随 $\,\,{\beta _m}^\prime $ 增大而减小。因此在对双通道对消系统实施干扰时，可根据需要选取合适的调制频率 ${f_m}$ ，再结合式(19)设置余弦调制指数 $\,\,{\beta _m}$ 以满足 $\,\,{\beta _m}^\prime $ 在1—2。

多通道对消技术对多种类型的干扰信号均具有良好的抑制性能，因此本文对传统散射波干扰信号进行方位向余弦调相改进，并分析了其对双通道对消系统的影响效果。研究结果表明：该干扰方法在SAR单通道成像中可形成多个方位向虚假散射场景；在SAR双通道对消中可改变补偿相位的估计结果，使得真实场景成像在方位向上被重复搬移，造成多个影像重叠的效果，并且通过设置余弦调制频率和指数等干扰参数可有效控制干扰效果。本文干扰方法具有灵活可控、可实施性强、对侦察依赖度低和干扰隐蔽性好的特点，为对抗常规SAR和多通道对消抗干扰技术提供了有效途径。鉴于方位向相位调制的干扰方法能够影响多通道SAR对接收信号相位信息的提取结果，因此可为下一步对抗其他类型多通道SAR系统提供更多具有针对性的干扰思路和具有特定效果的干扰方案。