出版日期: 2019-01-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20197518
2019 | Volumn23 | Number 1
上一篇 | 下一篇

全波形激光雷达回波分解方法

李洪鹏¹ , 李国元² , 蔡志坚³ , 吴冠豪¹

1. 清华大学精密仪器系精密测试技术及仪器国家重点实验室，北京 100084

2. 国家测绘地理信息局卫星测绘应用中心，北京 100048

3. 苏州大学物理光电与能源学部，苏州 215006

收稿日期: 2018-01-08

基金项目: 国家高分遥感测绘应用示范系统课题(编号：AH1601-8)；国家自然科学基金(编号：51405317)；江苏省自然基金(编号：BK20140358)

第一作者简介: 李洪鹏，1992年生，男，硕士研究生，研究方向为激光雷达及其波形分析。E-mail：lhp15@mails.tsinghua.edu.cn

通信作者简介: 吴冠豪，1981年生，男，副教授，研究方向为激光雷达及光频梳测量。E-mail：guanhaowu@mail.tsinghua.edu.cn

摘要

全波形激光雷达的回波中携带了被测目标的距离与特征信息，为了获取这些信息，本文提出了一种回波分解方法。本方法将原始的全波形回波分解为几个独立的高斯脉冲，并得到其函数表达式，从而提取出被测目标的距离等信息。分解过程中，首先，采用可变阈值的经验模态分解滤波法(EMD-soft)对原始波形进行滤波和噪声水平评估；其次，采用一套应对多种波形组成的初始参数估计方法，获取后续拟合所需的初始参数；最后，采用LM(Levenberg-Marquardt)优化算法对回波进行拟合优化，从而获取全波形回波中包含的独立高斯脉冲及其函数表达式。仿真波形的分解实验表明，分解误差在0.1 ns量级，换算成距离误差为15 mm，通过实验室自制的全波形激光雷达实验系统获取的回波的分解实验表明，分解的距离误差小于0.1 m。对比另外两种高斯分解方法对于相同仿真与实验数据的分解结果可以看出，本方法在分解成功率与精度上都有较大的提高。回波分解后的独立高斯脉冲中，除距离外还含有被测目标的反射率、粗糙度、面型等丰富的信息，回波分解方法作为回波分析的基础，将在遥感、测绘等生产与科研领域中发挥非常重要的作用。

关键词

全波形激光雷达, 回波分解, 经验模态分解(EMD), LM(Levenberg–Marquardt)优化算法

Full-waveform LiDAR echo decomposition method

LI Hongpeng¹ , LI Guoyuan² , CAI Zhijian³ , WU Guanhao¹

1.State Key Laboratory of Precision Measurement Technology and Instruments, Department of Precision Instrument, Tsinghua University, Beijing 100084, China

2.Satellite Surveying and Mapping Application Center, NASG, Beijing 100048, China

3.College of Physics, Optoelectronics and Energy, Soochow University, Suzhou 215006, China

Abstract

The echoes of full-waveform light detection and ranging (LiDAR) contain information on the targets such as distances and properties. To access such information, we demonstrate an echo decomposition method based on soft-thresholding Empirical Mode Decomposition (EMD-soft) filter, Levenberg–Marquardt (LM) optimization, and a method to estimate the initial parameters consisting of a variety of waveforms. This method decomposes raw full-waveform echoes into independent Gaussian pulses and derives their function expressions. Distances and properties of the targets can be extracted from the parameters of these Gaussian pulses. First, EMD-soft is used to filter the noise of raw echoes and estimate the amount of noise. Then, initial parameters for follow-up optimization are estimated through peak and inflection points of the filtered echoes by a given process. Lastly, after these initial parameters are input, LM optimization is applied to optimize the parameters, and function expressions of Gaussian pulses can be obtained through the parameters. Finally, information on the targets can be accurately extracted. Simulations and experiments are carried out to evaluate the performance of the proposed method. Simulated waveforms are generated by adding Gaussian white noise into a waveform consisting of several independent Gaussian pulses. Decomposition experiments of these simulated waveforms indicate that the decomposition error of this method is around 0.1 ns, which means 15 mm in ranging error. In actual experiments, a laboratory-built full-waveform LiDAR experimental system is utilized to generate and obtain echoes. Decomposition experiments of these real waveforms also show that the ranging error of this method is less than 0.1 m. Compared with two other Gaussian decomposition methods in decomposing the same echoes mentioned above, this method shows enhanced decomposition success rate and accuracy. The proposed method realizes high success rate and accuracy decomposition. It can provide reliable data for the subsequent analysis and will play an important role in many fields, such as remote sensing and mapping. Compared with other decomposition methods, the EMD-soft we used does not have a threshold of filter frequency, that is, it will be effective in any frequency, unlike some other filters that will make mistakes when close to their thresholds. In addition, EMD-soft does not need a given kernel function or parameter, which means it is a more generic method to deal with various LiDAR echoes. LM optimization is one of the most popular algorithms for optimizing LiDAR echoes, but requiring high-accuracy initial parameters is a big problem for the algorithm. Sometimes if the initial parameters do not have enough accuracy, the algorithm may converge to a local minimum instead of a global minimum and lead to a wrong fitting. Thus, in this method, a special process is realized in the section on evaluating initial parameters and enhancing the optimization effect from another way. Echo decomposition is the foundation of echo analysis. We will try to extract more properties of targets from the decomposed waveforms and build the functional relationship of these properties with the parameters of waveforms in future work.

Key words

full-waveform LiDAR, echo decomposition, Empirical Mode Decomposition (EMD), LM (Levenberg–Marquardt) optimization

1 引　言

激光雷达是一种以激光作为光源的主动式遥感技术。激光光源发射一束短脉冲激光，经过目标的后向散射后，使用探测器接收这一回波脉冲，通过高精度的时间测量系统，获取出射脉冲和回波脉冲之间的飞行时间，即可借此计算出目标与测量系统之间的距离(Wagner 等，2006)。而相比普通的激光雷达，全波形激光雷达通过数字化采样获取了回波脉冲的完整波形(Leeuwen 等，2011)，从中不仅可以获取目标的距离信息，还可以提取出激光足印内目标的几何与物理特征，如粗糙度(Shi 等，2013)、倾斜角(Mahoney 等，2014；Li 等，2012)、森林冠盖结构(Kotchenova 等，2003；Hovi和Korpela，2014；Bye 等，2017)、水深(Pan 等，2015)等，此外，全波形回波数据也可以用来辅助地物分类(Koenig和Höfle，2016)。

全波形回波脉冲可以认为是在一个激光脚印中，不同距离的多个目标面散射后产生的单回波脉冲的叠加。因此，可以通过分解全波形回波的方式获取对应不同目标面的单脉冲，进而由分析这些单脉冲的参数得到相应目标面的距离与其他特征信息(Mallet和Bretar，2009)。分解全波形回波的方法通常包含对原始波形的滤波与拟合，滤波的同时需要进行噪声水平的估计，拟合过程则包括初始参数估计和拟合优化两部分(Hofton 等，2000)。

当前常用的全波形回波滤波法主要有低通滤波、维纳滤波(Jutzi和Stilla，2006)、高斯平滑滤波(Hofton 等，2000；Xu 等，2016)和小波分解滤波(Zhou 等，2013；Li 等，2017)等。低通滤波对于频率在截止频率附近的噪声的滤波效果较差。维纳滤波需要对输入信号与预期输出信号之间的互相关向量的预估计，实现难度较大。而高斯平滑滤波存在一个核心问题，即如何选取合适的高斯核函数的脉宽参数，脉宽的变化会对滤波的结果产生极大的影响。同样，小波分解滤波也需要人为选择小波基函数，而小波基函数的选择目前缺少一般性的选择原则。因而，本文使用了可变阈值的经验模态分解滤波法 (EMD-soft)对全波形回波进行滤波，并同时估计其噪声水平。

目前广泛使用在全波形回波拟合优化上的算法主要是LM (Levenberg-Marquard)算法(Qin 等，2012；Ma 等，2017；Marquardt，1963)与期望最大化EM(Expectation Maximization)算法(Soederman 等，2005；Dempster 等，1977)，两种方法都具有较高的拟合速度与拟合精度，但也面临着相同的问题，即两种方法都对于初始参数的准确性具有非常高的要求，如果输入的初始参数与期望值差距太大，会导致拟合收敛到局部最小值，而不是所需的全局最小值，甚至导致拟合发散。因此，本文着重完善了LM算法初始参数估计过程，得到更加准确的初始参数，进而提高拟合精度。

2 回波分解算法

2.1 分解模型

全波形激光雷达系统中使用的激光脉冲近似为高斯函数，因此本文选择高斯函数作为分解模型，此时获取的全波形回波可以表示为式(1)所示的高斯模型

$G(t) = \sum\limits_{i = 1}^N {{a_i}{{\rm{e}}^{ - \frac{{{{(t - {t_i})}^2}}}{{f_i^2/(4\ln 2)}}}} + n(t)} $

(1)

式中，N为回波中的高斯脉冲数，a_i、t_i、f_i分别为第i个高斯脉冲的幅值、位置与半高宽， $n(t)$ 为噪声带来的残余误差，上述表达式中 ${f_i}$ 可以直接对应高斯函数的半高宽，因此使用该表达式便于参数的对应。式中，每一个高斯脉冲都由相应的目标面的散射特性决定。

2.2 滤波与噪声水平估计

由于全波形回波在获取过程中，会加入由背景光、光电探测器和模数转换器等带来的噪声，在拟合与分解之前需要对采集到的原始波形进行滤波，这里我们采用的是EMD-soft滤波法。

经验模态分解EMD(Empirical Mode Decomposition)理论认为，任何信号都是由一些不同的本征模态函数IMF(Intrinsic Mode Function)组成的

$X(t) = \sum\limits_{j = 1}^n {{{\rm{IMF}}_j}(t) + {r_n}(t)} $

(2)

式中，X(t)表示原始信号，IMF_j(t)表示分解出来的n个本征模态函数，r_n(t)表示分解后的余项，也即信号的单调趋势项。每个IMF必须符合以下两个条件：两个零点之间只能存在一个极值点，且由其局部最大值和局部最小值定义的上下包络必须均值为零。通过反复从信号中减去上下包络的均值，直到残量满足IMF的条件的方法获取IMF，而后对被减去的部分重复上述步骤，获取更多的IMF直到最终剩余的单调趋势项，即完成了整个EMD过程(Huang 等，1998；Li 等，2014)。

从滤波的角度来看，EMD过程中，逐个提取出的IMF分别包含了不同频率的分量，先提取出的IMF包含了较高频率，后提取出的IMF包含较低频率，最终剩余一个单调趋势项，因而通过舍去含不同频率分量的IMF，即可实现不同的滤波效果，由于全波形回波中噪声的频率远高于高斯脉冲的频率，本文采用舍弃较高频率的IMF来实现低通滤波的效果，即

${F_0}(t) = \sum\limits_{j = p + 1}^n {{{\rm{IMF}}_j}(t) + {r_n}(t)} $

(3)

式中， ${F_0}(t)$ 为滤波后的波形，舍去前p个IMF。

然而直接舍去前p个IMF有可能会丢失部分有用的信息，因此，需要对EMD过程进行一些改进，从而将可能的有用信息从被舍去的IMF中提取回来，由于该改进方法采用了一个可变的阈值，或者说柔性的阈值，因而称之为EMD-soft滤波法。在EMD过程结束后，通过下述方法从被舍去的IMF中提取有用信息 ${s_j}(t)$ (Boudraa 等，2013)

${\tau _j} = {\sigma _j}\sqrt {2\log L} $

(4)

${\sigma _j} = {{\rm{MAD}}_j}/0.6745$

(5)

$ {{\rm{MAD}}_j} = {\rm{Median}}|IM{F_j}(t) - {\rm{Median}}[{{\rm{IMF}}_j}(t)]| $

(6)

${s_j}(t) = \left\{ \begin{array}{l} {{\rm{IMF}}_j}(t) - {\tau _j},{{\rm{IMF}}_j}(t) \geqslant {\tau _j}\\ 0,\left| {{{\rm{IMF}}_j}(t)} \right| < {\tau _j}\\ {{\rm{IMF}}_j}(t) + {\tau _j},{{\rm{IMF}}_j}(t) \leqslant - {\tau _j} \end{array} \right.$

(7)

式中， $j \leqslant p$ ， ${\sigma _j}$ 为对 ${{\rm{IMF}}_j}$ 的噪声估计，L为 ${{\rm{IMF}}_j}$ 的数组长度。将提取出的 ${s_j}(t)$ 加到 ${F_0}(t)$ 中即得到了经过EMD-soft滤波法处理后的回波波形 $F(t)$

$F(t) = {F_0}(t) + \sum\limits_{j = 1}^p {{s_j}(t)} $

(8)

滤波完成后，可以对噪声水平进行估计

${\rm{Noise}}(t) = X(t) - F(t)$

(9)

将 ${\rm{Noise}}(t)$ 的均值与标准差记为 ${\mu _n}$ 与 ${\sigma _n}$ 。

2.3 初始参数估计

由于后续的拟合优化需要提供较为准确的初始参数，即分解模型中a_i、t_i、f_i的估计，因而在优化之前需要对滤波后的回波进行初始参数的估计。通过数值微分获取 $F(t)$ 的一阶与二阶导数，并分别由一阶、二阶导数的零点得到 $F(t)$ 的极值点与拐点。

由于滤波并不能完全去除原始波形中的噪声，残余的一些噪声可能会带来错误的极值点与拐点，所以为了避免这一问题，需要设定一个噪声阈值 $t{h_n}$

$t{h_n}{\rm{ = }}{\mu _n} + 3{\sigma _n}$

(10)

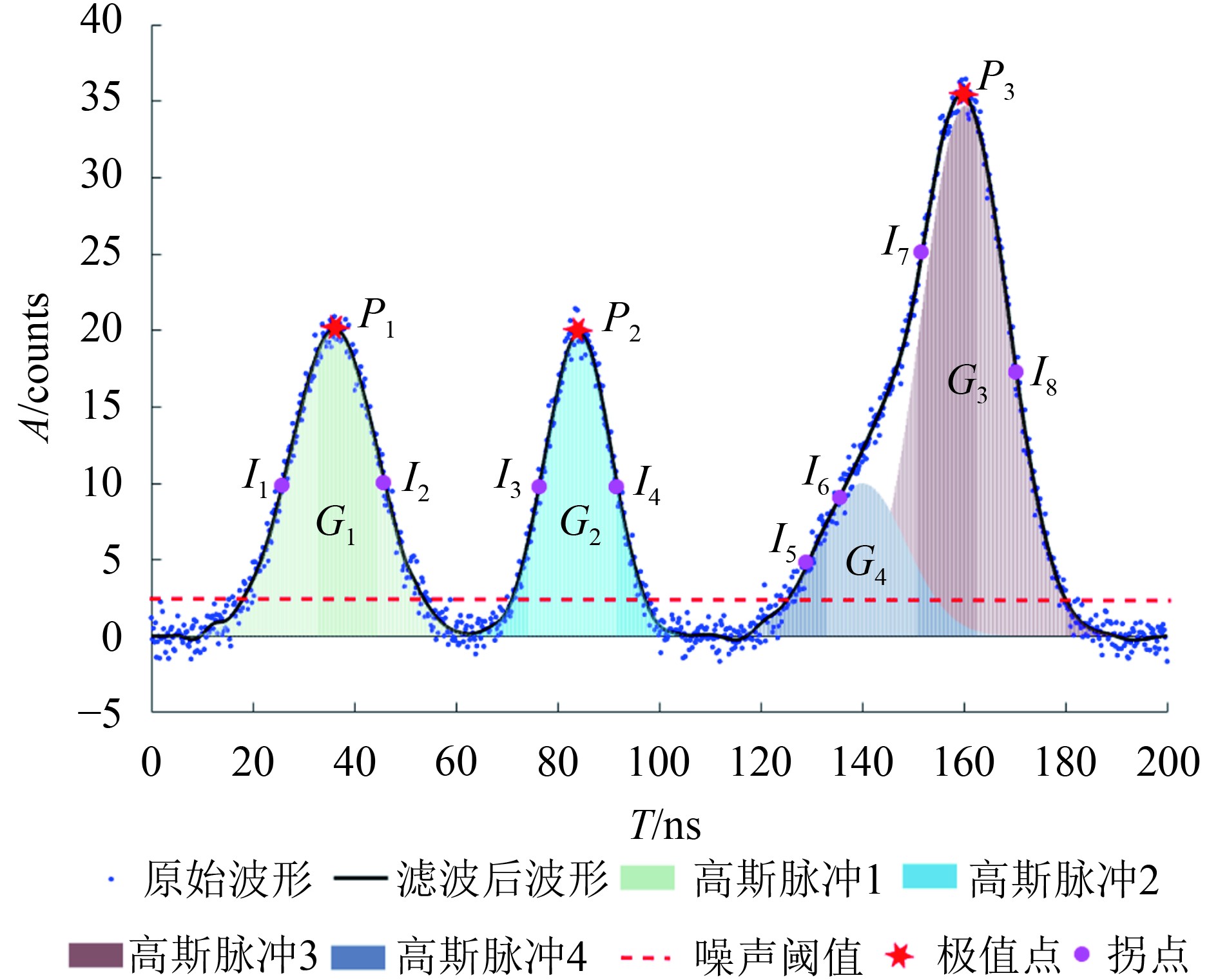
${\mu _n}$ 与 ${\sigma _n}$ 为上一节中得到的噪声的均值与标准差。而后，在获取极值点与拐点的过程中，如果该点的幅值小于 $t{h_n}$ ，则认为该点是一个错误的极值点或拐点，将其忽略。此外，在计算一阶与二阶导数的过程中，还可以对导数进行EMD-soft滤波，以进一步减少残余噪声带来的误判。

全波形回波中的高斯脉冲，存在相互独立与相互交叠两种情况，相互独立的高斯脉冲可以通过极值点来确定其数量、幅值与位置，而相互交叠的高斯脉冲在一些情况下由于两个脉冲距离过于接近，其中一个脉冲的极值点被另一个脉冲掩盖，则需要通过其他的方法估计其初始参数。图1是一个含有4个高斯脉冲的全波形回波，4个高斯脉冲分别记为 ${G_1}$ 、 ${G_2}$ 、 ${G_3}$ 、 ${G_4}$ ，可以看到， ${G_1}$ 与 ${G_2}$ 为独立高斯脉冲，而 ${G_3}$ 与 ${G_4}$ 则相互交叠， ${G_3}$ 的极值点被 ${G_4}$ 掩盖，因而整个回波中只能得到3个极值点，将高斯脉冲数N暂记为3。

图 1 一个含有4个高斯脉冲的全波形回波

Fig. 1 A full-waveform echo with four Gaussian pulses

对于独立脉冲例如 ${G_1}$ ，其对应的极值点为 ${P_1}({t_{p1}}, {a_{p1}})$ ，则 ${a_{p1}}$ 、 ${t_{p1}}$ 可以作为 ${G_1}$ 幅值与位置的初始参数，而对于独立脉冲，极值点 ${P_1}$ 左右两侧的单调区间均只有一个拐点，即 ${I_1}({t_{I_1}}, {a_{I_1}})$ 与 ${I_2}({t_{I_2}}, {a_{I_2}})$ ，则其在时间轴上的差 ${f_1} = {t_{I_1}} + {t_{I_2}}$ 可以直接作为 ${G_1}$ 半高宽的初始参数。

对于相互交叠的脉冲例如 ${G_3}$ 与 ${G_4}$ ，只能得到一个极值点 ${P_3}$ ，但在 ${P_3}$ 左侧的单调区间中有3个拐点 ${I_5}$ 、 ${I_6}$ 、 ${I_7}$ ，我们把这种在某一极值点一侧的单调区间中有多于1个拐点的情况作为有脉冲被交叠掩盖的标志，此时将高斯脉冲数N的值改为N+1，并由 ${P_3}({t_{p3}}, {a_{p3}})$ 得到 ${G_3}$ 的幅值与位置的初始参数。 ${G_3}$ 的半高宽与 ${G_4}$ 的初始参数则需要进一步的分析：

对于一个高斯函数

$g(t) = {a_0}{{\rm{e}}^{ - \frac{{{{(t - {t_0})}^2}}}{{f_0^2/(4\ln 2)}}}}$

(11)

任意横坐标 $t$ 与中心位置 ${t_0}$ 的距离为 $\Delta t = \left| {t - {t_0}} \right|$ ，已知一高斯函数上任意两点的横坐标与中心位置的距离 $\Delta {t_1}$ 、 $\Delta {t_2}$ ，及其幅值比 ${a_1}/{a_2}$ ，可以求得该函数的半高宽 ${f_0}$

$\frac{{{a_1}}}{{{a_2}}} = \frac{{{a_0}{{\rm{e}}^{ - \frac{{\Delta t_1^2}}{{f_0^2/(4\ln 2)}}}}}}{{{a_0}{{\rm{e}}^{ - \frac{{\Delta t_2^2}}{{f_0^2/(4\ln 2)}}}}}} = {{\rm{e}}^{\frac{{\Delta t_2^2 - \Delta t_1^2}}{{f_0^2/(4\ln 2)}}}}$

(12)

即

${f_0} = 2\sqrt {\frac{{\Delta t_2^2 - \Delta t_1^2}}{{\ln \displaystyle\frac{{{a_1}}}{{{a_2}}}}}\ln 2} $

(13)

因而对于 ${G_3}$ ，其左侧拐点受到 ${G_4}$ 的影响，位置并不在半高宽处，但可以通过上述公式，由 ${P_3}$ 两侧与其最接近的两个拐点，即 ${I_7}({t_{I_7}}, {a_{I_7}})$ 与 ${I_8}({t_{I_8}}, {a_{I_8}})$ 来确定，独立脉冲的半高宽估计，是此方法在所取两个拐点恰好为半高宽对应的两点时的特殊情况。

而对于 ${G_4}$ ，由于 ${I_6}$ 并不一定恰好处在其极值点所在的位置，而且在有些情况下，由于 ${G_4}$ 与 ${G_3}$ 距离过近，会出现只能获取 ${I_5}$ 一个拐点的情况，因而对于这种极值点被掩盖的脉冲，需要采用另一种方法进行初始参数估计。认为 ${I_5}({t_{I_5}}, {a_{I_5}})$ 为 ${G_4}$ 的一个半高宽对应点，则幅值的初始参数可以由式(14)进行估计

${a_4} = 2({a_{I_5}} - {\mu _n}) + {\mu _n} = 2{a_{I_5}} - {\mu _n}$

(14)

而后在全波形回波中找到幅值最接近 ${a_4}$ 的点，其横坐标即可作为 ${G_4}$ 的位置初始参数，进而 ${I_5}$ 与该点在横轴上距离的两倍可作为 ${G_4}$ 的半高宽初始参数。

通过上述的所有方法，即可实现对回波中所有高斯脉冲的初始参数估计。

2.4 拟合优化

在经过前述的滤波与初始参数估计后，获取了回波中高斯脉冲的数量N以及每一个高斯脉冲对应函数表达式的幅值、位置和半高宽，即a_i、t_i、f_i的初始估计，利用这些参数对滤波后的回波 $F(t)$ 进行非线性最小二乘拟合，可以获取更加准确的高斯脉冲参数。

Levenberg-Marquardt(LM)法是一种被广泛用于激光雷达回波数据拟合优化的算法，它是对Gauss-Newton(GN)法的改进，通过加入参数 ${\mu _k}$ ，将GN法与最速下降法结合起来，在所拟合的数据接近收敛点时，算法趋于GN法，拥有GN法的快速收敛性，而当所拟合的数据远离收敛点时，算法趋于最速下降法，拥有最速下降法的强适应性，使LM法可以更加快速有效的完成拟合优化(Marquardt，1963)。

LM法的迭代公式如下

$\left\{ \begin{array}{l} {x_{k + 1}} = {x_k} + {d_k}\\ {d_k} = - {({{J}}_k^{\rm{T}}{{{J}}_k} + {\mu _k}I)^{ - 1}}{{J}}_k^{\rm{T}}{{{F}}_k} \end{array} \right.$

(15)

式中，F为N个高斯函数相加组成的拟合目标函数，N为之前获取的高斯脉冲数，J为F的Jacobian矩阵。当目标函数与回波 $F(t)$ 之差达到设定的阈值或迭代次数达到设定的上限，迭代停止，即可得到经过拟合优化后精度更高的高斯脉冲函数表达式，完成回波的分解。

3 仿真与结果

为了检验本分解方法的有效性与分解精度，使用高斯函数之和并加入高斯白噪声的方法对全波形回波进行仿真，采样率与采样时间分别设置为5 GHz和199 ns，与后面实验中采集实测回波时的参数相同。

仿真的函数表达式如下

$G(t) = \sum\limits_{i = 1}^N {{a_i}{{\rm{e}}^{ - \frac{{{{(t - {t_i})}^2}}}{{f_i^2/(4\ln 2)}}}} + n(t)}, 0 \leqslant t \leqslant 199$

(16)

式中，t为采样时间，N为回波中高斯脉冲的数量，设为1—4的随机整数，a_i、t_i、f_i为第i个高斯脉冲的幅值、位置与半高宽，分别设为3—30的随机整数、40—160 ns的随机数和10—20 ns的随机整数， $n(t)$ 为高斯白噪声，仿真中按照信噪比分别为15 dB、25 dB、35 dB、40 dB设置4组，每组的仿真总次数为500次。图2是一包含4个高斯脉冲，信噪比25 dB的仿真全波形回波。

图 2 仿真全波形回波

Fig. 2 A simulated full-waveform echo

分解实验中，将本方法与另外两种高斯分解方法进行对比，两种方法分别记为Hofton法(Hofton 等，2000)、Duong法(Duong，2010)，通过相同的评价参数比较3种方法的分解效果。

定义一些评价参数对仿真试验的结果进行评价。分解成功率S

$S{\rm{ = }}\frac{{{N_S}}}{{{N_0}}}$

(17)

式中， ${N_0}$ 为该组仿真的总回波数，此处为500， ${N_S}$ 为分解成功的回波数，这里定义满足分解后高斯脉冲数量与设定值相同，且每个高斯脉冲的位置与设定值误差小于1 ns这两个条件的回波分解为分解成功的回波。

其他评价参数有幅值、位置、半高宽与设定值之差的均值μ_a、μ_t、μ_f及其标准差σ_a、σ_t、σ_f，4种方法的分解结果如表1所示，分别列出了4种方法对于上述4组信噪比不同的仿真回波的分解结果评价参数值。

表 1 不同信噪比下的仿真评价参数
Table 1 Evaluation parameters of simulation under different SNRs

下载CSV

分解方法	信噪比/dB	S/%	μ_a	μ_t /ns	μ_f /ns	σ_a	σ_t /ns	σ_f /ns
Hofton法	15	46.5	–2.04	0.806	0.424	3.85	0.967	0.988
	25	62.3	–1.32	0.592	0.309	2.27	0.411	0.610
	35	77.6	–0.905	0.498	0.228	1.68	0.265	0.291
	40	87.8	–0.356	0.086	0.122	0.674	0.120	0.144
Duong法	15	48.6	–1.75	0.824	0.324	3.70	0.704	1.374
	25	62.9	–1.10	0.601	0.231	2.46	0.323	0.747
	35	79.8	–0.851	0.502	0.170	1.69	0.102	0.409
	40	88.2	–0.322	0.090	0.112	0.623	0.064	0.187
本文方法	15	78.3	–0.347	0.016	0.242	0.439	0.138	0.343
	25	79.4	–0.175	–0.004	0.170	0.241	0.119	0.257
	35	87.5	–0.107	0.001	0.091	0.112	0.033	0.085
	40	91.5	–0.096	0.001	0.078	0.066	0.010	0.032

由表1中的仿真结果可以看出，本文方法分解成功率在78.3%以上，位置与半高宽分解误差在0.1 ns量级，对应测距误差为15 mm，即厘米量级。随着信噪比的提高，分解的成功率与精度等都会有相应的提升，当原始波形信噪比达到40 dB时，分解成功率可以达到91.5%，位置与半高宽的分解误差也会达到0.01 ns量级，对应测距误差达到毫米量级，这也说明实际使用中分解方法的有效性与精度同时也受到硬件条件的较大影响。而对比其他两种方法，本方法的分解成功率有了极大的提高，同时分解误差也有了明显的下降。从表格中的数据也可以看出，本方法在信噪比较低的情况下具有更明显的优势，这一方面是由于EMD-soft滤波算法较其他两种算法使用的高斯平滑滤波的滤波效果更好，同时也是得益于本方法中初始参数估计算法相较于其他两种算法，对于交叠脉冲的参数估计以及参数估计的准确性都有较大的提高。

4 实验与结果

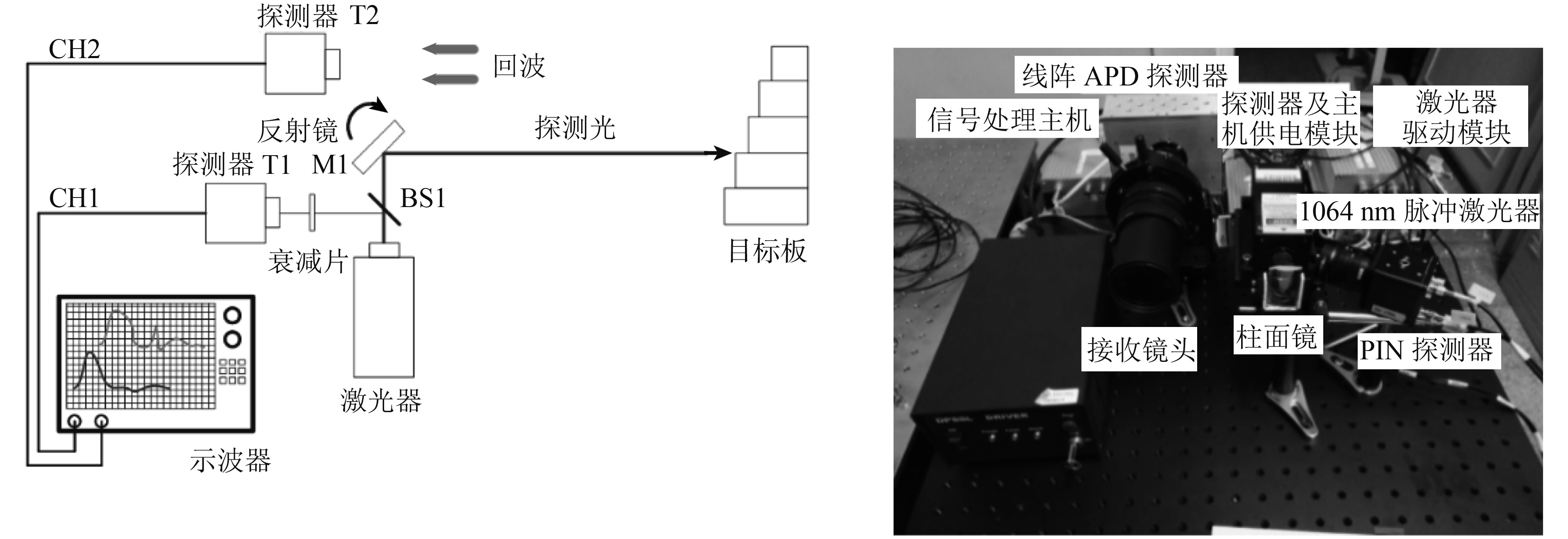
使用实验室自制的全波形激光雷达实验系统获取实测的全波形回波，并使用本方法进行分解。所用的激光雷达系统结构如图3所示，脉冲激光器波长为1064 nm，发射脉冲半高宽为15 ns，脉冲出射后分为两束，一束由光电探测器(PIN)T1接收作为出射波，另一束作为探测光经目标面散射后由雪崩二极管(APD)探测器T2接收作为回波，并使用示波器或采集卡采集全波形数据。

图 3 激光雷达实验系统

Fig. 3 LiDAR experimental system

实测回波的分解实验通过分解含有两个高斯脉冲的回波，计算出两个高斯脉冲对应的目标面间的距离，并对比实际目标面间距，来验证分解方法的精度。

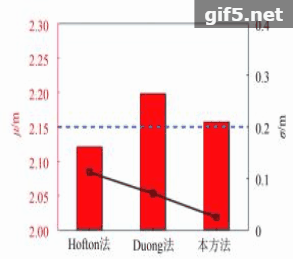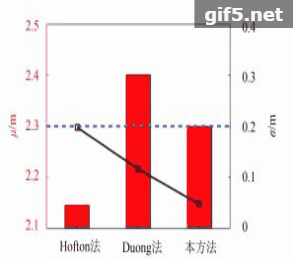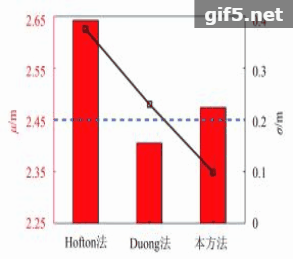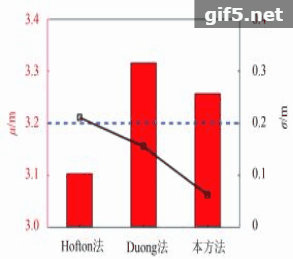
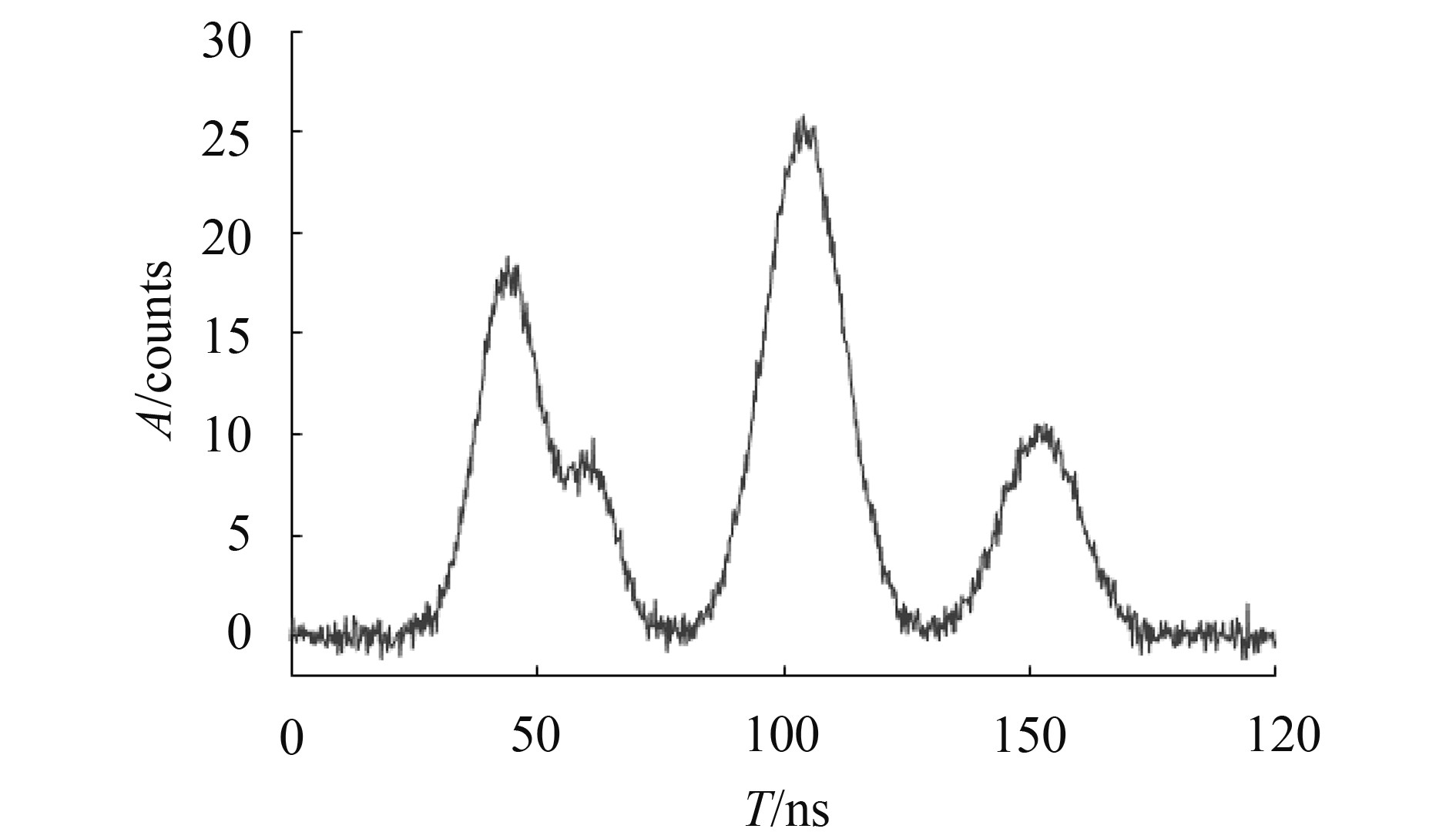
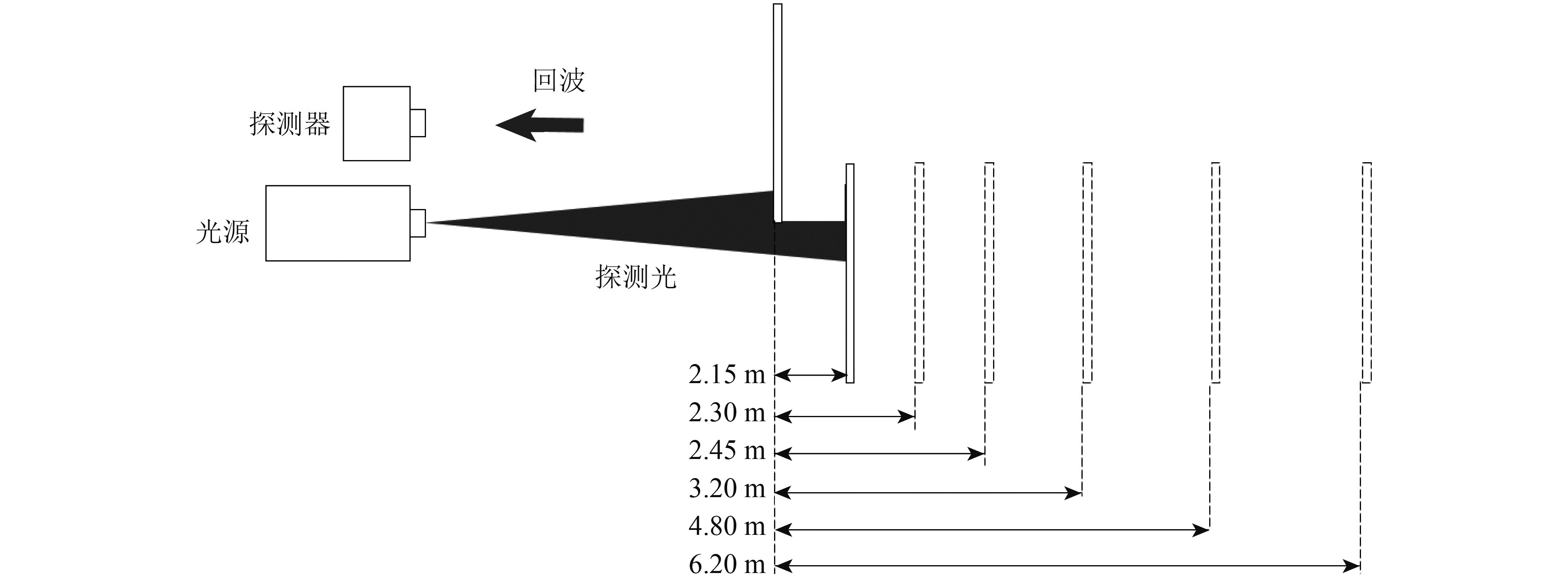
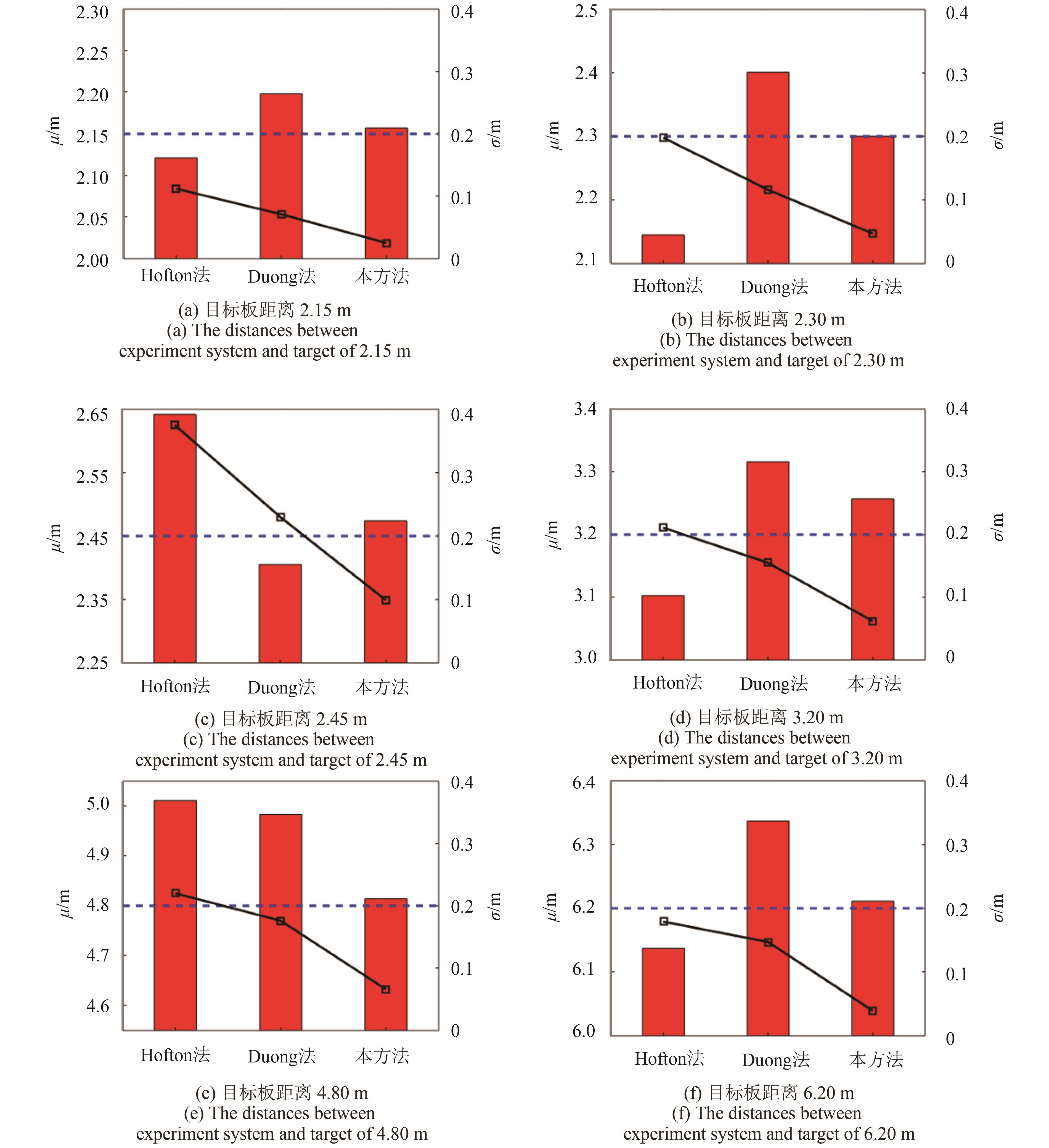
在距实验系统一定距离处设置两块目标板，使其各有一部分处于同一激光脚印中，调整两块目标板的距离，分别在2.15 m、2.30 m、2.45 m、3.20 m、4.80 m、6.20 m距离下各采集30组回波数据，图4是实验中目标板的分布图，图5是上述6组距离下的实测波形，图5(a)—(f)分别对应这6组距离，随着两目标板距离的增加，回波中的两个高斯脉冲在时间轴上的距离也逐渐增加，由交叠状态逐渐分离。将回波数据使用本分解方法以及前述的另外两种方法进行分解，得到两个高斯脉冲的时间差并换算为距离值，30组回波的距离平均值 $\mu $ 与标准差 $\sigma $ 如图6所示。

图 4 实验中目标板的分布图

Fig. 4 Distribution of the target boards setting in experiment

图 5 实测波形

Fig. 5 Measured waveforms

图 6 不同距离下分解回波得到的距离平均值与标准差(红色条形和黑色线分别代表回波分解得到的距离值的平均值 $\mu $ 和标准差 $\sigma $ ，蓝色线代表实际距离)

Fig. 6 Means and standard deviations of the distances obtained from decomposing echoes (Red bars and black lines represent the means $\mu $ and standard deviations $\sigma $ of distances derived from decomposition of the echoes respectively, blue lines represent the real distances)

由图6的实验结果可以看出，本方法的分解结果较其他两种方法更接近实际值，且多组回波分解的标准差也明显小于其他两种方法，证明了本方法分解误差更小，稳定性更好，实验中最大分解误差小于0.1 m，也在厘米量级，经过对噪声水平的估计，实测波形的信噪比约为27 dB，而误差与25 dB信噪比下的仿真结果处于同一数量级，考虑到实际实验中存在硬件系统或环境影响导致的波形变型等问题会影响到拟合效果，可以认为实验结果与仿真结果相符。

此外，3种算法在分解实际波形时的分解误差相比于分解仿真波形时，均有了一定的增大，其产生的原因主要在于回波实验中的APD探测器，APD管与后续跨阻放大电路中用到的运放等元器件对于脉冲信号的响应均会有一定的延迟，而该延迟时间相对于标称值存在一定的误差。查阅所用APD管与运放等的数据手册可知，其延迟时间的误差之和约为0.3 ns，即该误差会为单次测距结果加入约4.5 cm的误差，这一结果也符合实测数据与仿真数据分解后误差的增大量。该误差仅为单次测量中可能产生的偏差，是一个在真值附近浮动的随机误差，在实际测量中，在测量速度允许的范围内，通过多次测量取平均值的方法即可极大的消除其影响，上述的实测实验中，30次测量平均后均值存在的误差已经与仿真实验结果相近，证明了多次测量取均值可以消除该误差。

5 结　论

本文实现了一种基于EMD-soft滤波与LM优化算法的全波形激光雷达回波分解方法，通过对仿真波形和实测回波波形的分解，验证了本方法的有效性，同时得到了本方法将回波分解后的精度在0.1 ns量级，对应的距离精度在厘米量级，随着波形信噪比的提高，分解精度也会相应提高，达到毫米量级，实现了对全波形激光雷达回波的高精度分解，为后续进一步的回波分析提供了可靠的原始数据，将在遥感、测绘等生产与科研领域中发挥非常重要的作用。

相较于已有的回波分解方法，本方法采用的滤波算法不需要针对不同的回波数据设定不同的滤波参数，具有更好的普适性与可靠性；提出的初始参数估计方法提高了拟合初始参数的精度，进而提高了LM算法的拟合效果。与其他两种高斯分解方法的对比也直接证明了本方法在分解成功率上具有显著的优势，在分解精度上也有了明显的提升。

本方法可以从全波形回波数据中获取所有独立高斯脉冲的幅值、位置、半高宽等参数，其中除文中已提取到的距离信息外还有很多的其他的信息如反射率、粗糙度、面型等可以进行进一步的提取与分析。回波分解方法是回波分析的基础，接下来的工作中，我们将基于本分解方法与现有的实验系统，尝试提取出更多的特征信息，建立目标特征与回波参数的对应函数关系，实现回波与复杂面型之间的反演，并通过实验系统进行验证。

参考文献(References)

Boudraa A O, Cexus J C and Saidi Z. 2013. EMD-based signal noise reduction. International Journal of Signal Processing, 1 (1): 33–37.

Bye I J, North P R J, Los S O, Kljun N, Rosette J A B, Hopkinson C, Chasmer L and Mahoney C. 2017. Estimating forest canopy parameters from satellite waveform LiDAR by inversion of the FLIGHT three-dimensional radiative transfer model. Remote Sensing of Environment, 188 : 177–189. [DOI: 10.1016/J.RSE.2016.10.048]

Dempster A P, Laird N M and Rubin D B. 1977. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological), 39 (1): 1–38.

Duong H V. 2010. Processing and application of ICESat large footprint full waveform laser range data. Delft: Delft University of Technology

Hofton M A, Minster J B and Blair J B. 2000. Decomposition of laser altimeter waveforms. IEEE Transactions on Geoscience and Remote sensing, 38 (4): 1989–1996. [DOI: 10.1109/36.851780]

Hovi A and Korpela I. 2014. Real and simulated waveform-recording LiDAR data in juvenile boreal forest vegetation. Remote Sensing of Environment, 140 : 665–678. [DOI: 10.1016/j.rse.2013.10.003]

Huang N E, Shen Z, Long S R, Wu M C, Shih H H , Zheng Q N, Yen N C, Tung C C and Liu H H. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings: Mathematical, Physical and Engineering Sciences, 454 (1971): 903–995. [DOI: 10.1098/RSPA.1998.0193]

Jutzi B and Stilla U. 2006. Range determination with waveform recording laser systems using a Wiener Filter. ISPRS Journal of Photogrammetry and Remote Sensing, 61 (2): 95–107. [DOI: 10.1016/J.ISPRSJPRS.2006.09.001]

Koenig K and Höfle B. 2016. Full-waveform airborne laser scanning in vegetation studies—a review of point cloud and waveform features for tree species classification. Forests, 7 (9): 198 [DOI: 10.3390/F7090198]

Kotchenova S Y, Shabanov N V, Knyazikhin Y, Davis A B, Dubayah R and Myneni B R. 2003. Modeling lidar waveforms with time-dependent stochastic radiative transfer theory for remote estimations of forest structure. Journal of Geophysical Research, 108 (D15): 4484 [DOI: 10.1029/2002JD003288]

Li D, Xu L J and Li X L. 2017. Full-waveform LiDAR echo decomposition based on wavelet decomposition and particle swarm optimization. Measurement Science and Technology, 28 (4): 045205 [DOI: 10.1088/1361-6501/AA5C1E]

Li D, Xu L J, Li X L and Wu D. 2014. A novel full-waveform LiDAR echo decomposition method and simulation verification//Proceedings of 2014 IEEE International Conference on Imaging Systems and Techniques. Santorini, Greece: IEEE, 184–189 [DOI: 10.1109/IST.2014.6958470]

Li X L, Xu L J, Tian X R and Kong D M. 2012. Terrain slope estimation within footprint from ICESat/GLAS waveform: model and method. Journal of Applied Remote Sensing, 6 (1): 063534 [DOI: 10.1117/1.JRS.6.063534]

Ma H C, Zhou W W, Zhang L and Wang S Y. 2017. Decomposition of small-footprint full waveform LiDAR data based on generalized Gaussian model and grouping LM optimization. Measurement Science and Technology, 28 (4): 045203 [DOI: 10.1088/1361-6501/AA59F3]

Mahoney C, Kljun N, Los S O, Chasmer L, Hacker J M, Hopkinson C, North P R J, Rosette J A B and van Gorsel E. 2014. Slope Estimation from ICESat/GLAS. Remote Sensing, 6 (10): 10051–10069. [DOI: 10.3390/RS61010051]

Mallet C and Bretar F. 2009. Full-waveform topographic lidar: State-of-the-art. ISPRS Journal of Photogrammetry and Remote Sensing, 64 (1): 1–16. [DOI: 10.1016/J.ISPRSJPRS.2008.09.007]

Marquardt D W. 1963. An algorithm for least-squares estimation of nonlinear Parameters. Journal of the Society for Industrial and Applied Mathematics, 11 (2): 431–441. [DOI: 10.1137/0111030]

Pan Z G, Glennie C, Hartzell P, Fernandez-Diaz J C, Legleiter C and Overstreet B. 2015. Performance assessment of high resolution airborne full waveform LiDAR for shallow river bathymetry. Remote Sensing, 7 (5): 5133–5159. [DOI: 10.3390/RS70505133]

Qin Y C, Vu T T and Ban Y F. 2012. Toward an optimal algorithm for LiDAR waveform decomposition. IEEE Geoscience and Remote Sensing Letters, 9 (3): 482–486. [DOI: 10.1109/LGRS.2011.2172676]

Shi J C, Menenti M and Lindenbergh R. 2013. Parameterization of surface roughness based on ICESat/GLAS full waveforms: a case study on the tibetan plateau. Journal of Hydrometeorology, 14 (4): 1278–1292. [DOI: 10.1175/JHM-D-12-0130.1]

Soederman U, Persson A, Toepel J and Ahlberg S. 2005. On analysis and visualization of full-waveform airborne laser scanner data. Proceedings of SPIE 5791, Laser Radar Technology and Applications X, Orlando, Florida, United States: SPIE, 184–192 [DOI: 10.1117/12.604655]

van Leeuwen M, Hilker T, Coops N C, Frazer G, Wulder M A, Newnham G J and Culvenor D S. 2011. Assessment of standing wood and fiber quality using ground and airborne laser scanning: a review. Forest Ecology and Management, 261 (9): 1467–1478. [DOI: 10.1016/J.FORECO.2011.01.032]

Wagner W, Ullrich A, Ducic V, Melzer T and Studnicka N. 2006. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS Journal of Photogrammetry and Remote Sensing, 60 (2): 100–112. [DOI: 10.1016/J.ISPRSJPRS.2005.12.001]

Xu L J, Li D and Li X L. 2016. A high success rate full-waveform lidar echo decomposition method. Measurement Science and Technology, 27 (1): 015205 [DOI: 10.1088/0957-0233/27/1/015205]

Zhou Z R, Hua D X, Wang Y F, Yan Q, Li S C, Li Y and Wang H W. 2013. Improvement of the signal to noise ratio of Lidar echo signal based on wavelet de-noising technique. Optics and Lasers in Engineering, 51 (8): 961–966. [DOI: 10.1016/J.OPTLASENG.2013.02.011]

摘要

关键词