出版日期: 2018-01-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20187247
2018 | Volumn22 | Number s1
上一篇 | 下一篇

主喜马拉雅逆冲带的震间与同震重力场变化

周新¹ , 万晓云² , 申旭辉¹

1. 中国地震局地壳应力研究所地壳动力学重点实验室, 北京 100085

2. 钱学森空间技术实验室, 北京 100094

收稿日期: 2017-06-16

基金项目: 国家自然科学基金(编号：41574021，41404019，41674026)；中国地震局地壳应力研究所中央级公益性科研院所基本科研业务专项资助项目(编号：ZDJ2017-23)；中国科学院太空应用重点实验室开放基金(编号：CSU-WX-A-KJ-2016-044)；中国博士后科学基金(编号：2014M550804)

第一作者简介: 周新，1983年生，男，副研究员，研究方向为地震大地测量学。E-mail：zhouxin05@mails.ucas.ac.cn

中图分类号: P228

文献标识码: A

摘要

为对中国自主重力/重力梯度卫星在陆地地震研究中提供理论依据，本文选取了主喜马拉雅逆冲断层(MHT)，模拟了断层在同震和震间滑移产生的大地水准面、重力变化和重力梯度变化。首先给出了大地测量数据反演断层滑动分布的马尔可夫链—蒙特卡洛方法，实际反演中，Markov链的总长度由4×10⁷个模型组成，燃烧阶段和采样阶段的长度均为2×10⁷个模型，重采样的间隔为1000，初始温度设为100，终止温度为0.1。再次给出了基于反向滑移模型估计震间断层的耦合度。利用GPS和InSAR数据，对2×10⁴个重采样的模型取平均后，反演得到MHT的同震滑移和震间耦合分布，结果表明：2015年M_w 7.8尼泊尔地震同震破裂并未达到地表，最大滑移量约为6 m，地震矩为1.02×10²¹ Nm，相当于M_w 7.9，与其他手段得到的结果一致；MHT的震间耦合模型表明MHT在中上地壳以上部分在震间均处于闭锁状态，积累的能量相当于每年一个M 7地震。基于以上反演的断层滑移/滑移亏损模型，模拟了MHT同震和震间的重力场变化。变形地表面的同震重力变化呈南北两极分布，范围为–261—125 μgal，理论上能够被陆地重力测量所检测到。长波长的震间空间重力/重力梯度变化信号难以被当前重力卫星观测到；对冰川等大尺度质量效应进行改正后的同震重力/重力梯度变化有望被提高测量精度的下一代重力卫星检测出。本研究成果对中国未来发射的自主重力卫星数据在地震发生和孕育方面的应用研究将提供有益的启示。

关键词

GPS, InSAR, 重力场, 同震, 震间, 主喜马拉雅逆冲带

Coseismic and interseismic gravity field change along the Main Himalaya Thrust

ZHOU Xin¹ , WAN Xiaoyun² , SHEN Xuhui¹

1.Key Laboratory of Crustal Dynamics, Institute of Crustal Dynamics, CEA, Beijing 100085, China

2.Qian Xuesen Laboratory of Space Technology, Beijing 100094, China

Abstract

Low-low tracking gravimetric satellite Gravity Recovery and Climate Experiment (GRACE) with a spatial resolution of 330 km can detect gravity field change due to mass migration of the Earth. Numerous studies show that coseismic and postseismic gravity changes caused by several megathrust earthquakes (>M_w 8.8) in the ocean can be detected by GRACE. The gravity gradient satellite Gravity field and steady-state Ocean Circulation Explorer (GOCE) can provide a global gravity and geoid model with high accuracy and a high spatial resolution of 80 km. However, GOCE measurements cannot be used to detect gravity signals induced by any earthquake because of high-frequency noise. Previous studies focused only on the oceanic earthquake and gravity change but not fault creep during the interseismic period. In this paper, we simulate the gravity and gravity gradient changes caused by interseismic coupling of the Main Himalaya Thrust, as well as the coseismic rupture of the 2015 Nepal M_w 7.8 event. The MHT, where most crustal deformation occurs, absorbs half of the total India–Eurasia convergence rate (~20 mm/yr). Large earthquakes that recur along the Himalaya front must be related to the MHT rupture, for example, the 2015 Nepal earthquake. We first jointly invert the coseismic slip distribution of the 2015 Nepal event, which occurred at the seismic gap between the 1505 M 8.5 and 1934 M 8.2 events, using Markov chain Monte Carlo approach from GPS and InSAR observations. The InSAR data from ALOS-2 are resampled by using the quadtree technique. Green’s function is computed by using a spherically layered dislocation theory. The inverted average slip model shows that the maximum slip is approximately 6±0.7 m, and the seismic moment is approximately 1.02×10²¹ Nm, which is equivalent to M_w 7.9. The result is similar to that of other studies. Then, we invert the interseismic slip deficit of the MHT from GPS data that are post-processed by removing the block rotation effect based on the backslip model. The interseismic coupling model, which is converted from the slip deficit, shows that almost all 20 km of the uppermost MHT was locked during the interseismic period. It includes the coseismic slip region of the 2015 Nepal event. The seismic moment deficit is approximately 6.8×10¹⁹Nm/yr, which is consistent with other studies. We compute the gravity changes at the Earth surface with a full wavelength on a 3’× 3’ grid on the basis of the coseismic slip and interseismic slip deficit models. After considering the gravity change by vertical deformation, coseismic gravity change at the deformed surface has a dipolar distribution of gravity increase at the north of the epicenter and a decrease at the south. The magnitude of gravity change ranges from –261 μGal to 125 μGal and can be detected by traditional land gravimetry. The gravity change at Lhasa is –0.12 μGal, which was detected by using a superconductor gravimeter. Unlike the coseismic gravity change, the interseismic gravity change rate of the MHT after free air correction around the MHT ranges from –0.65 μGal/yr to 1.4 μGal/yr, which is difficult for gravimeters to detect with an accuracy of 10 μGal. We synthesize geoid, gravity, and gravity gradient tensor changes with long wavelengths caused by coseismic slip and interseismic slip deficit of the MHT by using spherical harmonic expansion of gravity changes. The truncation degrees of geoid and gravity are 60, and that of the gravity gradient tensor is 250, which is consistent with that of GRACE and of GOCE. In addition, similar to GRACE data post-process, geoid and gravity are smoothed by using a DDK3 filter, which is useful for damping the high-frequency noise. Gravity satellite is not sensitive to crustal vertical deformation; thus, gravity changes of the full wavelength without free air correction are used to expand into spherical harmonics. Results show that coseismic geoid and gravity changes with 60 degrees are distributed at the surface with a dipolar pattern. For the coseismic phase, the magnitude of geoid change is –0.2–0.3 mm, and that of gravity change is –0.9–1.2 μGal, which cannot be detected by GRACE with an observation accuracy of approximately 2 μGal. The synthetic interseismic geoid and gravity changes have an opposite pattern to the coseismic signals. The magnitudes of interseismic geoid and gravity are –0.026–0.014 mm/yr and –0.11–0.08 μGal/yr, respectively. The synthetic interseismic signals are much smaller than those values because of glacier melting on high mountains. The space coseismic gravity gradient of T_rr has a dipolar pattern with a magnitude of –27–31 mE; components of T_rθ and T_θθ have a tripolar pattern, and the magnitudes are –27–20 mE and –22–19 mE. The signals of the other three components are weaker at approximately ±10 mE. Unlike coseismic signals, all components of the interseismic gravity gradient tensor have a tripolar pattern in the range of –4–4 mE. Indubitably, gravity and gravity gradient changes with a low degree due to interseismic coupling of the MHT may not be detected by gravimetric satellite directly given their weaker signals compared with changes due to glacier mass migration or land water storage change. However, after careful correction for other sources, we can extract the gravity or gravity gradient change from next-generation gravimetric satellites, the measurement accuracy of which will be improved by new techniques such as laser ranging and an accurate gradiometer in the future.

Key words

GPS, InSAR, gravity field, coseismic, interseismic, the Main Himalaya Thrust

1 引　言

断层破裂引起的近场地壳变形和重力变化能够被现代大地测量或遥感手段，如GNSS、干涉合成孔径雷达(InSAR)和陆地/卫星重力测量等所观测到(Jónsson 等，2002；Imanish 等，2004；Zhou 等，2014；Lindsey 等，2015)，而且大型地震事件引起的远场变形也能够被GPS观测到(Zhou 等，2014)。这些观测物理量均能够被弹性地震位错理论所解释 (Okada，1985；Okubo，1992；Sun和Okubo，1993；Sun 等，1996；Wang 等，2006)。除此之外，断层的慢滑动(如余滑)和长期蠕动引起的非地震地壳变形同样能够被高精度的GPS和InSAR所观测到(Heki 等，1997；Loveless和Meade，2010)。反过来，可以利用这些大地测量和遥感观测资料来约束震源参数、滑移分布或断层在震间期的闭锁/耦合分布(Ader 等，2012；Loveless和Meade，2010)。

低轨道的重力卫星(Gravity Recovery and Climate Experiment，(GRACE)；Gravity Field and Stead-state Ocean Circulation Explore，(GOCE))的发射、运行和观测从空间上提供了前所未有的高精度、高分辨率的全球重力场和大地水准面模型，广泛应用于固体地球物理学、海洋学、冰川学、陆地水资源和气候变化等学科，对地球科学产生了深远影响。低—低卫星跟踪测距模式的GRACE卫星由两颗分别搭载加速度计、GPS接收机和测距仪的卫星组成，两颗卫星之间可以进行微波测距，当地球质量发生变化时，两颗卫星之间的距离也随之发生变化。GRACE卫星不仅能够观测到陆地水/地下水储量变化、全球海平面变化和极地冰川融化等大尺度地球质量的迁移(Tapley 等，2004；Chen 等，2005；Chambers 等，2004；Velicogna和Wahr，2006)，而且能够检测到大型地震产生的重力场变化。理论上一个M 8以上的地震均有可能被GRACE检测出来，但由于卫星数据的高频噪声和其他地球物理因素的影响，目前GRACE仅能够检测出2004年苏门答腊M_w 9.3、2010年智利M_w 8.8和2011年日本东北M_w 9.0地震同震和震后黏滞性调整产生的重力场变化(Han 等，2006，2010，2011；De 等，2009；Panet 等，2007；Cambiotti 等，2011；Zhou 等，2014)。反之，利用GRACE观测到的空间重力变化能够约束地震事件的震源参数(Han 等，2011；Cambiotti 等，2011)。需要指出的是，GRACE卫星观测的重力场信号含有高频噪声，重力变化图像呈南北条带，需要经过空间平滑提高信噪比后才能使用。

重力梯度卫星GOCE的主要目的是提供具有高空间分辨率和高精度的全球重力场和大地水准面模型，空间分辨率可达80 km。理论上，重力梯度是重力的一阶导数，引力位的二阶导数，对地球质量迁移应该更加敏感，以上地球物理信号应该都能够被检测出。事实上，由于GOCE卫星的梯度计精度未达预期以及高频噪声过大，很难检测出同震重力/重力梯度变化信号。尽管如此，搭载了3对加速度计的重力梯度卫星GOCE依然能够可以当作空间地震仪，可以观测到大地震引起的大气密度波动信号(Garcia 等，2013)。

以上利用重力卫星研究地震问题都是基于重力变化这一物理量，且均针对发生在海洋板片俯冲带的特大地震事件的同震和震后物理问题，并未考虑震间期断层闭锁或蠕动等过程。本文选取了较为典型的大陆碰撞造山带——主喜马拉雅逆冲带，模拟了2015年M_w 7.8尼泊尔地震的同震以及断层在震间期闭锁的大地水准面、重力变化和重力梯度变化，为下一代重力卫星研究地震循环周期过程提供参考。同时，本文也将计算地面重力变化，讨论利用陆地重力仪记录监测地震孕育的可能性。

2 主喜马拉雅逆冲带的构造背景

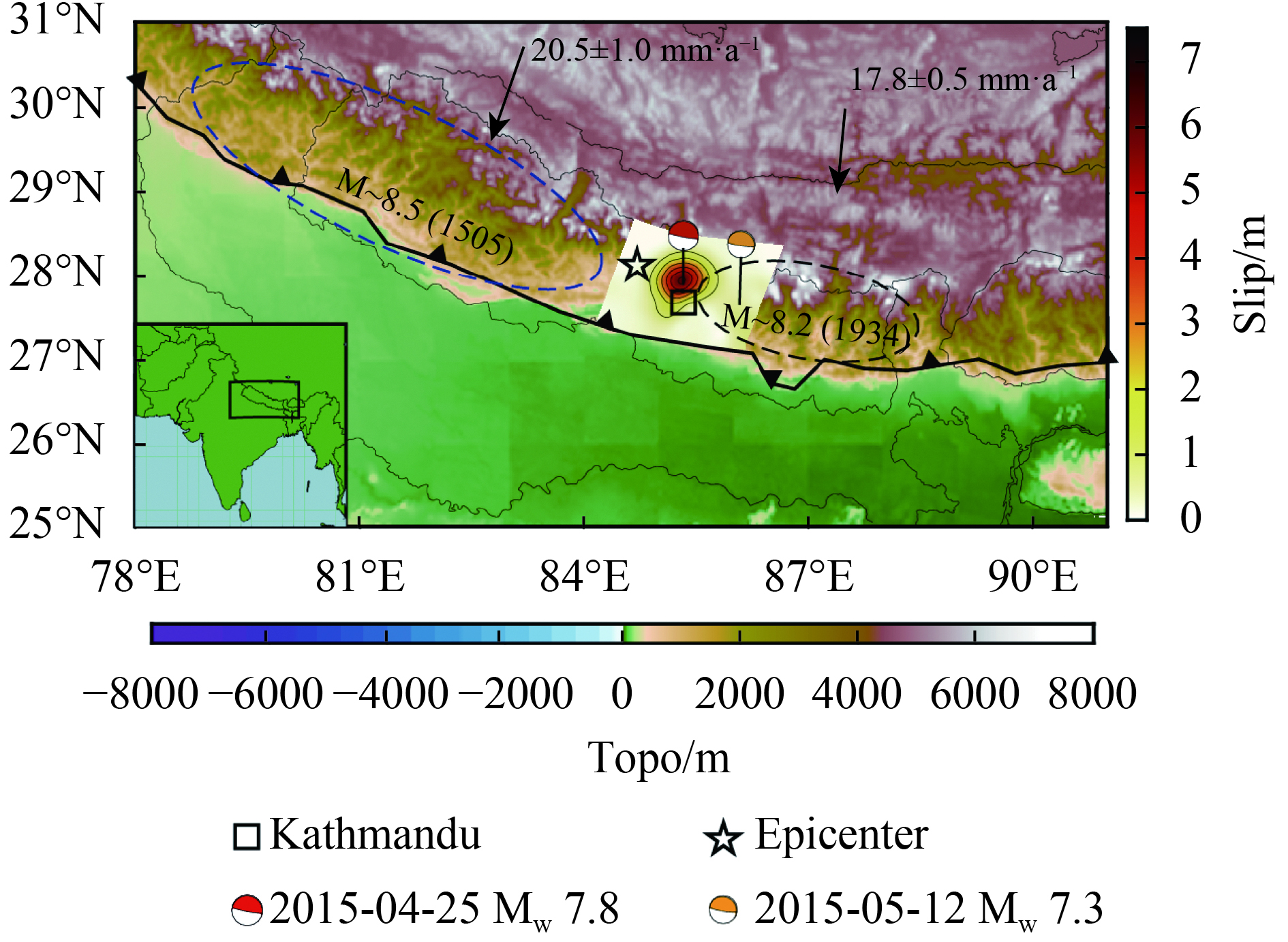
位于尼泊尔中部的喜马拉雅是地球上最为典型的碰撞造山带，印度洋板块向亚欧板块持续不断的俯冲运动将青藏高原推高，并伴随着地壳的快速缩短和增厚(Avouac，2003)。尼泊尔中部的收敛速率被沿着喜马拉雅山脚且出露地表面的逆冲断层，即主喜马拉雅逆冲断层(MHT)所吸收。MHT吸收了大约20 mm/a的收敛速率，为印度板块和欧亚板块总收敛速率的一半(Bettinelli 等，2006)。在一阶近似下，可以认为喜马拉雅推覆在印度地壳块体之上，且内部变形几乎为0，则大地震事件主要重复发生在喜马拉雅前缘，都伴随着MHT的破裂(Bilham，2004)。古地震的研究表明该地区在历史上发生过超过M_w 8.5的地震(图1)(Kumar 等，2006，2010)。大量的大地测量结果表明MHT在震间期闭锁，从地表面一直向北100 km，直至一个带有韧性流的次水平剪切区(Cattin和Avouac，2000；Ader 等，2012)。忽略微弱的非弹性变形产生的震间应变，MHT闭锁部分在震间期吸收了喜马拉雅在尼泊尔地区20 mm/a的弹性缩短变形。震间期积累的弹性应变足以产生M 8.0以上的地震(Molnar，1987)。2015年4月25日尼泊尔廓尔喀M_w 7.8—M_w7.9地震便发生在MHT上，距离加德满都80 km，向北倾斜约10º，震源深度约为15 km，事件主震发生在1505年和1934年两个历史地震之间的空区上(图1)(Mugnier 等，2013；Sapkota 等，2013；Avouac 等，2015)。图1中，2015年地震震中由USGS给出，主震和余震的震源机制解来自GCMT (Global Centroid Moment Tensor catalog)，喜马拉雅的收敛速率(Ader 等，2012)。

图 1 主喜马拉雅逆冲的构造背景图

Fig. 1 Tectonic background of the Main Himalaya Thrust (MHT)

3 数据和断层模型

为了得到MHT在震间期以及2015廓尔喀M_w 7.8地震同震的重力/重力梯度变化率，首先需要得到断层在震间期的耦合(或闭锁)分布和同震的滑移分布。为此，本文选择了用GPS和差分干涉合成孔径雷达DInSAR数据对断层滑移分布进行反演。

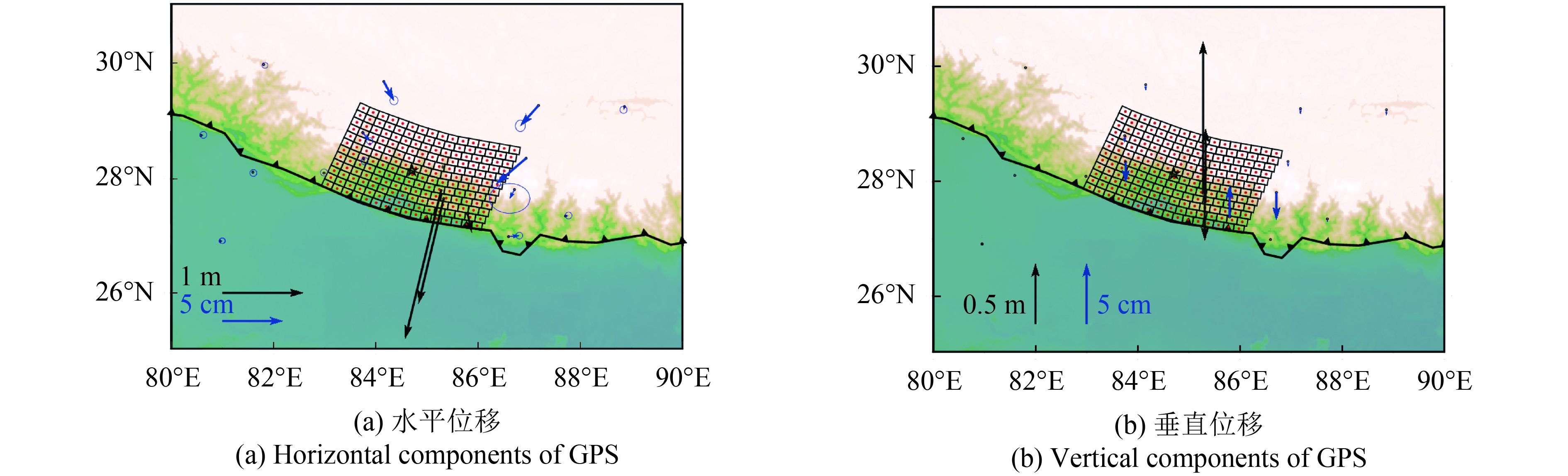
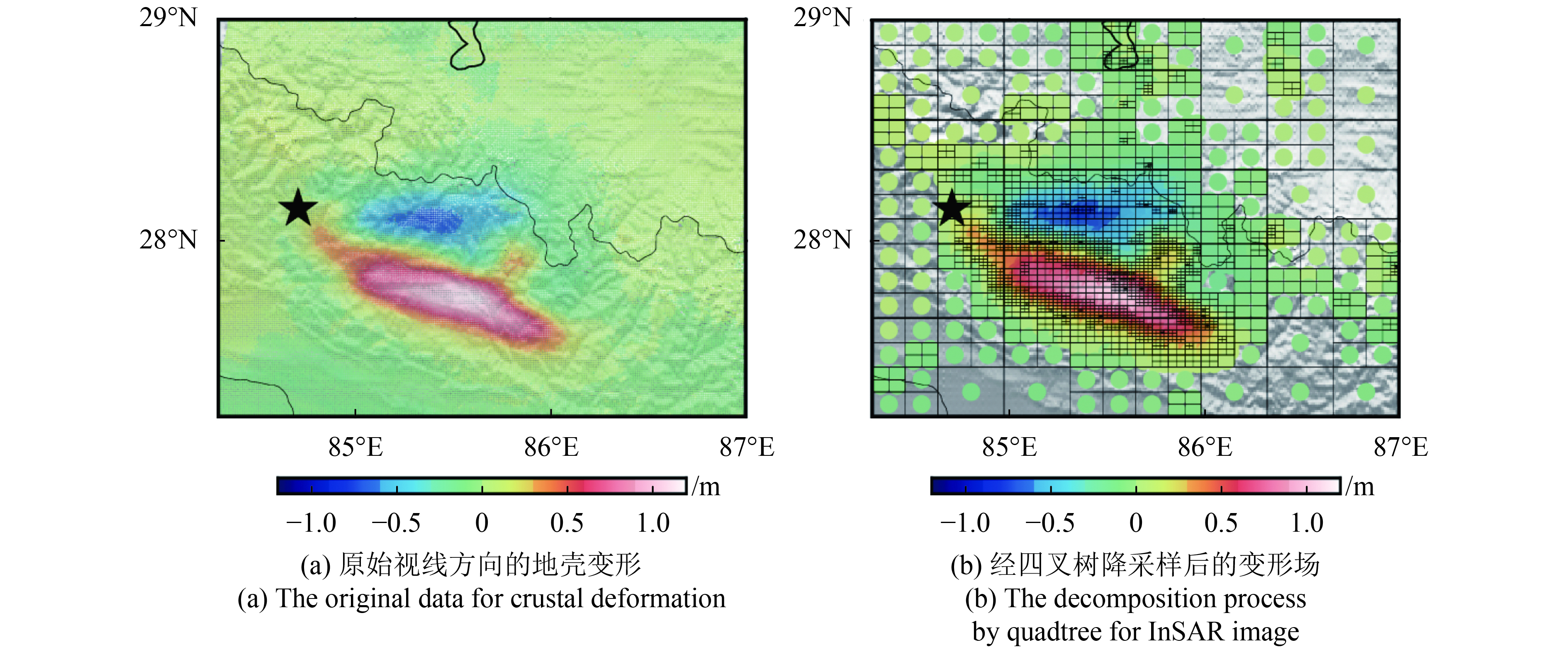
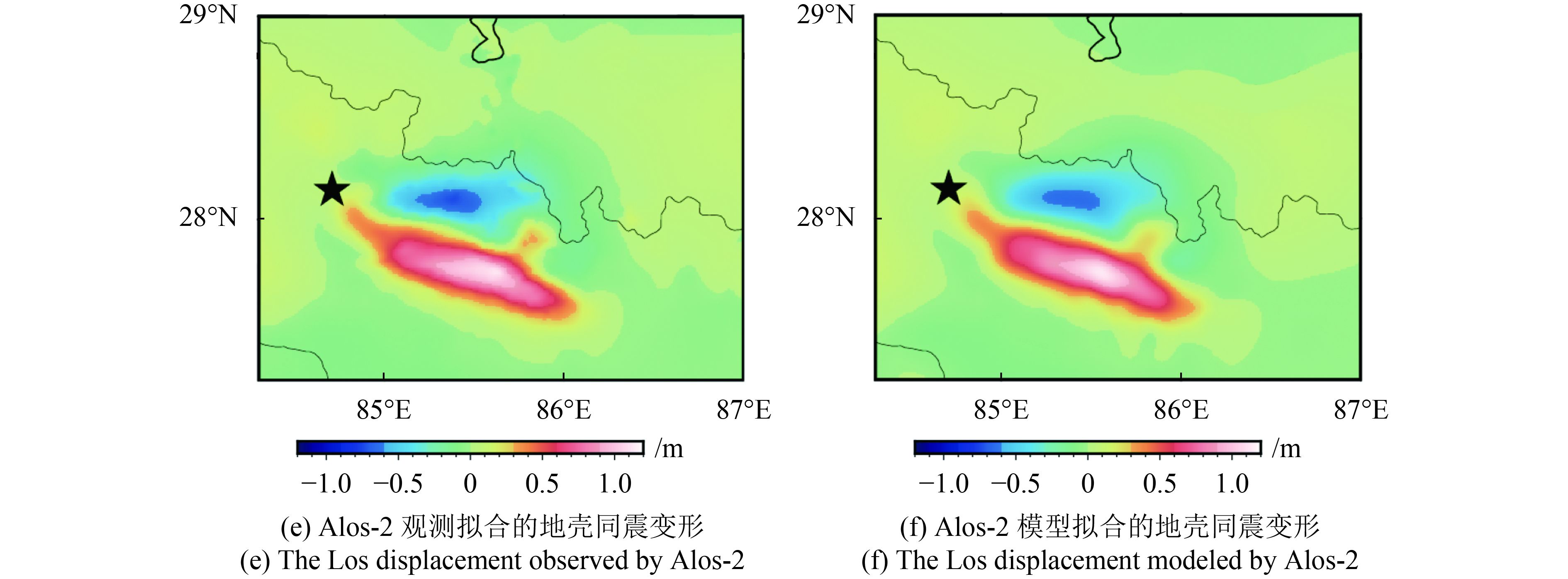
这里采用了苏小宁等人(2015)给出的19个GPS连续站观测的位移和Lindsey等人(2015)给出的DInSAR数据反演2015年廓尔喀地震的同震滑移分布。连续GPS观测站大多位于高原一侧，其中超过10个站点位于震中附近。最大变形发生在震中东南靠近板块边界的测站，水平位移为1.89 m，垂直位移为1.26 m(图2)。整个GPS位移方向表明该地震为一次近纯逆冲破裂事件。DInSAR视线方向(LOS)变形来自ALOS-2遥感卫星的降轨(Path 48)数据，观测时间为2015年2月22日—2015年5月3日，时间跨度包括M_w 7.8地震，不包括M_w 7.3的余震，LOS方向变形约为–0.5—1 m。地壳变形图像通过四叉树技术进行重采样，像素点数量由94555个下降到2245个(图3)。降采样后的InSAR数据与GPS数据一起用于同震滑移分布的反演。

图 2 GPS观测的2015年尼泊尔廓尔喀地震同震变形和用于断层滑移反演的子断层模型

Fig. 2 The coseismic displacements of 2015 Nepal thrust event observed by GPS and the fault model discretized into 192 patches

图 3 用于反演2015尼泊尔地震的InSAR变形数据

Fig. 3 The InSAR displacements used to slip inversion for the 2015 Nepal earthquake

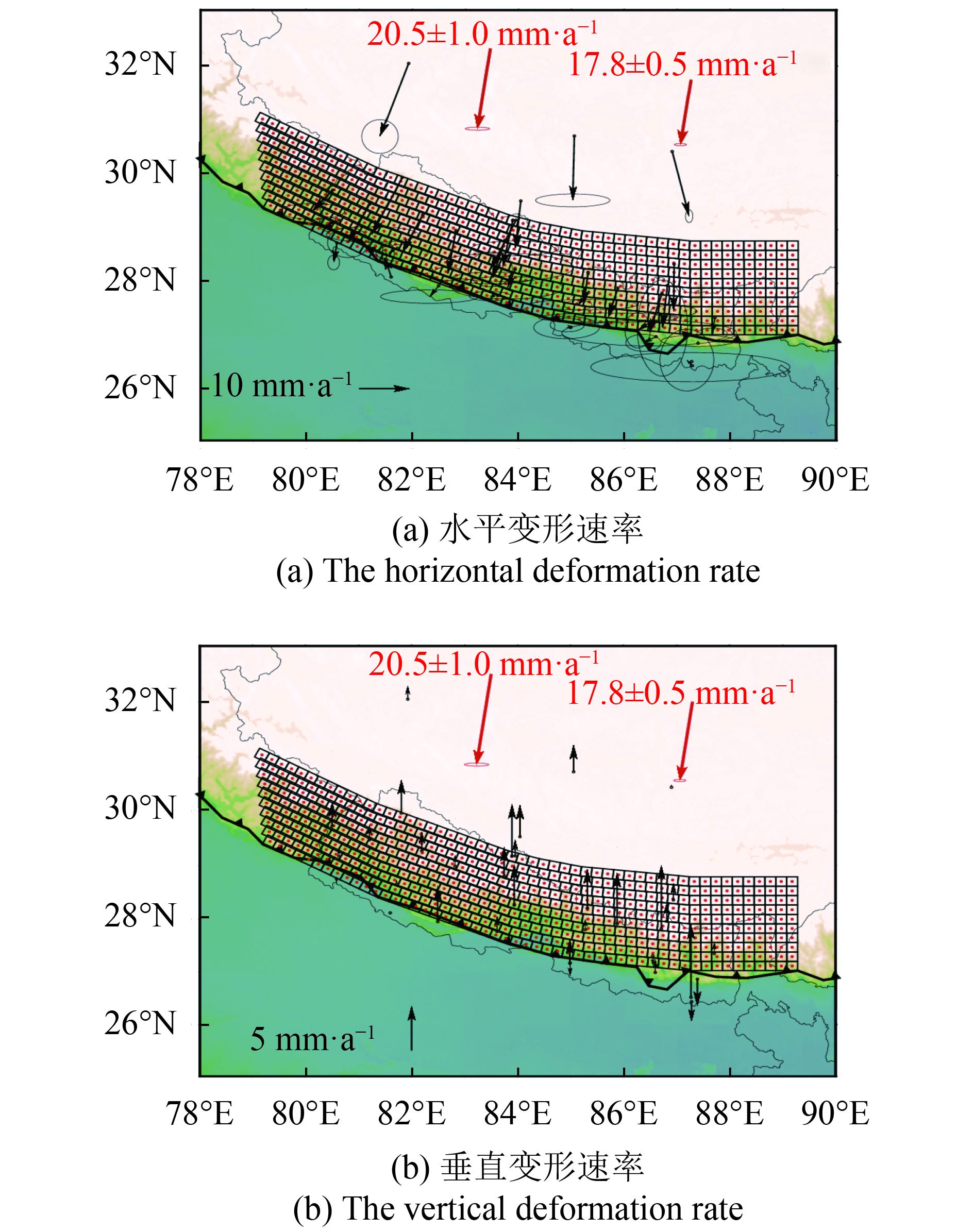
震间期的断层闭锁反演选用的是Ader等人(2012)给出的38个连续GPS站的速率，每个GPS站都包括东西、南北和垂向3个方向。测量时间在20年平静期内，除了一次M6.5级地震外，无其他大地震发生，适合用来确定MHT的震间耦合。为了得到MHT相对于印度板块的长期运动速率，需要通过去除块体的旋转效应。这里采用了Ader等人(2012)给出的欧拉极：(–1.34º±3.31º，51.4º±0.3º)，角速度为0.5029±0.0072º/M·a^–1。图4给出了已经扣除了块体水平旋转后的喜马拉雅块体相对于印度板块的GPS运动速率，由图4可知，纬度上从北向南，越靠近喜马拉雅前缘地表断层线，GPS运动速率越小，变形被MHT所吸收。尽管主要的变形发生在水平方向，但垂直方向在反演断层耦合度时仍然使用。同时，远场青藏高原稳定块体相对于印度板块的运动速率采用Ader等人(2012)给出的结果。在经度85º东西两侧长期速率不均匀，东侧为17.8±0.5 mm/a，西侧为20.5±1.0 mm/a。

图 4 主喜马拉雅逆冲带相对于印度板块的震间连续GPS运动速率(Ader 等，2012)和用于反演断层闭锁的子断层模型(红色矢量表示远场青藏高原稳定块体的长期运动速率)

Fig. 4 The motion velocity of the MHT relative to the Indian plate observed by continuous GPS (Ader et al, 2012) and the fault model that is discretized into 520 subfaults (Red vector represents the motion velocity of the far field stable Tibetan block with little internal deformation)

4 方　法

4.1 同震滑移的反演方法

利用GPS、InSAR等观测资料反演断层的滑移分布的问题可以写为

${\bf{\Sigma }}_{\bf{d}}^{{\bf{ - 1/2}}}{\bf{Gs}} = {\bf{\Sigma }}_{\bf{d}}^{{\bf{ - 1/2}}}{\bf{d}} + {\bf{e}}$

(1)

$\alpha {\bf{Ls}} = 0 + {\bf{\delta }}$

(2)

(1)式中， ${\bf{G}}$ 为格林函数，其意义为断层上单位滑移分量引起的变形； ${\bf{s}}$ 为滑移矢量； ${\bf{d}}$ 为观测的地表变形， ${{\bf{\Sigma }}_{\bf{d}}}$ 为观测数据的协方差； ${\bf{e}}$ 为模型空间(等式左边)和数据空间之间的距离。格林函数与地球模型有关，可以由位错理论模型得到。为了避免相邻子断层之间的滑移分布出现不合理的反向滑动，需要利用(2)式对断层面进行平滑。(2)式中， ${\bf{L}}$ 为平滑约束算子， ${\bf{\delta }}$ 为滑移模型的粗糙度； $\alpha $ 为正则化/平滑因子。考虑到实际的物理意义，平滑算子选用拉普拉斯算子 ${\nabla ^2}$ ，即断层面的应力降最小。为了得到更加集中的滑移分布形状，还需要施加非负约束，即

${\bf{s}} \geqslant 0$

(3)

可以用非负最小二乘求解式(1)—(3)的目标函数(Lawson和Hanson，1974)，其中，确定平滑因子 $\alpha $ 是首要问题。本文采用了Fukuda和Johnson (2008)提出的一种在贝叶斯框架下的马尔可夫—蒙特卡罗(MCMC)方法同时反演出断层滑移分布 ${\bf{s}}$ 和平滑因子 $\alpha $ 。并且在MCMC方法中，采用了模拟退火来避免因多峰的目标分布引起的局部最小以及加快可行解的收敛，详细算法见(周新，2017)。在实际计算时，先燃烧掉一段马尔可夫链，对剩余的链进行重采样，最终求得平均的可接受模型。

在利用GPS和DInSAR数据反演时，需要对两种不同的数据加权。可以将权重因子作为未知参数与滑移矢量和平滑因子一起用MCMC方法进行反演得到，由于GPS和DInSAR数据的数量差异较大，难以通过反演过程自动选择出合适的权重因子。考虑到GPS观测的精度较高，通过试验在拟合DInSAR数据的情况下，尽量给GPS施加较大的权重。

4.2 断层震间闭锁的反演方法

为了能够利用位错模型得到断层在震间期的闭锁/耦合度，需要利用反向滑移模型。由图4可知，扣除块体旋转运动速率后，喜马拉雅块体远场的长期运动速率大于MHT前缘，换言之，靠近MHT的运动速率相对于远场方向向北，与逆冲断层引起的地壳变形反向，表现为正断层滑移产生的位移方向。由位错理论模型可知，这种运动速率的亏损是由断层的滑移亏损引起的。故利用相对运动速率亏损，通过4.1节的断层滑移反演方法可以得到震间滑移亏损，进一步通过下式计算震间耦合度 $C$

$C = \frac{{\Delta {s_i}}}{v}$

(4)

式中， $\Delta {s_i}$ 为子断层的滑移亏损， $v$ 为长期滑移速率。理论上，沿着MHT不存在瞬时滑移，耦合度应介于[0, 1]。耦合度为0表示该子断层以长期滑移速率蠕动；耦合度为1表示子断层在震间完全闭锁。若耦合度为负值，意味着子断层上的滑移速率大于长期速率；耦合度大于1则表示子断层的向与长期速率相反的方向蠕动。

4.3 断层模型

为了利用上述方法从观测数据中得到断层滑移分布，需要对主喜马拉雅逆冲断层进行离散。对于2015年尼泊尔地震，根据其他机构和研究给出的震源机制解，本文将断层倾角设定为11º，走向根据板块边界线的变化给出(图2)。将断层划分为16×12个子断层，每个子断层面积为20 km×15 km。对于逆冲破裂事件，为了允许反演结果滑移能够达到地表，采用自由边界条件约束断层边界上的滑移(Zhou 等，2014)。为了避免不合理的反向滑移，反演时将滑移角限定在[45º，135º]。格林函数 ${\bf{G}}$ 采用球体分层位错理论模型(Sun 等，1996)计算得到，地球模型选用PREM模型(Dziewonski和Anderson，1981)。

与上述2015年尼泊尔地震同震断层模型的划分类似，断层的倾角设为11º，走向可以随板块边界线变化(图4)。断层划分为52×10个子断层，每个子断层面积为20 km×20 km。选用拉普拉斯算子对断层面的滑移进行平滑约束，滑移角约束在[–135º，–45º]。格林函数的计算和地球模型的选取与同震滑移反演一致。

4.4 模拟重力及重力梯度变化的方法

利用上述方法反演得到的断层同震滑移分布和震间滑移亏损，通过球体位错理论模型(Sun和Okubo，1993)可以正演模拟地表面的重力变化。地球外部引力位和重力变化可以分别表达为球谐函数展开式：

$\begin{aligned}& \quad \delta \psi (r, \theta, \lambda) = \frac{{G{m_e}}}{a}{\sum\limits_{\ell = 0}^N {\sum\limits_{m = 0}^\ell {\left({\frac{a}{r}} \right)} } ^{\ell + 1}} \\ & \left({{C_{\ell m}}\cos m\lambda + {S_{\ell m}}\sin m\lambda } \right){\bar P_{\ell m}}(\cos\theta)\end{aligned}$

(5)

$\begin{aligned}& \qquad\delta g(r, \theta, \lambda) = \frac{{G{m_e}}}{{{a^2}}}{\sum\limits_{\ell = 0}^N {\sum\limits_{m = 0}^\ell {\left({\frac{a}{r}} \right)} } ^{\ell + 2}} \\ & \left({\ell + 1} \right)\left({{C_{\ell m}}\cos m\lambda + {S_{\ell m}}\sin m\lambda } \right){\bar P_{\ell m}}(\cos\theta)\end{aligned}$

(6)

式中， $\delta \psi $ 和 $\delta g$ 分别是引力位和重力的变化； $(r, \theta, \lambda)$ 为球坐标，分别为地心距离、余纬和经度； $G$ 为万有引力常数， ${m_e}$ 是地球质量， $a$ 为地球半径； ${C_{\ell m}}$ 和 ${S_{\ell m}}$ 为球谐系数， $\ell $ 和 $m$ 分别为阶和次， $N$ 为最大阶数； ${\bar P_{\ell m}}$ 为完全规格化的勒让德函数。由位错理论计算的地表重力变化可以得到球谐系数：

${C_{\ell m}} = \frac{1}{{{g_0}}}\iint_{\theta, \lambda } {\frac{{\delta g(a, \theta, \lambda)}}{{\left({\ell + 1} \right)}}\cos m\lambda {{\bar P}_{\ell m}}(\cos\theta)d\Omega }$

(6)

${S_{\ell m}} = \frac{1}{{{g_0}}}\iint_{\theta, \lambda } {\frac{{\delta g(a, \theta, \lambda)}}{{\left({\ell + 1} \right)}}\sin m\lambda {{\bar P}_{\ell m}}(\cos\theta)d\Omega }$

(7)

式中， ${g_0} = \displaystyle\frac{{G{m_e}}}{{{a^2}}}$ ， $d\Omega = \sin \theta d\theta d\lambda $ 为面积元素。重力卫星GRACE观测的大地水准面和重力变化需要经过平滑处理

$\begin{aligned}\delta {N^s}(a, \theta, \lambda) = & a\sum\limits_{\ell = 0}^{{N^s}} {\sum\limits_{m = 0}^\ell {\left({{W_{\ell m}}{C_{\ell m}}\cos m\lambda + {V_{\ell m}}{S_{\ell m}}\sin m\lambda } \right)} } \\ & {{\bar P}_{\ell m}}(\cos\theta)\end{aligned}$

(8)

$\begin{aligned}& \qquad \delta {g^s}(a, \theta, \lambda) = {g_0}\sum\limits_{\ell = 0}^{{N^s}} {\sum\limits_{m = 0}^\ell {\left({\ell + 1} \right)} }\\ & \left({{W_{\ell m}}{C_{\ell m}}\cos m\lambda + {V_{\ell m}}{S_{\ell m}}\sin m\lambda } \right){{\bar P}_{\ell m}}(\cos\theta) \end{aligned}$

(9)

式中， ${W_{\ell m}}$ 和 ${V_{\ell m}}$ 为滤波器系数，本文采用DDK3滤波器(Kusche，2007)； ${N^s}$ 是卫星的最大阶数，对于GRACE， ${N^G} = 60$ ；对于GOCE， ${N^G} = 250$ 。

重力梯度张量的变化为对称张量

${\bf{T}} = \left({\begin{array}{*{20}{c}} {{T_{rr}}}&{{T_{r\theta }}}&{{T_{r\lambda }}} \\ {{T_{\theta r}}}&{{T_{\theta \theta }}}&{{T_{\theta \lambda }}} \\ {{T_{\lambda r}}}&{{T_{\lambda \theta }}}&{{T_{\lambda \lambda }}} \end{array}} \right)$

(10)

且 ${T_{ij}} = {T_{ji}}{\text{ }}(i \ne j)$ ，同样可用球谐函数表达

${T_{rr}} = \frac{{{\partial ^2}\delta \psi }}{{\partial {r^2}}} = \frac{{G{m_e}}}{{{a^2}}}{\sum\limits_{\ell = 0}^N {\sum\limits_{m = 0}^\ell {\left({\frac{a}{r}} \right)} } ^{\ell + 3}}\left({\ell + 1} \right)\left({\ell + 2} \right)\left({{C_{\ell m}}\cos m\lambda + {S_{\ell m}}\sin m\lambda } \right){\bar P_{\ell m}}(\cos\theta)$

(11)

${T_{r\theta }} = \frac{{{\partial ^2}\delta \psi }}{{r\partial r\partial \theta }} = - \frac{{G{m_e}}}{{{a^3}}}{\sum\limits_{\ell = 0}^N {\sum\limits_{m = 0}^\ell {\left({\frac{a}{r}} \right)} } ^{\ell + 3}}\left({\ell + 1} \right)\left({{C_{\ell m}}\cos m\lambda + {S_{\ell m}}\sin m\lambda } \right){\bar P'_{\ell m}}(\cos\theta)$

(12)

${T_{r\lambda }} = \frac{{{\partial ^2}\delta \psi }}{{r\sin \theta \partial r\partial \lambda }} = - \frac{{G{m_e}}}{{{a^3}}}{\sum\limits_{\ell = 0}^N {\sum\limits_{m = 0}^\ell {\left({\frac{a}{r}} \right)} } ^{\ell + 3}}\frac{{\left({\ell + 1} \right)m}}{{\sin \theta }}\left({ - {C_{\ell m}}\sin m\lambda + {S_{\ell m}}\cos m\lambda } \right){\bar P_{\ell m}}(\cos\theta)$

(13)

${T_{\theta \theta }} = \frac{{{\partial ^2}\delta \psi }}{{{r^2}\partial {\theta ^2}}} = \frac{{G{m_e}}}{{{a^3}}}{\sum\limits_{\ell = 0}^N {\sum\limits_{m = 0}^\ell {\left({\frac{a}{r}} \right)} } ^{\ell + 3}}\left({{C_{\ell m}}\cos m\lambda + {S_{\ell m}}\sin m\lambda } \right){\bar P''_{\ell m}}(\cos\theta)$

(14)

${T_{\theta \lambda }} = \frac{{{\partial ^2}\delta \psi }}{{r\sin \theta \partial \theta \partial \lambda }} = \frac{{G{m_e}}}{{{a^3}}}{\sum\limits_{\ell = 0}^N {\sum\limits_{m = 0}^\ell {\left({\frac{a}{r}} \right)} } ^{\ell + 3}}\frac{m}{{\sin \theta }}\left({ - {C_{\ell m}}\sin m\lambda + {S_{\ell m}}\cos m\lambda } \right){\bar P'_{\ell m}}(\cos\theta)$

(15)

${T_{\lambda \lambda }} = \frac{{{\partial ^2}\delta \psi }}{{{r^2}{{\sin }^2}\theta \partial {\lambda ^2}}} = - \frac{{G{m_e}}}{{{a^3}}}{\sum\limits_{\ell = 0}^N {\sum\limits_{m = 0}^\ell {\left({\frac{a}{r}} \right)} } ^{\ell + 3}}\frac{{{m^2}}}{{{{\sin }^2}\theta }}\left({{C_{\ell m}}\cos m\lambda + {S_{\ell m}}\sin m\lambda } \right){\bar P_{\ell m}}(\cos\theta)$

(16)

5 结　果

5.1 2015年尼泊尔同震滑移模型

利用MCMC方法，由GPS和DInSAR数据反演了2015年尼泊尔地震的同震滑移分布。在反演过程中，Markov链的总长度由4×10⁷个种子组成，燃烧阶段和采样阶段的长度均为2×10⁷个种子，重采样的间隔为1000。模拟退火过程中，初始温度设为100，终止温度为0.1，通过10⁵步从初始温度冷却到终止温度。对状态空间重采样后，得到2×10⁴个模型，去除最大和最小各2.5%的样本后，对剩余模型进行平均得到滑移模型及其误差(图5(a)、(b))。反演结果表明，滑移分布集中在震中东侧，最大滑移达到~6±0.7 m，滑移方向几乎垂直于走向，主要破裂未到地表。基于PREM地球模型的剪切模量，计算反演得到的地震矩为1.02×10²¹ Nm，相当于M_w7.9。该结果与其他研究结果较为一致，比单独用GPS反演得到的地震矩稍大(周新，2017)，原因是本文加入了DInSAR资料进行了联合反演。同震滑移的误差最大不超过0.7 m，较均匀地分布在断层上(图5(b))。图5(c)—(f)给出了GPS和DInSAR的观测数据和模型拟合值，由此可知联合反演模型能够同时解释GPS变形和InSAR降轨图像。由图1可知，2015尼泊尔地震事件发生在1505年M 8.5和1934年M 8.2两次历史地震之间的空区上，破裂更靠近1934年地震区域。

5.2 MHT震间耦合模型

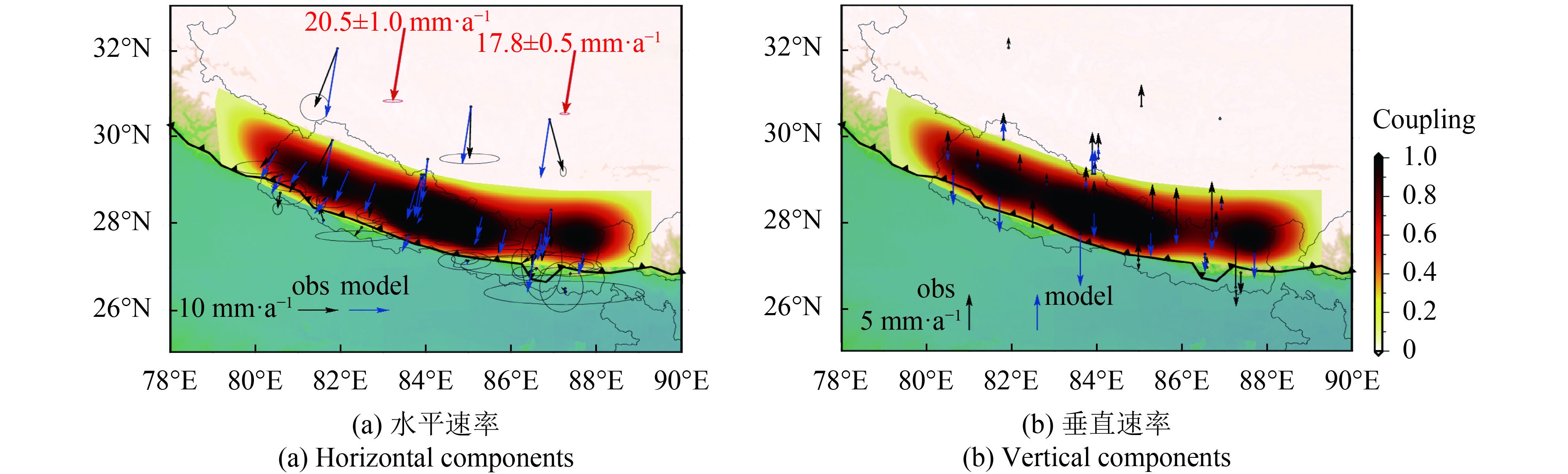
利用与同震滑移模型的反演相同的MCMC方法，用扣除刚体旋转和块体长期运动效应后的GPS速率反演得到滑移亏损率分布，再由式(4)转化为MHT的震间耦合，结果如图6所示。结果表明，MHT在震间几乎都处于闭锁状态，从地表面到20 km处于完全闭锁，包括2015年尼泊尔地震的同震滑移区。整个MHT的地震矩亏损率为6.8×10¹⁹Nm·a^–1，与Ader等人(2012)给出的结果一致。图6的GPS拟合结果显示位于断层上的GPS观测和模型计算的水平位移符合较好，垂直位移存在差异，较远场的水平位移无法完全符合。震间反向滑移模型不能够完全解释较远场的GPS观测。本文的断层耦合模型与Ader等人(2012)给出的结果相比，闭锁深度较深，差异是由于所用数据和反演方法的不同引起的。这里只采用了38个连续GPS站的观测数据，Ader等人(2012)还采用了定期复测资料。本文的反演中只加入平滑约束，用MCMC得到的一个平均模型；Ader等人(2012)则加入0阶的约束，通过拟合误差和地震矩亏损率的图形关系得到最佳模型。

图 6 由GPS资料反演的MHT震间耦合分布(黑色和蓝色矢量分别表示观测和模型拟合的GPS速率)

Fig. 6 Interseismic coupling model of the MHT inverted from GPS velocity observation (Black and blue vectors represent observed and modeled velocities, respectively)

5.3 地表重力变化

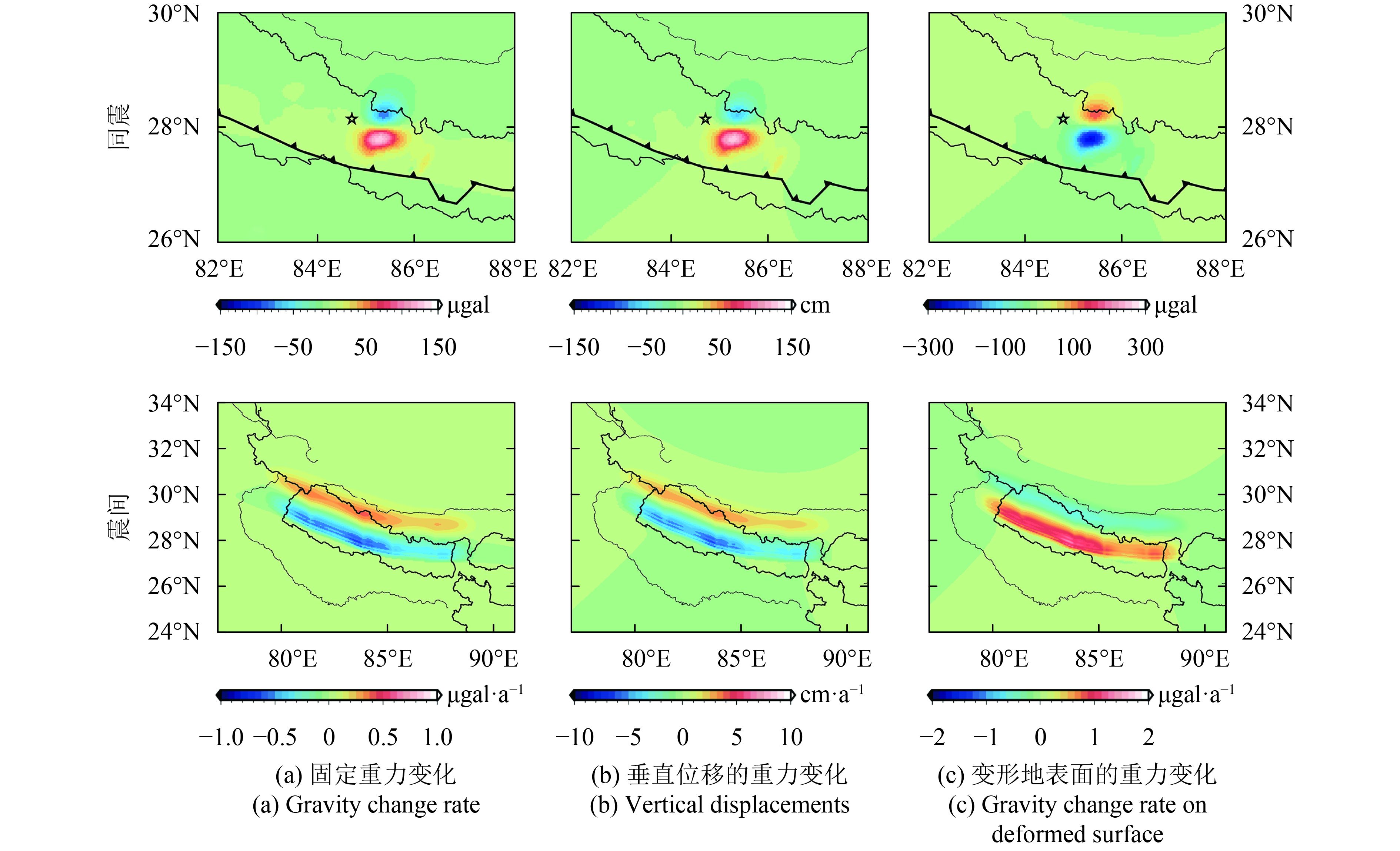
基于2015年尼泊尔地震的同震滑移模型(图5(a))，利用球体位错模型模拟3′×3′的同震重力场变化，结果如图7所示。在固定地表面(即无变形的地表)上，同震重力变化范围为–80—130 μgal，信号呈非对称的南正北负两极分布，重力增加幅度大于重力减小，这种非对称是由逆冲断层的低倾角所致。在地表面的重力仪器除了观测到地球质量的迁移外，重力仪还随着地壳垂直位移而运动，垂直变形产生重力变化。通过同震滑移分布计算得到的垂直位移信号与固定地表面的重力变化信号相似，也是呈南正北负非对称分布，幅度范围为–0.67—1.27 m。顾及地壳垂直运动引起的自由空气重力变化后，在变形地表面上的重力变化信号与固定地表面的相反，呈南负北正分布，变化范围为–261—125 μgal。该同震重力变化信号足以被陆地重力测量手段所检测到。显著的重力变化信号仅集中在断层最大滑移约150 km的地表区域，在较远场的信号快速衰减。距离滑移区域最近的连续重力观测站是拉萨(91ºE，29.6ºN)，其理论重力变化为0.12 μgal，有可能被高精度的超导重力仪检测出。

图 7 基于滑移/滑移亏损模型模拟的MHT同震和震间地表固定点重力变化、垂直位移和变形地表面的重力变化

Fig. 7 Simulated coseismic gravity change and interseismic gravity change rate on fixed surface and on deformed surface along the MHT based on the slip/slip deficit model

图 5 由GPS和DInSAR变形资料联合反演的2015年尼泊尔地震同震滑移分布及其反演误差

Fig. 5 The coseismic fault slip distribution of the 2015 Nepal earthquake jointly inverted from GPS and DInSAR data by using MCMC method

与同震重力变化模拟过程相同，利用震间滑移亏损模型计算得到固定地表面和变形地表面的震间重力变化率。如图7(e)—(g)所示，固定地表面的震间重力变化率呈南负北正非对称分布，变化范围为–0.72—0.39 μgal·a⁻¹；垂直速率分布与固定地表面的重力变化率相似，也为南负北正的非对称分布，幅度范围为–6.9—3.4 mm·a^–1；考虑自由空气改正后，变形地表面上的重力变化率为–0.65—1.4 μgal·a^–1，呈南正北负分布。尽管在震间断层闭锁区域分布整个断层面，直到20 km深处，但由于变化率极其微小，难以被10 μgal精度的重力仪观测到，仅能够被绝对重力仪和超导重力仪检测到。

5.4 空间重力/重力梯度变化

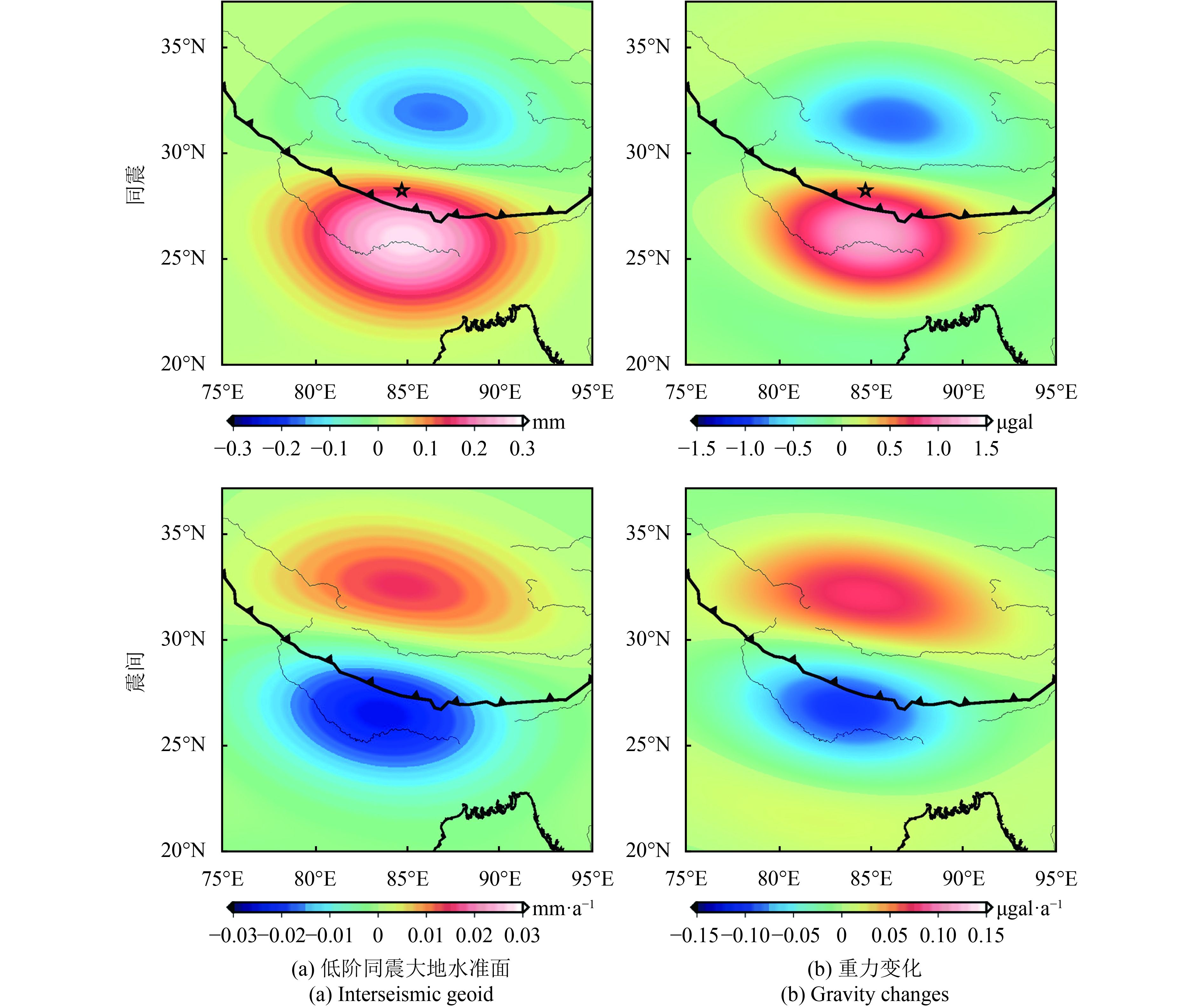
重力卫星对地壳位移不敏感，故空间重力场变化只考虑无变形地表面的情况。将固定地表面的重力变化按照式(6)和式(7)进行球谐展开，并截断到GRACE和GOCE观测的最大阶数(GRACE为60，GOCE为250)，再通过式(8)—(16)计算空间大地水准面、重力和重力梯度的变化。与GRACE观测数据处理一致，使用了DDK3滤波器(Kusche，2007)对空间大地水准面和重力信号进行平滑。如图8(a)、(b)所示，空间同震大地水准面和重力变化均为南正北负分布，大地水准面的变化幅度为–0.2—0.3 mm，重力变化幅度为–0.9—1.2 μgal。GRACE观测的重力变化不确定度在2 μgal左右，该信号难以被GRACE检测到。

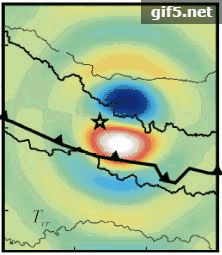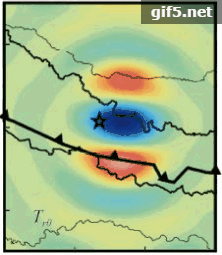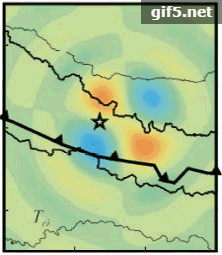
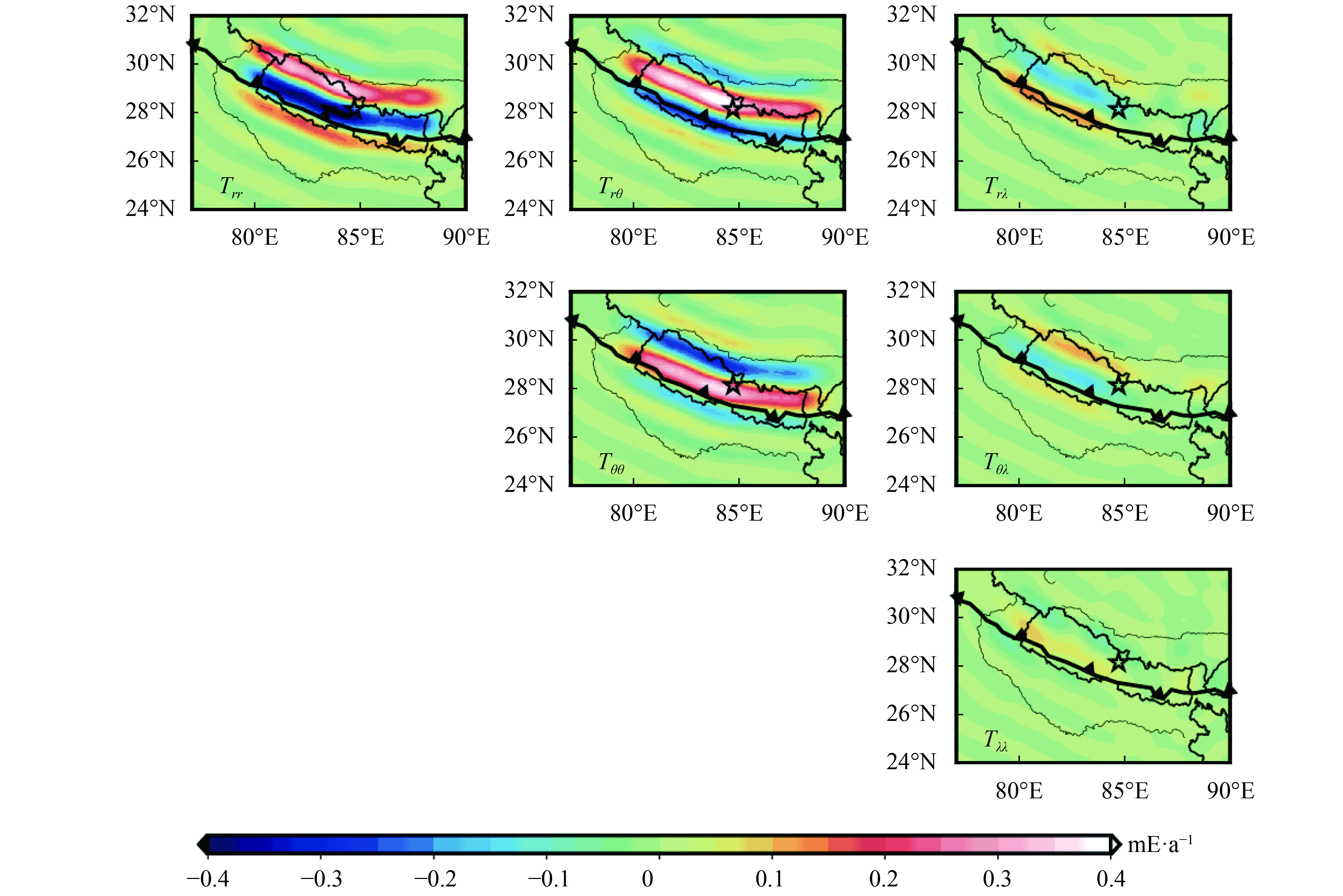
图 8 模拟的MHT在同震和震间期的低阶同震大地水准面和重力变化(该结果只考虑了60阶的重力场长波长部分，并施加了DDK3滤波器进行空间平滑处理)

Fig. 8 Coseismic and interseismic geoid and gravity changes along the MHT with low degree are simulated by using spherical dislocation theory. The upper row is for coseismic changes, the bottom is for interseismic changes (We here only consider the long wavelength of gravity field with 60 degrees and apply a DDK3 filter to smooth the results)

图9给出了模拟的2015年尼泊尔地震的同震重力梯度变化。考虑到重力梯度张量的对称性，这里只给出了6个分量的分布图。为了与GOCE卫星的分辨率一致，球谐展开截断到250阶。与空间大地水准面和重力变化的处理不同，重力梯度的变化并未施加空间平滑。如图9所示， ${T_{rr}}$ 、 ${T_{r\theta }}$ 和 ${T_{\theta \theta }}$ 三个分量的信号最为显著。其中， ${T_{rr}}$ 呈南正北负分布，变化范围约为–27~31 mE； ${T_{r\theta }}$ 和 ${T_{\theta \theta }}$ 均呈正—负—正的分布形状，变化范围分别为–27—20 mE以及–22—19 mE。 ${T_{r\lambda }}$ 、 ${T_{\theta \lambda }}$ 和 ${T_{\lambda \lambda }}$ 均呈多象限分布，变化范围为±10 mE。

图 9 位错理论模型模拟的2015尼泊尔地震引起的空间250阶重力梯度变化

Fig. 9 Gravity gradient tensor changes with 250 degrees caused by the 2015 Nepal earthquake are simulated by spherical dislocation theory

同上述过程，模拟了MHT在震间闭锁的空间大地水准面、重力和重力梯度变化率，结果如图8(c)，(d)和图10所示。震间信号分布与同震相反，经过空间平滑后的大地水准面变化幅度为–0.026—0.014 mm·a^–1，重力变化范围为–0.11—0.08 μgal·a^–1。与同震重力梯度变化分布相似， ${T_{rr}}$ 、 ${T_{r\theta }}$ 和 ${T_{\theta \theta }}$ 3个分量的信号强度大于 ${T_{r\lambda }}$ 、 ${T_{\theta \lambda }}$ 和 ${T_{\lambda \lambda }}$ ，不同的是震间重力梯度变化率的形状几乎均呈正—负—正或负—正—负分布，最大变化范围为±0.4 mE。

图 10 位错理论模型模拟的MHT震间 250阶重力梯度变化

Fig. 10 Interseismic gravity gradient tensor changes summated to 250 degrees of the MHT

6 讨　论

MHT为陆地上典型的逆冲断层，尽管从有限的近场连续GPS记录可以反演得到断层在震间期的滑移亏损，但GPS数量仍显不足，断层的空间分辨率不高(Ader 等，2012)。为了得到更高分辨率的断层震间应力积累分布，需要提高连续GPS观测站的密度。

本文模拟的2015年尼泊尔同震重力变化与付广裕等人(2015)给出的在分布形状上相似，变化幅度不同，付广裕等人(2015)的结果为–120—60 μgal。差异是由所用的同震滑移模型不同引起的：付广裕等人(2015)用的模型是美国地质调查局(USGS)用远震波形数据反演得到的，本文的滑移模型是由GPS和遥感数据得到的。有研究表明，在一些陆地地震前，重力观测网有明显的变化，如2013年四川芦山M_s 7.0(祝意青等，2013)。通过本文的模拟计算发现一次M_w 7.8—7.9地震前断层闭锁积累应力期间，重力变化仅为1 μgal·a^–1的量级，难以解释精度10 μgal的重力仪观测到的几十微伽的重力变化。另外，引起喜马拉雅前缘质量迁移的因素颇多，最为显著的是高山上的冰川融化。想要从重力观测中得到与断层活动相关的信号，需要对冰川质量源引起的重力变化加以改正。

GRACE卫星的空间分辨约为330 km，仅能够观测到大尺度的重力变化，受到卫星轨道高度(~500 km)和观测信号的高频噪声的影响，难以捕捉到2015年尼泊尔地震的信号。下一代低—低跟踪模式的重力卫星需要降低轨道高度和利用激光测距代替微波测距，有望提高检测地震信号的能力。青藏高原边缘的质量变化复杂，经空间平滑后±0.15 μgal·a^–1重力变化率的信号完全被冰川等大尺度的质量变化信号所淹没，难以被现阶段的低—低跟踪卫星观测到。邹正波等人(2015)分析了GRACE卫星数据，得到了MHT区域2003年—2008年重力增加，2009年—2014年重力减小，且2015年尼泊尔地震前重力变化形状与同震相似。事实上，尽管将卫星观测重力变化时间序列分段分析，在未扣除其他气候变化因素，难以直接讨论MHT长期运动引起的重力变化信号。在未来提高低—低跟踪重力卫星测距精度的同时，需要对水文、冰川、湖泊等较大尺度显著的质量变化源进行更准确的建模，去除这些影响后的重力变化有望用于检测MHT震间闭锁引起的长期重力变化。

理论上重力梯度是重力的一阶导数，信号应该被放大；实际中，重力梯度卫星GOCE的梯度仪精度不足以及轨道较低引起的高频噪声过大，目前难以检测到同震重力梯度变化信号。未来重力梯度卫星应用于检测M 8以上的地震信号，需要具备在80 km空间分辨率下观测到固定地表面上30 mE重力梯度信号的能力。

7 结　论

本文对利用GPS数据对MHT的震间耦合进行了反演，同时结合InSAR观测资料反演了发生于该断层上2015年尼泊尔地震的同震滑移分布。基于断层滑移/滑移亏损模型，对同震和震间重力场变化，包括大地水准面、重力和重力梯度的变化进行了模拟，讨论了陆地和卫星重力测量检测地震及地震孕育的可能性。得到的主要结论如下：

(1)利用MCMC方法，由连续GPS和ALOS-2数据反演的2015年尼泊尔地震同震滑移模型破裂并未达到地表，最大滑移约为6±0.7 m，地震矩为1.02×10²¹ Nm，相当于M_w7.9。

(2)连续GPS数据反演的MHT震间耦合模型表明几乎整个MHT的20 km深度之上在震间均处于闭锁状态，地震矩亏损率为6.8×10¹⁹Nm/a。

(3)变形地表面的同震重力变化呈南负北正两极分布，震间重力变化率信号呈反对称分布。同震重力信号可以被陆地重力测量所检测到，位于远场的拉萨重力变化有望被超导重力仪检测到。震间重力变化率难以被10 μgal精度的重力仪观测到。

(4)经过截断、平滑的同震和震间重力/重力梯度变化信号难以被当前重力卫星检测出；对冰川等大尺度质量变化源进行改正后，有望被提高测量精度的下一代重力卫星检测到。

参考文献(References)

Ader T, Avouac J P, Liu-Zeng J, Lyon-Caen H, Bollinger L, Galetzka J, Genrich J, Thomas M, Chanard K, Sapkota S N, Rajaure S, Shrestha P, Ding L and Flouzat M. 2012. Convergence rate across the Nepal Himalaya and interseismic coupling on the main Himalayan thrust: implications for seismic hazard. Journal of Geophysical Research, 117 (B4): B04403 [DOI: 10.1029/2011JB009071]

Avouac J P. 2003. Mountain building, erosion, and the seismic cycle in the Nepal Himalaya. Advances in Geophysics, 46 : 1–80. [DOI: 10.1016/S0065-2687(03)46001-9]

Avouac J P, Meng L S, Wei S J, Wang T and Ampuero J P. 2015. Lower edge of locked Main Himalayan Thrust unzipped by the 2015 Gorkha earthquake. Nature Geoscience, 8 (9): 708–711. [DOI: 10.1038/ngeo2518]

Bettinelli P, Avouac J P, Flouzat M, Jouanne F, Bollinger L, Willis P and Chitrakar G R. 2006. Plate motion of India and Interseismic strain in the Nepal Himalaya from GPS and DORIS measurements. Journal of Geodesy, 80 (8/11): 567–589. [DOI: 10.1007/s00190-006-0030-3]

Bilham R. 2004. Earthquakes in India and the Himalaya: tectonics, geodesy and history. Annals of Geophysics, 47 (2/3): 839–858. [DOI: 10.4401/ag-3338]

Cambiotti G, Bordoni A, Sabadini R and Colli L. 2011. GRACE gravity data help constraining seismic models of the 2004 Sumatran earthquake. Journal of Geophysical Research, 116 (B10): B10403 [DOI: 10.1029/2010JB007848]

Cattin R and Avouac J. 2000. Modeling mountain building and the seismic cycle in the Himalaya of Nepal. Journal of Geophysical Research, 105 (B6): 13389–13407. [DOI: 10.1029/2000JB900032]

Chambers D P, Wahr J and Nerem R S. 2004. Preliminary observations of global ocean mass variations with GRACE. Geophysical Research Letters, 31 (13): L13310 [DOI: 10.1029/2004GL020461]

Chen J L, Rodell M, Wilson C R and Famiglietti J S. 2005. Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment (GRACE) water storage estimates. Geophysical Research Letters, 32 (14): L14405 [DOI: 10.1029/2005GL022964]

De Linage C, Rivera L, Hinderer J, Boy J P, Rogister Y, Lambotte S and Biancale R. 2009. Separation of coseismic and postseismic gravity changes for the 2004 Sumatra-Andaman earthquake from 4.6 yr of GRACE observations and modelling of the coseismic change by normal-modes summation. Geophysical Journal International, 176 (3): 695–714. [DOI: 10.1111/j.1365-246X.2008.04025.x]

Dziewonski A M and Anderson D L. 1981. Preliminary reference earth model. Physics of the Earth and Planetary Interiors, 25 (4): 297–356. [DOI: 10.1016/0031-9201(81)90046-7]

Fu G Y, Gao S H, Zhang G Q, She Y W and Sun H P. 2015. Gravitational isostasy background and surface deformation response characteristics of the 2015 Nepal M_S8.1 earthquake . Chinese Journal of Geophysics, 58 (6): 1900–1908. [DOI: 10.6038/cjg20150606] ( 付广裕, 高尚华, 张国庆, 佘雅文, 孙和平. 2015. 2015年尼泊尔M_S8.1地震的地壳重力均衡背景与地表形变响应特征 . 地球物理学报, 58 (6): 1900–1908. [DOI: 10.6038/cjg20150606] )

Fukuda J and Johnson K M. 2008. A fully Bayesian inversion for spatial distribution of fault slip with objective smoothing. Bulletin of the Seismological Society of America, 98 (3): 1128–1146. [DOI: 10.1785/0120070194]

Garcia R F, Bruinsma S, Lognonné P, Doornbos E and Cachoux F. 2013. GOCE: the first seismometer in orbit around the Earth. Geophysical Research Letters, 40 (5): 1015–1020. [DOI: 10.1002/grl.50205]

Han S C, Shum C K, Bevis M, Ji C and Kuo C Y. 2006. Crustal dilatation observed by GRACE after the 2004 Sumatra-Andaman Earthquake. Science, 313 (5787): 658–662. [DOI: 10.1126/science.1128661]

Han S C, Sauber J and Luthcke S. 2010. Regional gravity decrease after the 2010 Maule (Chile) earthquake indicates large-scale mass redistribution. Geophysical Research Letters, 37 (23): L23307 [DOI: 10.1029/2010GL045449]

Han S C, Sauber J and Riva R. 2011. Contribution of satellite gravimetry to understanding seismic source processes of the 2011 Tohoku-Oki earthquake. Geophysical Research Letters, 38 (24): L24312 [DOI: 10.1029/2011GL049975]

Heki K, Miyazaki S and Tsuji H. 1997. Silent fault slip following an interplate thrust earthquake at the Japan Trench. Nature, 386 (6625): 595–598. [DOI: 10.1038/386595a0]

Imanishi Y, Sato T, Higashi T, Sun W K and Okubo S. 2004. A network of superconducting gravimeters detects submicrogal coseismic gravity changes. Science, 306 (5695): 476–478. [DOI: 10.1126/science.1101875]

Jónsson S, Zebker H, Segall P and Amelung F. 2002. Fault slip distribution of the 1999 M_w 7.1 hector mine, California, earthquake, estimated from satellite radar and GPS measurements . Bulletin of the Seismological Society of America, 92 (4): 1377–1389. [DOI: 10.1785/0120000922]

Kumar S, Wesnousky S G, Rockwell T K, Briggs R W, Thakur V C and Jayangondaperumal R. 2006. Paleoseismic evidence of great surface rupture earthquakes along the Indian Himalaya. Journal of Geophysical Research, 111 (B3): B03304 [DOI: 10.1029/2004JB003309]

Kumar S, Wesnousky S G, Jayangondaperumal R, Nakata T, Kumahara Y and Singh V. 2010. Paleoseismological evidence of surface faulting along the northeastern Himalayan front, India: timing, size, and spatial extent of great earthquakes. Journal of Geophysical Research, 115 (B12): B12422 [DOI: 10.1029/2009JB006789]

Kusche J. 2007. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. Journal of Geodesy, 81 (11): 733–749. [DOI: 10.1007/s00190-007-0143-3]

Lawson C and Hanson R. 1974. Solving least squares problems. Englewood Cliffs, New Jersey: Prentice Hall

Lindsey E O, Natsuaki R, Xu X H, Shimada M, Hashimoto M, Melgar D and Sandwell D T. 2015. Line-of-sight displacement from ALOS-2 interferometry: M_w7.8 Gorkha earthquake and M_w 7.3 aftershock . Geophysical Research Letters, 42 (16): 6655–6661. [DOI: 10.1002/2015GL065385]

Loveless J P and Meade B J. 2010. Geodetic imaging of plate motions, slip rates, and partitioning of deformation in Japan. Journal of Geophysical Research, 115 (B2): B02410 [DOI: 10.1029/2008JB006248]

Molnar P. 1987. The distribution of intensity associated with the 1905 Kangra earthquake and bounds on the extent of the rupture zone. Journal of Geological Society of India, 29 (2): 211–229.

Mugnier J L, Gajurel A, Huyghe P, Jayangondaperumal R, Jouanne F and Upreti B. 2013. Structural interpretation of the great earthquakes of the last millennium in the central Himalaya. Earth-Science Reviews, 127 : 30–47. [DOI: 10.1016/j.earscirev.2013.09.003]

Okada Y. 1985. Surface deformation due to shear and tensile faults in a half-space. Bulletin of the Seismological Society of America, 75 (4): 1135–1154.

Okubo S. 1992. Potential and gravity changes due to shear and tensile faults in a half-space. Journal of Geophysical Research, 97 (B5): 7137–7144. [DOI: 10.1029/92JB00178]

Panet I, Mikhailov V, Diament M, Pollitz F, King G, De Viron O, Holschneider M, Biancale R and Lemoine J M. 2007. Coseismic and post-seismic signatures of the Sumatra 2004 December and 2005 March earthquakes in GRACE satellite gravity. Geophysical Journal International, 171 (1): 177–190. [DOI: 10.1111/j.1365-246X.2007.03525.x]

Sapkota S N, Bollinger L, Klinger Y, Tapponnier P, Gaudemer Y and Tiwari D. 2013. Primary surface ruptures of the great Himalayan earthquakes in 1934 and 1255. Nature Geoscience, 6 (1): 71–76. [DOI: 10.1038/ngeo1669]

Su X N, Wang Z, Meng G J, Xu W Z and Ren J W. 2015. Pre-seismic strain accumulation and co-seismic deformation of the 2015 Nepal M_S8.1 earthquake observed by GPS . Chinese Science Bulletin, 60 (22): 2115–2123. [DOI: 10.1360/N972015-00534] ( 苏小宁, 王振, 孟国杰, 徐婉桢, 任金卫. 2015. GPS观测的2015年尼泊尔M_S8.1级地震震前应变积累及同震变形特征 . 科学通报, 60 (22): 2115–2123. [DOI: 10.1360/N972015-00534] )

Sun W K and Okubo S. 1993. Surface potential and gravity changes due to internal dislocations in a spherical earth-I. Theory for a point dislocation. Geophysical Journal International, 114 (3): 569–592. [DOI: 10.1111/j.1365-246X.1993.tb06988.x]

Sun W K, Okubo S and Vaníček P. 1996. Global displacement caused by point dislocations in a realistic earth model. Journal of Geophysical Research, 101 (B4): 8561–8577. [DOI: 10.1029/95JB03536]

Tapley B D, Bettadpur S, Ries J C, Thompson P F and Watkins M M. 2004. GRACE measurements of mass variability in the Earth system. Science, 305 (5683): 503–505. [DOI: 10.1126/science.1099192]

Velicogna I and Wahr J. 2006. Measurements of time-variable gravity show mass loss in Antarctica. Science, 311 (5768): 1754–1756. [DOI: 10.1126/science.1123785]

Wang R J, Lorenzo-Martín F and Roth F. 2006. PSGRN/PSCMP-A new code for calculating co- and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory. Computers and Geosciences, 32 (4): 527–541. [DOI: 10.1016/j.cageo.2005.08.006]

Zhou X, Cambiotti G, Sun W and Sabadini R. 2014. The coseismic slip distribution of a shallow subduction fault constrained by prior information: the example of 2011 Tohoku (M_w9.0) megathrust earthquake . Geophysical Journal International, 199 (2): 981–995. [DOI: 10.1093/gji/ggu310]

Zhou X. 2017. Markov chain Monte Carlo method used to invert for fault slip from geodetic data. Journal of Geodesy and Geodynamics, in print, 37(10): 996—1002 [DOI: 10.14075/j.jgg.2017.10.002 (周新. 2017. 利用大地测量数据反演断层滑移分布的MCMC方法. 大地测量与地球动力学, 37(10): 996—1002 [DOI: 10.14075/j.jgg.2017.10.002])

Zhu Y Q, Wen X Z, Sun H P, Guo S S and Zhao Y F. 2013. Gravity changes before the Lushan, Sichuan, M_S=7.0 earthquake of 2013 . Chinese Journal of Geophysics, 56 (6): 1887–1894. [DOI: 10.6038/cjg20130611] ( 祝意青, 闻学泽, 孙和平, 郭树松, 赵云峰. 2013. 2013年四川芦山M_S7.0地震前的重力变化 . 地球物理学报, 56 (6): 1887–1894. [DOI: 10.6038/cjg20130611] )

Zou Z B, Li H, Wu Y L, Wu G J and Kang K X. 2015. Characteristics of satellite time-variable gravity field before M8.1 Nepal earthquake . Journal of Geodesy and Geodynamics, 35 (4): 547–551. [DOI: 10.14075/j.jgg.2015.04.001] ( 邹正波, 李辉, 吴云龙, 吴桂桔, 康开轩. 2015. 尼泊尔M8.1地震震前卫星重力场时变特征 . 大地测量与地球动力学, 35 (4): 547–551. [DOI: 10.14075/j.jgg.2015.04.001] )

摘要

关键词