|
收稿日期: 2017-06-29
基金项目: 国家自然科学基金(编号:41374083,61427817)
第一作者简介: 李瑞锋,1974年生,女,高级工程师,研究方向为航天遥感数据处理与定标技术。E-mail:941532669@qq.com
中图分类号: P223
文献标识码: A
|
摘要
重力卫星搭载的加速度计用于测量非保守力。加速度计的偏差和标度因数在空间随环境变化而缓慢变化,需要实施外部标定,以方便正确应用于数据处理。很多文献研究了动力学标定法、定轨标定方法、能量标定法等,在快速性、高精度性等方面有待提高。本文提出了加速度标定方法,建立数学模型,用于重力卫星的加速度计标定。结果表明,该方法是一种有效的标定方法,在目前的数据条件下,其标校达到10−8—10−9 m/s2水平,标校效果X方向参数最优,Z轴次之,Y轴最差。加速度标校法受到先验地球重力场模型的影响,需要采用迭代方法,逐步逼近真实的加速度计参数。如果提高GNSS轨高产品采样率,可提高总加速度计算精度,从而提高加速度计的定标精度。加速度标定方法是一种有效、快速、精度较高的标定方法,提供精确的标定参数,可以在重力卫星数据处理中使用。
关键词
重力卫星, 加速度计, 定标, 加速度标校法
Abstract
Satellite gravimetry is a technique of surveying the earth’s gravity and geoid and their changing signal. The data are used in geodesy science, environment monitoring, seismic, hydrology, and ocean science. An accelerometer is a core payload in the satellite-to-satellite tracking model or satellite gravity gradiometry and is used to sense non-gravity forces. An accelerometer cannot survey a non-conservative force absolutely for its bias, drift, scale, and second-order terms. Parameters change with the environment, status, and time. Thus, the accelerometer should be calibrated and validated. The accelerometer STAR is loaded on the Challenging Mini-Satellite Payload for Geophysical Research and Application (CHAMP) satellite and has an accuracy of 10−8—10−9 m/s2. The SuperStar accelerometer is loaded on the Gravity Recovery And Climate Experiment (GRACE) satellite, and its accuracy is improved to 10−9—10−10 m/s2. The GRADIO accelerometer is loaded on the Gravity field and steady-state Ocean Circulation Explorer (GOCE) satellite, and its accuracy is 10−11—10−12 m/s2. With the improving accuracy, additional requirements are needed to calibrate the accelerometer. In terms of data type, the three calibration methods are as follows: The first method is direct calibration, where non-gravity force model data are used to compare the output of the accelerometer. The second is the dynamic method, where GNSS data are used to determine the satellite orbit and the accelerometer bias parameters together. The third is the integrated method, where all data are used to determine the total coefficients of the gravity model and the bias of the accelerometer. In addition, the energy domain, the cross point, and the gravity up-continue methods are used to calibrate the accelerometer. The energy domain method is based on persistence energy. The dissipative energy is deduced by the satellite position and velocity. Then, the parameters of the accelerometer are evaluated from the dissipative energy. Its accuracy is not better because the dissipative energy cannot be calculated precisely given the error of the satellite position and velocity. The cross point method is based on the hypothesis that the force of satellite, which crosses a point twice, is equivalent. Evidently, it is an inaccurate method. The gravity up-continue method is used to calibrate the gravity gradiometer. All these methods have been used to calibrate the accelerometer on CHAMP and GRACE. Results indicate that the dynamic and integrated methods are appropriate for external calibration. A new calibration method called the acceleration domain method is proposed. The calibration method is discussed, and the mathematic model is deduced. The acceleration domain method is used to calibrate the GRACE accelerometer. Results indicate that the total calibration accuracy is 10−8—10−9 m/s2. The best calibration is that of the X-axis parameters, followed by the Z-axis parameters, and then the Y-axis. The acceleration domain method effectively determines the accelerometer parameters. The calibration method is affected by the prior earth gravity model. Thus, iterative procedures should be applied. The accuracy of total acceleration, which is calculated from GNSS data, is related to the position sample rate. Thus, if the GNSS data rate is increased, then the calibration accuracy is improved. If the GNSS data rate is 1 s, and the calibration accuracy is 10−9—10−10 m/s2, then the accuracy is improved 8–10 times.
Key words
satellite gravimetry mission, accelerometer, calibration, acceleration calibration method
1 引 言
重力卫星用于测量地球重力场和大地水准面及其变化,在地球科学、环境监测、地震、水文、海洋等领域具有重要应用价值。重力卫星中无论是跟踪型卫星还是梯度重力测量型卫星,均搭载高精度静电悬浮加速度计,用于测量轨道空间处的非保守力或者差分测量地球重力梯度。星载高精度加速度计是相对测量仪器,存在仪器偏差、标度因数、二阶项等参数,使得输出的非保守力与真实的非保守力存在偏差。而且,上述仪器参数在地面检验过程中,由于受到重力加速度的限制,仅能给出粗略检验值,需要进一步在轨标校和外部标校。另外,加速度计参数是变化量,与仪器所处的环境、时间等因素有关,需要以一定的频度和一定精度实施标校,以期获得较好的非保守力测量结果。
加速度计参数标校包括地面、在轨和外部标校3个过程。地面校准是加速度计研制厂家在出厂前利用地面设备进行加速度计参数标校,给出尽可能准确的标校参数数值,供卫星用户数据在数据处理中使用。在轨校准是在轨利用外部输入标准非保守力进行标校,方法主要包括3种:(1)推进器推力标定方法,采用推力器提供标准推力,假设在短时间内非保守力平稳无变化,则依据加速度计测量的推力,实现加速度计的在轨标定。(2)旋转卫星标定法,通过引入周期力矩,使得卫星产生周期性晃动,生成标准离心力,进一步采用加速度计测量的离心力标定加速度计参数。(3)引力标定方法,改变星体内部引力分布,引入标准变化引力,依据加速度计测量数据的变化标定加速度计参数。在轨标定方法可以测量加速度计的分辨率、质心重合度、标度因数和安装误差等,但是受到各类控制力的准确度影响,标定加速度计参数精度有限。外部校准方法可归纳为5种方法:(1)直接法:利用加速度计在轨测量非保守力数据与标准的模型计算的非保守力进行比对,标校参数;(2)能量法:计算出卫星一段时间内的耗散能,用来估计加速度计参数;(3)交叉点法:基于在升降轨交叉点处卫星受力环境一致,实现加速度计参数估计;(4)动力学方法:基于GPS实测轨道数据、重力场模型、加速度计数据等同时进行定轨和加速度计参数校准;(5)整体法:将重力场模型参数、加速度计参数一起估计。
CHAMP(Challenging Mini-satellite Payload)卫星搭载法国研制的Star加速度计,测量精度达到10−8—10−9 m/s2(Reigber 等,2002)。GRACE(Gravity Recovery And Climate Experiment)卫星搭载了法国研制的SuperStar加速度计,测量精度提高一个数量级,达到10−9—10−10 m/s2水平(Tapley 等,2004)。GOCE(Gravity field and steady-state Ocean Circulation Explorer)卫星搭载的GRADIO加速度计,其精度水平再提高2个数据量级,达到10−11—10−12 m/s2水平。测量能力逐步增强,也给加速度计定标提出了更严苛的要求(Drinkwater 等,2007)。
国际上,德国地学中心(GFZ)、慕尼黑大学、丹弗大学、美国空间中心等相关研究机构在加速度计偏值和标度因素标校方面取得了丰富研究成果。德国地学中心在标校CHAMP卫星上STAR加速度计参数中采用了动力学标校方法,即利用卫星轨道数据采用动力学方法同时估计卫星轨道参数和加速度计参数,将标校参数公布给卫星用户使用。研究表明如果以GPS数据替代轨道数据,动力学法标校的加速度计参数结果较差,估计尺度参数偏离1较明显。但是,如能同时估计重力场参数,则标校结果得到明显改善(Neumayear,2005;Perosanz 等,2005)。美国德克萨斯大学空间研究中心(CSR)用动力学法进行标校,将加速度计参数与GPS定轨参数、KBR校准参数看作待定参量,与重力场球谐系数一起估计。CSR和GFZ都是采取一天估算一次偏值,一天或一个月估算一次标度因数。GOCE卫星项目组成立了专门校准组,开展在轨梯度仪内部校准工作,利用离子和冷气推进器使得卫星晃动引入的牵连加速度作为校准输入源(梯度仪每个加速度计单元离卫星质心距离较远,偏心距离达到几十厘米,旋转引起的牵连加速度大)进行在轨标校。这一方法在轨内部标定精度非常有限,而且无法解决偏值的在轨内部校准,因此最终校准参数还是需要通过外部校准方法来解决。针对GOCE卫星,也提出利用高精度地面区域重力测量数据沿拓到卫星轨道高度来校准梯度仪偏值和标度因数。
中国开展了很多重力卫星标校方法研究。基于能量法,利用现有重力场模型标定重力卫星加速度参数,研究证明尺度、偏差和偏差漂移参数都有明显的周期变化,但各主周期项略有差异,标校精度一定程度上取决于所选重力场模型精度(徐天河和杨元喜,2005;徐新禹 等,2008)。利用卫星轨迹交叉点可以标定重力卫星加速度参数,算例验证算法有效。采用整体法,在解算位系数的同时对加速度计数据的尺度和偏差进行标校,计算结果表明该方法几乎不受参考重力场模型影响,可明显改善重力场模型的恢复精度(张兴福和沈云中,2007;邹贤才 等, 2007, 2015)。研究动力学定轨中对加速计参数进行方法校标,获得了较好的标校结果,是一种快速校标方法(熊永清 等,2011)。研究了重力测量卫星中加速度计在轨参数校准方法,如推进器推力标定、旋转卫星标定、引力标定等方法,结果表明在轨标定方法可以测量加速度计的分辨率、质心重合度、标度因数和安装误差,但是加速度计参数标定精度受限,仍需用外部校准方法标校加速度计参数(周泽兵 等,2009;祝竺 等,2010)。采用迭代算法对加速度计的标度因子和零偏进行估算,算法能有效标定出加速度计参数,并且对较大偏差的初值同样适用,且迭代过程收敛迅速,计算量小,非线性适应性较强(戴邵武 等,2014)。研究提出一种旋转加速度计重力梯度仪标定方法,给出了重力梯度零位和标度系数计算式,并在重力梯度半物理仿真系统上进行了验证(钱学武和蔡体菁,2016)。基于动力学方法,将KBR测量系统观测到的星间加速度作为观测量,选用高精度的地球重力场模型,利用扩展卡尔曼滤波算法实现加速度计参数的在轨标定,仿真结果表明加速度计的标度因子和零偏估计误差均在0.2%以内(辛宁 等,2016)。
在能量法、交叉点方法、动力学标校方法、整体标校法中取得大量的研究成果,但是尚未见对于加速度标校方法系统研究报道,对这一方法研究上还很欠缺。基于此,本文提出并详细研究加速度标校法,并将这一方法用于实际重力卫星加速度计标校。
2 加速度标校法理论模型
加速度标校法基本原理是基于卫星轨道计算卫星总加速度,扣除利用已知高精度重力场模型、固体潮模型和海潮模型计算轨道处保守力,得到卫星受到的非保守力,以此为标准观测值估计加速度计偏值和标度因素,实现对于加速度计的标校。
根据卫星动力学方程可导出卫星受到非保守力表达式为
| ${{{a}}_{{{ng}}}} = {{\ddot r}} - {{{a}}_{{g}}} - {{{a}}_{{t}}}$ | (1) |
式中,
导出观测值与加速度计参数函数关系式如下
| ${{AX}} = {{L}}$ | (2) |
式中,
依据最小二乘原理,加速度计的参数估计值可以依据下式求出:
| ${{\hat X}} = {{{(}}{{{A}}^{{\rm T}}}{{A)}}^{ - {{1}}}} \cdot {{{A}}^{{\rm T}}}{{L}}$ | (3) |
相应误差表示式为
| $\begin{gathered} {{\hat \sigma }^2} = {{{V}}^{{\rm T}}}{{V}}/(m - n) \\ {{Q}} = {{{(}}{{{A}}^{{\rm T}}}{{A)}}^{ - {{1}}}} \\ {m_{{x_i}}} = \hat \sigma \sqrt {{Q_{ii}}} \\ \end{gathered} $ | (4) |
式中,
卫星总加速度通常有两种计算方法,第1种方法是采用事后处理方法对低轨卫星精密定轨,得到低轨卫星位置和速度,再采用数值差分算法对卫星轨道二次微分或对卫星速度一次微分得到卫星总加速度,这一方法称为位置微分法或速度微分法;第2种方法是对星载GPS距离观测数据二次微分得到高低卫星星间加速度观测值,建立星间加速度观测值与低轨卫星加速度间关系,采用最小二乘方法估计低轨卫星加速度,称为相位加速度法。本文研究采用了位置微分法和速度微分法。显然,总加速度的计算精度会影响加速度标定法的效果。总加速度的计算精度改善不仅与观测精度提高有关,而且有赖于重力卫星轨道位置和速度精度和采样率的提高,如采样间隔由60 s提高到1 s,根据误差传播定律可将导出加速度精度提高8—10倍。
非保守力计算主要采用模型方法进行计算,各项累加后得到总的保守力。非保守力计算需要采用先验重力场模型计算地球引力,则加速度标校法受到先验地球重力场模型的影响。为解决这一问题,提出采用迭代方法,在不断更新重力场模型的过程中逐步改善加速度计参数估计值。
3 算例分析
以GRACE_A卫星和GRACE_B卫星数据为例,用加速度标定方法估计加速度计的偏值和标度因素参数,估计结果分别列于表1和表2。
表 1 GRACE_A卫星加速度计的偏值和标度因素估计结果
Table 1 The evaluated bias and scale of the GRACE_A accelerometer
| 方向 | 偏值
(10−8 m/s2) |
偏值误差
(10−8 m/s2) |
标度因素 | 标度因素误差
(10−2) |
| X | –5.81 | 0.41 | 0.93 | 2.92 |
| Y | 21.70 | 3.89 | 0.19 | 3.14 |
| Z | –131.40 | 0.99 | 1.39 | 8.96 |
表 2 GRACE_B卫星加速度计的偏值和标度因素估计结果
Table 2 The evaluated bias and scale of the GRACE_B accelerometer
| 方向 | 偏值/
(10−8 m/s2) |
偏值误差
/(10−8 m/s2) |
标度因素 | 标度因素误差
/(10−2) |
| X | –4.88 | 0.22 | 0.98 | 2.76 |
| Y | 11.63 | 4.31 | 0.04 | 1.32 |
| Z | –95.17 | 1.35 | 1.34 | 8.38 |
由表1和表2可见,两颗卫星的加速度计偏值估计误差为10−8—10−9 m/s2的水平,在卫星飞行方向即X方向的估计精度较其他两个方向高一个数量级。加速度计标度因素估计误差为10–2的水平,X方向标度因素较接近1,Z方向稍差,Y方向最差,原因在于Y方向是加速度计非敏感轴,而且此方向的非保守力最小,在10−9 m/s2的水平。
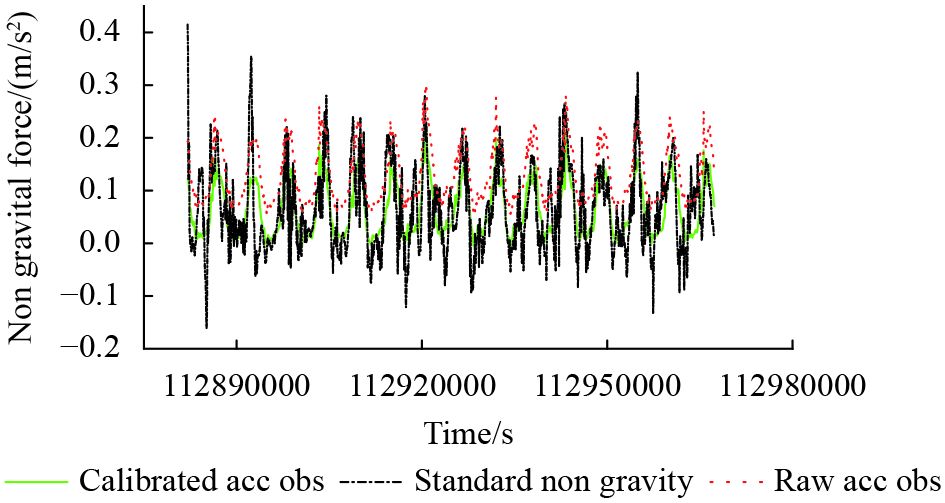
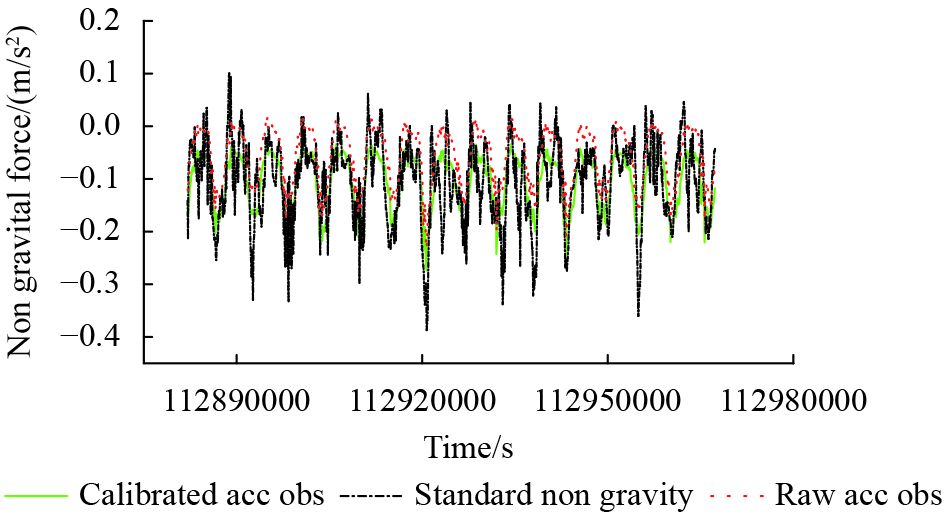
利用估计得到的加速度计参数标校观测值,得到校准后的加速度计数据。为比较期间,将两者和导出的非保守力观测值一同表示在图1和图2中,图1和图2分别对应GRACE-A和GRACE-B卫星加速度计输出数据。
由图1和图2可见,标校后的加速度计观测值与导出非保守力符合得较好。A卫星的加速度计观测值与导出非保守力差值的均值和标准差分别为–4.1×10−11 m/s2和5.9×10−8 m/s2,相应B卫星而言分别为–3.4×10−11 m/s2和5.6×10−8 m/s2。
为进一步分析加速度方法的标校结果,估计了4天的加速度计参数,每天得到一组结果,A卫星加速度计偏值和标度因素估计结果分别列于表3和表4,相应于B卫星结果列于表5和表6。
表 3 卫星A加速度计的偏值估计结果
Table 3 The evaluated bias of GRACE_A accelerometer
| /(10−8 m/s2) | |||||
| X方向 | X方向误差 | Y方向 | Y方向误差 | Z方向 | Z方向误差 |
| –7.01 | 0.72 | 12.80 | 3.24 | –132.16 | 0.92 |
| –4.25 | 0.53 | 15.31 | 3.90 | –129.11 | 0.94 |
| –7.85 | 0.54 | 20.93 | 4.01 | –125.73 | 1.01 |
| –6.67 | 0.71 | 38.93 | 3.99 | –128.20 | 0.97 |
表 4 卫星A加速度计的标度因素估计结果
Table 4 The evaluated scale of GRACE_B accelerometer
| X方向 | X方向误
差/(10−2) |
Y方向 | Y方向误
差/(10−2) |
Z方向 | Z方向误
差/(10−2) |
| 0.92 | 4.03 | 0.09 | 2.19 | 1.54 | 8.23 |
| 0.75 | 3.48 | 0.11 | 2.63 | 1.24 | 8.41 |
| 0.95 | 3.83 | 0.15 | 2.69 | 0.97 | 9.02 |
| 0.89 | 5.35 | 0.26 | 2.67 | 1.23 | 8.72 |
表 5 卫星B加速度计的偏值估计结果
Table 5 The evaluated bias of GRACE_B accelerometer
| /(10−8 m/s2) | |||||
| X方向 | X方向误差 | Y方向 | Y方向误差 | Z方向 | Z方向误差 |
| –6.03 | 0.27 | 10.17 | 2.70 | –88.52 | 1.13 |
| –5.55 | 0.25 | 12.51 | 3.92 | –90.16 | 1.32 |
| –4.79 | 0.24 | 14.99 | 3.63 | –99.48 | 1.50 |
| –5.98 | 0.26 | 26.56 | 4.32 | –93.09 | 1.50 |
表 6 卫星B加速度计的标度因素估计结果
Table 6 The evaluated scale of GRACE_B accelerometer
| X方向 | X方向误
差/(10−2) |
Y方向 | Y方向误
差/(10−2) |
Z方向 | Z方向误
差/(10−2) |
| 0.91 | 2.80 | 0.03 | 0.74 | 1.61 | 6.67 |
| 0.91 | 3.50 | 0.04 | 1.08 | 1.54 | 7.78 |
| 1.14 | 3.89 | 0.04 | 1.00 | 1.01 | 8.77 |
| 0.88 | 5.01 | 0.08 | 1.18 | 1.36 | 8.73 |
由表3—6数据分析可见,加速度法标校精度在10−8 m/s2—10−9 m/s2水平,可以较好标校X方向的加速度计观测值,Z轴次之,Y轴最差。Y轴差的原因有二,一则Y周是加速度计的非敏感轴,观测精度较差;二是该方向的非保守力量级较小,仅为10–9 m/s2水平,与导出非保守力的误差水平相当或略小。
4 结论与讨论
本文提出了一种新的加速度计标校方法-加速度定标法。该方法突破了传统的动力学标定法、轨道标定法和能量法,是一种在卫星加速度域实现的定标方法。与动力学标定法和轨道标定法比较,该法具有计算简便、获取标校参数快捷的优点;与能量标定方法比较,具有高精度的特点,可作为重力卫星数据处理中的快速定标方法应用,也是对传统定标方法的一种补充。
研究表明本文提出的加速度定标法是一种有效、快速的加速度计标定方法,可用于重力卫星加速度计的偏值和标度因数标校。在现有GRACE卫星数据条件下,标校精度达到10–8—10–9 m/s2水平,可以为后续的精处理提供较高精度的标校参数。加速度标校法的精度主要受到导出总加速度精度和先验地球重力场模型精度的影响,前者可以通过提高总加速度精度和重力场模型精度进一步改善标校精度,后者可采用迭代方法,逐步逼近真实的加速度计参数,进一步改善标校精度。
在本文研究试验中,由于目前重力卫星的标准轨道产品的采样率为60 s,暂时无法获得1 s采样率的轨道产品,对于提高采样率可以进一步提高导出加速度精度的理论分析结论还未进行试验数据验证。后续工作将进一步收集1 s采用率的轨道数据,开展相关试验分析,验证采样率提高可以提高导出加速度精度的分析结论。
参考文献(References)
-
Dai S W, Wan L and Xu S H. 2014. Accelerometer calibration method based on Iterative calculation. Ship Electronic Engineering, 34 (1): 63–65, 95. [DOI: 10.3969/j.issn1672-9730.2014.01.018] ( 戴邵武, 万龙, 徐胜红. 2014. 基于迭代计算的加速度计标定方法. 舰船电子工程, 34 (1): 63–65, 95. [DOI: 10.3969/j.issn1672-9730.2014.01.018] )
-
Drinkwater M R, Haagmans R, Muzi D, Popescu A, Floberghagen R, Kern M and Fehringer M. 2007. The GOCE gravity mission: ESA’s first core Earth explorer. Proceedings of the 3rd International GOCE User Workshop. Frascati, Italy: European Space Agency
-
Perosanz F, Biancale R, Lemoine J M, Vales N, Loyer S and Bruinsma S. 2005. Evaluation of the CHAMP accelerometer on two years of mission//Reigber C, Lühr H, Schwintzer P and Wickert J, eds. Earth Observation with CHAMP, Results from Three Years in Orbit. Berlin Heidelberg: Springer: 77–82 [DOI: 10.1007/3-540-26800-6_12]
-
Qian X W and Cai T J. 2016. Calibration method for gravity gradiometer of rotating accelerometer. Journal of Chinese Inertial Technology, 24 (4): 427–430, 436. [DOI: 10.13695/j.cnki.12-1222/o3.2016.04.002] ( 钱学武, 蔡体菁. 2016. 旋转加速度计重力梯度仪标定方法. 中国惯性技术学报, 24 (4): 427–430, 436. [DOI: 10.13695/j.cnki.12-1222/o3.2016.04.002] )
-
Reigber C, Balmino G, Schwintzer P, Biancale R, Bode A, Lemoine J M, König R, Loyer S, Neumayer H, Marty J C, Barthelmes F, Perosanz F and Zhu S Y. 2002. A high-quality global gravity field model from CHAMP GPS tracking data and accelerometry (EIGEN-1s). Geophysical Research Letters, 29 (14): 37-1–37-4. [DOI: 10.1029/2002GL015064]
-
Tapley B D, Bettadpur S, Watkins M and Reigber C. 2004. The gravity recovery and climate experiment: mission overview and early results. Geophysical Research Letters, 31 (9): L09607 [DOI: 10.1029/2004GL019920]
-
Xin N, Qiu L D, Zhang L H and Liu N J. 2016. On-orbit calibration algorithm of electrostatic accelerometer for gravity measurement satellite. Spacecraft Engineering, 25 (1): 25–30. [DOI: 10.3969/j.issn.1673-8748.2016.01.004] ( 辛宁, 邱乐德, 张立华, 刘乃金. 2016. 一种重力测量卫星静电加速度计在轨标定算法. 航天器工程, 25 (1): 25–30. [DOI: 10.3969/j.issn.1673-8748.2016.01.004] )
-
Xiong Y Q, Wang H B, Xu X L and Zhao C Y. 2011. The calibration research for GRACE accelerometer. Scientia Sinica (Physica, Mechanica and Astronomica), 41 (11): 1319–1327. [DOI: 10.1360/132010-1234] ( 熊永清, 汪宏波, 许晓丽, 赵长印. 2011. GRACE加速仪资料定标研究. 中国科学(物理学 力学 天文学), 41 (11): 1319–1327. [DOI: 10.1360/132010-1234] )
-
Xu T H and Yang Y X. 2005. Spectral analysis on time series of calibration parameters of CHAMP accelerometer. Chinese Journal of Space Science, 25 (2): 143–148. [DOI: 10.3969/j.issn.0254-6124.2005.02.011] ( 徐天河, 杨元喜. 2005. CHAMP卫星加速度计标校参数序列的谱分析. 空间科学学报, 25 (2): 143–148. [DOI: 10.3969/j.issn.0254-6124.2005.02.011] )
-
Xu X Y, Li J C, Wang Z T and Zou X C. 2008. Calibration of GRACE accelerometer using reference gravity field model based on energy balance approach. Geomatics and Information Science of Wuhan University, 33 (1): 72–75. ( 徐新禹, 李建成, 王正涛, 邹贤才. 2008. 利用参考重力场模型基于能量法确定GRACE加速度计校准参数. 武汉大学学报(信息科学版), 33 (1): 72–75. )
-
Zhang X F and Shen Y Z. 2007. Calibration of CHAMP accelerometer data with dynamical method. Geomatics and Information Science of Wuhan University, 32 (2): 176–179. [DOI: 10.3321/j.issn:1671-8860.2007.02.021] ( 张兴福, 沈云中. 2007. 利用动力学法标校CHAMP卫星加速度计数据. 武汉大学学报(信息科学版), 32 (2): 176–179. [DOI: 10.3321/j.issn:1671-8860.2007.02.021] )
-
Zhou Z B, Bai Y Z, Zhu Z and Zhang X M. 2009. In-orbit calibration methods of accelerometer parameters on satellite-borne gravimetry. Chinese Space Science and Technology, 29 (6): 74–80. [DOI: b10.3321/j.issn:1000-758X.2009.06.012] ( 周泽兵, 白彦峥, 祝竺, 张晓敏. 2009. 卫星重力测量中加速度计在轨参数校准方法研究. 中国空间科学技术, 29 (6): 74–80. [DOI: b10.3321/j.issn:1000-758X.2009.06.012] )
-
Zhu Z, Zhang X M and Zhou Z B. 2010. In-orbit verification for accelerometers using rotating spacecraft method. Journal of Astronautics, 31 (5): 1362–1367. [DOI: 10.3873/j.issn.1000-1328.2010.05.018] ( 祝竺, 张晓敏, 周泽兵. 2010. 利用旋转卫星法开展加速度计在轨检验研究. 宇航学报, 31 (5): 1362–1367. [DOI: 10.3873/j.issn.1000-1328.2010.05.018] )
-
Zou X C, Li J C, Luo J and Xu X Y. 2007. Calibration of onboard accelerometer by dynamic method. Geomatics and Information Science of Wuhan University, 32 (12): 1152–1155. [DOI: 10.3969/j.issn.1671-8860.2007.12.016] ( 邹贤才, 李建成, 罗佳, 徐新禹. 2007. 星载加速度计的动力法校准. 武汉大学学报(信息科学版), 32 (12): 1152–1155. [DOI: 10.3969/j.issn.1671-8860.2007.12.016] )
-
Zou X C, Li J C Zhong L P and Xu X Y. 2015. Calibration of the accelerometers Onboard GRACE with the dynamic method. Geomatics and Information Science of Wuhan University, 40 (3): 357–360. [DOI: 10.13203/j.whugis20130269] ( 邹贤才, 李建成, 衷路萍, 徐新禹. 2015. 动力法校准GRACE星载加速度计. 武汉大学学报(信息科学版), 40 (3): 357–360. [DOI: 10.13203/j.whugis20130269] )