出版日期: 2018-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20187145
2018 | Volumn22 | Number 6
上一篇  |  下一篇
  
城市扩张CA模型的参数敏感性分析
expand article info 张亦汉 , 乔纪纲 , 刘婉华 , 蔡思锐 , 丁倩欣 , 陈小微
广东财经大学 地理与旅游学院, 广州 510320
收稿日期: 2017-05-26
基金项目: 国家自然科学基金(编号：41531176，41371376)；广东省自然科学基金（编号：2014A030313605）
第一作者简介: 张亦汉，1985年生，男，副教授，研究方向为地理信息模型与数据同化。E-mail：zyh4184@163.com
通信作者简介: 乔纪纲，1973年生，男，副教授，研究方向为遥感与地理信息模型。E-mail：qjg821@263.com
中图分类号: TP79
文献标识码: A

摘要

以广州市番禺区为研究区，构建了相应的城市扩张CA模型，从采样、邻域结构和微观元胞尺度等方面研究了CA模型的敏感性。首先通过改变模型采样比例、样本各个类别的比例等研究样本对模型参数的影响。然后分析不同的邻域结构与模型模拟精度的关系，并从微观尺度分析邻域元胞对中心元胞的影响。最后从空间尺度上分析CA模型在各种不同分辨率下的模拟结果，用景观指数剖析模拟结果的形态，同时在元胞摩尔邻域内分析其3×3邻域的城市发展密度变化情况。实验表明：(1)适当提高采样比例，会得到精度较高的权重，但训练样本中城市用地的比例应该与城市用地的转变量在全区的占比相匹配。(2)不论是采用摩尔邻域还是冯诺依曼邻域，模拟精度均随着空间尺度的增加而降低。在同一空间尺度下，采用摩尔邻域的模拟结果略好。相比冯诺依曼4个邻域元胞，摩尔邻域中的角点对中心元胞具有更大的影响。(3)随着空间分辨的降低，模拟结果的斑块数、斑块密度、聚集度和分形维度值在减少，结构变得简单，而且在微观的摩尔邻域中城市发展密度正在减少，即由高密度向低密度转换。

关键词

元胞自动机, 城市扩张, 敏感性, 景观指数, 邻域结构

Parameter sensitivity analysis of urban cellular automata model
expand article info ZHANG Yihan , QIAO Jigang , LIU Wanhua , CAI Sirui , DING Qianxin , CHEN Xiaowei
School of Geography and Tourism, Guangdong University of Finance and Economics, Guangzhou 510320, China

Abstract

Land-use change is the hotspot in the research on global change and sustainable development. The change of urban land use has attracted the attention of many scholars. Cellular Automata (CA) model, which is characterized by its powerful space–time dynamic simulation capability, is one of the important tools for urban land-use change. However, existing research does not systematically analyze the effect of sampling, neighborhood, structure, and different resolutions in the CA model. Therefore, this paper intends to carry out systematic sensitivity analysis in an urban CA model to obtain the quantitative accuracy effect by different factors, such as sampling and neighborhood structure, and the optimal model simulation results. The critical part of CA models is transition rules, which are usually represented by exogenous impact factors such as roads, highways, and towns. These factors (variables) can be addressed by incorporating multicriteria evaluation (MCE) form into CA, which is transformed from MCE into a logistic form to obtain the parameters with a more objective method. This study applies the Monte Carlo method to create different sample ratios that can be used to obtain the weight of the CA model. We also test the CA model’s sensitivity by using different neighborhood structures. Landscape metrics are adopted to verify the accuracy of simulation results in different spatial resolutions. These methods can help determine the best combination for the CA model. After the model is applied to Panyu, the core area of the Pearl River Delta, simulation results can be obtained by using three combinations and processes. First, different sampling ratios and category proportions are used to study the parameter changes under different sample groups. Second, different neighborhood structures are used to find the relationship between model accuracy and neighborhood structure. Finally, the simulation results and changes in different resolutions, landscape index, and 3×3 micro-neighborhood are analyzed. Different simulation results are determined for different combinations of sample ratio, neighborhood, and spatial resolution. Our findings are as follows: (1) High precision weights can be obtained using high sampling ratios, and the proportion of urban in the sample should be consistent with the change rate in the study area. (2) Regardless of which kind of neighborhood structure is used, the simulation accuracy decreases with low-resolution data. However, the simulation accuracy of the Moore neighborhood will be better than that of the Von Neumann neighborhood. The corner cells have a greater effect than the adjacent cells. (3) The patch number, patch density, concentration, and fractal dimension values fall with low-resolution data. The structure of simulation results becomes simple, and the development density of the Moore neighborhood decreases.

Key words

cellular automata, urban expansion, sensitivity, landscape index, neighborhood structure

1 引　言

土地利用变化是全球变化与可持续发展研究的核心和热点，其中城市用地的扩张变化更是引起了众多学者的关注(刘纪远 等，2002；王雷 等，2012)。一些学者利用遥感和GIS技术进行多时像的城市用地变化研究，也有一些学者关注城市用地的过程模拟(Li和Yeh，2004；张亦汉 等，2011)。元胞自动机(CA)模型因其强大的时空动态模拟能力，被认为是土地利用变化模拟的重要方法和主要工具之一(Guang和Clarke，2010；Li 等，2011；Chen 等，2014)。CA模型是由Wolfram提出的空间、时间离散且通过局部规则获得全局涌现特征的动力学模型，常被用于地理格局和过程的建模和模拟。城市扩张研究常采用遥感影像等栅格数据作为数据源，与CA模型的离散空间具有天然的相似性，因此越来越多的学者运用CA模型进行城市扩张研究工作(White和Engelen，1993；Wu，2002；Li和Yeh，2002；Liu 等，2010，2014)。

CA模型主要包括转换规则、元胞大小、邻域大小以及邻域形状等方面。由于CA模型由众多因素共同制约，因此其敏感性的研究是CA模型研究城市扩张不可回避的问题(柯新利 等，2010)。其中，转换规则是CA模型的核心，规则中的参数值大小对城市扩张模拟的结果有决定性的作用(Li和Liu，2006)。元胞大小可以反映输入数据的空间尺度特征，即栅格数据(如遥感)的空间分辨率(柯新利 等，2010)。邻域大小及形状指元胞空间邻近关系的范围大小，是邻域元胞对中心元胞的作用力体现(吴浩 等，2013)。利用CA模型模拟城市扩张时，模拟结果往往会随着这些因素的空间尺度变化而发生改变。一些学者进行了相关的敏感性分析，如Wu(2002)、柯新利等人(2010)、王羊等人(2011)、Li等人(2014)进行了转换规则、元胞大小和邻域设置的敏感性分析。但以上研究都较少涉及采样、邻域结构、微观元胞尺度影响等，因此本文拟在城市扩张CA模拟研究中进行系统的敏感性分析，定量获取采样、邻域结构、微观元胞尺度对CA模型造成的精度影响，并尝试获取最优的模型模拟结果。

2 模型与方法

城市系统是动态的复杂系统，具有开放性、动态性、自组织性和非平衡性的特点，城市的发展变化受到自然、社会、经济、文化、政治等多种要素的影响，其行为过程具有高度的复杂性(Li和Yeh，2004；Zhang 等，2015)。在城市发展模拟中，与城市社会经济模型等城市发展模型相比，CA模型因具有自组织性、“自下而上”的研究思路、高分辨率的空间尺度和城市空间的动态变化对城市发展的反馈作用等特点，被认为是模拟复杂城市系统非常有效的模型之一(黎夏 等，2009；Lin和Li，2015)。研究表明，用CA模型模拟城市发展时，元胞的城市发展概率主要与邻近范围元胞的状态、离区中心的最短距离、离地铁站的最短距离、离道路的最短距离等变量相关(刘小平 等，2007；Chen 等，2012)。

在基于逻辑回归的城市扩张CA模型中(Wu，2002)，某元胞t+1时刻发展为城市用地的概率 $p_{{\rm{d}},ij}^t$ 为

$p_{{\rm{d}},ij}^t = RA \cdot Pg \cdot {\rm{con}}(s_{i,j}^t) \cdot \varOmega _{ij}^t$ (1)

式中，随机项RA=1+(–lnr)α。其中r为[0，1]的随机数，α为控制随机变量大小的参数，取值范围是1—10的整数(White和Engelen，1993；Li和Yeh，2002)。开发适宜性 $Pg = \displaystyle\frac{1}{{1 + \exp ( - {z_{ij}})}}$ 。其中 ${z_{ij}} = $ $ a + \displaystyle\sum\limits_k {{b_k}} $ ${x_k} $ ，a为常数项，bk为空间变量的权重，xk为空间变量，如离公路的最短距离、离市中心的距离等。约束条件函数 ${\rm{con}}(s_{ij}^t)$ 。其值域范围0—1， $s_{ij}^t$ 为t时刻元胞的状态，如果该状态越有利于城市发展的状态(如元胞为开发用地等)，则 ${\rm{con}}(s_{ij}^t)$ 的值越接近于1；若该状态为不利于城市发展的状态(如元胞为水体)，则其取值越接近于0。邻域函数 $\varOmega _{ij}^t = \displaystyle\frac{{\displaystyle\sum\limits_{3 \times 3} {{\rm{con}}({s_{ij}} = {\rm{urban}})} }}{{3 \times 3 - 1}}$ ，表示t时刻元胞的3×3邻域对其的影响值。得出单元发展概率后，还要判断一个单元是否发展为城市用地，在文章中是给定一个阈值(0—1)，比较单元发展概率与阈值的大小。

${S_{t + 1}}(ij) = \left\{ {\begin{array}{*{20}{c}}{{\rm{Developed}},p_{{\rm{d}},ij}^t > {p_{{\rm{threshold}}}}\& \& \gamma \leqslant \beta }\\{{\rm{Undeveloped}},p_{{\rm{d}},ij}^t > {p_{{\rm{threshold}}}}||\gamma > \beta }\end{array}} \right.$ (2)

式中，γ为随机变量，β=1/K，K为迭代次数。

建立逻辑回归模型后，将模型参数及模拟起始影像输入到模型中，便可以“自下而上”地模拟出城市的扩张过程。计算开发适宜性的各个空间变量权重是对随机采样的训练样本经逻辑回归得到的。

3 分析与讨论

3.1 研究区与数据准备

本文以珠江三角洲核心地区的广州市番禺区为研究区，其总面积为786.2 km2。番禺区由于经济和人口不断增长，经历了快速的土地利用变化。根据遥感TM图像的土地利用分类结果，1999年番禺城市用地面积为134.6 km2，但是到了2008年用地面积增长到255.60 km2，城市扩张的年增长率达6.8%。根据其经济增长速度，番禺的土地消耗较快且高于全国平均水平(年扩张率为3%)。它位于广州市南部地区，邻近佛山市，是广州高铁枢纽所在地，广佛同城化的支点之一，区位优势显著。随着广州市城市发展的战略推进，番禺区成为广州市南部发展战略的支点。伴随着城市人口和经济的飞速发展，番禺也面临着资源、生态、粮食、人口等多方面的问题。通过CA模型敏感性分析，可以精确地模拟并预测城市扩张情况，对于城市快速发展区域的政策制定也具有重要的借鉴意义。

选用该区域1999年和2008年的遥感TM影像，7个波段、对地分辨率30 m。采用ENVI软件对影像进行大气纠正和几何纠正，再通过查找同名点对影像进行配准。在ENVI软件中挑选了两组样本，训练样本和测试样本。训练样本用于监督分类，并将全区分为城市用地、开发用地、耕地、林地、基塘、水体和园地。测试样本用于检查分类结果，数据显示测试样本的分类精度可达到92%，满足后续研究与分析等要求(Li和Yeh，1998)。研究表明，城市扩张往往与一系列的空间距离变量相关，本文运用ArcGIS获取了离区中心距离，离地铁线的距离，离地铁站的距离，离(普通)道路距离和离镇中心的距离(图1)。


图 1 番禺区空间距离变量
Fig. 1 Spatial distances variables of Panyu

3.2 样本敏感性分析

当CA模型应用到具体的研究区时，参数校正过程是必要的(Wu，2002；Liu 等，2008)。参数校正需要先验知识的输入，即需要训练样本进行参数训练。针对不同研究区有可能需要采用不同采样比例的训练样本，因此文中对研究区的采样比例进行敏感性分析。为了方便对比，本文均采用蒙特卡罗随机采样，采样比例分别为1%、3%、5%、10%、15%、20%、25%、30%、40%和50%。在不同的采样比例下，训练的置信度均大于90%(α $ \leqslant $ 0.1))，精度均达到80%(表1)。实验发现测试样本的精度随着采样比例的增加而略有提高。采用更多的样本进行训练，会得到精度较高的权重，但是训练的运算量也是相对较大的(表2)。若使用较小比例的样本获取权重，将会得到误差较大的权重。因此本文使用40%采样比例以减少训练时间，同时保证参数校正的精度。

表 1 采样比例与权重、精度的关系
Table 1 The relationship of sample ratio and parameters，accuarcy

下载CSV 
比例/% 区中心 地铁线 地铁站 道路 镇中心 测试精度/%
1 –0.90 –3.58 2.23 –21.19 –2.99 80.44
3 –1.31 –4.89 3.34 –24.07 –2.17 80.65
5 –1.45 –6.93 5.57 –20.78 –2.44 80.59
10 –1.42 –5.14 3.69 –21.99 –2.41 80.64
15 –1.40 –5.14 3.83 –20.63 –2.66 80.66
20 –1.35 –5.68 4.49 –21.32 –2.72 80.62
25 –1.38 –5.43 4.04 –21.14 –2.37 80.66
30 –1.34 –5.28 3.89 –19.05 –2.64 80.67
40 –1.37 –5.35 4.04 –20.18 –2.59 80.70
50 –1.36 –5.10 3.78 –19.64 –2.69 80.64

表 2 权重的统计指标
Table 2 Statistics of weight

下载CSV 
参数 区中心 地铁线 地铁站 道路 镇中心
极差 0.55 3.35 3.34 5.02 0.83
方差 0.02 0.67 0.71 1.90 0.05
均值 –1.33 –5.25 3.89 –21.00 –2.57

从表1和表2中可以发现，虽然采样比例均不相同，但是各个参数的权重变化相对较小。其中，区中心、地铁线、地铁站、道路和镇中心的权重极差分别为0.55、3.35、3.34、5.02和0.83。当采样比例大于15%时，其极差更小，分别只有0.06、0.58、0.71、2.27和0.36。本文也采用了方差用来度量使用不同采样比例获取权重的偏离程度。区中心、地铁线、地铁站、道路和镇中心的权重方差分别为0.024、0.668、0.705、1.895和0.053，从数值中可以看出各个参数的偏离程度较少。特别是采样比例为40%的各个权重值，它们与均值的偏离程度分别只有3.20%、1.84%、3.79%、3.91%和0.98%。由于各个空间变量均为归一化的之后进行采样，因此从表1中还可以看出对城市扩张影响由大到小分别为道路、地铁线、地铁站、镇中心和区中心。

获取模型参数需要足够样本数据，对于多种不同土地利用的样本数据，其训练样本数据均应满足一定要求(Li和Yeh，1998)。为了更好地理解不同土地利用类别的比例对模型参数获取的影响，本文将土地利用数据重分类成两种类别，城市用地与非城市用地。同时根据不同的城市与非城市比例进行采样，其中城市用地与非城市用地的样本总数等于研究区40%的采样量。本文设定样本中城市用地的比例分别为1%、3%、5%、10%、15%、20%、30%、40%和50%(表3)。从表3中可以看出，当采样样本中城市用地的比例为1%、3%、4%、10%和15%时，其测试精度均能达到81%，而当城市用地的比例大于20%时，其精度迅速下降。当城市用地的比例为50%时，测试精度只有40%。这是由于当城市用地的比例过大时，这时对非城市用地的不转变情况估计不足，因此造成了较大的误差。通过计算可以发现研究区在1999年—2008年，城市用地转变量占比约为15.5%，因此本文认为样本中城市用地的比例应该与城市用地的转变量在全区的占比相匹配。

表 3 样本中城市比例与权重、精度的关系
Table 3 The relationship of urban percentage and parameters, accuracy

下载CSV 
比例/% 区中心 地铁线 地铁站 道路 镇中心 精度/%
1 –0.86 –4.12 2.73 –21.12 –2.98 81.47
3 –1.03 –5.54 4.02 –20.18 –2.69 81.45
5 –1.33 –5.81 4.45 –20.00 –2.76 81.48
10 –1.29 –4.53 3.34 –19.39 –2.78 81.50
15 –1.41 –5.05 3.60 –18.71 –2.51 81.48
20 –1.51 –5.88 4.65 –20.73 –2.62 79.57
30 –1.31 –5.48 4.07 –19.66 –2.82 67.11
40 –1.51 –6.03 4.64 –20.66 –2.75 52.52
50 –1.65 –6.16 5.08 –23.22 –2.77 40.02

3.3 邻域结构敏感性分析

在元胞自动机中，往往会采用两种不同的邻域结构，摩尔邻域和冯诺依曼邻域(图2)。在标准摩尔邻域中，中心元胞(红色)有8个邻居。而在标准冯诺依曼邻域中，中心元胞中只有4个邻域。本文将测试两种不同邻域结构在不同的空间尺度下的模拟结果，模拟结果的精度如表4所示。


图 2 元胞自动机的邻域结构
Fig. 2 Neighborhood structure of CA model

表 4 多尺度和不同邻域结构下的模拟精度
Table 4 The simulation accuracy in different neighbor structure and spatial resolution

下载CSV 
空间分辨率/m 精度
摩尔邻域 冯诺依曼
50 80.57 50.43
100 79.83 79.78
200 79.89 79.88
500 76.10 75.97

从表4中可知，不论是采用摩尔邻域还是冯诺依曼邻域，模拟精度均随着空间尺度的增加而降低。在同一空间尺度下，采用摩尔邻域的模拟结果略好。在空间分辨率为50 m、100 m、200 m和500 m，采用摩尔邻域的模拟精度比采用冯诺依曼邻域的模拟精度分别高0.14%、0.05%、0.01%和0.13%。在两种不同的邻域结构中，中心元胞只受到与其最邻近的元胞的影响，也有一些学者认为，应该考虑其扩展邻域(图2)，如5×5扩展邻域、7×7扩展邻域(黎夏和叶嘉安，2005；吴浩 等，2013)。

因此，本文分析在CA模型在同一空间尺度下，不同邻域结构不同邻域大小的模拟结果(表5)。从表5中可知，使用3×3摩尔邻域，其模拟结果的精度可达到80.57%。当运用更大的5×5扩展邻域时，模拟结果的精度有所降低，精度为80.48%。当采用7×7和9×9邻域时，其模拟精度有所提高，分别为80.51%和80.52%。总体上，使用冯诺依曼邻域的模拟结果精度比使用摩尔邻域的精度略低。在3×3、5×5、7×7和9×9的扩展冯诺依曼邻域中，其精度分别80.43%、80.47%、80.50%和80.51%，并随着邻域元胞个数的增加而增加。

表 5 不同邻域结构和邻域大小的模拟结果
Table 5 The simulation accuracy in different neighborhood structure and size

下载CSV 
邻域大小 精度
摩尔邻域 冯诺依曼
3×3 80.57 80.43
5×5 80.48 80.47
7×7 80.51 80.50
9×9 80.52 80.51

从微观尺度上看，不同的位置的邻域元胞对中心元胞的贡献不一，本文统计了番禺区新增城市用地的摩尔邻域的城市用地情况(图3)。由图3中可以看出，中心元胞上下左右(即冯诺依曼邻域)4个元胞对中心元胞的影响均约为11%。相比而言，摩尔邻域中的角点(左上、左下、右上、右下)对中心元胞有较大的影响，约为14%。从图2中可以看出，冯诺依曼5×5扩展邻域中包含摩尔邻域所有元胞，也包含了影响相对较大的摩尔邻域4个角点，因此本文认为其模拟精度会随着角点的增加而增加。


图 3 邻域位置对城市扩张的影响
Fig. 3 Impact of neighbor location to urban expansion

3.4 空间尺度敏感性分析

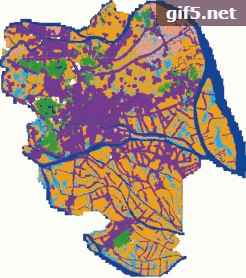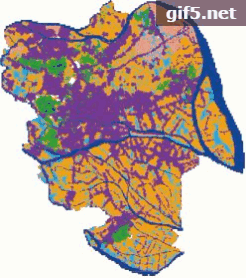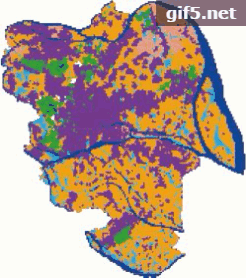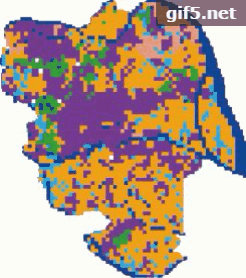
本文对元胞大小为50 m×50 m的原始数据进行重采样，得到元胞大小分别为100 m×100 m、200 m×200 m和500 m×500 m的数据。在此基础上，采用文中的CA模型分别在4个不同的尺度上对研究区的城市扩张进行了模拟，模拟结果如图4所示。从图4中可以看出，随着数据空间分辨率的降低，模拟结果与真实情况之间的差别越来越大。


图 4 不同分辨率的模拟结果
Fig. 4 Simulation results using different resolutions

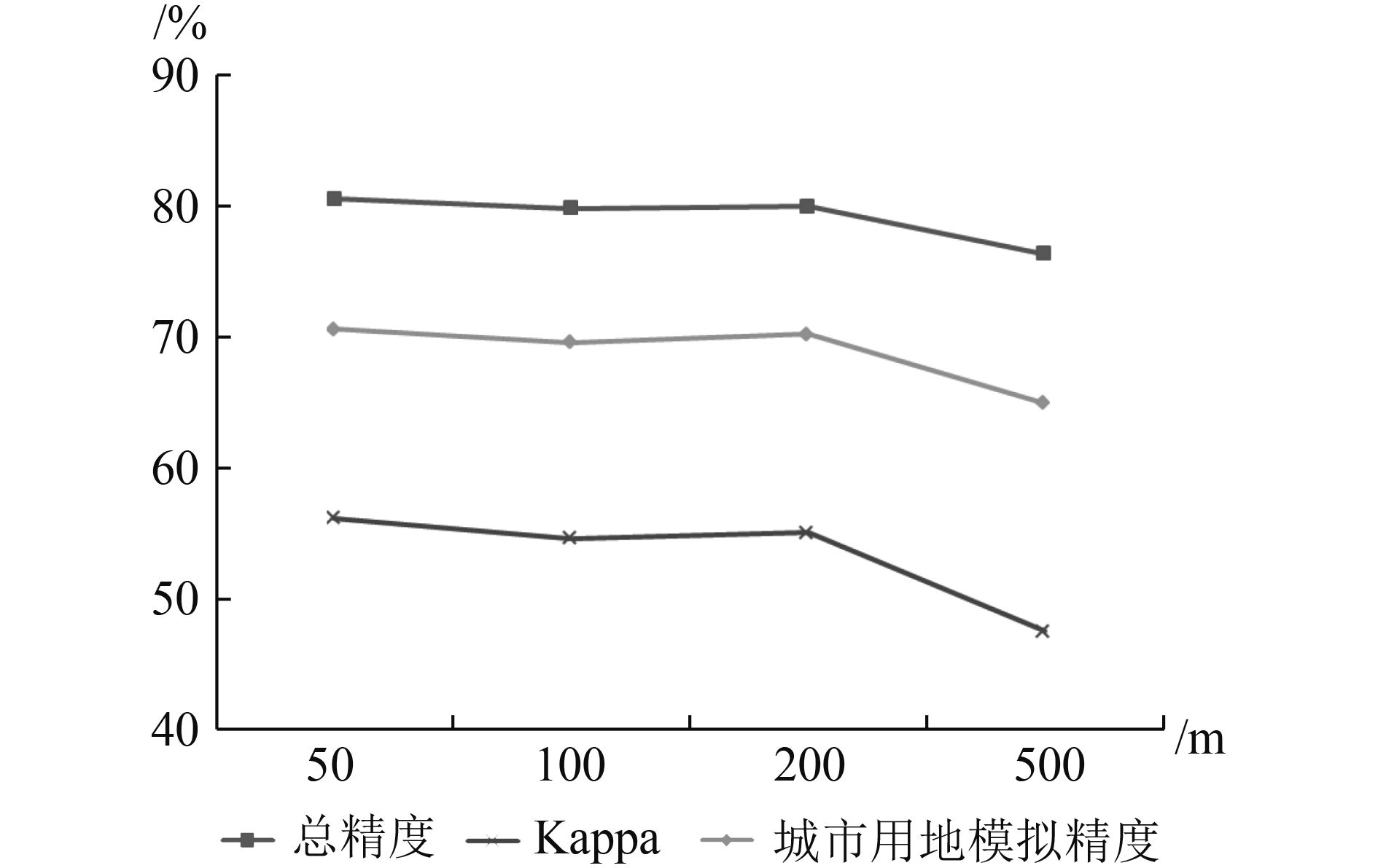
本文采用总精度、Kappa系数和城市用地模拟精度进行点对点对比分析，以此制作出模拟精度与空间尺度之间的关系图(图5)。从总体上看，不论是总精度、Kappa，还是城市用地的模拟精度都是随着空间尺度的增加而降低。其中，空间尺度从50 m增加到200 m时，其总精度、Kappa和城市用地的模拟精度变化较小，分别从80.57%降至79.98%、0.56降至0.55、70.58%降至70.18%，但是当空间尺度从200 m增加到500 m时，各个指标降幅明显，总精度从79.98%降至76.36%、Kappa系数从0.55降至0.47和城市用地的模拟精度从70.18%降至64.94%。


图 5 不同分辨率下的CA模拟精度
Fig. 5 Simulation accuracy using different resolutions

学者们采用一些指标衡量模拟结果的空间形态，其中景观指数指标被认为能够很好地反映模拟结果的空间形态(彭建 等，2006)。因此本文选择了景观指数中的斑块数(NP)、斑块密度(PD)、分形维度(FRAC)和聚集度(AI)等分析结果(表5)，其中斑块数(NP)和斑块密度(PD)可以直观地反映出城市用地总体统计情况；分形维度(FRAC)可以较好地反映斑块形状复杂程度；聚集度(AI)能够反映城市用地在景观上团簇的情况；这些指标可以帮助理解和评价该地区的景观现状和城市用地利用格局。从表6中可知，随着空间分辨率的降低，斑块数、斑块密度和聚集度均在逐渐下降。其中斑块数从145下降到47，斑块密度从0.19下降到0.06，聚集度从91.20下降到68.95。这表明分辨率从50 m到500 m，较小的斑块均合并到邻近的大斑块中，斑块面积增加，但是斑块个数和斑块密度均减少。对于小斑块合并而形成的较大斑块，也会显得相对孤立，因此其聚集度指数同样也下降。分形维度可以反映内部结构复杂性的一个指标，可以看出随着空间分辨率的降低，其分形维度值从1.09减少到1.02，这表明低分辨率的结构变得简单。

表 6 模拟结果的景观指数
Table 6 Landscape metrics of simulation results in different resolutions

下载CSV 
分辨率/m NP PD AI FRAC
50 145 0.19 91.20 1.09
100 117 0.15 77.91 1.05
200 62 0.08 72.43 1.03
500 47 0.06 68.95 1.02

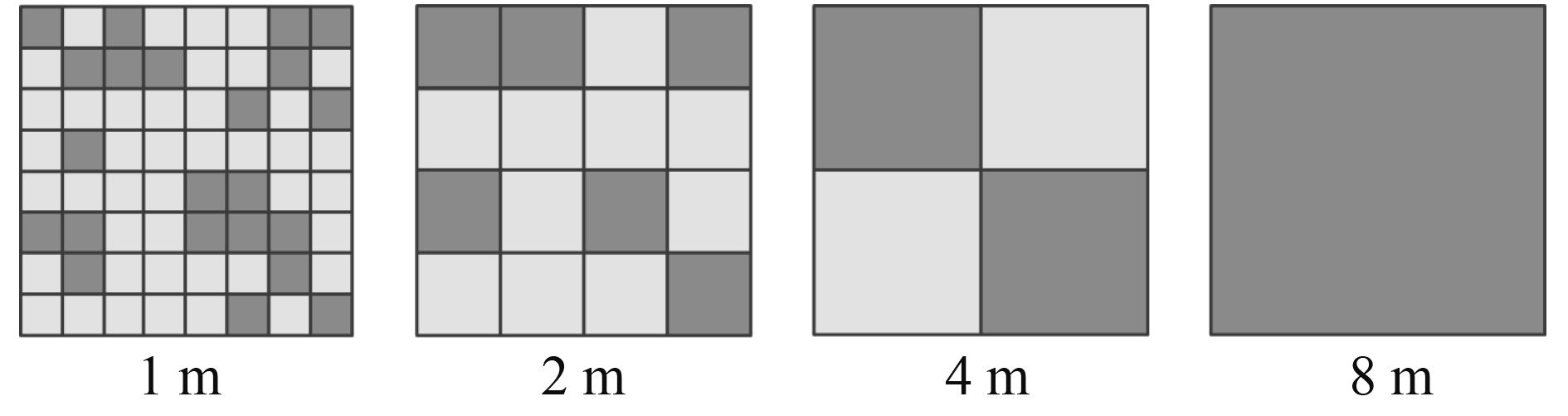
从CA模型的转换式(1)分析，在不同空间尺度下，模拟结果的精度有很大变化主要是因为随着元胞空间尺度的增大，孤立元胞增多，孤立元胞具有较低的邻域发展密度，导致较小的转换概率值，本文也绘制出不同空间尺度下元胞空间的变化情况(图6)。从图6中可以发现，当空间分辨率从1 m变成2 m，元胞的最大邻域发展密度有所下降，从5/8减少到4/8。随着空间尺度的增加，其元胞的邻域发展密度变得越小，即从4/8(2 m)到2/8(4 m)、1/8(8 m)。


图 6 不同分辨率下的元胞邻域空间变化
Fig. 6 Changes of cell neighborhood in different resolutions

为了更好地理解不同空同尺度下的元胞邻域发展密度，本文统计了1999年和2008年遥感影像在50 m×50 m、100 m×100 m、200 m×200 m和500 m×500 m空间分辨率下的邻域城市元胞个数(表7)。通过统计发现，不论是1999年还是2008年，随着空间尺度的增加，邻域城市个数为8的个数比例在下降。这表明通过降尺度，城市发展密度正在减少，即由高密度向低密度转换。从表7中也可以看出，邻域城市元胞个数为1、2、3和4的，通过降尺度，其比例不断增加。而邻域城市元胞为6、7和8的几乎均有下降的趋势。

表 7 不同分辨率下摩尔邻域的城市元胞占比
Table 7 Urban cells percentage of Moore neighborhood in different resolutions

下载CSV 
/%
个数 1999年 2008年
50 m 100 m 200 m 500 m 50 m 100 m 200 m 500 m
0 69.1 59.5 54.5 44.6 50.5 40.1 32.6 18.7
1 4.0 9.2 15.9 23.2 4.5 8.9 14.3 20.9
2 4.1 8.7 9.2 12.8 4.5 8.9 11.2 16.2
3 5.0 6.9 6.1 7.0 6.0 8.6 8.6 13.5
4 3.7 4.2 4.2 5.2 4.7 6.3 6.6 9.1
5 3.3 3.2 3.2 3.5 4.9 5.7 5.8 8.8
6 2.2 2.5 2.4 2.0 3.6 4.6 5.6 6.2
7 1.8 2.1 2.0 1.1 3.1 4.6 5.8 4.3
8 6.9 3.8 2.5 0.7 18.2 12.2 9.5 2.2

4 结　论

本文从3个不同的角度(采样比例、邻域结构和空间分辨率)研究CA模型的敏感性，系统地分析了采样比例、空间分辨率对模拟精度的影响，并创新性地从微观角度分析邻域结构对中心元胞的贡献。研究表明在获取CA模型权重(参数)时可以通过提高采样比例以得到更好的结果，但是相应地，训练的运算量较大的。同时也发现，若训练样本中不同土地利用类型的比例与真实转换情况一致将有助于获取更好的模型参数。CA模型的模拟精度会随着空间尺度而变化。但在同一空间尺度下，摩尔邻域中的角点(左上、左下、右上、右下)对中心元胞有较大的影响，约为14%。冯诺依曼4个元胞对中心元胞的影响均约为11%。不论是总精度、Kappa，还是城市用地的模拟精度都是随着空间尺度的增加而降低，而且斑块数、斑块密度和聚集度均在逐渐下降。分形维度值在减少，表明低分辨率的结构变得简单。通过降尺度，城市发展密度正在减少，即由高密度向低密度转换。下一步研究工作将从更长的时间序列和更多的空间分辨率研究CA模型的敏感性趋势。

参考文献(References)

  • Chen Y M, Li X, Liu X P, and Ai B. 2014. Modeling urban land-use dynamics in a fast developing city using the modified logistic cellular automaton with a patch-based simulation strategy. International Journal of Geographical Information Science, 28 (2): 234–255. [DOI: 10.1080/13658816.2013.831868]
  • Chen Y M, Li X, Wang S J and Liu X P. 2012. Defining agents’ behaviour based on urban economic theory to simulate complex urban residential dynamics. International Journal of Geographical Information Science, 26 (7): 1155–1172. [DOI: 10.1080/13658816.2011.626780]
  • Guang Q F and Clarke K C. 2010. A general-purpose parallel raster processing programming library test application using a geographic cellular automata model. International Journal of Geographical Information Science, 24 (5): 695–722. [DOI: 10.1080/13658810902984228]
  • Ke X L, Deng X Z and He S J. 2010. Scale sensitivity and its causality for geo-cellular automata modelling. Geographical Research, 29 (5): 863–872. [DOI: 10.11821/yj2010050010] ( 柯新利, 邓祥征, 何书金. 2010. 地理元胞自动机模型的尺度敏感性及原因. 地理研究, 29 (5): 863–872. [DOI: 10.11821/yj2010050010] )
  • Li X and Liu X P. 2006. An extended cellular automaton using case‐based reasoning for simulating urban development in a large complex region. International Journal of Geographical Information Science, 20 (10): 1109–1136. [DOI: 10.1080/13658810600816870]
  • Li X and Yeh A G O. 1998. Principal component analysis of stacked multi-temporal images for the monitoring of rapid urban expansion in the Pearl River Delta. International Journal of Remote Sensing, 19 (8): 1501–1518. [DOI: 10.1080/014311698215315]
  • Li X and Yeh A G O. 2002. Neural-network-based cellular automata for simulating multiple land use changes using GIS. International Journal of Geographical Information Science, 16 (4): 323–343. [DOI: 10.1080/13658810210137004]
  • Li X and Yeh A G O. 2004. Data mining of cellular automata’s transition rules. International Journal of Geographical Information Science, 18 (8): 723–744. [DOI: 10.1080/13658810410001705325]
  • Li X and Ye J A. 2005. Cellular automata for simulating complex land use systems using neural networks. Geographical Research, 24 (1): 19–27. [DOI: 10.3321/j.issn:1000-0585.2005.01.003] ( 黎夏, 叶嘉安. 2005. 基于神经网络的元胞自动机及模拟复杂土地利用系统. 地理研究, 24 (1): 19–27. [DOI: 10.3321/j.issn:1000-0585.2005.01.003] )
  • Li X, Lao C H, Liu X P and Chen Y M. 2011. Coupling urban cellular automata with ant colony optimization for zoning protected natural areas under a changing landscape. International Journal of Geographical Information Science, 25 (4): 575–593. [DOI: 10.1080/13658816.2010.481262]
  • Li X, Li D, Liu X P and He J Q. 2009. Geographical simulation and optimization system (GeoSOS) and its cutting-edge researches. Advances in Earth Science, 24 (8): 899–907. [DOI: 10.3321/j.issn:1001-8166.2009.08.007] ( 黎夏, 李丹, 刘小平, 何晋强. 2009. 地理模拟优化系统GeoSOS及前沿研究. 地球科学进展, 24 (8): 899–907. [DOI: 10.3321/j.issn:1001-8166.2009.08.007] )
  • Li X C, Liu X P and Yu L. 2014. A systematic sensitivity analysis of constrained cellular automata model for urban growth simulation based on different transition rules. International Journal of Geographical Information Science, 28 (7): 1317–1335. [DOI: 10.1080/13658816.2014.883079]
  • Lin J Y and Li X. 2015. Simulating urban growth in a metropolitan area based on weighted urban flows by using web search engine. International Journal of Geographical Information Science, 29 (10): 1721–1736. [DOI: 10.1080/13658816.2015.1034721]
  • Liu J Y, Liu M L, Zhuang D F, Zhang Z X and Deng X Z. 2002. Study on spatial pattern of land-use change in China during 1995—2000. Science in China Series D: Earth Sciences, 32 (12): 1031–1040. [DOI: 10.3969/j.issn.1674-7240.2002.12.008] ( 刘纪远, 刘明亮, 庄大方, 张增祥, 邓祥征. 2002. 中国近期土地利用变化的空间格局分析. 中国科学(D辑), 32 (12): 1031–1040. [DOI: 10.3969/j.issn.1674-7240.2002.12.008] )
  • Liu X P, Li X, Liu L, He J Q and Ai B. 2008. A bottom-up approach to discover transition rules of cellular automata using ant intelligence. International Journal of Geographical Information Science, 22 (11/12): 1247–1269. [DOI: 10.1080/13658810701757510]
  • Liu X P, Li X, Shi X, Zhang X H and Chen Y M. 2010. Simulating land-use dynamics under planning policies by integrating artificial immune systems with cellular automata. International Journal of Geographical Information Science, 24 (5): 783–802. [DOI: 10.1080/13658810903270551]
  • Liu X P, Li X, Yeh A G O, He J Q and Tao J. 2007. Discovery of transition rules for geographical cellular automata by using ant colony optimization. Science in China Series D: Earth Sciences, 50 (10): 1578–1588. [DOI: 10.1007/s11430-007-0083-z]
  • Liu X P, Ma L, Li X, Ai B, Li S Y and He Z J. 2014. Simulating urban growth by integrating landscape expansion index (LEI) and cellular automata. International Journal of Geographical Information Science, 28 (1): 148–163. [DOI: 10.1080/13658816.2013.831097]
  • Peng J, Wang Y L, Zhang Y, Ye M T and Wu J S. 2006. Research on the influence of land use classification on landscape metrics. Acta Geographica Sinica, 61 (2): 157–168. [DOI: 10.11821/xb200602005] ( 彭建, 王仰麟, 张源, 叶敏婷, 吴健生. 2006. 土地利用分类对景观格局指数的影响. 地理学报, 61 (2): 157–168. [DOI: 10.11821/xb200602005] )
  • Wang L, Li C C, Ying Q, Cheng X, Wang X Y, Li X Y, Hu L Y, Liang L, Yu L, Huang H B and Gong P. 2012. China’s urban expansion from 1990 to 2010 determined with satellite remote sensing. Chinese Science Bulletin, 57 (16): 1388–1399. ( 王雷, 李丛丛, 应清, 程晓, 王晓昳, 李雪艳, 胡娈运, 梁璐, 俞乐, 黄华兵, 宫鹏. 2012. 中国1990～2010年城市扩张卫星遥感制图. 科学通报, 57 (16): 1388–1399. )
  • Wang Y, Gao Y, Zhao L, Zhao Z Q and Li S C. 2011. Scale sensitive analysis of cellular automata model. Acta Scientiarum Naturalium Universitatis Pekinensis, 47 (4): 750–758. [DOI: 10.13209/j.0479-8023.2011.105] ( 王羊, 高阳, 赵琳, 赵志强, 李双成. 2011. 元胞自动机模型的尺度敏感性分析. 北京大学学报(自然科学版), 47 (4): 750–758. [DOI: 10.13209/j.0479-8023.2011.105] )
  • White R and Engelen G. 1993. Cellular automata and fractal urban form: a cellular modelling approach to the evolution of urban land-use patterns. Environment and Planning A: Economy and Space, 25 (8): 1175–1199. [DOI: 10.1068/a251175]
  • Wu F L. 2002. Calibration of stochastic cellular automata: the application to rural-urban land conversions. International Journal of Geographical Information Science, 16 (8): 795–818. [DOI: 10.1080/13658810210157769]
  • Wu H, Zhou L, Shi W Z, Chen X L, Yang H S, Cheng Z P and Ye L P. 2013. Scale sensitive of cellular automata model for the simulation of land use change based on orthogonal experiment. Scientia Geographica Sinica, 33 (10): 1252–1258. [DOI: 10.13249/j.cnki.sgs.2013.10.013] ( 吴浩, 周璐, 史文中, 陈晓玲, 杨海生, 程志萍, 叶露萍. 2013. 基于正交试验设计的土地利用变化元胞自动机模拟过程的尺度敏感性分析. 地理科学, 33 (10): 1252–1258. [DOI: 10.13249/j.cnki.sgs.2013.10.013] )
  • Zhang Y H, Li X, Liu X P and Qiao J G. 2011. The CA model based on data assimilation. Journal of Remote Sensing, 15 (3): 475–491. [DOI: 10.11834/jrs.20110114] ( 张亦汉, 黎夏, 刘小平, 乔纪纲. 2011. 基于数据同化的元胞自动机. 遥感学报, 15 (3): 475–491. [DOI: 10.11834/jrs.20110114] )
  • Zhang Y H, Li X, Liu X P and Qiao J G. 2015. Self-modifying CA model using dual ensemble Kalman filter for simulating urban land-use changes. International Journal of Geographical Information Science, 29 (9): 1612–1631. [DOI: 10.1080/13658816.2015.1037305]
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体