出版日期: 2018-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20187234
2018 | Volumn22 | Number 4
上一篇 | 下一篇

红外卫星云图和相关向量机的有眼热带气旋客观定强模型

戴李杰¹ , 张长江¹ , 薛利成¹ , 马雷鸣² , 鲁小琴³

1. 浙江师范大学数理与信息工程学院，金华 321004

2. 上海市气象局中心气象台，上海 200030

3. 中国气象局上海台风研究所，上海 200030

收稿日期: 2017-06-23

基金项目: 国家自然科学基金(编号：41575046，41475059)；浙江省科技厅公益性技术应用研究计划(编号：2016C33010)；上海市自然科学基金(编号：15ZR1449900)

第一作者简介: 戴李杰，1990年生，男，硕士研究生，研究方向为图像处理及应用、机器学习与模式识别。E-mail：dlj16823@163.com

通信作者简介: 张长江，1974年生，男，教授，研究方向为图像处理、机器学习、多尺度几何分析与应用。E-mail：zcj74922@zjnu.edu.cn

中图分类号: TP751.1

文献标识码: A

摘要

热带气旋TC (Tropical Cyclone)是全球影响最严重的自然灾害之一。TC强度和路径的准确预报，对于减轻其带来的灾害影响至关重要。本文基于静止红外卫星云图和相关向量机RVM (Relevance Vector Machine)构建有眼TC客观定强模型。首先，利用高斯平滑对红外卫星云图进行去噪；然后，利用基于测地活动轮廓GAC (Geodesic Active Contour)模型的偏微分方程PDE (Partial Differential Equation)法对有眼TC的眼壁进行分割，提取眼壁的亮温梯度信息，计算眼壁亮温梯度的最大值及梯度数据不同概率时的均值，从而构造与TC强度密切相关的特征因子；最后，利用RVM构建单特征因子、多特征因子与近地面最大中心风速的客观定强模型，研究不同特征维度对TC客观定强误差的影响。实验结果表明，在单特征因子的模型定强中，95%概率眼壁亮温梯度均值的定强误差最小，相比利用单特征因子所构建的定强模型，多特征因子的模型定强误差更小，即多特征因子中包含更多与TC强度相关的特征信息。在多特征因子的模型定强中，二特征因子优于三特征因子模型，说明应当合理选择特征因子维数，并非越多越好。本文所用RVM模型具有良好的高维非线性处理能力，能对TC强度进行有效估计。

关键词

热带气旋, 红外卫星云图, 图像分割, 相关向量机, 机器学习, 客观定强

Eyed tropical cyclone intensity objective estimation model based on infrared satellite image and relevance vector machine

DAI Lijie¹ , ZHANG Changjiang¹ , XUE Licheng¹ , MA Leiming² , LU Xiaoqin³

1.College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua 321004, China

2.Shanghai Central Meteorological Observatory, Shanghai Meteorological Bureau, Shanghai 200030, China

3.Shanghai Typhoon Institute of China Meteorological Administration, Shanghai 200030, China

Abstract

A Tropical Cyclone (TC) is an influential natural hazard in the world. Thus, the forecasting accuracy of intensity and track is important to reduce the impacts of this disaster. In recent years, a remote sensing satellite cloud image gradually becomes the main means of monitoring a TC. In this study, an eyed TC intensity objective estimation model based on geostationary infrared satellite cloud image and Relevance Vector Machine (RVM) is proposed. First, the infrared satellite cloud image is denoised through a Gaussian smoothing method. Second, a TC eye area is segmented using a Partial Differential Equation (PDE) based on a Geodesic Active Contour (GAC) model. Third, the brightness temperature gradient data of the eyewall are obtained, and the maximum of brightness and different mean brightness temperature gradients with various probabilities are calculated. Thus, the characterization factors that are closely related to the TC intensity are structured. Finally, the TC intensity objective estimation model based on the RVM is established (single and multiple characterization factors) to study the influence of different characteristic dimensions on a TC intensity estimation error. Experimental results show that the estimation model that is established using the mean brightness temperature gradient of the TC eyewall with a probability of 95% performs better than the other models in studying intensity estimation model that is established using a single characterization factor. The error of the intensity estimation model established using multiple characterization factors is lower than that of the single characterization factor. That is, the multiple characterization factors contain additional characteristic information that is related to the TC intensity. In the study of the intensity estimation model established using multiple characterization factors, the estimation model performs better in the two characterization factors (the maximum of brightness and mean brightness temperature gradients with a probability of 95%) than in the three characterization factors. Therefore, not all " more” is better. Hence, the dimension of the characterization factor should be reasonably selected. Three types of RVM kernel functions are used in the experiments. Results show that all RVM kernel functions are efficient in estimating the TC intensity. Cauchy kernel function is suitable for the estimation model established using multiple characterization factors. The RVM model proposed in this study has a favorable high-dimensional nonlinear processing capability. Therefore, this model can effectively estimate the TC intensity.

Key words

tropical cyclone, infrared satellite image, image segmentation, relevance vector machine, machine learning, intensity objective estimation

1 引　言

濒临中国的西北太平洋是全球热带气旋TC (Tropical Cyclone)活动最为频繁的海域之一，平均每年约有27个TC生成，约占全球总数的1/3(赵海坤和吴立广，2015)。因此，TC强度和路径的准确预报，对预防和减轻其带来的灾害影响至关重要。

近年来，国内外各类观测手段和数值预报技术的发展推动了TC路径预报水平的不断提高，但是，TC强度的预报能力却进展非常缓慢。其主要原因一方面是TC定强能力不足，另一方面是对影响TC强度的机制仍不清楚，而这两方面又密切联系。TC定强的较低精度阻碍了TC强度预报的进展(Harnos和Nesbitt，2011；DeMaria 等，2014)。

目前TC定强方法主要包括基于极轨卫星微波资料和静止卫星云图资料。在极轨卫星资料方面，目前主要以微波资料为主进行定强，如刘喆等人(2008)利用AMSU-A亮温估测西北太平洋区域TC强度。Jaiswal和Kishtawal(2011)将数据挖掘技术与QuickScat卫星海洋风散射计所获数据相结合，对TC强度进行预测。但是由于微波资料容易受到强降水的干扰及极轨卫星的时间分辨率不高的原因，往往不能全面捕捉TC强度变化及其相关的内部对流结构演变。此外由于极轨卫星的时间分辨率不高(每颗卫星每天只有两次观测)，往往不能全面捕捉TC强度变化及其相关的内部对流结构演变，不能满足业务要求。而静止卫星资料时间分辨率高，目前被更多应用于TC定强。长期以来，业务上基于静止卫星资料的TC定强主要借助于Dvorak方法。早期，Dvorak(1973)提出使用红外卫星云图来确定TC强度，并且在1975年形成基于卫星云图的TC定强理论(Dvorak，1975)，然后对TC定强技术进行了两次改进(Dvorak和Wright，1977；Dvorak，1984)。由于Dvorak技术的主观性较大，先后有多位研究者对其进行改进，并提出一些客观TC定强技术(Zehr，1989；Velden 等，1998；Olander和Velden，2007)。近年来也有学者利用静止红外卫星云图提取TC的结构特征并结合线性(Zhao 等，2016)和非线性建模技术(Piñeros 等，2008，2011；钱金芳等，2015)和方位角的亮温信息(Fetanat 等，2013；鲁小琴等，2014；Knaff 等，2015)进行TC定强。

周知，热带气旋的眼壁区是冷暖气流交换最为强烈的地方，往往也是风速最为强烈的地方。在红外卫星云图上眼壁处的亮温梯度恰好能够用于刻画眼墙处的对流交换的强弱程度，进一步能够被间接用于描述热带气旋的强度大小(陈渭民，2003)。如前所述，近年来已经有部分学者应用红外卫星图像的亮温梯度采用非线性模型间接估计TC强度并取得了较好的效果(Piñeros 等，2011)。近年来，人工智能算法在图像识别、数据挖掘及预测等领域得到许多应用，相比线性回归法，机器学习算法具有更优秀的高维非线性建模能力。鉴于卫星资料在提高TC定强及强度预报精度中的重要性，本文基于风云2号(FY-2C和FY-2E)静止卫星的红外云图和相关向量机RVM (Relevance Vector Machine)构建TC客观定强模型(分别构建单特征因子、多特征因子与近地面最大中心风速的客观定强模型)，对有眼TC的强度进行客观估计。在此基础上将TC定强资料用于TC强度预报，可望提高中国TC强度预报的准确度，为防台减灾提供技术支撑。

2 红外卫星云图和相关向量机的有眼TC客观定强模型

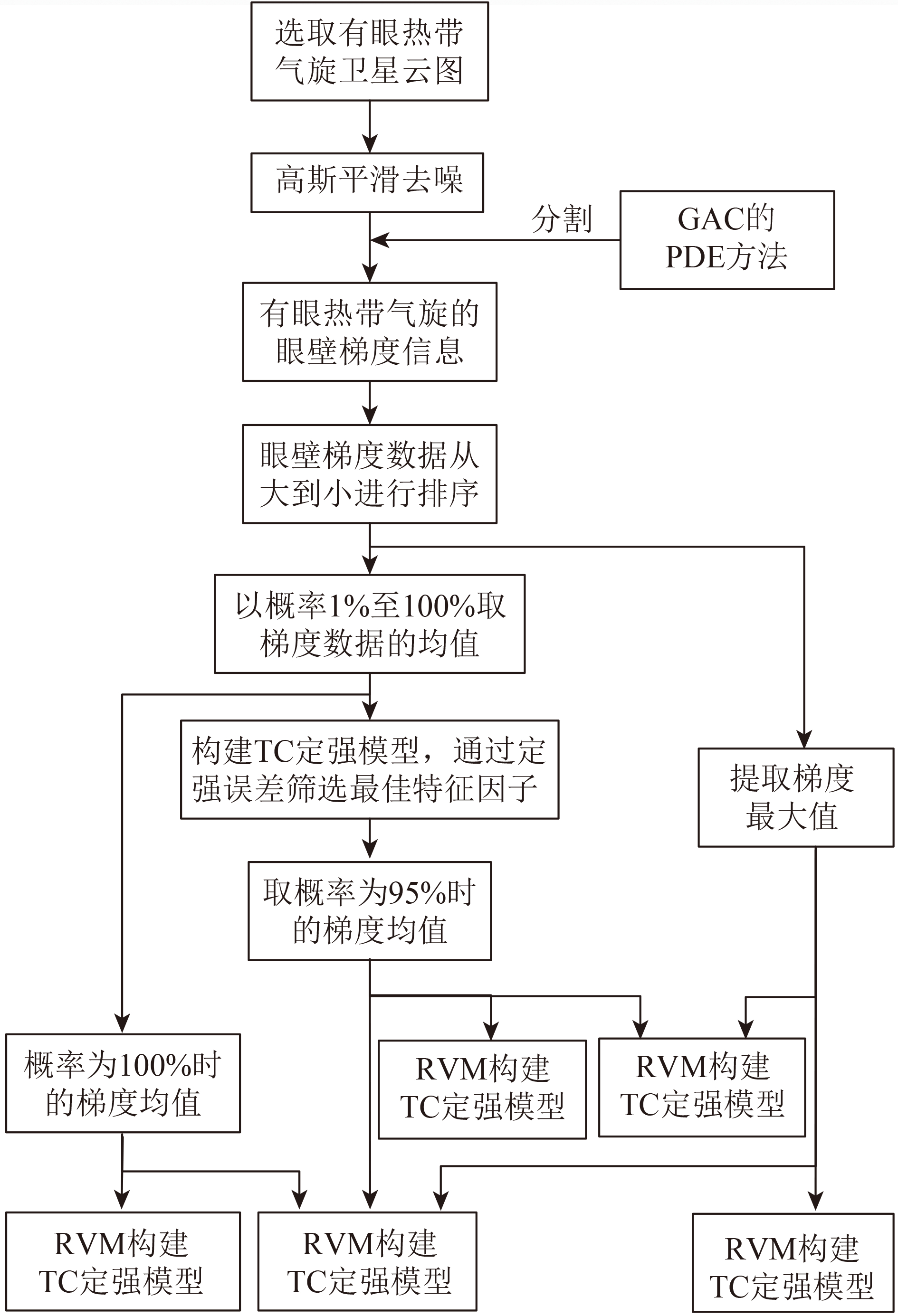
在大气环流中，当温度较高的暖流与温度较低的冷流相遇时，容易产生多雨天气。而当TC来临时常常伴随大风大雨，尤其在眼壁附近区域的最大风速区，雨水量非常得明显，因此，在最大风速区域，冷暖流交替也是最强烈的(杨波，2011；钱金芳等，2015)。在红外卫星云图中，TC眼壁处的亮温变化相当强烈，则眼壁处的亮温梯度信息就反映了眼壁亮温变化的剧烈程度，即眼壁处的亮温梯度信息反映了眼壁区域的最大风速。由于TC年鉴的中心风速描述的是TC底层中心附近最大平均风速，因此本文采用眼壁梯度最大值及不同概率下的梯度均值作为刻画有眼TC强度的特征因子，分别构建基于单特征及多特征因子的TC客观定强模型。基于红外云图和相关向量机的有眼TC客观定强模型流程图如图1所示。

图 1 红外卫星云图和相关向量机的有眼TC客观定强模型流程图

Fig. 1 Flow chart of eyed TC intensity objective estimation model based on infrared satellite image and RVM

2.1 GAC模型的TC眼壁分割

TC眼区信息对于TC定强和强度预报有重要的意义。但是，在实际研究中经常使用主观分析来定位TC眼区。因此，自动且准确地使用卫星云图来分割TC眼壁显得非常重要。由于有眼TC的眼壁轮廓通常是一条不规则的闭合曲线，经典的图像分割方法可能会导致部分TC眼壁轮廓断裂而难以成功用于分割TC眼壁。基于偏微分方程PDE (Partial Differential Equation)的图像处理法比傅里叶变换和小波变换更具局部适应性(杨波，2011)，能较好地处理上述问题，因此，本文用基于PDE的图像分割方法对有眼TC的眼壁进行分割处理。

基于PDE的图像分割的众多方法中，活动轮廓模型应用最为广泛。Kass等人(1988)提出活动轮廓模型，即Snakes模型，也称参数模型。但是，Snakes模型的能量函数依赖于参数，不同的参数会形成不同的能量函数，最终将得到不同的目标边缘。另外，若演化曲线远离了目标边缘，则可能得到错误的边缘，因此Snakes模型的初始化演化曲线的位置选取也很重要。Osher和Sethian (1988)提出了水平集方法(Level Set Method)，该方法不仅克服了Snakes模型的缺点，拓宽了Snakes模型的应用范围，也发展了活动轮廓模型的理论。

图像处理领域有两类主要的形变模型：参数活动模型和几何形变模型。Caselles等人(1993)和Malladi等人(1995)以曲线演化理论和水平集方法为基础，分别独立提出几何活动轮廓模型，该模型通过更新水平集函数使轮廓线运动。Caselles等人(1997)提出测地活动轮廓GAC (Geodesic Active Contour)模型，该模型主要的优势是没有自由参数，能获得唯一且准确的目标边缘。本文采用基于GAC模型来分割有眼TC的眼壁，进而获得眼壁梯度信息。

GAC模型是基于活动轮廓模型，主要思想是将图像分割问题转化为最小化一个封闭曲线 $ C\left( p \right)$ 的“能量”泛函 $ {E}\left( {C\left( p \right)} \right)$ ，该能量函数可表示为

$\begin{aligned}{E}\left( {C\left( p \right)} \right) = & \alpha \mathop \int \nolimits_0^1 {\left| {C'\left( p \right)} \right|^2}{\rm{d}}p + \beta \mathop \int \nolimits_0^1 {\left| {C''\left( p \right)} \right|^2}{\rm{d}}p - \\ &\lambda \mathop \int \nolimits_0^1 \left| {\nabla I\left( {C\left( p \right)} \right)} \right|{\rm{d}}p\end{aligned}$

(1)

式中， $p $ 是曲线 $ C$ 的位置参数， $ \alpha$ 、 $\beta $ 、 $ \lambda$ 都是正值常量。Caselles等人(1993)提出：当 $\beta=0 $ 时，曲线平滑仍可实现，即公式可表示为

${E}\left( {C\left( p \right)} \right)= \alpha \mathop \int \nolimits_0^1 {\left| {C'\left( p \right)} \right|^2}{\rm{d}}p - \lambda \mathop \int \nolimits_0^1 \left| {\nabla I\left[ {C\left( p \right)} \right]} \right|{\rm{d}}p$

(2)

定义一个严格递减的函数 $ g:[0,+\infty]$ ，当 $r\to \infty $ 时， $g(r)\to 0 $ 。因此， $ -|\nabla I|$ 可以被 $ g(|\nabla I|)^2$ 代替，然后获得一个一般形式的能量函数：

${E}\left( {C\left( p \right)} \right) = \alpha \mathop \int \nolimits_0^1 {\left| {C'\left( p \right)} \right|^2}{\rm{d}}p + \lambda \mathop \int \nolimits_0^1 {{g}}{\left( {\left| {\nabla I\left[ {C\left( p \right)} \right]} \right|} \right)^2}{\rm{d}}p$

(3)

式中， $E[C(p)] $ 依赖于曲线的形状、位置及位置参数 $p $ 。将活动轮廓模型转变为GAC模型后，可避免参数 $ p$ 。然后，“能量”泛函可写成为

${L_R}\left( C \right) = \mathop \int \nolimits_0^{L\left( C \right)} {{g}}\left( {\left| {\nabla I\left[ {C\left( p \right)} \right]} \right|} \right){\rm{d}}s$

(4)

式中， $L(C) $ 是欧几里得弧长， $L_R(C) $ 是加权后的弧长。根据曲线演化规则和水平集数值化方案的图像分割，可得：

$\begin{aligned}\frac{{\partial u}}{{\partial t}} = & \delta \left| {\nabla u} \right| = \left( {{{g}}\left( I \right)\left( {c + \kappa } \right) + \nabla {{g}} \cdot \frac{{\nabla u}}{{\left| {\nabla u} \right|}}} \right)\left| {\nabla u} \right| = \\ &{{g}}\left( I \right)c\left| {\nabla u} \right| + {{g}}\left( I \right)\kappa \left| {\nabla u} \right| + \nabla {{g}} \cdot \frac{{\nabla u}}{{\left| {\nabla u} \right|}}\left| {\nabla u} \right| = \\ &c{{g}}\left( I \right)\left| {\nabla u} \right| + div\left( {{{g}}\left( I \right)\frac{{\nabla u}}{{\left| {\nabla u} \right|}}} \right)\left| {\nabla u} \right|\end{aligned}$

(5)

式中，c为一个可调参数，通常与演化速度有关，κ为欧几里得曲率。

最终，采用基于双曲型方程的迎风差分方法(王申林，2001)计算式(5)离散化后的方程。由于式(5)的系数 $cg(I) $ 总为正值，故该项的迎风方案为

${Q_{1,ij}} = c{{g}}\left( I \right)\nabla _{ij}^{\left( - \right)}$

(6)

不确定式(5)中的系数 ${s_{ij}} = div{\left( {{{g}}\left( I \right)\displaystyle\frac{{\nabla u}}{{\left| {\nabla u} \right|}}} \right)_{ij}}$ 为正值还是负值，故该项的迎风方案为

${Q_{2,ij}} = \max \left( {{s_{ij}},0} \right)\nabla _{ij}^{\left( - \right)} + \min \left( {{s_{ij}},0} \right)\nabla _{ij}^ + $

(7)

最终，得到显式方案为

$u_{ij}^{n + 1} = u_{ij}^n + \Delta t\left( {{Q_{1,ij}} + {Q_{2,ij}}} \right)$

(8)

2.2 TC眼壁分割结果

本文选用中国FY-2号(FY-2C和FY-2E)静止卫星的红外1通道的有眼TC云图作为有眼TC客观定强的云图资料。现以2014年1419号热带气旋黄蜂(2014年10月08日00时——世界时间)为例，利用基于GAC模型的PDE方法分割有眼TC的眼部区域，并提取眼壁的亮温梯度信息(图2)。

图 2 有眼TC的眼壁分割过程

Fig. 2 Eyewall segmentation process of eyed TC

图2(a)为从红外卫星云图中截取出来的TC区域云图，图2(b)为经过高斯滤波平滑后的TC云图，图2(c)为分割方法的分割初始状态云图，图2(d)为分割结束后的TC云图，并已从TC眼壁提取亮温梯度信息。由图2可知，TC眼壁呈不规则的轮廓线，本文所用的分割方法能有效且准确地分割TC眼区，有利于进一步提取眼壁亮温梯度信息。

2.3 RVM概述

近年来，机器学习算法在图像处理、生物特征识别、机器视觉、数据挖掘和智能预测等领域取得很大的进展。在1999年和2001年，Michael提出相关向量机RVM (Relevance Vector Machine) (Tipping，1999，2001)。相比支持向量机SVM (Support Vector Machine)，RVM是基于贝叶斯的概率学习模型，能获得更稀疏化的模型和给出预测的概率信息，并且不受核函数必须满足Mercer条件的约束。本文所用为RVM回归模型，故对回归模型原理进行如下概述。

对于训练样本 $\left\{ {{{{x}}_{n}},{{{t}}_{n}}} \right\}_{n = 1}^N $ ，其中 $\left\{ {{{{x}}_{n}}} \right\}_{n = 1}^N $ 为输入向量， ${{{t}}_{n}} $ 为输出向量，假设输入和输出都是独立同分布，则关系可表示为

${{{t}}_{n}} = y\left( {{{{x}}_{n}};{{w}}} \right) + {\varepsilon _n}$

(9)

式中， ${\varepsilon _n}$ 为独立同分布的高斯噪声，即 $\varepsilon \in {N}\left( {0,{\sigma ^2}} \right) $ 。由式(9)可得 ${p}\left( {{{{t}}_{n}}|{{x}}} \right) = {N}({{{t}}_{n}}|{{y}}\left( {{{{x}}_{n}}} \right),{\sigma ^2})$ 。RVM模型的输出可表示为

${y}\left( {{{x}};{{w}}} \right) = \mathop \sum \limits_{i = 1}^N {\omega _i}{{K}}\left( {{{x}},{{{x}}_{{i}}}} \right) + {\omega _0}$

(10)

式中， ${K}\left( {{{x}},{{{x}}_{i}}} \right)$ 为核函数， ${{w}} = {\left[ {{\omega _0},{\omega _1}, \ldots ,{\omega _N}} \right]^{\rm T}}$ 为权值向量。常用的核函数主要有以下几种：

线性核函数：

${{K}}\left( {{{x}},{{{x}}_{{i}}}} \right) = {{x}}^{\rm{T}}{{{x}}_{{i}}}$

(11)

多项式核函数：

${K}\left( {{{{x}}},{{{x}}_{{i}}}} \right) = {\left( {\gamma {{x}}^{\rm{T}}{{{x}}_{{i}}} + r} \right)^d},\gamma > 0$

(12)

Gauss核函数：

${K}\left( {{{{x}}},{{{x}}_{{i}}}} \right) = {\exp}\left( { - \frac{{{{\left\| {{{{x}}} - {{{x}}_{{i}}}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)$

(13)

Cauchy核函数：

${K}\left( {{{{x}}},{{{x}}_{{i}}}} \right) = {\left( {\frac{{{||{{x}}} - {{{x}}_{{i}}}||^2}}{\sigma } + 1} \right)^{ - 1}}$

(14)

Sigmoid核函数：

${{K}}\left( {{{{x}}},{{{x}}_{{i}}}} \right) = {\rm{tanh}}\left( {\gamma {{x}}^{\rm{T}}{{{x}}_{{i}}} + r} \right)$

(15)

核函数的作用是将低维中线性不可分的问题转化到高维中线性可分的问题，从而解决许多低维中难以处理的高维非线性问题，也体现了RVM的高维非线性处理能力。各种核函数中应用最广泛的是Gauss核函数，即径向核函数RBF(Radial Basis Function)，Gauss核对数据中的噪声有着较好的抗干扰能力，核函数中的参数影响了函数作用的范围，若核函数带宽设置得过小，则容易导致过拟合；若设置得过大，则会导致过平滑。所以，设置合理的核函数带宽对RVM的分类或回归模型有重要的影响。本文基于RVM构建TC客观定强模型，并分别选择Gauss核、Poly3核和Cauchy核来测试TC定强模型的误差结果。

3 数据资料及构造建模特征因子

本文选用FY-2C和FY-2E静止卫星中红外1通道的有眼TC云图作为有眼TC定强的实验数据。风云卫星以每间隔1 h记录一个TC从形成到消散的全过程，中国气象局上海台风研究所提供的TC年鉴资料是每间隔3 h或6 h。一般而言，当TC底层近中心风速达到32.7 m/s以上时，即TC强度达到台风及以上的级别，才有可能出现TC眼区。本文从2005年—2014年内共132个TC中选取有眼TC云图，最终选取473幅对应有年鉴资料的有眼TC云图，把年鉴中的强度值作为TC强度的参考值。

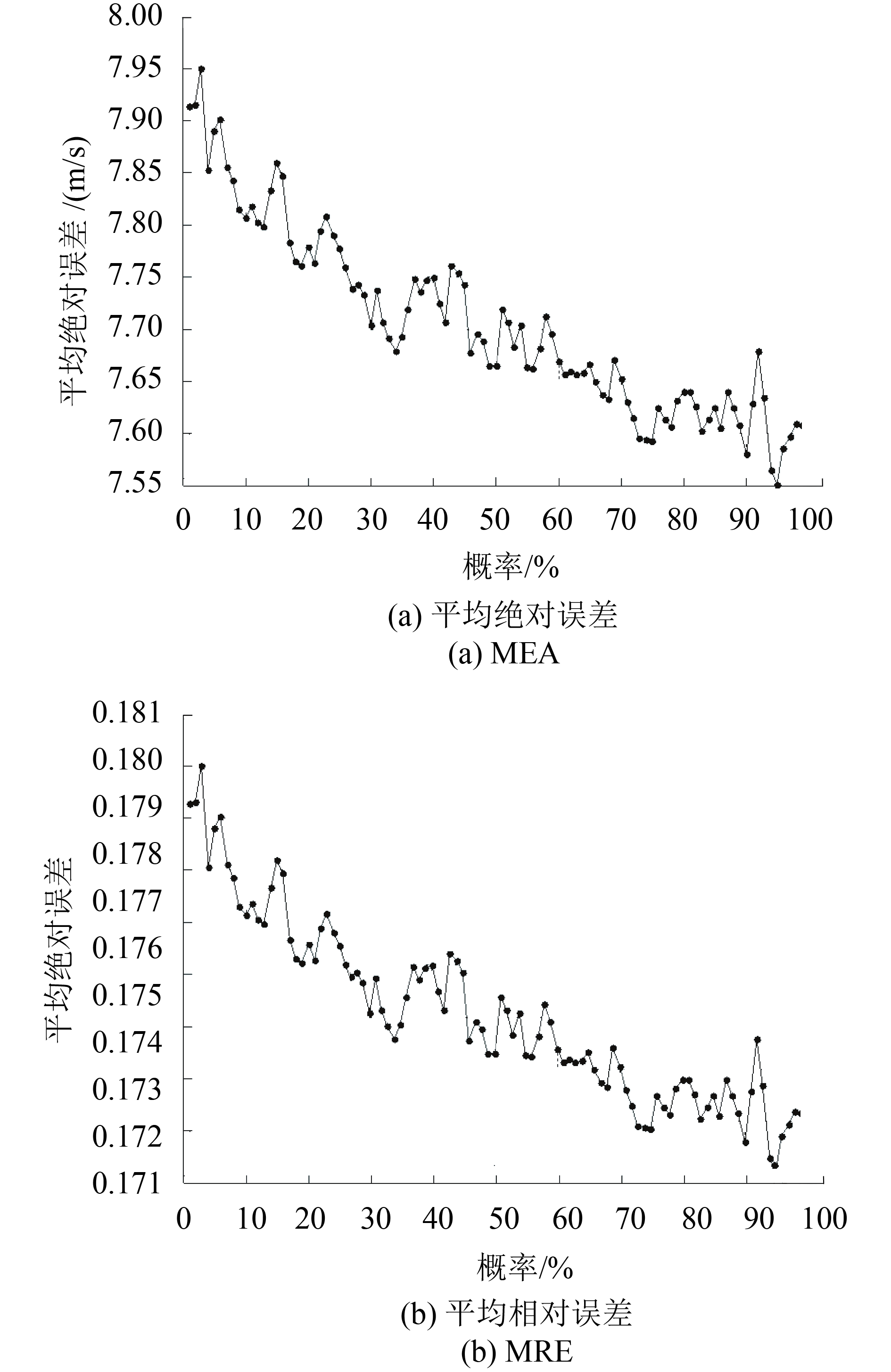
在TC最大风速区域，冷暖流交替是最强烈的。在红外卫星云图中，眼壁处的亮温梯度信息反映了眼壁区域的最大风速。首先，利用高斯滤波对红外卫星云图进行平滑去噪，消除卫星辐射计扫描云图所产生的噪声。然后，利用基于GAC模型的PDE方法分割有眼TC的眼区，并提取眼壁亮温信息，计算获得眼壁的亮温梯度信息，从而计算获得眼壁亮温梯度的最大值，然后将眼壁亮温梯度数据按照从大到小进行排序，从1%—100%(间隔1%)不同的概率取眼壁亮温梯度均值，从而获得不同概率下的梯度均值。本文利用气象部门常用的线性回归LR (Linear Regression)方法测试不同概率梯度均值的定强误差，以此构造与TC强度密切相关的最佳特征因子，测试样本量为473个，本文采用循环测试法，即每次只留一个作为测试样本，其余作为训练样本，以此循环473次，测试结果如图3所示。

图 3 不同概率的眼壁梯度均值作为TC强度特征因子的误差曲线

Fig. 3 Error curve using mean of eyewall’s gradient in different probability as TC intensity characteristic factor

在建模之前，先将数据都归一化至[0,1]范围，归一化公式如下

${x_k} = \left( {{x_k} - {x_{\min}}} \right)/\left( {{x_{\max}} - {x_{\min}}} \right)$

(16)

式中， ${x_{\min}}$ 为数据序列中的最小值； $ {x_{\max}}$ 为数据序列中的最大值。

由图3(a)可知，平均绝对误差MAE (Mean Absolute Error )曲线呈现先下降后上升的走势，而当概率为95%时，MAE曲线达到最低点，可知利用95%概率时的梯度均值所建立定强模型的MAE最小。由图3(b)可知，平均相对误差MRE (Mean Relative Error)曲线也呈现先下降后上升的走势，当概率为95%时，MAE曲线达到最低点，可知利用95%概率时的梯度均值所建立定强模型的MRE最小。综上所述，概率95%的眼壁亮温梯度均值最适用于构建有眼TC客观定强模型。

由于概率100%的梯度均值能反映眼壁整体的亮温变化速率信息，梯度最大值能够反映眼壁一圈的亮温变化速率最快信息。本文利用RVM分别构建单特征因子、多特征因子与中心风速的客观定强模型。分别研究眼壁亮温梯度最大值、100%梯度均值、95%梯度均值与中心风速的定强模型。在此基础上，增加特征因子的维数，研究梯度最大值、95%梯度均值与中心风速的定强模型，研究梯度最大值、100%梯度均值、95%梯度均值与中心风速的定强模型。

4 实验结果及分析

本文利用RVM分别构建单特征因子、多特征因子与中心风速的客观定强模型。RVM分别选取Gauss核、Poly3核和Cauchy核进行测试，共473个样本点，采用留一法进行循环测试473次。在建模之前，先将数据都归一化到[0,1]范围，消除各维数据之间的数量级差异，有利于提高定强模型的准确度，归一化公式为式(16)。本文所有实验的软硬件环境：硬件环境为DELL工作站，处理器为Intel Xeon 2.80 GHZ，内存4 G，操作系统为Windows 7 Service Pack 1，程序运行的软件版本为Matlab R2014a。

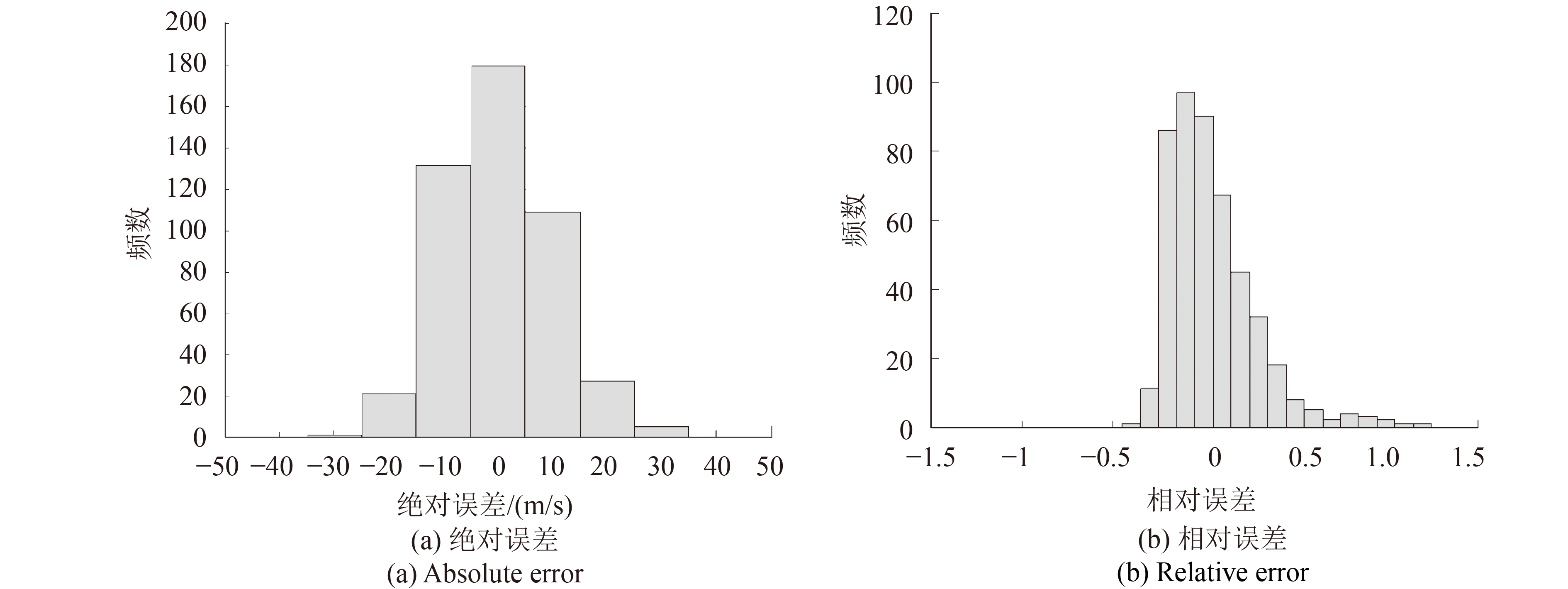
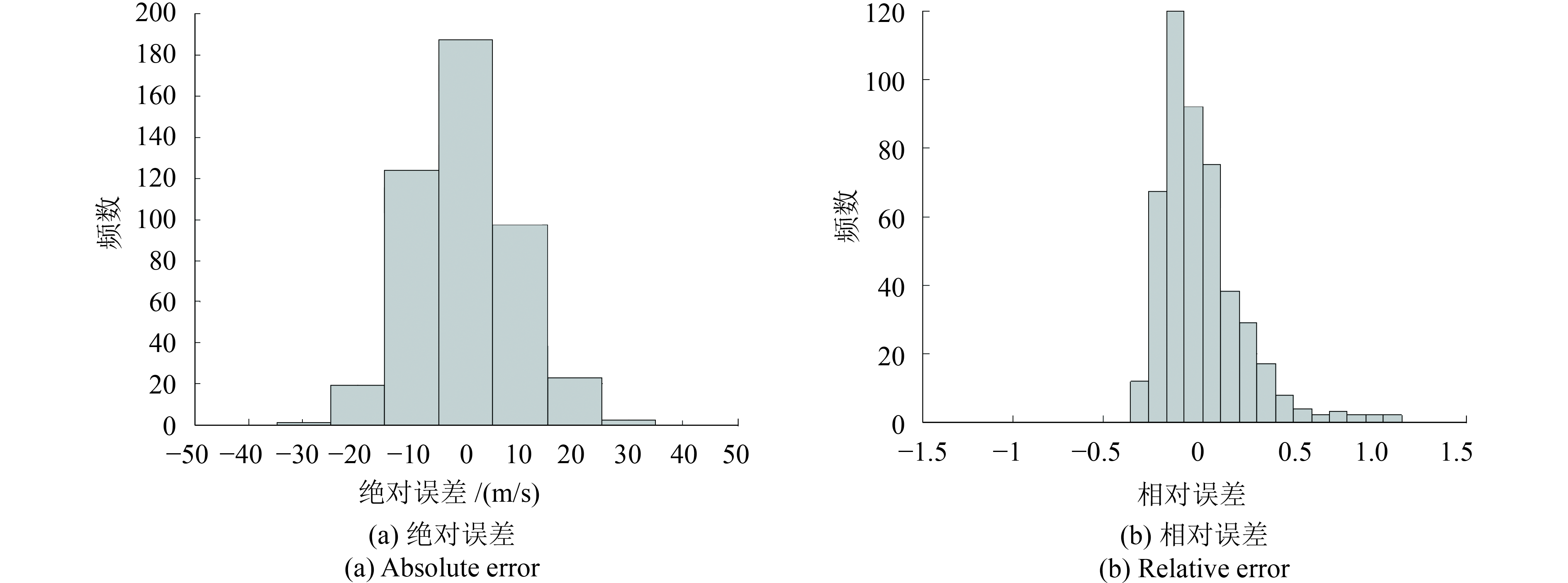
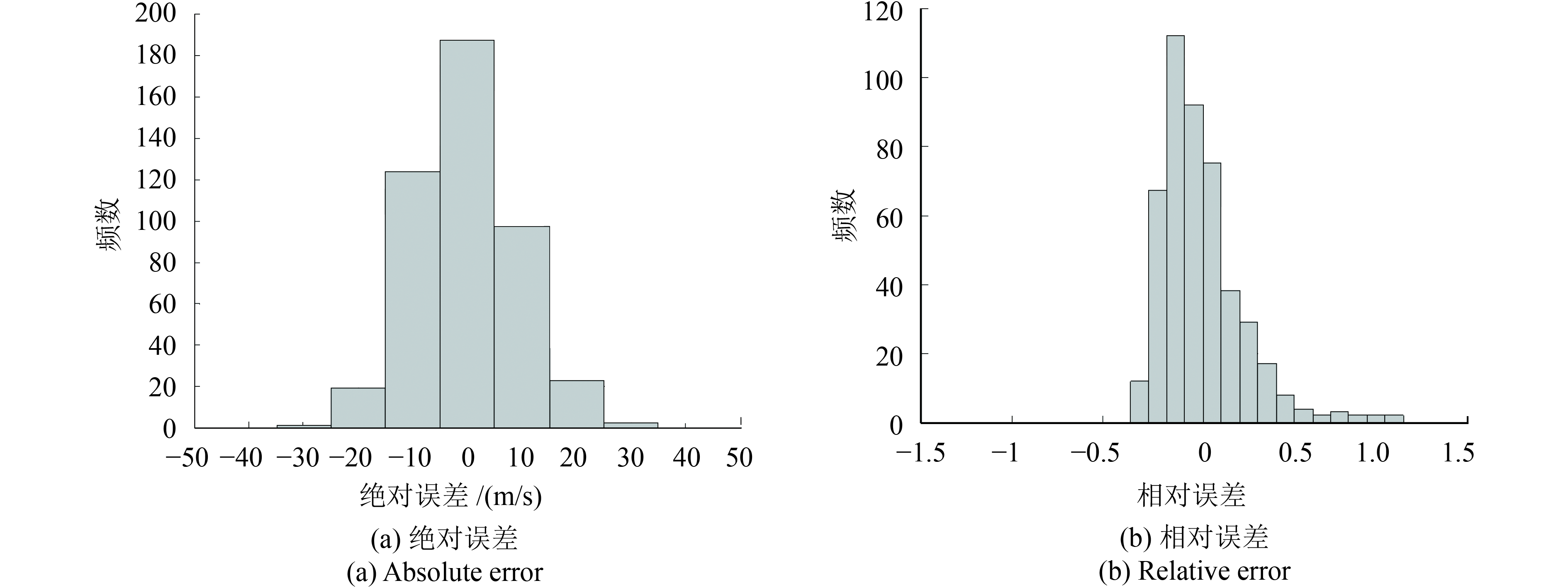
本文基于RVM构建眼壁梯度最大值与中心风速的定强模型，TC定强的绝对误差柱状图的最小误差区间为(–5, 5]，区间宽度为10 m/s，误差区间分别向两边扩展，相对误差柱状图的最小误差区间为(–0.05, 0.05]，区间宽度为0.1，误差区间分别向两边扩展，并且本文所有的绝对误差与相对误差柱状图都采用上述误差间隔。

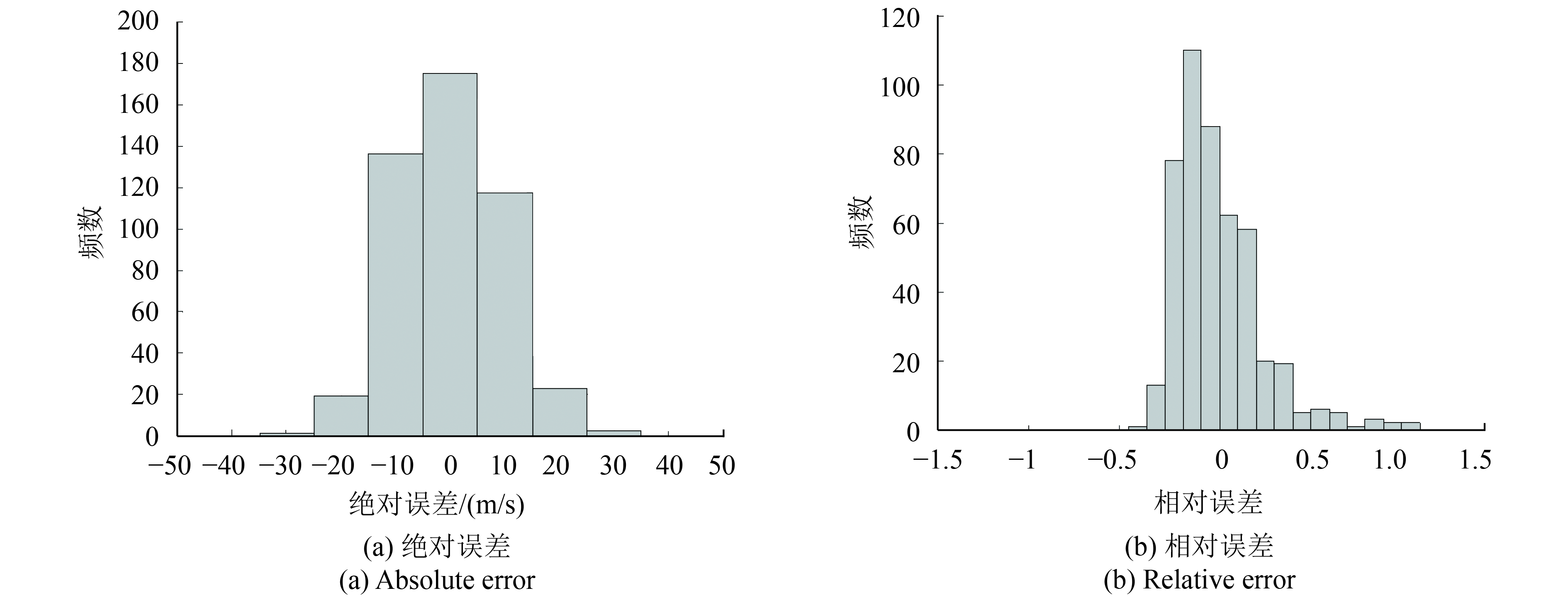
分别利用RVM建立TC强度与眼壁亮温梯度最大值、眼壁亮温梯度均值、95%眼壁亮温梯度均值、眼壁亮温梯度最大值+95%眼壁亮温梯度均值、眼壁亮温梯度最大值+眼壁亮温梯度均值+95%眼壁亮温梯度均值的定强模型，其定强的绝对误差和相对误差柱状图如图4—8所示。在同个定强模型中，不同核函数的定强误差相差不大，因此，展示相对较好的核函数的误差柱状图。

图 4 核函数为Poly3时的RVM定强模型(眼壁亮温梯度最大值)的误差柱状图

Fig. 4 Error histogram of intensity estimation model (maximum of eyewall’s brightness temperature gradient) using Poly3 kernel function

图 5 核函数为Poly3时的RVM定强模型(眼壁亮温梯度均值)的误差柱状图

Fig. 5 Error histogram of intensity estimation model (mean of eyewall’s brightness temperature gradient) using Poly3 kernel function

图4—8为利用基于不同核函数的RVM构建定强模型的误差柱状图，当选择相应RVM核函数时，不同模型各自的定强效果最佳。由图4—6可知，当利用单特征因子构建定强模型时，各个定强模型的定强误差相近，但都有少量的点落在误差较大区间。由图7—8可知，当利用多个特征因子构建定强模型时，模型定强误差比基于单特征因子的模型小，绝对误差落在最小区间(–5, 5]的数量更多，相对误差落在区间(–0.15, –0.05]的数量更多。综上所述，本文所提出的RVM定强模型能对有眼TC强度进行有效估计，并且算法性能稳定。相比利用单特征因子所构建的定强模型，基于多特征因子的RVM模型的定强误差更小，得益于RVM具有处理高维非线性问题的能力，特征因子维数的增加，将更有利于构建较高精度的RVM定强模型。

图 6 核函数为Cauchy时的RVM定强模型(95%眼壁亮温梯度均值)的误差柱状图

Fig. 6 Error histogram of intensity estimation model (95% mean of eyewall’s brightness temperature gradient) using Cauchy kernel function

图 7 核函数为Cauchy时的RVM定强模型(眼壁亮温梯度最大值+95%眼壁亮温梯度均值)的误差柱状图

Fig. 7 Error histogram of intensity estimation model (maximum, 95% mean of eyewall’s brightness temperature gradient) using Cauchy kernel function

图 8 核函数为Cauchy时的RVM定强模型(眼壁亮温梯度最大值+95%眼壁亮温梯度均值+眼壁亮温梯度均值)的误差柱状图

Fig. 8 Error histogram of intensity estimation model (maximum, 95% mean, mean of eyewall’s brightness temperature gradient) using Cauchy kernel function

本文利用RVM分别构建单特征因子、多特征因子与中心风速的客观定强模型，采用不同核函数的定强模型误差如表1所示。

由表1可知，对于利用不同特征因子所构建的定强模型，采用不同的RVM核函数所构建的模型误差相接近，说明该3种核函数都能用作构建有眼TC定强模型。在利用单特征因子所构建的定强模型中，误差最小的是基于95%眼壁亮温梯度均值的定强模型。相比单特征因子的定强模型，多特征因子定强模型的误差更小，并且发现当RVM核函数采用Cauchy核的时候，定强模型的误差最小，说明Cauchy核更适用于构建基于高维特征因子的定强模型。随着特征因子维数的增加，体现出本文所提出的RVM模型在处理高维非线性问题上的优势，能对TC强度进行有效估计。同时发现，利用3个特征因子所构建的模型的定强误差略大于两个特征因子的模型，由于相比两特征因子，三特征因子增加了100%眼壁亮温梯度均值，而这一特征与95%眼壁亮温梯度均值有较大部分特征信息重叠，即存在特征信息冗余，而且从表1可知，与单独利用95%眼壁亮温梯度均值相比，单独利用100%眼壁亮温梯度均值建模会产生更大的误差，从而导致三特征因子的定强模型误差较二特征因子的定强模型略大。

表 1 不同定强模型的MAE和MRE比较
Table 1 Comparison of MAE and MRE of different intensity estimation model

下载CSV

核函数	MAE/(m/s)			MRE/%
核函数	Gauss	Poly3	Cauchy	Gauss	Poly3	Cauchy
眼壁亮温梯度最大值	7.82	7.84	7.83	17.64	17.66	17.60
100%眼壁亮温梯度均值	7.53	7.53	7.54	16.95	16.96	16.98
95%眼壁亮温梯度均值	7.53	7.53	7.52	16.95	16.96	16.90
两特征因子	7.35	7.43	7.32	16.49	16.67	16.43
三特征因子	7.36	7.44	7.32	16.54	16.71	16.45
注：两特征因子为95%眼壁亮温梯度均值+梯度最大值，三特征因子为100%梯度均值+95%梯度均值+梯度最大值。

5 结　论

本文基于红外卫星云图和相关向量机构建有眼TC客观定强模型，分别研究利用单特征因子、多特征因子与中心风速的客观定强模型，并分别对RVM中Gauss核、Poly3核及Cauchy核函数进行测试。经实验得出以下结论：

(1)对于单特征因子的有眼TC定强，利用95%概率眼壁亮温梯度均值构建TC定强模型的误差最小。RVM模型的算法性能稳定，能有效地估计有眼TC强度。

(2)本文在研究利用单特征因子构建模型的基础上，增加特征因子的维数。相比利用单特征因子所构建的定强模型，基于多特征因子的RVM模型定强误差减小了，体现了RVM模型处理高维非线性问题的优势，这也是机器学习算法在处理高维问题上的优势。同时可发现，虽然总体多特征因子定强模型优于单特征因子模型，但是也不是特征因子越多越好，正确选择适当数量的特征因子建立定强模型才能取得满意的定强结果，如在本文中二特征因子优于单特征因子和三特征因子模型。对于多特征因子的有眼TC定强，当RVM核函数为Cauchy核时，定强误差MAE和MRE都最小，由此可见，Cauchy核函数适用于多特征因子的有眼TC定强。本文所提出的RVM定强模型可对有眼TC强度进行有效估计，且定强精度较高，在此基础上将TC定强资料用于TC强度预报，可望提高我国TC强度预报的准确度，为防台减灾提供技术支撑。

(3)本文采用图像处理技术结合GAC模型对TC眼壁进行分割，从而提取眼壁亮温梯度信息，利用RVM构建TC客观定强模型。在后续的工作中，将利用深度学习技术进行TC定强研究，例如近年来在计算机视觉、数据挖掘及预测等领域表现优秀的卷积神经网络。卷积神经网络在训练过程中，可提取并学习图像中与TC强度密切相关的特征信息，从而可免去前期的特征提取工作，并且由于其深层的网络结构，可学习到更丰富、全面的特征信息，有利于提高TC客观定强精度。

参考文献(References)

Caselles V, Catté F, Coll T and Dibos F. 1993. A geometric model for active contours in image processing. Numerische Mathematik, 66 (1): 1–31. [DOI: 10.1007/BF01385685]

Caselles V, Kimmel R and Sapiro G. 1997. Geodesic active contours. International Journal of Computer Vision, 22 (1): 61–79. [DOI: 10.1023/A:1007979827043]

Chen W M. 2003. Weixing Qixiangxue. Beijing: China Meteorological Press: 300–336 (陈渭民. 2003. 卫星气象学. 北京: 气象出版社: 300–336)

DeMaria M, Sampson C R, Knaff J A and Musgrave K D. 2014. Is tropical cyclone intensity guidance improving?. Bulletin of the American Meteorological Society, 95 (3): 387–398. [DOI: 10.1175/BAMS-D-12-00240.1]

Dvorak V F. 1973. A Technique for the Analysis and Forecasting of Tropical Cyclone Intensities from Satellite Pictures. NOAA Technical Memorandum NESS 45 (Revision of NOAA TM NESS 36). Washington DC: U.S. Department of Commerce: 19

Dvorak V F. 1975. Tropical cyclone intensity analysis and forecasting from satellite imagery. Monthly Weather Review, 103 (5): 420–430. [DOI: 10.1175/1520-0493(1975)103<0420:TCIAAF>2.0.CO;2]

Dvorak V F. 1984. Tropical Cyclone Intensity Analysis Using Satellite Data. NOAA Technical Report NESDIS 11. Washington DC: U.S. Department of Commerce: 1–47

Dvorak V F and Wright S. 1977. Tropical cyclone intensity analysis using enhanced infrared satellite data//Proceeding of the 11th Technical Conference on Hurricanes and Tropical Meteorology. Washington, DC: National Environmental Satellite Service/NOAA, 268–273

Fetanat G, Homaifar A and Knapp K R. 2013. Objective tropical cyclone intensity estimation using analogs of spatial features in satellite data. Weather and Forecasting, 28 (6): 1446–1459. [DOI: 10.1175/WAF-D-13-00006.1]

Harnos D S and Nesbitt S W. 2011. Convective structure in rapidly intensifying tropical cyclones as depicted by passive microwave measurements. Geophysical Research Letters, 38 (7): L07805 [DOI: 10.1029/2011GL047010]

Jaiswal N and Kishtawal C M. 2011. Prediction of tropical cyclogenesis using scatterometer data. IEEE Transactions on Geoscience and Remote Sensing, 49 (12): 4904–4909. [DOI: 10.1109/TGRS.2011.2153862]

Kass K, Witkin A and Terzopoulos D. 1988. Snakes: active contour models. International Journal of Computer Vision, 1 (4): 321–331. [DOI: 10.1007/BF00133570]

Knaff J A, Longmore S P, Demaria R T and Molenar D A. 2015. Improved tropical-cyclone flight-level wind estimates using routine infrared satellite reconnaissance. Journal of Applied Meteorology and Climatology, 54 (2): 463–478. [DOI: 10.1175/JAMC-D-14-0112.1]

Liu Z, Li W B, Han Z G, Yao Z G, Zhang F Y and Zhu Y J. 2008. Estimating the intensity of tropical cyclone in Western North Pacific basin with AMSU——a brightness temperature. Chinese Journal of Geophysics, 51 (1): 51–57. [DOI: 10.3321/j.issn:0001-5733.2008.01.008] ( 刘喆, 李万彪, 韩志刚, 姚志刚, 张凤英, 朱元竞. 2008. 利用AMSU-A亮温估测西北太平洋区域热带气旋强度. 地球物理学报, 51 (1): 51–57. [DOI: 10.3321/j.issn:0001-5733.2008.01.008] )

Lu X Q, Lei X T, Yu H and Zhao B K. 2014. An objective TC intensity estimation method based on satellite data. Journal of Applied Meteorological Science, 25 (1): 52–58. [DOI: 10.11898/1001-7313.20140106] ( 鲁小琴, 雷小途, 余晖, 赵兵科. 2014. 基于卫星资料进行热带气旋强度客观估算. 应用气象学报, 25 (1): 52–58. [DOI: 10.11898/1001-7313.20140106] )

Malladi R, Sethian J A and Vemuri B C. 1995. Shape modeling with front propagation: a level set approach. IEEE Transactions on Pattern Analysis and Machine Intelligence, 17 (2): 158–175. [DOI: 10.1109/34.368173]

Olander T L and Velden C S. 2007. The advanced Dvorak technique: continued development of an objective scheme to estimate tropical cyclone intensity using geostationary infrared satellite imagery. Weather and Forecasting, 22 (2): 287–298. [DOI: 10.1175/WAF975.1]

Osher S and Sethian J A. 1988. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. Journal of Computational Physics, 79 (1): 12–49. [DOI: 10.1016/0021-9991(88)90002-2]

Piñeros M F, Ritchie E A and Tyo J S. 2008. Objective measures of tropical cyclone structure and intensity change from remotely sensed infrared image data. IEEE Transactions on Geoscience and Remote Sensing, 46 (11): 3574–3580. [DOI: 10.1109/TGRS.2008.2000819]

Piñeros M F, Ritchie E and Tyo J S. 2011. Estimating tropical cyclone intensity from infrared image data. Weather and Forecasting, 26 (5): 690–698. [DOI: 10.1175/WAF-D-10-05062.1]

Qian J F, Zhang C J, Yang B and Ma L M. 2015. Typhoon inner core wind speed modeling method by RBFNN and PDE based on infrared cloud image. Infrared and Laser Engineering, 44 (2): 438–444. [DOI: 10.3969/j.issn.1007-2276.2015.02.007] ( 钱金芳, 张长江, 杨波, 马雷鸣. 2015. 红外云图的台风内核风速建模的RBFNN和PDE方法. 红外与激光工程, 44 (2): 438–444. [DOI: 10.3969/j.issn.1007-2276.2015.02.007] )

Tipping M E. 1999. The relevance vector machine//Advances in Neural Information Processing Systems 12. Denver, Colorado, USA: NIPS: 652–658

Tipping M E. 2001. Sparse Bayesian learning and the Relevance vector machine. Journal of Machine Learning Research, 1 : 211–244. [DOI: 10.1162/15324430152748236]

Velden C S, Olander T L and Zehr R M. 1998. Development of an objective scheme to estimate tropical cyclone intensity from digital geostationary satellite infrared imagery. Weather and Forecasting, 13 (1): 172–186. [DOI: 10.1175/1520-0434(1998)013<0172:DOAOST>2.0.CO;2]

Wang S L. 2001. The upwind difference method for first-order hyperbolic equation. Journal of Shandong University, 36 (4): 386–393. [DOI: 10.3969/j.issn.1671-9352.2001.04.006] ( 王申林. 2001. 一阶双曲型方程的迎风差分方法. 山东大学学报(自然科学版), 36 (4): 386–393. [DOI: 10.3969/j.issn.1671-9352.2001.04.006] )

Yang B. 2011. Wind Field Retrieval for Typhoon Based on Partial Differential Equation and Machine Learning. Jinhua: Zhejiang Normal University (杨波. 2011. 基于偏微分方程和机器学习的台风风场反演方法研究. 金华: 浙江师范大学 [DOI: 10.7666/d.y1950553])

Zehr R. 1989. Improving objective satellite estimates of tropical cyclone intensity//Proceeding of 18th Conference on Hurricanes and Tropical Meteorology. San Diego, CA: American Meteorological Society: J25-J28

Zhao H K and Wu L G. 2015. Review on climate change of tropical cyclone in the Northwest Pacific. Journal of the Meteorological Sciences, 35 (1): 108–118. [DOI: 10.3969/2014jms.0009] ( 赵海坤, 吴立广. 2015. 西北太平洋热带气旋气候变化的若干研究进展. 气象科学, 35 (1): 108–118. [DOI: 10.3969/2014jms.0009] )

Zhao Y, Zhao C F, Sun R Y and Wang Z X. 2016. A multiple linear regression model for tropical cyclone intensity estimation from satellite infrared images. Atmosphere, 7 (3): 40 [DOI: 10.3390/atmos7030040]

摘要

关键词