出版日期: 2017-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20177026
2017 | Volumn21 | Number 6
上一篇 | 下一篇

多源卫星观测的全球海洋次表层温度异常信息提取

黎文娥¹ , 苏华¹ , 汪小钦¹ , 严晓海²

1. 福州大学地理空间信息技术国家地方联合工程研究中心空间数据挖掘与信息共享教育部重点实验室，福州 350002

2. 厦门大学—美国特拉华大学近海海洋研究与管理联合研究所，厦门 361005

收稿日期: 2017-03-20; 优先数字出版日期: 2017-11-01

基金项目: 国家自然科学基金(编号：41601444)；国家海洋局“全球变化与海气相互作用”专项(编号：GASI-IPOVAI-01-04)；国家自然科学基金(编号：41630963)；国家自然科学基金(编号：41476007)；福建省自然科学基金(编号：2017J01657)；中国博士后科学基金面上资助(编号：2016M600495，2017T100466)；海西政务大数据应用协同创新中心资助(编号：2015750401)

第一作者简介: 黎文娥(1992—　)，女，硕士研究生，研究方向为中深层海洋遥感。E-mail：1836682015@qq.com

通讯作者简介: 苏华(1985—　)，男，副研究员，研究方向为海洋环境遥感。E-mail：suhua@fzu.edu.cn

中图分类号: TP79

文献标识码: A

摘要

基于表层卫星遥感观测的中深层海洋遥感对于了解海洋内部异常及其动力过程有重要意义。如何从现有的海洋表层遥感观测资料提取海洋内部关键动力环境信息场是具有挑战性的海洋遥感技术前沿。本文采用支持向量回归(SVR)方法，通过卫星遥感观测获取的多源海表参量(海表高度异常(SSHA)、海表温度异常(SSTA)、海表盐度异常(SSSA)和海表风场异常(SSWA))，选择最优参量输入组合，感知海洋次表层温度异常(STA)，并用实测Argo数据作精度验证。结果表明SVR模型可准确估算全球尺度的STA(1000 m深度以浅)；当SVR输入变量为2个(SSHA、SSTA)、3个(SSHA、SSTA、SSSA)、4个(SSHA、SSTA、SSSA、SSWA)时对应的平均均方差(MSE)分别为0.0090、0.0086、0.0087，平均决定系数(R²)分别为0.443、0.457、0.485。因此，除了SSHA和SSTA外，SSSA与SSWA的输入对SVR模型的估算有积极影响，有助于提高STA的估算精度。在全球增暖与减缓背景下，该研究可为从表层卫星遥感观测提取海洋内部热力异常信息研究提供重要技术支持，有利于拓展卫星对海观测范围。

关键词

多源卫星观测, 次表层温度异常, 支持向量回归, 信息提取, 全球海洋

Estimation of global subsurface temperature anomaly based on multisource satellite observations

LI Wen′e¹ , SU Hua¹ , WANG Xiaoqin¹ , YAN Xiaohai²

1.Key Laboratory of Spatial Data Mining and Information Sharing of Ministry of Education, National Engineering Research Centre of Geo-spatial Information Technology, Fuzhou University, Fuzhou 350002, China

2.Xiamen University/University of Delaware Joint Institute for Coastal Research and Management (Joint-CRM), Xiamen University, Xiamen 361005, China

Abstract

Subsurface thermal structure of the global ocean is a key factor that reflects the impact of global climate variability and change. Accurately determining and describing the global subsurface and deeper ocean thermal structure from satellite measurements are becoming even more important for understanding the ocean interior anomaly and dynamic processes during recent global warming and hiatus. The extent to which such surface remote sensing observations can be used to develop information about the global ocean interior is essential but challenging. This work proposes a Support Vector Regression (SVR) method, a popular machine learning method for data regression used to estimate Subsurface Temperature Anomaly (STA) in the global ocean. The SVR model can well estimate the global STA upper 1000 m through a suite of satellite remote sensing observations of sea surface parameters [including Sea Surface Height Anomaly (SSHA), Sea Surface Temperature Anomaly (SSTA), Sea Surface Salinity Anomaly (SSSA), and Sea Surface Wind Anomaly (SSWA)] with in situ Argo data for training and testing at different depth levels. In this study, we employed the Mean Squared Error (MSE) and squared correlation coefficient (R²) to assess the performance of SVR on STA estimation. Results from the SVR model were validated to test the accuracy and reliability using the worldwide Argo STA data (upper 1000 m depth). The average MSE and R² of the 15 levels are 0.0090/0.0086/0.0087 and 0.443/0.457/0.485 for two attributes (SSHA, SSTA)/three attributes (SSHA, SSTA, SSSA)/four attributes (SSHA, SSTA, SSSA, SSWA) SVR, respectively. The estimation accuracy was improved by including SSSA and SSWA for SVR input (MSE decreased by 0.4%/0.3% and R² increased by 1.4%/4.2% on average). The estimation accuracy gradually decreased with the increase in depth from 500 m. With the increase in depth, the absolute value of STA became smaller, i.e., it became more indistinctive in the spatial heterogeneity. The STA became less intensive in the deeper ocean due to the water stratification and stability. Results showed that SSSA and SSWA, in addition to SSTA and SSHA, are useful parameters that can help estimate the subsurface thermal structure and improve the STA estimation accuracy. Moreover, an obvious advantage for SVR is the absence of limitation on the input of sea surface parameters. Therefore, we can figure out more potential and useful sea surface parameters from satellite remote sensing as input attributes to further improve the STA sensing accuracy from SVR machine learning. This study provides a helpful technique for studying thermal variability in the ocean interior, which has played an important role in recent global warming and hiatus from satellite observations over global scale.

Key words

multisource satellite observation, subsurface temperature anomaly, support vector regression, information extraction, global ocean

1 引　言

海洋内部的3维动力过程非常复杂，诸多重要的物理海洋现象与过程都存在于海表以下一定深度范围内(Klemas和Yan，2014)。全球大空间尺度海洋3维热盐结构的估算对海洋内部动力过程研究是至关重要的。然而，海洋内部动力过程研究对海洋内部观测数据而言是一项重大挑战，全球有限的Argo浮标观测数据仍远远满足不了要求(王喜冬等，2011)，实测数据稀少严重制约了海洋内部现象的机制和过程的研究。利用海洋3维热盐结构数据集，可以估算海洋次表层流场，并模拟海洋内部运动特征(Wilson和Coles，2005)。此外，近十几年来全球表面出现增暖减缓(Kosaka和Xie，2013；Chen和Tung，2014)，通过卫星对进出地球能量收支的估算(Trenberth和Fasullo，2013)，以及大量的研究发现，全球尺度的中深层海洋(300—2000 m)增暖在全球表面增暖减缓过程中扮演重要角色(Song和Colberg，2011；Balmaseda 等，2013；Chen和Tung，2014；Drijfhout 等，2014；Huber和Knutti，2014)，故准确估算全球海洋次表层热力结构显得愈发重要。由于海洋内部现场观测受到诸多因素限制而导致数据稀疏和缺失，卫星遥感无法直接探测海洋内部热力信息，因此基于表层卫星遥感观测间接推测海表以下热力结构信息很有必要。虽然不同的洋盆具有不同的水文环境特征，但这些特征并非各自独立的，它们因洋流等海洋动力因素紧密相连，因此将全球海洋作为一个整体进行研究，探索全局海洋内部变异特征，具有重要意义。

虽然卫星遥感仅能直接获取海表参数信息，但很多海洋内部物理现象都会在海洋表面有所表征，因而结合海表表征现象与机制模型，可推演海洋内部动力过程的关键参数(Wang 等，2013；Klemas和Yan，2014)。目前国内外多类型卫星传感器提供了丰富的多时空尺度海表观测数据，这为开展海洋内部热力信息遥感反演提供重要的数据支持。如何从现有的海洋表层遥感观测资料及历史现场观测数据挖掘出有用的海洋内部关键动力环境信息是当前海洋遥感亟需解决的重要问题(Ali 等，2004)。卫星高度计可重复测量海面高度异常及大尺度海面空间变化，结合卫星高度计和其他卫星传感器，通过与实测数据建立经验统计模型，可推演出海洋内部动力环境信息。海洋次表层温度异常(STA)与动力高度异常(DHA)存在很高的空间相似性(Mayer 等，2001；Willis 等，2003；Klemas和Yan，2014)。通过历史观测的不同深度层位的STA和DHA建立线性回归方程，可从DHA简单快速估算出不同层位的STA(Willis 等，2003)。Khedouri等人(1983)首次引入卫星高度计数据估算墨西哥湾暖流海域的温度结构。Fischer(2000)尝试结合海表高度异常(SSHA)和海表温度异常(SSTA)来估算赤道处的垂向温度结构，指出海表多变量观测可用来估算海洋内部温度结构。Ali等人(2004)利用神经网络通过使用阿拉伯海锚系的海表温度(SST)、海表高度(SSH)、风应力、净辐射通量及净热通量数据估算海洋内部温度结构。Guinehut等人(2004, 2006, 2009, 2012)结合卫星遥感和Argo浮标数据估算并改进了海洋内部3维热盐结构场。Wu等人(2012)应用自组织神经网络模型(SOM)在北大西洋海区从海表温度异常(SSTA)和海表高度异常(SSHA)估算海洋内部温度结构，取得较好的反演效果。Liu等人(2014)，采用海洋表层+内部的准地转方法(isQG)，通过SSH、SST和SSS反演得到次表层的流速和密度场。Su等人(2015)采用支持向量机(SVM)机器学习方法，从表层多源卫星遥感观测(SST、SSH、SSS)估算印度洋STA，提高了海洋内部温度结构的反演精度，为中深海热力参量遥感研究提供有力的技术手段。同时，卫星海洋观测还被其他相关学者用来研究海洋的内部特征(Fox 等，2002；Swart 等，2010；Meijers 等，2011)，海洋表层遥感观测越来越多的被用于海洋内部动力环境信息的估算研究。

综上所述，结合现场观测的动力模型或单纯基于海表和次表层参量的统计关系模型是估算海洋次表层热力结构信息的基本方法。但是，过往的统计方法较多依赖回归分析进行空间建模，缺乏高级机器学习模型的应用，并且模型输入参量较为单一。此外，全球尺度的估算模型较为欠缺，精度也有待提高。本研究面向全球海洋内部，采用支持向量回归(SVR)方法，基于海表多源卫星观测数据(海表高度(SSH)、海表温度(SST)、海表盐度(SSS)及海表风场(SSW))，选择最优输入参数组合，构建SVR机器学习模型，估算全球海洋次表层温度异常(STA)，利用Argo现场观测数据开展精度评价，最终建立适合全球尺度的STA估算模型，以期为中深层海洋数据集构建以及优化中深层海洋增暖分析提供遥感技术支持。

2 研究区及数据

2.1 研究区概况

全球海洋覆盖地球表面积的71%，蓄积全球97%的水量。全球海洋在全球气候变化过程中起到至关重要的调制作用，能够吸收因温室气体增加导致全球增暖的大部分热量，起到储热器和缓冲器的作用。本文所指的全球海洋是介于–180°E—180°E，–78.375°N—77.625°N，包括太平洋、大西洋和印度洋。

2.2 多源卫星观测与Argo数据

本研究采用的多源海表卫星观测及Argo实测数据具体如下：(1)海表高度数据(SSH)，采用AVISO卫星高度计，分辨率为0.25°×0.25°产品(自1993年起)(http://www.aviso.altimetry.fr [2016-03-14])；(2)海表温度数据(SST)，使用遥感系统的SST 0.25°×0.25°数据产品，来自AQUA卫星的Advanced Microwave Scanning Radiometer for EOS (AMSR-E)传感器，SST产品精度为0.5 ℃(2002年—2011年)(http://www.remss.com/missions/amsre[2016-03-14])；(3)海表盐度数据(SSS)，选取具有较长观测时间跨度及精度较好的欧空局的Soil Moisture and Ocean Salinity (SMOS) 1°×1°海表盐度产品(自2009年起)，平均误差为0.006 pss，标准差为0.287 pps (http://eopi.esa.int [2016-03-15])；(4)海表风场数据(SSW)，采用具有较高精度和适用性多平台交叉校正(CCMP)的海面风场数据集(Atlas 等，2011)。CCMP风场数据采用增强变分分析法，具有较高时空分辨率和全球海洋覆盖能力的新型卫星遥感资源，空间分辨率为0.25°×0.25°，时间跨度从1987年至2011年(ftp://podaac.jpl.nasa.gov/ocean_wind/ccmp [2016-08-30])；(5)现场观测Argo数据，用于模型训练与验证的标记。这里采用空间格网化的Argo分层观测数据集1°×1°产品，从海表0 m深度至2000 m深度共有27个标准层位，各层位都包括了温度、盐度及绝对动力高度等观测信息，时间跨度从2005年1月至2015年12月。Argo格网数据是基于变分分析方法将离散的海洋实测观测数据变分插值在3维空间格网中，从而实现全球范围覆盖(http://apdrc.soest.hawaii.edu/projects/Argo/data/gridded/On_standard_levels/index-1.html [2016-03-18])。

2.3 数据预处理

所有观测数据集大部分覆盖全球海洋，空间分辨率统一到1°×1°，时间分辨率统一为每月(monthly)，海表遥感观测与Argo现场观测时相保持一致。所有表层遥感参量(包括SSH、SST、SSS与SSW)均减去各自气候平均态(climatology)获得各参量异常值(anomaly)(如SSHA=SSH–SSHC，其中SSHC是SSH的气候平均态)，目的是为了单纯考虑海表参量异常信号，避免混入气候态季节变动信号对机器学习建模产生干扰。Argo实测次表层温度(ST)也同样减去其气候平均态得到次表层温度异常(STA)。

3 方　法

3.1 支持向量机

支持向量机(SVM)是Cortes和Vapnik(1995)首先提出的，是一种监督式机器学习的方法(Hsu 等，2010)。它通过寻求结构风险最小(SRM)原则(Vapnik 等，1997)，根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折中，以期获得最好的泛化能力。同时，它在解决小样本、非线性及高维模式识别中表现出众多特有的优势(Huang 等，2002)，并能够推广应用到函数拟合等其他机器学习问题中。SVM的基本思想是借助非线性映射(即核函数)，将多维的数据映射到一个更高维的特征空间，在这个空间寻找并构建一个最优分隔超平面(OSH)，最大化不同类型的数据间隔(Weston和Watkins，1999)。

3.2 支持向量回归

支持向量回归(SVR)(Vapnik 等，1997)是SVM最常用的形式之一。本研究采用ε-SVR，是通过引入ε不敏感损失函数，即最大能容忍ε大小的偏差，当且仅当模型预测值f(x)与真实值y，满足|f(x)–y|>ε时，才计算损失。这样可以实现具有较强鲁棒性的回归，保留了SVM的优点(冼广铭和曾碧卿，2008)。SVR的预测和泛化能力很大程度上取决于其核函数的选取，常用的核函数有Sigmoid核函数、多项式核函数(Polynomial)、线性核函数(Linear)及径向基核函数(RBF)。通过不同核函数的对比实验发现RBF是最佳选择，且以往大量研究也表明，在通常情况下RBF也是SVR应用的最合理选择，尤其对于高维小样本的研究，此核函数具有较强的适用性(Hsu 等，2010)。本文通过LIBSVM工具包(Chang和Lin，2013)进行SVR空间建模。

3.3 实验设置

以径向基(RBF)为核函数的支持向量回归(SVR)有两个关键的参数，惩罚系数(C)以及Gamma(G)系数。由于这两个系数的设置对实验结果会有很大影响，我们采用格网搜索(Grid-Search)或交叉验证(Cross-Validation)的方法来定量的分析并确定最优系数C与G组合。因为交叉验证法(或格网搜索法)评估的结果具有很好的稳定性和保真性(Hsu 等，2010)，大量的实验也证明该方法获得的系数组合可靠性很好。为了探讨不同海表参量输入对SVR模型估算的影响，本研究建立3种不同海表参量输入组合的SVR模型，均以RBF为核函数，并通过交叉验证确定各自的最优C和G组合。获得结果如下：4个输入参量SVR(SSHA、SSTA、SSSA、SSWA)对应G=8，C=1；3个输入参量SVR(SSHA、SSTA、SSSA)对应G=16，C=1；2个输入参量SVR(SSHA、SSTA)对应G=32，C=0.5。

图1展示如何利用海表多源遥感观测数据(SSHA、SSTA、SSSA、SSWA)通过SVR模型估算次表层温度异常(STA)(以500 m深度为例)，构建基于表层遥感观测的全球海洋STA遥感估算模型。首先，构建训练数据集。选择表层遥感观测SSHA、SSTA、SSSA与SSWA作为模型的输入参量，利用Argo实测STA作为训练标记和测试标记，并随机选取一定比例的表层观测数据集作为训练数据集(训练数据占60%，测试数据占40%，两个数据集完全独立)，所有数据集均归一化处理；其次，进行SVR训练。构建合适的SVR模型，选择RBF作为核函数，通过交叉验证确定最优的C和G系数组合。使用训练数据集(SSHA_X、SSTA_X、SSSA_X与SSWA_X)作为SVR训练的输入数据，同时用Argo STA作为训练标记，通过SVR训练获得次表层分层位的STA预测模型；最后，进行SVR估算。利用SVR训练获得的分层位STA预测模型，以表层观测数据集(SSHA_C、SSTA_C、SSSA_C与SSWA_C)作为模型输入参量，估算并获得次表层各层位STA(如500 m深度STA)，并利用Argo STA作为测试标记进行实测验证，评估SVR模型在次表层各深度层位的STA估算精度。

图 1 利用海表多源遥感观测数据通过支持向量回归模型估算全球海洋次表层热力结构(STA)流程图(以500 m深度为例)

Fig. 1 Flowchart for STA (e.g., 500 m depth) estimation in the Global Ocean using a support vector regression approach, SSHA、SSTA、SSSA and SSWA are from satellite remote sensing observations of sea surface

4 结果与分析

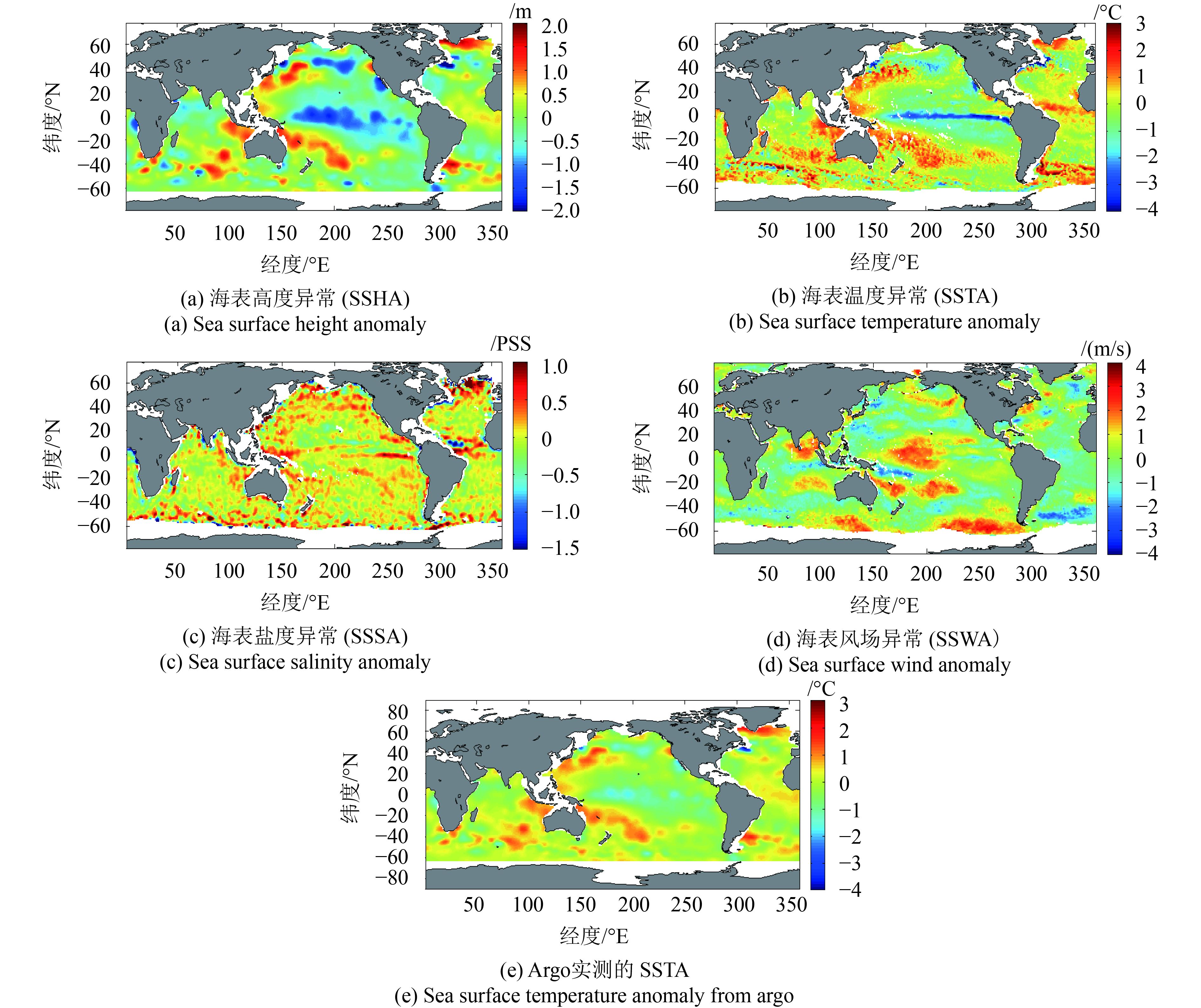
卫星遥感观测可获得海表高度、海表温度、海表盐度及海表风场等信息。图2展示了卫星遥感获得的多源海表参量(时间为2010年10月)，其中包括SSHA(取值范围为–2—2 m)，SSTA(取值范围为– 4—3 ℃)，SSSA(取值范围为–1.5—1 pss)，SSWA(取值范围为– 4—4 m/s)。在全球海洋表面，这些海表参量都表现出各自独特的空间特性，具有明显的空间异质性。如海表高度在太平洋赤道处呈现异常高值(西部)和异常低值(中部)(图2(a))；海表温度呈明显的纬向分布，太平洋赤道东、中部附近呈现异常低温(图2(b))，Nino3.4指数为–1.5 ℃(http://www.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ensoyears.shtml [2017-04-06])。西北和西南太平洋则呈现异常高值状态。大西洋中部和南部地区也呈现明显的异常高值。热带印度洋东部温度要明显高于印度洋西部，这是因为热带印度洋存在一种典型的海温异常型——印度洋偶极子(IOD)(李崇银和穆明权，2001)，且为负IOD(图2(b))；海表盐度呈现纬向带状较均匀分布状态(图2(c))；海表风场整体上呈现纬向带状并在经向上高低交替分布(图2(d))。

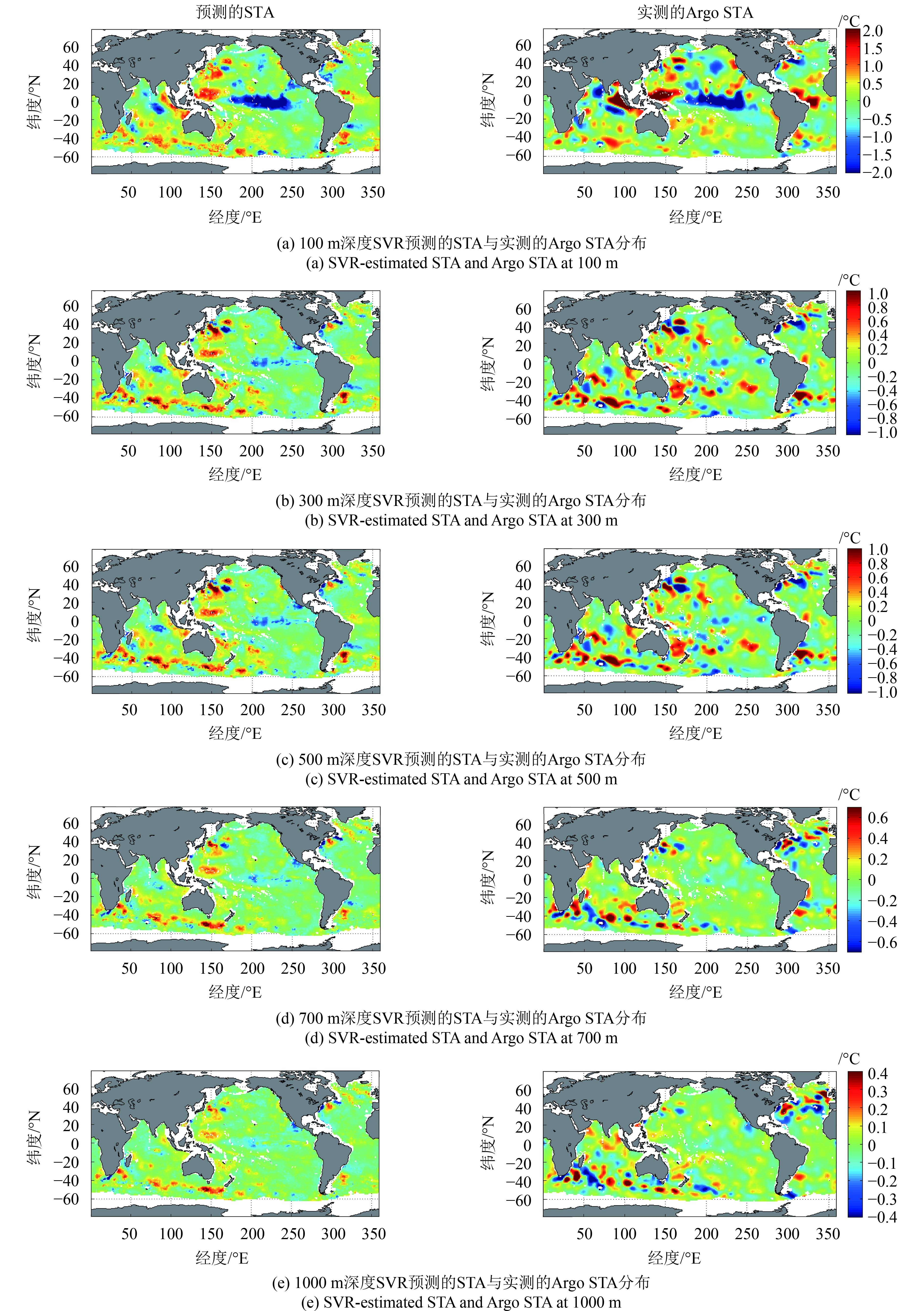
图 2 卫星遥感观测获得的多源海表参量与Argo实测SSTA分布图，时间均为2010年10月，空间分辨率统一为1°×1°

Fig. 2 The monthly SSHA, SSTA, SSSA, SSWA and Argo SSTA for the global ocean from satellite remote sensing observations with the same 1°×1° spatial resolution on October 2010

本研究面向全球海洋内部的不同深度层位，输入表层多源遥感观测参量，采用支持向量回归方法构建反演模型并估算全球海洋分层位STA。这里设立3组不同参量输入组合的SVR对照实验：第1组，SVR输入参量为SSHA和SSTA；第2组，SVR输入参量为SSHA、SSTA和SSSA；第3组，SVR输入参量为SSHA、SSTA、SSSA和SSWA。图3展示第3组4个输入参量SVR的STA估算结果。

图 3 2010年10月不同深度层位下，4参量SVR估算的STA及其对应的实测Argo STA

Fig. 3 The SVR-estimated (four-attributes SVR) STA compared with Argo gridded STA at different levels (depths)

采用Argo实测分层STA验证SVR估算的分层STA，直观地从空间分布上看，两者吻合的比较好，预测的异常区域和实测的分布格局较为一致。随着深度的增加，在某些区域两者的空间吻合度会有所降低(如在北大西洋和南印度洋)(图3)。同时海水温度总体上渐趋稳定，STA的变化强度也越来越小，空间异质性也逐渐不明显，这和海洋内部与表层动力差异有关。在100 m深度，太平洋赤道中西部的次表层出现大范围的异常低温，STA可低至–2 ℃(图3(a))；300—1000 m的STA空间分布比较类似，但与100 m深度的STA空间分布相差较大(图3)，这与热带太平洋上层的拉尼娜现象有关，而中深层海洋(300 m以深)的热力环境相对表层较为稳定；此外，边界附近的STA相对洋盆中心更加显著，这是受到边界流的影响，3大洋的西边界更加突出；700 m深的STA总体上呈纬向带状分布，在北大西洋和南印度洋尤为明显，这受该区域强烈的环流及动力环境影响所致(图3(d)—(e))。

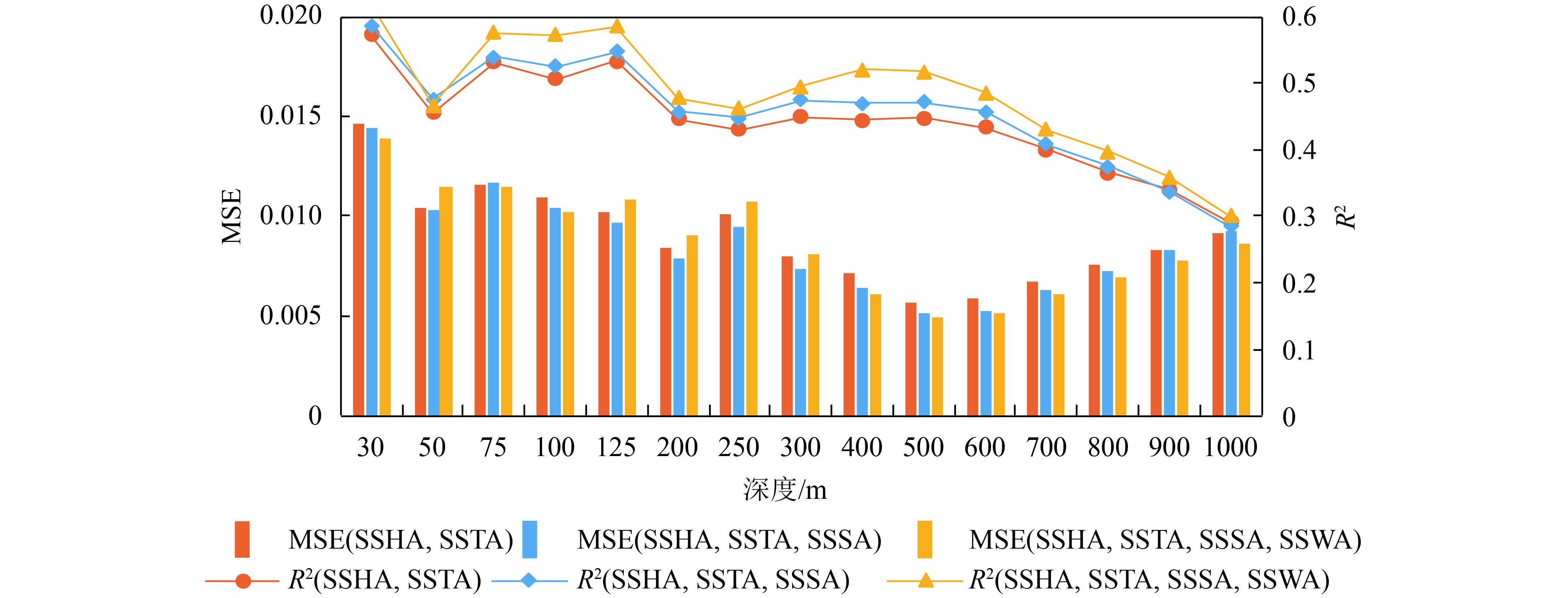
本研究采用均方差(MSE)与决定系数(R²)定量评价模型估算精度(表1)，在同一深度层位下，在SVR输入中增加SSSA与SSWA两个参量时，整体上MSE减小而R²增大，估算精度有所提升。随着深度(500 m以深)的增加，MSE增大而R²减小，说明SVR的预测能力降低，即估算精度下降(图3和表1)。对于4参量SVR，在100 m深度时所对应的MSE=0.0102，R²=0.572；300 m时，MSE=0.008，R²=0.496；500 m时，MSE=0.005，R²=0.517；700 m时，MSE=0.0061，R²=0.431；1000 m时，MSE=0.0086，R²=0.3。总体来说，SVR预测模型较为稳定，估算结果也较为可靠，随着深度的增加预测精度会有所下降。

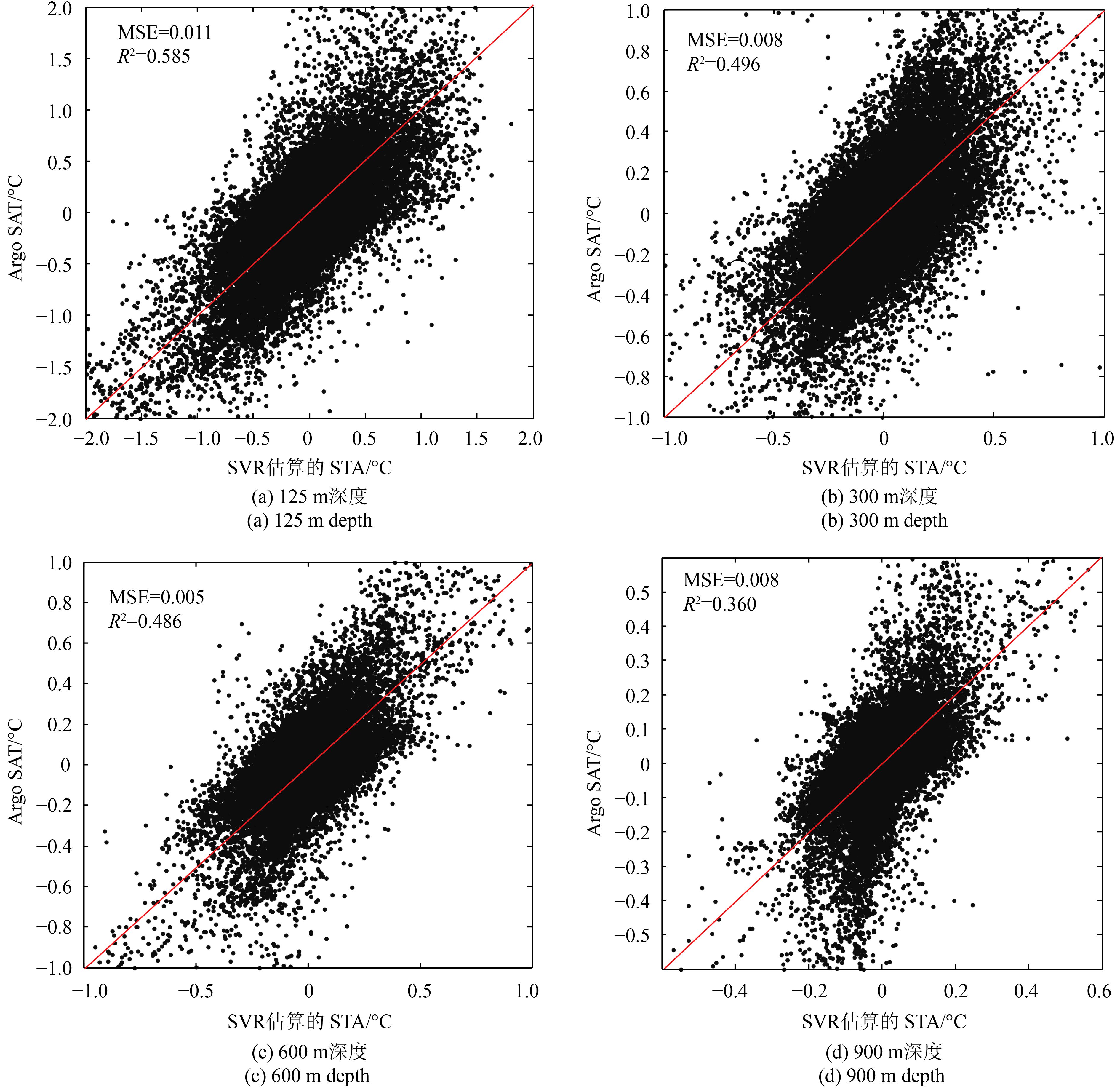
总体上，4个输入参量SVR估算精度最好，3个输入参量SVR估算精度次之，2个输入参量SVR估算精度最低，但仍可保持较好结果。分析不同深度层位的平均决定系数(R²)和均方差(MSE)，4个输入参量SVR的平均MSE为0.0087(最大/最小值为0.0139/0.0050)，R²均值为0.485(最大/最小值为0.619/0.300)；3个输入参量SVR的平均MSE为0.0086(最大/最小值为0.0144/0.0051)，R²均值为0.457(最大/最小值为0.586/0.285)；2个输入参量SVR的平均MSE为0.0090(最大/最小值为0.0146/0.0057)，R²均值为0.443(最大/最小值为0.573/0.292)。因此，输入参量SSSA与SSWA对模型预测有积极影响，估算精度略有提升，且4个输入参量SVR模型的STA估算效果最佳(表1与图4)。图4展示了不同参量输入组合的SVR模型在不同深度层位的STA预测精度评价(MSE和R²)。从图中可发现随着深度的增加MSE总体上呈现先降后升的趋势，而R²是先波动后下降(500 m深度为拐点)。深度在500 m以浅，估算精度有所波动，但总体精度可保持较好水平，这可能与全球海洋上层复杂的动力过程及混合层与温跃层的扰动有关。在500 m以深，MSE增加而R²减少，即模型预测能力降低，估算精度下降，这可能是由于中深层海水层化状态较为稳定，且深度越深海洋内部的物理现象越难在表层表征，并越难为卫星遥感所探测。此外，图4更直观的显示了增加海表盐度以及海表风场输入对提高SVR模型的预测精度有积极影响，可在一定程度上提升模型估算精度。图5散点图展示了4参量SVR模型估算的STA与Argo实测的STA之间的相关性与均方差(125 m(MSE=0.011，R²=0.585)、300 m(MSE=0.008，R²=0.496)、600 m(MSE=0.005，R²=0.486)和900 m(MSE=0.008，R²=0.360))。通过散点回归可直观检验模型估算精度(采用Argo实测的STA验证SVR预测的STA)，若图5中的数据点越均匀密集地分布在等值线上，则二者相关性越高且均方差越小。结果表明，大部分的预测结果与观测值较为接近，随着深度增加相关系数随之降低，即估算精度有所下降(图5)。通过散点图验证再次证明SVR可较好地预测全球海洋STA，估算结果可信度较高。

表 1 在不同深度，SVR输入参量分别为2个、3个、4个时所对应的均方差(MSE)与决定系数(R²)
Table 1 The performance measures comparison of 4-attributes, 3-attributes and 2-attributes of SVR for STA estimation at different depths by employing MSE and R²

下载CSV

深度/m	MSE	R²
深度/m	(SSHA, SSTA)/(SSHA, SSTA, SSSA)/(SSHA, SSTA, SSSA, SSWA)	(SSHA, SSTA)/(SSHA, SSTA, SSSA)/(SSHA, SSTA, SSSA, SSWA)
30	0.0146/0.0144/0.0139	0.573/0.586/0.619
50	0.0104/0.0104/0.0114	0.455/0.476/0.467
75	0.0116/0.0117/0.0114	0.532/0.539/0.576
100	0.0110/0.0105/0.0102	0.507/0.525/0.572
125	0.0103/0.0097/0.0108	0.533/0.548/0.585
200	0.0084/0.0078/0.0090	0.447/0.457/0.478
250	0.0105/0.0094/0.0107	0.430/0.449/0.462
300	0.0081/0.0074/0.0080	0.449/0.474/0.496
400	0.0071/0.0064/0.0061	0.445/0.470/0.520
500	0.0057/0.0051/0.0050	0.447/0.472/0.517
600	0.0058/0.0053/0.0051	0.434/0.457/0.486
700	0.0067/0.0063/0.0061	0.400/0.409/0.431
800	0.0076/0.0073/0.0070	0.366/0.375/0.398
900	0.0083/0.0083/0.0078	0.340/0.338/0.360
1000	0.0092/0.0093/0.0086	0.292/0.285/0.300

图 4 基于SVR模型的全球海洋15个不同深度层位STA估算结果的精度评价(评价指标采用均方差(MSE)和决定系数(R²)

Fig. 4 The performance measures comparison of 4-attributes (SSHA, SSTA, SSSA, SSWA), 3-attributes (SSHA, SSTA, SSSA) and 2-attributes (SSHA, SSTA) SVR for STA estimation at different depths (15 levels) based on MSE and R²

图 5 不同深度下SVR(4参量输入)估算的STA与Argo实测的STA相关性散点图

Fig. 5 The scatter plots between SVR-estimated (4-attributes SVR) and Argo STA in different depth levels

5 结　论

本文面向全球海洋内部，充分利用表层多源卫星观测资料(SSH、SST、SSS及SSW)，通过SVR机器学习方法，构建合理可靠的大尺度遥感模型，估算全球海洋内部热力异常(1000 m深度以浅的STA)，通过Argo实测的STA做验证，利用均方差(MSE)和决定系数(R²)进行精度评价，结果表明本文所构建的基于SVR的STA估算模型稳定可靠，精度较高。

本研究通过构建不同海表参量输入组合的对比实验分析不同参量输入对STA估算的影响。结果表明，4个参量输入的SVR模型具有最高的估算精度，3个参量SVR和2个参量SVR次之。因此，除海表高度、海表温度外，海表盐度和海表风场也是影响STA估算的积极因子，有助于提高全球STA的估算精度。

此外，在同种输入变量条件下，不同深度的STA估算精度也有所差异。随着深度的增加，MSE总体趋势表现为先减小后增大，R²则波动比较大，但从500以深估算精度出现较明显下降。随着深度的不断增加，全球海洋的STA变化幅度越来越小，因海水层化热力状态趋于稳定，STA空间异质性也较不显著。

综上，本文提出了基于海表多源遥感观测感知全球海洋次表层热力异常的技术方法，有利于发展基于机器学习的深海遥感技术，可为中深层海洋观测数据集的构建提供遥感技术支持，进而更全面认识海洋内部动力环境信息，优化当前全球增暖与减缓期间的中深海变异分析。然而，机器学习模型的海表输入参量较有限，同时缺乏对估算结果的动力机理解译，STA感知精度也有待提高，未来可以在这些方面进一步深入探究。

志谢感谢AVISO提供的海表高度数据，Remote Sensing Systems(RSS)提供的AMSR-E海表温度数据，European Space Agency (ESA) Earth Online提供的海表盐度数据，Cross-Calibrated Multi-Platform (CCMP)提供的海表风场数据，以及International Pacific Research Center(IPRC)提供的Argo格网数据。

参考文献(References)

Ali M M, Swain D and Weller R A. 2004. Estimation of ocean subsurface thermal structure from surface parameters: a neural network approach. Geophysical Research Letters, 31 (20): L20308 [DOI: 10.1029/2004GL021192]

Atlas R, Hoffman R N, Ardizzone J, Leidner S M, Jusem J C, Smith D K and Gombos D. 2011. A cross-calibrated, multiplatform ocean surface wind velocity product for meteorological and oceanographic application. Bulletin of the American Meteorological Society, 92 (2): 157–174. [DOI: 10.1175/2010BAMS2946.1]

Balmaseda M A, Trenberth K E and Källén E. 2013. Distinctive climate signals in reanalysis of global ocean heat content. Geophysical Research Letters, 40 (9): 1754–1759. [DOI: 10.1002/grl.50382]

Chang C C and Lin C J. 2013. LIBSVM: a library for support vector machines. [2015-11-23]. http://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf

Chen J N, Song G T, Chu J T and Xu L Y. 2003. Oceanic temperature anomalous signal pathway in the equatorial Pacific. Advances in Water Science, 14 (2): 152–157. [DOI: 10.3321/j.issn:1001-6791.2003.02.005] ( 陈锦年, 宋贵霆, 褚健婷, 许兰英. 2003. 赤道太平洋次表层海水温度异常的信号通道. 水科学进展, 14 (2): 152–157. [DOI: 10.3321/j.issn:1001-6791.2003.02.005] )

Chen X Y and Tung K K. 2014. Varying planetary heat sink led to global-warming slowdown and acceleration. Science, 345 (6199): 897–903. [DOI: 10.1126/science.1254937]

Drijfhout S S, Blaker A T, Josey S A, Nurser A J G, Sinha B and Balmaseda M A. 2014. Surface warming hiatus caused by increased heat uptake across multiple ocean basins. Geophysical Research Letters, 41 (22): 7868–7874. [DOI: 10.1002/2014GL061456]

Fischer M. 2000. Multivariate projection of ocean surface data onto subsurface sections. Geophysical Research Letters, 27 (6): 755–757. [DOI: 10.1029/1999GL010451]

Fox D N, Teague W J, Barron C N, Carnes M R and Lee C M. 2002. The modular ocean data assimilation system (MODAS). Journal of Atmospheric and Oceanic Technology, 19 (2): 240–252. [DOI: 10.1175/1520-0426(2002)019<0240:TMODAS>2.0.CO;2]

Guinehut S, Coatanoan C, Dhomps A L, Le Traon P Y and Larnicol G. 2009. On the use of satellite altimeter data in Argo quality control. Journal of Atmospheric and Oceanic Technology, 26 (2): 395–402. [DOI: 10.1175/2008JTECHO648.1]

Guinehut S, Dhomps A L, Larnicol G and Le Traon P Y. 2012. High resolution 3-D temperature and salinity fields derived from in situ and satellite observations. Ocean Science, 8 (5): 845–857. [DOI: 10.5194/os-8-845-2012]

Guinehut S, Le Traon P Y and Larnicol G. 2006. What can we learn from Global Altimetry/Hydrography comparisons?. Geophysical Research Letters, 33 (10): L10604 [DOI: 10.1029/2005GL025551]

Guinehut S, Le Traon P Y, Larnicol G and Philipps S. 2004. Combining Argo and remote-sensing data to estimate the ocean three-dimensional temperature fields–a first approach based on simulated observations. Journal of Marine Systems, 46 (1/4): 85–98. [DOI: 10.1016/j.jmarsys.2003.11.022]

Hsu C W, Chang C C and Lin C J. 2010. A practical guide to support vector classification. National Taiwan University. [2016-08-16]. http://www.vis.lbl.gov/~romano/mlgroup/papers/practical-svm-guide.pdf

Huang C, Davis L S and Townshend J R G. 2002. An assessment of support vector machines for land cover classification. International Journal of Remote Sensing, 23 (4): 725–749. [DOI: 10.1080/01431160110040323]

Huber M and Knutti R. 2014. Natural variability, radiative forcing and climate response in the recent hiatus reconciled. Nature Geoscience, 7 (9): 651–656. [DOI: 10.1038/NGEO2228]

Khedouri E, Szczechowski C and Cheney R. 1983. Potential oceanographic applications of satellite altimetry for inferring subsurface thermal structure // Proceedings of OCEANS’83. San Francisco, CA, USA: IEEE: 274–280 [DOI: 10.1109/OCEANS.1983.1152138]

Klemas V and Yan X H. 2014. Subsurface and deeper ocean remote sensing from satellites: an overview and new results. Progress in Oceanography, 122 : 1–9. [DOI: 10.1016/j.pocean.2013.11.010]

Kosaka Y and Xie S P. 2013. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature, 501 (7467): 403–407. [DOI: 10.1038/nature12534]

Li C Y and Mu M Q. 2001. The dipole in the equatorial Indian Ocean and its impacts on climate. Chinese Journal of Atmospheric Sciences, 25 (4): 433–443. [DOI: 10.3878/j.issn.1006-9895.2001.04.01] ( 李崇银, 穆明权. 2001. 赤道印度洋海温偶极子型振荡及其气候影响. 大气科学, 25 (4): 433–443. [DOI: 10.3878/j.issn.1006-9895.2001.04.01] )

Liu L, Peng S Q, Wang J B and Huang R X. 2014. Retrieving density and velocity fields of the ocean’s interior from surface data. Journal of Geophysical Research, 119 (12): 8512–8529. [DOI: 10.1002/2014JC010221]

Mayer D A, Molinari R L, Baringer M O and Goni G J. 2001. Transition regions and their role in the relationship between sea surface height and subsurface temperature structure in the Atlantic Ocean. Geophysical Research Letters, 28 (20): 3943–3946. [DOI: 10.1029/2001GL013331]

Meijers A J S, Bindoff N L and Rintoul S R. 2011. Estimating the four-dimensional structure of the southern ocean using satellite altimetry. Journal of Atmospheric and Oceanic Technology, 28 (4): 548–568. [DOI: 10.1175/2010JTECHO790.1]

Song Y T and Colberg F. 2011. Deep ocean warming assessed from altimeters, gravity recovery and climate experiment, in situ measurements, and a non-Boussinesq ocean general circulation model. Journal of Geophysical Research, 116 (C2): C02020 [DOI: 10.1029/2010JC006601]

Su H, Wu X B, Yan X H and Kidwell A. 2015. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurement: a support vector machine approach. Remote Sensing of Environment, 160 : 63–71. [DOI: 10.1016/j.rse.2015.01.001]

Swart S, Speich S, Ansorge I J and Lutjeharms J R E. 2010. An altimetry-based gravest empirical mode south of Africa: 1. development and validation. Journal of Geophysical Research, 115 (C3): C03002 [DOI: 10.1029/2009JC005299]

Trenberth K E and Fasullo J T. 2013. An apparent hiatus in global warming?. Earth’s Future, 1 (1): 19–32. [DOI: 10.1002/2013EF000165]

Vapnik V, Golowich S E and Smola A. 1997. Support vector method for function approximation, regression estimation, and signal processing // Mozer M, Jordan M and Petsche T, eds. Advances in Neural Information Processing Systems 9. Cambridge, MA: MIT Press: 281–287

Wang J B, Flierl G R, LaCasce J H, McClean J L and Mahadevan A. 2013. Reconstructing the ocean’s interior from surface data. Journal of Physical Oceanography, 43 (8): 1611–1626. [DOI: 10.1175/JPO-D-12-0204.1]

Wang X D, Han G J, Li W and Qi Y Q. 2011. Reconstruction of ocean temperature profile using satellite observations. Journal of Tropical Oceanography, 30 (6): 10–17. [DOI: 10.11978/j.issn.1009-5470.2011.06.010] ( 王喜冬, 韩桂军, 李威, 齐义泉. 2011. 利用卫星观测海面信息反演三维温度场. 热带海洋学报, 30 (6): 10–17. [DOI: 10.11978/j.issn.1009-5470.2011.06.010] )

Weston J and Watkins C. 1999. Support vector machines for multi-class pattern recognition // Verleysen M, ed. Proceedings of the 7th European Symposium on Artificial Neural Networks. Bruges: D-Facto Press

Willis J K, Roemmich D and Cornuelle B. 2003. Combining altimetric height with broadscale profile data to estimate steric height, heat storage, subsurface temperature, and sea-surface temperature variability. Journal of Geophysical Research, 108 (C9): 3292 [DOI: 10.1029/2002JC001755]

Wilson C and Coles V J. 2005. Global climatological relationships between satellite biological and physical observations and upper ocean properties. Journal of Geophysical Research, 110 (C10): C10001 [DOI: 10.1029/2004JC002724]

Wu X B, Yan X H, Jo Y H and Liu W T. 2012. Estimation of subsurface temperature anomaly in the north Atlantic using a self-organizing map neural network. Journal of Atmospheric and Oceanic Technology, 29 (11): 1675–1688. [DOI: 10.1175/JTECH-D-12-00013.1]

Xian G M and Zeng B Q. 2008. ε-SVR algorithm and its application. Computer Engineering and Applications, 44 (17): 40–42. [DOI: 10.3778/j.issn.1002-8331.2008.17.012] ( 冼广铭, 曾碧卿. 2008. ε-支持向量回归机算法及其应用. 计算机工程与应用, 44 (17): 40–42. [DOI: 10.3778/j.issn.1002-8331.2008.17.012] )

摘要

关键词