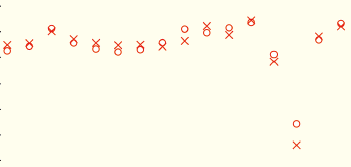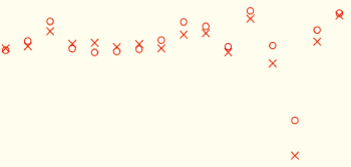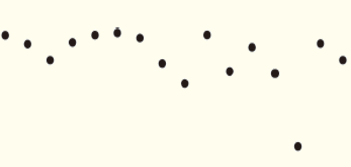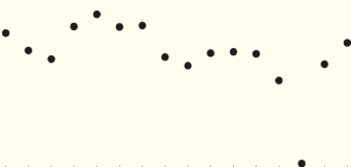出版日期: 2017-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176351
2017 | Volumn21 | Number 6
上一篇  |  下一篇
  
多目标的卫星仪器宽动态非线性定标
expand article info 王玲 , 胡秀清 , 陈林
1. 中国气象局 国家卫星气象中心，北京 100081
2. 中国气象局 中国遥感卫星辐射测量和定标重点开放实验室，北京 100081
收稿日期: 2016-11-01; 优先数字出版日期: 2017-11-01
基金项目: 国家自然科学基金(编号：41401417)
第一作者简介: 王玲(1986—　)，女，博士研究生，研究方向为卫星传感器可见–近红外通道辐射定标。E-mail：lingw@cma.gov.cn
中图分类号: TP701
文献标识码: A

摘要

传统的场地辐射定标方法由于定标样本少，难以覆盖遥感器动态范围，且不能发现仪器辐射响应是否存在非线性特性。针对这一问题，本文提出了基于多种亮暗等级的地球稳定目标(盐湖、沙漠和海洋)的卫星传感器宽动态非线性辐射定标方法。该方法以MODIS和NCEP数据产品作为稳定目标的地表特性、大气状况的先验知识库，利用大气辐射传输模型计算的多个稳定目标的大气层顶辐射值为定标基准，以二次多项式为定标方程，实现宽动态的非线性辐射定标，并以Aqua/MODIS观测值作为参考，对定标基准的精度进行评估。结果显示，对于反射太阳波段，辐射传输模型的计算值与MODIS观测值间的偏差均值在2%以内。最后，以气象卫星遥感器MERSI为例，基于2014年在稳定目标上空获取的大量定标样本，对其反射太阳通道的辐射响应特性进行研究，从而确定辐射定标方案和辐射定标方程的系数，然后采用敦煌试验场的同步实测数据对定标结果进行验证。结果表明，除了940 nm的水汽强吸收通道，其他通道的定标精度基本在5%以内。

关键词

辐射定标, 稳定目标, MERSI, MODIS, 非线性

Wide dynamic nonlinear radiometric calibration of optical satellite sensors using multiple stable earth targets
expand article info WANG Ling , HU Xiuqing , CHEN Lin
1.National Satellite Meteorological Center, China Meteorological Administration, Beijing 100081, China
2.Key Laboratory of Radiometric Calibration and Validation for Environmental Satellites, China Meteorological Administration, Beijing 100081, China

Abstract

In order to obtain quantitative information from satellite measurements, the satellite radiometer must first be calibrated. Calibration is a critical step to ensure data quality and to meet the needs of quantitative remote sensing in a broad range of scientific applications. One of the least expensive and increasingly popular methods of on-orbit calibration has been the use of pseudo invariant calibration sites. However, most of the researchers are tend to use one of these sites to monitor the multi-temporal stability of satellite sensors using time series analysis. A wide dynamic absolute calibration method by using multiple stable earth targets is presented here. This method relies on calculated Top-Of-Atmosphere (TOA) radiances over bright desert and salt lake sites as well as dark ocean targets. These simulated radiances represent the " reference” and are done using the 6S radiative transfer code with MODerate-resolution Imaging Spectroradiometer (MODIS) products and National Centers for Environmental Prediction (NCEP) reanalysis data for surface reflectance, aerosol optical depth, ozone amount and water vapor load estimation. When associating the simulated radiances with the sensor observed Digital Number (DN) using quadratic polynomial, the calibration coefficients can be obtained. The accuracy of the calibration results are determined by the accuracy of the " reference”, and this " reference” accuracy are assessed through using MODIS L1B data, which is characterized by high calibration accuracy (<2%), during one year period. Then, this method are applied to Medium-Resolution Imager (MERSI) onboard the second Chinese Polar Orbital Meteorological Satellite of FY-3A and FY-3C to study the radiometric response characteristics, so that the best calibration strategy can be determined. Finally, the determined calibration strategy is applied to FY-3A/MERSI and FY-3C/MERSI respectively, and the calculated calibration coefficients are validated based on the field observation data obtained at China Dunhuang Calibration Test Site on August 16, 2014. With the field observation data and 6S radiative transfer code, the TOA reflectance for MERSI solar bands are simulated and are used to validate the TOA reflectance calculated with the calibration coefficients obtained through the calibration method using Multiple Stable earth Targets (MST) proposed here. The comparison results demonstrate that calibration " reference” has high accuracy with relative bias between simulation and observation less than ±2%. Study of radiometric response characteristics FY-3A/MERSI and FY-3C/MERSI shows that radiometric response of FY-3A/MERSI is linear, while FY-3C/MERSI is non-linear. Hence, during their calibration processes, linear calibration method using MST is applied to FY-3A/MERSI, and non-linear calibration for FY-3C/MERSI. Validation results show that the relative differences of TOA reflectance between the one obtained from the calibration method using MST and the one obtained from 6S simulation using In-situ measurements are within ±%5 for most solar bands of MERSI. Compared with the traditional two-point calibration method, calibration trough using MST has the following advantages: (1) covering a wider dynamic range of satellite sensors, hence be good at characterize their radiometric response characteristic, (2) be helpful to reduce the calibration uncertainty with a large amount of calibration samples, and (3) can achieve efficient, real-time absolute radiation calibration for satellite sensors.

Key words

radiometric calibration, stable targets, MERSI, MODIS, nonlinear

1 引　言

卫星遥感以其快速、大面积、长期重复观测等独特优势，成为研究全球资源、环境和气候变化的重要手段。在这些研究领域中，科学家们更关注卫星观测资料所反映的地–气系统反射和辐射的绝对物理量。这对遥感信息由定性走向定量提出了迫切需求，而辐射定标是实现遥感信息定量化的基本前提(田庆久 等，1998；Smith 等，2002；顾行发 等，2013)。

卫星仪器在轨运行期间辐射定标的方法主要有星上定标和在轨替代定标。中国的卫星普遍没有搭载反射太阳谱段的星上定标系统(唐军武 等，2005)，即使有，如中分辨率光谱成像仪MERSI (胡秀清 等，2009；Hu 等，2012；孙凌 等，2013)，星上定标器也会因为恶劣的太空环境和强烈的太阳辐射等因素产生一定程度的衰减，不适合作为卫星辐射定标的基准源(高彩霞 等，2013)，只能依靠在轨替代定标的方法更新定标系数。经过20 多年的努力，该领域的学者提出了许多替代定标方法，包括场地定标法、交叉定标法和稳定目标定标法(孙凌 等，2013；Dinguirard和Slater，1999；Chander 等，2010)。其中，场地定标法是一种有效且广泛应用的辐射定标方法。近年来，韩启金等人(2013，2015) 提出了高分卫星多场地宽动态辐射定标的概念，以解决现有单场地定标的动态问题。但是该方法只有高、中、低3种定标场，样本数量有限，难以很好地描述仪器辐射效应是否存在非线性特性，且需要开展大量的场地同步测量，比较费时、费力，定标频次有限(如一年1—2次)，难以实现高频次的定标(Chander 等，2010；孙凌 等，2013)。稳定目标定标法既可避免场地定标中需要进行卫星同步测量的问题，也可弥补交叉定标中需要依赖其他卫星传感器的不足，具有成本低、定标频次高等优势，是未来辐射定标的一个发展趋势(巩慧 等，2010)。但是，目前这方面的研究工作主要侧重对遥感器辐射响应变化跟踪监测的相对辐射定标(Masonis和Warren，2001；Kim 等，2013)，绝对辐射定标方面的研究较少。Govaerts等人(2004)在这一方面开展了初步的研究工作，并应用在静止气象卫星Meteosat的绝对辐射定标中，对于红–近红外波段定标精度约为3%。之后却鲜见这方面的研究，直到最近，Helder等人(2013)基于Libya4沙漠目标，使用Terra/MODIS和EO-1/Hyperion建立了一个简化的经验辐射定标模型。该模型只考虑太阳天顶角变化对大气顶表观反射率的影响，只能计算星下点观测条件下，目标上空的大气顶表观反射率。Mishra等人(2014)对这一模型进行了改进，可实现非星下点观测、不同大气条件下目标上空表观反射率的模拟计算，并对不同特性的卫星传感器，如Aqua/MODIS、Landsat 8/OLI、ENVISAT/MERSI进行了定标试验，定标精度可达3%左右。但这些方法仍采用的是两点(冷空和稳定目标)的线性定标方案。孙凌等人(2013) 利用稳定目标具有时间稳定性的特征，提出了使用4个沙漠目标和1个海洋目标，在一个时间段内的数据样本，对FY-3A/MERSI进行宽动态定标跟踪的方法。由于沙漠目标在小于600 nm的较短波段处反射率较低(<0.3)，属于暗目标。因此，对于小于600 nm的波段，表观反射率的动态范围比较有限，最大只能达到0.2—0.25。王玲等人(2015)在利用多个稳定目标对FY-3C/MERSI辐射定标精度进行检验时，发现选用在较短波段处具有较高反射率(>0.3)的白沙(white sands)和玻利维亚盐湖(Uyuni salt Flats)，能有效提高该波段的动态范围，约是孙凌等人(2013)研究结果的2倍。但是这一研究没有选取海洋目标，因此，低端目标数据点相对较少。然而，对于具有非线性响应特性的遥感器，如FY-3C/MERSI，其辐射定标系数存在显著的目标依赖性，即，定标系数会随着目标辐射的动态发生变化(Xu 等，2014)，因此，此时需要大量的目标样本尽可能覆盖遥感器的动态范围，并采用非线性定标方案或分段线性的定标方案，才能获得较高精度的定标结果。

鉴于以上问题，本文选取了全球范围内15个不同亮暗等级的盐湖、沙漠和海洋稳定目标，以MODIS和NCEP数据产品作为稳定目标的地表特性、大气状况的先验知识库，基于6 S大气辐射传输模型(Vermote 等，1997) 建立了一套多目标宽动态非线性辐射定标方法，并利用具有较高定标精度的Aqua/MODIS观测数据，对该方法的定标基准(即辐射传输模型计算的大气顶表观反射率)精度进行了评估；最后，以FY-3A/MERSI和FY-3C/MERSI为例，利用该方法对两者的太阳反射波段辐射响应特性进行分析，在此基础上确定了辐射定标方案，并采用敦煌试验场的同步实测数据对绝对辐射定标系数进行检验分析，探讨基于多个稳定目标进行气象卫星传感器宽动态非线性辐射定标的适用性。

2 定标方法介绍

2.1 方法原理

国际地球观测卫星委员会(CEOS)的定标与真实性检验工作组(WGCV)在全球范围内选取了一系列辐射稳定且空间分布均匀的目标场地，这些场地被广泛用于卫星传感器反射太阳波段的绝对辐射定标或辐射响应稳定性评估(Cosnefroy 等，1996；Teillet 等，2007)。本文在之前研究选取的沙漠、盐湖稳定目标基础上(王玲 等，2015)，新添加了3个低亮度的海洋目标，分别位于太平洋、大西洋和印度洋区内，用以弥补之前研究缺少低端响应目标(大气顶反射率<0.1)的不足。各个稳定目标的名称和地理位置见表1。

表 1 文章使用的地球稳定目标及其位置分布
Table 1 The selected earth stable targets and their locations

下载CSV 
序号 站名 经度/°E 纬度/°N 序号 站名 经度/°E 纬度/°N
1 Algeria5 2.23 31.02 9 Sudan1 28.22 21.74
2 Arabia2 50.96 20.13 10 Sonora –114.1 31.95
3 Dunhuang 94.27 40.18 11 Uyuni Salt –67.45 –20.22
4 Libya1 13.35 24.42 12 White Sands –106.35 32.92
5 Libya4 23.39 28.55 13 Pacific Ocean 135.0 15.0
6 Mali –4.85 19.12 14 Indian Ocean 80.0 –20.0
7 Mauritania2 –8.78 20.85 15 Atlantic Ocean –45.0 20.0
8 Niger2 10.59 21.37

由辐射传输理论可知，假定地表为朗伯表面，卫星传感器入瞳处的表观反射率可表示为

${\rho ^*}\left( {{\theta _{\rm{v}}},{\theta _{\rm{s}}},{\varphi _{\rm{v}}} - {\varphi _{\rm{s}}}} \right) = {T_{\rm{g}}}\left( {{\theta _{\rm{v}}},{\theta _{\rm{s}}}} \right)\left[ {{\rho _{{\rm{r}} + {\rm{a}}}} + T\left( {{\theta _{\rm{s}}}} \right)T\left( {{\theta _{\rm{v}}}} \right)\frac{\rho }{{1 - s\rho }}} \right]$ (1)

式中，θv、θs分别为观测天顶角和太阳天顶角；φv、φs分别为观测方位角和太阳方位角；T(θs)为入射方向(太阳–目标路径)的大气散射透过率；T(θv)为观测方向(目标阳路径)的大气散射透过率；Tg为气体吸收通过率，ρr+a为由分子散射加气溶胶散射所构成的路径辐射反射率，S是大气球面反照率，ρ为地表反射率。

对卫星传感器通道i的等效反射率可由式(2)计算得到

$\rho _{{\rm{eq}}i}^* = \frac{{\mathop \smallint \nolimits_{{\textit{λ} _1}}^{{\textit{λ} _2}} {\rho ^*}\left( \textit{λ} \right){f_i}\left(\textit{λ} \right){\rm{d}}\left(\textit{λ} \right)}}{{\mathop \smallint \nolimits_{{\textit{λ}_1}}^{{\textit{λ}_2}} {f_i}\left( \textit{λ} \right){\rm{d}}\left( \textit{λ} \right)}}$ (2)

式中， $\rho _{{\rm{eq}}i}^*$ 是卫星通道i的等效反射率；ρ*(λ)是大气层顶卫星入瞳处的光谱反射率；fi(λ)为归一化的卫星通道i的光谱响应函数；λ1和λ2是卫星通道i的光谱响应范围。

通常情况下，卫星传感器输出信号与其入瞳处的辐射之间多采用线性关系，但是由于光学器件的问题，仪器的辐射响应也可能是非线性的。因此，为了更真实的反映仪器辐射效应特性，通道i的等效反射率与该通道计数值DN之间的关系可以表示为

$\rho _{{\rm{eq}}i}^*\cos \left( {{\theta _s}} \right)/d_{\rm{ES}}^2 = k_i^2 \cdot DN_i^2 + k_i^1 \cdot D{N_i} + k_i^0$ (3)

式中，dES为日地距离； $k_i^2$ ， $k_i^1$ ， $k_i^0$ 分别是卫星通道i的二次项和一次性定标系数及截距。当 $k_i^2$ 等于0，即为通常使用的线性定标方案。若将式(3)的左边用 $\rho _{{\rm{eq}}i}^{**}$ 表示，则式(3)可以简化为

$\rho _{{\rm{eq}}i}^{**} = k_i^2 \cdot DN_i^2 + k_i^1 \cdot D{N_i} + k_i^0$ (4)

式中， $\rho _{{\rm{eq}}i}^{**}$ 是利用卫星观测时刻的太阳天顶角和日地距离对卫星通道等效反射率进行订正后的结果，以下称为订正后的卫星通道等效反射率(adjusted reflectance)。要求解式(4)中的3个定标系数至少需要3组观测样本，通常使用的定标方法只有两组观测，即目标场地与冷空，无法获得仪器的非线性项，而在本研究中，通过使用多个地球稳定目标，可以很好地解决这一问题。

2.2 方法流程

晴空稳定目标区识别：对15个不同亮暗等级的地球稳定目标，选取其中心3×3窗口像元区域为研究区，采用空间均一性准则，即目标区的DN方差系数>0.1去除被云污染的目标区(Kim 等，2014)。海洋稳定目标区还要去除太阳耀斑角<40°、表面风速>7 m/s的观测，以避免太阳耀斑和白沫(white cap)的污染。太阳耀斑角计算如式(5)所示。表面风速由NCEP每日4次(four-times daily)的纬向风速(U-wind)和经向风速(U-wind)再分析资料(Kalnay 等，1996)计算得到。该资料一天4次的当地时间分别为0:00、6:00、12:00和18:00，使用时选取离卫星过境时刻最近的时间。

${\rm{cos}}{\theta _{\rm{r}}} = {\rm{sin}}{\theta _{\rm{v}}}{\rm{sin}}{\theta _{\rm{s}}}{\rm{cos}}\psi + {\rm{cos}}{\theta _{\rm{v}}}{\rm{cos}}{\theta _{\rm{s}}}$ (5)

式中，θr为太阳耀斑角； $ \psi $ 是相对方位角。

辐射传输模拟：结合观测时刻的实际光照条件和观测几何、大气和地表特性参数以及卫星通道光谱响应函数，使用6 S大气辐射传输模型(Vermote 等，1997)，计算成功识别出的晴空稳定目标区的大气顶光谱辐射。其中，沙漠稳定目标的地表双向反射率采用MODIS全球0.05°×0.05°空间分辨率的BRDF产品(MCD43C1)计算获得，具体计算过程参考王玲等人(2015)的文献。海洋稳定目标的表面特性参数使用6 S辐射传输模型提供的CLEARW地表模型参数。大气特性参数，如550 nm气溶胶光学厚度、臭氧总量和水汽总量，来自MODIS的全球1°×1°的大气日产品。其中，海洋目标上空气溶胶光学厚度采用Terra/MODIS的结果，即MOD08产品；沙漠目标上空采用Auqa/MODIS的深蓝算法结果，即MYD08产品。

定标系数计算：在一段时间范围内，如一天或一个月，对于待定标的卫星通道i，通过对不同目标的观测，可以得到多组卫星观测计数值和辐射传输模型计算的卫星通道等效光谱辐射数据对，即[ $\rho _{{\rm{eq}}i}^{**}$ (g, t), DNi(g, t)]。其中，g代表第g个稳定目标，g≤15；t表示卫星过境时刻。最后，根据最小二乘优化准则(式(6))求解通道i的定标系数Gi和Ii。

$\sum {(\rho _{{\rm{eq}}i}^{*{\rm{*}}}\left( {g,t} \right) - {G_i} \cdot D{N_i}\left( {g,t} \right) - {I_i})^2} \to \min$ (6)

3 定标基准不确定性评估

由2.2节可知，本文提出的定标方法中，辐射传输模型计算的大气顶表观反射率是卫星传感器的定标基准(calibration reference)(Govaerts 等，2004)，这一定标基准的准确性决定了最终定标结果的精度。在辐射传输计算时，输入参数几乎全部来自卫星产品和气候数据集，这些参数的不准确性和辐射传输模式本身都会影响大气顶辐射的计算精度。

针对定标基准的不确定性评估，选取了一个具有较高定标精度的MODIS卫星观测数据(约2%，Xiong 等，2007)。参与评估分析的MODIS数据为2014年AQUA/MODIS L1B级定标后的表观反射率数据MYD02 1 km和地理定位数据MYD03 1 km。在15个稳定目标上空共获取了2874景影像数据，每个目标的数据量约为150—230。参与分析的波段为MODIS的前7个波段，中心波长分别为659 nm, 865 nm, 460 nm, 555 nm, 1240 nm, 1640 nm和2130 nm。

采用2.2节所述的方法流程，针对MODIS的观测几何和波段响应函数，模拟计算MODIS过境时刻晴空稳定目标区的大气顶表观反射率，并与MODIS的观测值进行对比。为进一步去除残留云的影响，对比时剔除了波段1(659 nm)大气顶反射率观测值大于0.6的数据(孙凌 等，2013)。定标基准的精度采用观测值和辐射模拟值之间的相对偏差表示(式(7))

$bias = \left( {\rho _{{\rm{est}}}^* - \rho _{{\rm{mea}}}^*} \right)/\rho _{{\rm{mea}}}^*$ (7)

式中， ${\rho _{{\rm{mea}}}^*}$ 是MODIS观测的表观反射率， ${\rho _{{\rm{est}}}^*}$ 是辐射传输模型计算的表观反射率。


图 1 2014年MODIS观测的大气顶表观反射率与辐射模拟值的散点图
Fig. 1 Scatter plots between the observed TOA reflectance by AQUA/MODIS and that calculated from the atmospheric radiative transfer model

图1给出了2014年晴空稳定目标区MODIS观测值与模拟值的比对散点图，以及观测值与模拟值之间的线性拟合关系，定标基准的精度估计bias(相对偏差均值±相对偏差标准差)和参与对比分析的稳定目标样本数N。为便于展示，图1中的12个稳定目标根据865 nm处的地表反射率值(参见王玲等人(2015)文中的图1)分成3种类型，即较高亮度的目标Desert1，包括：White Sands、Libya1、Libya4和Mali；中等亮度的目标Desert2，包括：Algeria5、Arabia2、Mauritania2和Sonora；低亮度的目标Desert3，包括：Niger2、Sudan1、Uyuni salt Flats和Dunhuang。

由图1可以看出，辐射传输模拟值与MODIS观测值之间具有很好的相关性，除了波段6的相关系数R为0.98外，其他波段都达到了0.99。从辐射数据的动态范围来看，各个波段表观反射率都有比较大的取值范围，最小值基本在0.05—0.1(波段7除外，大约为0.2)；最大值略有差异，波长较短的蓝(band3)、绿(band4)波段约为0.5，波长较长的近红外(band2)和短波红外波段(band5—7)约为0.7，位于中间波长的红波段(band1)，取值也在两者之间，约为0.6，这与王玲等人(2015)的研究结果一致。不同之处在于，本研究通过海洋目标的使用，可见光波段(band3—4、band1)处，反射率<0.1的低端响应数据样本明显增多，近红外波段(band2)也有少量的增加。由于清洁水体在大于1.1 μm的波段处，反射率很低，几乎趋近于零，因此band6和band7几乎没有海洋目标的数据样本。图1中给出的精度估计结果(bias)表明，对反射太阳波段范围内的7个波段，辐射传输模型的计算值与MODIS观测值间的偏差均值在2%以内，偏差标准差为3%—4%，说明本文提出的多目标宽动态辐射定标能够提供较高精度的定标基准，应用到卫星传感器实际辐射定标中也有望获得较高精度的定标结果。因此，为了检验该方法在实际定标工作中的效果，以下部分对FY-3A/MERSI反射太阳波段进行了辐射定标实验。

4 定标方法应用

4.1 MERSI辐射定标方案选取

风云三号(FY-3)是中国新一代极轨气象卫星，目前该系列已有3颗(A、B和C)在轨运行。其中，FY-3A和FY-3C分别于2008 年5月27日和2013年9月23日在太原卫星发射中心成功发射。两颗卫星设计相同，均携带有11个有效载荷，具有全球、多光谱综合观测地球系统的能力(张鹏 等，2012)。中分辨率光谱成像仪MERSI是星上搭载的一个关键光学成像仪，具有19个反射太阳波段(0.41—2.13 μm)和一个红外发射波段(11.25 μm)，扫描幅宽为2900 km×10 km，可实现每天一次的全球扫描覆盖。

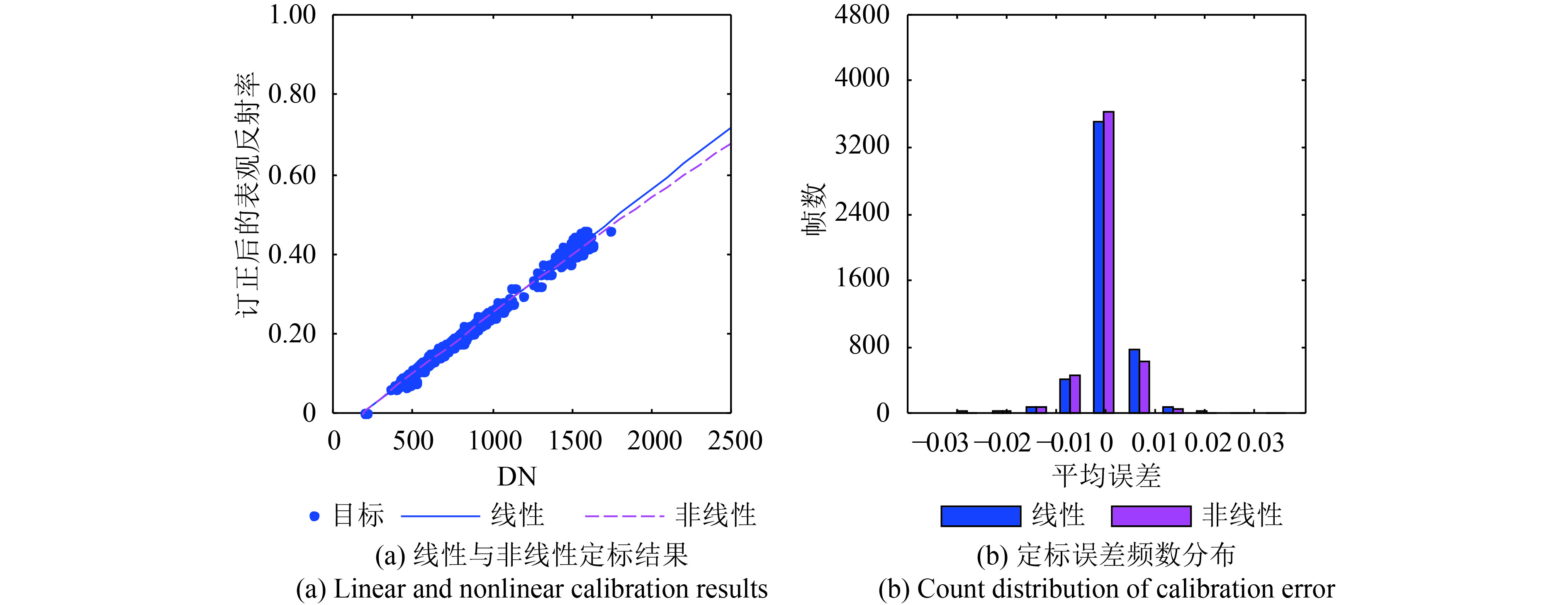
为了降低仪器辐射性能衰减给辐射响应分析带来的不确定性，采用FY-3A/MERSI在晚期(2014年1月—12月)获取的全球稳定目标的观测样本进行分析。图2显示的是波段2(中心波长550 nm)的计数值(DN)与订正后的表观反射率(Adjusted Reflectance)的对应关系图2(a)及不同拟合方法误差均值分布图2(b)。


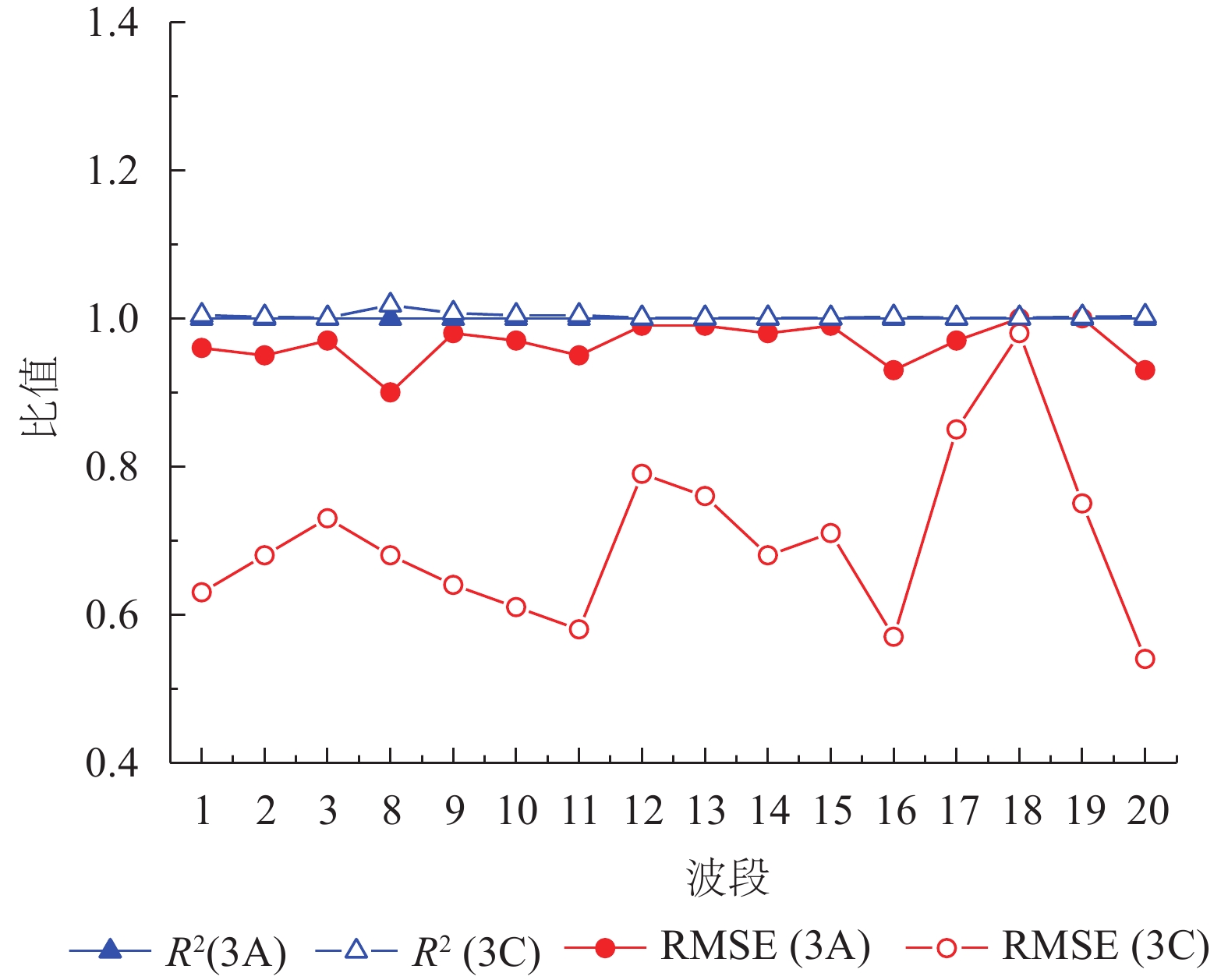
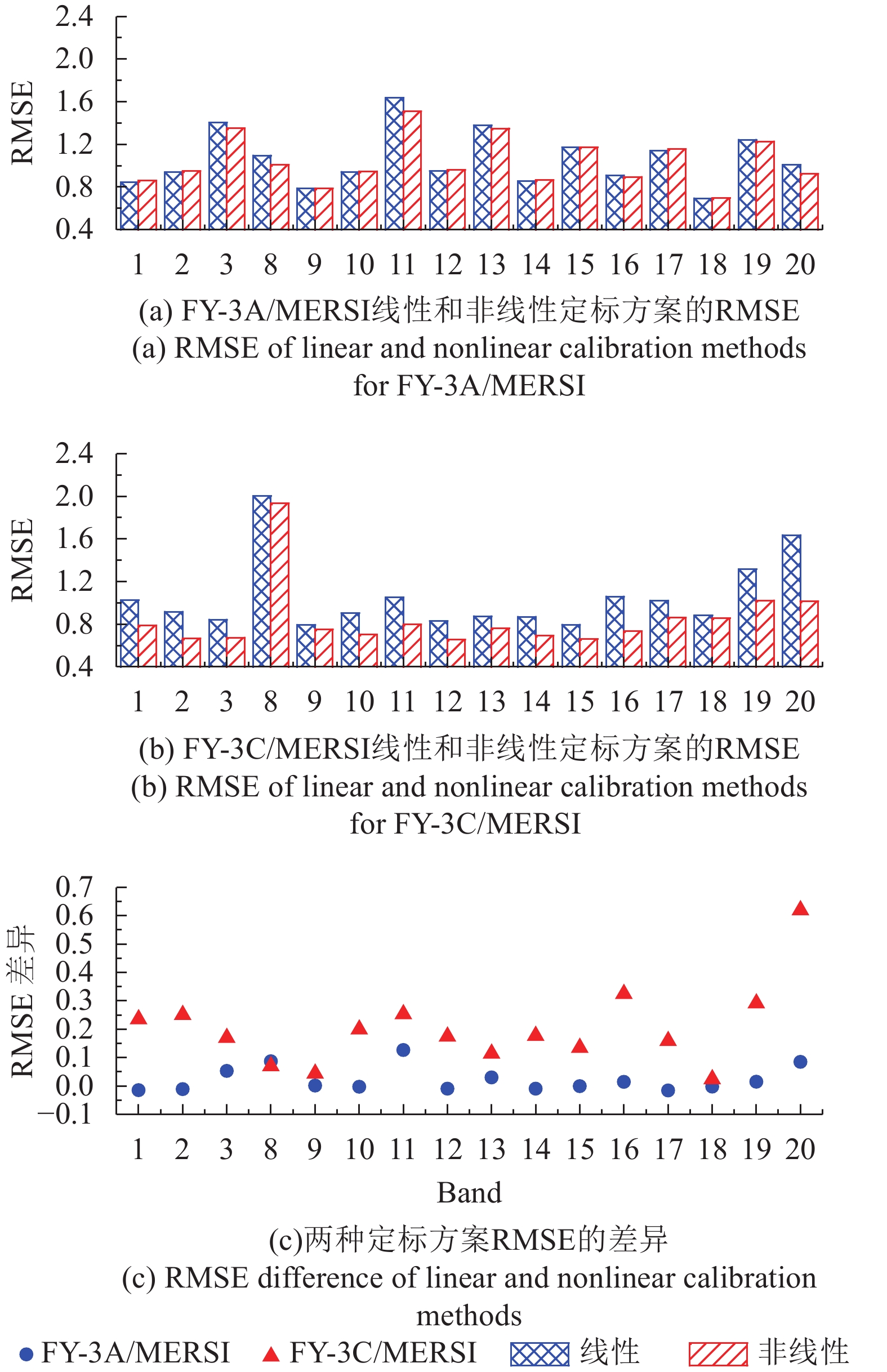
图 2 FY-3A/MERSI波段2线性和非线性定标曲线(2014-01—2014-12)及定标误差(即反射率平均误差)频数分布
Fig. 2 Linear and nonlinear calibration for FY-3A/MERSI band2 (2014-01—2014-12) and the count distribution of calibration error (i.e., reflectance Mean Error (ME)) for different calibration methods

由图2可见，对于波段2，线性拟合和二次非线性拟合曲线比较接近，误差大小都近似正态分布，误差均值都接近于0。由于篇幅限制，其他波段只给出拟合方法的误差统计结果，如表2所示。可以看出，FY-3A/MERSI所有波段非线性拟合方法与线性拟合方法的误差结果比较接近，误差均值ME(Mean Error)接近0，均方根误差RMSE (Root Mean Square Error)在0.01以内。二次拟合与线性拟合的RMSE差异除了波段8略大外，其他波段都在5%以内(图3)。有关FY-3A/MERSI辐射响应衰变规律研究表明(Chen 等，2014)，波段8(中心波长412 nm)存在严重的衰减，因此这也会给通道的辐射响应带来一定的非线性，所以在计算波段8的辐射定标系数时，应尽量采用较短时期内的观测样本。从拟合优度R2来看，二次拟合与线性拟合的R2值都在0.995以上，拟合效果都较好，且两者的比值为1(图3)，这说明二次非线性拟合与线性拟合相比并没有明显的优势。因此对于FY-3A/MERSI的反射太阳通道可以采用线性拟合方法进行定标计算，即式(4)中的k2取值为0。需要说明的是由于FY-3A/MERSI的波段6和波段7处在无辐射制冷的异常状态，波段4从2014年出现冷空观测异常，因此这里没有对这3个波段进行处理。

表 2 线性与非线性拟合优度(R2)及误差统计(FY-3A/MERSI)
Table 2 Goodness of fit (R2) and error statistics for linear and nonlinear calibration method (FY-3A/MERSI)

下载CSV 
波段 波长/nm ME RMSE R2
线性 非线性 线性 非线性 线性 非线性
1 470 –4.20E–16 –2.43E–17 0.0059 0.0057 0.996 0.996
2 550 3.50E–16 2.12E–16 0.0047 0.0045 0.998 0.998
3 650 –1.39E–16 1.06E–16 0.0058 0.0056 0.999 0.999
8 412 1.96E–16 –9.60E–18 0.0071 0.0064 0.995 0.996
9 443 2.03E–16 –7.12E–18 0.0049 0.0048 0.997 0.997
10 490 2.50E–16 2.58E–17 0.0048 0.0047 0.997 0.998
11 520 1.08E–16 –9.42E–17 0.0047 0.0044 0.998 0.998
12 565 5.67E–18 –2.06E–19 0.0043 0.0042 0.999 0.999
13 650 –2.14E–16 3.57E–17 0.0057 0.0056 0.999 0.999
14 685 –6.05E–17 –4.18E–18 0.0056 0.0055 0.999 0.999
15 765 –2.80E–16 1.50E–16 0.0061 0.0060 0.998 0.998
16 865 –6.62E–16 6.83E–17 0.0072 0.0067 0.999 0.999
17 905 –2.00E–16 6.83E–18 0.0080 0.0078 0.997 0.997
18 940 –2.18E–16 1.90E–17 0.0053 0.0053 0.995 0.995
19 980 –8.28E–17 4.26E–18 0.0083 0.0083 0.998 0.998
20 1030 3.23E–17 5.39E–17 0.0097 0.0090 0.998 0.998


图 3 线性和非线性辐射定标的均方根误差(RMSE)比值及拟合优度(R2)比值
Fig. 3 The RMSE and R2 ratio of linear calibration to nonlinear calibration for MERSI reflective solar bands (2014-01—2014-12)

由于FY-3C/MERSI从2015年5月发生故障停止工作，因此这里也采用2014年1月—12月的全球稳定目标观测数据，分别采用一次线性和二次多项式拟合的方法，对其辐射响应特性的分析。图4显示的是波段2的拟合结果。由图4可见，对于波段2线性拟合和非线性拟合曲线之间的差异较大，而两种拟合方法的误差分布类似，近似正态分布。误差均值(ME)、均方根误差(RMSE)及拟合优度(R2)值如表3所示。可以看出，对于表中列出的波段，非线性拟合方法与线性拟合方法的误差均值都接近0，即误差呈正态分布。从拟合优度R2来看，线性拟合的R2值均低于非线性拟合的值，但差异较小，除了波段8非线性拟合与线性拟合的比值略高于1外，其他波段约为1(图3)。与FY-3A/MERSI类似，波段8的非线性特性可能与该通道在轨运行期间的衰减有关。RMSE差异比较明显：线性拟合的RMSE波段8最大为0.0188，其他波段约为0.007—0.015，非线性拟合的RMSE也是波段8最大，但小于线性拟合的值，为0.0127，其他波段的RMSE也小于线性拟合的值，为0.005—0.010。非线性拟合与线性拟合的RMSE比值(图3)显示，除了波段18接近1外，其他波段主要集中在0.5—0.8，其中，波段11，16和20的比值最小在0.5附近，说明FY-3C/MERSI的通道具有明显非线性响应特性，且波段11，16，20的非线性特性最为显著，这与Chen等人(2014)基于发射前室外太阳反射定标测量资料对FY-3C/MERSI非线性特性的分析结论一致。因此，对于FY-3C/MERSI的反射太阳通道最好采用非线性拟合方法进行定标计算。


图 4 FY-3C/MERSI波段2线性和非线性定标曲线(2014-01—2014-12)及定标误差(即反射率平均误差)频数分布
Fig. 4 Linear and nonlinear calibration for FY-3C/MERSI band2 (2014-01—2014-12) and the count distribution of reflectance mean error for different calibration methods

表 3 线性与非线性拟合优度(R2)及误差统计(FY-3C/MERSI)
Table 3 Goodness of fit (R2) and error statistics for linear and nonlinear calibration method (FY-3C/MERSI)

下载CSV 
波段 波长/nm ME RMSE R2
线性 非线性 线性 非线性 线性 非线性
1 470 3.35E–16 –6.16E–17 0.0082 0.0052 0.994 0.997
2 550 1.29E–16 –2.53E–17 0.0075 0.0051 0.996 0.998
3 650 –3.40E–16 –4.13E–18 0.0091 0.0066 0.997 0.999
8 412 6.40E–17 7.61E–17 0.0188 0.0127 0.967 0.985
9 443 –6.72E–18 –3.04E–17 0.0106 0.0068 0.989 0.995
10 490 3.87E–17 –9.07E–17 0.0084 0.0051 0.994 0.998
11 520 –9.42E–17 –5.81E–17 0.0084 0.0048 0.994 0.998
12 565 3.60E–16 1.67E–17 0.0079 0.0062 0.996 0.998
13 650 –3.39E–16 3.66E–17 0.0091 0.0069 0.997 0.998
14 685 –2.94E–16 –1.28E–16 0.0092 0.0063 0.997 0.999
15 765 2.33E–16 8.73E–18 0.0090 0.0064 0.997 0.999
16 865 1.27E–16 7.41E–17 0.0110 0.0063 0.998 0.999
17 905 –3.17E–16 1.60E–19 0.0103 0.0088 0.996 0.997
18 940 –3.58E–17 1.44E–17 0.0102 0.0099 0.984 0.985
19 980 –1.06E–16 –1.59E–16 0.0136 0.0102 0.995 0.997
20 1030 3.23E–17 5.39E–17 0.0097 0.0090 0.998 0.998

4.2 MERSI辐射定标结果验证

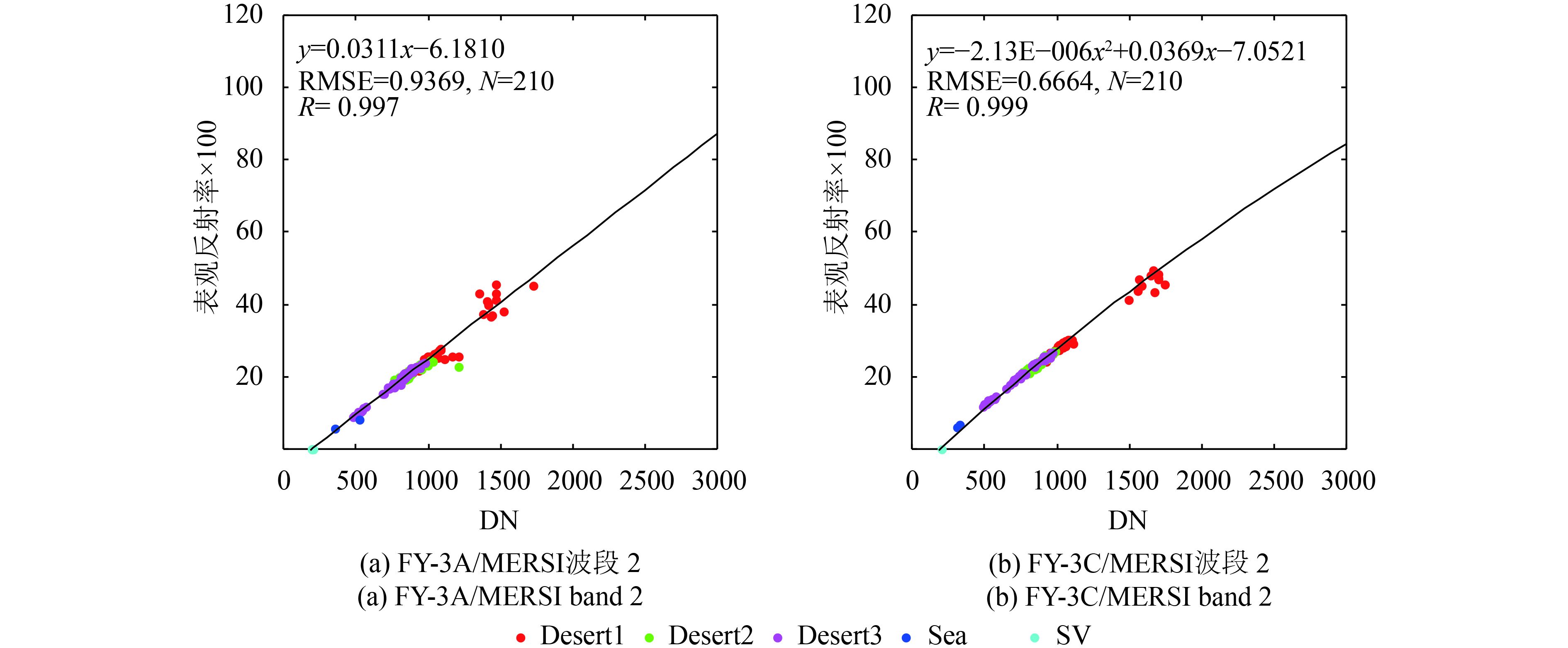
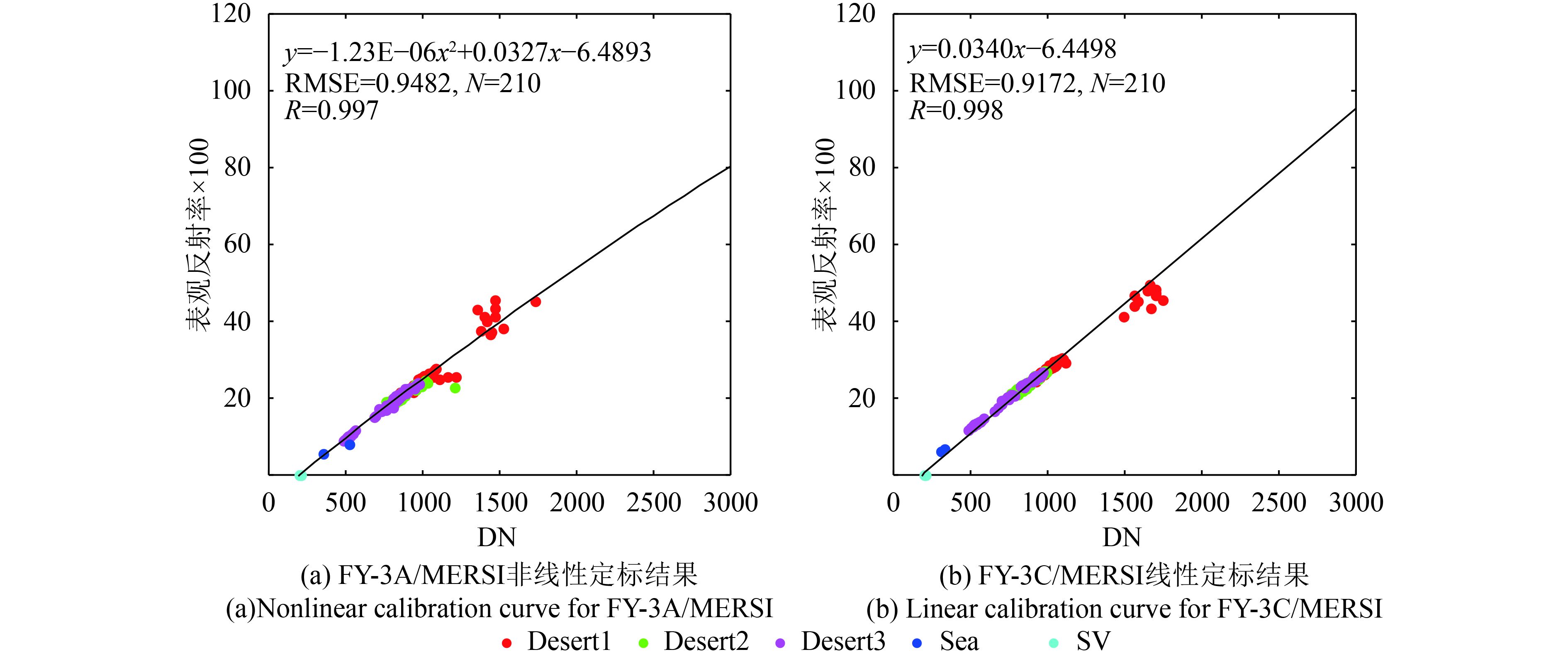
根据4.1的分析，为了减小由于仪器衰减，如波段8，对定标结果精度的影响，这里采用2014年8月16日前一个月的MERSI全球观测数据，进行辐射定标计算。以波段2为例，根据2.2节的辐射定标流程，对FY-3A/MERSI和FY-3C/MERSI分别采用线性和非线性(二次多项式)定标方案，获取的8月16日反射太阳波段的辐射定标结果如图5所示。图5(a)和图5(b)分别是FY-3A和FY-3C MERSI波段2(550 nm)的计数值(DN)与经太阳天顶角和日地距离订正后的大气顶表观反射率模拟值( $\rho _{\,\,{\rm{eq}}}^{**}$ )的比对散点图及拟合结果。图5中给出了定标公式、均方根误差(RMSE)、相关系数(R)和稳定目标样本数(N)。其余各个通道的结果见表4。需要说明的是，除了稳定目标观测样本(Desert1，Desert2，Desert3和Sea)，卫星传感器的冷空观测值SV(Space View)也参与辐射定标计算中。


图 5 2014年8月16日FY-3A/MERSI与FY-3C/MERSI波段2(550 nm)多目标绝对辐射定标曲线(样本数据时间：2014-07-16—2014-08-16)
Fig. 5 Multi-targets radiometric calibration curve for FY-3A/MERSI and FY-3C/MERSI band2 on August 16, 2014 (samples time: 2014-07-16—2014-08-16)

表 4 2014年8月16日MERSI多目标绝对辐射定标系数
Table 4 Multi-targets calibration coefficients for MERSI on August 16, 2014

下载CSV 
波段 波长/nm FY-3A FY-3C
$k_i^1$ $k_i^0$ RMSE R $k_i^2$ $k_i^1$ $k_i^0$ RMSE R
1 470 0.0403 –11.0179 0.8446 0.996 –2.0334E–06 0.0377 –8.4481 0.7892 0.997
2 550 0.0311 –6.1810 0.9369 0.997 –2.1266E–06 0.0369 –7.0521 0.6664 0.999
3 650 0.0227 –3.1017 1.4029 0.996 –1.8684E–06 0.0332 –6.2120 0.6730 0.999
8 412 0.0395 –3.8615 1.0946 0.994 –2.9950E–07 0.0219 –3.4512 1.9316 0.984
9 443 0.0354 –1.9523 0.7876 0.997 –1.1694E–06 0.0287 –4.0966 0.7507 0.997
10 490 0.0296 –2.6070 0.9422 0.996 –1.2696E–06 0.0303 –6.6080 0.7033 0.998
11 520 0.0219 –1.2586 1.6351 0.989 –1.2323E–06 0.0300 –5.5354 0.7969 0.998
12 565 0.0237 –1.4217 0.9497 0.997 –1.2648E–06 0.0283 –5.1507 0.6544 0.999
13 650 0.0207 –1.1990 1.3790 0.996 –8.5411E–07 0.0261 –6.0750 0.7608 0.999
14 685 0.0216 –1.2971 0.8538 0.999 –1.1850E–06 0.0276 –3.6134 0.6921 0.999
15 765 0.0301 –2.4082 1.1711 0.998 –9.6973E–07 0.0255 –5.0943 0.6607 0.999
16 865 0.0219 –1.4739 0.9088 0.999 –1.2600E–06 0.0286 –3.1258 0.7347 0.999
17 905 0.0250 –1.7407 1.1388 0.997 –1.9400E–06 0.0313 –7.5483 0.8610 0.999
18 940 0.0302 –2.9371 0.6924 0.995 –3.6500E–06 0.0346 –4.2549 0.8561 0.993
19 980 0.0275 –3.4319 1.2424 0.997 –2.8500E–06 0.0373 –7.9137 1.0225 0.999
20 1030 0.0341 –2.0483 1.0076 0.999 –3.2500E–06 0.0397 –8.6739 1.0147 0.999

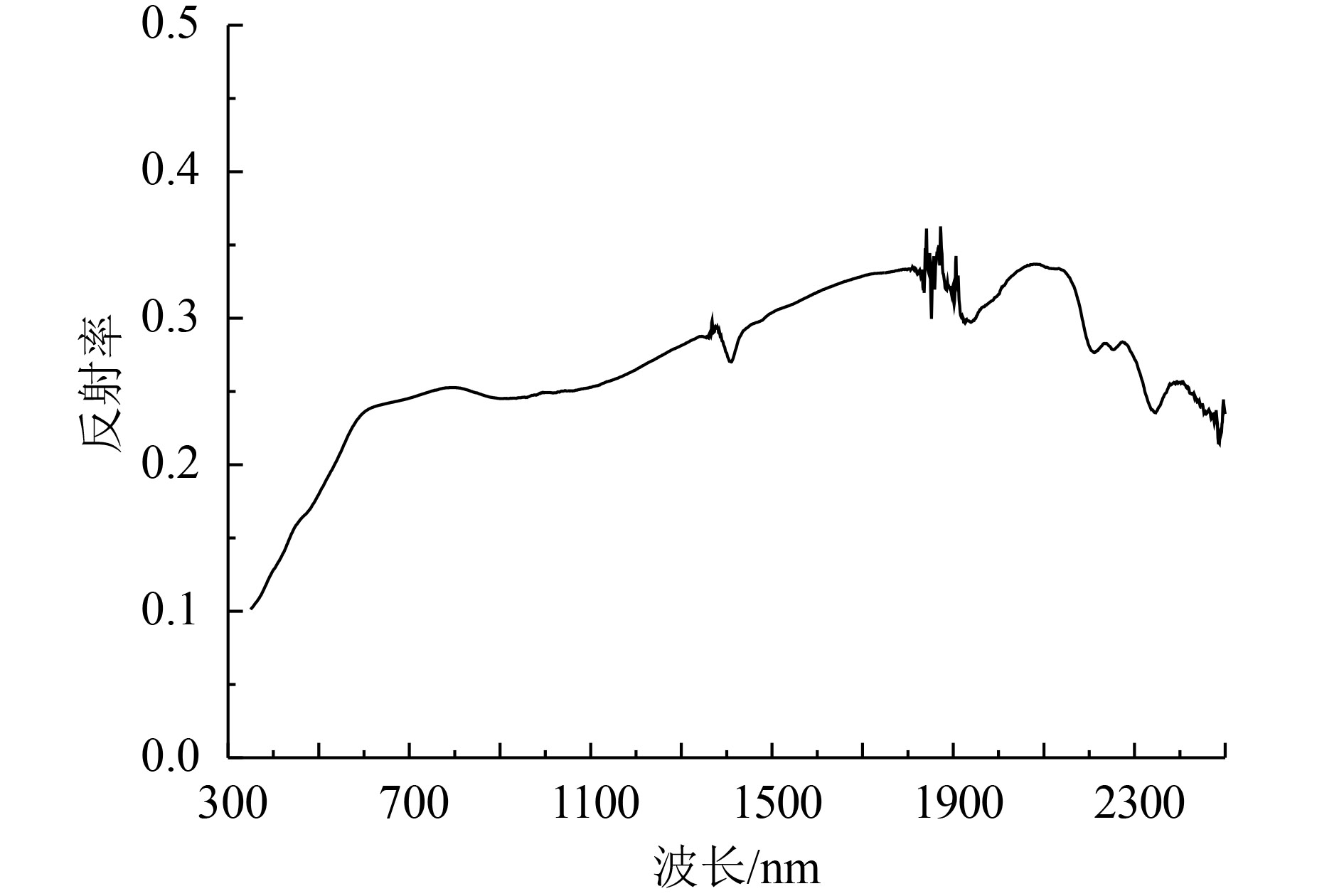
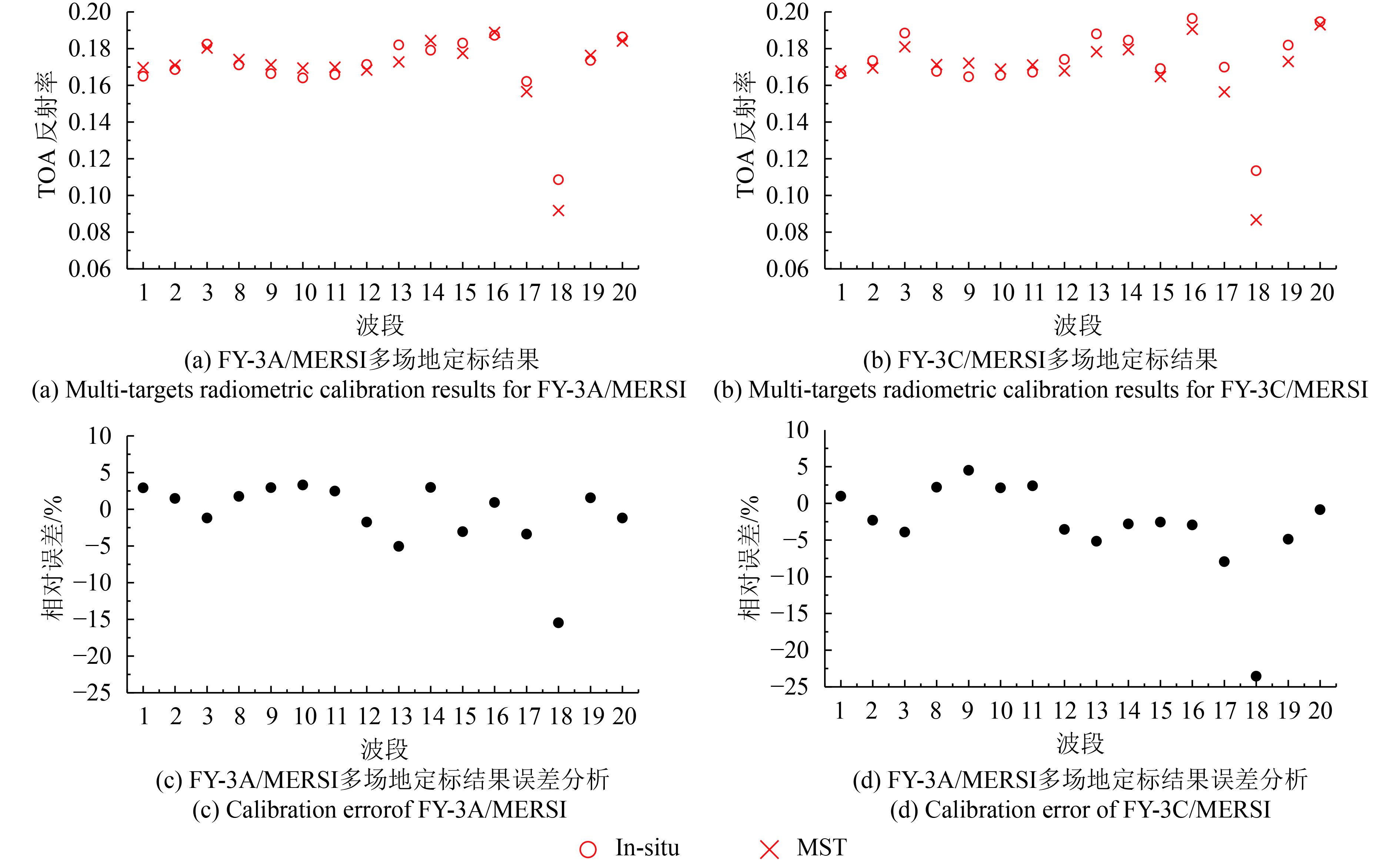
自2002年起，基于同步现场测量的敦煌场地替代定标法已成为风云系列卫星的业务定标手段，每年夏季都会开展一次同步定标观测试验，期间开展卫星过前后1 h的地表反射率、气溶胶光学特性、大气温湿度廓线等的测量。基于2014年8月16日同步观测的敦煌场地地表反射率(图6)和大气参数(表5)，结合卫星观测角度参数(表5)和波段响应函数，利用6 S辐射传输模型计算FY-3A/MERSI和FY-3C/MERSI过境时刻的大气顶表观反射率，作为绝对辐射定标系数检验的参考真值，间接对定标系数进行验证分析。FY-3A和FY-3C的计算结果分别在图7(a)和图7(b)中以红色空心圆表示。

表 5 2014年8月16日MERSI同步观测试验场地参数信息
Table 5 The in-situ measurement information on August 16, 2014 for MERSI

下载CSV 
日期 τa/(550 nm) 水汽/(g/cm2) 臭氧(DU) SolZ/(°) SenZ/(°) SolA/(°) SenA/(°)
FY-3A 0.096 0.888 285.2 40.8744 15.330 119.890 102.1189
FY-3C 0.116 0.888 285.2 30.6100 9.37 144.6822 –79.3156


图 6 2014年8月16日ASD同步测量的敦煌场地地表反射率光谱曲线
Fig. 6 Surface reflectance spectrum of Dunhuang obtained using ASD on August 16, 2014

基于多目标绝对辐射定标系数结果(表4)，反演2014年8月16日FY-3A和FY-3C MERSI在敦煌场地中心3×3窗口像元的大气顶表观反射率，计算结果分别在图7(a)和图7(b)中以红色×表示。与基于野外同步观测试验的结果相比，基于多目标绝对辐射定标系数反演的表观反射率与参考真值有高度一致性和很好的相关性，且两者的相对差异较小(图7(c)和图7(d))。除了波段18(940 nm)的平均相对偏差较大(~20%)外，其他通道基本都在5%以内。波段18辐射定标结果精度较差可能与该波段为水汽强烈吸收，大气透过率计算偏差较大有关。多场地辐射定标方法的水汽含量参数来源于MODIS大气产品，而野外观测的水汽含量来源于探空气球，两者之间会存在一定的差异，因此对于水汽敏感通道，辐射传输模型计算值会存在一定的偏差，而对于非水汽吸收通道，这一影响相对较小。


图 7 敦煌沙漠场地MERSI多目标绝对辐射定标结果(MST)和以及基于野外同步观测资料模拟结果(In-situ)对比
Fig. 7 Multi-targets radiometric calibration results for MERSI over Dunhuang desert and comparison with the reflectance calculated using the in-situ measurements

4.3 讨　论

为进一步说明文中给出的辐射定标方案的合理性，这里将采用与4.2节不同的辐射定标方案，对FY-3A/MERSI和FY-3C/MERSI进行定标处理，并将辐射定标结果与敦煌野外同步观测试验的结果进行对比验证。图8与图5类似，给出的是FY-3A和FY-3C MERSI波段2(550 nm)的辐射定标结果。但图8采用的辐射定标方案与图5不同：对FY-3A/MERSI，这里采用的是非线性辐射定标方案，FY-3C/MERSI则是线性辐射定标方案。与图5对比可以发现，对于FY-3A/MERSI，线性和非线性辐射定标方法的RMSE差异较小，线性定标方案的RMSE为0.937(图5(a))，非线性定标方案为0.948(图8(a))，非线性定标方案略高0.011；而FY-3C/MERSI的线性和非线性辐射定标方法的RMSE差异较大，线性定标方案为0.917(图8(b))，非线性定标方案为 0.666(图5(b))，线性定标方案比非线性定标方案高0.255。其他波段不同定标方案的RMSE对比如图9所示。由图9可以看出，其他波段不同定标方案的RMSE差异情况与波段2类似，即FY-3A/MERSI的线性和非线性辐射定标方法的RMSE差异较小(图9(a))，除了波段11略高于0.1外，其他波段都在0.1以内(图9(c))；FY-3C/MERSI的线性和非线性辐射定标方法的RMSE差异，除了波段18外，其他波段都高于0.1(图9(c))。


图 8 2014年8月16日FY-3A/MERSI波段2(550 nm)非线性定标曲线与FY-3C/MERSI线性辐射定标曲线(2014-07-16—2014-08-16)
Fig. 8 Nonlinear radiometric calibration curve for FY-3A/MERSI and linear calibration curve for FY-3C/MERSI of band2 on Aug. 16 2014 (2014-07-16—2014-08-16)


图 9 2014年8月16日MERSI反射太阳波段线性和非线性定标方案的RMSE对比
Fig. 9 RMSE comparison between linear and nonlinear calibration methods for MERSI reflective solar bands on August 16, 2014

与4.2节类似，图10(a)给出了FY-3A/MERSI采用非线性定标方案及FY-3C/MERSI采用线性定标方案对应的定标精度。当FY-3A/MERSI采用非线性定标方案时，除了水汽强吸收通道-波段18外，其他波段的定标精度均在5%以内。但是，当FY-3C/MERSI采用线性定标方案时，16个反射率太阳波段中，仅有5个波段(约占31%)的定标精度在5%以内(5%是目前国际上对卫星传感器反射太阳波段定标精度的最低要求)，大部分波段的定标精度绝约为7%—10%。将这里的标结果精度与图7定标结果精度相比，可以发现，对于FY-3A/MERSI两种定标方案之间的精度差异较小，除了波段16和波段20差异约为4%外，其他波段的差异均在±2%以内(图10(c))。但是，对于FY-3C/MERSI两种定标方案之间的精度差异较大，只有少数波段(波段1—2，波段8—9，波段18—19)的差异在±2%以内，绝大数波段的差异约为4%—5%，特别是波段19和波段20，定标精度的差异可达8%左右，是定标精度要求(5%)的1.6倍。这一结果与4.1节对MERSI辐射响应特性的分析结果(图3)有很好的一致性。4.1节的分析表明，FY-3A/MERSI的反射太阳波段的非线性特性不明显，因此，线性定标方案和非线性定标方案的定标精度差异较小；而FY-3C/MERSI大部分通道都具有非线性特性，这就解释了两种辐射定标方案的定标精度差异大以及当采用线性定标方案时，难以获得理想的定标精度较大的原因。


图 10 FY-3A/MERSI非线性定标方案的精度及与线性定标精度的差异和FY-3C/MERSI线性定标方案的定标精度及与非线性定标精度的差异
Fig. 10 Nonlinear calibration accuracy for FY-3A/MERSI and calibration accuracy difference between linear calibration, and linear calibration accuracy for FY-3C/MERSI and calibration accuracy difference between the nonlinear calibration

5 结　论

利用位于全球范围内的盐湖、沙漠、海洋等15个不同亮度等级的稳定目标，结合MODIS和NCEP的地表、大气参数产品，基于大气辐射传输模型对卫星通道大气顶光谱辐射的模拟计算，建立了卫星传感器反射太阳波段宽动态非线性辐射定标的方法。并以具有高定标精度的MODIS数据为参考，评估了该方法提供的定标基准的精度。最后，以搭载在气象卫星FY-3A和FY-3C上的MERSI遥感器为例，对其反射太阳波段进行了辐射响应特性分析和绝对辐射定标实验。研究结果表明：

(1) 通过使用盐湖、沙漠、海洋等多种亮度稳定目标可以更好的覆盖感器的动态范围。MODIS大气顶表观反射率模拟结果显示，表观反射率取值范围较大：最小值基本可到0.1以下(波段7除外)；最大值随波长的增加呈递增趋势：即，蓝(band3)、绿(band4)波段最小，约为0.5，近红外(band2)和短波红外波段(band5—7)最大，约为0.7，红波段(band6)居中。

(2) 该方法以大气辐射传输模型的卫星通道大气顶辐射值为定标基准，且模型输入参数全部来源于卫星和气候数据集，避免了场地同步测量，可以实现卫星传感器高效、实时的绝对辐射定标。同时，该方法的定标基准具有较高精度，对于MODIS反射太阳波段范围内的7个波段，大气顶辐射模拟值与观测值间的偏差均值在2%以内。

(3) 基于多目标宽动态非线性定标方法获得了FY-3A/MERSI和FY-3C/MERSI反射太阳通道的辐射响应特性及辐射定标方案。FY-3A/MERSI的反射太阳波段的非线性特性不明显，可采用传统的线性辐射定标方案；而FY-3C/MERSI大部分通道都具有非线性特性，其中，波段11，波段16，波段20最为显著，需采用非线性辐射定标方案。基于敦煌场地同步实验的验证结果显示该方法具有较高的定标精度，除了波段18(940 nm)较差(~20%)外，其他通道基本都在5%以内。

需要在下一步工作中解决的问题有：(1)在定标样本中，增加较短波长(<600 nm)处具有高反射率的稳定目标，如格林兰(Greenland)冰雪稳定目标，进一步提高较短波长处定标样本的反射率动态范围；(2)该方法的定标基准是大气辐射传输模型计算的卫星通道大气顶辐射值，因此辐射传输模型的输入参数精度直接影响定标基准精度，如何提高输入参数的精度，尤其地表反射率参数和水汽参数，需进一步研究。

志 谢 文中使用的MODIS数据来源于NSAA的LAADS Web网站，NCEP数据来源于NOAA的ESRL网站，在此表示感谢！

参考文献(References)

  • Chander G, Xiong X X, Choi T and Angal A. 2010. Monitoring on-orbit calibration stability of the Terra MODIS and Landsat 7 ETM+ sensors using pseudo-invariant test sites. Remote Sensing of Environment, 114 (4): 925–939. [DOI: 10.1016/j.rse.2009.12.003]
  • Chen L, Xu N, Li Y, Wu R H, Xu X Q and Zhang P. 2014. FY-3C/MERSI pre-launch calibration for reflective solar bands//Proceedings of SPIE Earth Observing Missions and Sensors: Development, Implementation, and Characterization III. Beijing, China: SPIE, 9264: 92640Z [DOI: 10.1117/12.2070397]
  • Cosnefroy H, Leroy M and Briottet X. 1996. Selection and characterization of Saharan and Arabian desert sites for the calibration of optical satellite sensors. Remote Sensing of Environment, 58 (1): 101–114. [DOI: 10.1016/0034-4257(95)00211-1]
  • Dinguirard M and Slater P N. 1999. Calibration of space-multispectral imaging sensors: a review. Remote Sensing of Environment, 68 (3): 194–205. [DOI: 10.1016/S0034-4257(98)00111-4]
  • Gao C X, Jiang X G, Ma L L and Huo H Y. 2013. Review of radiometric cross-calibration. Arid Land Geography, 36 (1): 139–146. ( 高彩霞, 姜小光, 马灵玲, 霍红元. 2013. 传感器交叉辐射定标综述. 干旱区地理, 36 (1): 139–146. )
  • Gong H, Tian G L, Yu T, Gu X F, Gao H L and Li X Y. 2010. Vicarious radiometric calibration and validation of CBERS02B CCD data. Journal of Remote Sensing, 14 (1): 1–12. [DOI: 10.11834/jrs.20100101] ( 巩慧, 田国良, 余涛, 顾行发, 高海亮, 李小英. 2010. CBERS02B卫星CCD相机在轨辐射定标与真实性检验. 遥感学报, 14 (1): 1–12. [DOI: 10.11834/jrs.20100101] )
  • Govaerts Y M, Clerici M and Clerbaux N. 2004. Operational calibration of the Meteosat radiometer VIS band. IEEE Transactions on Geoscience and Remote Sensing, 42 (8): 1900–1914. [DOI: 10.1109/TGRS.2004.831882]
  • Gu X F, Tian G L, Yu T, Li X Y, Gao H L and Xie Y. 2013. Radiation Calibration of the Space-Based Optical Satellite Sensor: Principle and Method. Beijing: Science Press: 6–11 (顾行发, 田国良, 余涛, 李小英, 高海亮, 谢勇. 2013. 航天光学遥感器辐射定标原理与方法[M]. 北京: 科学出版社: 6–11)
  • Han Q J, Fu Q Y, Pan Z Q, Wang A C and Zhang X W. 2013. Absolute radiometric calibration and validation analysis of ZY-3 using artificial targets. Infrared and Laser Engineering, 42 (S1): 167–173. [DOI: 10.3969/j.issn.1007-2276.2013.z1.033] ( 韩启金, 傅俏燕, 潘志强, 王爱春, 张学文. 2013. 资源三号卫星靶标法绝对辐射定标与验证分析. 红外与激光工程, 42 (S1): 167–173. [DOI: 10.3969/j.issn.1007-2276.2013.z1.033] )
  • Han Q J, Zhang X W, Qiao Z Y, Yang L, Pan Z Q and Liu L. 2015. Wide dynamic radiometric calibration of GF-1 PMS sensors using multi-test sites. Infrared and Laser Engineering, 44 (1): 127–133. [DOI: 10.3969/j.issn.1007-2276.2015.01.023] ( 韩启金, 张学文, 乔志远, 杨磊, 潘志强, 刘李. 2015. 高分一号卫星PMS相机多场地宽动态辐射定标. 红外与激光工程, 44 (1): 127–133. [DOI: 10.3969/j.issn.1007-2276.2015.01.023] )
  • Helder D, Thome K J, Mishra N, Chander G, Xiong X X, Angal A and Choi T. 2013. Absolute radiometric calibration of Landsat using a pseudo invariant calibration site. IEEE Transactions on Geoscience and Remote Sensing, 51 (3): 1360–1369. [DOI: 10.1109/TGRS.2013.2243738]
  • Hu X Q, Liu J J, Qiu K M, Fan T X, Zhang Y X, Rong Z G and Zhang L J. 2009. New method study of sites vicarious calibration for SZ-3/CMODIS. Spectroscopy and Spectral Analysis, 29 (5): 1153–1159. [DOI: 10.3964/j.issn.1000-0593(2009)05-1153-04] ( 胡秀清, 刘京晶, 邱康睦, 范天锡, 张玉香, 戎志国, 张立军. 2009. 神舟3号飞船中分辨率成像光谱仪场地替代定标新方法研究. 光谱学与光谱分析, 29 (5): 1153–1159. [DOI: 10.3964/j.issn.1000-0593(2009)05-1153-04] )
  • Hu X Q, Sun L, Liu J J, Ding L, Wang X H, Li Y, Zhang Y, Xu N and Chen L. 2012. Calibration for the solar reflective bands of medium resolution spectral imager onboard FY-3A. IEEE Transactions on Geoscience and Remote Sensing, 50 (12): 4915–4928. [DOI: 10.1109/TGRS.2012.2214226]
  • Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Leetmaa A, Reynolds R, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo K C, Ropelewski C, Wang J, Jenne R and Joseph D. 1996. The NCEP/NCAR 40-year reanalysis project. Bulletin of the American Meteorological Society, 77 (3): 437–471. [DOI: 10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2]
  • Kim W, Cao C Y and Liang S L. 2014. Assessment of radiometric degradation of FY-3A MERSI reflective solar bands using TOA Reflectance of pseudoinvariant calibration sites. IEEE Geoscience and Remote Sensing Letters, 11 (4): 793–797. [DOI: 10.1109/LGRS.2013.2279134]
  • Masonis S J and Warren S G. 2001. Gain of the AVHRR visible channel as tracked using bidirectional reflectance of Antarctic and Greenland snow. International Journal of Remote Sensing, 22 (8): 1495–1520. [DOI: 10.1080/01431160121039]
  • Mishra N, Helder D, Angal A, Choi J and Xiong X X. 2014. Absolute calibration of optical satellite sensors using Libya 4 pseudo invariant calibration site. Remote Sensing, 6 (2): 1327–1346. [DOI: 10.3390/rs6021327]
  • Smith D L, Mutlow C T and Rao C R N. 2002. Calibration monitoring of the visible and near-infrared channels of the Along-Track Scanning Radiometer-2 by use of stable terrestrial sites. Applied Optics, 41 (3): 515–523. [DOI: 10.1364/AO.41.000515]
  • Sun L, Hu X Q, Guo M H and Xu N. 2013. Multisite calibration tracking for FY-3A MERSI solar bands. Advances in Meteorological Science and Technology, 3 (4): 84–96. [DOI: 10.3969/j.issn.2095-1973.2013.04.009] ( 孙凌, 胡秀清, 郭茂华, 徐娜. 2013. 风云三号A星中分辨率光谱成像仪反射太阳波段的多场地定标跟踪. 气象科技进展, 3 (4): 84–96. [DOI: 10.3969/j.issn.2095-1973.2013.04.009] )
  • Tang J W, Gu X F, Niu S L, Ma C F and Min X J. 2005. Water target based cross-calibration of CBERS-02 CCD camera with MODIS data. Science in China Series E Engineering and Materials Science, 35 (SI): 61–71. [DOI: 10.3321/j.issn:1006-9275.2005.z1.005] ( 唐军武, 顾行发, 牛生丽, 马超飞, 闵祥军. 2005. 基于水体目标的CBERS-02卫星CCD相机与MODIS的交叉辐射定标. 中国科学E辑-信息科学, 35 (SI): 61–71. [DOI: 10.3321/j.issn:1006-9275.2005.z1.005] )
  • Teillet P M, Barsi J A, Chander G and Thome K J. 2007. Prime candidate earth targets for the post-launch radiometric calibration of space-based optical imaging instruments//Proceedings of SPIE 6677, Earth Observing System XII. San Diego, CA, USA: SPIE [DOI: 10.1117/12.733156]
  • Tian Q J, Zheng L F and Tong Q X. 1998. Comparison and analysis for in-flight calibration of SPOTBased on methods of test site and on-boarding calibration. Journal of Remote Sensing, 2 (1): 13–18. [DOI: 10.11834/jrs.19980103] ( 田庆久, 郑兰芬, 童庆禧. 1998. SPOT地面场定标与星上定标结果的比较分析. 遥感学报, 2 (1): 13–18. [DOI: 10.11834/jrs.19980103] )
  • Vermote E F, Tanré D, Deuzé J L, Herman M and Morcette J J. 1997. Second simulation of the satellite signal in the solar spectrum, 6S: an overview. IEEE Transactions on Geoscience and Remote Sensing, 35 (3): 675–686. [DOI: 10.1109/36.581987]
  • Wang L, Hu X Q and Chen L. 2015. FY-3C/MERSI calibration for solar band using multi-reflectance stable targets. Optics and Precision Engineering, 23 (7): 1911–1920. [DOI: 10.3788/OPE.20152307.1911] ( 王玲, 胡秀清, 陈林. 2015. 基于多种亮度稳定目标的FY-3C/中分辨率光谱成像仪的反射太阳波段辐射定标. 光学 精密工程, 23 (7): 1911–1920. [DOI: 10.3788/OPE.20152307.1911] )
  • Xiong X X, Sun J Q, Barnes W, Salomonson V, Esposito J, Erives H and Guenther B. 2007. Multiyear on-orbit calibration and performance of Terra MODIS reflective solar bands. IEEE Transactions on Geoscience and Remote Sensing, 45 (4): 879–889. [DOI: 10.1109/TGRS.2006.890567]
  • Xu N, Chen L, Wu R H, Hu X Q, Sun L and Zhang P. 2014. In-flight intercalibration of FY-3C visible channels with AQUA MODIS. Proceedings of SPIE Earth Observing Missions and Sensors: Development, Implementation, and Characterization III. Beijing, China: SPIE, 9264: 926408 [DOI: 10.1117/12.2071185]
  • Zhang P, Yang H, Qiu H, Ma G, Yang Z D, Lu N M and Yang J. 2012. Quantitative remote sensing from the current Fengyun 3 satellites. Advances in Meteorological Science and Technology, 2 (4): 6–11. [DOI: 10.3969/j.issn.2095-1973.2012.04.001] ( 张鹏, 杨虎, 邱红, 马刚, 杨忠东, 卢乃锰, 杨军. 2012. 风云三号卫星的定量遥感应用能力. 气象科技进展, 2 (4): 6–11. [DOI: 10.3969/j.issn.2095-1973.2012.04.001] )
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体