|
收稿日期: 2017-01-19; 优先数字出版日期: 2017-11-01
基金项目: 全球变化与海汽相互作用专项(编号:GASI-03-03-01-01)
第一作者简介: 王梅竹(1991— ),女,博士研究生,研究方向为海洋遥感、图像消旋以及图像拼接。E-mail:wangmeizhu2013@163.com
通讯作者简介: 冯旗(1964— ),男,研究员,研究方向为航天光电遥感系统。E-mail:fengqi168@vip.sina.com
中图分类号: TP73
文献标识码: A
|
摘要
极轨海洋卫星的时间分辨率低,不能及时感知快速变化的海洋现象及海洋突发事件,因此,发展静止轨道海洋成像辐射计势在必行。静止轨道卫星可以长时间观测指定海域,但是视场小,需要通过二维指向镜等方式扩大卫星的观测区域。本文意在通过提出漏扫判断方法,给出合理的扫描方式,保证高轨面阵扫描无地理信息遗漏。首先,本文在分析二维指向镜成像原理的基础上,给出了指向镜子图像成像特性以及不同方向、大小的电机转角所引入的像面旋转。其次,画出了子图像的边界包络图,直观地给出了扫描角度变化与图像覆盖程度的关系。最后,提出了两种无缝拼接的判断方法:栅格法和几何相交法,栅格法能够判断出图像覆盖次数,几何法速度快、准确度高。实验结果表明应用本文的两种方法得到了不同扫描角度间隔下地球边缘有无漏扫的情况,找到基于本文光学系统、可覆盖全球且无缝拼接图像的最大俯仰、方位转角间隔,为电机转角步距的设置提供理论依据,保证不漏扫的同时提高载荷的时间分辨率。
关键词
像旋, 无缝, 静止轨道, 二维指向镜, 漏扫
Abstract
Geostationary satellites can perform high-frequency observation in the same area of the Earth. To extend the area of observation, we use a two-dimensional pointing mirror combined with a frame sensor. A two-dimensional pointing mirror can acquire image information in a short time, and its small volume and low weight render it an appropriate device loaded on the satellite. However, imaging theory of the pointing mirror indicates that image rotation and non-linear error reduce the geometric accuracy of image and may cause missing scans. To address the problem, we first analyze the imaging characteristics of each slot and calculate the rotation angle. We numerically analyze different types of angular error introduced from pitch and azimuth rotation. Then, we propose a mechanism by which the pointing angle affects image coverage. We provide a flow chart of cover rate analysis and figures showing the cover area of different pointing angles. Boundary diagrams of slots are drawn to display the relationship between angular variations and cover rate. After numerical analysis, we find a better way to observe the Northern Hemisphere. Then, we develop two judging methods of seamless stitching: grid method and geometric intersection method. The grid method is used to grid the pointing plane and label cover time on each grid point, whereas the geometric intersection method is used to determine whether the image information is missing on the basis of intersecting relations of the slot envelope. Different situations of geometric intersection are listed. The two methods are also compared. The grid method can determine the coverage time, and the geometric method has great advantages of speed and accuracy. Finally, the two methods have been used to obtain the cover situation of the edge of the Earth at different scanning angles, to find the maximum pitch and azimuth angle interval of the proposed optical system, which can cover the global area and seamless splicing images. When the point mirror is rotating in azimuth, image rotation is more obvious with an increase in motor angle. When the mirror is rotating in pitch, the rotation angle increases with a decrease in pitch angle. Thus, the relative location of the follow-up optical elements should be considered to obtain a low rotation angle of key observation area. This process provides the theoretical basis for setting the turning step of the motor and ensures that the time resolution of the load is increased without geometric information leakage.
Key words
image rotation, seamless, geostationary, two-dimensional pointing mirror, missing scan
1 引 言
与极轨卫星相比,地球静止轨道遥感卫星可以对同一区域进行高频次观测,从而提高观测的时间分辨率。由于受探测器像素规模、光学系统视场限制,需要依靠扫描镜或指向镜扩大观测范围,目前采用的方案基本为两类:线列探测器推扫结合二维扫描;面阵探测器凝视结合二维指向(周世椿,2010)。
线列结合二维扫描的方式包括自旋加步进的对地二维扫描和双扫描镜机械扫描,双扫描镜机械扫描方式为东西往复式扫描、南北步进式扫描(王淦泉和陈桂林,2014;殷东羽,2016;惠彬 等,2005)。本文采用的面阵探测器结合二维指向的方式是通过一面指向镜俯仰、方位两个方向的旋转,指向待观测的区域,通过改变指向镜的两维电机转角进行成像,并对成像子图像拼接,扩大卫星观测范围。二维指向镜方式可在短时间内获取指定位置图像信息,体积小,重量轻。但是,当指向镜绕两坐标轴旋转时,系统视轴和电机转角存在非线性关系,指向镜反射后的图像,有像旋。
很多研究工作曾围绕此类问题展开。扫描轨迹的非线性最初在双轴检流扫描计中提出(Pelsue,1983),在两轴转动的光学扫描仪中被重视。Hafez和Sidler(1999;Hafez 等,2003)、杨志卿等人(2004)提出了轨迹非线性偏差函数和补偿方法。像旋问题则在摆扫结合45度镜(张锷和龚惠兴,1999;孙德新和王建宇,2005;陈强 等,2012;张树青 等,2014)、推扫结合二维扫描镜(惠彬 等,2005;王武 等,2015)以及凝视结合二维指向镜(李淑英和周世椿,2008;吴凡和王大鹏,2009)中均有出现。像旋的存在,会使像面畸变,特征错位(王昱 等,2012),原本完全覆盖的多块扫描区域内出现漏扫点。
因此,本文在分析扫描非线性和像旋对静止卫星二维指向成像影响的基础上,对扫描角度变化与图像覆盖程度的关系进行了研究,提出无缝扫描判断方法,保证在存在像旋的情况下,合理调整电机转角,使多幅图像的拼接图无地理信息遗漏,且覆盖面积大、扫描效率高。提高载荷扫描效率,即可以提高静止卫星的时间分辨率,这是静止卫星的关键参数之一。
2 二维指向镜成像分析
2.1 二维指向镜工作原理
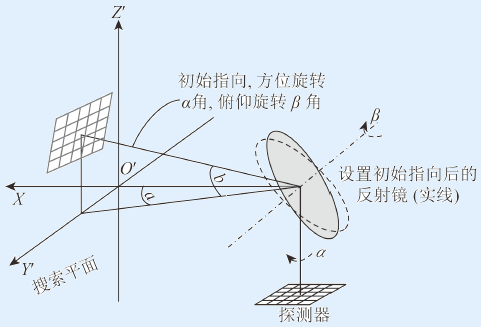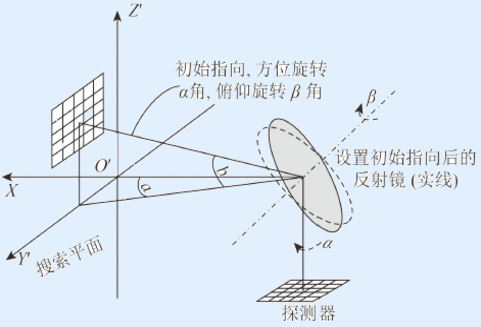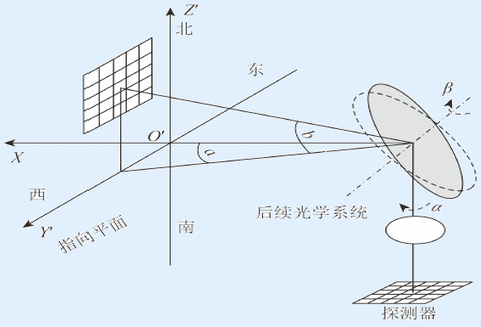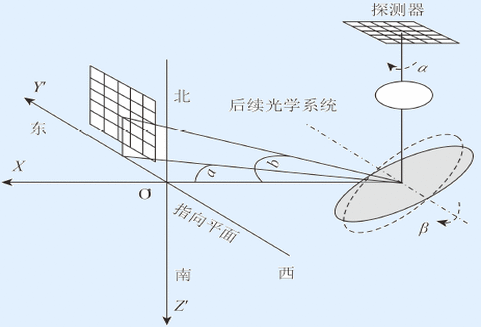
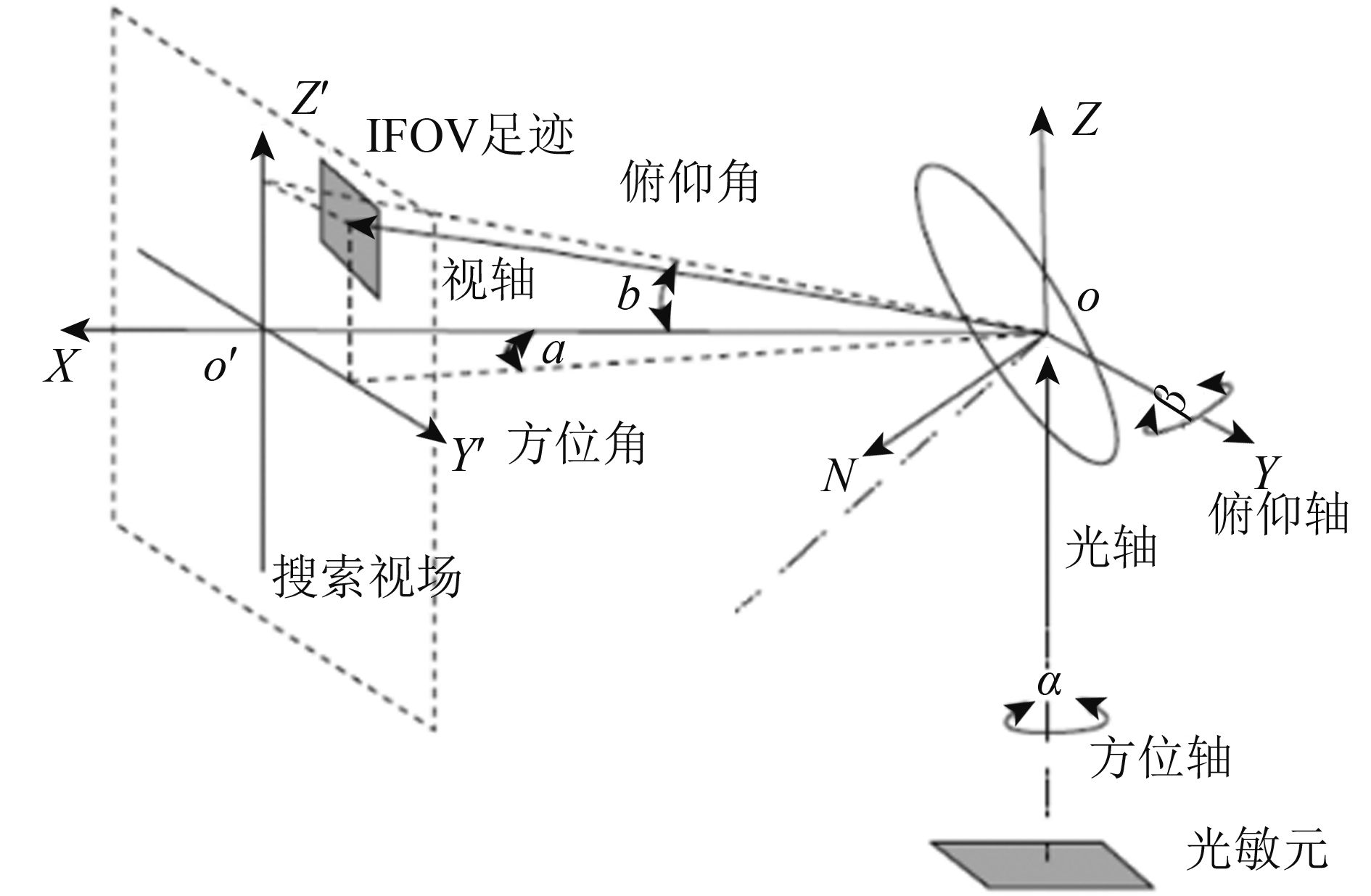
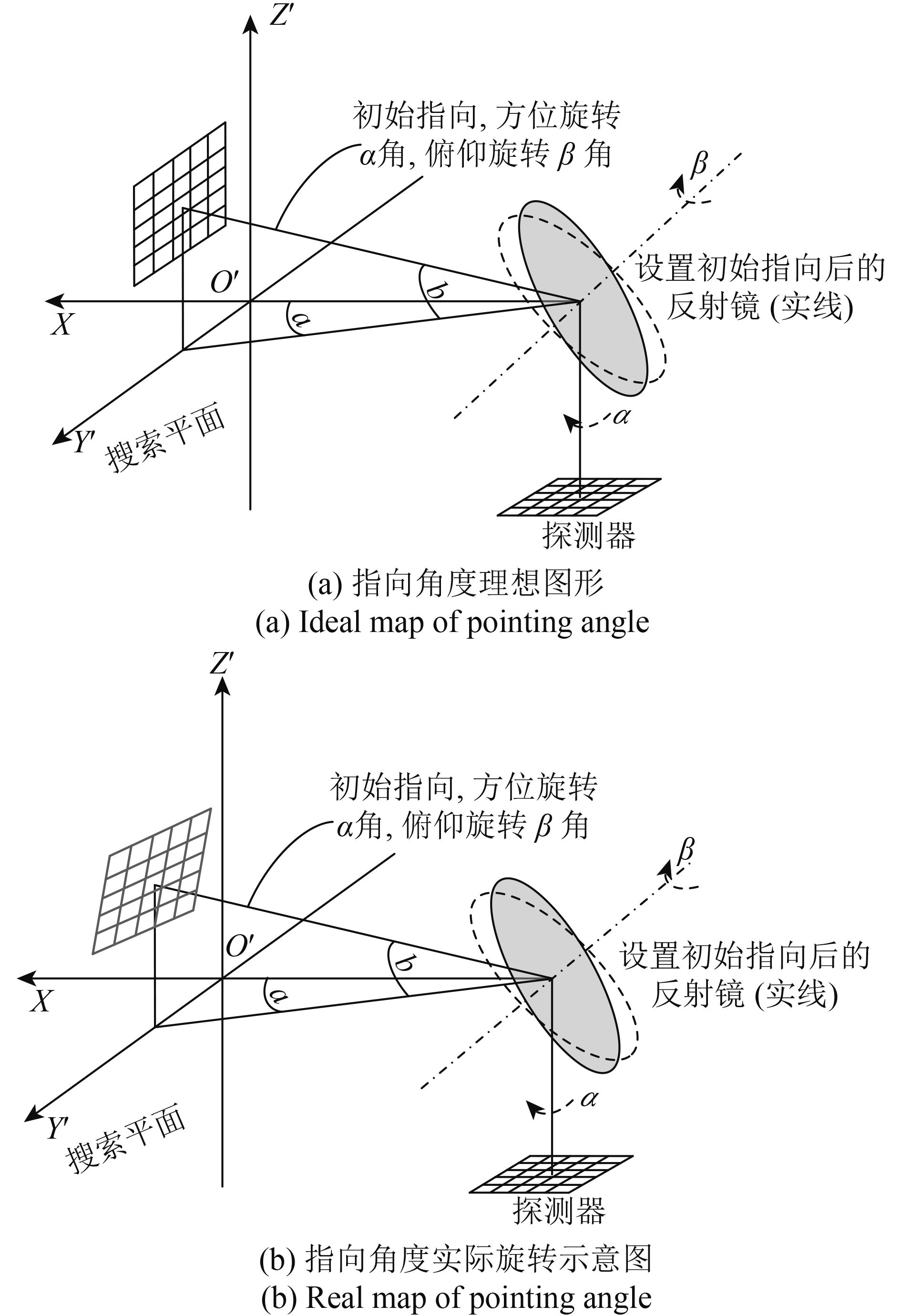
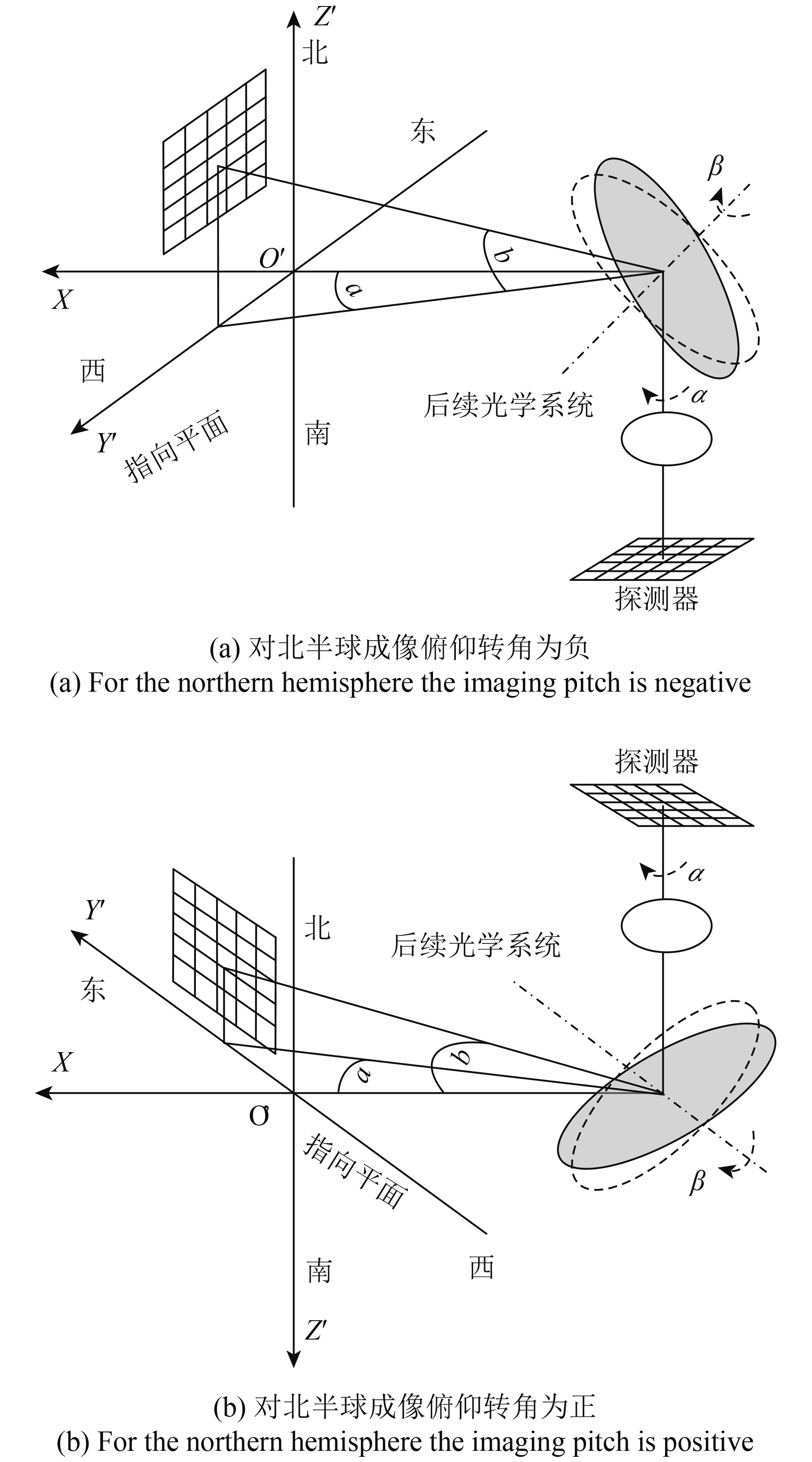
如图1所示,Y’O’Z’组成的平面为指向平面,即物面;光敏元为像面。
根据光路可逆,实际计算中,由于光敏元是标准的矩形,可将其当作物,由光敏元经反射镜反射到在指向平面对应的图像可视为像,这样便于得到光敏元的地面覆盖区域示意图。
图1中椭圆形为二维指向镜,它可以绕Y轴、Z轴旋转,O点位于镜面中心位置。其中,Y轴为俯仰轴,Z轴为方位轴,光轴与Z轴重合,经指向镜反射后的光线称为视轴,视轴随指向镜的旋转而发生变化,视轴与指向视场的交点为扫描轨迹。
指向镜电机转角分别为:α—绕方位轴Z转动,方位转角;β—绕俯仰轴γ转动,俯仰转角。α、β的正方向均符合右手螺旋定则。
视轴指向角分别为:a—方位角,视轴在水平面投影与X轴夹角;b—俯仰角,视轴在垂直面投影与X轴夹角。
假设二维指向镜法向量
|
${{R}} = \left( {\begin{array}{*{20}{c}}{1 - 2N_x^2}&{ - 2{N_x}{N_y}}&{ - 2{N_x}{N_z}}\\[5pt]{ - 2{N_x}{N_y}}&{1 - 2N_y^2}&{ - 2{N_y}{N_z}}\\[5pt]{ - 2{N_x}{N_z}}&{ - 2{N_y}{N_z}}&{1 - 2N_z^2}\end{array}} \right)$
|
(1) |
则矢量A经二维指向镜反射后的出射矢量为
|
${{R}} = \left( {\begin{array}{*{20}{c}}0&0&1\\[5pt]0&1&0\\[5pt]1&0&0\end{array}} \right)$
|
(2) |
假设指向镜绕单位矢量
|
${{{S}}_{P,\theta }} = \left( {\begin{array}{*{20}{c}}{\cos \theta + 2P_x^2{{\sin }^2}\theta /2}&{ - {P_z}\sin \theta + 2{P_x}{P_y}{{\sin }^2}\theta /2}&{{P_z}\sin \theta + 2{P_x}{P_y}{{\sin }^2}\theta /2}\\{{P_z}\sin \theta + 2{P_x}{P_y}{{\sin }^2}\theta /2}&{\cos \theta + 2P_y^2{{\sin }^2}\theta /2}&{ - {P_x}\sin \theta + 2{P_z}{P_y}{{\sin }^2}\theta /2}\\{ - {P_y}\sin \theta + 2{P_x}{P_z}{{\sin }^2}\theta /2}&{{P_x}\sin \theta + 2{P_z}{P_y}{{\sin }^2}\theta /2}&{\cos \theta + 2P_y^2{{\sin }^2}\theta /2}\end{array}} \right)$
|
(3) |
当指向镜绕Z轴转动α,Y轴转动β时,可得到坐标转换矩阵G10。
|
$\begin{aligned}{{{G}}_{10}} = & {{{S}}_{k,\alpha }} \cdot {{{S}}_{j,\beta }} = \\ &\left( {\begin{array}{*{20}{c}}{\cos \alpha \cos \beta }&{ - \sin \alpha }&{\cos \alpha \sin \beta }\\[5pt]{\sin \alpha \cos \beta }&{\cos \alpha }&{\sin \alpha \sin \beta }\\[5pt]{ - \sin \beta }&0&{\cos \beta }\end{array}} \right)\end{aligned}$
|
(4) |
假设A经由已转动α、β角的二维指向镜反射,其出射矢量
|
${{A'}} = ({{{G}}_{10}} \cdot {{R}} \cdot {{G}}_{10}^{ - 1}) \cdot {{A}}$
|
(5) |
2.2 扫描轨迹
假设光轴
2.3 子图像特性
根据1.1节中的假设,光敏元经一定角度的二维指向镜反射,在指向平面内对应的区域为子图像。由于
为量化像面旋转,本文用视轴的偏转角作为像旋角。取
|
${{OP'}} = \left( {\begin{array}{*{20}{c}}{ - {{\cos }^2}\alpha \sin 2\beta - {{\sin }^2}\alpha }\\[5pt]{ - \sin 2\alpha \left( {\sin 2\beta - 1} \right)/2}\\[5pt]{ - \cos \alpha \cos 2\beta }\end{array}} \right)$
|
(6) |
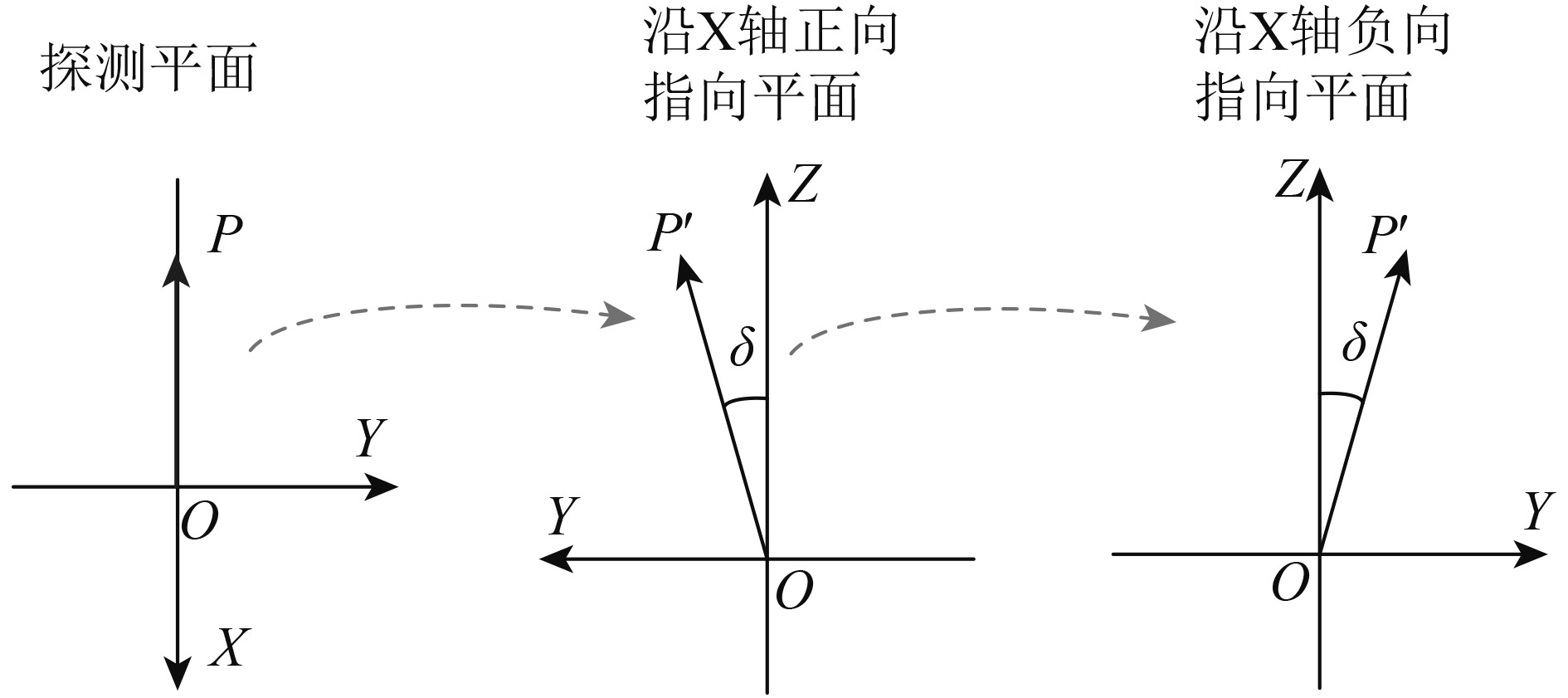
如图3所示,OP′与Z轴正方向的夹角δ为像旋角,像旋角的正负由正切值决定
|
$\tan \delta = \frac{{O{{P'}_y}}}{{O{{P'}_z}}} = \frac{{\sin \alpha (\sin 2\beta - 1)}}{{\cos 2\beta }}$
|
(7) |
由式(7)可得出:
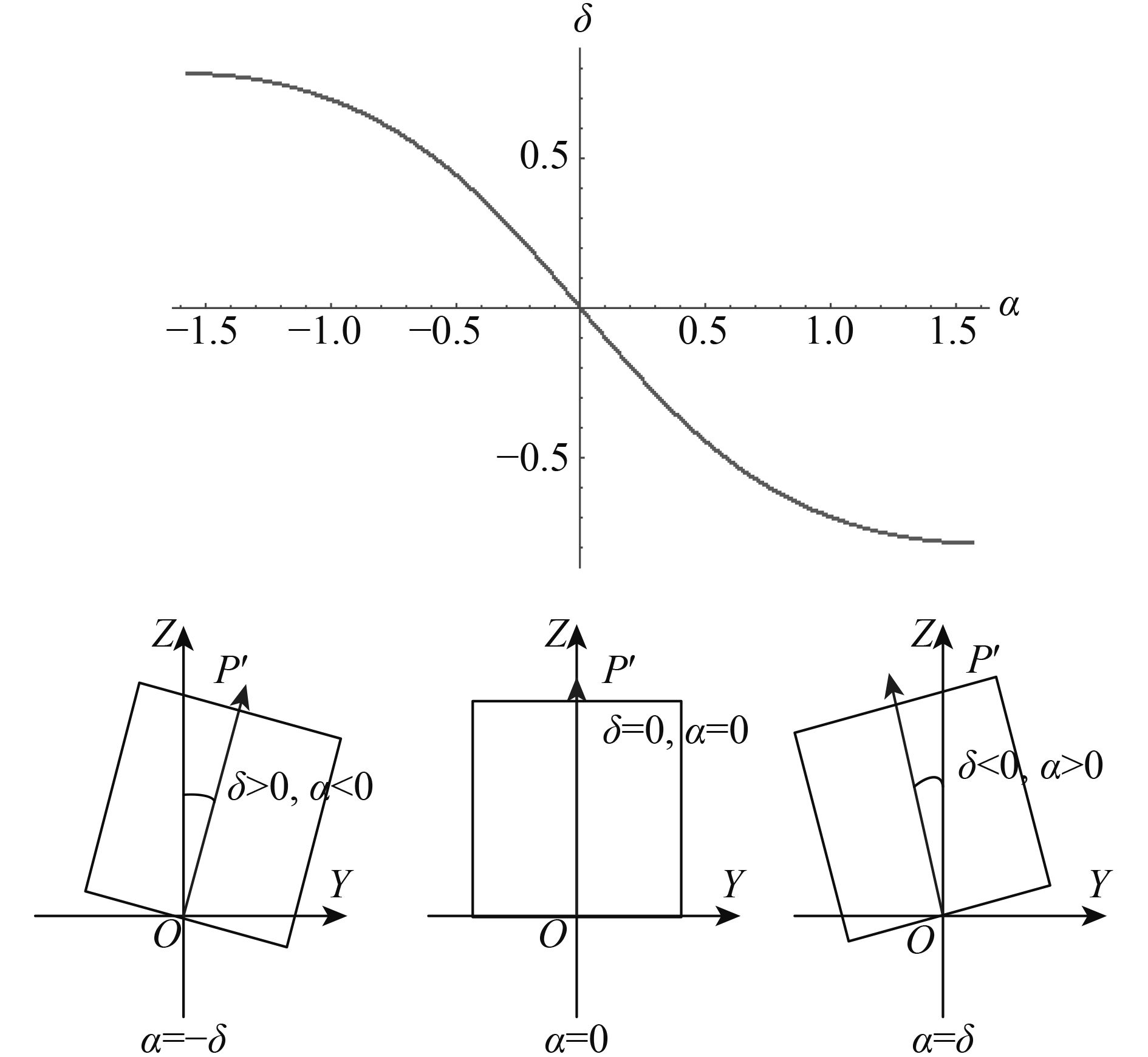
(1) α=0处无像旋,即当指向镜方位转角为零,只进行俯仰扫描时,不存在像旋。
(2) β=0时,
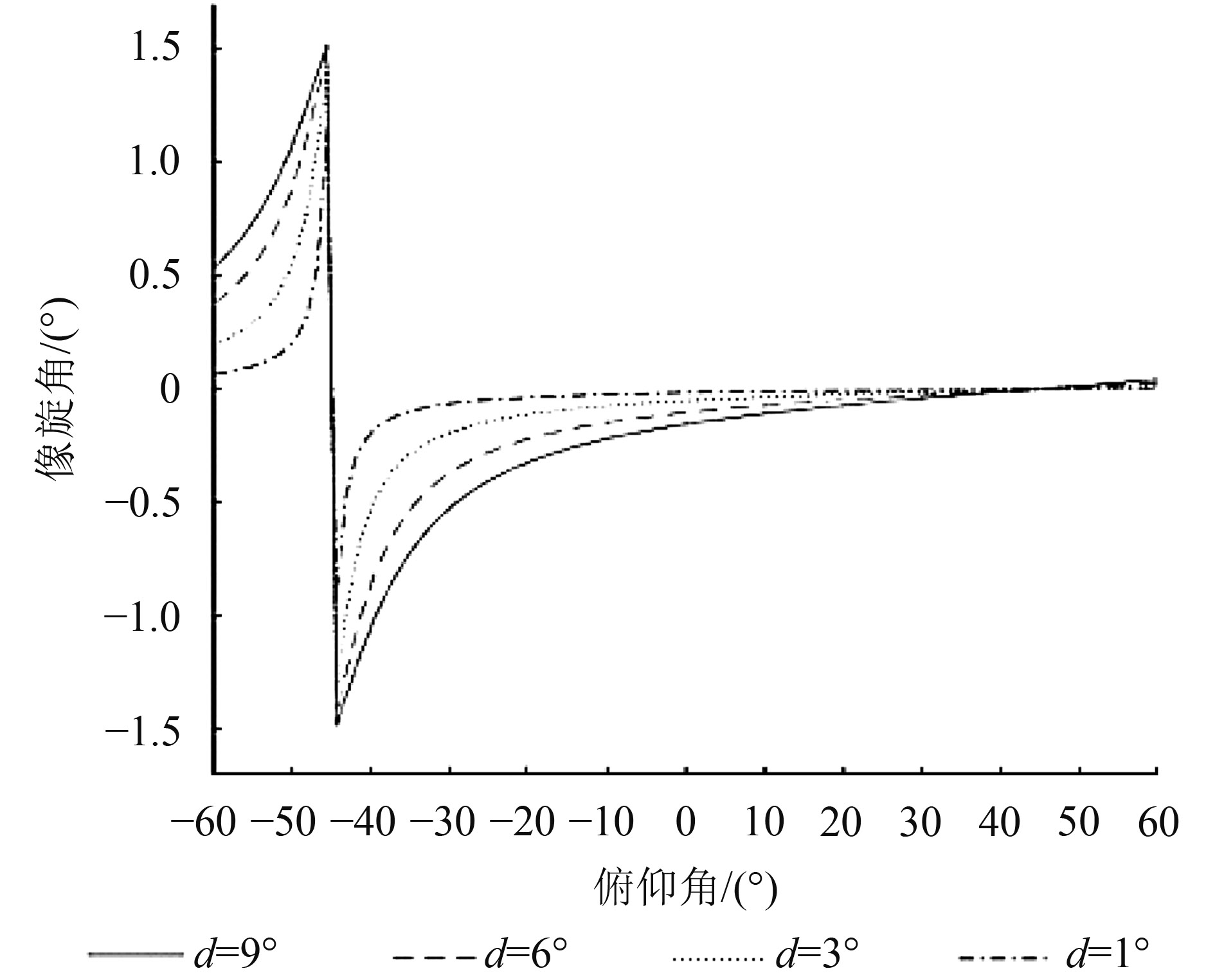
(3) α≠0,β≠0时,如图5所示是δ随β的变化,曲线关于β=45°对称,在β=–45°—45°区间内单调递增,像旋角绝对值逐渐减小。同时,方位角|α|越小,像旋角绝对值越小,α=–δ的图像关于δ=0镜像对称。
根据图5,β角变化对像旋角的影响,本文可以得出结论:
(1) 在–45°—45°之间,随着β增大,像旋角绝对值会减小,像面旋转情况有所好转;
(2) 对重点监测区域进行成像时,建议在可实现的情况下,选择δ曲线单调递增而不超过0、δ尽可能大,即像旋角绝对值尽可能小的一段进行成像,像面旋转会得到有效控制,漏扫情况会随之减少,扫描效率也可提高;
(3) β=0处不是一个特殊的值,因此在光学设计中,可以考虑引入初始偏置角度,从而控制图像的像旋程度。
3 扫描角度变化与图像覆盖程度的关系
为使观察角度更为广阔,指向镜初始指向可以有一定的旋转,如图6所示,扫描镜从虚线处方位旋转α角,俯仰旋转β角得到初始指向。再以初始指向为中心东西、南北各扫描五幅子图像。与子图像内部像旋相似,指向镜的初始转角会带来25幅图像的整体倾斜,如图6所示。
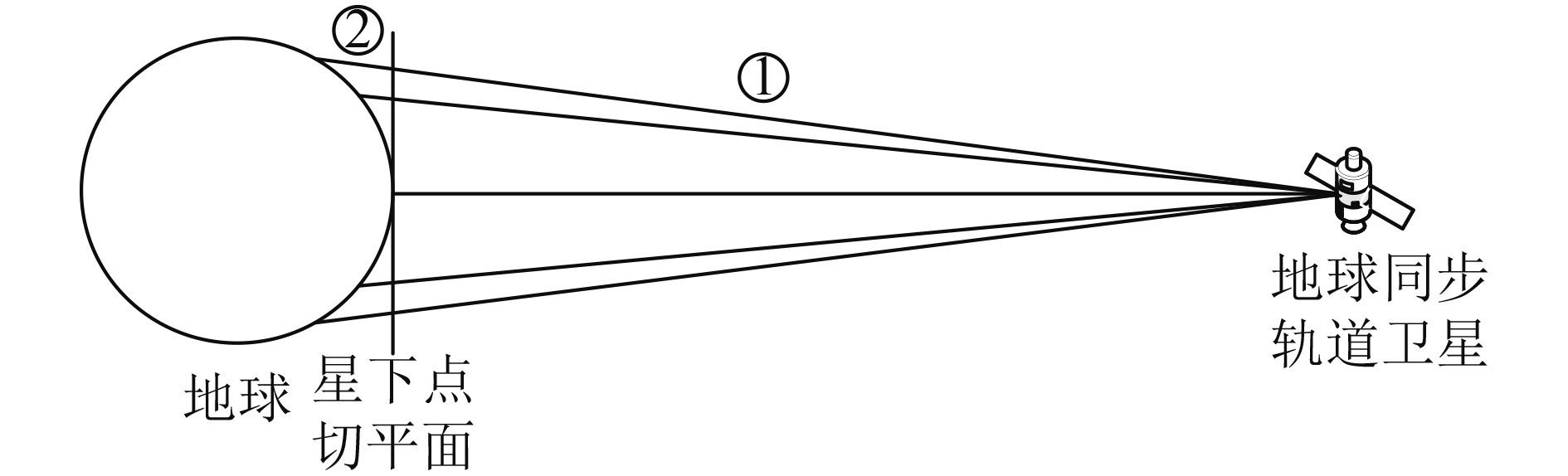
实际上,对于远在35800 km的地球同步轨道卫星而言,地球曲率会影响成像,使像面扭曲。但是,这种形变并不会改变子图像是否漏扫的性质。如图7所示,星下点切平面可视为指向平面,如果在星下点切平面成像无漏扫,则对地球的成像也无漏扫;反之,会漏扫。
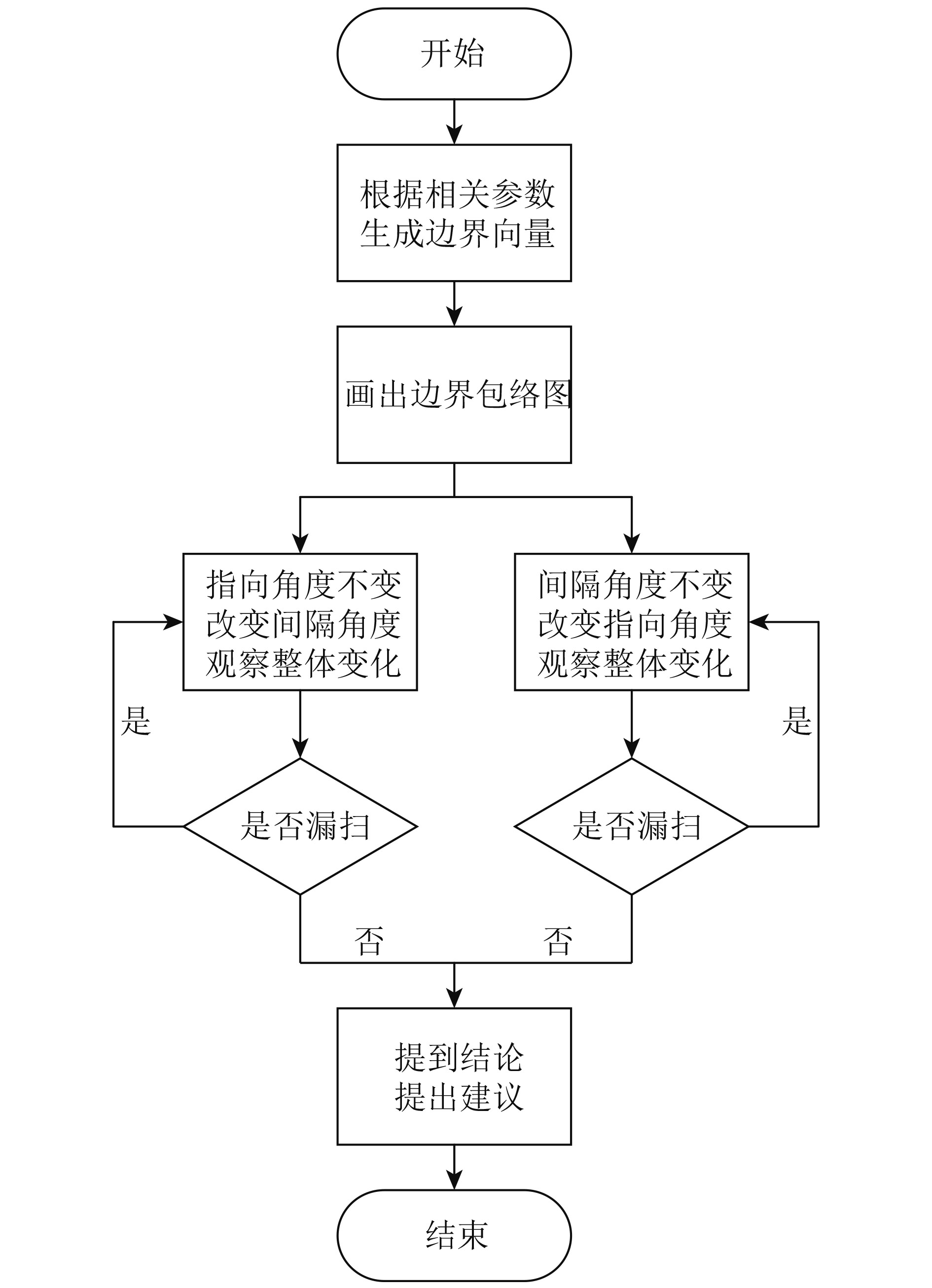
在子图像特性中,由于线段经线性变换后得到的是线段,为得到指向角度、间隔角度和覆盖程度的关系,选取探测器中心点和边缘点组成的向量经过已知的矩阵计算,得到每幅子图像的边界图。25幅边界图放在一个坐标系内观察则可以得到图像覆盖程度。计算分析过程如图8所示。
由图8流程可以得到不同指向角度或不同间隔角度的边界包络图。
本文中用到的系统参数如表1所示。
表 1 本文用到的系统参数
Table 1 Parameter of system in this article
| 内容 | 参数 |
| 波段 | 可见近红外 |
| 轨道高度 | 35800 km |
| 探测器像元大小 | 12 μm×12 μm |
| 面阵规模 | 2048×2048 |
| 子图像个数 | 5×5 |
| 焦距 | 1714 mm |
| 角分辨率 | 7 μrad |
| 子图像视场 | 0.82°×0.82° |
3.2 改变子图像间隔角度,指向角度不变
指向角度不变,子图像阵列的整体偏移程度不变,改变字图像间隔角度,子图像间的重叠面积会有不同。以视轴指向角度(5°, 5°)为例,同一个细节处,不同间隔角度的覆盖情况如表2所示。由于视轴指向角与电机转角存在如式(8)(9)的关系(李淑英和周世椿,2008)
|
$a = \alpha $
|
(8) |
|
$b \approx 2\beta $
|
(9) |
在视轴指向角改变一个单位时,电机方位转角转动近似为俯仰转角的2倍,所以表2中默认设置方位转角是俯仰转角的2倍,间隔角度值为俯仰转角β。
表 2 扫描间隔的影响
Table 2 Influence of different scan interal
| /(°) | |||
| 俯仰间隔角 | 0.39 | 0.40 | 0.41 |
| 覆盖情况 |
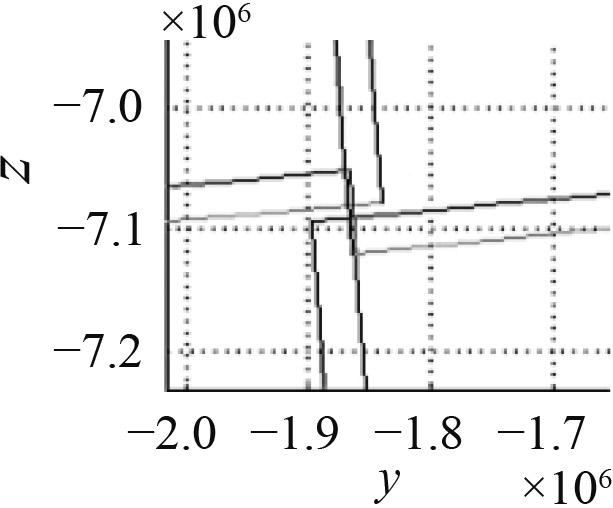 全部覆盖 全部覆盖
|
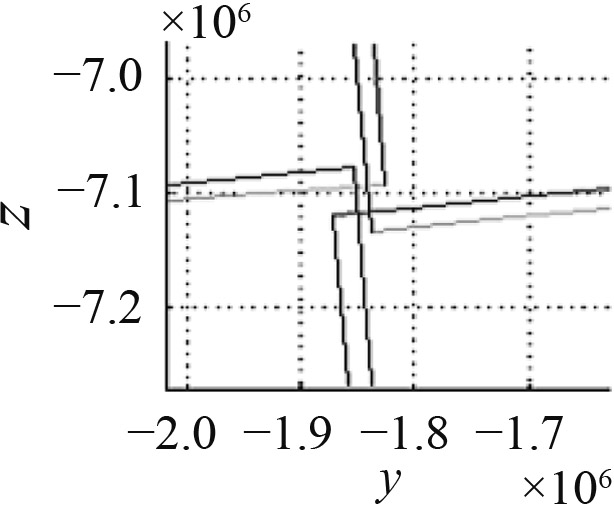 有漏扫 有漏扫
|
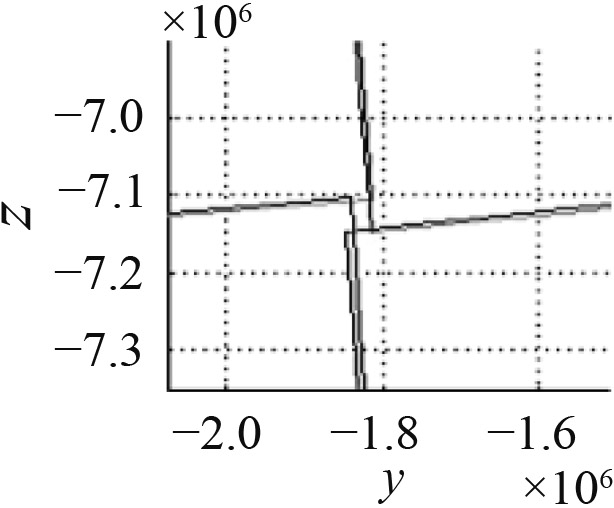 漏扫面积大 漏扫面积大
|
4 无缝拼接的判断方法
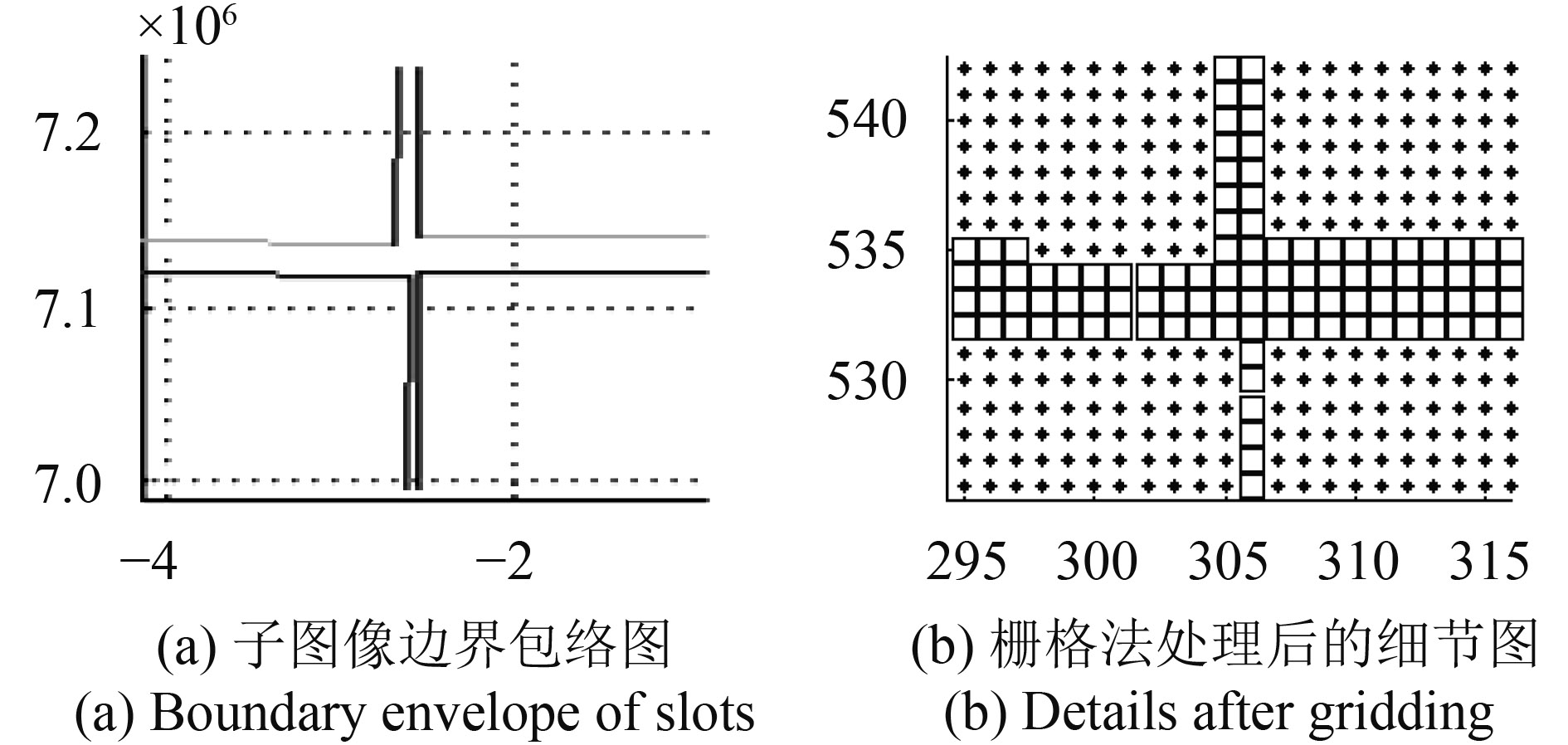
查看边界包络图是否存在漏扫情况,如果单用眼看,要放大交叠区域观察,有时还会存在漏扫点不明显容易误判的情况,如图11所示。通过有效的判断算法进行处理,可以快速、简便地得到是否漏扫的信息,以及漏扫部位、漏扫原因等。基于此,本文提出两种漏扫判断算法:栅格法和几何相交法。
4.1 栅格法
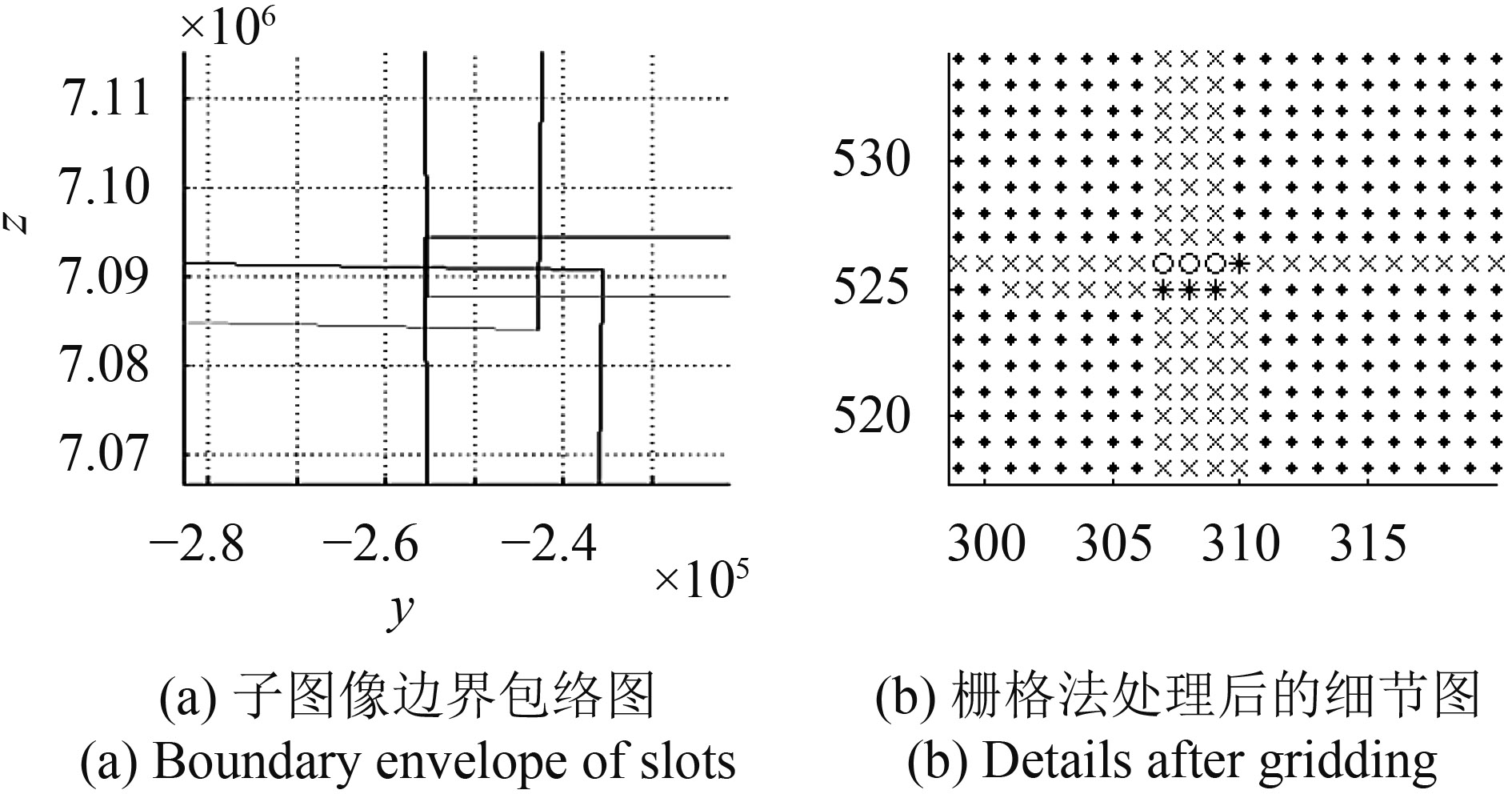
栅格法是将指向平面栅格化,每个子图像的边界包络线内的栅格赋值1,包络线外赋值0。在计算分析中,取无像旋处单个像素的尺寸对应指向平面的大小为栅格单位。栅格化后的细节如图12、13所示,图12为覆盖不完全的示意图,方块值为0(无覆盖),圆点为1(覆盖一次);图13为覆盖完全并有重叠的示意图,圆点值为1,“x”为2,“*”为3,“o”为4,数字分别表示覆盖的次数。
这样,栅格法可以很直接地统计重叠面积,同时,方便计算每个格点的覆盖次数,为之后的处理提供了便利,这是它的优势;然而,栅格化的计算引入的量化误差是不可避免的,为使量化误差尽可能小,需要缩小栅格的大小,这会降低计算速度,难以对漏扫进行实时监测,同时,在航天系统面阵大小很大的情况下,庞大的数据量也会增加系统的负担。考虑到上述原因,本文对算法进行了改进,通过几何相交法更快,更准确地判断是否出现漏扫。
4.2 几何相交法
几何相交法是利用不漏扫情况下包络线的相交关系来判断图像是否漏扫的。几何相交法需要的重叠条件如表3所示。
表 3 几何相交法需要的重叠条件
Table 3 Requirements of overlap for method geometry intersection
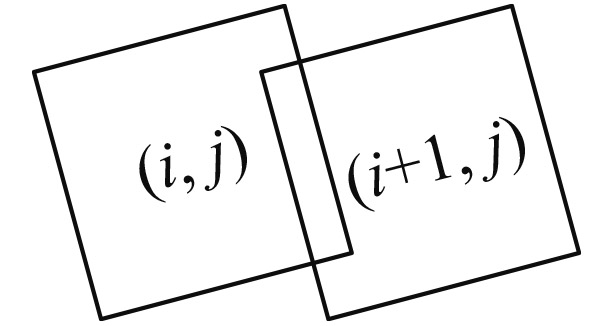
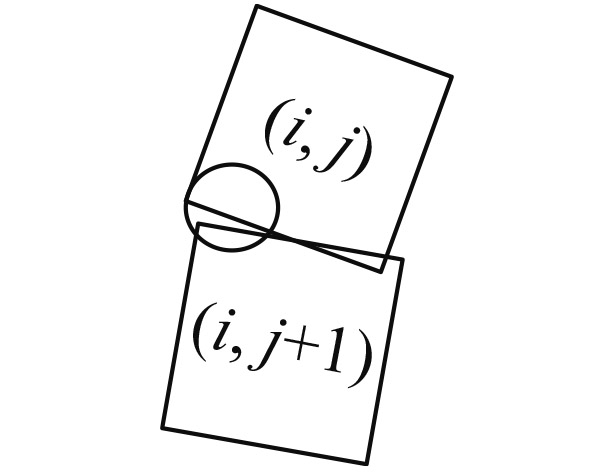
| 重叠方式 | 定义 | δ,α | 子图像重叠示意图 | 子图像未完全覆盖示意图 | 判断条件 |
| 方位扫描重叠 | 俯仰角一定,做方位扫描时,相邻两个子图像的邻边有四边形重叠区域 | δ>0α<0 |

|
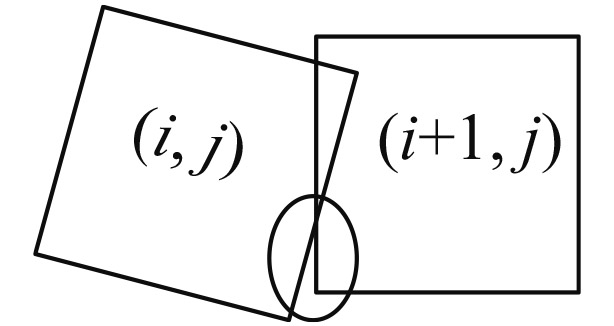
|
(i, j)上边界&(i+1, j)左边界相交 (i, j)右边界&(i+1, j)下边界相交 |
| δ<0α>0 |
|
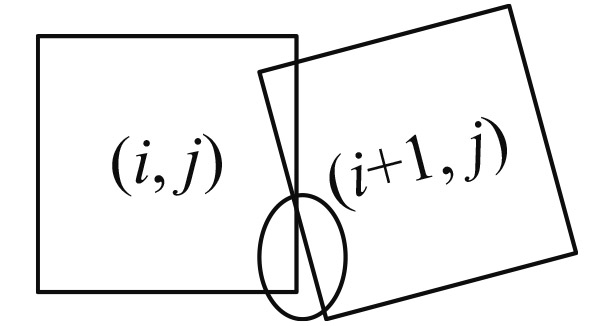
|
(i, j)下边界&(i+1, j)左边界相交 (i, j)右边界&(i+1, j)上边界相交 | ||
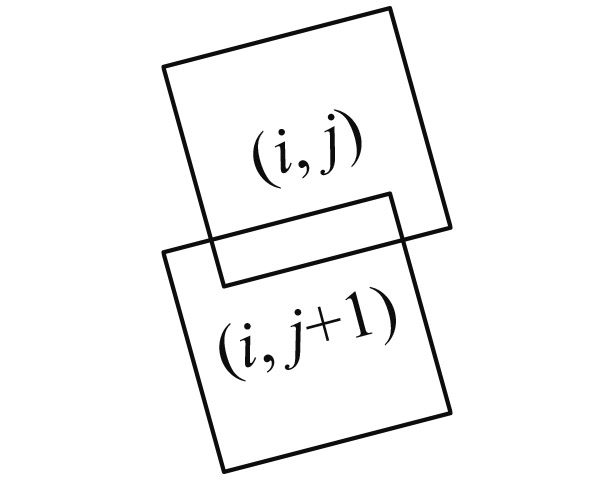
| 俯仰扫描重叠 | 在同一列,相邻两个子图像的邻边有四边形重叠覆盖区域 | δ>0α<0 |

|
|
(i, j)下边界&(i, j+1)左边界相交(i, j)右边界&(i, j+1)上边界相交 |
| δ<0α>0 |
|

|
(i, j)下边界&(i, j+1)左边界相交(i, j)右边界&(i, j+1)上边界相交 |
表3中第5列的未完全覆盖示意图中,有交叉重叠区域,但是圈出来的地方并没有完全覆盖;表3第4列的字重叠示意图为四方形重叠区域。
这样区分的原因如下:以方位扫描重叠δ>0为例,图14中(i, j)的右边界与(i, j+1)的左边界斜率相近,但并不平行,出现图14(a)情况时的扫描间隔角度必然比图14(b)的间隔角度要大,因为要出现圈住的区域。而当方位扫描间隔角度很小,图形如图14(b)所示时,仍会出现漏扫的情况,如图14(c)。因此要避免发生图14(a)中的情况,其他重叠方式和δ值可依此类推。
当相邻子图像分别满足方位、俯仰扫描重叠的条件后,仍然会出现漏扫的部分,这时,需要考虑对角重叠。对角重叠的判断条件如表4所示。
表 4 几何相交法对角重叠的几种情况
Table 4 Conditions of diagonal overlap for method geometry intersection
| δ,α | 子图像漏扫示意图 | 子图像重叠示意图 | 判断条件 | 备注 |
| δ>0αall<0 |

|
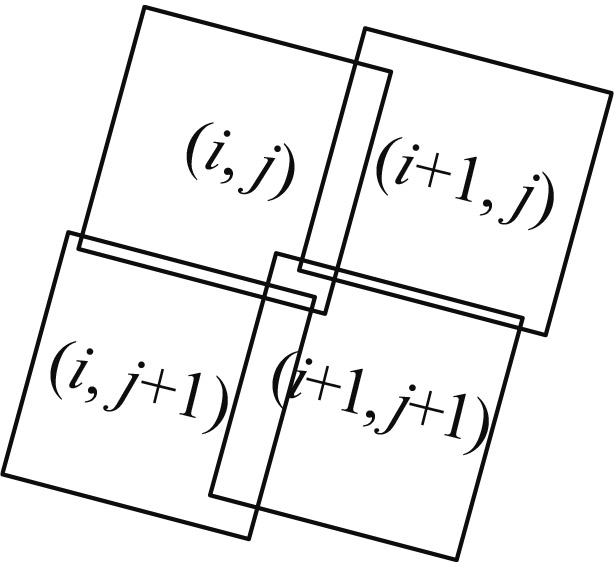
|
子图像(i, j)与(i+1, j+1)有重合区域 | 需要满足方位扫描重叠和俯仰扫描重叠的条件 |
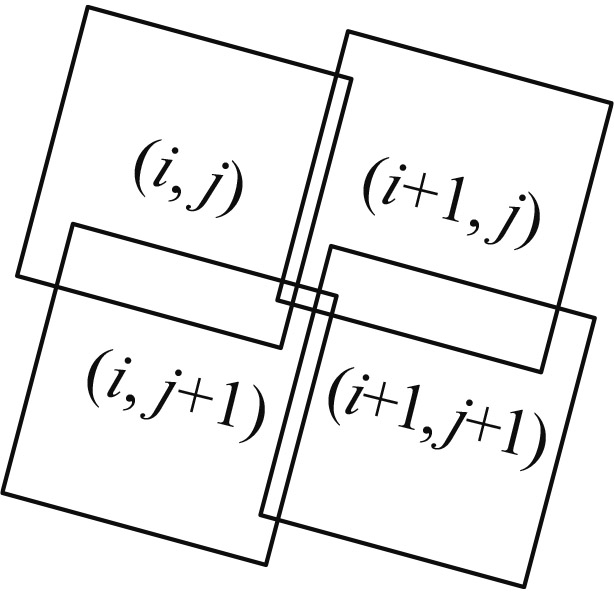
|
子图像(i+1, j)与(i, j+1)有重合区域 | 需要满足方位扫描重叠和俯仰扫描重叠的条件 | ||
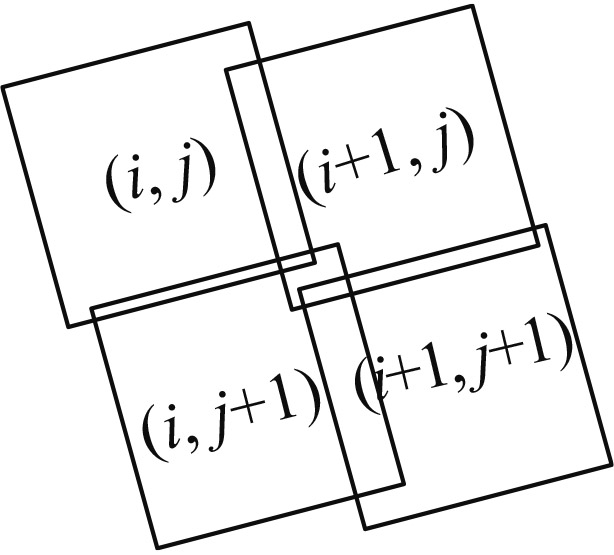
| δ<0αall>0 |
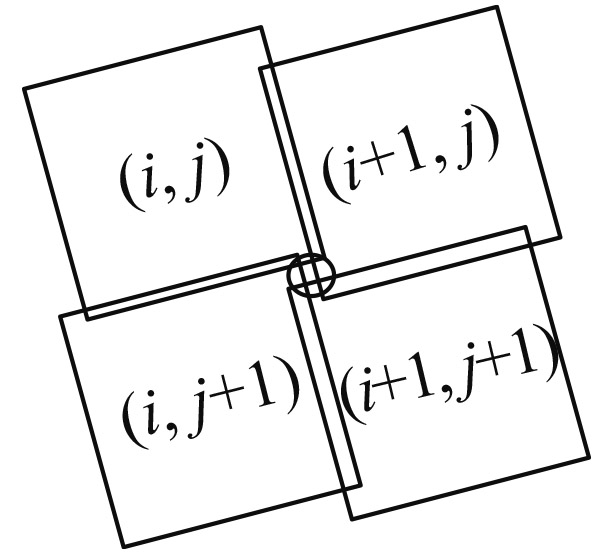
|
|
子图像(i+1, j)与(i, j+1)有重合区域 | 需要满足方位扫描重叠和俯仰扫描重叠的条件 |
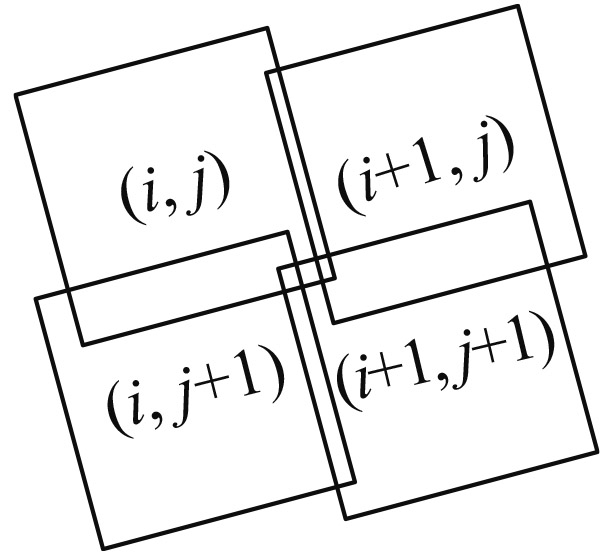
|
子图像(i, j)与(i+1, j+1)有重合区域 | 需要满足方位扫描重叠和俯仰扫描重叠的条件 | ||
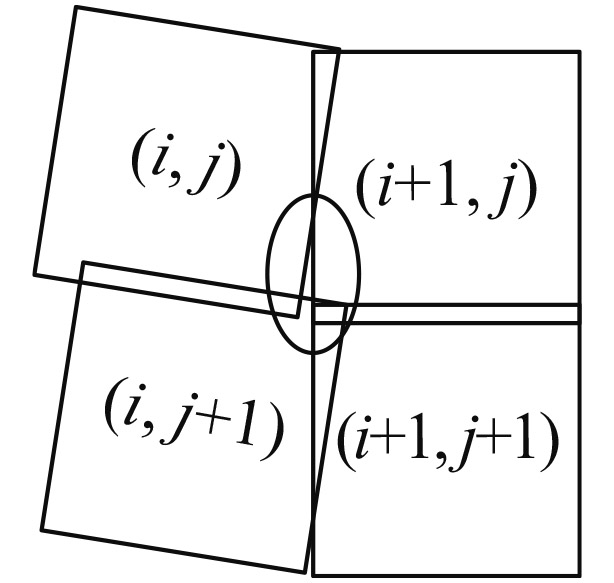
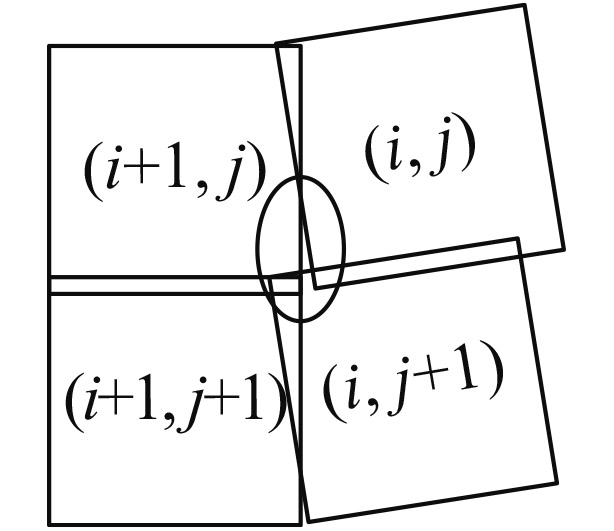
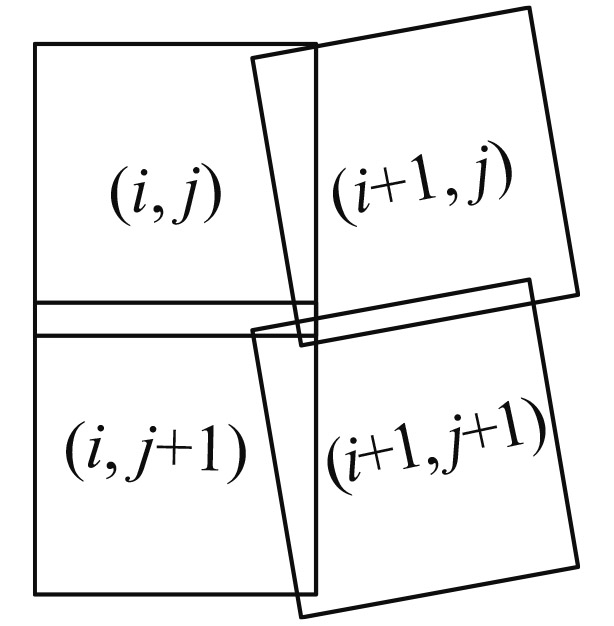
| αleft<0αright=0 |
|
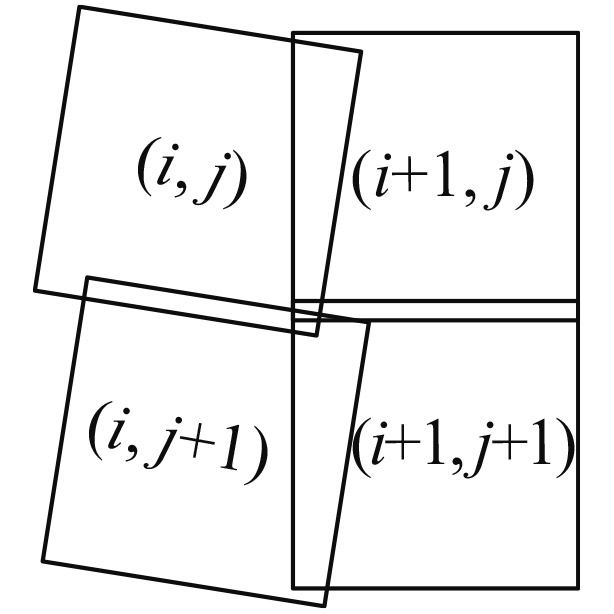
|
子图像(i, j)与(i+1, j+1)有重合区域 | 不需要满足方位扫描重叠的条件 |
| αleft=0αright>0 |
|
|
子图像(i+1, j)与(i, j+1)有重合区域 | 不需要满足方位扫描重叠的条件 |
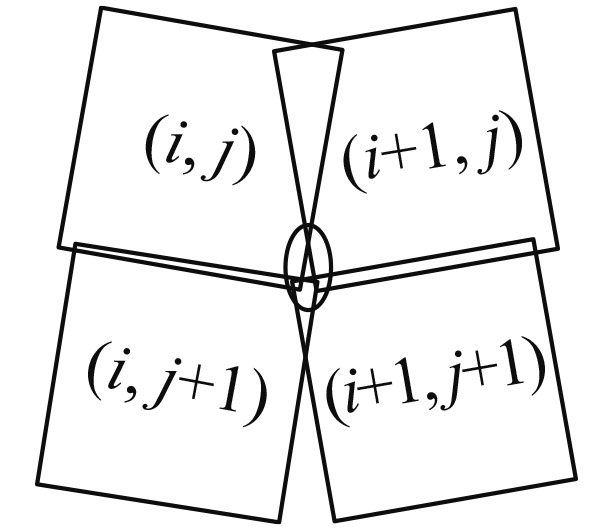
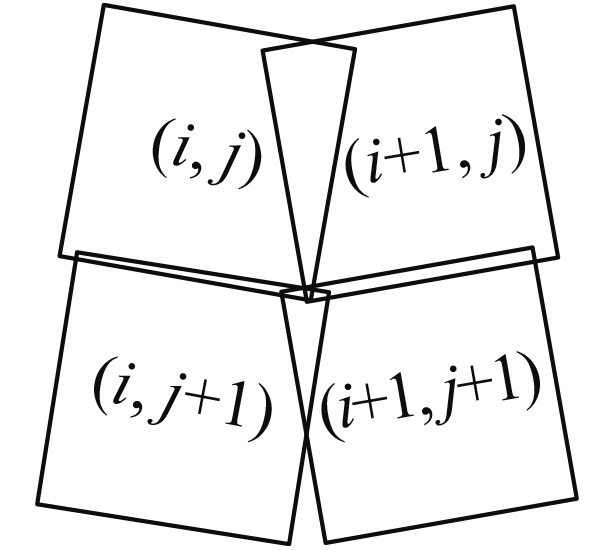
| αleft<0αright>0 |
|
|
子图像(i, j)与(i+1, j)的重叠区域S1,子图像(i+1, j+1)、(i+1, j+1)的重合区域S2,S1与S1有重叠 | 不需要满足方位扫描重叠的条件 |
综上所示为几何相交法的判断方法,它的优势是速度快,准确度高,无量化误差,但是逻辑复杂,需要多次计算总结经验后才能给出全面的判断依据,不过,判断依据一旦设定,对后面各种角度偏转的漏扫判断是准确快速的。
4.4 漏扫判断过程与无缝拼接条件
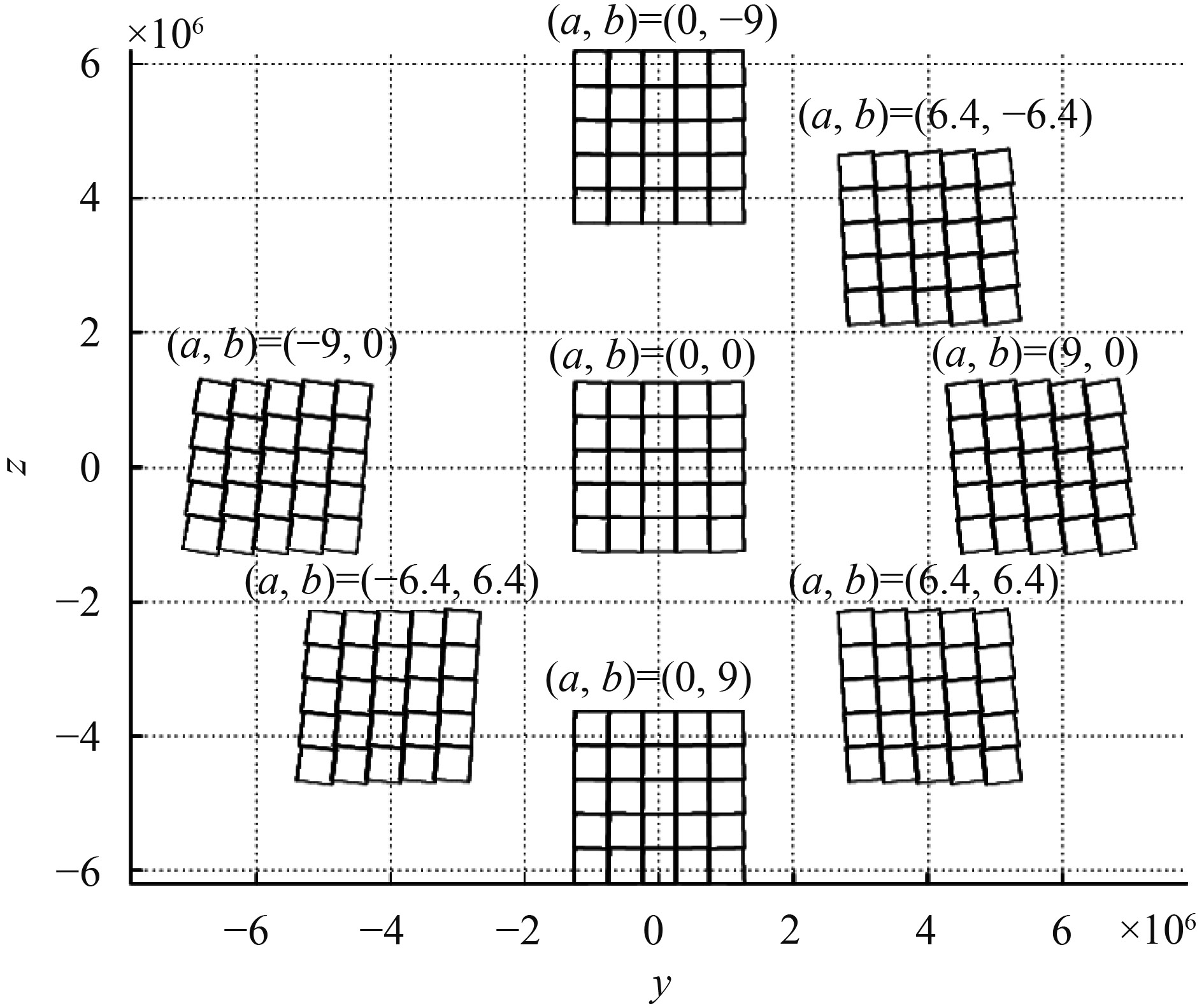
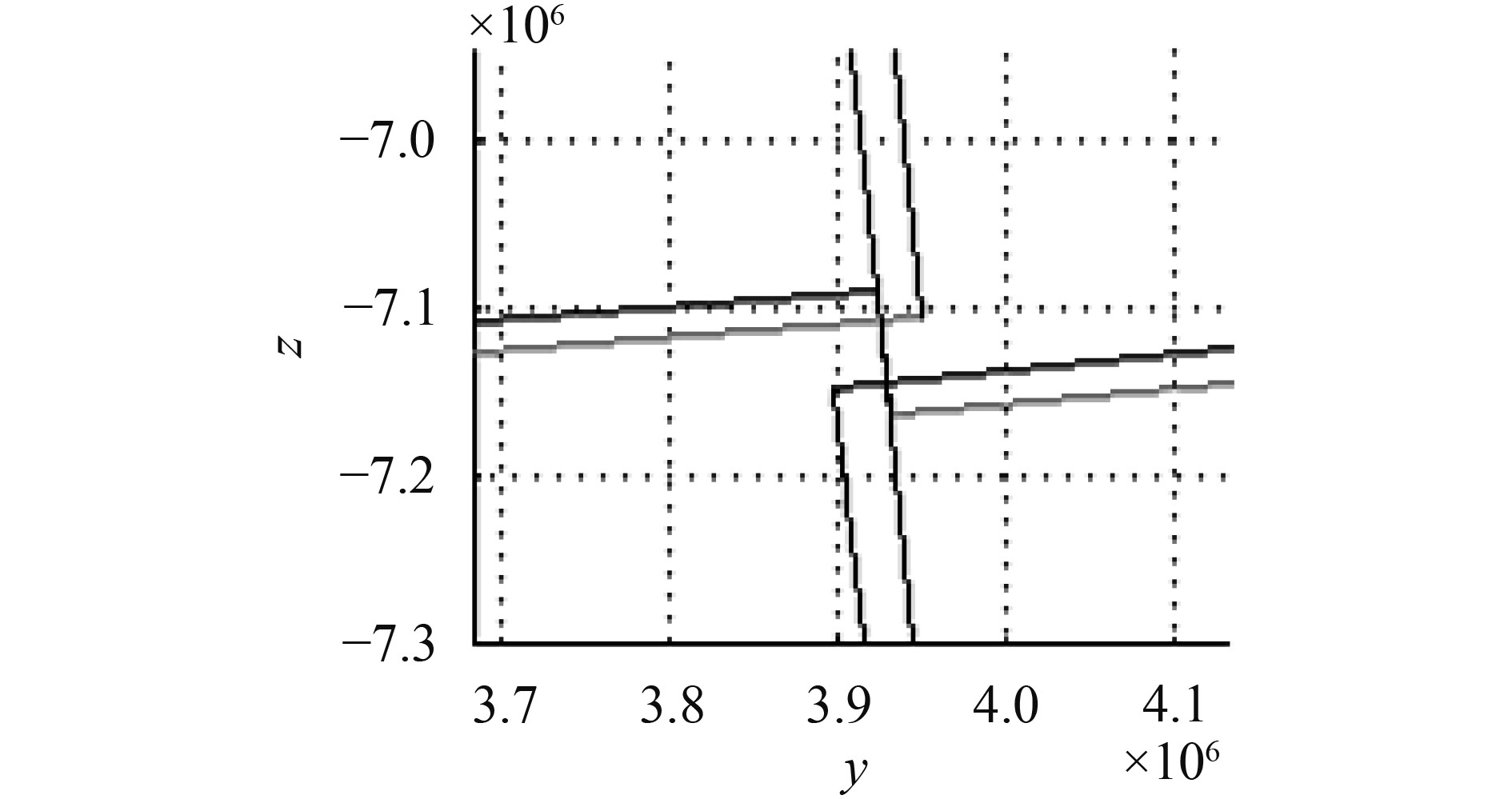
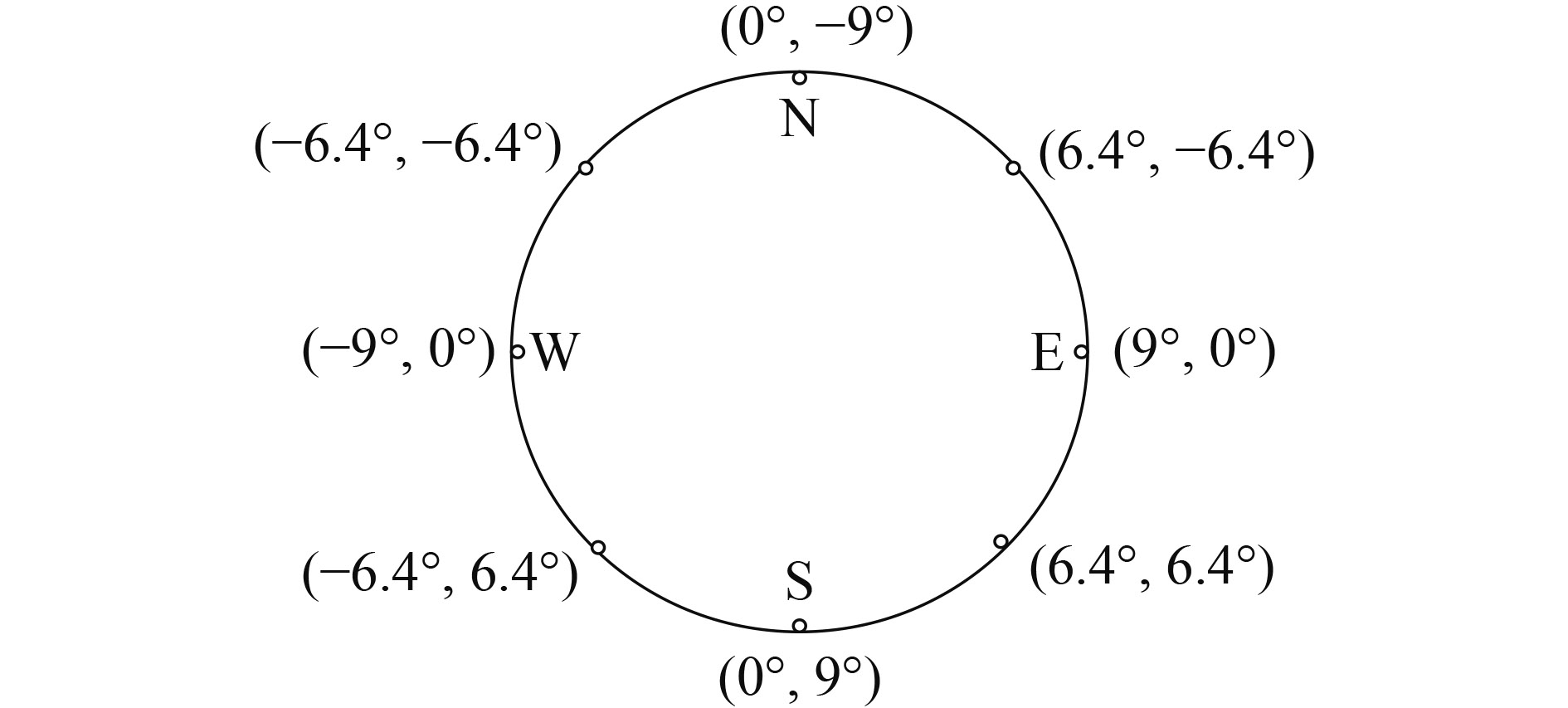
为使指向镜对整个地球的扫描拼接图像无漏扫,需要研究二维指向镜对地球边缘成像无漏扫的最大间隔角度。根据地球静止卫星的轨道高度35800 km以及地球的平均半径6371 km,可以大致计算出静止卫星对地球边缘的张角,本文取如图15中8点,根据3.2节、3.3节中的判断方法,逐次改变俯仰、方位转角间隔,找到指向八点时临界漏扫的俯仰转角的分布范围,即从边缘位置全部能覆盖的0.36°到全部漏扫的0.41°。在这个范围内,以0.01°为间隔,画出边界包络图,查看不同指向、不同间隔角度的漏扫情况。如表6所示,其中1为全部覆盖,0为出现漏扫的情况。
表6中,带*的八组(a,b)°在俯仰转角间隔为0.40°的包络图可参见图9。(a,b)°=(6.4°, 6.4°)、(–6.4°, 6.4°)、(6.4°, –6.4°)、(–6.4°, –6.4°)这4组数据的覆盖情况不同,是因为a=±6.4°的图像关于a=0°对称;而在0附近b=±6.4°并没有对称关系,b值越大,像旋角越小,覆盖情况越好。
表 6 不同指向、不同间隔角度覆盖情况
Table 6 Situation of covering with different angle
| /(°) | |||||||
| (a,b) | (α,β) | 角度间隔 | |||||
| 0.36 | 0.37 | 0.38 | 0.39 | 0.40* | 0.41 | ||
| (9, 0)* | (9, 0) | 1 | 0 | 0 | 0 | 0 | 0 |
| (–9, 0)* | (–9, 0) | 1 | 0 | 0 | 0 | 0 | 0 |
| (6.4, 6.4)* | (6.4, 3.2) | 1 | 1 | 1 | 0 | 0 | 0 |
| (–6.4, 6.4)* | (–6.4, 3.2) | 1 | 1 | 1 | 0 | 0 | 0 |
| (6.4, –6.4)* | (6.4, –3.2) | 1 | 1 | 0 | 0 | 0 | 0 |
| (–6.4, –6.4) | (–6.4, –3.2) | 1 | 1 | 0 | 0 | 0 | 0 |
| (0, 9)* | (0, 4.5) | 1 | 1 | 1 | 1 | 1 | 0 |
| (0, –9)* | (0, –4.5) | 1 | 1 | 1 | 1 | 1 | 0 |
| (0, 0)* | (0, 0) | 1 | 1 | 1 | 1 | 1 | 0 |
| (0, 5) | (0, 2.1) | 1 | 1 | 1 | 1 | 1 | 0 |
| (0, –5) | (0, –2.1) | 1 | 1 | 1 | 1 | 1 | 0 |
| 注:标记*的8组(a,b)在俯仰转角间隔为0.40°的包络图可参见图9。 | |||||||
因此,基于本文的光学系统,对35800 km处的地球进行成像,为得到覆盖全球、可无缝拼接的图像,俯仰、方位转角间隔应最大设置为0.36°、0.72°。
5 结 论
由于前人更多是对二维指向镜的成像进行分析,成像像旋的影响、不同指向角间隔角的影响程度并未深入研究。本文提供了更为详细的研究,提出扫描镜在方位、俯仰两个方向拥有不同的旋转特性,并给出了两种无缝拼接的判断方法。
同时,通过对二维指向镜成像的分析,得知当指向镜在东西方向转动时,电机转角越大,子图像的旋转越明显。指向镜在南北方向转动时,由于子图像旋转程度随俯仰角的增大而减小,所以光学设计中要考虑后续光学系统的相对位置从而使重点观测区域覆盖广、无漏扫。实际应用中,可以利用本文提出的两种判断漏扫的方法来判断一定指向角度、扫描间隔、图像大小等条件下漏扫的情况;也可以指定观测区域,得到不漏扫的角度条件,从而设置电机的转角大小。在已知需要观测区域的面积时,通过漏扫判断条件,找到最大的电机转角间隔,这样可以提高扫描效率,使4幅子图像就能覆盖原本需要5幅子图像才能覆盖的区域,减少成像时间,提高静止轨道卫星的时间分辨率。
另外,本文提出的判断漏扫的方法,在图像配准、拼接中还需要一定的延伸。根据不同的配准算法,确定两幅子图像需要重合的面积,对需要做漏扫判断的子图像进行剪裁,确保剪裁后的子图像仍不会漏扫,这样可以保证子图像做配准的区域足够,实现无缝拼接。
鉴于本文是基于地球曲面投影到赤道切平面的研究,虽然漏扫判断结果对曲面和平面无区别,但是,电机扫描转角的设置以及覆盖区域的面积会随着地球经纬度而变化。因此,下一步的研究重点将放在观测区域经纬度对二维指向扫描方式的影响上。
参考文献(References)
-
Chen Q, Hu Y, Gong C L, Li Z Q, Zhou Y and Liu Y N. 2012. Destriping method for mid-infrared image. Journal of Remote Sensing, 16 (1): 93–104. [DOI: 10.11834/jrs.20120433] ( 陈强, 胡勇, 巩彩兰, 李志乾, 周颖, 刘银年. 2012. 中波红外图像条纹处理方法. 遥感学报, 16 (1): 93–104. [DOI: 10.11834/jrs.20120433] )
-
Hafez M and Sidler T C. 1999. Fast-steering two-axis tilt mirror for laser pointing and scanning//Proceedings of the SPIE 3834, Microrobotics and Microassembly. Boston, MA, US: SPIE, 3834: 172–181[DOI: 10.1117/12.357822]
-
Hafez M, Sidler T and Salathé R P. 2003. Study of the beam path distortion profiles generated by a two-axis tilt single-mirror laser scanner. Optical Engineering, 42 (4): 1048–1057. [DOI: 10.1117/1.1557694]
-
Hui B, Pei Y T and Wang G Q. 2005. Optical analysis of space two-axus scanning mirror. Chinese Journal of Quantum Electronics, 22 (5): 810–813. [DOI: 10.3969/j.issn.1007-5461.2005.05.029] ( 惠彬, 裴云天, 王淦泉. 2005. 二维扫描镜扫描特性理论分析. 量子电子学报, 22 (5): 810–813. [DOI: 10.3969/j.issn.1007-5461.2005.05.029] )
-
Li S Y and Zhou S C. 2008. Analysis of the imaging characteristics of the two-dimensional pointing mirror. Opto-Electronic Engineering, 35 (5): 17–22. [DOI: 10.3969/j.issn.1003-501X.2008.05.004] ( 李淑英, 周世椿. 2008. 二维指向镜的成像特性分析. 光电工程, 35 (5): 17–22. [DOI: 10.3969/j.issn.1003-501X.2008.05.004] )
-
Lian T S. 1988. Conjugate Theory of Reflecting Prism. Beijing: Beijing Institute of Technology Press: 1–3 (连铜淑. 1988. 反射棱镜共轭理论: 光学仪器的调整与稳象. 北京: 北京理工大学出版社: 1–3)
-
Pelsue K. 1983. Precision, post-objective, two-axis, galva-nometer scanning//Proceedings of the SPIE 390, High Speed Read/Write Techniques for Advanced Printing and Data Handling. Los Angeles: SPIE, 390: 70–78 [DOI: 10.1117/12.935036]
-
Sun D X and Wang J Y. 2005. Scan track of system using 45° Mirror and its effect on the correction of image rotation. Journal of Infrared and Millimeter Waves, 24 (1): 19–22. [DOI: 10.3321/j.issn:1001-9014.2005.01.005] ( 孙德新, 王建宇. 2005. 45°镜系统扫描轨迹分析及其对像旋校正的影响. 红外与毫米波学报, 24 (1): 19–22. [DOI: 10.3321/j.issn:1001-9014.2005.01.005] )
-
Wang G Q and Chen G L. 2014. Two-dimensional scanning infrared imaging technology on geosynchronous orbit. Infrared and Laser Engineering, 43 (2): 429–433. [DOI: 10.3969/j.issn.1007-2276.2014.02.016] ( 王淦泉, 陈桂林. 2014. 地球同步轨道二维扫描红外成像技术. 红外与激光工程, 43 (2): 429–433. [DOI: 10.3969/j.issn.1007-2276.2014.02.016] )
-
Wang W, Hong P, Wang B and Yu H. 2015. Characteristic analysis of two-dimensional scanning mirror rotating. Optics and Optoelectronic Technology, 13 (2): 82–86. ( 王武, 洪普, 王波, 余徽. 2015. 二维扫描镜像旋特性分析. 光学与光电技术, 13 (2): 82–86. )
-
Wang Y, Hu G J, Long H and Zhang T T. 2012. CCD image seamless mosaic on characteristic and dislocation fitting. Journal of Remote Sensing, 16 (S1): 98–101. [DOI: 10.11834/jrs.20120020] ( 王昱, 胡国军, 龙辉, 张廷涛. 2012. 特征与错位拟合的CCD图像无缝拼接. 遥感学报, 16 (S1): 98–101. [DOI: 10.11834/jrs.20120020] )
-
Wu F and Wang D P. 2009. Analysis of scanning traces characteristics of the two-axis pointing mirror in the mode of scanning in given area. Electro-Optic Technology Application, 24 (4): 16–20. [DOI: 10.3969/j.issn.1673-1255.2009.04.005] ( 吴凡, 王大鹏. 2009. 二维指向镜的定域扫描方式的扫描特性分析. 光电技术应用, 24 (4): 16–20. [DOI: 10.3969/j.issn.1673-1255.2009.04.005] )
-
Yang Z Q, Wu D X and Zheng Y C. 2004. Study of angular non-linearity in 2-D optical scanning. Laser Technology, 28 (3): 262–265. [DOI: 10.3969/j.issn.1001-3806.2004.03.009] ( 杨志卿, 吴登喜, 郑永超. 2004. 二维光学扫描中扫描角度非线性研究. 激光技术, 28 (3): 262–265. [DOI: 10.3969/j.issn.1001-3806.2004.03.009] )
-
Yin D Y. 2016. The Study of the Scan-Mirror’s Dynamic Precision Measuring Method Based on the Digital Imaging Technique. Shanghai: Graduate University of Chinese Academy of Sciences(Shanghai Institute of Technical Physics): 1–3 (殷东羽. 2016. 基于数字图像的扫描镜动态精度测量方法研究. 上海: 中国科学院研究生院(上海技术物理研究所): 1–3)
-
Zhang E and Gong H X. 1999. Research and application of system for offsetting the image rotation from 45° rotating scan mirror. Journal of Infrared and Millimeter Waves, 18 (2): 125–132. [DOI: 10.3321/j.issn:1001-9014.1999.02.006] ( 张锷, 龚惠兴. 1999. 消除45°旋转扫描反射镜像旋转系统的研究及应用. 红外与毫米波学报, 18 (2): 125–132. [DOI: 10.3321/j.issn:1001-9014.1999.02.006] )
-
Zhang S Q, Zhang Y, Zhou C H and Wang Z L. 2014. Image motion model of azimuthally photography for satellite borne TDICCD camera. Infrared and Laser Engineering, 43 (6): 1823–1829. [DOI: 10.3969/j.issn.1007-2276.2014.06.023] ( 张树青, 张媛, 周程灏, 王治乐. 2014. 星载TDICCD相机方位扫描像移模型研究. 红外与激光工程, 43 (6): 1823–1829. [DOI: 10.3969/j.issn.1007-2276.2014.06.023] )
-
Zhou S C. 2010. Introduction to Advanced Infrared Optoelectronic Engineering. Shanghai: Shanghai Institute of Technical Physics of the Chinese Academy of Sciences: 319–328 (周世椿. 2010. 高级红外光电工程导论. 上海: 中国科学院上海技术物理研究所研究生部: 319–328)