|
收稿日期: 2016-11-01; 优先数字出版日期: 2017-09-01
基金项目: 国家自然科学基金(编号:61572437,41301473)
第一作者简介: 范菁(1969— ),女,教授,主要研究方向为森林虚拟仿真与可视化。E-mail:fanjing@zjut.edu.cn
中图分类号: TP701
文献标识码: A
|
摘要
在多云多雨的地区,光学遥感存在着获取无云数据困难的难题,这会导致时间序列应用中可用数据匮乏。因此,本文面向稀疏时间序列遥感数据,根据噪声造成遥感影像上归一化差分植被指数(NDVI)被低估的事实,提出了一种知识引导的拟合方法。首先,在遥感影像预处理的基础上,利用先验知识和时序差分法对噪声进行识别和剔除;然后,采用高斯二阶模型对原始数据进行拟合;最后,根据拟合残差更新权重,进行迭代拟合,重复上述过程直至获得稳定的结果。本文以Landsat 8 OLI作为数据源,对浙江省杭州地区的森林数据进行拟合,结果表明:在稀疏时间序列数据的情况下,本文方法与MODIS数据拟合结果的相关系数达到0.92,关键时点(如NDVI峰值点等)的时间误差在5 d;相比当前主流方法的0.88与 8 d具有更高的精度。
关键词
稀疏时间序列数据, 迭代加权, 数据拟合, Landsat 8, 高斯模型
Abstract
Time series remote sensing plays an important role in forest monitoring, and the performance of the fitting method of time series Normalized Difference Vegetation Index (NDVI) determines the precision of phenology parameter estimation. However, in cloudy and rainy areas, obtaining cloud free remote sensing data for time series application is greatly difficult, leading to the difficulty in precisely fitting the time series NDVI. We present a knowledge-guided fitting method for sparse time series remote sensing data, given that the NDVI is underestimated by noise. First, we use prior knowledge and time difference method to identify and remove the noise, and then the Gaussian second-order model is used to fit the original data. Third, the iterative fitting is carried out by updating the weights of original data according to the fitting residuals. Finally, this process is repeated until a stable result is obtained. We use NDVI derived from Landsat 8 OLI as the data source to fit the forest data in Hangzhou, Zhejiang province. MODIS data are used as the referenced data to test accuracy of fitting result. The correlation coefficient between the fitting result of sparse time series data and the MODIS data fitting results is 0.92, and the difference of the day of max NDVI is five days, which indicates the proposed can be used to estimate the growth intensity, growth period, and other biological parameters effectively, the result is closer to the MODIS data fitting result compared with the state of art method. Our research provides the knowledge-guided fitting method, which is more effective than the other conventional methods, especially for the sparse time series data. This method reduces the human subjective influence and the excessive disturbance caused by the noise in the original data, making the fitting result more close to the actual fitting curve. The advantages of this method include less input parameters, fast converge, and the stability of fitting result. However, the proposed method suppresses the noise in the fitting processing to obtain relatively smooth fitting curve, which also may lead to the loss of the curve information; further improvements can be performed in the future.
Key words
sparse time series data, iterative weighted, data fitting, Landsat 8, Gaussian model
1 引 言
遥感卫星按照相同的观测角度、光谱通道和获取条件对地表进行观测,获取的时间序列遥感数据记录了地表现象的发生和发展规律,已成为研究森林演替、物候变化、农情监测、农作物估产、城市扩张等地表时空特征的重要数据来源,并取得了良好的应用效果(Ma 等,2012;Verbesselt 等,2010;杨浩 等,2011;Fu和Weng,2016)。然而,受获取时刻光照强度、大气状况等因素影响,遥感器获取的测量值中包含大量与地表信息无关的噪声,辐射校正仅能够一定程度消除辐射畸变,但残存的辐射畸变依然是地表应用的重要制约。同时,云影造成数据上部分区域缺失,使得同一地区对地观测的时间间隔变长,可用数据变少。可以看出,辐射畸变与云影依然是时序应用的重要限制性因素。
遥感时序数据拟合将不同时刻获取的离散数据点拟合成一条曲线,并利用拟合值代替原始值进行处理和分析。时序数据拟合一方面能够克服上述各种因素造成的噪声,另一方面能够将不规则时间采样的离散数据转化为连续的曲线,从而估计任意时刻的数据(Hird和McDermid,2009)。根据拟合模型的不同,经典的遥感时序数据拟合大致可以分为滤波去噪法、傅里叶拟合法和高斯拟合法3种类型:(1)滤波法在滑动窗口内通过平均等运算,达到抑制噪声、获取平滑曲线的目标。如Savitzky-Golay滤波器能保证波段信号的形状宽度不变,从而体现植被的物候规律,但是滑动窗口大小和方向等参数对结果影响较大(Chen 等,2004;Kim 等,2014)。(2)傅里叶拟合方法是将离散数据点表示为一系列余(正)弦波的线性或者非线性叠加,该类型方法具有拟合地表周期性现象的内在优势(Roerink 等,2000;Carrão 等,2010);(3)高斯拟合法通过最小二乘法采用高斯模型对时序数据进行重建,实现平滑去噪(Hird 等,2009)。
同时,国内外研究者也提出了一些改进和其他相关的时序数据拟合方法。例如,非对称高斯拟合(AG拟合)是一个“整体—局部”相结合的高斯拟合模型,该方法首先利用一个滑动窗口获取NDVI时序数据的谷值和峰值,再分别对位于谷值和峰值之间的NDVI时序数据进行分段局部拟合,从而表达植被物候变化规律 (Jönsson和Eklundh,2002, 2004)。Beck等人(2006)以高纬度地区为实验区,采用double logistic函数拟合法重建MODIS NDVI数据,与非对称高斯拟合相比,该方法能够更有效的估计作物的生长期。此外,为了利用影像的多波段特点,有的方法将时序遥感数据拟合为一个曲面,如多项式趋势面(polynomial trend surface)和搭配面 (collection surface),前者能够得到较为平滑的结果,在拟合渐变地物上具有优势,而后者在拟合突变方面具有更好的效果(Mello 等,2013)。
不同算法的NDVI拟合效果与数据本身的噪声类型及最终的应用目的相关,需要结合实际情况对时序重建方法进行选择,但整体来说,高斯类模型能够获得较为均衡的拟合结果(Atkinson 等,2012)。
然而,上述方法适用于噪声较少的数据,诸如MODIS数据。但由于MODIS空间分辨率较低,无法满足较高分辨率场景的应用需求。影像分辨率较高的Landsat系列卫星从20世纪70年代开始,不间断的获取数据,具有良好的时间连续性。该数据的时间采样间隔是16 d,但因为云影的存在使得数据的时间间隔进一步拉长,时间采样变得不均匀,无法通过最大值合成进行噪声抑制或剔除,这种现象在多云多雨地区尤其严重。
针对Landsat这类稀疏、噪声较多、时间采样不均匀而分辨率较高的时序数据,适用的拟合方法相对较少。张霞等人(2010)通过引入异常值的检测,对传统的傅里叶谐波分析的时序拟合进行了优化,剔除了异常数据值,提高了数据拟合的真实性,将其称为改进傅里叶方法。为了进一步提高拟合结果的真实性,本文基于云影等多种类型噪声造成NDVI被低估的先验知识,提出一种知识引导的稀疏时间序列遥感数据拟合方法,最终获得鲁棒的拟合结果。
2 基本原理
在可见光与近红外通道,云和雾霾的存在,使得影像上相应区域不包含地表信息或者信息发生扭曲,成为被动遥感的主要噪声来源,主要体现在:(1)云和雾霾在可见光以及近红外波段的高反射,将太阳辐射大量反射并被传感器接收,相当于在各个通道掺入功率相同的白噪声,使得影像变得模糊;(2)将包含地表信息的短波辐射反射回地表,使得到达传感器的电磁辐射量较少,植被高反射的近红外波段减少尤其严重,从而造成影像整体偏暗,对比度降低。
归一化差分植被指数(NDVI)、叶面积指数(LAI)等是描述地表特征的定量指标,其中NDVI能够部分消除辐射误差,广泛的应用于监测植被生长状态、植被覆盖度,是一种最常用的定量指标,计算方法为
|
${\rm{NDVI}} = \frac{{NIR - R}}{{NIR + R}}$
|
(1) |
式中,NIR和R分别表示近红外波段和红波段的DN值或者反射率。根据上述分析可知,一方面,云和雾霾本身的反射使得NIR和R同时增大;另一方面,云和雾霾将部分地表辐射反射回地表,使得NIR和R同时减小,但近红外波段值的影响相对较大。上述两个因素的综合作用使得NDVI测量值较真实值低,并得到了广泛的证实(Beck 等,2006)。具体到时间序列数据上,噪声的存在使得相邻时间采样值出现“陡升陡降”的现象,容易导致时间序列数据的拟合结果发生扭曲,影响作物生长期等物候参数的提取和估计。
针对此问题,本文采用以Landsat为代表的中等分辨率稀疏时间序列数据,基于噪声造成NDVI低估的先验知识,提出一种知识引导的时序数据拟合方法,具体包含两点:(1)识别时序数据中明显的噪声;(2)根据拟合结果定量评价数据质量,并确定权重,使得拟合曲线向着上方移动,逐渐接近NDVI真实值,提高拟合结果的精度。
3 方 法
同一地区不同时间获取的n景影像I,按照时间
|
${{I}} = < {I_{{t_1}}},{I_{{t_2}}},\cdots,{I_{{t_n}}} > $
|
(2) |
某一像素在n景影像I上NDVI时间序列值
|
${{{N}}^{(r,c)}} = < N_{{t_1}}^{(r,c)},N_{{t_2}}^{(r,c)},\cdots,N_{{t_n}}^{(r,c)} > $
|
(3) |
式中,r,c表示该像素所在的行列号。受噪声的影响,NDVI时间序列值中存在“陡升陡降”的现象,不利于生长期等特征值的估计与提取。时序拟合是将不均匀时间采样的离散NDVI值
|
${{f}}({{{N}}^{(r,c)}}) = < f(N_{{t_1}}^{^{(r,c)}}),f(N_{{t_2}}^{^{(r,c)}}),\cdots,f(N_{{t_n}}^{^{(r,c)}}) > $
|
(4) |
并使用拟合值
高斯模型具有良好的均衡拟合结果以及主观误差较小等特点,因而本文采用高斯模型作为基础进行时序拟合,该模型f表示为
|
$f({N_t}) = G({N_{{t_{\varepsilon 1}}}}) + G({N_{{t_{\varepsilon 2}}}}) = {a_1}{{\rm{e}}^{ - {{\left(\frac{{Nt - {b_1}}}{{{c_1}}}\right)}^{^2}}}} + {a_2}{{\rm{e}}^{ - {{\left(\frac{{Nt - {b_2}}}{{{c_2}}}\right)}^{^2}}}}$
|
(5) |
式中,a1、b1、c1和a2、b2、c2为模型待估计的参数,
|
$Q(N) = \arg \min \sum\limits_{i = 1}^n {{{({N_{{t_i}}} - f({N_{{t_i}}}))}^2}} $
|
(6) |
通过解算上述模型,获得优化的拟合结果。
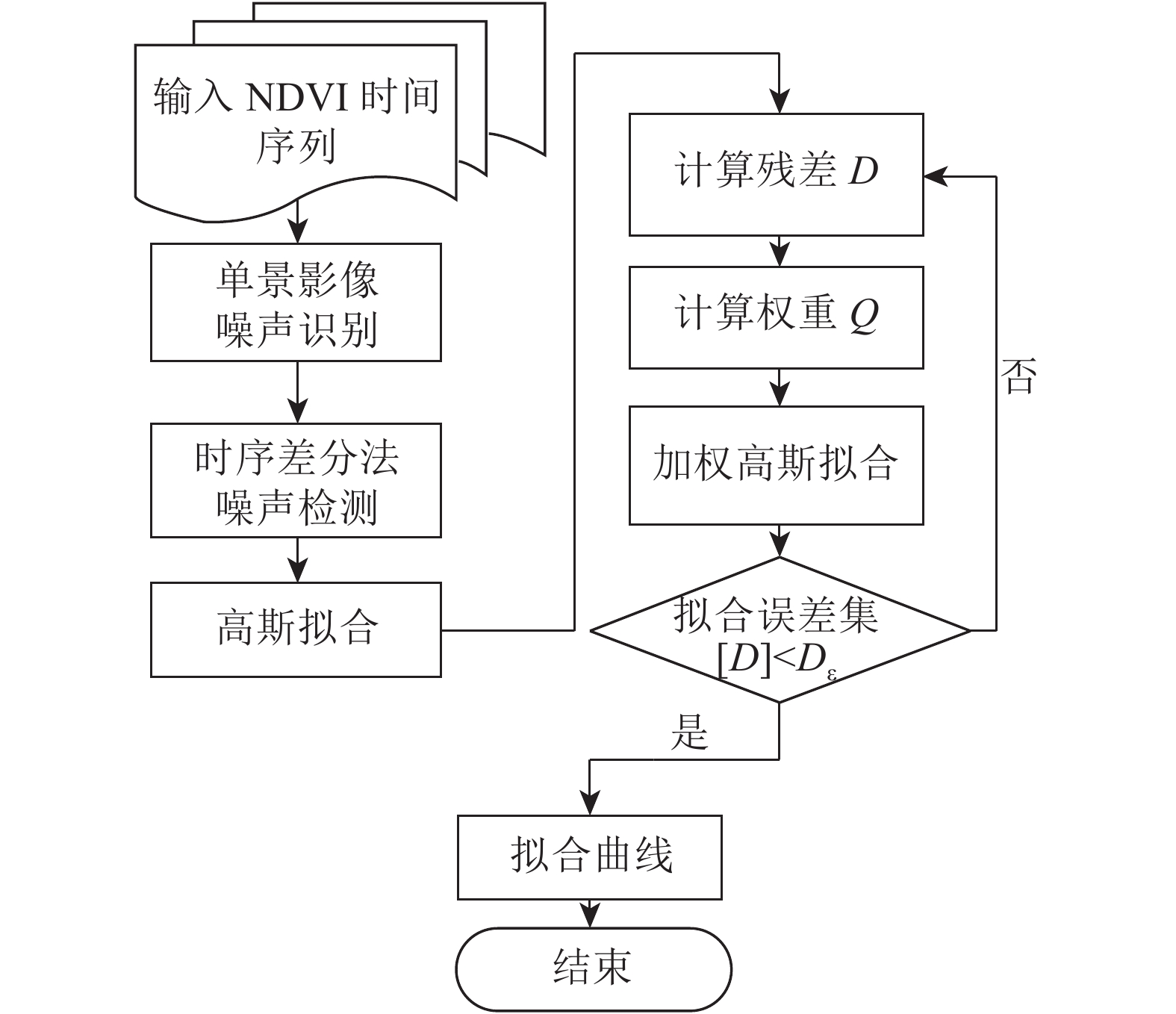
本文以高斯模型为基础,再使用最小二乘方法进行参数求解和拟合,设计并实现知识引导时序数据拟合方法,其过程为如图1所示:首先根据单期遥感影像和时序影像识别噪声并加以剔除;再将保留的时序数据利用二阶高斯模型进行初步拟合。由于噪声使得NDVI低估,并使得拟合曲线整体偏小,根据残差设置各个采样时间点的权重,以实现高斯模型的迭代优化,最终获得稳定的拟合曲线。以下分为噪声数据识别、权重估计与迭代优化两个过程描述本文方法的原理及其实现细节。
3.1 噪声数据识别
云和云阴影一般是通过云的反射率较高而阴影的反射率较低的特点进行阈值分割,云影检测已经得到了广泛的研究,拥有多种成熟的算法(Zhu和Woodcock,2012)。Landsat 8 OLI数据提供了质量评估波段QA(Quality Assessement Band),包含各个像素的云可信度(cloud confidence)和卷云可信度(cirrus confidence)等信息。本文主要目标是利用云影识别结果剔除NDVI时间序列数据中的明显噪声点,因而不再深入讨论云影检测方法,而是直接采用Landsat 8 OLI数据提供的QA波段作为云掩膜输入,也可以利用其他先进的云影掩膜算法的结果作为云掩膜输入。
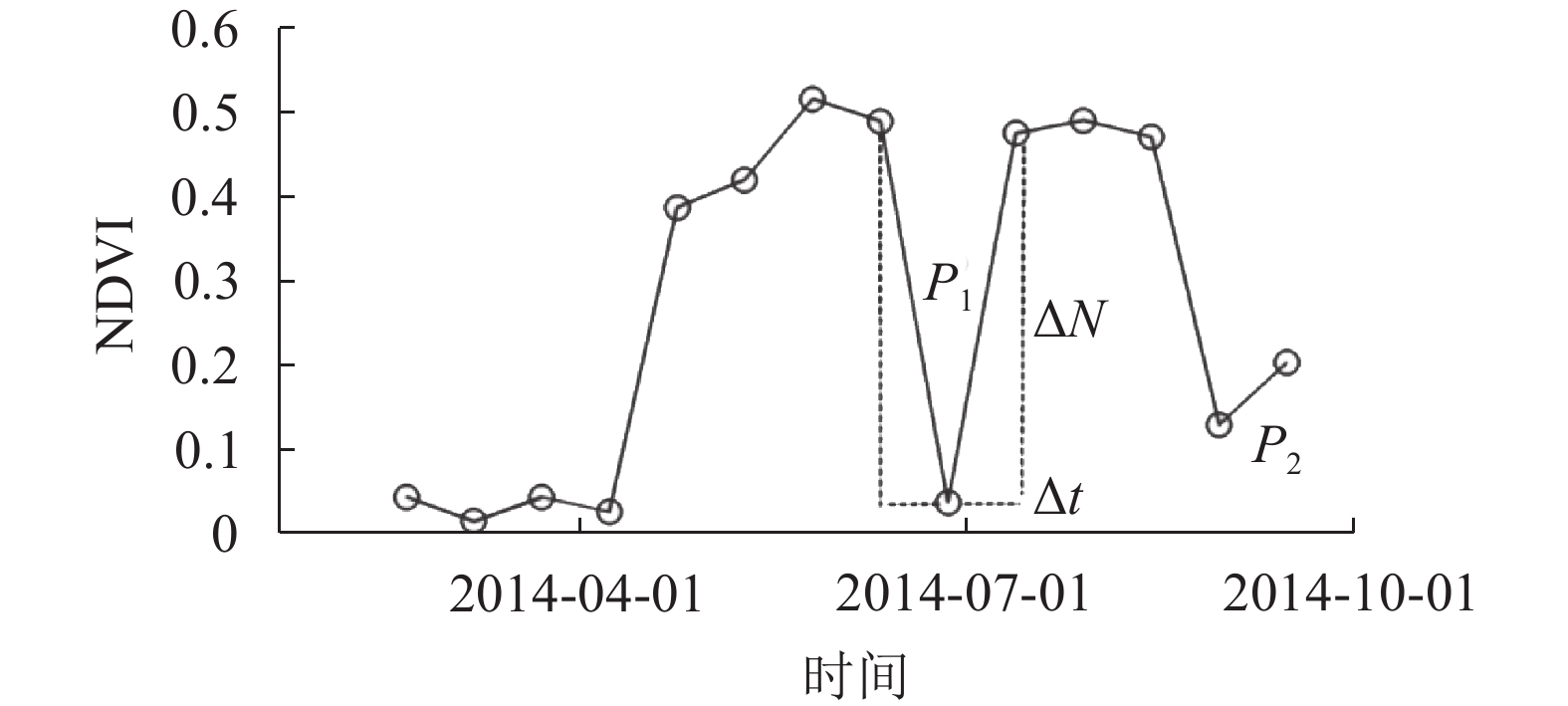
上述云影掩模仅对于厚云作用比较明显,而难于识别薄云、雾霾等,因而,需要进一步对其进行处理。植被的生长(或者衰落)是一个循序渐进的过程,表现为时间序列NDVI值上缓慢的变化。自然灾害(森林大火)或者人为扰动等因素使得地表植被迅速破坏,从而造成NDVI陡降;但是对于植被的生长过程,即使是树木移栽等过程也需要一段时间的恢复,NDVI陡升的可能性相对较小。因而,可以通过NDVI时间序列值上“陡升陡降”的突变来进一步识别时间序列NDVI噪声。图2是某一地区2014年NDVI随时间变化的曲线,可以看出:P1点数据是陡降之后又出现陡升现象,并回到接近原来的水平,从而可以判定为噪声。P2点数据的陡降和陡升现象都没有P1点明显,在NDVI陡降的随后NDVI缓慢恢复,因而可能一次人为的扰动,也可能是噪声,需要结合其他特征予以进一步判断。
根据以上分析,本文的突变点提取方法为计算某一时间点ti上NDVI随时间的变化率
|
${\theta _{{t_i}}} = \frac{{\Delta N}}{{\Delta t}} = \frac{{{N_{{t_i}}} - {N_{{t_{i + 1}}}}}}{{{t_i} - {t_{i + 1}}}}$
|
(7) |
式中,
|
${\theta _\varepsilon } = 3\frac{{{N_{\rm{Max}}} - {N_{\min }}}}{{t({N_{\max }}) - t({N_{\min }})}}$
|
(8) |
即突变的变化率不能大于从最大值与最小值变化率的3倍。
本文利用QA波段和突变点检验法对明显噪声点进行识别和剔除,继而利用保留数据进行高斯拟合,得到较为准确的初始拟合结果。需要说明的是:为了不破坏原始数据的时序序列,剔除的噪声数据的权重值设置为0,不将其从原始数据队列中删除,从而不改变原始的序列。
3.2 权重估计与迭代优化
上述去噪过程能够较好地剔除厚云等,然而薄云、雾霾等因素仍然会造成NDVI被低估,使得NDVI的初步拟合曲线依然位于真实NDVI曲线的下方。因而,需要对每个数据点进行权重评估,以抑制位于初始拟合曲线下方的数据对于迭代结果的影响。
一般地,考虑第k次迭代拟合,其相对于上一次的拟合残差
|
$d_{{t_i}}^{k,k - 1} = f(N_{{t_i}}^k) - f(N_{{t_i}}^{k - 1})$
|
(9) |
式中,
|
${{{D}}^{k,k - 1}} = \{ d_{{t_1}}^{k,k - 1},d_{{t_2}}^{k,k - 1},...,d_{{t_n}}^{k,k - 1}\} \sim N({\mu ^k},{({\sigma ^k})^2})$
|
(10) |
一般来说,
|
$w_{{t_i}}^k = \frac{1}{{{\sigma ^{k,k - 1}}\sqrt {2\pi } }}{{\rm{e}}^{ - \frac{{{{(d_{{t_i}}^{k,k - 1} - d_{\min }^{k,k - 1})}^2}}}{{2{{({\sigma ^{k,k - 1}})}^2}}}}}$
|
(11) |
式中,
在获得遥感影像数据点的权重值后,将原最小二乘法迭代模型进行修改,加入权重值,将其修改成带权重的最小二乘拟合,表示为
|
$Q({N^k}) = \arg \min \sum\limits_{i = 1}^n {w_{{t_i}}^{k,k - 1} \times {{({N_{{t_i}}} - f(N_{{t_i}}^k))}^2}} $
|
(12) |
将优化后的NDVI数据集和权重集代入高斯模型,利用带权的最小二乘法解算得到新的拟合结果。
迭代过程的目标是获得稳定的拟合结果,因而迭代过程结束的条件一般是达到最大迭代次数或者获得稳定的结果,记相邻两次的迭代残差变化绝对值为
|
$\left| {d_{{t_i}}^{k,k - 1}} \right| = |f(N_{{t_i}}^k) - f(N_{{t_i}}^{k - 1})| < {D_\varepsilon }$
|
(13) |
式中,
(1) 分别计算各个数据点的初始拟合残差向量
(2) 根据残差向量
(3) 利用加权最小二乘拟合法再次进行NDVI曲线拟合;
(4) 判断残差
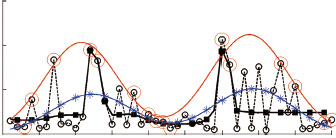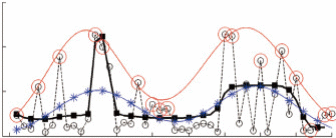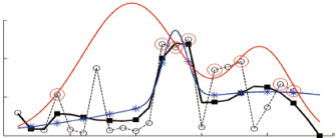
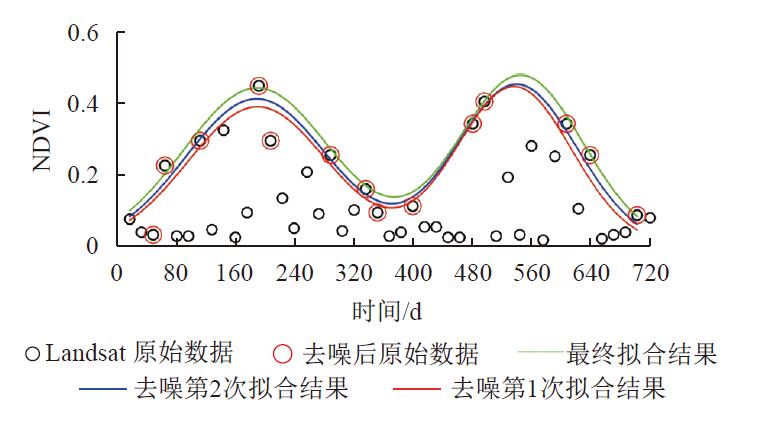
图3给出杭州地区某个地表类型为森林的像素迭代拟合过程。图像中噪声数据很多,仅存稀疏的高质量数据点,通过本文方法拟合,曲线不断地抬升,最终获得稳定的拟合结果。从图3中还可以看出,本文方法与支持向量机分类的原理类似,仅少数分布在管壁上的样本点(即支持向量)对分类结果起作用,而本文方法上仅少数高质量的样本点对拟合结果起作用,从而在稀疏有效数据的情况下获得较高的拟合精度。
4 实 验
4.1 实验数据与实验方法
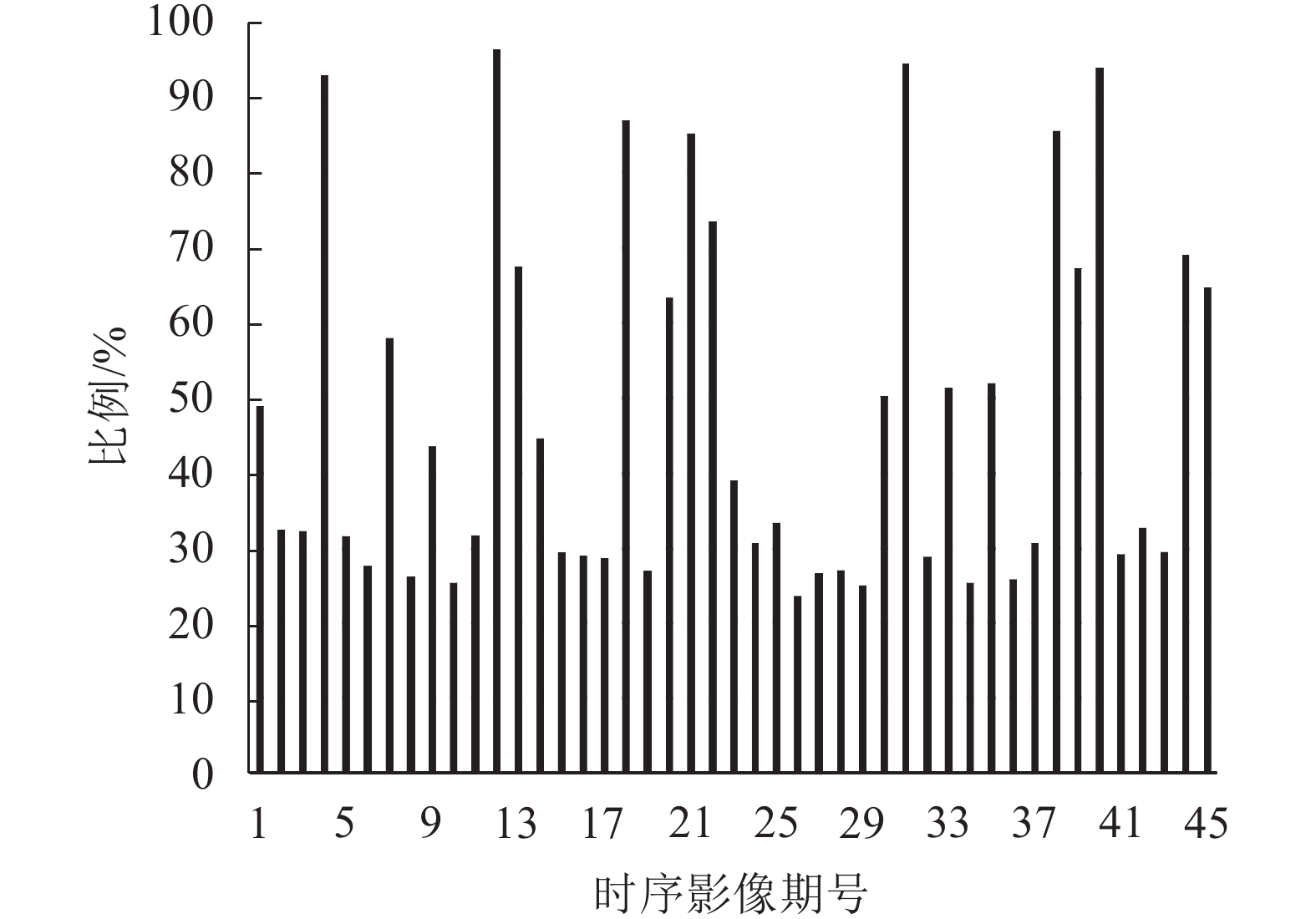
本文选取了Landsat 8获取的OLI数据进行实验,数据涵盖2014年到2015年时间内的所有数据,共45景,空间分辨率为30 m,时间分辨率为16 d。影像在World Reference System(WRS)坐标系中的Path为129,Row为31,研究区位于浙江省中部和北部,该区域属于亚热带季风气候,植被覆盖度较高,为亚热带常绿阔叶林(如马尾松等)以及毛竹等。多云多雨的气候条件使得无云数据的获取尤其困难,总共45景数据中,根据QA波段的统计(图4),无云影比例高于50%的影像数目不足1/3,平均各个像素的每年的有效像元数目仅为8个左右,且分布不均匀,较长时间内均缺乏有效的观测象元。
本文采用MODIS MOD13Q1 v6的数据作为验证,该数据的空间分辨率为250 m,搭载在Terra和Aqua卫星的两台传感器能够在1—2 d内实现对全球表面进行一次观测。该数据产品是16天最大NDVI合成的数据产品,能够较好的克服云影噪声的影响,同时由于光谱通道较多,从而更好地描述获取时刻的大气等条件以进行精确的大气校正。因而,本文将其作为标准数据来评价本文方法的实验结果。由于MODIS数据和Landsat 8数据空间分辨率不同,以Landsat为中心的8×8个数据点区域的均值和MODIS中的相应位置数据点进行时序拟合结果的比较。
本文采用二阶高斯拟合、AG拟合以及张霞等人(2010)改进傅里叶拟合作为对比方法。首先将二阶高斯拟合法、AG拟合法和本文方法进行目视判断,以定性的评价拟合结果。在此基础上,分别与MODIS数据拟合结果进行定量比较,具体指标包括相关系数、峰谷值天数差、峰值偏离度以及动态时间弯曲距离(DTW)等。其中,相关系数是指两条曲线的相似性,相关系数越高,两条拟合曲线的线性相关性越好;峰谷值时差是拟合曲线从谷值到峰值的所经历的天数,是生长期估计的基础;峰值偏离度是以MODIS数据拟合曲线的峰值所在天数为标准,其他拟合曲线的峰值所在天数与其的差值;DTW能够较好地评价曲线间的距离,从而表征拟合的绝对精度。
本文从影像上选取20处地表覆被类型为森林、农作物的像素进行实验,选择依据是面积大于8×8均质的区域,以利于和MODIS结果比较。首先DN值转化为天顶反射率TOA,再计算NDVI。本文通过读取Landsat OLI数据中的QA波段,剔除卷云噪声(cirrus)、云噪声(cloud)、冰雪(snow/ice)等信息可信度二进制表示为10和11的数据,继而用突变点检测法对原始数据进行噪声数据的剔除。然后再对保留的数据采用本文方法及其对比方法进行拟合。
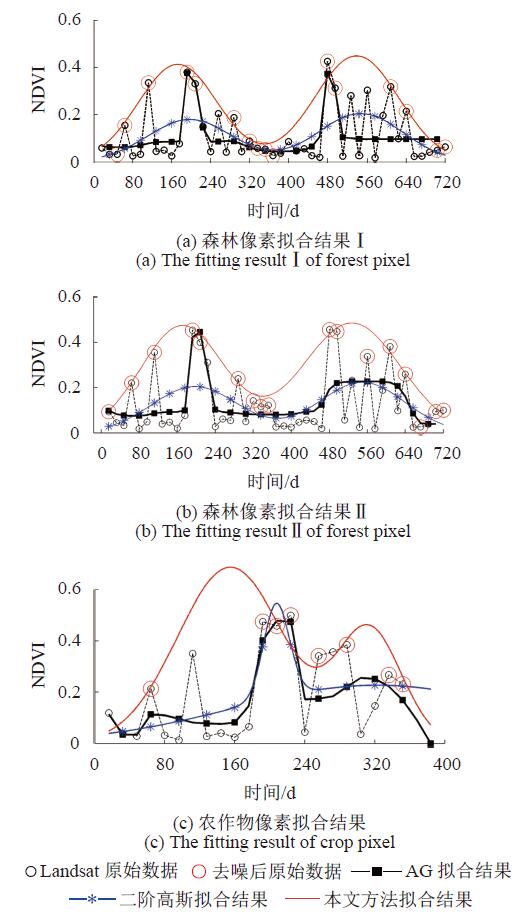
4.2 实验结果与分析
图5给出了3组实验的结果。其中,图5(a)(b)为一年单峰谷的森林,图5(c)表示一年多峰谷值的农作物。从实验结果中可以看出:(1)基于二阶高斯的时序拟合法和本文方法都较好地表现了森林的生长物候特点,即NDVI指数的拟合曲线走势大致相同,而AG拟合法由于噪声比例较大,导致数据的估计严重偏低;(2)本文方法的拟合结果值高于原始数据及其他拟合方法的结果,从而更有可能贴近真实值,即植被物候特性的描述更加准确;而二阶高斯拟合法和AG拟合法普遍比原始数据值偏小,造成NDVI被低估;(3)本文方法能够有效地保持地物的多峰谷特性,从而获得更好的拟合结果,而对于对比的二阶高斯拟合方法在一个周期内有效数据太少,不能有效的识别峰谷,从而导致拟合失败。
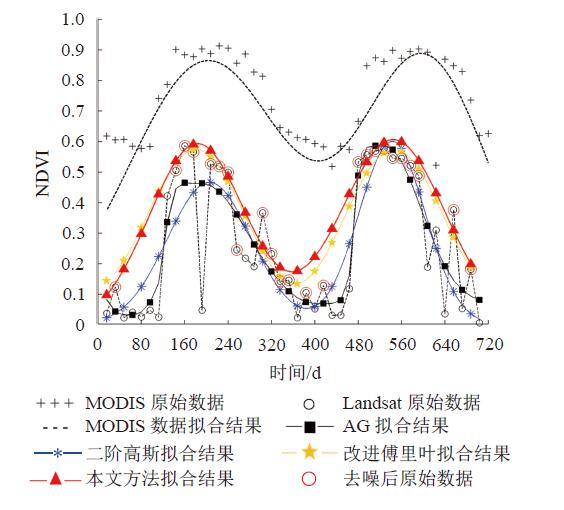
图6给出了一组本文方法和对比方法的结果与MODIS参考结果的数据对比情况。从中可以看出:与AG拟合结果相比,本文的迭代加权拟合结果和MODIS拟合结果具有更相似的曲线走势,相同的植被生长期和衰退期等物候特点。与改进傅里叶拟合方法和二阶高斯拟合结果相比,由于本文的方法去除了噪声数据,并通过迭代的权重计算使得拟合结果更加接近MODIS拟合结果,即更可能接近植被指数的真实值。然而Landsat 8数据中仍然存在很多噪声、传感器响应等影响,导致MODIS数据拟合结果中的植被指数相对迭代加权拟合法的植被指数仍然存在偏差。总体看来,本文的迭代加权拟合法已经能够在稀疏时序数据的情况进行拟合,获得类似于MODIS数据的拟合结果。
对20组森林实验点计算了上述统计指标的算术平均值。从表1中可以看出,本文的迭代加权拟合法与MODIS数据的相关系数最高,所以拟合结果与MODIS数据拟合结果线性相关性最好。从峰谷值时差和峰值偏离度两方面看,本文方法结果较为接近MODIS数据拟合结果,改进的傅里叶方法次之,由此看出本文方法的NDVI最大值拐点时刻最接近MODIS数据拟合结果。而由于噪声较多,AG拟合法无法获得正确的拟合结果。从以上3个特征值说明本文的方法在曲线走势上相较另外两种方法更为接近真实值。从DTW距离可以看出,本文的方法从曲线数值上更加接近MODIS数据拟合结果值。
表 1 拟合曲线特征值表
Table 1 The table fit the curve characteristic value
| 特征值 | 二阶高斯拟合法 | 改进傅里叶拟合 | AG拟合法 | 迭代加权拟合法 | MODIS数据高斯拟合 |
| 相关系数 | 0.865 | 0.8856 | 0.772 | 0.9282 | 1 |
| 峰谷值时差/d | 157 | 171 | – | 180 | 202 |
| 峰值偏离度/d | 18.579 | 8.314 | – | 5.16 | 0 |
| DTW距离 | 4.703 | 3.153 | 5.160 | 2.552 | 0 |
在此基础上,将NDVI从底部增加10%作为返青期,提取了浙江省的森林返青期,并将其与MODIS提取结果、物候观测资料进行了比较,误差在5 d之内,从而为利用中分辨率稀疏有效数据获得类似于MODIS高时间数据分辨率数据的拟合结果提供了可能。
4.3 参数设置
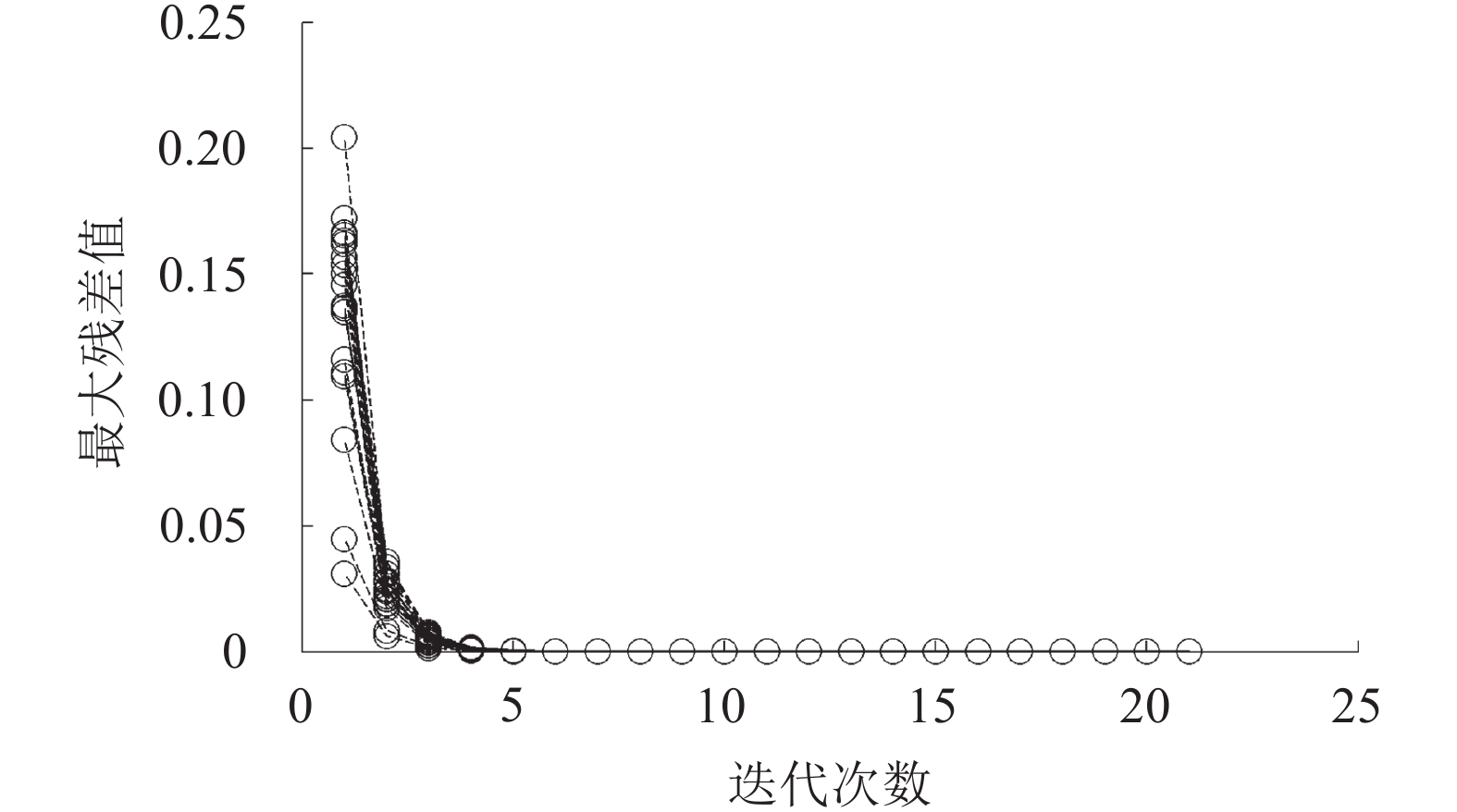
本文算法应用的一个关键因素是算法的收敛性,即算法能否获得稳定的拟合结果。从理论上来看,当算法获得较好的拟合结果,最大残差值应趋近于0。图7给出了上述20组实验的前后两次拟合最大残差
5 结 论
针对仅具有稀疏有效数据的情况,本文基于云影噪声造成NDVI被低估的先验知识,实现噪声识别并建立数据质量评价方法,定量评估权重,通过加权拟合将数据质量的先验知识融入到算法。经过不断迭代拟合,获取稳定的拟合结果。与当前主流的方法相比,本文方法能够获取较好的结果,定量与定性方法都表明本文方法能够获得更加接近高时间分辨率MODIS数据拟合的结果。
该方法减少了人为主观影响和原始数据中噪声造成的过度扰动,使得拟合结果更为客观真实。方法的输入参数较少,算法能够快速收敛,且稳定性较好。
然而,本文的研究也存在一些不足,例如,稀疏有效数据对于关键时点数据等问题的定量评价不足;一年之内至少需要多少有效的数据等进行时序拟合需要进一步评估;权重的绝对准确性需要定量评价,并与Landsat中类似分辨率的数据进行比较和确定;由于本文使用的实验数据相对稀疏,且拟合结果对于噪声进行了抑制,导致曲线相对平滑,使得曲线中的信息含量偏少,一种理想方式是对缺失的噪声数据进行估计,以生成信息丰富的曲线。
参考文献(References)
-
Atkinson P M, Jeganathan C, Dash J and Atzberger C. 2012. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sensing of Environment, 123 : 400–417. [DOI: 10.1016/j.rse.2012.04.001]
-
Beck P S A, Atzberger C, Høgda K A, Johansen B and Skidmore A K. 2006. Improved monitoring of vegetation dynamics at very high latitudes: a new method using MODIS NDVI. Remote sensing of Environment, 100 (3): 321–334. [DOI: 10.1016/j.rse.2005.10.021]
-
Carrão H, Gonçalves P and Caetano M. 2010. A nonlinear harmonic model for fitting satellite image time series: analysis and prediction of land cover dynamics. IEEE Transactions on Geoscience and Remote Sensing, 48 (4): 1919–1930. [DOI: 10.1109/TGRS.2009.2035615]
-
Chen J, Jönsson P, Tamura M, Gu Z H, Matsushita B and Eklundh L. 2004. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sensing of Environment, 91 (3/4): 332–344. [DOI: 10.1016/j.rse.2004.03.014]
-
Fu P and Weng Q H. 2016. A time series analysis of urbanization induced land use and land cover change and its impact on land surface temperature with Landsat imagery. Remote Sensing of Environment, 175 : 205–214. [DOI: 10.1016/j.rse.2015.12.040]
-
Hird J N and McDermid G J. 2009. Noise reduction of NDVI time series: an empirical comparison of selected techniques. Remote Sensing of Environment, 113 (1): 248–258. [DOI: 10.1016/j.rse.2008.09.003]
-
Jönsson P and Eklundh L. 2002. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Transactions on Geoscience and Remote Sensing, 40 (8): 1824–1832. [DOI: 10.1109/TGRS.2002.802519]
-
Jönsson P and Eklundh L. 2004. TIMESAT—a program for analyzing time-series of satellite sensor data. Computers and Geosciences, 30 (8): 833–845. [DOI: 10.1016/j.cageo.2004.05.006]
-
Kim S R, Prasad A K, El-Askary H, Lee W K, Kwak D A, Lee S H and Kafatos M. 2014. Application of the Savitzky-Golay filter to land cover classification using temporal MODIS vegetation indices. Photogrammetric Engineering and Remote Sensing, 80 (7): 675–685. [DOI: 10.14358/PERS.80.7.675]
-
Ma T, Zhou C H, Pei T, Haynie S and Fan J F. 2012. Quantitative estimation of urbanization dynamics using time series of DMSP/OLS nighttime light data: a comparative case study from China’s cities. Remote Sensing of Environment, 124 : 99–107. [DOI: 10.14358/PERS.80.7.675]
-
Mello M P, Vieira C A O, Rudorff B F T, Aplin P, Santos R D C and Aguiar D A. 2013. STARS: a new method for multitemporal remote sensing. IEEE Transactions on Geoscience and Remote Sensing, 51 (4): 1897–1913. [DOI: 10.1109/TGRS.2012.2215332]
-
Roerink G J, Menenti M and Verhoef W. 2010. Reconstructing cloud free NDVI composites using Fourier analysis of time series. International Journal of Remote Sensing, 21 (9): 1911–1917. [DOI: 10.1080/014311600209814]
-
Verbesselt J, Hyndman R, Newnham G and Culvenor D. 2010. Detecting trend and seasonal changes in satellite image time series. Remote Sensing of Environment, 114 (1): 106–115. [DOI: 10.1016/j.rse.2009.08.014]
-
Zhu Z and Woodcock C E. 2014. Automated cloud, cloud shadow, and snow detection in multitemporal Landsat data: an algorithm designed specifically for monitoring land cover change. Remote Sensing of Environment, 152 : 217–234. [DOI: 10.1016/j.rse.2014.06.012]
-
Yang H, Huang W J, Wang J H, Yang G J, Tu N M, Yang X D and Wang D C. 2011. Monitoring rice growth stages based on time series HJ-1A/1B CCD images. Transactions of the Chinese Society of Agricultural Engineering, 27 (4): 219–224. [DOI: 10.3969/j.issn.1002-6819.2011.04.038] ( 杨浩, 黄文江, 王纪华, 杨贵军, 屠乃美, 杨小冬, 王大成. 2011. 基于HJ-1A/1B CCD时间序列影像的水稻生育期监测. 农业工程学报, 27 (4): 219–224. [DOI: 10.3969/j.issn.1002-6819.2011.04.038] )
-
Zhang X, Li R, Yue Y M, Liu B and Liu H X. 2010. Improved algorithm for reconstructing vegetation index image time series based on Fourier harmonic analysis. Journal of Remote Sensing, 14 (3): 437–447. [DOI: 10.11834/jrs.20100303] ( 张霞, 李儒, 岳跃民, 刘波, 刘海霞. 2010. 谐波改进的植被指数时间序列重建算法. 遥感学报, 14 (3): 437–447. [DOI: 10.11834/jrs.20100303] )