高光谱遥感是在多光谱遥感基础上发展起来的能够同时获取光谱信息和空间信息的遥感技术，其光谱分辨率为纳米级，光谱波段数多达数百个，为地物分类和目标识别提供丰富的光谱信息，因此高光谱图像常用于地物的精细分类(童庆禧 等，2006)。然而，由于Hughes现象，高光谱图像的分类精度随波段数目增加而降低(Hughes，1968)。在训练样本稀少时，研究如何提升高光谱图像分类精度，具有重要的理论意义和应用价值。

由于成像光谱仪波段狭窄导致光成像能量不足，相对于全色和多光谱图像，高光谱图像噪声比较严重。在样本稀少、样本质量较差或可信度较低等情况下，噪声将会对高光谱图像的分类结果造成严重影响。近年来，许多高光谱图像降噪方法被提出，如主成分分析法(PCA)、多维分析法(Liu 等，2012)、全方差法(Yuan 等，2012)等。其中，PCA是一种经典的高光谱图像降维方法，每一个主成分都与前面的主成分线性无关且在剩余成分中包含的信息量(即方差)最大。然而，当噪声的能量较大时，信息量大的主成分分量反而信噪比较低，因此PCA变换并不能保证图像质量更高的主成分分量排在前面(张兵和高连如，2011)，可能出现信噪比低的主成分被选为特征波段，而信噪比相对较高的编号较大的主成分被丢弃，导致高光谱图像信息损失和分类精度降低。

为解决这个问题，应该在PCA变换前尽量消除高光谱图像中的强噪声。根据强噪声具有稀疏性的特点，首先利用稀疏与低秩矩阵分解方法将高光谱图像分解成低秩的信号矩阵和稀疏的噪声矩阵，从而将强噪声从高光谱图像数据中分离。然后，利用PCA变换对低秩的信号矩阵降维，同时消除高斯弱噪声。最后，利用边缘保持的滤波方法消除分类结果图的“椒盐噪声”。本文方法通过多级降噪滤波依次去除高光谱图像的强噪声、弱噪声和分类结果图中的噪声，提高高光谱图像的分类精度和质量。

本文使用3种图像降噪滤波方法，包括稀疏与低秩矩阵分解方法、PCA方法和引导滤波方法。由于PCA方法的相关资料较多，主要介绍其他两种降噪滤波方法。

稀疏与低秩矩阵分解法SLRMD(Sparse and Low Rank Matrix Decomposition)(Wright 等，2009)假设一个2维矩阵 ${{D}} \in {{\bf{R}}^{m \times n}}$ 可以分解为1个稀疏矩阵E和1个低秩矩阵A，分解的数学模型可表示为式(1)的最优化问题

$\begin{array}{*{20}{c}}{\mathop {\rm{min}}\limits_{A,{{E}}} {{\left\| {{A}} \right\|}_*} + \lambda {{\left\| {{E}} \right\|}_1}}\\{\begin{array}{*{20}{c}}{{\rm{s}}{\rm{.t}}{\rm{.}}}&{{{D}} = {{A}} + {{E}}}\end{array}}\end{array}$

(1)

式中， ${\left\| \cdot \right\|_*}$ 是矩阵的核范数，它是矩阵奇异值之和，是矩阵秩的凸近似； ${\left\| \cdot \right\|_1}$ 是矩阵的1范数，它是矩阵各元素绝对值之和，是矩阵0范数的凸近似； $\lambda $ 表示权重系数。

SLRMD的实现方法包括迭代阈值法(Wright 等，2009)、加速邻近梯度法(Beck和Teboulle，2009)、增广拉格朗日乘子法、ALM(Augmented Lagrange Multiplier Method)(Lin 等，2009)等。林宙辰等人提出了两种效率较高的ALM方法，即精确增广拉格朗日乘子法，EALM(Exact ALM)和非精确增广拉格朗日乘子法，IALM(Inexact ALM)，后者运算速度可以达到加速邻近梯度法的5倍且同样能够收敛到式(1)中最优化问题的最优解。

增广拉格朗日乘子法(ALM)是针对罚函数法由于罚参数过大引起的数值计算上的困难，结合拉格朗日函数，对非可行点加以惩罚的最优化方法。具体来说，针对式(2)的等式约束最优化问题

$\begin{array}{*{20}{c}}{\min f({{X}})\begin{array}{*{20}{c}}{}&{}\end{array}}\\{\begin{array}{*{20}{c}}{{\rm{s}}{\rm{.t}}{\rm{.}}}&{h({{X}}) = 0}\end{array}}\end{array}$

(2)

构造增广拉格朗日函数

$\begin{array}{l}L({{X}},{{\varLambda}} ,\mu ) = \\f({{X}}) + \left\langle {{\varLambda}} \right.,\left. {h({{X}})} \right\rangle + \displaystyle\frac{\mu }{2}\left\| {h({{X}})} \right\|_{\rm{F}}^2\end{array}$

(3)

式中， $\mu $ 是罚参数， $\mu > 0$ ； ${{\varLambda}} $ 是拉格朗日乘子， $\left\langle {\left. {{{A}},{{B}}} \right\rangle } \right. = {\mathop{\rm trace}\nolimits} ({{A}}{{{B}}^{\rm{T}}})$ 表示两个矩阵内积。ALM通过迭代获得下面无约束最优化问题的解：

${{X}} = \arg \mathop {\min }\limits_{{X}} L({{X}},{{\varLambda}} ,\mu )$

(4)

针对SLRMD最优化问题(1)，令 ${{X}} = ({{A,E}})$ ， $f({{X}}) = {\left\| {{A}} \right\|_*} + \lambda {\left\| {{E}} \right\|_1}$ ， $h({{X}}) = {{D}} - {{A}} - {{E}}$ ，构造如下增广拉格朗日函数

$\begin{array}{l}{\mathop{\rm L}\nolimits} ({{A}},{{E}},{{\varLambda }},\mu ) = \\[5pt]{\left\| {{A}} \right\|_*} + \lambda {\left\| {{E}} \right\|_1} + \left\langle {{{{{\varLambda}} ,D}} - {{A}} - {{E}}} \right\rangle + \\[5pt] \displaystyle\frac{\mu }{2}\left\| {{{D}} - {{A}} - {{E}}} \right\|_{\mathop{\rm F}\nolimits} ^2\end{array}$

(5)

在求解式(5)时，首先固定E、 ${{\varLambda }}$ 、μ，求解使 ${\mathop{\rm L}\nolimits} ({{A}},{{E}},{{\varLambda }},\mu )$ 最小的A；然后固定A、 ${{\varLambda}} $ 、μ，求解使 $L({{A}},{{E}},{{\varLambda }},\mu )$ 最小的E，反复迭代直至算法收敛。为了方便求解计算A、E，可以利用软阈值求解公式(Lin 等，2009)

$\begin{array}{l}{{U}}{S_\varepsilon }({{S}}){{{V}}^{\rm{T}}}\\ = \arg \mathop {\min }\limits_{{X}} \varepsilon {\left\| {{X}} \right\|_*} + \frac{1}{2}\left\| {{{X}} - {{W}}} \right\|_{\rm{F}}^2\end{array}$

(6)

${S_\varepsilon }({{W}}) = \arg \mathop {\min }\limits_{{X}} \varepsilon {\left\| {{X}} \right\|_1} + \frac{1}{2}\left\| {{{X}} - {{W}}} \right\|_{\rm{F}}^2$

(7)

式中， $({{U}},{{S}},{{V}}) = svd({{W}})$ ， $svd$ 是奇异值分解函数； ${S_\varepsilon }(x)$ 的定义如式(8)所示 $(\varepsilon > 0)$ ，是软阈值收缩算子。

${S_\varepsilon }(x) \buildrel\textstyle.\over= \left\{ {\begin{array}{*{20}{c}}{x - \varepsilon } \,\,\,\,\, \quad \\[5pt]{x + \varepsilon } \,\,\,\,\,\, \quad \\[5pt]{0} \,\,\,\,\, \, \quad\end{array}} \right.\begin{array}{*{20}{c}}\!\!\!\!{x > \varepsilon }\\[5pt]{x < - \varepsilon }\\[5pt]{\left| x \right| \leqslant \varepsilon }\end{array}$

(8)

SLRMD方法能够从高光谱图像中分离出低秩的矩阵，而低秩矩阵意味着矩阵的列或行相关性更强、噪声更低，因此许多研究者提出利用SLRMD方法对高光谱图像进行降噪或分类。

引导滤波GF(Guided Filter)通过引导图像控制滤波器的输出是一种高效边缘保持滤波方法(He 等，2010)。引导图像可以是输入图像本身，也可以是其他边缘清晰的图像，如PCA变换后的第一主成分分量。引导滤波方法假定在引导图像I和滤波输出q之间存在一个局部线性模型，即在以像素k为中心的窗口 ${{{\omega }}_{{k}}}$ 内，q是I的一个线性变换：

$\begin{array}{*{20}{c}}{{{{q}}_i} = {{{a}}_k}{{{I}}_i} + {{{b}}_k},}&{\forall i \in {{{\omega }}_{{k}}}}\end{array}$

(9)

式中， $({{{a}}_k},{{{b}}_k})$ 在 ${{{\omega }}_{{k}}}$ 内是常数。对式(9)的两边求导，可得 $\nabla {{O}} \approx a\nabla {{I}}$ ，这意味着仅当引导图像I有一条边时，滤波输出q中才会有一条边，达到了边缘保持的目的。系数a_k和b_k的值可以通过最小化下面的能量函数获得：

${\mathop{\rm E}\nolimits} ({{{a}}_k},{{{b}}_k}) = \sum\limits_{i \in {{{\omega }}_{{k}}}} {({{({{{a}}_k}{{{I}}_i} + {{{b}}_k} - {{{p}}_i})}^2} + \varepsilon {{a}}_k^2)} $

(10)

式中，p是输入图像； $\varepsilon $ 是正则化参数，避免a_k的值过大。上式的最优解能够最小化滤波输入p和输出q之间的差异。

由于一个像素i同时包含在多个局部窗口 ${{{\omega }}_{{k}}}$ 内，每个窗口 ${{{\omega }}_{{k}}}$ 计算的q_i值都是不同的，因此最终滤波输出可以通过对所有可能的q_i值求均值得到，其中 $\left| \omega \right|$ 是窗口 ${{{\omega }}_{{k}}}$ 内像素的数量。

${{{q}}_i} = \frac{1}{\omega }\sum\limits_{k,i \in {{{\omega }}_{{k}}}} {({{{a}}_k}{{{I}}_i} + {{{b}}_k})} $

(11)

引导滤波方法在计算机视觉和计算机图形学等领域应用很广泛，包括图像降噪、细节平滑/增强、图像去雾等。Kang等人(2014a)将引导滤波方法应用于SVM分类结果的后处理，去除分类图中的“椒盐噪声”，使高光谱图像分类精度有显著提高。

现有的SLRMD方法大多是利用高光谱图像波段之间的相关性，即矩阵列之间的高相关性进行低秩矩阵分解(Lu 等，2013；Zhang 等，2014；Zhao和Yang，2015)，但也有利用斑块内部像素之间的相关性，即矩阵行之间的高相关性进行低秩矩阵分解(Xu 等，2015)。本文结合这两种矩阵分解方法的优点，提出了分别利用斑块内部像素之间的相关性和波段之间的相关性进行矩阵分解，也就是两阶段的稀疏与低秩矩阵分解TSLR(Two-phase Sparse and Low Rank matrix decomposition)。具体过程如下：首先，对高光谱图像进行分割，将每个斑块的像素数据组成1个子矩阵，对该子矩阵进行稀疏与低秩矩阵分解；然后，合并所有的低秩子矩阵，对合并后的2维矩阵进行稀疏与低秩矩阵分解。因此，TSLR方法能够充分利用斑块内部像素矩阵的低秩性和高光谱图像光谱矩阵的低秩性，从行和列两个方向上消除高光谱图像中的强噪声。

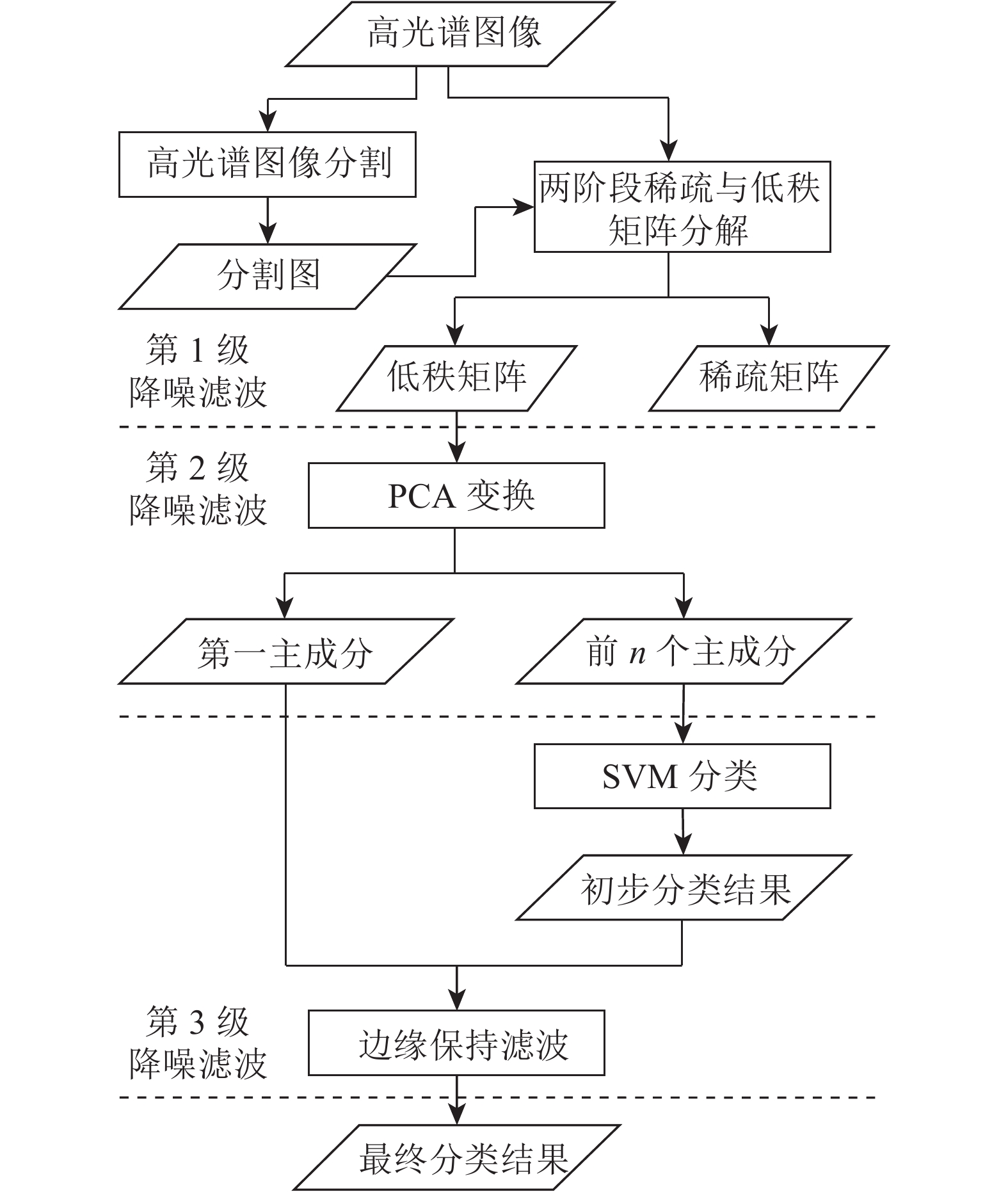
高光谱图像中大多数噪声是随机的能量较低的高斯白噪声，少部分是稀疏的能量较高的强噪声。由于强噪声和高斯白噪声分布模型不同，因此很难用单一的降噪方法同时进行有效的噪声消除。为此，本文提出了应用多种降噪滤波的方法分别消除高光谱图像中不同类型的噪声，获得高信噪比的特征波段，提高高光谱图像的分类精度。由于像素级分类器的分类结果中“椒盐噪声”现象比较严重，本文利用像素类别之间的空间相关性对那些错误标记的像素类别进行校正，同时保持分类结果中的地物边缘与真实地物边缘一致。图1是基于多级降噪滤波的高光谱图像分类方法总体流程图。

总体流程：首先，利用面向对象的图像分割方法将高光谱图像分割成若干个斑块，这些斑块信息将用于两阶段稀疏与低秩矩阵分解方法对高光谱图像进行降噪，消除图像中的强噪声。然后，利用PCA变换对分解后的低秩矩阵进行降维，去掉后面噪声较多的主成分，保留前n个信噪比较高的主成分。进而，利用SVM分类器和训练样本进行分类，得到一个初步的分类结果。最后，利用第一主成分作为引导图像，对SVM分类器的初步分类结果进行边缘保持滤波，生成最终的分类结果图。

基于多级降噪滤波的高光谱图像分类步骤：

(1) 使用面向对象的分割方法对高光谱图像进行分割，生成分割图 ${{S}} = \{ {{{S}}^{(1)}},{{{S}}^{(2)}}, \cdots ,{{{S}}^{(P)}}\} $ 。(2) 稀疏与低秩矩阵分解(第1阶段)：　 $\begin{array}{*{20}{c}}{for}&{r = 1:p}\end{array}$ 　构造矩阵 ${{{D}}^{(r)}} \in {{\bf {R}}^{\left| {{{S}}(r)} \right| \times n}}$ ， $\left| \cdot \right|$ 表示集合的基数， ${{{D}}^{(r)}}$ 中的每一行对应同质斑块 ${{{S}}^{(r)}}$ 中的一个像素；　 ${{{D}}^{(r)}}$ 转置，使矩阵每一列对应一个像素；　 $\{ {{{A}}^{(r)}},{{{E}}^{(r)}}\} = {\mathop{\rm IALM}\nolimits} ({{{D}}^{(r)}})$ ，IALM函数表示利用非精确增广拉格朗日乘子法对矩阵做稀疏与低秩分解， ${{{A}}^{(r)}}$ 是分解后的低秩矩阵， ${{{E}}^{(r)}}$ 是分解后的噪声矩阵；　 $end$ (3) 稀疏与低秩矩阵分解(第2阶段)：　1)构造低秩矩阵 ${{A}} = \{ {{{A}}^{(1)}},{{{A}}^{(2)}}, \cdots ,{{{A}}^{(p)}}\} $ ，将各个斑块的低秩数据组织成图像矩阵A；　2)A转置，使A的每一列对应一个光谱波段；　3) $\{ {{A'}},{{E'}}\} = {\mathop{\rm IALM}\nolimits} ({{A}})$ ，对矩阵A做稀疏与低秩分解；(4) PCA变换： ${{A''}} = {\text{PCA}}({{A'}},dims)$ ， $dims$ 表示新的特征空间的维数；(5) 利用SVM分类器和训练样本集T对数据集 ${{A''}}$ 分类，得到分类图 ${{M}} = {\mathop{\rm SVM}\nolimits} ({{A''}},{{T}})$ ；(6) 将高光谱图像的第一主成分作为引导图像，对分类图进行引导滤波，去除“椒盐噪声”，输出分类图 $ClassMap = {\rm{GF}}({{M}},{\rm{PCA}}({{D}},1))$ 。

(1) Indian Pines。利用机载可见光/红外成像光谱仪(AVIRIS)获取的来自印第安纳州西北部Indian Pines农业试验场的高光谱图像。主要地物类型包括玉米、大豆、苜蓿、小麦、燕麦、草、树等，部分地物还进行了细分，比如玉米分为免耕法、少耕法和传统耕作法3种类型，总共16种地物。图像空间分辨率为20 m，220个波段，光谱范围为400—2500 nm。Indian Pines图像很多波段噪声严重，从数据集删除20个水吸收严重的波段(104—108, 150—163, 200)，最后得到200个波段。图2给出了Indian Pines三波段假彩色图和地面真值图。

(2) University of Pavia。利用反射光学系统成像光谱仪(ROSIS-03)获取的来自帕维亚大学的高光谱图像。主要地物类型包括柏油马路、草地、砂砾、树、金属板、裸露土壤、沥青屋顶、砖地和阴影，总共9种对象。图像空间分辨率为1.3 m，103个波段，光谱范围为430—860 nm。图3给出了University of Pavia三波段假彩色图和地面真值图。

以Indian Pines高光谱数据集为例验证稀疏与低秩矩阵分解方法的降噪效果。图4是Indian Pines高光谱图像的第1—3波段，这3个波段都受到噪声污染，第1波段噪声尤其严重。图5是矩阵分解后的低秩图像的第1—3波段。从图5可以看出，图像降噪的效果非常明显，而且降噪后的波段之间表现出较强的相关性。

图6给出了Indian Pines图像在矩阵分解前后某一列像素的光谱，图6(b)和图6(c)分别是蓝色实线所在的列像素光谱在矩阵分解前后的结果。根据图6(b)中的地面真值数据，蓝色实线所在的列共包含了5种地物类型，从上到下分别为：免耕玉米、草树混生、少耕大豆、小麦、少耕玉米。从图6可以看出原始图像的像素光谱中包含了很多噪声信息，尤其是在前几个波段和最后几个波段；低秩图像的像素光谱变得非常平滑，除了第2类地物光谱变化比较大之外，其他地物类型的像素光谱都高度相似，因而矩阵是低秩的。第2类地物(红色斑块内)是草和树的混生区，地物分布不均匀导致像素光谱多样化。

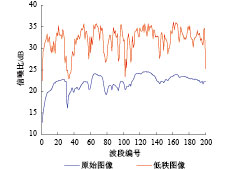
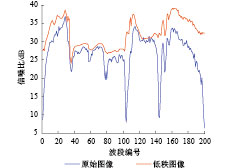
信噪比SNR(Signal-to-Noise Ratio)是衡量遥感图像质量的重要指标。由于真实的高光谱图像理论上无法获得对应的无噪声的波段，因此常用的图像信噪比评价指标，如峰值信噪比(PSNR)、结构相似性指数(SSIM)都不能应用。为此，本文引入了光谱/空间维去相关法和局部方差估计法对图像信噪比进行估计。

光谱和空间维去相关法SSDC(Spectral and Spatial De-Correlation method)是一种专门针对高光谱图像的噪声评估方法，它利用高光谱图像空间维和光谱维存在高相关性的特点，通过多元线性回归去除具有高相关性的信号，利用得到的残差图像对噪声进行估算。该方法受地物覆盖类型影响小，并且可以自动执行，是目前较为稳定的高光谱图像噪声评估方法。将高光谱图像波段的平均值与估算得到的噪声值之比转成dB数就是波段的信噪比。

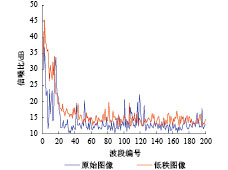
另一种图像信噪比的估计方法是计算图像信号与噪声的功率谱之比。但通常功率谱难以计算，可以近似估计图像信噪比，即信号与噪声的方差之比。首先计算图像中所有像素的局部方差，然后将局部方差的最大值认为是信号方差，最小值是噪声方差，求出它们的比值，再转成dB数，最后用经验公式修正(邹谋炎，2001)。该方法通常被称为局部方差估计法LVE(Local Variance Estimation method)。

图7和图8分别为采用SSDC方法和LVE方法对Indian Pines高光谱图像信噪比估计的结果。可以看出，尽管SSDC方法和LVE方法的计算原理不同，对图像信噪比估计的结果差异较大，但低秩矩阵分解后高光谱图像的信噪比都有显著的提高，在图像光谱范围的两端尤为明显。

下面分析稀疏与低秩矩阵分解对主成分分析的影响。图9是对原始图像和低秩图像做PCA变换后各个主成分分量的信噪比。由于相邻主成分分量光谱不相关，并且各个主成分分量的均值接近于0，因此只能采用LVE方法来估计信噪比。可以看出，原始图像中某些编号较小/特征值较大的主成分，如第7、8、10主成分信噪比极低，但编号比它们大的某些主成分信噪比较高。如果特征提取是根据编号顺序选择光谱特征，则噪声图像极有可能被包含在特征组合中，从而对图像分类造成严重影响。低秩图像经过PCA变换后，编号较小的主成分信噪比都相对较高，没有出现个别主成分信噪比极低的情况，这是由于强噪声已经从图像中去除，特征值大的主成分信号强度也较大，因此图像信噪比较高。

表1是对原始图像和低秩图像做PCA变换后前15个主成分特征值和累加贡献率。可以看出，原始图像PCA变换后前15个主成分累加贡献率为99.823%，而低秩图像PCA变换后前5个主成分的累加贡献率已经达到99.837%。可见，经过SLRMD降噪后图像信息量集中度更高。

本节使用两个高光谱数据集阐述各种图像降噪方法对高光谱图像分类精度的影响。每一种方法都是采用高斯径向基核函数的SVM作为分类器，参数通过五重交叉验证获得。对比的方法包括：像素级SVM、SLRMD(SLR-SVM)、PCA(PCA-SVM)、应用SLRMD和PCA的降噪方法(SLR-PCA-SVM)、两阶段SLRMD降噪方法(TSLR-SVM)、应用TSLR和PCA的降噪方法(TSLR-PCA-SVM)、应用TSLR和PCA对图像降噪处理并对分类结果滤波的方法(TSLR-PCA-GF)。基于图像融合和递归滤波的高光谱图像特征提取方法(IFRF)被用来同本文方法进行对比(Kang 等，2014b)。每次训练样本是从可用样本集中随机选取，剩余所有样本都作为测试样本。所有结果都是通过30次蒙特卡洛运行后计算均值和标准差获得。

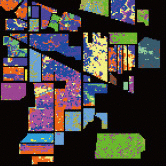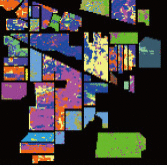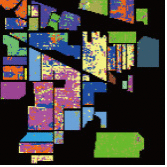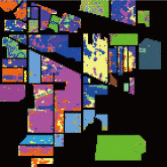
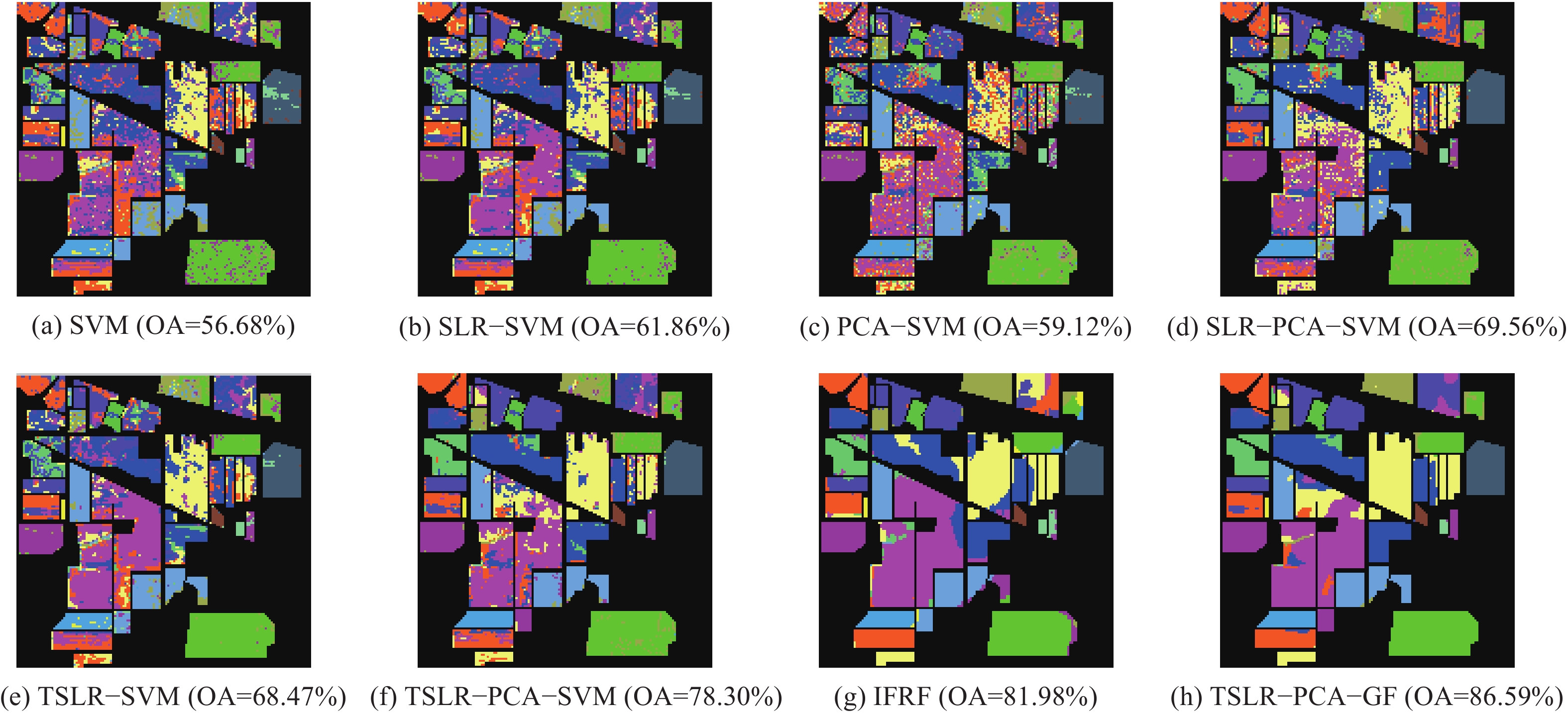
对于Indian Pines图像，每个类别中随机选取12个样本作为训练样本，燕麦因为样本数目太少只选取10个训练样本。训练样本占总样本数的1.85%。表2给出了各种方法的总体精度(OA)、平均精度(AA)、Kappa系数和不同地物类型的分类精度(CA)。每一个数据项的左边是30次重复实验的均值，右边是30次重复实验的标准差。从表2中可以看出，由于样本数目太少，大部分分类方法的精度都较低，SVM分类器的总体精度只有58.79%。PCA-SVM方法的总体精度比SVM还要低2.78%，这是因为降维后前15个主成分包含4个噪声严重的图像，从而影响了分类精度。SLR-SVM方法的总体精度比SVM高3.02%，但SLRMD与PCA结合的方法SLR-PCA-SVM总体精度比SVM提高9.51%，说明这两种方法具有互补性。SLRMD方法去除了强噪声之后，前15个主成分中没有噪声严重的图像。TSLR-SVM方法的总体精度比SVM高6.72%，比SLR-SVM方法提高了3.7%，TSLR与PCA结合的方法TSLR-PCA-SVM总体精度比SVM提高了18.71%，这是因为TSLR方法能够更加有效地去除强噪声，减少了强噪声对PCA主成分排序的干扰。TSLR-PCA-GF方法消除了分类图中的“椒盐噪声”，分类精度最高，比SVM方法提高25.85%，比IFRF方法提高6.04%。图10是某一次实验获得的地物分类图，可以看出TSLR-PCA-GF方法的分类结果更平滑且接近于地面真值图。

对于University of Pavia图像，每个类别中随机选取19个样本作为训练样本，训练样本占总样本数的0.4%。表3给出了各种方法的总体精度、平均精度、Kappa系数和每一种地物的分类精度。数据项的左边是30次重复实验的均值，右边是30次重复实验的标准差。从表3中可以看出，由于样本数目太少，SVM分类器的总体精度只有74.12%。PCA-SVM方法的总体精度比SVM还要低1.58%，SLR-SVM方法的总体精度比SVM低0.69%，说明该图像中强噪声较少，SLRMD方法降噪效果不明显，但SLR与PCA结合的方法SLR-PCA-SVM总体精度比SVM提高4.48%，再次验证了这两种降噪方法具有互补性。TSLR-SVM方法的总体精度比SVM提高了3.2%，但TSLR与PCA结合的方法TSLR-PCA-SVM总体精度比SVM提高了13.2%，证明了这两种降噪方法对于高光谱图像分类都是非常重要的。TSLR-PCA-GF方法的分类精度达到了93.11%，比SVM高18.99%。IFRF方法在样本稀少时分类精度不高，总体精度均值只有79.2%。图11是某一次实验获得的地物分类图，可以看出TSLR-PCA-GF方法的分类结果接近于地面真值图。

本文利用稀疏与低秩矩阵分解、PCA变换和引导滤波3种方法之间的互补性，实现高光谱图像精细分类的多级降噪滤波方法，解决了由于高光谱图像波段狭窄导致信噪比较低和分类结果较差的问题。其中，高光谱图像的强噪声分两个阶段去除：第1阶段是利用斑块内部像素光谱的相关性，通过稀疏与低秩矩阵分解去除像素中的强噪声；第2阶段是利用相邻波段的相关性，通过稀疏与低秩矩阵分解去除波段的强噪声。高光谱图像中的弱噪声将利用PCA去除，而分类结果图中的“椒盐噪声”将利用引导滤波方法去除。实验结果表明，这些降噪方法组合不仅能够显著改善噪声严重波段的图像质量，而且在样本稀少时同样能够获得较高的分类精度。

高光谱图像噪声来源复杂，类型多样，传统降噪方法是以PCA为代表的特征空间变换方法，认为信息量较大的投影方向是图像信号，信息量较小的投影方向是图像噪声。然而，由于高光谱图像中可能存在强噪声，很容易出现噪声方向被当作主成分提取出来，从而严重影响降维后的高光谱图像质量和分类精度。近年来兴起的以稀疏与低秩矩阵分解为代表的降噪方法认为噪声是稀疏的，去除噪声后的图像信号是强相关的，也即是低秩的，因此通过低秩矩阵分解可以将噪声从图像信号中分离出去。实际上，高光谱图像中只有强噪声是稀疏的，能量低的高斯白噪声是普遍存在的，因此上述假设是不完全成立的。在两幅真实高光谱图像上的实验结果也表明，单独使用这两种方法时对分类精度影响不大，甚至还略有下降。然而，本文将这两种互补的降噪方法组合应用后，图像分类精度提高10%和4%左右。将SLRMD方法升级为两阶段SLRMD方法后，分类精度提高19%和13%左右。最后应用引导滤波的目的是对分类结果图进行平滑，结果使图像分类精度进一步提高了6%左右。

本文对高光谱图像中存在的噪声类型划分还较粗糙，只大致分为强噪声和弱噪声两种类型，并给出了不同的处理方法。下一步工作包括细分高光谱图像的噪声类型，分析其信号特征和规律，研究更加有针对性的噪声消除方法，从而进一步提升高光谱图像的质量和提高图像分类精度。