|
收稿日期: 2016-12-12; 优先数字出版日期: 2017-09-01
基金项目: 国家自然科学基金(编号:41371222);国家重大科技专项(编号:2012ZX07101-010)
第一作者简介: 姜勃(1990— ),男,硕士研究生,研究方向为水体辐射传输及遥感应用。E-mail:nuist309@163.com
通讯作者简介: 赵巧华(1972— ),男,教授,研究方向为水光学、大气光学及环境遥感。E-mail:qhzhao@nuist.edu.cn
中图分类号: X122
文献标识码: A
|
摘要
漫衰减系数常用于计算水体浑浊度和划分水体等级,是水中生物进行光合作用等生态过程中的重要参数。本文假设水体固有光学特性(IOPs)不随垂直剖面变化,水体表面为镜面。通过Monte Carlo方法模拟追踪光子在水中的运动过程,统计大量光子在不同深度上的能量分布,计算出下行漫衰减系数Kd值。结果表明:在450 nm,550 nm和650 nm波长处模拟的Kd值基本上小于实测Kd值,对应后向散射概率为3%的散射相函数模拟的相对误差最小,适合用于构建太湖水体的Kd值反演模型。进一步分析入射天顶角、b/a值对Kd值变化的影响,结果发现:在b/a较大的情况下,散射相函数成为影响Kd值变化的主要因素。当b/a值大于9时,入射天顶角从10°变化到80°时,Kd值的变化率小于10%,可忽略入射天顶角的变化对Kd值的影响。利用单一散射相函数模拟不同波长处的Kd值,发现悬浮颗粒物浓度较高且以无机颗粒物为主体时,450—550 nm内模拟值大于实测值,550—650 nm内则相反,说明随着波长的增加,水体中颗粒物的散射呈现出前向散射减弱、后向散射增强的变化趋势。在反演不同波长处的Kd值时需考虑到散射相函数的光谱变化所造成的误差。
关键词
Monte Carlo, 数值模拟, 漫衰减系数, 入射天顶角, 散射相函数
Abstract
The diffuse attenuation coefficient (Kd) is an important property related to the penetration and availability of light underwater, which is of fundamental interest in studies of primary production, physical and biological process. The remote sensing estimation of diffuse attenuation coefficient can reveal the change of underwater light field, which is one of the main ways to obtain the diffuse attenuation coefficient. Models developed in the recent decades were mainly based on theoretical and numerical(radiative transfer)simulations. In this paper, a Monte Carlo calculation procedure has been developed for modeling of the penetration of light into turbid inland waters found at Meiliang Bay of Taihu Lake. We assume the water optical homogeneously, inherent optical properties (IOPs) do not change with depth, the water surface as a mirror, We can use the Monte Carlo method to simulate the movement process of photons in the water, energy distribution statistics of a large number of photons at different depths, calculate the downward diffuse attenuation coefficient value. We use several phase function with different backscatter fraction and overall shape as comparison. The results indicate that in the same condition of sun zenith angle and absorb coefficient (a)、scatter coefficient (b), simulated Kd values appear quite different when choose different scattering phase function. Simulated Kd values based on phase function applied to ocean or slightly turbid waters are less than the measured values. Within 450 nm, 550 nm, 650 nm band, the relative error between simulated Kd value with phase function that have a backscatter fraction of 0.03 and measured Kd value is the minimum. The phase function that have a backscatter fraction of 0.03 is more appropriate to develop a semi-analytical model based on inland turbid lake water than particular normalized phase function used in ocean water. We use the MC model to discuss the relationship between variation of sun zenith angle and phase function and Kd value. It turns out under the condition of high values of b/a, phase function become the main factor to effect the change of Kd value. When b/a values are greater than 9, the incident zenith angle changes from 10° to 80°, the rate of change in Kd values is less than 10%, so the impact of the variation of the sun zenith angle on the change of Kd value is negligible. Using a single wavelength scattering phase function to simulate Kd values at different wavelength. It’s found that in more turbid water, when the wavelength are less than 550 nm, simulated values are greater than measured values, in contrast, when the wavelength are greater than 550 nm, simulated values are less than measured values, which indicate that with the increase of wavelength, the scattering properties of particulate matter in water appear a variation trend that it’s weaken in the forward scattering and heighten in the backward scattering. When we develop the remote sensing model of Kd value for inland lake water type. We should consider the difference of scattering properties of water. Under different concentration of suspended matter and different wavelength, we should consider the spectral variation of the phase functions and use the phase function with the correct backscatter fraction.
Key words
Monte Carlo, numerical simulation, diffuse attenuation coefficient, zenith angle, scattering phase function
1 引 言
根据辐射传输理论,在光学性质均一的水体中,光的辐射强度随深度增加呈近似指数型衰减,下行漫衰减系数(Kd)表征了整个下行光场的分布情况,是一重要的表观光学量(AOP)。无论是计算水体的浑浊度、真光层深度,划分水体等级(Jerlov,1976);还是研究例如浮游植物光合作用等一系列的生物、化学过程(Platt 等,1988;Marra 等,1995),Kd值都有着不可或缺的作用。海洋清洁水体的Kd值的反演主要以经验算法为主,这种算法的劣势在于不能指出影响Kd值变化的因素,且在二类水体上反演精度较差。为了克服经验算法的局限性,许多学者做了大量关于漫衰减系数(Kd)与固有光学量(IOPs)之间关系的定量研究,并构建了一系列半分析估算模型(Kirk, 1981, 1984, 1991;Gordon,1989;Liu 等,2002;Lee 等,2005)。由于内陆湖泊水体的光学特性存在区域差异,半分析模型仍存在参数上的不确定性,移植性较差(Wang 等,2009;Pan和Zimmerman,2010)。国内主要集中研究太湖水体漫衰减系数在不同季节、不同湖区以及不同深度上的漫衰减系数的差异(张运林 等,2003;黄昌春 等,2009)。在计算Kd值时主要根据不同深度上的Ed值进行推算,缺乏漫衰减系数数值模拟方面的研究。
Monte Carlo方法采用一种较为灵活的方式给出辐射传输方程的数值解,它利用计算机模拟大量光子的运动轨迹,再将其转化为对应的辐射能量。国外已经有大量研究利用Monte Carlo方法来研究水下光场分布(Gordon和McCluney,1975;Kirk, 1981, 1984, 1994, 2003),但研究对象主要是海洋与近岸水体,有关内陆富营养化湖泊水体方面的研究较少。
太湖属于典型的内陆富营养浅水湖泊,由于风浪作用导致水体悬浮泥沙含量较高。悬浮泥沙等无机悬浮颗粒物对光的衰减主要体现为散射,所以太湖水体的散射尤其是后向散射特性与一类水体相比有较大差异(乐成峰 等,2009)。过去在使用辐射传输模型模拟一类或近海水体的漫衰减系数时主要考虑到水体各光学组分的吸收和入射天顶角对Kd值的影响,关于散射相函数对Kd值模拟的影响的研究较少。本文采用Monte Carlo方法对太湖梅梁湾水体下行漫衰减系数Kd进行模拟,通过输入不同水体类型的散射相函数进行比较,进而探讨在不同入射光场条件、b/a值条件下,散射相函数前向、后向散射的变化对Kd值变化的影响,为构建适用于太湖水体Kd值反演的半分析模型提供一定的理论基础。
2 数据与方法
2.1 辐射数据
采样时间:2015-04-17,2015-04-22,2015-05-16,2015-05-19,2015-05-21,2015-06-20,2015-07-27,2015-07-29,2015-08-06,2015-09-26和2015-10-15。实验地点:太湖梅梁湾中国科学院太湖生态网络站栈桥头。实验期间天气状况良好,基本无云或有少量的云。风速较小,湖面可近似为水平。利用Trios水下光谱仪测定水面以下的光谱数据,该仪器可同时测量上行辐亮度(Lu)、上行辐照度(Eu)和下行辐照度(Ed),波段测量范围为320—950 nm,光谱分辨率为3.3 nm,可重采样为1 nm,与吸收、散射系数光谱分辨率对应。测量深度初步设定为0—1.5 m,深度间隔为10 cm。入射辐射包括太阳直接辐射和天空漫辐射。在无云的情况下,天空漫辐射可以看成是各向同性辐射。将仪器置于水面以上,用挡板挡住太阳直射方向测天空漫射部分(Edsky),移开档板测总的入射辐射,相减得到太阳直射部分(Edsun),用来粗略计算太阳直射光与天空漫射光的比例(Mobley,1994)。
2.2 固有光学量(IOP)的测定
采集测量点的表层水样,带回实验室分析各组分浓度及其光学特性,包括总悬浮物、色素颗粒物、非色素颗粒物和有色可溶性有机物(CDOM)的光谱吸收系数。根据Lambert Beer定律,水体的总吸收系数可表示为各种物质吸收系数的线性相加(Kirk,1994)
|
$a(\textit{λ}) = {a_{\rm{w}}}(\textit{λ}) + {a_{\rm{p}}}(\textit{λ}) + {a_{{\rm{CDOM}}}}(\textit{λ})$
|
(1) |
式中,aw(λ),ap(λ),aCDOM(λ)分别表示纯水,悬浮颗粒物和可溶性有机物的吸收系数。
2.2.1 悬浮颗粒物吸收系数测定
总悬浮颗粒物的吸收采用定量滤膜技术(QFT)(Mitchell,1990)。先使用滤膜过滤一定体积的水样,在紫外分光光度计下测量滤膜的吸光度OD(λ),最后利用吸光度来计算吸收系数。其中为了消除散射带来的影响,要对吸光度进行校正(Clevel和Weidemann,1993),公式如下
|
$O{D^*}\left(\textit{λ} \right) = 0.378OD\left( \textit{λ} \right) + 0.523O{D^2}\left( \textit{λ} \right)$
|
(2) |
式中,OD*(λ)为校正后的吸光度。利用吸光度计算吸收系数的公式为(Cleveland和Weidemann,1993)
|
${a_p}\left( \textit{λ} \right) = 2.303 \times \frac{S}{V}OD\left( \textit{λ} \right)$
|
(3) |
式中,V为被过滤水样的体积,S为沉积在滤膜上的颗粒物的有效面积。
2.2.2 CDOM吸收系数的测定
用GF/F孔径为0.22 μm的Millipore膜过滤水样,在分光光度计下测定其吸光度OD(λ),然后根据公式进行计算(Bricaud 等,1981)
|
${a_{{\rm{CDOM}}}}\left( \textit{λ} \right) = 2.303 \times \frac{{OD\left(\textit{λ} \right)}}{r}$
|
(4) |
式中,OD(λ)是分光光度计所测的吸光度,r是比色皿的宽度(光程)。在CDOM浓度较高的内陆湖泊中使用比色皿宽度在1—5 cm内,本次实验采用4 cm宽度的比色皿。对aCDOM(λ)进行散射校正,校正公式如下(Bricaud 等,1981;Green和Blough,1994)
|
${a_{{\rm{CDOM}}}}\left( \textit{λ} \right) = {a_{{\rm{CDOM}}}}\left( {\textit{λ} '} \right) - {a_{{\rm{CDOM}}}}\left( {\textit{λ} '} \right) \cdot \textit{λ} /{\textit{λ} ^0}$
|
(5) |
式中,aCDOM(λ′)为未校正吸收系数,λ0为参考波长,一般选用700 nm或者750 nm。
纯水的光谱吸收经过多次研究被证明是一个较稳定的值,可认为是常数。具体参照之前论文中所给出的数值(Pope和Fry,1997)。
2.2.3 散射系数的计算
总散射系数的计算遵循光学闭合原理,即散射系数为衰减系数和吸收系数之差,太湖水体主要光学组分分为4种(纯水、色素颗粒物、无机颗粒物和CDOM),通常忽略CDOM的散射贡献,总散射系数可表示为
|
$b(\textit{λ} ) = {b_{\rm{w}}}(\textit{λ}) + {b_{{\rm{ph}}}}(\textit{λ} ) + {b_{\rm{d}}}(\textit{λ} )$
|
(6) |
式中,bw(λ),bph(λ)和bd(λ)分别为纯水、色素颗粒物和无机悬浮颗粒物的散射系数。纯水的散射系数可参照之前文献所给出的数值(Smith和Baker,1981)。色素颗粒物和无机颗粒物的散射系数可表示为单位体积散射系数与颗粒物浓度的乘积
|
$b(\textit{λ}) = {b_{{\rm{ph}}}}^*(\textit{λ}){C_{{\rm{OSS}}}} + {b_d}^*(\textit{λ} ){C_{{\rm{ISS}}}}$
|
(7) |
式中,
2.3 漫衰减系数Kd的计算
通常认为在光学性质均一的水体中,入射光的辐射能量随深度呈指数型衰减,某一深度z处下行漫衰减系数Kd(z)定义为
|
${K_{\rm{d}}}(\textit{z}) = - \frac{1}{{{E_{\rm{d}}}(\textit{z})}}\frac{{{\rm{d}}{E_{\rm{d}}}(\textit{z})}}{{{\rm{d}}\textit{z}}}$
|
(8) |
在实际研究Kd(z)值时,通常用整个水柱内平均漫衰减系数
|
${{{\overline K }_{\rm d}}} ({\textit{z}_0} \to \textit{z}) = \frac{1}{{\Delta {\textit{z}}}}\ln \left( {\frac{{{E_{\rm d}}({\textit{z}_0})}}{{{E_{\rm d}}(\textit{z})}}} \right)$
|
(9) |
将拟合所得到的各深度的下行辐照度与实测的下行辐照度求相关,只有当R2≥0.97,深度数≥3时,水体介质的光学性质可近似看作均一(Mobley,1994)。其中部分测量时间450 nm,550 nm及650 nm拟合的相关系数的平方见表1。
表 1 实测的下行辐照度与指数拟合得到的下行辐照度间的相关系数
Table 1 The linear correlation coefficient between the downward irradiance by measured under water and the data fited by exponential decay
| 观测时间 | 450 nm(n=10) | 550 nm(n=10) | 650 nm(n=10) |
| 4月22日12点 | 0.9787 | 0.9859 | 0.9775 |
| 5月16日10点 | 0.9764 | 0.9943 | 0.9940 |
| 5月16日11点 | 0.9819 | 0.9938 | 0.9939 |
| 5月16日12点 | 0.9852 | 0.9951 | 0.9950 |
| 5月21日10点 | 0.9890 | 0.9913 | 0.9911 |
| 5月21日11点 | 0.9898 | 0.9930 | 0.9928 |
| 5月21日12点 | 0.9912 | 0.9927 | 0.9895 |
| 6月20日10点 | 0.9919 | 0.9747 | 0.9650 |
| 6月20日11点 | 0.9949 | 0.9946 | 0.9940 |
| 6月20日12点 | 0.9914 | 0.9951 | 0.9940 |
| 9月26日11点 | 0.9129 | 0.9948 | 0.9947 |
| 9月26日12点 | 0.9260 | 0.9895 | 0.9860 |
| 注:n为样本数。 | |||
对于总悬浮物和有机、无机颗粒物浓度测量采用常规的干燥、烘烧、称重的方法测定,在此不再赘述。
2.4 Monte Carlo方法
Monte Carlo方法是一种用计算机模拟随机抽样统计来解决辐射传输问题的数值方法,它将光在介质中的能量传输看成是一个个光子在介质中运动过程的集合。运动过程包括穿过水—气界面,被水体吸收和与颗粒物碰撞发生散射等一系列事件。事件之间是相互独立的。每个事件发生的概率由水体自身光学特性决定。本文所编写的Monte Carlo程序的算法原理来自文献(Leathers和Mobley,2004)。在此只简单介绍散射相函数和光子运动过程。
2.4.1 散射相函数
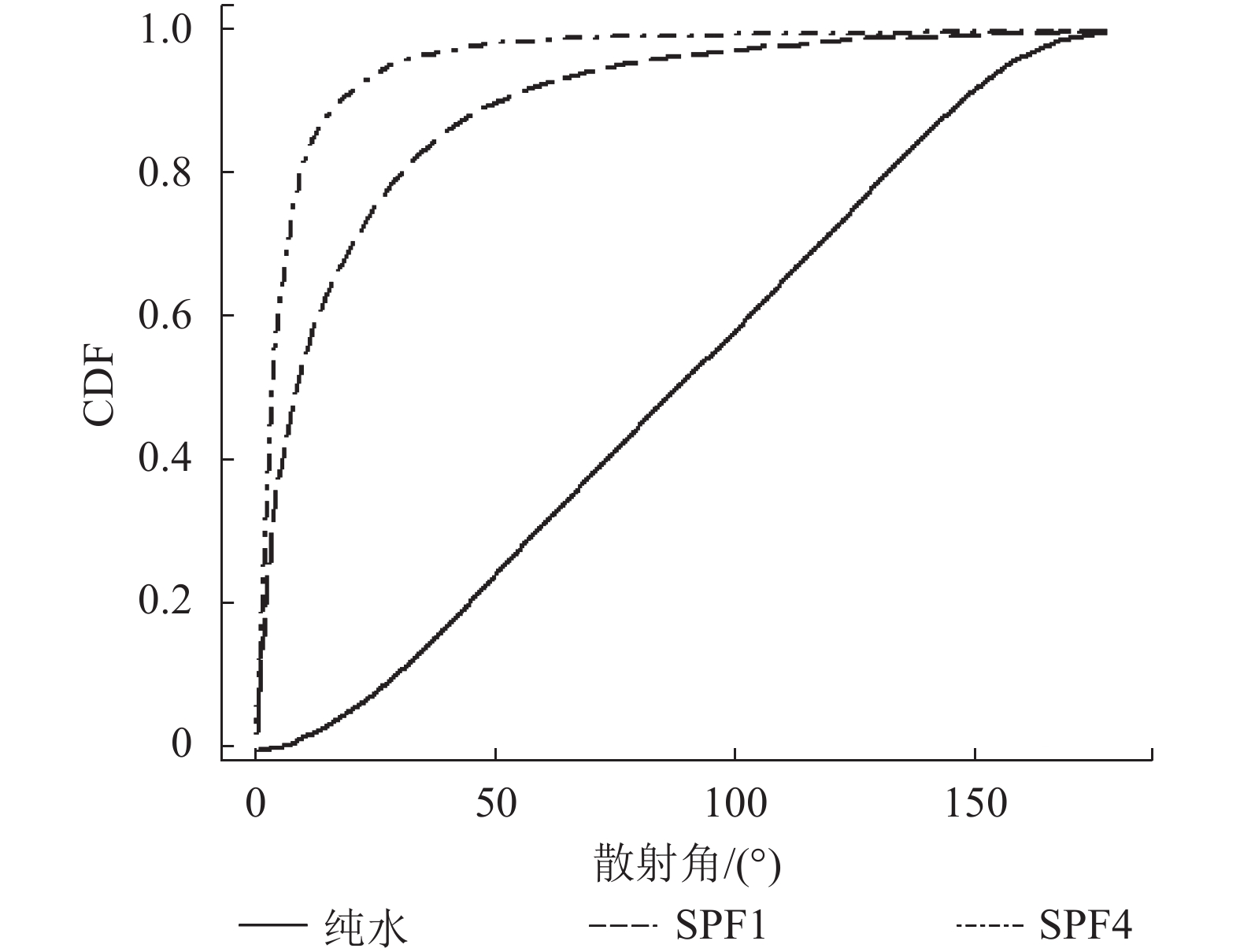
散射相函数定义为体散射函数β(θ)与散射系数b的比值,其表征了在不同散射角度、单位路径长度上辐射能量强弱分布,是归一化的体散射函数。根据散射相函数可以计算出光子的散射方向。辐射传输模型中使用的散射相函数主要来自于:(1)基于Mie散射理论或其他数学理论的数值模拟(Fournier和Forand,1994;Haltrin,1999a);(2)实验室和原位实测数据。本文分别采用了Petzold(1972)实测的海洋水体体散射函数数据和Michael等人(2003)实测的近海浑浊水体的体散射函数数据。Petzold(1972)所测的数据中选取turbid harbor类型体散射函数,测量波长为514 nm,散射系数为1.8 m–1,比本次实验所采集水样的散射系数小了一个数量级。与Petzold(1972)所测的数据相比,Michael等人(2003)观测的水体浑浊度更高,选取其中4种体散射函数,散射系数最大值达到9 m–1,更接近于本次采集水样的散射值,测量波长为550 nm。这里分藻类颗粒物和无机悬浮颗粒物两种情况来选取散射相函数,每种散射相函数要对应相应的后向散射概率(Mobley 等,2002)。目前对太湖地区浮游植物的后向散射概率研究较少,Morel(1980)、Sathyendranath等人(1989)研究得出叶绿素的后向散射概率在0.5%左右,Haltrin(1999b)的研究认为,浮游植物的后向散射概率为0.64%。无机悬浮颗粒物的后向散射概率在不同地区的差异较大,在太湖地区,孙德勇等人(2008)利用实测的太湖水体的散射和后向散射系数,计算得到后向散射概率变化范围为0.2%—3%,马荣华等人(2008)研究400—700 nm颗粒物后向散射概率范围的平均值为0.03±0.015。本文选取的散射相函数对应的散射系数和后向散射概率见表2,其中SPF4代表藻类颗粒物的散射相函数,
表 2 几种散射相函数对应的b与bb
Table 2 b and bb of several scattering phase functions
| 名称 | b/(m–1) | bb/b |
| SPF_th | 1.824 | 0.019 |
| SPF1 | 9.262 | 0.033 |
| SPF2 | 5.366 | 0.027 |
| SPF3 | 2.364 | 0.011 |
| SPF4 | 3.396 | 0.005 |
2.4.2 光子运动过程
将入射光看作由大量光子组成,为提高计算效率将单个光子看作带权重的光子束。首先光子束在穿过水气界面进入水体时,被水面反射的概率为
|
$r = \frac{1}{2}\left[ {\frac{{{{\sin }^2}({\theta ^i} - {\theta ^t})}}{{{{\sin }^2}({\theta ^i} + {\theta ^t})}}} \right. + \left. {\frac{{{{\tan }^2}({\theta ^i} - {\theta ^t})}}{{{{\tan }^2}({\theta ^i} + {\theta ^t})}}} \right]$
|
(10) |
式中,θi和θt分别为入射角和折射角,折射后的光子束的权重为(1–r)。光子束在水中与介质发生碰撞事件,分为吸收和散射两种,每次碰撞后光子束的权重乘以一个系数ω(单次散射反照率:ω=b/c)。经过多次碰撞后,光子的权重值会降低到一个很小的阈值,我们将阈值设为10–6,当权重值小于阈值或运动的垂直距离超过最大深度时,结束本次计算,重新下一次循环。在两次碰撞事件之间,光子束运动的几何距离为
|
$l = - \ln (\xi )/c$
|
(11) |
式中,ξ为计算机生成的随机数,c为衰减系数。光子束在碰撞后运动方向会发生改变,这里假设水平方向上各向同性,只考虑在垂直方向上的角度的变化,新的运动方向计算为
|
$\sin \alpha ' = \sin \alpha \cos \theta + \cos \alpha \sin \theta \cos \phi $
|
(12) |
式中,α和α'分别为初始、新的方向与垂直方向的夹角。θ和φ分别为空间散射角的垂直与水平分量,θ的计算与散射相函数有关,先将散射相函数按散射角积分得到概率累积分布函数(CDF)P(θ),计算公式为
|
$P(\theta ) = 2{{\pi }}\int_0^\theta {\tilde \beta (\theta )} \sin (\theta ){\rm{d}}\theta $
|
(13) |
纯水及SPF1,SPF4的概率累积分布函数见图1,利用P(θ)和散射角一一对应的关系制作查找表,使P(θ)为计算机生成的随机数,利用查找表计算θ。将循环的次数设置为1000000以上,在所有光子运动追踪结束后计算每层深度上的光子束权重和,可以转化为对应的辐照度值。
3 结果与分析
3.1 模型的验证
本文根据Mobley等人(1993)提出的关于辐射传输数值模拟的标准问题进行模型的验证。假设条件为(1)水—气界面水平,无风浪影响;(2)水体光学特性各向同性;(3)没有天空漫射影响;(4)太阳可看做点光源且入射天顶角为60°;(5)入射水面上单位面积内辐照度设为1 w·m–2·nm–1;(6)忽略非弹性散射和其他内光源;(7)水体的散射是水中颗粒物引起的。由于本文主要是计算漫衰减系数,所以只比较了Ed值。模拟的结果如表3所示,Ed1表示本文模拟结果,Ed2表示mobley等人(1993)的文献中给出的标准结果。从表3对比结果来看,本文模拟结果与文献中给出的标准结果基本一致,可保证模型的正确性。
表 3 本文模拟结果与mobley等人(1993)的文献中标准结果对比
Table 3 The comparison between simulated result and standard result mobley, et al. (1993)
| 光学深度τ | ω0=0.2 | ω0=0.9 | |||||
| Ed1/w·m–2·nm–1 | Ed2/w·m–2·nm–1 | 相对误差/% | Ed1/w·m–2·nm–1 | Ed2/w·m–2·nm–1 | 相对误差/% | ||
| 1 | 1.63E-1 | 1.62E-1 | 0.62 | 4.15E-1 | 4.13E-1 | 0.48 | |
| 5 | 2.25E-1 | 2.27E-3 | 0.88 | 1.86E-1 | 1.87E-1 | 0.24 | |
| 10 | 1.28E-5 | 1.30E-5 | 1.54 | 6.83E-2 | 6.85E-2 | 0.29 | |
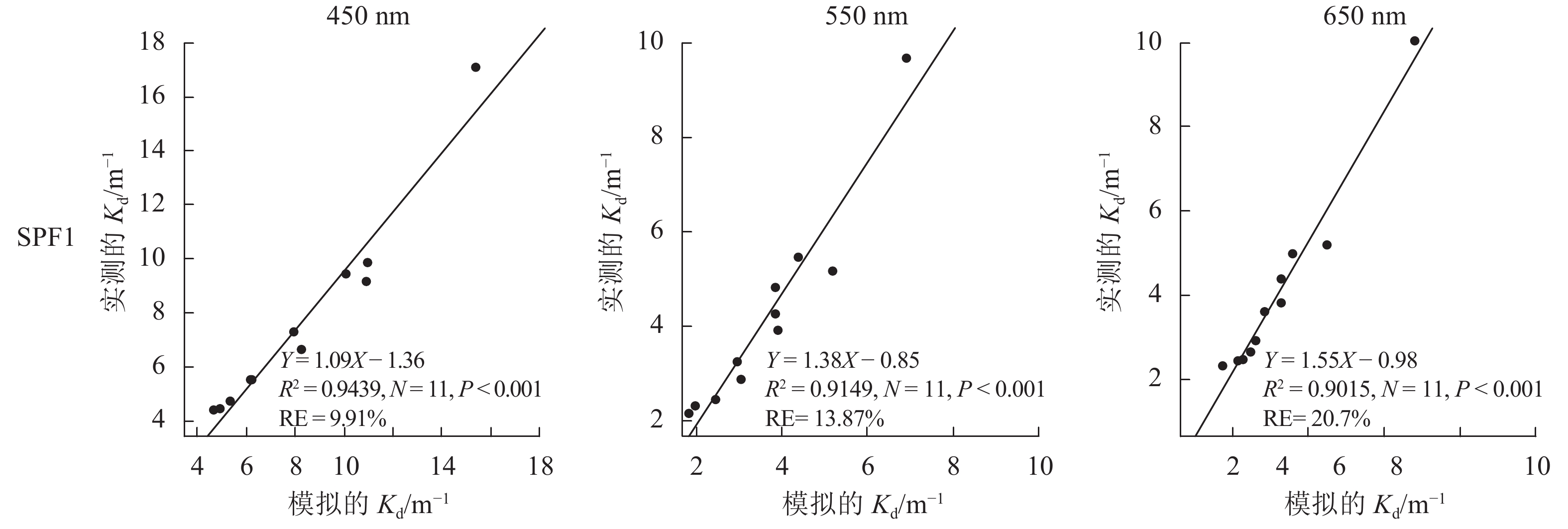
3.2 Kd值模拟值与实测值的比较
在早期运用辐射传输原理研究海洋水体时,一般认为散射相函数的差异尤其是前向小角度散射的变化对Ed或R没有太大的影响(Gordon,1992)。在后来的研究中,Mobley等人(2002)通过对水下光场的数值模拟,发现散射相函数的差异(尤其对应不同的后向散射概率)会造成辐照度、辐亮度和遥感反射率发生变化。Lee等人(2005)在使用Hydrolight模型模拟Kd值时选用不同的散射相函数进行对比,发现在吸收、散射系数不变的情况下,散射相函数的差异会造成Kd模拟值的变化。本文假设藻类颗粒物的散射相函数为SPF4,改变无机颗粒物的散射相函数(SPF1,SPF2,SPF3,SPF_TH)。将太阳高度角、太阳直射与天空漫射比、散射相函数、水体各光学组分的吸收和散射系数输入Monte Carlo模型(具体数值见表4,表5),选取了450 nm,550 nm和650 nm 3个不同的波长,计算各深度所对应的下行辐照度,再根据辐照度计算漫衰减系数Kd值,并与实测的Kd值进行比较。
表 4 水体各组分浓度及太阳高度角
Table 4 Concentration of water components and solar altitude
| 日期 | 太阳高度角(中午12时)/(°) | TSS/(mg/l) | OSS/(mg/l) | ISS/(mg/l) | Chla/(μg/l) |
| 2015-04-17 | 69.02 | 43.4—56.5 | 10.1—11.5 | 33.3—45.1 | 7.9—11.2 |
| 2015-04-22 | 70.75 | 25.8—51.6 | 7.2—23.7 | 18.5—27.8 | 12.5—29.9 |
| 2015-05-16 | 77.71 | 44.7—51.8 | 9.3—10.4 | 34.4—41.9 | 8.18—13.3 |
| 2015-05-19 | 78.38 | 20.4—25.2 | 8.7—10.6 | 10.3—16.4 | 12.8—16.7 |
| 2015-05-21 | 78.75 | 25.9—32.1 | 7.2—8.3 | 18.2—24.5 | 15.6—21.7 |
| 2015-06-20 | 82.18 | 19.5—62.7 | 9.6—20.2 | 9.5—44.6 | 22.7—77.8 |
| 2015-07-27 | 78.10 | 16.3—22.7 | 11.9—18.5 | 2.9—5.4 | 45.5—97.9 |
| 2015-07-29 | 77.60 | 35.7—53.8 | 31.7—46.0 | 5.8—9.3 | 55.1—181.8 |
| 2015-08-06 | 75.62 | 64.7—89.6 | 29.0—59.1 | 30.5—36.5 | 148.6—274.3 |
| 2015-09-26 | 57.75 | 43.2—48.2 | 10.1—13.9 | 31.6—34.3 | 4.7—9.3 |
| 2015-10-15 | 50.45 | 5.9—54.5 | 0.3—30.8 | 5.6—47.6 | 21.7—151.6 |
表 5 模型所输入的吸收、散射系数及太阳直射所占比
Table 5 Input absorbing and scattering coefficients and the ratio of sun direct
| 日期 | 吸收系数/(m–1) | 藻类颗粒物散射系数/(m–1) | 无机颗粒物散射系数/(m–1) | 太阳直射所占比/(m–1) | |||||||||||
| 450 nm | 550 nm | 650 nm | 450 nm | 550 nm | 650 nm | 450 nm | 550 nm | 650 nm | 450 nm | 550 nm | 650 nm | ||||
| 2015-04-17 | 5.08 | 1.75 | 1.09 | 1.14 | 2.66 | 1.66 | 15.95 | 14.03 | 13.44 | 0.57 | 0.63 | 0.66 | |||
| 2015-04-22 | 3.44 | 1.20 | 1.13 | 1.54 | 3.06 | 1.78 | 14.55 | 10.96 | 9.81 | 0.66 | 0.75 | 0.81 | |||
| 2015-05-16 | 3.69 | 1.24 | 1.10 | 1.85 | 3.68 | 2.07 | 27.44 | 20.73 | 17.92 | 0.59 | 0.64 | 0.68 | |||
| 2015-05-19 | 2.88 | 0.90 | 0.86 | 2.36 | 4.25 | 2.53 | 11.66 | 7.97 | 7.3 | 0.51 | 0.56 | 0.61 | |||
| 2015-05-21 | 3.48 | 1.29 | 1.06 | 1.43 | 2.86 | 1.67 | 14.17 | 10.78 | 9.67 | 0.69 | 0.78 | 0.84 | |||
| 2015-06-20 | 3.20 | 1.03 | 1.04 | 2.89 | 5.07 | 3.41 | 8.7 | 5.77 | 5.95 | 0.46 | 0.52 | 0.57 | |||
| 2015-07-27 | 3.83 | 1.05 | 1.51 | 2.65 | 4.20 | 2.72 | 2.14 | 1.28 | 1.28 | 0.69 | 0.77 | 0.82 | |||
| 2015-07-29 | 8.12 | 1.81 | 2.56 | 7.34 | 12.42 | 9.27 | 5.13 | 3.28 | 3.77 | 0.66 | 0.73 | 0.77 | |||
| 2015-08-06 | 10.22 | 3.27 | 3.70 | 6.71 | 12.81 | 8.96 | 17.56 | 12.71 | 13.64 | 0.63 | 0.74 | 0.81 | |||
| 2015-09-26 | 6.08 | 2.12 | 1.16 | 2.67 | 5.15 | 3.01 | 24.94 | 18.17 | 16.33 | 0.30 | 0.34 | 0.38 | |||
| 2015-10-15 | 5.68 | 1.69 | 1.38 | 0.01 | 0.04 | 0.02 | 23.48 | 21.33 | 17.58 | 0.50 | 0.61 | 0.69 | |||
从图2的模拟结果上来看,选取不同的散射相函数,使用Monte Carlo方法模拟太湖水体的漫衰减系数,最大相对误差在40%以内。模拟的Kd值基本上小于实测的Kd值,这是因为和沿岸中度浑浊水体相比,太湖水体颗粒悬浮物浓度更高,模型低估了真实情况下由悬浮泥沙等无机颗粒物的散射引起的衰减。由散射所造成的误差主要体现在两个方面:一是4种散射相函数之间存在着较大差异,其中SPF1对应的相对误差范围为11.91%—20.7%,SPF2对应的相对误差为12.11%—28.53%,SPF3对应的相对误差为16.45%—38.38%,SPF_TH对应的相对误差为10.47%—33.68%。SPF1对应的散射系数和后向散射概率最大,与实测值之间的相对误差相对最小。SPF2、SPF3对应的后向散射概率依次降低,模拟的Kd值与实测值的相对误差也逐渐增大,可见选取对应合适后向散射概率的散射相函数能减小模型误差。由于太湖水体的光学特性具有时空差异性,对太湖水体的后向散射概率的研究并没有一个统一定论(马荣华 等,2008;孙德勇 等,2008;刘忠华 等,2012),其中马荣华等人(2008)在研究太湖水体后向散射特性时给出了不同波长处的后向散射概率,其中442 nm、488 nm处为0.017,532 nm处为0.033,676 nm处为0.054。就本文模拟结果来看,450—650 nm波段区间内的平均后向散射概率在3%左右。因此,散射相函数SPF1比SPF_TH更适合用于构建太湖水体的Kd值反演模型。二是不同波长处,散射相函数造成的误差也存在着差异,在450 nm上,4种散射相函数的相对误差之间的变化很小,为10.47%—16.45%,而在650 nm上,这种误差的变化扩大到20.7%—38.38%。虽然长波处的吸收和散射呈递减的趋势,但b/a值却呈递增趋势,450 nm处b/a值的范围为1.25—7.94,650 nm处b/a值增加到2.64—11.44,在模型中,b/a值决定了光子发生散射事件的概率,b/a值越大,光子被散射的次数越多,散射造成的误差越大。
3.3 不同太阳高度角、散射相函数下Kd值的变化
根据辐射传输原理,光在水中的衰减不仅受水体各光学组分(纯水,藻类、非藻类颗粒物,CDOM)吸收、散射特性影响,还与入射光场条件有关(Gordon,1992;Stramska和Frye,1997)。Kirk(1984, 1991)通过数值模拟进一步得出太阳高度角对Kd值的影响与b/a值有关,在以吸收为主的水体中,b/a值较小,Kd值与太阳高度角关系密切,随着b/a值的增加,Kd对太阳高度角的变化的敏感度在降低。太湖为典型二类水体,特别是梅梁湾处由于水浅,受到径流、风浪的影响,水体中悬浮颗粒物浓度、组分的变化造成了散射性质的差异,这种差异不仅体现在b/a值上,还与散射相函数有关。利用Monte Carlo模型,可以分析在不同的b/a值条件下,散射相函数、太阳高度角的变化对Kd值的影响。
假设入射光为太阳直射光,不考虑天空漫射的影响。吸收系数为2 m–1,b/a值分别设为0.5,1,3,6,9,12。入射天顶角(θ)设为10°—80°。输入的散射相函数为SPF1,SPF2,SPF3,SPF4。随着入射天顶角的增大,入射光在水中传输路径变长,光在水中的衰减越多,所以Kd值随入射天顶角的增加而增加。利用Kd值的变异系数(标准差比平均值)表征在不同b/a值条件下,散射相函数、太阳高度角的变化对Kd值的影响程度。当b/a为0.5,散射相函数为SPF1时,Kd值随θ变化的变异系数为14.49%;随着b/a值变大,Kd值的变异系数范围为13.86%(b/a=1,SPF1)—2.3%(b/a=12,SPF1)。由此可见,随着b/a值增大,入射天顶角的变化对Kd值影响降低,这与Kirk(1984)的研究结果相一致。此外,当b/a为0.5时,光在水中发生散射次数较少,散射相函数之间的差异对Kd值的影响程度相对较弱,Kd值随散射相函数变化的变异系数为1.31%(b/a=0.5,θ=10°)—1.82%(b/a=0.5,θ=80°),从图3中可以看出对应不同散射相函数的曲线近似平行。随着b/a值增加,光在水中发生散射次数增多,散射相函数的差异对Kd值的影响程度在增加。当b/a值为12时,Kd值随散射相函数变化的变异系数为14.28%(b/a=12,θ=10°)—19.85%(b/a=12,θ=80°),大于随θ变化的变异系数,说明在b/a较大的情况下,散射相函数成为影响Kd值变化的主要因素。
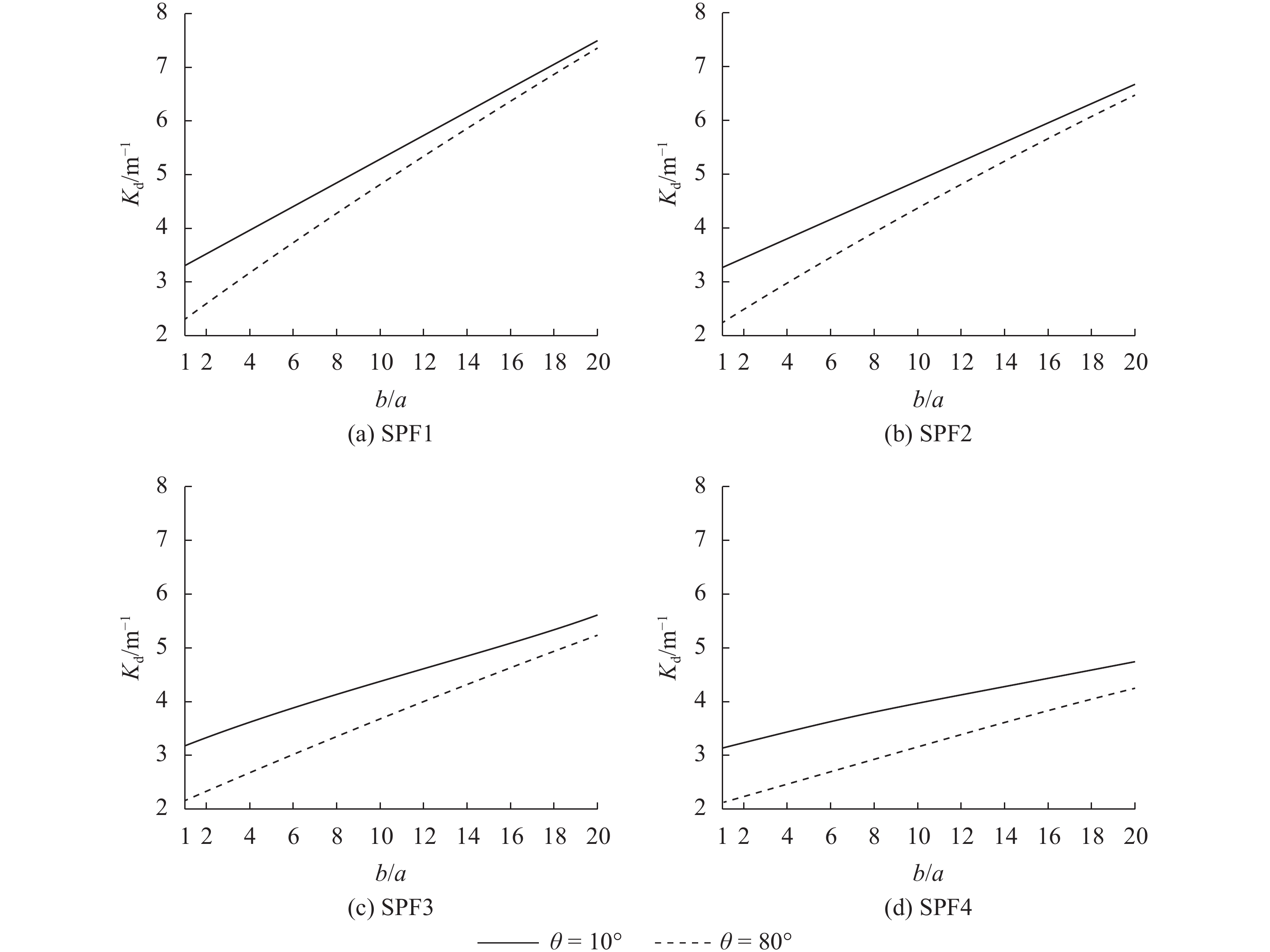
本次实验采集的水样b/a值在400—700 nm内范围为1—20,观测时太阳高度角在10°—80°范围内。对比4种散射相函数,分别模拟在入射天顶角为10°和80°条件下,Kd值随b/a变化的情况。根据图4所示,太阳高度角对漫衰减系数的影响不仅仅取决于b/a值的大小,还与散射相函数的选取有关。当散射相函数为SPF1时,入射天顶角从10°变化到80°时,Kd值增幅由30.56%变化到2.17%,当b/a值大于9时,Kd值的变化率小于10%,可忽略太阳高度角的变化对Kd值的影响;当散射相函数为SPF4时,Kd值随θ变化的增幅由32.04%变化到9.98%,当b/a值大于20时可忽略太阳高度角对Kd值的影响。
3.4 Kd值的光谱变化
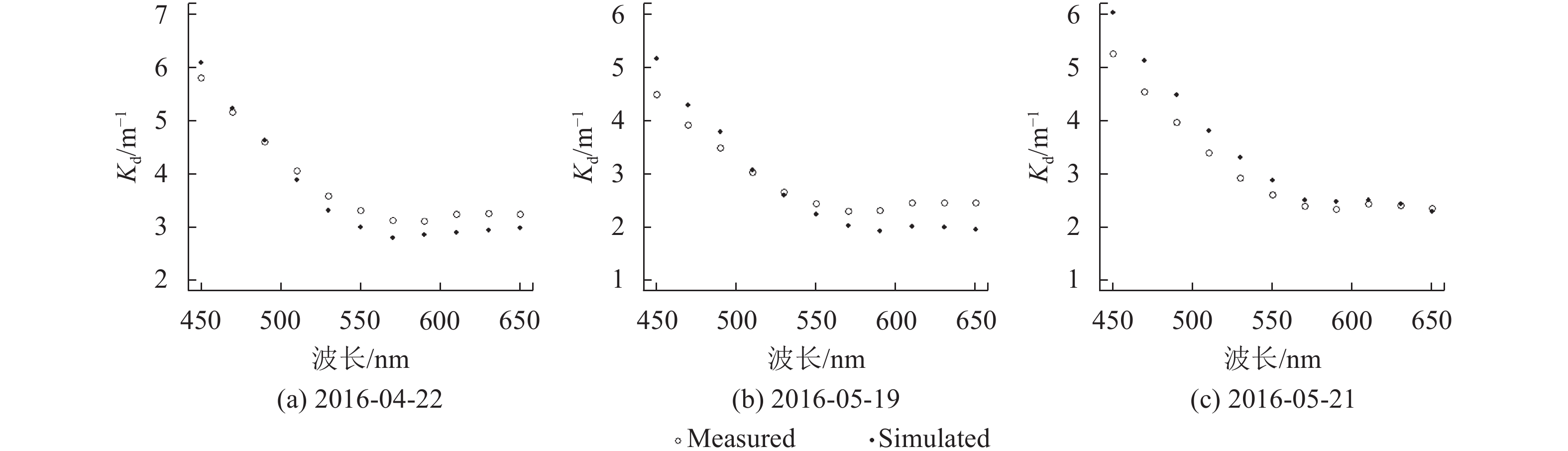
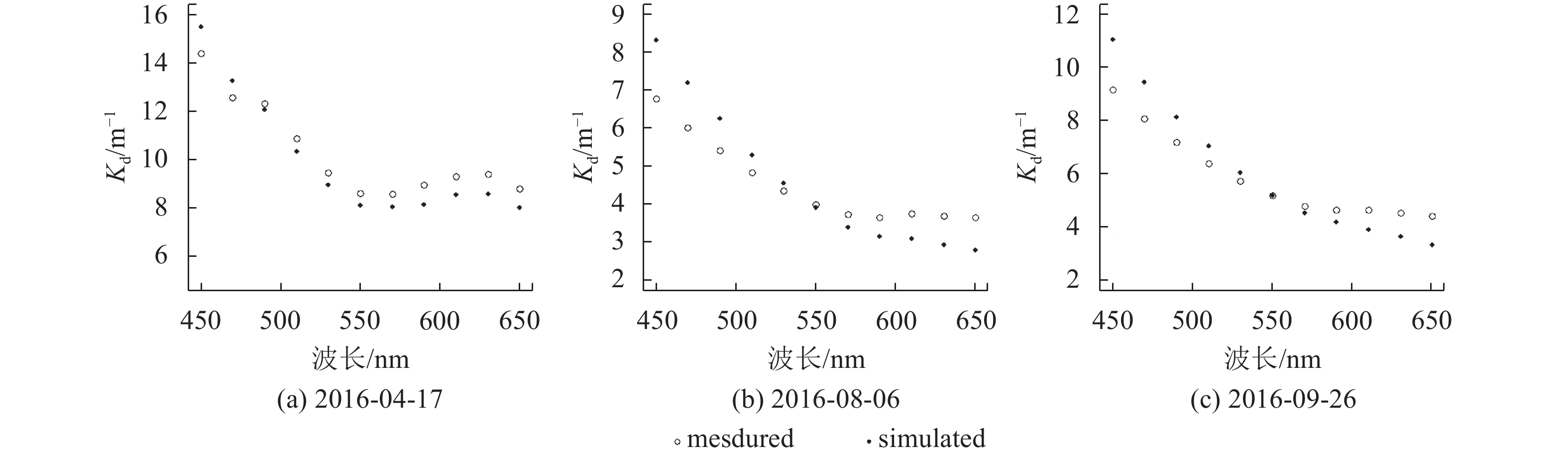
在利用辐射传输模型解决海洋水体光学问题时,许多研究通常忽略散射相函数的光谱变化,主要是因为海洋水体悬浮颗粒物浓度较低,水体散射较弱,不同波长处散射相函数变化较小(Sokolov 等,2010)。在模拟太湖水体Kd值时,是否可认为散射相函数的波长依赖性较弱还需要进一步验证。本文拟采用SPF1作为无机悬浮颗粒物的散射相函数输入模型,以20 nm为间隔模拟400–700 nm范围内的Kd值。模型模拟的结果与实测值对比如图5、6所示,可分为两种情况:(1) 4月22日、5月19、21日中午12时总悬浮物浓度在25.15—31.16 mg/l内,在400—700 nm内Kd值范围为2.0—8.7 m–1。4月22日和5月19日模拟值与实测值之间的差异在450—550 nm内很小,两者具有很好的一致性,在大于550 nm波段范围内,吸收系数较小,水体中各光学组分的散射成为光衰减的主要因素,由于散射相函数的光谱差异所造成的相对误差在增加。5月21日的情况正好相反,在450—550 nm波段范围内,模拟值要略大于实测值,说明在吸收较强时,水体中颗粒悬浮物的后向散射相对较弱。(2) 4月17日、8月6日和9月26日总悬浮物浓度较大,在44.3—75.8 mg/l内,Kd值范围为4.7—11.6 m–1。其中,4月17日和9月26日水体光学组分以无机颗粒物为主,色素颗粒物浓度较低,Kd值随波长增加呈单调递减趋势,在450—550 nm内真实的后向散射概率可能小于0.03,所以Kd的模拟值大于实测值。在550—650 nm内,真实的后向散射概率可能大于0.03,模型低估了后向散射对光衰减的影响。8月6日水样中色素颗粒物浓度较高,Kd值在675 nm处附近由于叶绿素的吸收作用形成了峰值。由于有机颗粒物对总悬浮颗粒物的后向散射贡献较低,所以在550—650 nm内模拟值与实测值之间的误差相对较小。
4 讨 论
Kirk(1981, 1984, 1991)利用Monte Carlo方法模拟水下光场得出了关于漫衰减系数与吸收、散射系数,入射天顶角之间关系的数学方程
|
${K_{\rm{d}}} = \frac{1}{{{\mu _0}}}{[{a^2} + ({g_1}{\mu _0} - {g_2})ab]^{0.5}}$
|
(14) |
式中,μ0为入射天顶角的平均余弦,系数g1和g2分别为0.425,0.19。Kirk(1981, 1984, 1991)认为散射相函数的光谱差异性较小,对许多沿岸和中等浑浊水体而言,后向散射概率定为0.019较为合适,所以他只选用了散射相函数SPF_TH输入MC模型来确定方程的系数。从本文的模拟结果来看,在540—560 nm波段范围内,后向散射概率为0.03的SPF1比SPF_TH更适合模拟太湖水体的下行漫衰减系数。太湖是典型的二类水体,悬浮颗粒物组成以悬浮泥沙等无机颗粒物为主,根据Mie散射理论,粒径的尺寸和相互之间的距离成反比,当水体浊度较大时,颗粒物粒径偏小且折射率高,对后向散射的贡献相对较大,所以选用后向散射概率较大的散射相函数更符合实际情况。太湖不同湖区悬浮颗粒物组成、含量不同,固有光学量空间变化较大,本次研究观测点在梅梁湾口,水中无机悬浮颗粒物含量较高,在大于520 nm波段上,b/a值基本上大于10,当太阳高度角从10°变化到80°时,Kd值的变化率小于10%,太阳高度角的变化对Kd值的影响可以忽略不计,一方面因为水体散射较强,光在进入水中迅速地被多次散射,传输方向偏离进入水中的初始方向,所以光场的分布结构更多与水体本身散射性质有关,而受入射光场边界条件(太阳高度角、太阳直射与天空漫射之比、水体表面波)影响较小;另一方面是因为根据式(7)线性拟合出来的平均漫衰减系数表征了水柱内的总体的衰减情况,由于太湖漫衰减系数较大,入射光的能量在60 cm深度以下基本上衰减到10%以下,呈现出渐进态光场特征,所以平均漫衰减系数表征的是渐进态光场的衰减情况,漫衰减系数表现为“准固有光学量”的性质,与太阳高度角相关性较低(Baker和Smith,1979)。
由于现场测量技术的限制,目前没有关于太湖水体确定的、先验的散射相函数数据可以利用,所以无法确定散射相函数的光谱变化。本文利用单一相函数SPF1去模拟不同波段处的Kd值,发现当悬浮物浓度较小(30 mg/l以内)时,在小于550 nm的波段内模拟值与实测值吻合得较好,说明在短波处散射相函数的光谱差异不大,散射相函数的波长依赖性只体现在大于550 nm的长波处;悬浮物浓度较大(大于40 mg/l)时,在小于540 nm的波段范围内会出现模拟值大于实测值的情况,而在大于540 nm的长波段处正好相反,说明随着波长的增加,散射相函数前向散射逐渐减弱,后向散射逐渐增强,后向散射概率随波长呈递增的趋势。最近的研究表明后向散射概率具有波长依赖性(Aas 等,2005),在不同的水体中,后向散射概率随波长的变化函数不同,如马荣华等人(2008)利用二次函数模拟后向散射概率的光谱变化,Aas等人(2005)则利用幂函数进行模拟,这种差别可能是由不同水体中颗粒物本质属性所造成的(Aas 等,2005)。本文通过模拟Kd值所推测出来的后向散射概率随波长呈现递增的趋势与马荣华学者研究一致,但是否符合实际情况,还需要进一步的实验验证。
5 结 论
本文利用Monte Carlo模型计算漫衰减系数Kd,采用几种不同的散射相函数进行对比,相比于标准海洋颗粒物散射相函数,后向散射概率为3%的散射相函数SPF1对应的相对误差最小,更适合用于构建太湖水体的Kd值反演模型。
当b/a值小于等于1时,入射天顶角的变化是影响Kd值变化的主要因素,随着b/a值的增加,入射天顶角的变化对Kd值的影响减弱,散射相函数对Kd值的影响增强。太湖梅梁湾水体中悬浮颗粒物较多,散射较强,当b/a值大于9时,可忽略太阳高度角的变化对漫衰减系数的影响。
选取不同悬浮物浓度的水样,使用单一散射相函数模拟不同波长处的Kd值。结果发现,当悬浮颗粒物浓度较小时(<35 mg/L),在小于550 nm波段范围内,模拟值与实测值吻合较好,在大于550 nm波段范围内,模拟值小于实测值;当悬浮物浓度较大(>40 mg/L)且以无机颗粒物为主体时,在短波处(<550 nm),模拟值大于实测值,而在长波处(>550 nm),模拟值小于实测值。在构建内陆湖泊水体的Kd值半分析遥感模型时,需考虑不同悬浮物浓度的大小以及组成的条件下散射相函数的选取。
参考文献(References)
-
Aas E, Høkedal J and Sørensen K. 2005. Spectral backscattering coefficient in coastal waters. International Journal of Remote Sensing, 26 (2): 331–343. [DOI: 10.1080/01431160410001720324]
-
Bricaud A, Morel A and Prieur L. 1981. Absorption by dissolved organic matter of the sea (yellow substance) in the UV and visible domains. Limnology and Oceanography, 26 (1): 43–53. [DOI: 10.4319/lo.1981.26.1.0043]
-
Clevel J S and Weidemann A D. 1993. Quantifying absorption by aquatic particles: a multiple scattering correction for glass-fiber filters. Limnology and Oceanography, 38 (6): 1321–1327. [DOI: 10.4319/lo.1993.38.6.1321]
-
Darecki M and Stramski D. 2004. An evaluation of MODIS and SeaWiFS bio-optical algorithms in the Baltic Sea. Remote Sensing of Environment, 89 (3): 326–350. [DOI: 10.1016/j.rse.2003.10.012]
-
Fournier G R and Forand J L. 1994. Analytic phase function for ocean water//Proceedings of SPIE 2258, Ocean Optics XII. Bergen, Norway: SPIE: 194–201 [DOI: 10.1117/12.190063]
-
Gordon H R and McCluney W R. 1975. Estimation of the depth of sunlight penetration in the sea for remote sensing. Applied Optics, 14 (2): 413–416. [DOI: 10.1364/AO.14.000413]
-
Gordon H R. 1989. Can the Lambert-Beer law be applied to the diffuse attenuation coefficient of ocean water?. Limnology and Oceanography, 34 (8): 1389–1409. [DOI: 10.4319/lo.1989.34.8.1389]
-
Gordon H R. 1992. Monte Carlo simulations for interpretation of irradiance measurements from moored instruments: preliminary results//Proceedings of SPIE 1750, Ocean Optics XI. San Diego, CA: SPIE: 366–370 [DOI: 10.1117/12.140663]
-
Green S A and Blough N V. 1994. Optical absorption and fluorescence properties of chromophoric dissolved organic matter in natural waters. Limnology and Oceanography, 39 (8): 1903–1916. [DOI: 10.4319/lo.1994.39.8.1903]
-
Haltrin V I. 1999a. Two-term Henyey-Greenstein light scattering phase function for seawater//Proceedings of IEEE 1999 International Geoscience and Remote Sensing Symposium. Hamburg: IEEE, 2 : 1423–1425. [DOI: 10.1109/IGARSS.1999.774652]
-
Haltrin V I. 1999b. Light scattering coefficient of seawater for arbitrary concentrations of hydrosols//Proceedings of 1997 IEEE International Geoscience and Remote Sensing. Singapore: IEEE, 1: 299–301 [DOI: 10.1109/IGARSS.1999.774652]
-
Haltrin V I. 1997. Light scattering coefficient of seawater for arbitrary concentrations of hydrosols// Geoscience and Remote Sensing, IGARSS’97. Remote Sensing-A Scientific Vision for Sustainable Development. IEEE International. IEEE, 1999:299–301
-
Huang C C, Li Y M, Le C F, Sun D Y, Wu L, Wang L Z and Wang X. 2009. Seasonal characteristics of the diffuse attenuation coefficient of Meiliang Bay waters and its primary contributors. Acta Ecologica Sinica, 29 (6): 3295–3306. [DOI: 10.3321/j.issn:1000-0933.2009.06.062] ( 黄昌春, 李云梅, 乐成峰, 孙德勇, 伍蓝, 王利珍, 王鑫. 2009. 太湖梅梁湾漫衰减系数季节性差异及其主导因素. 生态学报, 29 (6): 3295–3306. [DOI: 10.3321/j.issn:1000-0933.2009.06.062] )
-
Jerlov N G. 1976.Marine Optics.New York:Elsevier Scientific Publishing Company
-
Kirk J T O. 1981. Monte Carlo study of the nature of the underwater light field in, and the relationships between optical properties of, turbid yellow waters. Marine and Freshwater Research, 32 (4): 517–532. [DOI: 10.1071/MF9810517]
-
Kirk J T O. 1984. Dependence of relationship between inherent and apparent optical properties of water on solar altitude. Limnology and Oceanography, 29 (2): 350–356. [DOI: 10.4319/lo.1984.29.2.0350]
-
Kirk J T O. 1991. Volume scattering function, average cosines, and the underwater light field. Limnology and Oceanography, 36 (3): 455–467. [DOI: 10.4319/lo.1991.36.3.0455]
-
Kirk J T O. 1994. Light and Photosynthesis in Aquatic Ecosystems. Cambridge: Cambridge University Press
-
Le C F, Li Y M, Zha Y, Sun D Y and Lv H. 2009. Simulation of backscattering properties of Taihu Lake. Advances in Water Science, 20 (5): 707–713. [DOI: 10.3321/j.issn:1001-6791.2009.05.017] ( 乐成峰, 李云梅, 查勇, 孙德勇, 吕恒. 2009. 太湖水体后向散射特性模拟. 水科学进展, 20 (5): 707–713. [DOI: 10.3321/j.issn:1001-6791.2009.05.017] )
-
Leathers R A and Mobley C D. 2004. Monte Carlo Radiative Transfer Simulations for Ocean Optics: A Practical Guide. NRL/MR/5660-04-8819. Washington, DC: Naval Research Laboratory
-
Lee M E, Haltrin V I, Shybanov E B, Weidemann A D. 2003. Light scattering phase functions of turbid coastal waters measured in LEO-15 experiment in 2000// Oceans. IEEE, 2003:P2835-P2841 Vol.5.[DOI: 10.1109/OCEANS.2003.178358]
-
Lee Z P, Du K P and Arnone R. 2005. A model for the diffuse attenuation coefficient of downwelling irradiance. Journal of Geophysical Research: Oceans, 110 (C2): C02016 [DOI: 10.1029/2004JC002275]
-
Liu C C, Carder K L, Miller R L and Ivey J E. 2002. Fast and accurate model of underwater scalar irradiance. Applied Optics, 41 (24): 4962–4974. [DOI: 10.1364/AO.41.004962]
-
Ma R H, Song Q J, Li G Y and Pan D L. 2008. Estimation of backscattering probability of Lake Taihu waters. Journal of Lake Sciences, 20 (3): 375–379. [DOI: 10.18307/2008.0318] ( 马荣华, 宋庆君, 李国砚, 潘德炉. 2008. 太湖水体的后向散射概率. 湖泊科学, 20 (3): 375–379. [DOI: 10.18307/2008.0318] )
-
Marra J, Langdon C and Knudson C A. 1995. Primary production, water column changes, and the demise of a Phaeocystis bloom at the Marine Light-Mixed Layers site (59°N, 21°W) in the northeast Atlantic Ocean. Journal of Geophysical Research: Oceans, 100 (C4): 6633–6643. [DOI: 10.1117/12.869730]
-
Morel A, Ahn Y H. 1990.Optical efficiency factors of free-living marine bacteria: Influence of bacterioplankton upon the optical properties and particulate organic carbon in oceanic waters. Journal of Marine Research. 1990. Optical efficiency factors of free-living marine bacteria: Influence of bacterioplankton upon the optical properties and particulate organic carbon in oceanic waters. Journal of Marine Research, 48 (1): 145–175. [DOI: 10.1357/002224090784984632]
-
Mitchell B G. 1990. Algorithms for determining the absorption coefficient for aquatic particulates using the Quantitative Filter Technique//Proceedings of SPIE 1302, Ocean Optics X. Orlando, FL: SPIE: 137 [DOI: 10.1117/12.21440]
-
Mobley C D, Gentili B, Gordon H R, Jin Z H, Kattawar G W, Morel A, Reinersman P, Stamnes K and Stavn R H. 1993. Comparison of numerical models for computing underwater light fields. Applied Optics, 32 (36): 7484–7504. [DOI: 10.1364/AO.32.007484]
-
Mobley C D. 1994. Light and Water: Radiative Transfer in Natural Waters. New York: Academic Press
-
Mobley C D, Sundman L K and Boss E. 2002. Phase function effects on oceanic light fields. Applied Optics, 41 (6): 1035–1050. [DOI: 10.1364/AO.41.001035]
-
Pan X J and Zimmerman R C. 2010. Modeling the vertical distributions of downwelling plane irradiance and diffuse attenuation coefficient in optically deep waters. Journal of Geophysical Research: Oceans, 115 (C8): C08016 [DOI: 10.1029/2009JC006039]
-
Petzold T J. 1972. Volume Scattering Functions for Selected Ocean Waters. Scripps Institution of ceanography.San Diego, CA, Tech. Rep.
-
Platt T, Sathyendranath S, Caverhill C M and Lewis M R. 1988. Ocean primary production and available light: further algorithms for remote sensing. Deep Sea Research Part A. Oceanographic Research Papers, 35 (6): 855–879. [DOI: 10.1016/0198-0149(88)90064-7]
-
Pope R M and Fry E S. 1997. Absorption spectrum (380-700 nm) of pure water. II. Integrating cavity measurements. Applied Optics, 36 (33): 8710–8723. [DOI: 10.1364/AO.36.008710]
-
Sathyendranath S, Prieur L and Morel A. 1989. A three-component model of ocean colour and its application to remote sensing of phytoplankton pigments in coastal waters. International Journal of Remote Sensing, 10 (8): 1373–1394. [DOI: 10.1080/01431168908903974]
-
Smith R C and Baker K S. 1981. Optical properties of the clearest natural waters (200-800 nm). Applied Optics, 20 (2): 177 [DOI: 10.1364/AO.20.000177]
-
Snyder W A, Arnone R A, Davis C O, Goode W, Gould R W, Ladner S, Lamela G, Rhea W J, Stavn R, Sydor M and Weidemann A. 2008. Optical scattering and backscattering by organic and inorganic particulates in U. S. coastal waters. Applied Optics, 47 (5): 666–677. [DOI: 10.1364/AO.47.000666]
-
Sokolov A, Chami M, Dmitriev E and Khomenko G. 2010. Parameterization of volume scattering function of coastal waters based on the statistical approach. Optics Express, 18 (5): 4615–4636. [DOI: 10.1364/OE.18.004615]
-
Stramska M and Frye D. 1997. Dependence of apparent optical properties on solar altitude: experimental results based on mooring data collected in the Sargasso Sea. Journal of Geophysical Research: Oceans, 102 (C7): 15679–15691. [DOI: 10.1029/97JC00886]
-
Sun D Y, Li Y M, Wang Q, Le C F, Huang C C and Wu L. 2008. The scattering characteristics of Lake Taihu waters. Journal of Lake Sciences, 20 (3): 389–395. [DOI: 10.18307/2008.0320] ( 孙德勇, 李云梅, 王桥, 乐成峰, 黄昌春, 伍蓝. 2008. 太湖水体散射特性及其空间分异. 湖泊科学, 20 (3): 389–395. [DOI: 10.18307/2008.0320] )
-
Wang M H, Son S and Harding Jr L W. 2009. Retrieval of diffuse attenuation coefficient in the Chesapeake Bay and turbid ocean regions for satellite ocean color applications. Journal of Geophysical Research: Oceans, 114 (C10): C10011 [DOI: 10.1029/2009JC005286]
-
Zhang Y L, Qin B Q, Chen W M, Yang D T and Ji J. 2003. Analysis on distribution and variation of beam attenuation coefficient of Taihu Lake’s water. Advances in Water Science, 14 (4): 447–453. [DOI: 10.3321/j.issn:1001-6791.2003.04.011] ( 张运林, 秦伯强, 陈伟民, 杨顶田, 季江. 2003. 太湖水体光学衰减系数的分布及其变化特征. 水科学进展, 14 (4): 447–453. [DOI: 10.3321/j.issn:1001-6791.2003.04.011] )