出版日期: 2017-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176315
2017 | Volumn21 | Number 4
上一篇  |  下一篇
  
质心误差对分布式InSAR基线确定的影响及消除
expand article info 鞠冰 , 昌虓 , 谷德峰 , 段晓君 , 朱炬波 , 王正明
国防科学技术大学 理学院, 长沙 410073
收稿日期: 2016-09-09
基金项目: 国家自然科学基金(编号：91438202，61573367，61370013)
第一作者简介: 鞠冰(1986—　)，男，博士研究生，研究方向为卫星精密轨道确定及应用。E-mail：jucice@126.com
中图分类号: TP702
文献标识码: A

摘要

高精度星间基线确定是分布式InSAR干涉测量中的关键技术。针对卫星在轨运行期间的质心与地面标校结果不一致问题，仿真分析了星体系x、y、z不同方向1 cm质心误差对InSAR星间基线确定的影响。结果表明：x、y方向的质心误差对基线解算影响很小；z方向的质心误差对基线解算影响显著，使得InSAR基线产品中含有明显的系统误差。提出了两种消除卫星质心误差影响的方法：一是在星载GNSS定轨过程中增加轨道径向的经验加速度予以补偿；二是增加星体系z方向的质心偏差估计。实验结果表明，经两种方法处理后得到的InSAR基线3维误差由8.8 mm分别降至0.13 mm和0.09 mm，98%以上的卫星质心误差影响被消除。

关键词

卫星质心误差, 分布式InSAR, 星间基线确定, 星载GNSS, 经验加速度

Analysis and mitigation of the Center-of-Mass errors for InSAR baseline determination
expand article info JU Bing , CHANG Xiao , GU Defeng , DUAN Xiaojun , ZHU Jubo , WANG Zhengming
College of Science, National University of Defense Technology, Changsha 410073, China

Abstract

High-precision inter-satellite baseline determination is essential for the distributed InSAR system. The reduced dynamic orbit determination method, which employs onboard GNSS measurements and the dynamical constraints, is most extensively used to generate a baseline solution between two formation-fly satellites in low-Earth orbits. However, the reference point of the dynamical model is the center-of-mass (CoM) of the satellite rather than the phase center of the SAR antenna. Owing to the effect of structural deformation and the inevitable formation-keeping maneuvers, the CoM of a satellite in orbit is usually different from the point calibrated on ground. Thus, the effect of CoM errors must be carefully considered in GNSS-based precision baseline determination; otherwise, CoM errors are likely to induce systematic errors in the spatial baseline solution of the InSAR formation. Simulations are carried out in this study to analyze and mitigate the effect of CoM errors on the InSAR baseline determination. First, a constant CoM error of 1 cm is added to the x-, y-, and z-directions of the satellite-fixed frame. Simulation results show that the effect of such 1 cm error in the x- and y-directions are extremely tiny and can be safely neglected. By contrast, the effect of CoM error in the z-direction is significant, and the results in a systematic variation in the baseline product. In view of this, we further propose two independent methods in GNSS-based InSAR baseline determination to mitigate the z-component CoM errors by adding the following: (1) constant empirical acceleration in the radial direction; (2) an offset parameter in the z-direction of the satellite-fixed frame. The first method is based on dynamical modeling and does not need any extra correction for CoM variations. In addition, the first method is suitable for the mitigation of the CoM errors caused by formation-keeping maneuvers. The second method is based on geometric modeling, and an online calibration for the CoM errors is necessary. Moreover, the second method is suitable for the CoM calibration at the beginning of the in-orbit validation phase. Both methods are proven effective according to the numerical experiments. The 3D RMS caused by the simulated 1 cm CoM errors in the satellite-fixed z-direction can be reduced from 8.8 mm to 0.13 mm and 0.09 mm, respectively. Over 98% of the CoM errors can be mitigated. Using our proposed methods, the systematic errors caused by the CoM offset in the baseline solution can be considerably mitigated. Compared with traditional in-orbit CoM calibration, the proposed method not only avoids the complex design for satellite attitude control but also improves the efficiency of the InSAR system. The current research is based on simulations. Further validation of real data will be carried out in future studies.

Key words

Center-of-Mass errors, distributed InSAR, inter-satellite baseline determination, spaceborne GNSS, empirical acceleration

1 引　言

分布式InSAR系统是将合成孔径雷达(SAR)成像技术与卫星编队飞行相结合的一种新体制雷达系统，通过卫星近距离编队飞行和SAR天线的协同工作来完成干涉测量任务(Tu 等，2012)。相比于传统的星载InSAR系统，分布式InSAR可以突破时间去相干和基线长度限制，利用干涉成像技术实现地面目标的3维定位、地表形变和动目标监测等，极大地拓展了以往星载InSAR系统的干涉性能和测绘精度，已成为高分辨率对地观测领域的研究热点(Allende-Alba和Montenbruck，2016)。

星间基线的高精度确定是分布式InSAR系统干涉测量的前提和重要保证(Krieger 等，2013)，其精度要求极为苛刻，以德国TanDEM-X编队任务(Krieger 等，2005, 2007)为例，为实现高精度的地面高程测量目标(绝对高程精度10 m，相对高程精度2 m)，星间基线的确定精度须控制在1 mm以内(1D RMS)(汪丙南和向茂生，2009；Montenbruck 等，2011)。目前，星间基线的确定主要依靠基于全球卫星导航系统(GNSS)测量的缩减动力学绝对定轨(Wu 等，1991；Beutler 等，2006)和相对定轨技术(Moon 等，2012；Jäggi 等，2012)。然而，轨道动力学模型的作用点是卫星质心，而非SAR天线相位中心。利用星载GNSS获得的InSAR基线需要经过进一步的部位修正，将基线的参考点由卫星质心转换到SAR天线相位中心才能获得最终的基线产品。受轨道控制机动、卫星结构变形以及重力应力释放等因素的影响，卫星在轨运行期间的质心通常与地面标校的结果存在不一致。例如：TanDEM-X卫星入轨后的质心与地面标校值之间存在7 mm的偏差，并且受未来频繁的轨道控制机动影响，卫星燃料箱将逐渐变空，最终将导致卫星寿命期内的质心变化量达到10 cm(Wermuth 等，2011)。因此，在GNSS精密定轨中必须对卫星质心误差予以充分考虑，否则将导致InSAR基线产品中含有明显的系统误差。

目前，对卫星质心误差控制的研究主要集中在重力场探测卫星的应用，大多采用在轨标校技术，需要设计专门的姿态机动方案协作完成。其基本思想是通过姿态机动设计，利用加速度计等测量数据估计出质心偏差，从而达到修正和精确控制的目的。Bergman等人(1987)，Richfield等人(1988)和Tanygin和Williams(1997)分别设计了卫星在轨姿态机动方案，并研究了卫星质心的在轨标定算法。Wang等人(2010)给出了GRACE卫星的质心校准机动方案设计和校准精度。王本利等人(2010)研究了以磁力矩驱动卫星做周期性姿态晃动，联合使用加速度计和陀螺仪测量数据进行质心的在轨标定。在轨标校技术的局限性在于：一方面，姿态控制机动的设计和操作难度大，需要使用加速度计、陀螺仪等精密仪器的测量数据，工程实现较为复杂；另一方面，姿态控制机动和质心标定过程也会对SAR的正常工作带来干扰；再者，与重力场探测需要精确控制质心位置需求不同，对于分布式InSAR任务而言，质心只是其基线产品估计过程的一个中间环节，消除其对基线确定的影响才是最终目的。因此，本文通过增加卫星质心误差的建模以改进现有GNSS基线估计方法，直接消除其对InSAR基线确定的影响，避免引入额外的姿态机动设计而增加卫星控制复杂度。首先给出分布式InSAR基线确定以及星载GNSS绝对、相对定轨的基本原理，利用仿真系统地分析不同方向质心误差对InSAR基线确定精度的影响。在此基础上，进一步给出质心误差的消除策略。最后，通过数值实验验证方法的有效性。

2 分布式InSAR基线确定

分布式InSAR系统的干涉基线定义为：在同一地面目标点的主星成像时刻t1与辅星成像时刻t2，两颗卫星SAR天线相位中心的连线矢量(Tu 等, 2012)。干涉基线定义中包含主、辅星SAR天线的相对位置和相对时间关系，其中它们的相对位置关系被定义为空间域基线，相对时间关系被定义为时间域基线。时间域基线误差主要来自主辅图像的干涉时刻配准误差、授时误差等。其中干涉SAR图像配准误差一般优于0.1像素，GNSS卫星授时精度通常优于微秒量级(王青松 等, 2012)。尽管这些误差带来的基线误差可达厘米甚至分米量级，但这些基线误差将主要体现在方位向，对距离向的InSAR地理高程测量影响并不明显。空间域基线的高精度确定才是分布式InSAR系统星间基线确定的关键。

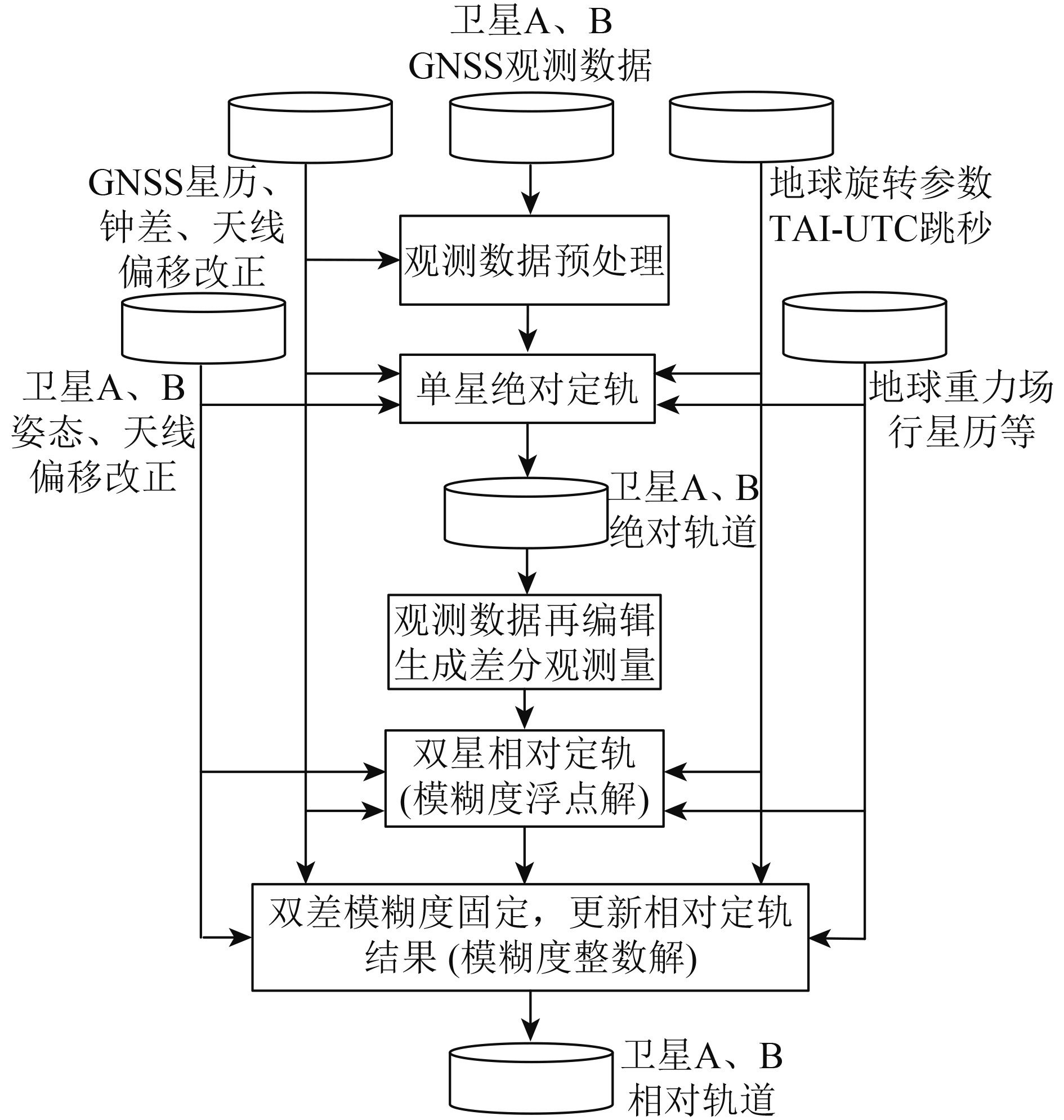
分布式InSAR星间基线测量主要通过星载GNSS差分手段(流程见图1)。首先，通过GNSS差分测量和地面高精度轨道解算，获得GNSS测量基线(主、辅卫星质心轨迹)；然后，通过部位修正，将基线的参考点由卫星质心转换到SAR天线相位中心，得到空间域基线(主、辅卫星SAR天线相位中心轨迹)；最后，将空间域基线插值重采样到主、辅星更高数据率的雷达成像时刻。其中，GNSS基线测量频率一般为1 Hz，SAR脉冲重复频率一般为3000 Hz左右，插值重采样方法可选取高阶Lagrange方法，此时对应插值方法本身带来的误差影响相对于1—2 mm量级的基线确定可忽略。用户根据主辅图像干涉时刻匹配后的时间关系，即可获得对应的干涉基线产品。


图 1 分布式InSAR基线确定处理流程
Fig. 1 Flow chart of the distributed InSAR baseline determination

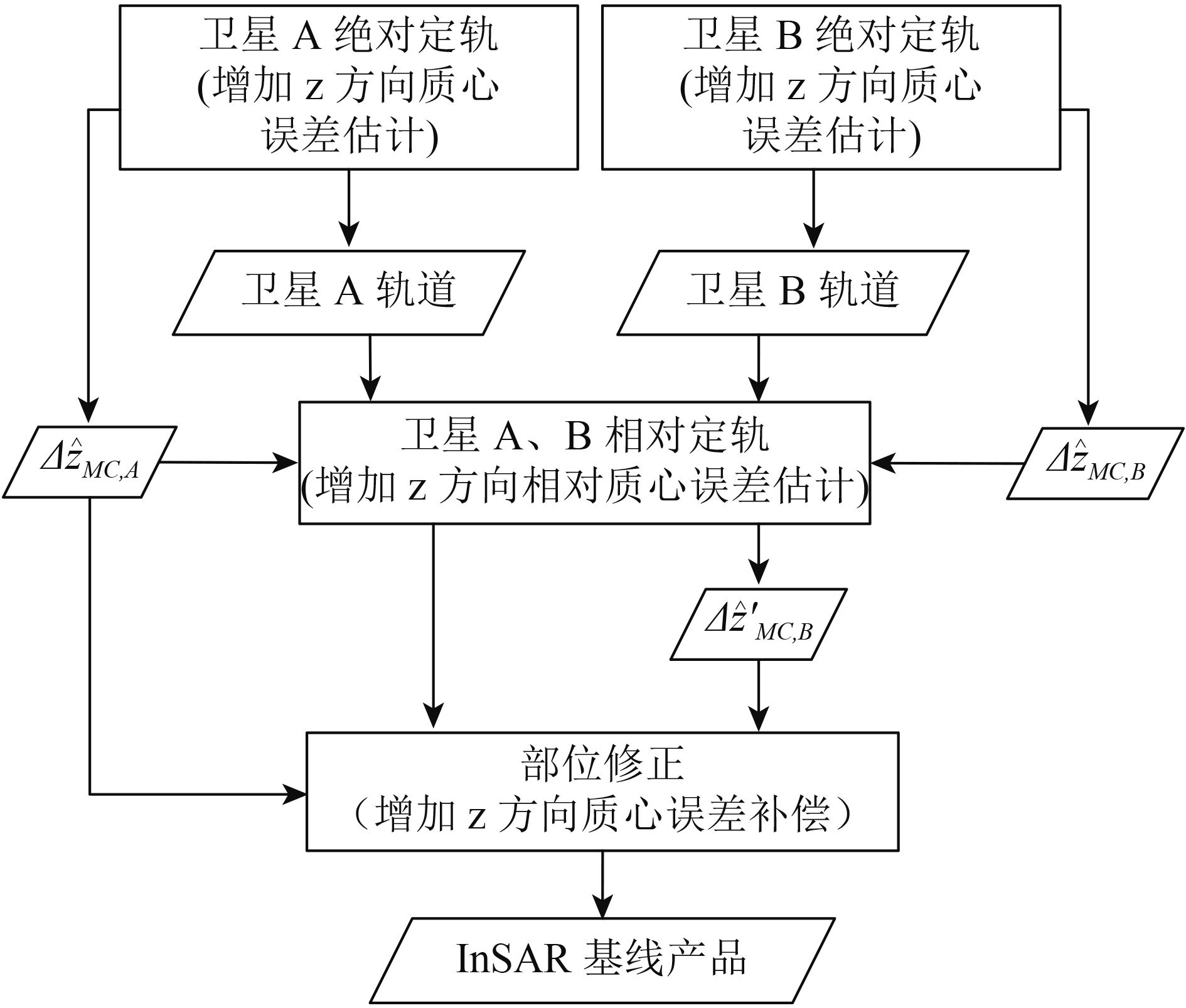
空间域基线确定主要通过GNSS单星绝对定轨和双星相对定轨技术来实现(流程见图2)。以双星编队为例，卫星A的轨道可通过单星GNSS绝对定轨技术来实现，卫星B的轨道则主要通过双星GNSS相对定轨来完成。二者的主要区别是双星GNSS相对定轨中采用CDGNSS技术(Kroes 等, 2005)，对两颗近距离编队飞行卫星的GNSS载波相位测量数据进行差分，可以减弱或消除各种公共误差影响，提高观测精度。同时，双星GNSS相对定轨中采用了双差模糊度固定技术，使得相对定轨精度更高。


图 2 GNSS单星定轨和双星相对定轨处理流程
Fig. 2 Flow chart of the GNSS based single-satellite orbit determination and inter-satellite relative orbit determination

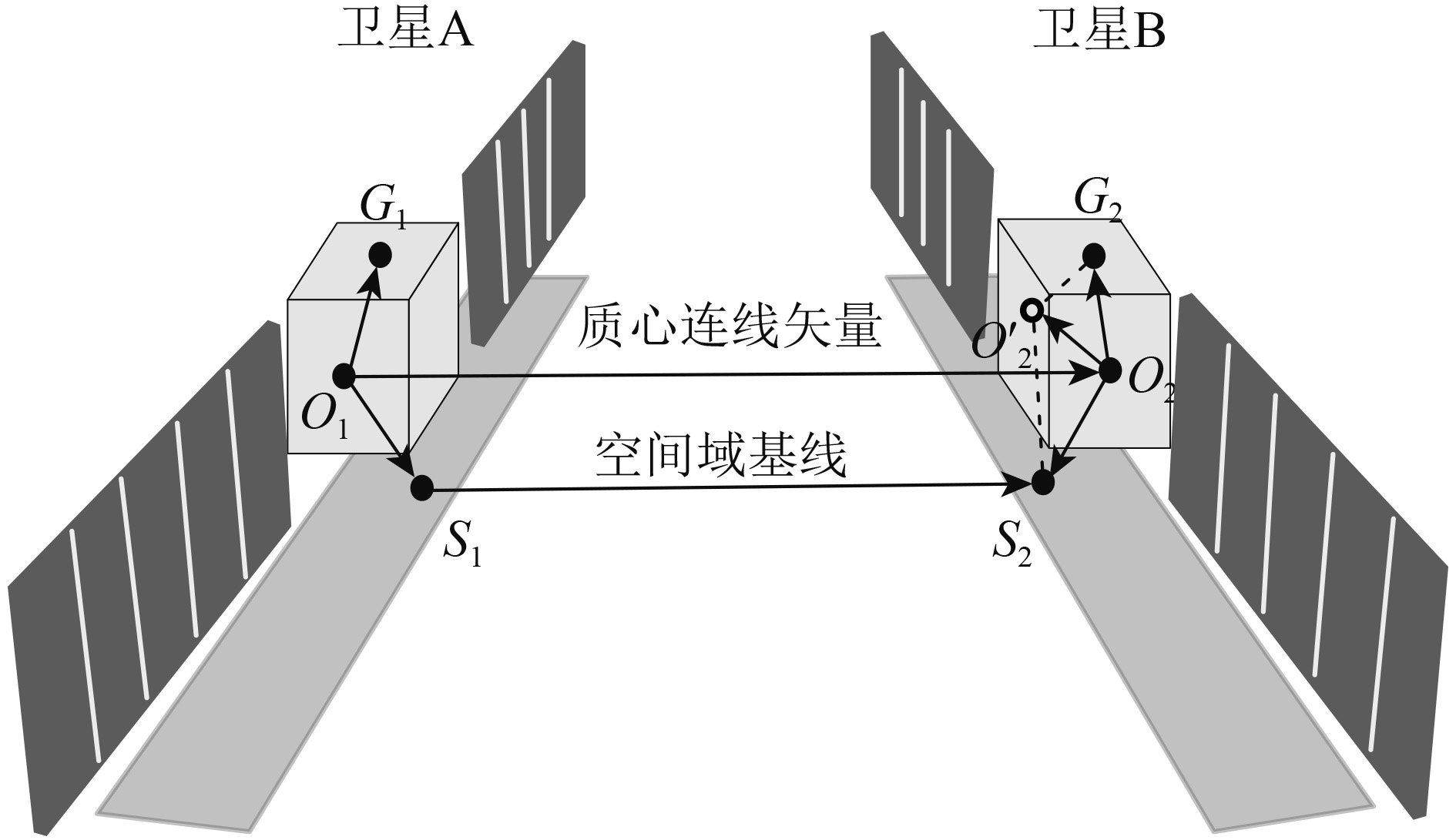
空间域基线处理中部位修正的目的是将基线参考点由卫星质心转换到SAR天线相位中心，其几何关系描述见图3。图中G1、G2是GNSS接收天线相位中心，O1、O2是卫星质心，S1、S2是SAR天线相位中心。根据图中的几何关系可得：

${{{S}}_1}{{{S}}_2}{\rm{ = }}{{{O}}_1}{{{O}}_2} + {{{O}}_2}{{{S}}_2} - {{{O}}_1}{{{S}}_1}$ (1)

式中， ${{{S}}_1}{{{S}}_2}$ 为卫星A、B的SAR天线相位中心连线矢量， ${{{O}}_1}{{{O}}_2}$ 为卫星A、B的质心连线矢量， ${{{O}}_1}{{{S}}_1}$ 、 ${{{O}}_2}{{{S}}_2}$ 分别为卫星A、B的质心与SAR天线相位中心连线矢量。


图 3 InSAR空间域基线天线部位修正示意图
Fig. 3 Antenna phase center corrections for InSAR spatial baseline

本文依托国防科技大学精密定轨软件工具包NUDTTK进行卫星质心误差的影响分析及建模消除研究。该软件已成功处理GRACE、CHAMP、Shiyan3、HY2等多颗卫星实测GNSS数据(Liu 等，2014, 2015；Gu 等，2016)，其中GRACE单星绝对定轨精度优于3 cm，双星相对定轨KBR检核精度优于1 mm(Ju 等，2017)。由于影响低轨卫星力学模型精度的主要因素是大气阻力，考虑到大气随地球旋转假设，残余的未模型化的摄动力影响主要体现在卫星轨道飞行方向(T)和法方向(N)。为此，引入T、N方向的分段线性样条经验加速度分量，以补偿未模型化的摄动力影响。NUDTTK采用的定轨模型和参数配置详见表1。

表 1 定轨模型及参数配置
Table 1 Configuration of models and parameters for orbit determination

下载CSV 
模型项 描述
地球重力场 GGM02C 100×100
固体潮 IERS Conventions 2010，4×4
极潮 IERS Conventions 2010
海潮 CSR 4.0
三体引力 太阳、月球和行星，DE405
太阳光压摄动 Canon-ball模型，每天估计1次光压系数Cr
大气阻力摄动 大气密度模型Jacchia-Gill71，每3 h估计1次大气阻力系数Cd
经验加速度 T、N方向30 min分段线性样条模型
相对论摄动 仅Schwarzschild项
岁差、章动 IAU 2000A
地球旋转参数 IERS Standard Rapid EOP

3 卫星质心误差对基线确定的影响

星载GNSS定轨采用卫星轨道动力学模型的先验约束来抑制测量误差。轨道力学模型的作用点是卫星质心，因此在星载GNSS定轨中需要对观测数据进行天线质心偏移改正，将测量数据参考点由GNSS天线相位中心修正到卫星质心。以卫星B为例，记GNSS天线参考点G2相对于卫星质心O2的真实偏移量为 ${{{r}}_{2G}}$ ，SAR天线参考点S2相对于卫星质心O2的真实偏移量为 ${{{r}}_{2S}}$ 。天线参考点相对于卫星质心的偏移量 ${{{r}}_{2G}}$ 、 ${{{r}}_{2S}}$ 一般在卫星发射前通过地面仪器精密测量给出。地面测量坐标系的三轴与星体系三轴的定义相同，坐标原点一般选取星体上的某个特征点，将各天线参考点坐标的测量结果减去卫星质心的测量结果，即可得到星体系下天线的质心偏移量。一方面，地面测量结果可能存在误差，尤其是卫星质心的测量。为了保证卫星质心测量结果的有效性，地面测量时一般要求太阳帆板展开，以保证与卫星在轨飞行状态一致。另一方面，分布式InSAR卫星编队入轨后需要频繁地进行轨道及编队保持机动，产生燃料消耗，从而导致卫星质心在轨发生变化。此外，卫星发射过程中的振动及在轨温度变化引起的热变形也会导致天线偏移的地面测量结果与在轨状态不一致。

假设卫星B质心的地面测量结果为 ${O'_2}$ ，其相对于真实卫星质心O2存在误差 ${{{O}}_{\rm{2}}}{{{O'}}_{\rm{2}}}$ (见图3)，不妨将该质心误差所导致的 ${{{r}}_{2G}}$ 、 ${{{r}}_{2S}}$ 误差记为 ${{\varDelta }}{{{r}}_{2G}}$ 、 ${{\varDelta }}{{{r}}_{2S}}$ ，则

${{\varDelta }}{{{r}}_{2G}} = {{\varDelta }}{{{r}}_{2S}} = - {{{O}}_{\rm{2}}}{{{O'}}_{\rm{2}}}$ (2)

式中， ${{\varDelta }}{{{r}}_{2G}}$ 和 ${{\varDelta }}{{{r}}_{2S}}$ 为系统性偏差，短时间内可以认为是常值固定偏差。GNSS天线质心偏移误差 ${{\varDelta }}{{{r}}_{2G}}$ 的存在会导致绝对定轨和相对定轨中的天线偏移修正环节存在偏差，其引起的每颗GNSS观测卫星视方向 ${{{e}}^j}$ 的距离观测误差为

$ \varepsilon _\rho ^j = {({{{e}}^j})^{\rm T}} \cdot {{\varDelta }}{{{r}}_{2G}}$ (3)

SAR天线质心偏移误差 ${{\varDelta }}{{{r}}_{2S}}$ 的存在则会导致SAR天线部位修正环节存在偏差，其引起的基线产品位置误差为 ${{\varDelta }}{{{r}}_{2S}}$ 。

以下给出卫星质心误差对基线产品影响的仿真分析。首先给定编队卫星A、B的轨道根数(见表2)，设置星间基线长度为1 km，积分生成编队卫星24小时的参考轨迹真值；配置GNSS和SAR天线安装位置(表3)；然后结合IGS提供的GNSS精密轨道、钟差产品，仿真生成星载GPS原始观测数据，包括双频伪码P1、P2和双频载波相位L1、L2。

表 2 仿真InSAR编队的轨道根数
Table 2 Orbital roots of the simulated formation flying InSAR satellites

下载CSV 
轨道根数 主星A 辅星B
半长轴a/km 7000 7000
偏心率e 7.1429×10–5 7.1429×10–5
轨道倾角i/(°) 97 96.9939
升交点赤经Ω/(°) 0.0071 –0.0036
近地点幅角w/(°) 0 120
平近点角M/(°) 0.0008 –120.0004

表 3 星体系下GNSS天线及SAR天线相位中心坐标
Table 3 Values of the GNSS and SAR antenna phase center coordinates in satellite-fixed frame

下载CSV 
/m
主星A 辅星B
GNSS天线坐标 x 0 0
y 0 0
z –1.8 –1.8
SAR天线坐标 x 0 0
y 0 0
z 0.2 0.2

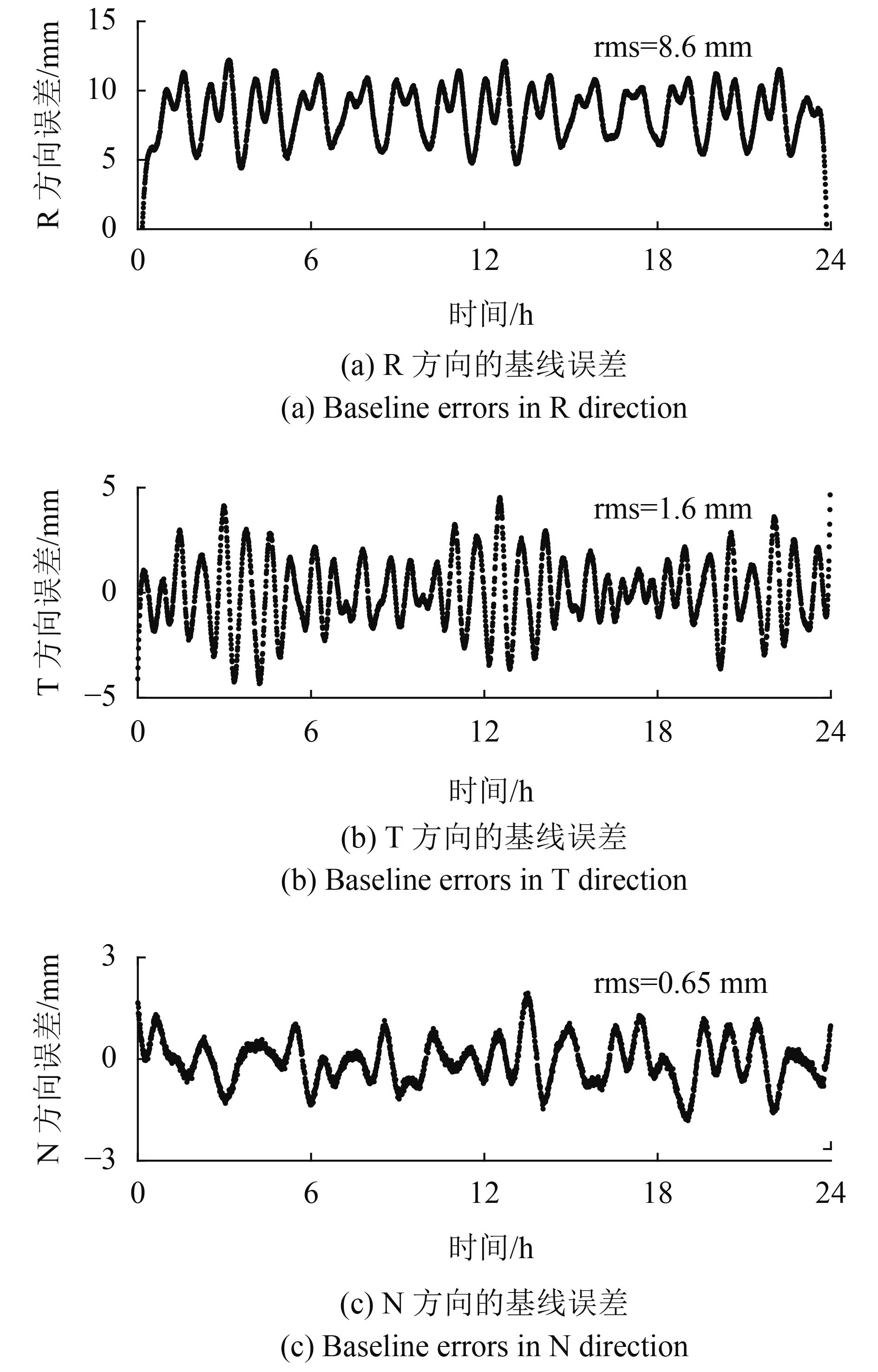
分别沿星体系x、y、z方向在卫星B中加入1 cm大小的质心误差，解算编队卫星A、B的空间域基线，得到基线产品。然后将基线产品与仿真基线真值进行比对，分析不同方向的质心误差对基线解算结果的影响。由图4可见：x方向的质心误差对基线产品影响很小。y方向的质心误差对基线解算的影响与x方向类似(限于篇幅，文中未给出具体误差分布)，二者均可被忽略。由图5可见：z方向的质心误差对基线产品影响差异较为显著，其中轨道径向(R)误差为8.6 mm，轨道飞行方向(T)误差为1.6 mm，轨道法向(N)误差0.65 mm，3维误差为8.8 mm。z方向的质心误差经过定轨中的力学模型平滑后分散到3个方向，呈现不规则的波动特性。产生该现象的主要原因是：x、y、z分别与轨道T、N、R方向相对应，表1中的定轨经验加速度仅添加了T、N方向分段线性样条参数，未考虑R方向。x、y方向的质心误差均会被定轨中的经验加速度参数所吸收，但z方向的质心误差无法被吸收。因此，z方向的质心误差影响必须在GNSS定轨中予以消除，否则基线产品中的系统误差将无法通过后续的基线标定(Gonzalez 等，2010；Antony 等，2013)进行校准。


图 4 x方向1 cm质心误差对基线确定精度的影响
Fig. 4 The effect of 1 cm center-of-mass error in x direction on baseline determination


图 5 z方向1 cm质心误差对基线确定精度的影响
Fig. 5 The effect of 1 cm center-of-mass error in z direction on baseline determination

4 卫星质心误差影响的消除

4.1 方法Ⅰ：增加轨道R方向经验加速度补偿

借鉴x、y方向的质心误差可以被轨道T、N方向经验加速度参数所吸收的原理，继续增加轨道R方向的经验加速度参数进行估计，以达到吸收z方向卫星质心偏差的目的。假设z方向存在卫星质心偏差Δ ${z_{MC}}$ ，则该偏差会被对应R方向的轨道经验加速度参数所吸收，此时会导致GNSS绝对定轨和相对定轨结果(质心轨迹)分别沿z方向存在一个常值的平移，而且平移的大小与 ${\rm{\varDelta }}{z_{MC}}$ 大小几乎相同。然后，在空间域基线部位修正中，将基线参考点由卫星质心转换到SAR天线相位中心时，会继续引入一个大小相同、方向相反的SAR天线相位中心坐标偏差– ${\rm{\varDelta }}{z_{MC}}$ ，从而将z方向卫星质心误差影响抵消，使得最终的InSAR基线产品几乎不受影响(原理见图6)。需要注意的是，为吸收z方向卫星质心偏差，仅添加R方向的常值经验加速度参数估计即可，若添加多组经验加速度参数，则需添加紧约束条件，以避免增加过多待估参数导致力学模型自身约束变弱，降低定轨精度。


图 6 增加轨道R方向经验加速度补偿卫星质心误差原理
Fig. 6 Center-of-mass error compensation by adding empirical acceleration in R direction

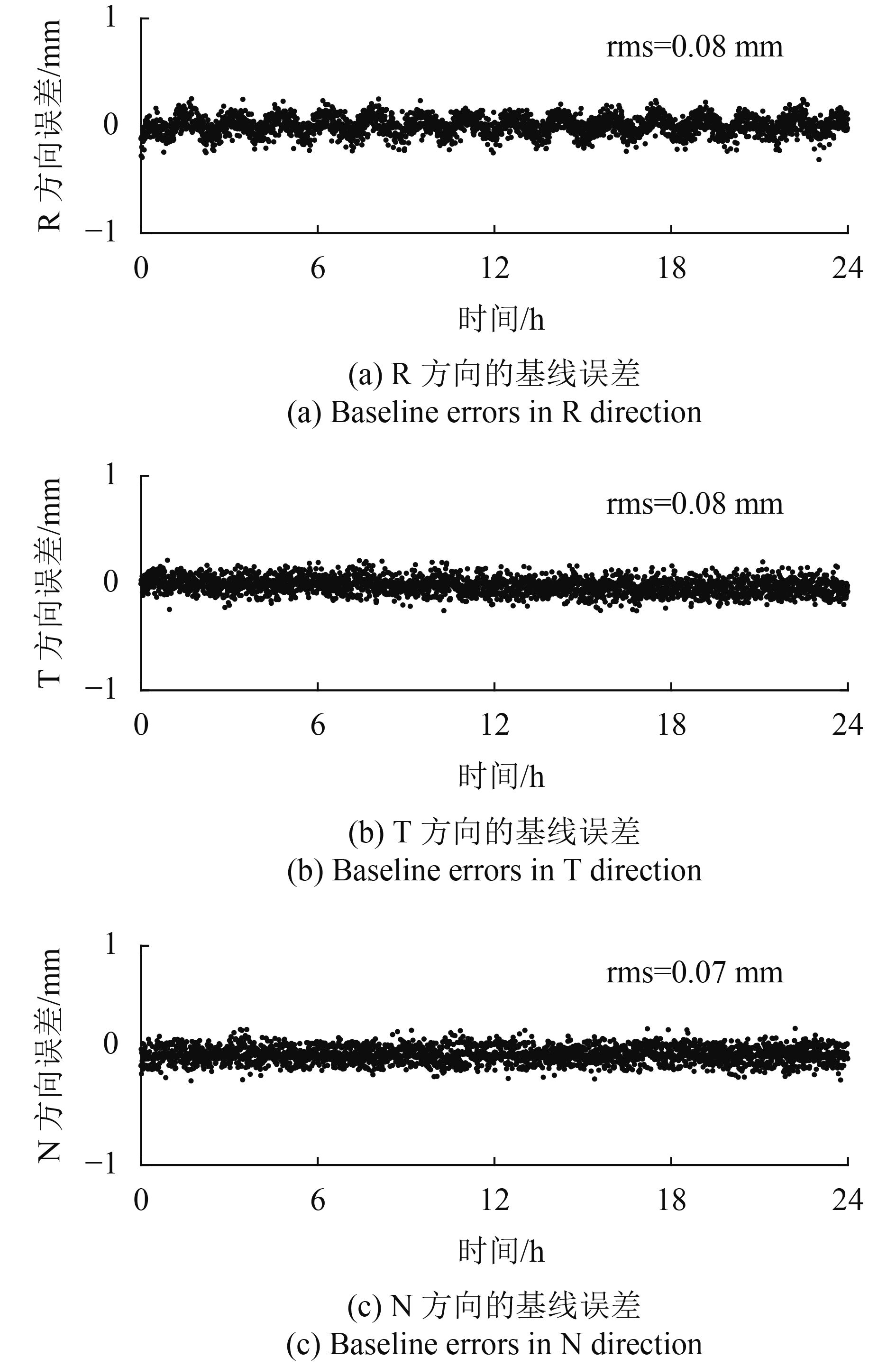
图7给出的仿真结果表明：经过方法I处理得到的基线产品误差为：R方向0.08 mm，T方向0.08 mm，N方向0.07 mm，3维0.13 mm；约98.5%的卫星质心误差影响得到有效消除，验证了方法Ⅰ能够有效抑制卫星质心误差的影响。


图 7 方法I卫星质心误差补偿效果
Fig. 7 The performance of center-of-mass error compensation using method I

4.2 方法Ⅱ：增加Z方向的质心偏差估计与补偿

假设z方向存在卫星质心偏差，分别在GNSS绝对定轨和相对定轨中添加一个待估参数 ${\rm{\varDelta }}{z_{MC}}$ 来实现该偏差的估计。此时，z方向的质心偏差将被待估参数 ${\rm{\varDelta }}{z_{MC}}$ 所吸收，并且不会引起GNSS绝对定轨和相对定轨结果(质心轨迹)存在偏差。在空间域基线部位修正中，将基线参考点由卫星质心转换到SAR天线相位中心时，会引入一个大小相同、方向相反的SAR天线相位中心坐标偏差– ${\rm{\varDelta }}{z_{MC}}$ 。因此，为了消除z方向的质心偏差对InSAR基线产品的影响，在部位修正过程中需利用 ${\rm{\varDelta }}{z_{MC}}$ 的估计结果进行误差补偿(原理见图8)。


图 8 增加z方向的质心偏差估计补偿卫星质心误差原理
Fig. 8 Center-of-mass error compensation by adding bias parameter in z direction

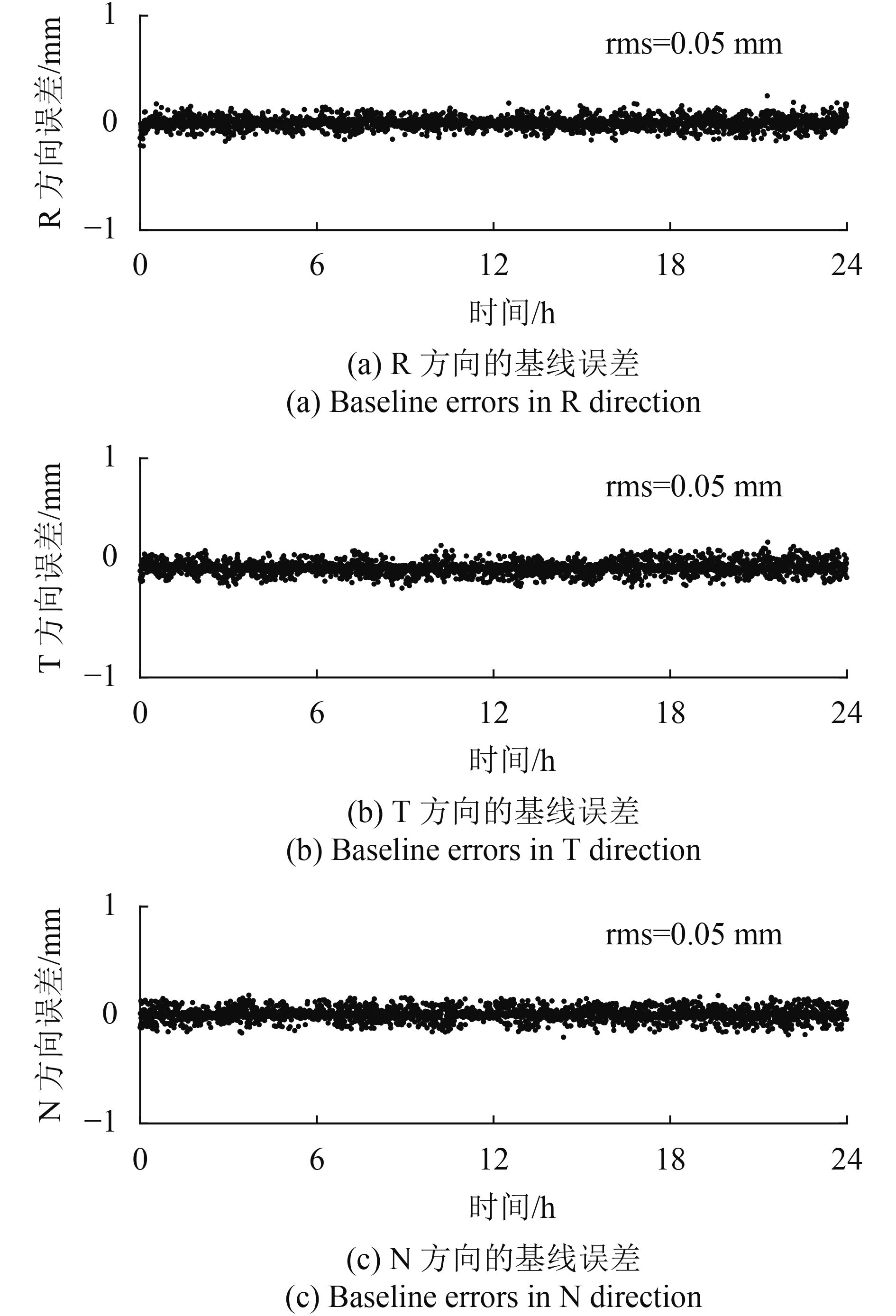
图9给出的仿真结果表明：经过方法Ⅱ处理得到的基线产品误差为：R方向0.05 mm，T方向0.05 mm，N方向0.05 mm，3维0.09 mm；约99%的卫星质心误差影响得到了有效的补偿，验证了方法Ⅱ能够有效抑制卫星质心误差的影响。


图 9 方法Ⅱ卫星质心误差补偿效果
Fig. 9 The performance of center-of-mass error compensation using method Ⅱ

5 结　论

针对卫星在轨运行期间的质心与地面标校结果不一致问题，研究了质心误差对分布式InSAR基线确定的影响及消除方法。仿真分析表明：星体系x、y方向的质心误差对基线解算影响很小，而z方向的质心误差对基线解算影响显著。提出了两种消除卫星z方向质心误差影响的方法：一是在星载GNSS定轨过程中增加轨道径向的常值经验加速度估计；二是增加星体系z方向的质心偏差估计。前者基于轨道动力学建模，无需对InSAR基线产品进行额外的质心偏移修正，适用于处理编队构型保持机动所造成的卫星质心微小扰动。后者基于几何法建模，需要对InSAR基线产品进行额外的质心偏移修正，适用于任务早期阶段的卫星质心在轨校准。实验结果表明：采用本文提出的方法，98%以上的卫星质心误差影响可被消除。与传统的在轨标校方法相比，避免了复杂的卫星姿态控制设计，既减少了卫星控制端的压力，又最大限度地保证了InSAR卫星的有效工作时间，对改进分布式InSAR雷达干涉测量精度具有重要的理论意义与应用价值。本文目前所开展的研究工作均基于模拟仿真数据，在下一步工作中将进行InSAR系统的在轨实测数据验证。

参考文献(References)

  • Allende-Alba G and Montenbruck O. 2016. Robust and precise baseline determination of distributed spacecraft in LEO. Advances in Space Research, 57 (1): 46–63. [DOI: 10.1016/j.asr.2015.09.034]
  • Antony J W, Gonzalez J H, Schwerdt M, Bachmann M, Krieger G and Zink M. 2013. Results of the TanDEM-X baseline calibration. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6 (3): 1495–1501. [DOI: 10.1109/JSTARS.2013.2258328]
  • Bergman E V, Walker B K and Levy D R. 1987. Mass property estimation for control of asymmetrical satellites. Journal of Guidance, Control, and Dynamics, 10 (5): 483–491. [DOI: 10.2514/3.20243]
  • Beutler G, Jäggi A, Hugentobler U and Mervart L. 2006. Efficient satellite orbit modelling using pseudo-stochastic parameters. Journal of Geodesy, 80 (7): 353–372. [DOI: 10.1007/s00190-006-0072-6]
  • Gonzalez J H, Bachmann M, Krieger G and Fiedler H. 2010. Development of the TanDEM-X calibration concept: analysis of systematic errors. IEEE Transactions on Geoscience and Remote Sensing, 48 (2): 716–726. [DOI: 10.1109/TGRS.2009.2034980]
  • Gu D F, Lai Y W, Liu J H, Ju B and Tu J. 2016. Spaceborne GPS receiver antenna phase center offset and variation estimation for the Shiyan 3 satellite. Chinese Journal of Aeronautics, 29 (5): 1335–1344. [DOI: 10.1016/j.cja.2016.08.016]
  • Jäggi A, Montenbruck O, Moon Y, Wermuth M, König R, Michalak G, Bock H and Bodenmann D. 2012. Inter-agency comparison of TanDEM-X baseline solutions. Advances in Space Research, 50 (2): 260–271. [DOI: 10.1016/j.asr.2012.03.027]
  • Ju B, Gu D F, Herring T A, Allende-Alba G, Montenbruck O and Wang Z M. 2017. Precise orbit and baseline determination for maneuvering low earth orbiters. GPS Solutions, 21 (1): 53–64. [DOI: 10.1007/s10291-015-0505-x]
  • Krieger G, Fiedler H, Hajnsek I, Eineder M, Werner M and Moreira A. 2005. TanDEM-X: mission concept and performance analysis//Proceedings of 2005 IEEE International Geoscience and Remote Sensing Symposium. Seoul, Korea: IEEE: 4890–4893 [DOI: 10.1109/IGARSS.2005.1526770]
  • Krieger G, Moreira A, Fiedler H, Hajnsek I, Werner M, Younis M and Zink M. 2007. TanDEM-X: A Satellite Formation for High-Resolution SAR Interferometry. IEEE Transactions on Geoscience and Remote Sensing, 45 (11): 3317–3341. [DOI: 10.1109/TGRS.2007.900693]
  • Krieger G, Zink M, Bachmann M, Bräutigam B, Schulze D, Martone M, Rizzoli P, Steinbrecher U, Walter Antony J, De Zan F, Hajnsek I, Papathanassiou K, Kugler F, Rodriguez Cassola M, Younis M, Baumgartner S, López-Dekker P, Prats P and Moreira A. 2013. TanDEM-X: a radar interferometer with two formation-flying satellites. Acta Astronautica, 89 : 83–98. [DOI: 10.1016/j.actaastro.2013.03.008]
  • Kroes R, Montenbruck O, Bertiger W and Visser P. 2005. Precise GRACE baseline determination using GPS. GPS Solutions, 9 (1): 21–31. [DOI: 10.1007/s10291-004-0123-5]
  • Liu J H, Gu D F, Ju B, Lai Y W and Yi D Y. 2015. Relative clock estimation method between two LEO satellites with a double-difference solution constraint. Acta Astronautica, 109 : 34–41. [DOI: 10.1016/j.actaastro.2014.12.014]
  • Liu J H, Gu D F, Ju B, Yao J, Duan X J and Yi D Y. 2014. Basic performance of BeiDou-2 navigation satellite system used in LEO satellites precise orbit determination. Chinese Journal of Aeronautics, 27 (5): 1251–1258. [DOI: 10.1016/j.cja.2014.03.006]
  • Montenbruck O, Wermuth M and Kahle R. 2011. GPS based relative navigation for the TanDEM-X mission-first flight results. Navigation, 58 (4): 293–304. [DOI: 10.1002/j.2161-4296.2011.tb02587.x]
  • Moon Y, Koenig R and Wermuth M. 2012. Operational precise baseline determination for TanDEM-X DEM processing//Proceedings of IEEE International Geoscience and Remote Sensing Symposium. Munich: IEEE: 1633–1636 [DOI: 10.1109/IGARSS.2012.6351215]
  • Richfield R F, Walker B K and Bergmann E V. 1988. Input selection for a second-order mass property estimator. Journal of Guidance, Control, and Dynamics, 11 (3): 207–212. [DOI: 10.2514/3.20295]
  • Tanygin S and Williams T. 1997. Mass property estimation using coasting maneuvers. Journal of Guidance, Control, and Dynamics, 20 (4): 625–632. [DOI: 10.2514/2.4099]
  • Tu J, Gu D F, Wu Y and Yi D Y. 2012. Error modeling and analysis for InSAR spatial baseline determination of satellite formation flying. Mathematical Problems in Engineering, 2012: Article ID 140301 [DOI: 10.1155/2012/140301]
  • Wang B L, Liao H and Han Y. 2010. On-Orbit calibration of satellite center of mass based on MME/EKF algorithm. Journal of Astronautics, 31 (9): 2150–2156. ( 王本利, 廖鹤, 韩毅. 2010. 基于MME/EKF算法的卫星质心在轨标定. 宇航学报, 31 (9): 2150–2156. )
  • Wang B N and Xiang M S. 2009. Relative height accuracy analysis of TanDEM-X system. Journal of Remote Sensing, 13 (1): 49–53. [DOI: 10.11834/jrs.20090106] ( 汪丙南, 向茂生. 2009. TanDEM-X系统相对测高性能分析. 遥感学报, 13 (1): 49–53. [DOI: 10.11834/jrs.20090106] )
  • Wang F R, Bettadpur S V, Save H and Kruizinga G. 2010. Determination of Center-of-Mass of gravity recovery and climate experiment satellites. Journal of Spacecraft and Rockets, 47 (2): 371–379. [DOI: 10.2514/1.46086]
  • Wang Q S, Qu J S, Huang H F, Yu A X and Dong Z. 2012. A method based on integrating real and complex correlation function for InSAR image coregistration. Acta Geodaetica et Cartographica Sinica, 41 (4): 563–569. ( 王青松, 瞿继双, 黄海风, 余安喜, 董臻. 2012. 联合实、复相关函数的干涉SAR图像配准方法. 测绘学报, 41 (4): 563–569. )
  • Wermuth M, Montenbruck O and Wendleder A. 2011. Relative navigation for the TanDEM-X mission and evaluation with DEM calibration results. Journal of Aerospace Engineering, Sciences and Applications, 3 (2): 28–38. [DOI: 10.7446/jaesa.0302.03]
  • Wu S C, Yunck T P and Thornton C L. 1991. Reduced-dynamic technique for precise orbit determination of low earth satellites. Journal of Guidance, Control, and Dynamics, 14 (1): 24–30. [DOI: 10.2514/3.20600]
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体