出版日期: 2017-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176374
2017 | Volumn21 | Number 4
上一篇 | 下一篇

面向对象影像多尺度分割最大异质性参数估计

马燕妮¹ , 明冬萍¹ , 杨海平²

1. 中国地质大学(北京) 信息工程学院，北京 100083

2. 浙江工业大学计算机学院，杭州 310014

收稿日期: 2016-10-09

基金项目: 国家自然科学基金(编号：41371347，41671369）

第一作者简介: 马燕妮(1992—　)，女，硕士研究生，研究方向为高空间分辨率遥感影像信息提取。E-mail：mayanni@cugb.edu.cn

通讯作者简介: 明冬萍(1976—　)，女，副教授，研究方向为遥感信息提取及地学尺度。E-mail：mingdp@cugb.edu.cn

中图分类号: TP701

文献标识码: A

摘要

多尺度分割是遥感影像分析的关键步骤，影像分割过程中的尺度参数选择直接关系到面向对象影像分析的质量和精度。首先，总结了面向对象影像分析中尺度概念的内涵，分析遥感影像空间和属性两大基本特征，依据空间统计和光谱统计获得理论上最优的空间尺度分割参数、属性尺度分割参数。其次，运用了基于谱空间统计的高分辨率影像分割尺度估计方法，分析了分形网络演化多尺度分割与影像谱空间统计特征的关系，进而将基于谱空间统计的面向对象影像分析尺度参数应用于分形网络演化多尺度分割算法中，最后，对其参数的合理性进行验证。研究采用高空间分辨率IKONOS和SPOT 5影像数据，选择建筑实验区和农田实验区进行空间和光谱特征统计，以进一步估计分割中的最佳尺度参数。使用分形网络演化方法对图像进行分割，利用监督分类对本文提出的尺度估计方法进行验证，验证结果表明尺度估计方法可以一定程度上保证后续的面向对象影像分类的精度。不同于以往分割后评价的尺度选择方法会需要大量的运算量，本文方法不需要先验知识的参与，且在分割前就可以自适应地估计出相对较为合适的尺度参数，提高了面向对象信息提取的自动化程度。

关键词

面向对象影像分析, 影像分割, 尺度估计, 尺度选择, 空间统计, 分形网络演化方法

Scale estimation of object-oriented image analysis based on spectral-spatial statistics

MA Yanni¹ , MING Dongping¹ , YANG Haiping²

1.School of Information Engineering, China University of Geosciences, Beijing 100083, China

2.School of Computer Science, Zhejiang University of Technology, Hangzhou 310014, China

Abstract

Multi-scale segmentation is the key step of analysis in remotely-sensed imagery. Scale parameter selection in the segmentation process is directly related to the quality and accuracy of object-oriented analysis. Only on the basis of experience for segmentation parameter choice that has less quantitative analysis ways, currently. These methods lack quantitative estimation before segmentation, with considerable workloads and low efficiency. From the perspective of scientific research, the scientificity and universality of these methods are poor. The objective of this paper is to use the quantitative method to determine the scale parameterin order to realize the automatic extracting target on the object-oriented analysis. This paper summarizes the concept of scale parameter in the object-oriented analysis. The commonly used segmentation scale parameters into spatial and attribute bandwidths were also analyzed. This paper used a spatial and spectral statistics-based scale parameter selection method for object-based information extraction from high spatial resolution remote sensing images. The relationship between Fractal Net Evolution Approach (FNEA) in multi-scale segmentation and spatial statistical characteristics was analyzed. Scale estimation based on spatial and spectral statistical characteristics was applied to FNEA in multi-scale segmentation. Meanwhile, the scale estimation approach proposed in this paper was verified by high spatial resolution image, namely IKONOS and SPOT 5 data. Construction and farmland areas were selected for spatial and spectral statistical characteristics, respectively, to further estimate the optimal scale parameters in segmentation. A series of supervised classification was performed to verify the reasonability of the predicted optimal scale parameter. The classification and accuracy assessment results show that the estimated scale by spatial statistical characteristics is basically close to the optimal one in the FNEA-based multi-scale segmentation. The proposed scale estimation approach can ensure the accuracy of the following object-oriented image classification. The method can be used to estimate the appropriate scale parameters before segmentation. In addition, it is an essentially data-driven method that requires nearly no prior knowledge; thus, it can enhance the efficiency and automatic degree of object-based image analysis.

Key words

object oriented image analysis, image segmentation, scale estimation, scale selection, spatial statistics, fractal net evolution approach

1 引　言

近50年来，全球对地观测技术得到快速发展，人类实现了在太空对地球的全方位观测。尤其是近年来高分辨率遥感影像的发展，使得我们能够获得极其丰富的关于地球表面的信息。在高分辨率遥感影像上，不仅地物的光谱特征更明显，而且具有更加丰富的结构、纹理、形状等细节信息。近十几年来面向对象影像分析方法OBIA (Object Based Image Analysis)(Walter, 2000, 2004)已逐渐成为高空间分辨率遥感信息提取的主流技术(Blaschke 等，2014)。由德国Definiens imaging公司推出的影像分析软件eCognition是世界上第一个面向对象智能化影像分析软件。突破了之前传统商业遥感软件单纯基于光谱信息进行影像分类的局限性，采取面向对象的思路进行信息提取，提高了高空间分辨率数据的自动识别精度。目前面向对象分析方法进行多尺度分割时大多使用eCognition软件。

多尺度分割的难点在于定义合适的尺度参数(Hay 等，2005)，尺度参数不合适会降低面向对象遥感信息提取的精度(Myint 等，2011；Dronova 等，2012)。目前，对于分割参数只能依据目视效果或多个尺度分割结果的评价来择优选择，这些方法均是通过分割后评价进行尺度的优化选择。依据分割评价是否需要参考数据的参与，分割评价过程又可分为监督评价和非监督评价。监督评价主要是将实际分割结果与参考数据对比，利用两者间的差异度量指标，如潜在分割误差、分割比率数量或欧几里得距离等来评价分割效果(Zhang，1997；Yang 等，2014，2015；Zhang 等，2015)；非监督评价主要是利用分割后单元内部的均质性和(或)分割单元之间的异质性来对分割效果进行评价(Jung，2007；Kim 等，2008；Drăgut 等，2010；Johnson和Xie，2011)，从而实现对分割尺度的优选。然而无论哪种方法，都是分割后评价，缺少分割前的定量估计，工作量大、效率低。从尺度科学研究的角度，其科学性和普适性欠佳。

此外，随着人工智能技术的发展，基于深度学习进行遥感识别也成为当前研究的主流(Pinheiro 等，2015；Ševo和Avramović，2016；Zhao和Du, 2016a, 2016b；Nogueira 等，2017)。深度学习技术依赖于大量样本，可对影像进行卷积计算自动提取特征并实现自组织学习，有大量样本参与遥感识别的情况下可以一定程度上回避尺度参数的预估计问题。但是目前的深度学习在遥感识别中的应用基本上还处在目标检测或场景分类阶段，深度学习的过程依然是一个黑箱操作，难以形成对场景和目标识别机理过程的直观理解。而从遥感认知的角度，在遥感目标尺度效应本质机理认知的基础上进行分割前尺度参数的预估计对于高分辨率的遥感应用仍然是至关重要，仍然具有重要的理论和应用价值。

研究普适性的尺度参数估计方法，对于面向对象影像分析自动化非常重要。本文基于遥感数据的固有特征，归纳影像分割尺度参数的一般含义，从空间和属性两大特征出发，将空间统计学应用于面向对象遥感影像分析的分割尺度参数估计，并进行了分类验证。

2 面向对象影像分析中的尺度与谱空间统计尺度估计的关系

面向对象影像处理一个必要的先决条件是成功的图像分割，其基本单元是面向对象(Definiens，2007)。面向对象遥感影像分析中尺度主要指影像对象在空间跨度上的大小；从影像对象提取算法(影像分割)的角度，面向对象影像分析中的尺度选择主要对应了多尺度分割算法中的尺度参数选择。

从地学研究的角度，尺度问题的本质是空间统计学的空间自相关或者尺度依赖思想，合适的尺度本质上是恰好能反映地物间空间相关性是否存在的一个临界点(Ming 等，2012)。基于这个理论前提，Ming等人(2012, 2015)提出了基于空间统计学的面向对象遥感影像分割尺度估计思想。总体上来说，遥感影像分割尺度参数估计的实质是基于原始影像上全局或者局部特征的一种统计估计，因此空间统计学方法无论从空间统计学的科学思想基础，还是在算法实现技术等方面，都是解决面向对象影像分析尺度参数选择问题的可行方法。

如明冬萍等人(2008)、陈杰等人(2011)和冯霞等人(2014)的研究表明，几乎所有的图像属性——颜色、纹理、形状都或多或少有着尺度效应。尺度是在一个通用的分割算法的基础上，结合局部和全局优化技术的同质化定义。一个尺度参数常常控制着面向对象影像大小。影像的光谱或空间信息是斑块间异质性标准的基础。斑块间合并的参数是基于其类别间的异质性标准(明冬萍等，2016)。从这个角度来说，面向对象影像分析中的尺度与谱空间统计尺度意义相同。

Ming等人(2012)从空间数据的空间和属性两大特征出发，将面向对象影像分析中多尺度分割的尺度参数概括为空间尺度分割参数(类别或斑块间的空间距离)、属性尺度分割参数(类别或斑块间的属性距离)。在这两个参数的基础上，可以结合具体的算法思想派生出更多的尺度参数，如区域生长中的斑块面积阈值参数则可以基于空间尺度分割参数采用简单几何计算来进行近似地代替，分水岭分割算法中的谷底阈值参数可以基于属性尺度分割参数近似来代替，或者区域生长分割算法中的最大异质度阈值参数也可以基于属性尺度分割参数近似来计算代替。

目前，eCognition软件的多分辨率分割(Multi-resolution segmentation)是自下而上的分割方法，其核心思想是分形网络演化思想FNEA(Fractal Net Evolution Approach)，即利用图像分割的方法得到的分割图斑，图斑还可以在不同尺度上聚合(Blaschke和Hay，2001)。本文以分形网络演化方法为例，阐述面向对象影像分析尺度参数与影像谱空间统计特征的关系，并对其进行验证。

3 基于异质度空间统计的影像分割尺度估计

对于组成一个影像场景的不同类型目标来说，绝对的最优尺度是不存在的，一个折衷的解决方案是计算理论上的最优尺度来近似地逼近或代替绝对的最优尺度。此时，面向对象分类的精度能最大程度地得到保证，信息能够被更好地被提取。

异质度空间统计，实质是谱空间统计。尽管尺度参数常常是依赖算法存在的，但是基于空间数据的空间和属性两大基本特征，可以依据空间统计和光谱统计获得理论上最优的空间尺度分割参数、属性尺度分割参数，这些参数可以部分地或者全部地应用于大多数的多尺度分割算法中(明冬萍等，2016)。以下仅简单介绍方法的基本过程，更详细的信息，可以参见Ming等人(2012, 2015)，明冬萍等人(2016)的文献。

3.1 最佳空间尺度分割参数

本文运用局部方差法和半方差法来确定空间尺度分割参数(记为d_s)，虽然具体方法有所不同，但都是对影像进行空间统计。因此理论上，两种方法所计算的最佳空间尺度分割参数的值相同。

3.1.1 局部方差法

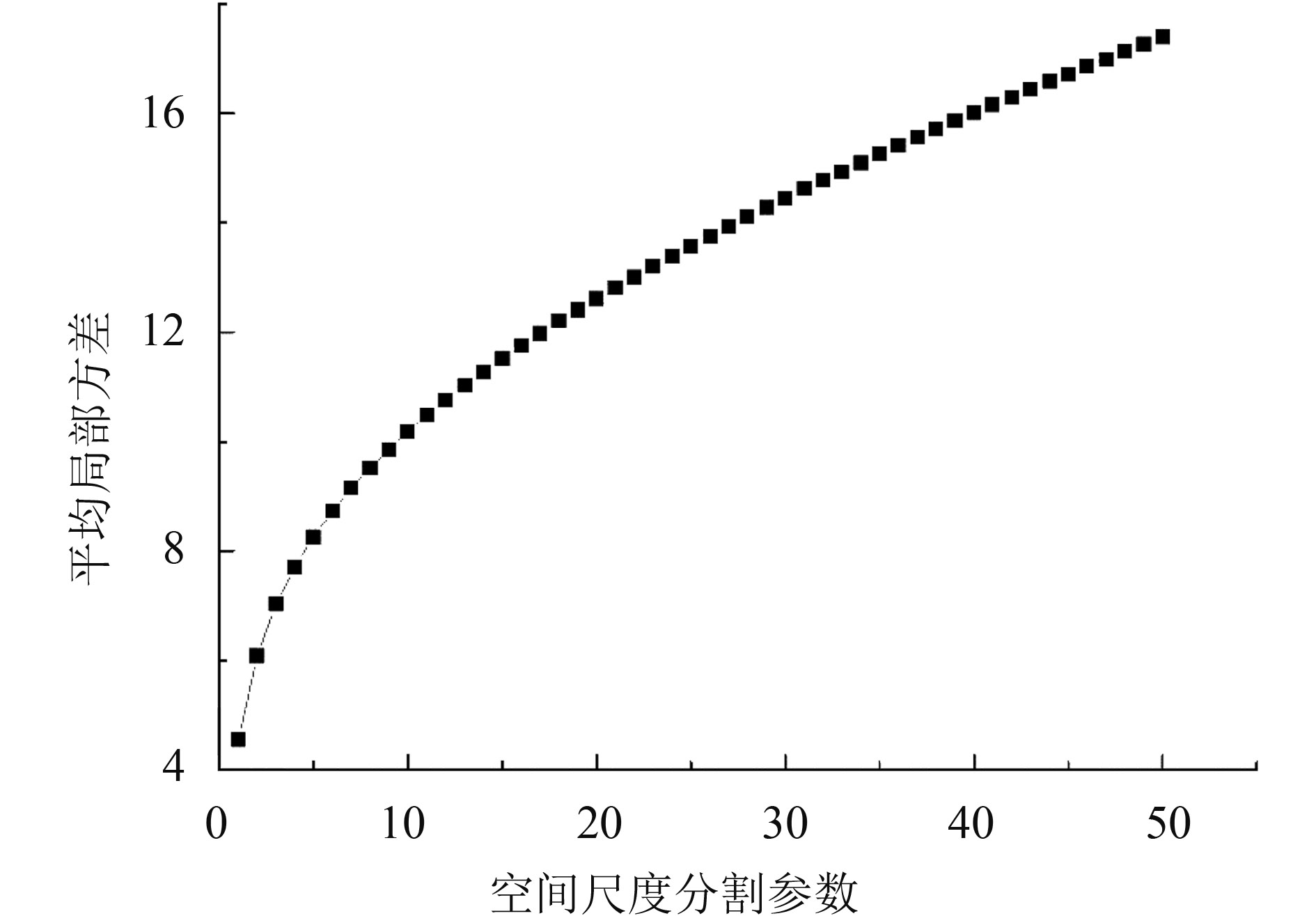
当不考虑地物空间分布各向异性，采用局部方差法(Woodcock和Strahler，1987；Woodcock 等1988)选取遥感应用的最优尺度。通过n×n像素移动窗计算窗口内的局部方差，产生局部方差图ALV(Average Local Variogram)，计算公式如下：

${\rm{ALV}} = \frac{{\mathop \sum\limits_{i = 0}^{M - 1} \mathop \sum\limits_{j = 0}^{N - 1} LV\left( {i,j} \right)}}{{MN}}$

(1)

式中，M和N表示原图像行列数大小，LV(i, j)表示第i行j列像元的局部方差，即该窗口尺寸n内的局部图像灰度值方差，反应各像元灰度值与局部创口灰度平均值的总的离散程度，其计算公式为

$LV\left( {i,j} \right) = \sqrt {\frac{{\mathop \sum\limits_{i = 0}^n \mathop \sum\limits_{j = 0}^n {{\left[ {f\left( {i,j} \right) - f} \right]}^2}}}{{{n^2}}}} $

式中，n表示窗口尺寸，i，j为局部窗口行列数，f(i, j)表示该局部窗口内第i行j列像元的灰度，f为该局部窗口像元灰度均质，反映该窗口图像中地物平均反射强度。

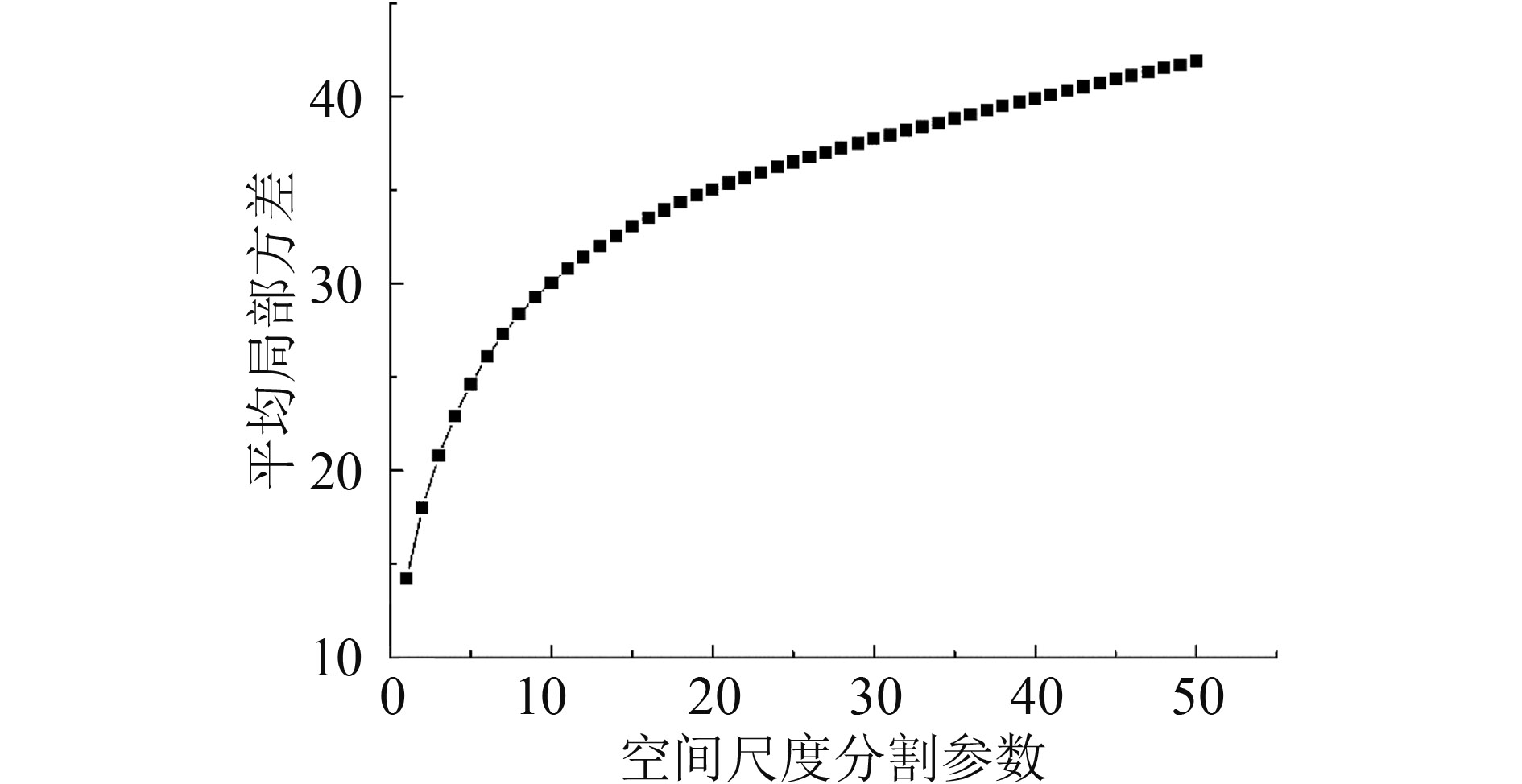
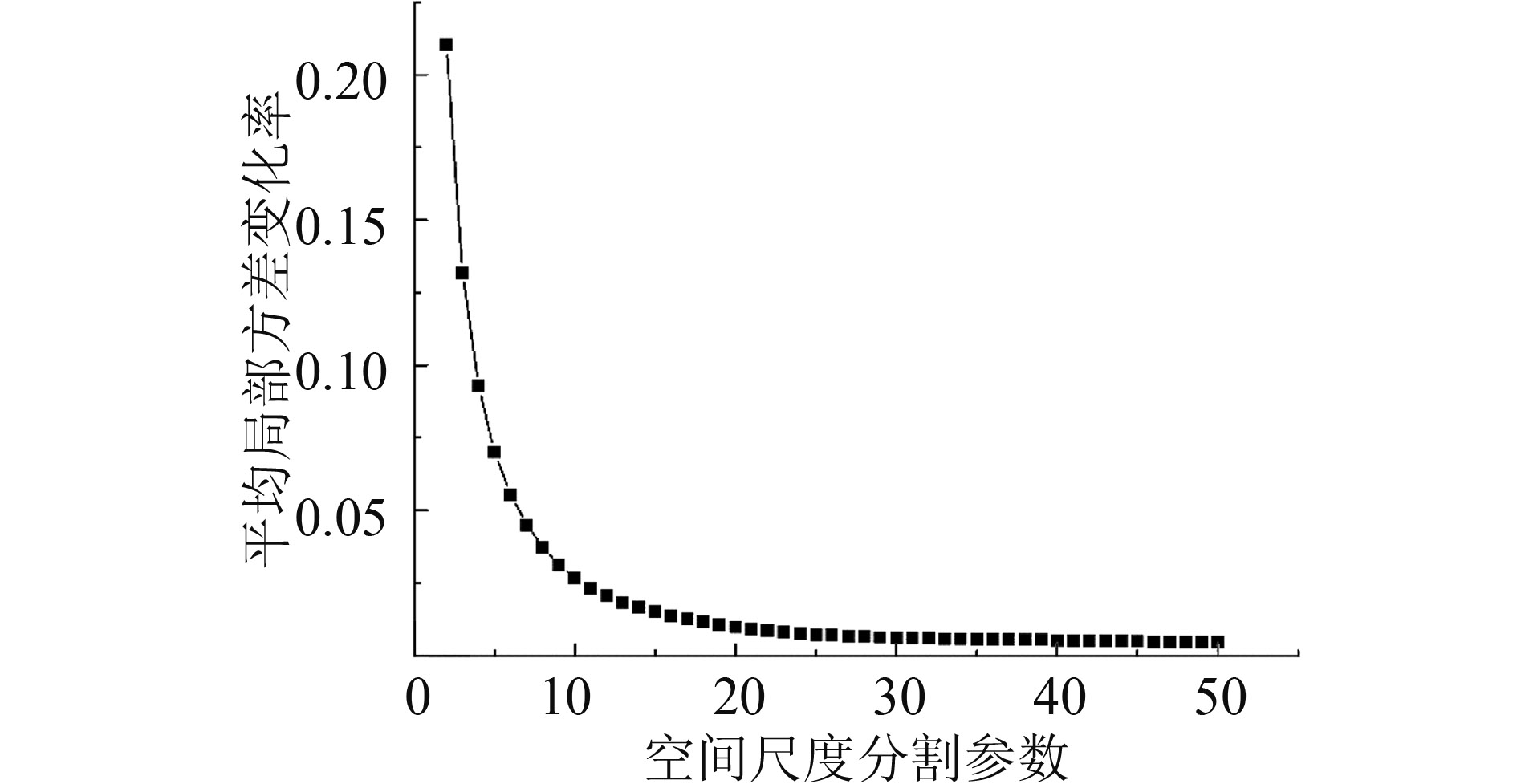
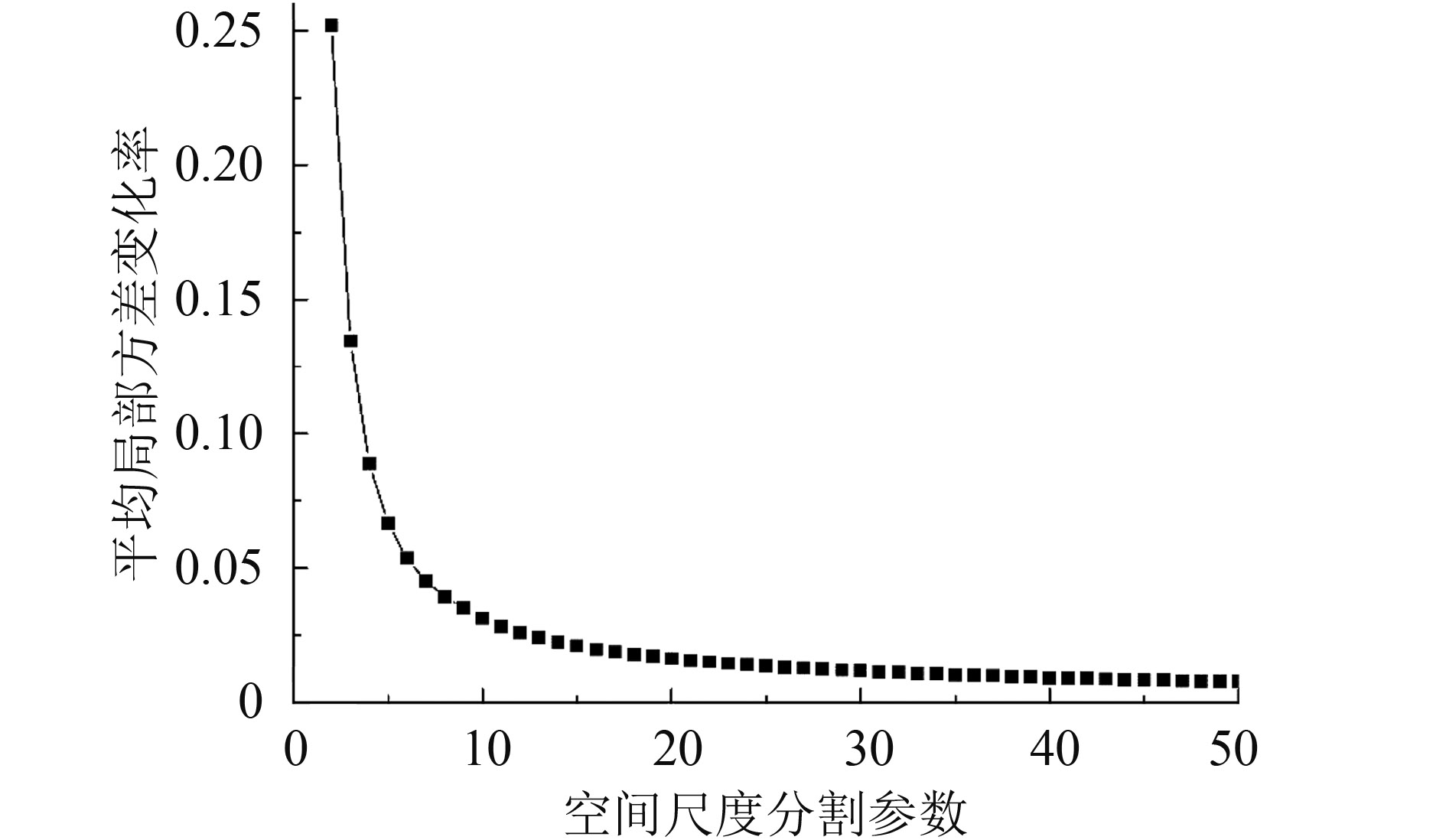
用平均局部方差随计算窗口尺寸变化的变化率来确定平均局部方差曲线变程。实际上，局部方差在数学上找不到这个极值点或者临界点。根据经验平均局部方差的变化率阈值设为0.01，即随着计算间隔d_s增大，第一次出现其变化率小于0.01时，其对应窗口尺寸d_s为最佳空间尺度分割参数。

3.1.2 半方差法

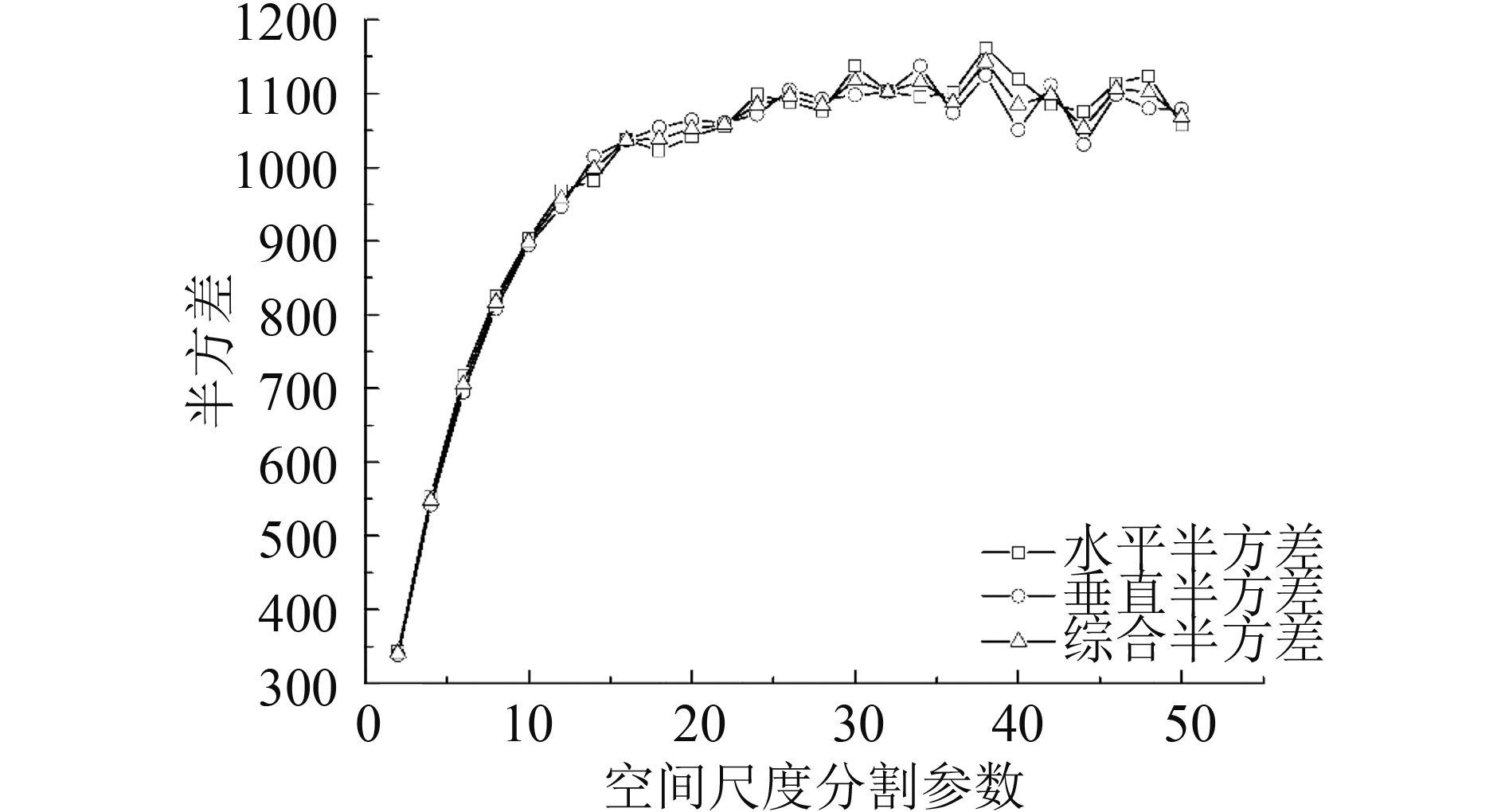
若考虑地物空间分布各向异性，在水平和垂直方向上，依据不同采样计算间隔，计算影像在不同方向上的半方差(Atkinson和Aplin，2004)。

变异函数值由式(2)计算：

${\gamma _{\rm{YY}}}\left( h \right) = \frac{1}{{2N\left( h \right)}}\mathop \sum \limits_{n = 1}^{N\left( h \right)} {\left[ {y\left( {{u_a}} \right) - y\left( {{u_a} + h} \right)} \right]^2}$

(2)

式中，γ_YY(h)表示间隔为h的样本的变异函数值，它反映了观测量在空间上的相关程度；N(h)表示空间间隔为h的样本点对个数；y(u_a)和y(u_a+h)表示a和a+h外图像像元DN值。

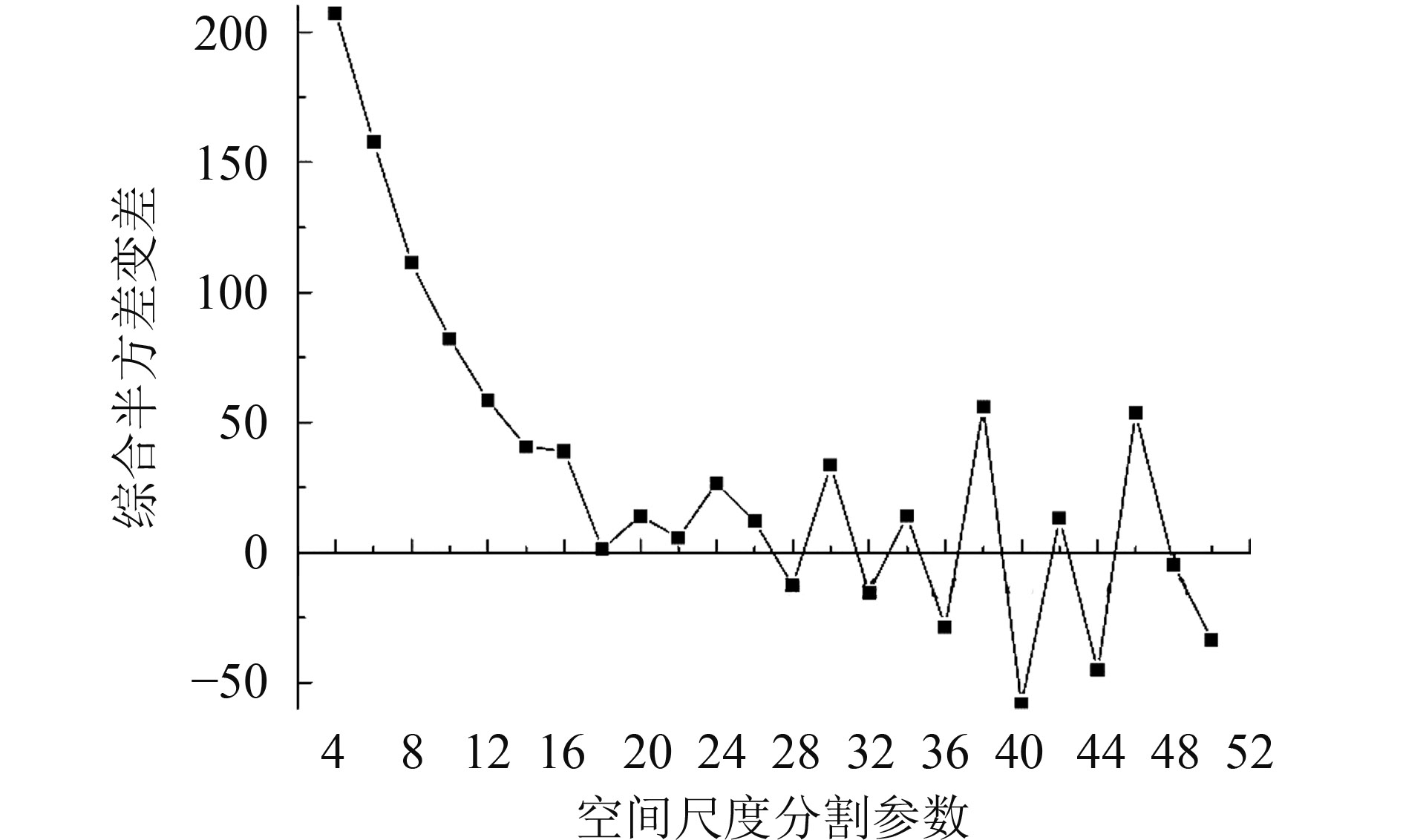
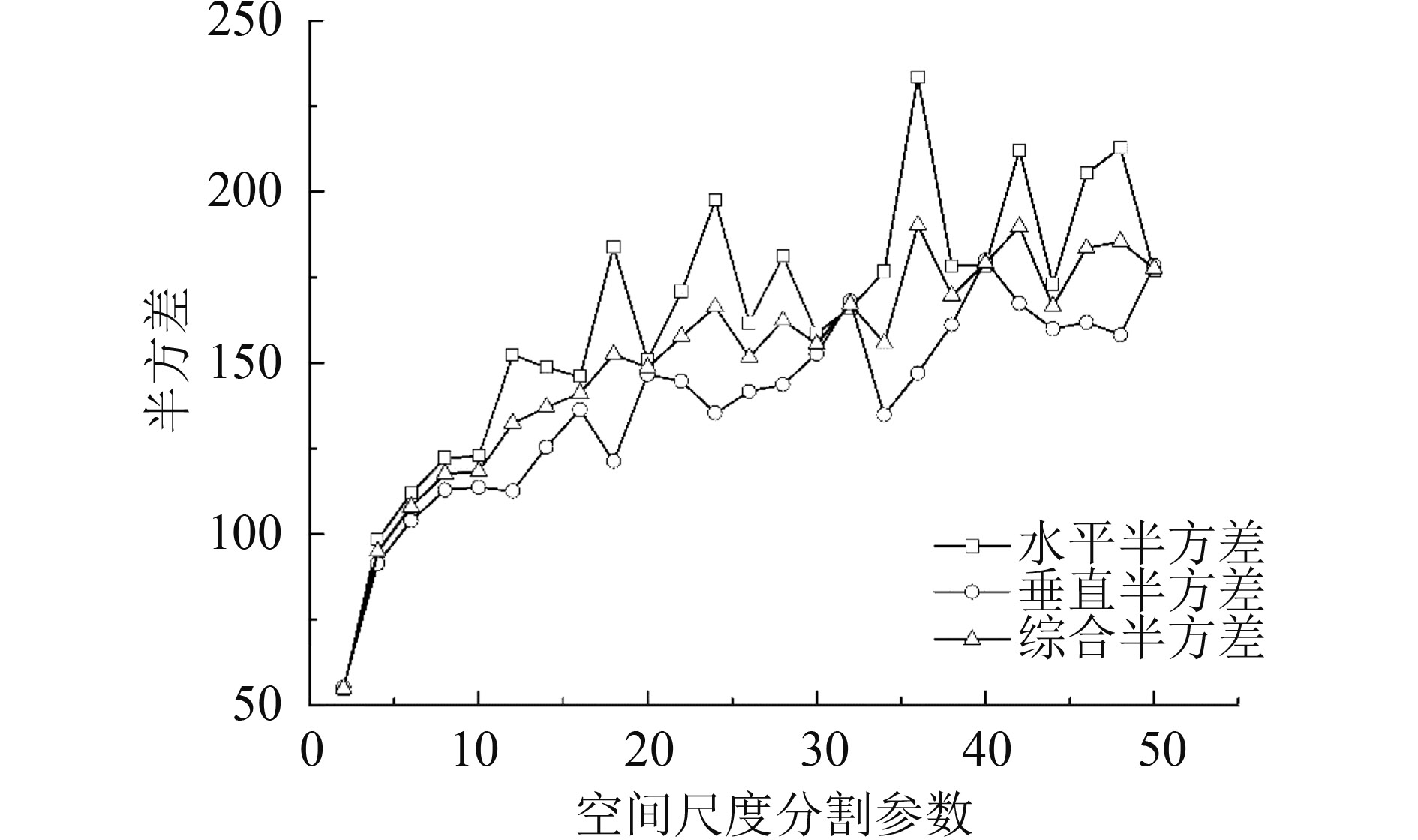
利用半方差随计算间隔变化的半方差曲线变差来确定半方差曲线的变程。因为半方差的平稳性较弱，曲线抖动较为剧烈，为了避免过分割问题，属性分割参数不能过小，因此取综合半方差变差第一次出现负值时，其对应窗口尺寸d_s为最佳空间尺度分割参数。

3.2 最佳属性尺度分割参数

一旦最佳空间尺度分割参数d_s被确定，则可以基于最佳空间尺度分割参数进一步估计最佳属性尺度分割参数h_r。对局部协方差进行最佳属性尺度分割参数估计，当有大量样本计算时，可以消除估计偏差(Comaniciu，2003)。更详细的最佳属性尺度分割参数数学证明见Comaniciu(2003)。

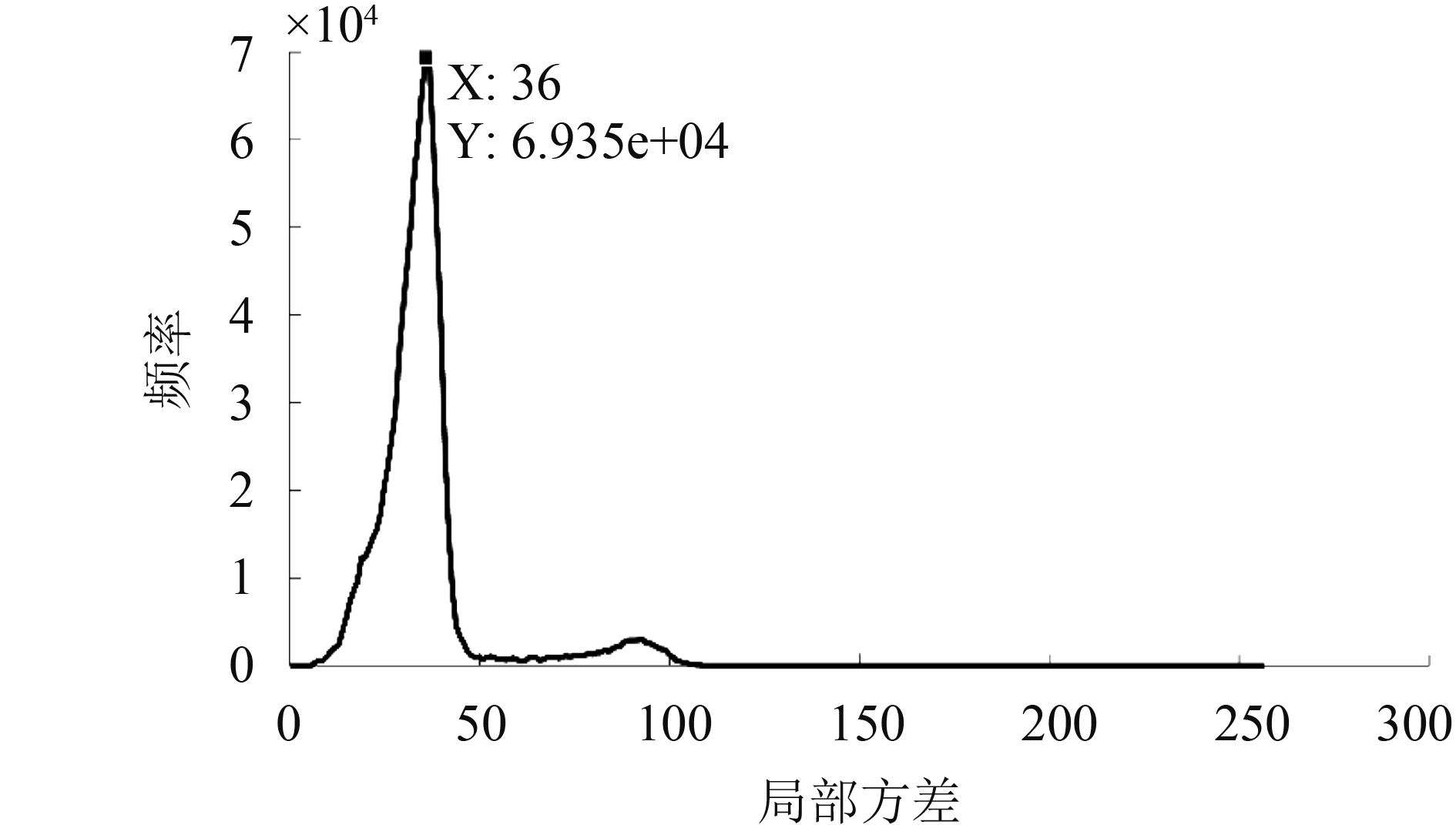
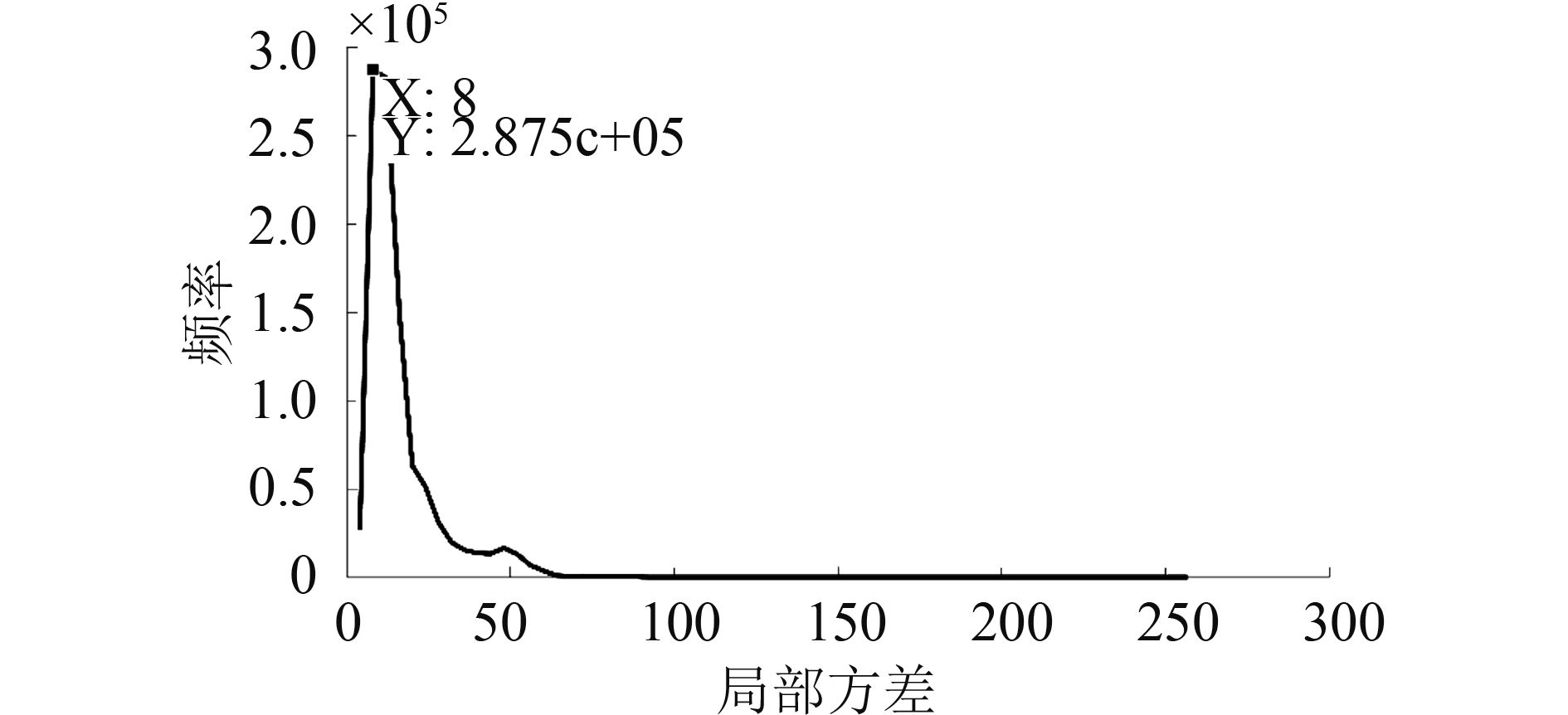
而本文所采用的方法，是对整幅图像进行局部方差遍历计算，保证了样本的数量最大化，进而对局部方差矩阵(窗口大小为2d_s+1)进行直方图统计来估计最佳属性尺度分割参数，能有效减少属性分割参数估计的偏差。为了避免过分割问题，属性分割参数不能过小，因此Ming等人(2015)提出局部方差直方图的第一个峰值对应的影像光谱值(从数学上为峰值的平方根)即为所估计的属性尺度分割参数h_r，而这个属性尺度分割参数的实质则是像元或者对象之间的光谱异质度。本文则采用了这个方法来估计分形网络演化算法的最大异质度参数。

4 分形网络演化方法

分形网络演化方法由Baatz和Schape(2000)提出，在面向对象影像分析中得到了广泛的使用。该算法(Benz 等，2004)利用模糊子集理论提取感兴趣的影像对象，在感兴趣的尺度范围内，影像的大尺度对象与小尺度对象同时存在，从而形成一个多尺度影像对象层次等级网络。其基本思想是基于像素从下向上的区域增长的分割算法，遵循异质性最小的原则，把光谱信息相似的邻近像元合并为一个同质的影像对象，分割后属于同一对象的所有像元都赋予同一含义。

(1)对象的光谱异质性。对象的光谱异质性可以采用如下的定义：

${h_c} = \mathop \sum \limits_c {w_c} \cdot {\sigma _c}$

(3)

式中，w_c是不同光谱波段的权重，σ_c是光谱值的标准差。标准差代表了影像灰度分布的波动情况，可以用来衡量整体差异，因此单个对象的光谱异质性可以理解为对象对应的各波段标准差的加权平均值。

对象合并前后的异质性用下面的式子来表示：

$\begin{array}{l}{h_{{\rm{color}}}} = \mathop \sum \limits_c {w_c}({n_{{\rm{merge}}}} \cdot {\delta _{c,{\rm{merge}}}} - ({n_{{\rm{obj}}1}} \cdot \\{\delta _{c,{\rm{obj}}1}} + {n_{{\rm{obj}}2}} \cdot {\delta _{c,{\rm{obj}}2}}))\end{array}$

(4)

式中，h_color为两个对象合并后得到的光谱异质性值和合并前对象obj1和obj2的各自光谱异质性值之和的差异，w_c表示参与分割合并的波段权重，n_merge，δ_{c, merge}分别表示合并后的区域面积和光谱方差，δ_{c, obj1}，n_obj1，δ_{c, obj2}，n_obj2分别为两个空间相邻区域的光谱方差和面积。

(2)对象的形状异质性。对象的形状异质性指标是由光滑度指数与紧凑度指数这两个子异质性指标所构成。所谓的紧凑度指数就是指对象的圆度，用来衡量区域接近圆形的程度，也可以作为衡量对象形状的规则程度的指标；平滑度指数和圆度有些类似，但是用来表示对象形状的平滑程度的，影像的平滑与否是衡量对象规则不规则的一种指标。

对象合并前后的形状异质性增量为光滑度指数增量和紧凑度指数增量的加权平均值，ω_smoothness与ω_compactness代表两者间的权重调配，两者的和为1，其表达形式为

${h_{{\rm{shape}}}} = {\omega _{{\rm{smoothness}}}} \times {h_{{\rm{smoothness}}}} + {\omega _{{\rm{compactness}}}} \times {h_{{\rm{compactness}}}}$

(5)

若平滑指标的权重较高，分割后的对象边界较为平滑，反之，若紧密指标的权重较高，分割后的对象形状较为紧密较接近矩形，根据不同的影像特性以及目标对象特性，两者间的权重调配亦有所不同，可依使用者的需求加以调整。加入形状的因子于影像分割的过程中，能约制对象形状的发展，使分割后的区域形状较平滑完整，较符合人的视觉习惯。

(3)对象的整体异质性。对象的整体异质性增量由光谱异质性增量和形状异质性增量的加权平均值所构成的。ω_color与ω_shape代表光谱与形状两者间的权重调配，两者之和为 1，同样可以依据使者的需求进行调整，其计算公式为

$sp = {\omega _{{\rm{color}}}} \times {h_{{\rm{color}}}} + {\omega _{{\rm{shape}}}} \times {h_{{\rm{shape}}}}$

(6)

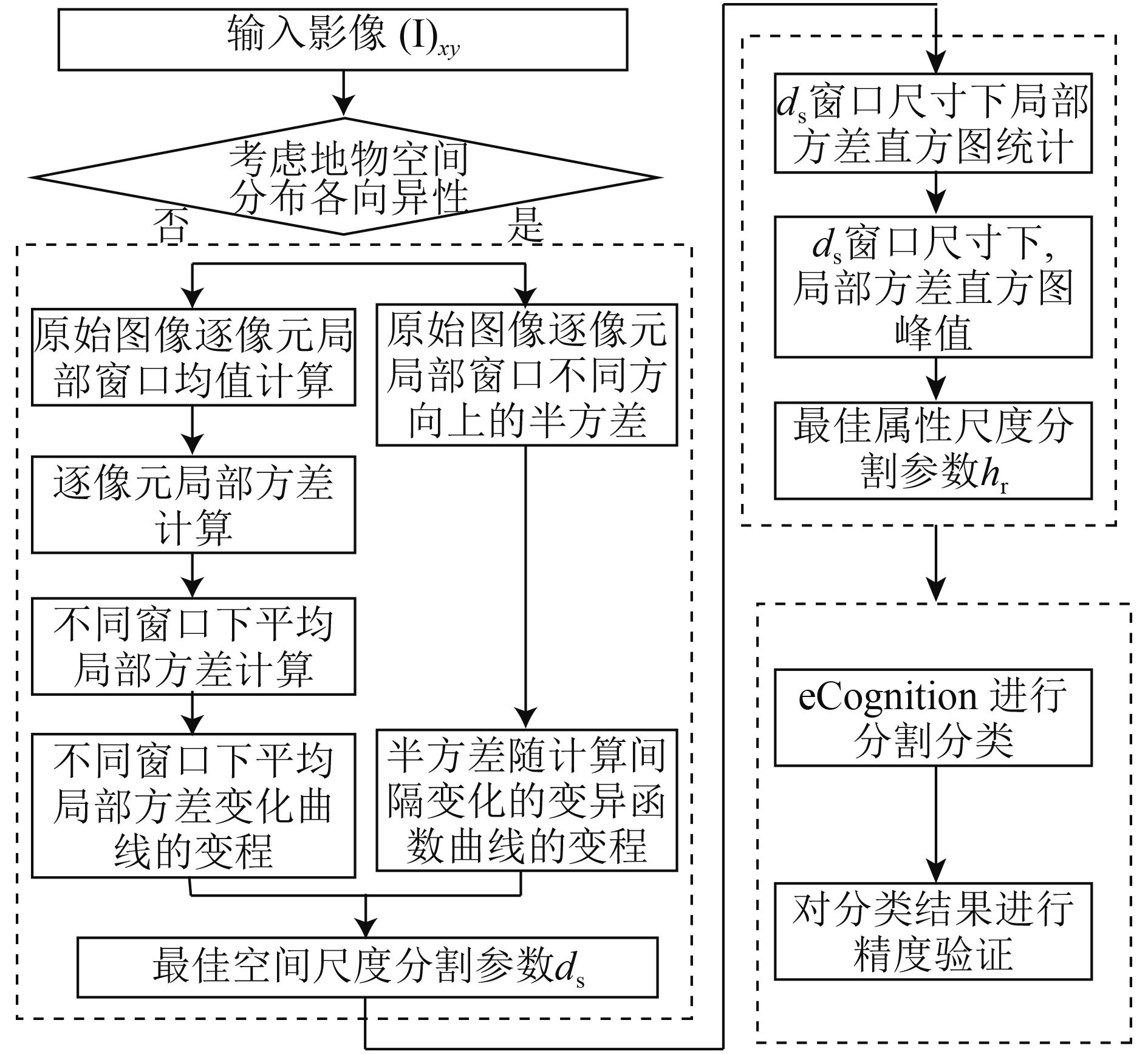
影像分割过程中对影像对象的空间特征、光谱特征和形状特征同时进行操作，因此生成的影像对象不仅包括了光谱同质性，而且包括了空间特征与形状特征的同质性。本文中不考虑形状异质性，即在分割中令形状参数的权重为0，此时其分割时考虑的整体异质性仅体现为光谱异质性。在形状参数的权重为0的前提条件下，分形网络演化的整体异质性尺度参数与本文基于异质度空间统计的属性尺度参数的意义近似相同。因此，将基于异质度空间统计的影像分割尺度估计方法应用于分形网络演化方法中，进行尺度参数的选择。图1是基于谱空间统计的尺度分割参数估计方法及分类验证流程示意图。

图 1 基于谱空间统计的尺度分割参数估计方法及分类验证流程示意图

Fig. 1 Workflow of selecting the optimal spatial bandwidth based on the semivariogram and validation on remote sensing classification

5 实　验

5.1 研究区及实验数据

实验分两组——建筑实验区和农田实验区。

建筑实验区(图2)所用数据为IKONOS影像。全色分辨率1 m，多光谱分辨率4 m。分为4个波段，分别为蓝色波段、绿色波段、红色波段和近红外波段。选用地区主体地物类别为建筑，大小1000像素×1000像素。

图 2 建筑实验区

Fig. 2 Experimental panchromatic high-spatial-resolution images (construction)

农田实验区(图3)所用数据为SPOT 5影像。全色分辨率为2.5 m，多光谱分辨率为10 m。分为4个波段，分别为绿色波段、红色波段、近红外波段和短波红外波段。选用地区主体地物类别为农田，大小1000像素×1000像素。

图 3 农田实验区

Fig. 3 Experimental panchromatic high-spatial-resolution images (farmland)

5.2 多尺度面向对象分类

多尺度面向对象分类实验采用eCognition Developer 9.0.2软件完成，其中分割采用基于分形网络演化的多分辨分割算法，形状指数(shape)设为0，此时的尺度参数(scale parameter)则由本文的光谱异质性来近似代替。分类过程采用了eCognition软件提供的模糊分类算法，即在样本选择的基础上，通过样本特征空间计算得出的隶属度、最小距离、均值距离来判定对象是否与样本对象属于同一个类别。

为了尽量降低人为主观因素的影响，提高精度评价结果的可信度，实验中同一影像的分类操作使用同一个分类样本库。同一影像的精度检验利用同一套基于像素的混淆矩阵(TTAMask)进行。保证影像分类过程中唯一的变量为光谱异质性尺度参数。

5.2.1 建筑实验区

结合建筑实验区(图2)影像，通过目视解译，将影像分为4类，分别为道路(road)、房屋(house)、树(tree)、草坪(lawn)。根据目视判断，初步认定在分割尺度为20时，房屋和道路分割结果较为理想；在尺度为25时，草坪和树木分割效果较为理想，在上述尺度下选择训练样本。在面向对象分类精度评价环节，利用ArcGIS生成10×10格网，目视判别其交点所代表地物，保证检验样本分布均匀，以此方式共选择检验样本100个。建筑实验区各地物类别训练样本和检验样本个数如表1所示。

表 1 建筑实验区样本列表
Table 1 Sample list of construction area

下载CSV

类别	训练样本个数	检验样本个数
房屋(house)	176	29
道路(road)	113	23
草坪(lawn)	71	18
树木(tree)	170	30
总计	530	100

分类中采用的分类特征包括归一化差值植被指数(NDVI)，亮度(Brightness)，灰度共生矩阵(GLCM Homogeneity(quick8/11))以及4个波段DN值作为分类指标。

5.2.2 农田实验区

结合农田实验区(图3)影像，通过目视解译，将影像分为5大类，分别为建筑区(construction)，农作物区(crop)，道路(road)，树木(tree)，水体(water)。其中，建筑区分为水泥地(cement floor)和住宅区(residential area)；农作物区分为高产作物区(high crop)、低产作物区(low crop)和无作物生长区(bare crop)；道路分为亮度高道路(bright road)和亮度低道路(dark road)。根据目视判断，初步认定分割尺度为15时，道路分割效果较为理想；尺度为20时，建筑区和树木分割效果较为理想；尺度为30时，农作物和水体分割效果较为理想，在上述尺度下选择训练样本。在面向对象分类精度评价环节，利用ArcGIS生成10×10格网，目视判别其交点所代表地物，保证检验样本分布均匀，以此方式共选择检验样本100个。农田实验区各类别训练样本和检验样本个数如表2所示。

表 2 农田实验区样本列表
Table 2 Sample list of farmland area

下载CSV

类别		训练样本个数	检验样本个数
建筑	水泥地(cement floor)	15	20
建筑	住宅区(residential area)	161	20
农田	高产作物区(high crop)	136	53
	低产作物区(low crop)	50
	无作物生长区(bare crop)	36
道路	高亮度道路(bright road)	34	10
道路	低亮度道路(dark road)	49	10
树木		93	11
水体		34	6
总计		608	100

分类中采用的分类特征包括归一化差值植被指数(NDVI)，亮度(Brightness)，灰度共生矩阵(GLCM Homogeneity(quick8/11))，形状指数(Shape index)，长宽比(Length/Width)以及4个波段DN值。

5.3 基于谱空间统计的高分辨率影像分割尺度参数估计

实验中采用不考虑地物空间分布各向异性的局部方差法和考虑地物空间分布各向异性的半方差法来确定最佳空间尺度分割参数d_s。首先基于半方差法，找到综合半方差变差第一次出现负值时的点，来确定最佳空间尺度分割参数d_s，再用局部方差法，找到其局部方差变化率小于0.01时的区间范围，来验证和评估这个点的可靠性，最终确定最佳空间尺度分割参数d_s。进而计算出最佳属性尺度分割参数h_r。

5.3.1 建筑实验区

计算建筑实验区局部方差(图4)与局部方差变化率(图5)；半方差(图6)与综合半方差变差(图7)，进而估计其适合尺度参数(图8)。如图4—7可知，建筑实验区影像的最佳空间尺度分割参数d_s为28，此时最佳属性尺度分割参数h_r为36。

图 4 建筑实验区局部方差

Fig. 4 ALV of construction area

图 5 建筑实验区局部方差变化率

Fig. 5 SCROC-ALV of building

图 6 建筑实验区半方差

Fig. 6 Semivariogram of construction area

图 7 建筑实验区综合半方差变差

Fig. 7 The change of synthetic semivariance of construction area

图 8 建筑实验区尺度参数估计

Fig. 8 Scale estimation of construction

5.3.2 农田实验区

计算农田实验区局部方差(图9)与局部方差变化率(图10)；半方差(图11)与综合半方差变差(图12)，进而估计其适合空间尺度参数(图13)。如图可知，农田实验区影像的最佳空间尺度分割参数d_s为20，此时最佳属性尺度分割参数h_r为8。

图 9 农田实验区局部方差

Fig. 9 Local variogram of farmland

图 10 农田实验区局部方差变化率

Fig. 10 SCROC-ALV of farmland

图 11 农田实验区半方差

Fig. 11 Semivariogram of farmland

图 12 农田实验区综合半方差变差

Fig. 12 Change of synthetic semivariance of farmland

图 13 农田实验区尺度参数估计

Fig. 13 Scale estimation of farmland

5.4 实验结果及分析

为了进一步分析影响面向对象分类精度的影像因素，本文分别进行了shape=0和shape=0.1条件下的两组分类实验，用以进行对比分析。

5.4.1 建筑实验区

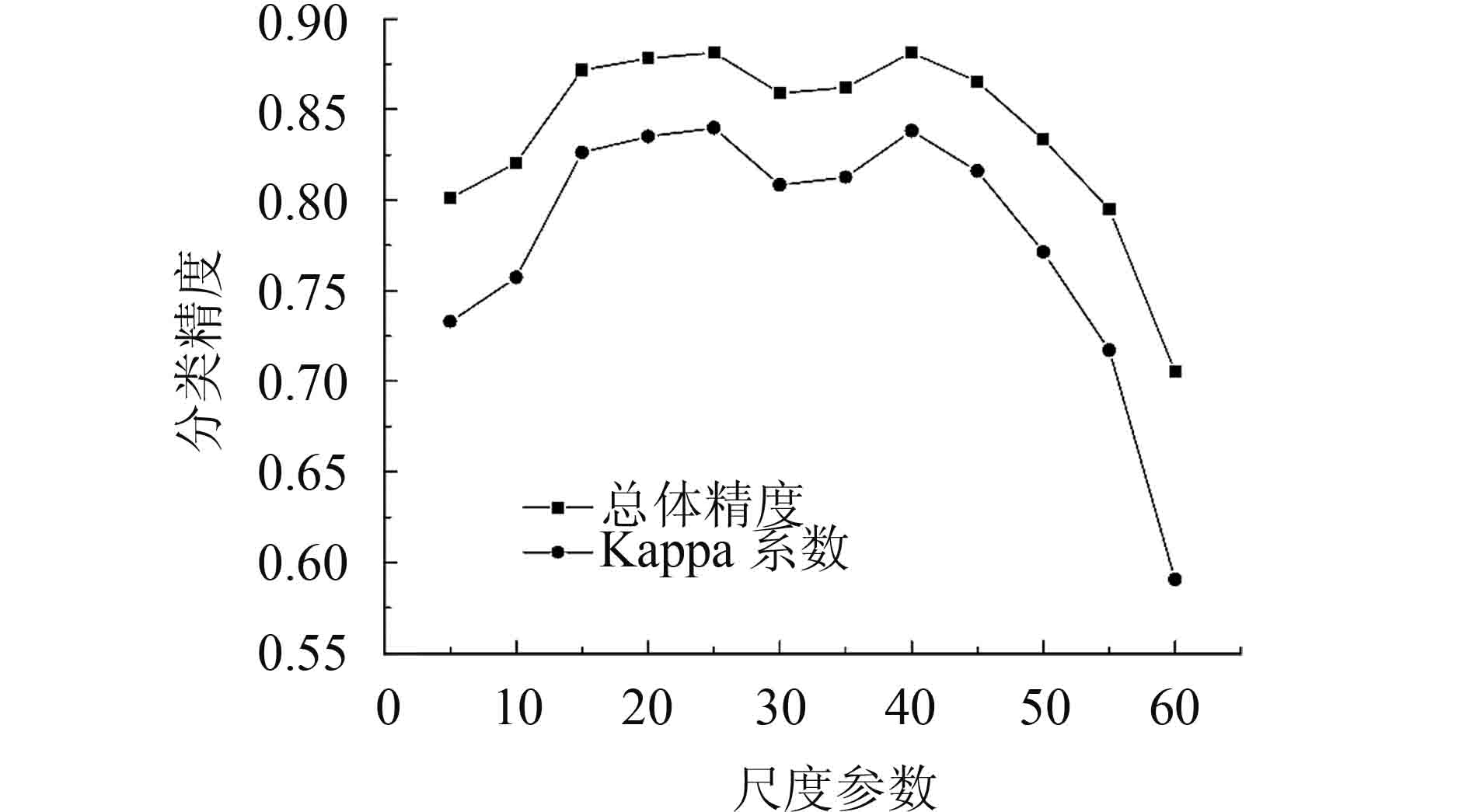
当shape=0时，分类精度如图14。总体精度趋势先升高后降低，中间有所波动。尺度在5—25时，精度处于上升状态。尺度在25—30时，精度总体保持很高，但有一定的下降趋势。尺度在35—40时，精度略有上升趋势。尺度在40—60时，精度呈下降趋势。在尺度选择25时精度最高，总体精度为0.8814103，Kappa系数为0.8398179。所预测最佳分割尺度为36，尺度在35时，总体精度为0.8621795，Kappa系数为0.8126152，与最高分类精度差距不大，基本满足分类要求。

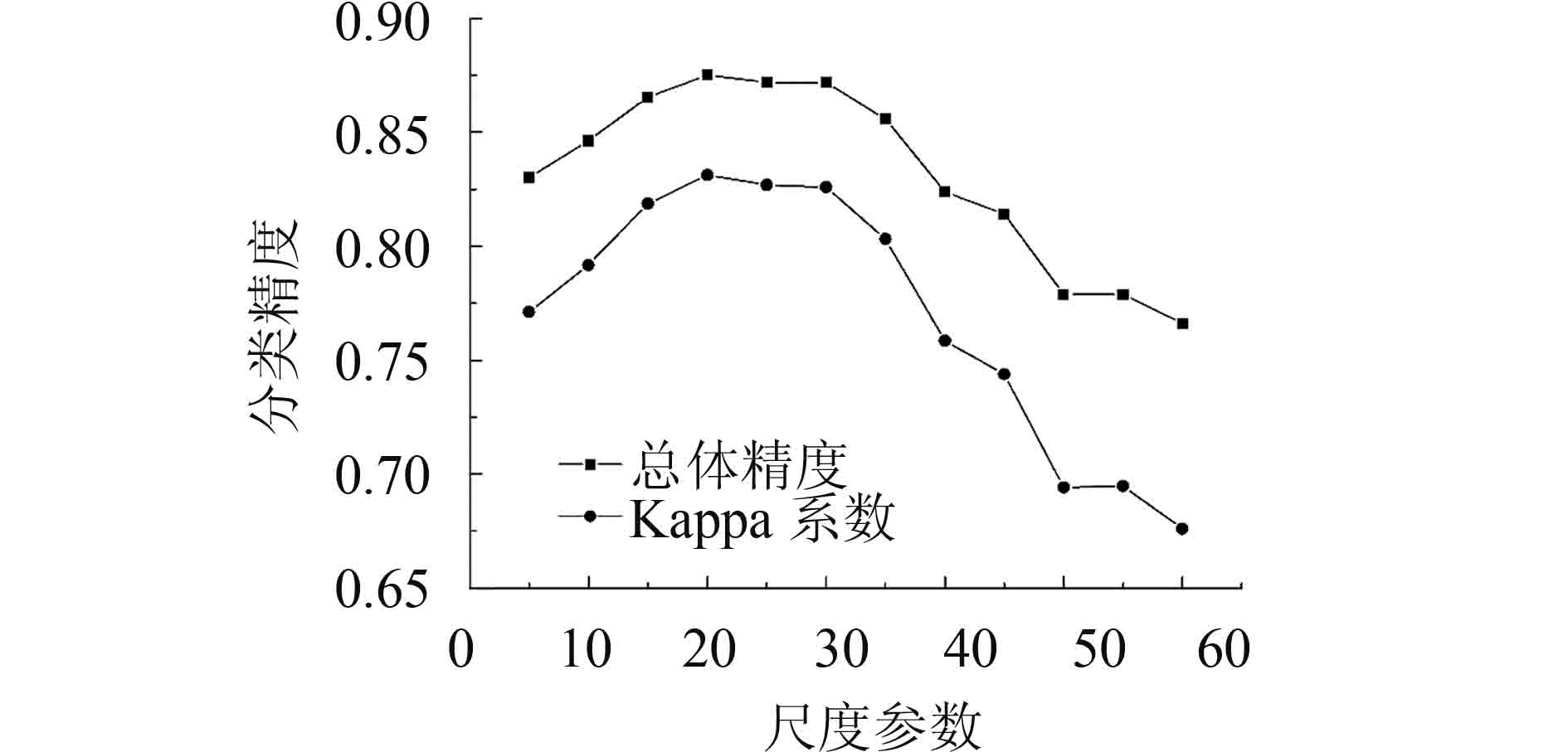
当shape=0.1时，分类精度如图15。总体精度的变化与上述情况略有不同，总体精度趋势是先升高后降低。尺度在5—20时，精度处于上升状态，在尺度为20时达到最高，总体精度达到0.875，Kappa系数为0.8311313，分类结果最好。尺度在20—30时，分类精度相差不大，处于精度较高的状态，但随着尺度增加，精度略有下降。尺度在30—60时，精度处于明显的下降趋势。

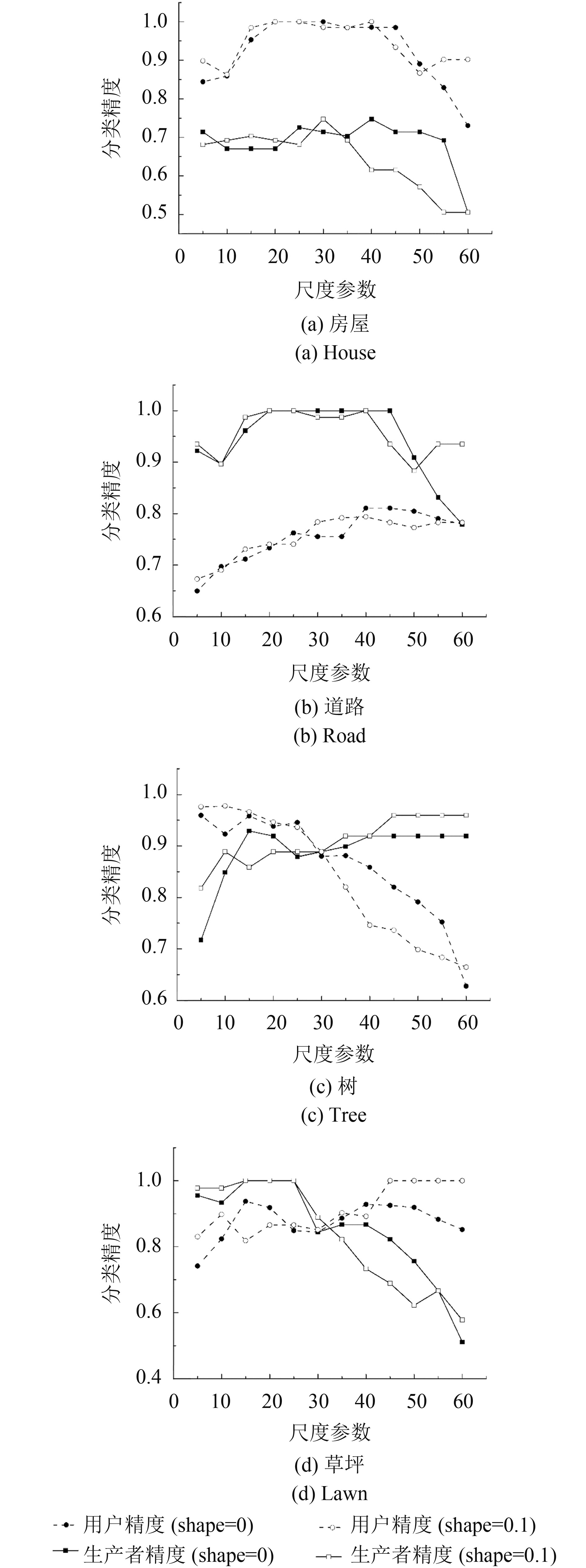
上述情况有所差别，原因在于分割时是否加入形状这一参数。对比各地物类别在shape=0和shape=0.1两种情况下随着尺度的变化趋势(图16)。

图 14 建筑实验区分类精度(shape=0)

Fig. 14 Classification accuracy of construction (shape=0)

图 15 建筑实验区分类精度(shape=0.1)

Fig. 15 Classification accuracy of construction (shape=0.1)

图 16 建筑实验区各地物类别在shape=0和shape=0.1时随尺度变化趋势

Fig. 16 The relationship of building’s classification accuracy and segmentation scale (shape=0, shape=0.1)

总体来说，四种地物类别在shape=0与shape=0.1时，随着尺度的增加，都有很明显的变化，说明四种地物类别对于尺度都很敏感。

对于道路, shape=0与shape=0.1两组变化趋势几乎一致。结合原始影像及分割过程会发现，虽然道路形状较为细长，但是分割过程中无法较为完整的提取道路，会把一条道路分为几个小块，在分类时归为一类。所以道路对于形状不敏感。

房屋、草坪、树木在shape=0与shape=0.1的精度虽然大致走势上较为相似，但数值差别较明显，说明其受形状影响较大。

建筑实验区土地利用分类图(shape=0，scale parameter=35)如图17。

图 17 建筑实验区土地利用分类图(shape=0，scale parameter=35)

Fig. 17 The land use classification map of building (shape=0，scale parameter=35)

5.4.2 农田实验区

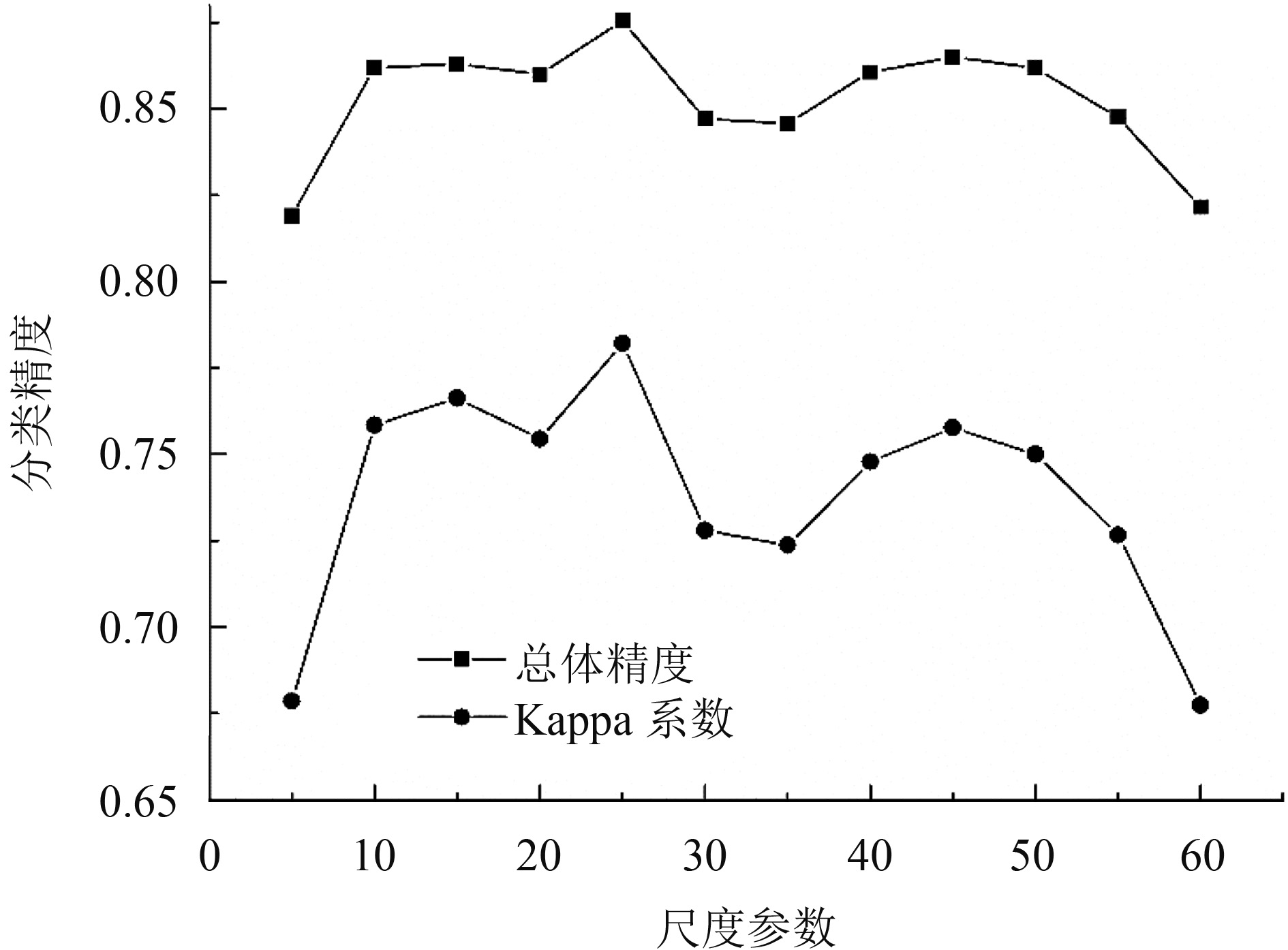
当shape=0时，分类精度如图18。总体精度趋势是先升高后降低，在降低的过程中略有波动。尺度在5—10时，精度处于上升状态。尺度在10—20时，精度略有降低。尺度在20—40时，精度变化不大。尺度在40—45时，精度略有下降。尺度在45—55时，精度略有上升，但整体变化不大。尺度在55—60时，精度有所下降。在尺度选择10时精度最高，总体精度为0.8531599，Kappa系数为0.7397017。上文所预测最佳分割尺度为8，与实际分类精度基本吻合。

图 18 农田实验区分类精度(shape=0)

Fig. 18 Classification accuracy of farmland (shape=0)

当shape=0.1时，分类精度如图19。总体精度的变化与上述情况略有不同，总体精度先升高，再有所降低，之后略有升高，最后走势呈降低趋势。尺度在5—25时，精度成上升趋势，其中，15—20时，精度有小幅度下降。尺度在25时，精度达到最高，总体精度为0.8754647，Kappa系数为0.7821495。尺度在25—35时，精度呈一定的下降趋势。尺度在35—45时，精度小幅提高。精度在45—60时，精度呈下降趋势。

图 19 农田实验区分类精度(shape=0.1)

Fig. 19 Classification accuracy of farmland (shape=0.1)

有上述趋势的差别，原因在于在分割时是否加入形状这一参数。对比各地物类别在shape=0和shape=0.1两种情况下随着尺度的变化趋势(图20)。

图 20 农田实验区各地物类别在shape=0和shape=0.1随尺度变化趋势

Fig. 20 The relationship of farmland’s classification accuracy and segmentation scale (shape=0, shape=0.1)

对于建筑区，shape=0与shape=0.1两组变化趋势基本相同。只有在尺度为15时，shape=0与shape=0.1的生产者精度有了异常升高。因为建筑区没有能够提出单独的房屋或单独水泥地，而是将其划为一片，无论分割结果如何，最终均归为一类，故建筑区对于形状不敏感。shape=0与shape=0.1的精度变化范围不大，说明建筑区对尺度并不敏感。

对于农作物区，shape=0与shape=0.1两组变化趋势几乎一致。说明对于农作物区而言，虽然其形状较为规整，呈四方形，但是因为面积较大，无论先开始分割是什么样子，最后在分类时都将归为一类，所以农田对于形状不敏感。shape=0与shape=0.1的生产者精度一直处于较高水平，用户精度随着尺度增加有所降低，但降低幅度不大，说明农作物区对尺度不敏感。

对于道路和树木而言，shape=0与shape=0.1的精度变化较明显，说明其受形状参数影响较大。在本实验区中，道路为平直细长的；树木主要存在于农作物区与农作物区之间，所以其形状也较为规则，所以在二者的影响下，shape=0和shape=0.1的分类精度变化明显。

对于水体来说，两组变化走势很相似，在影像中水体的面积非常小，所以它对整体的影响也不大。

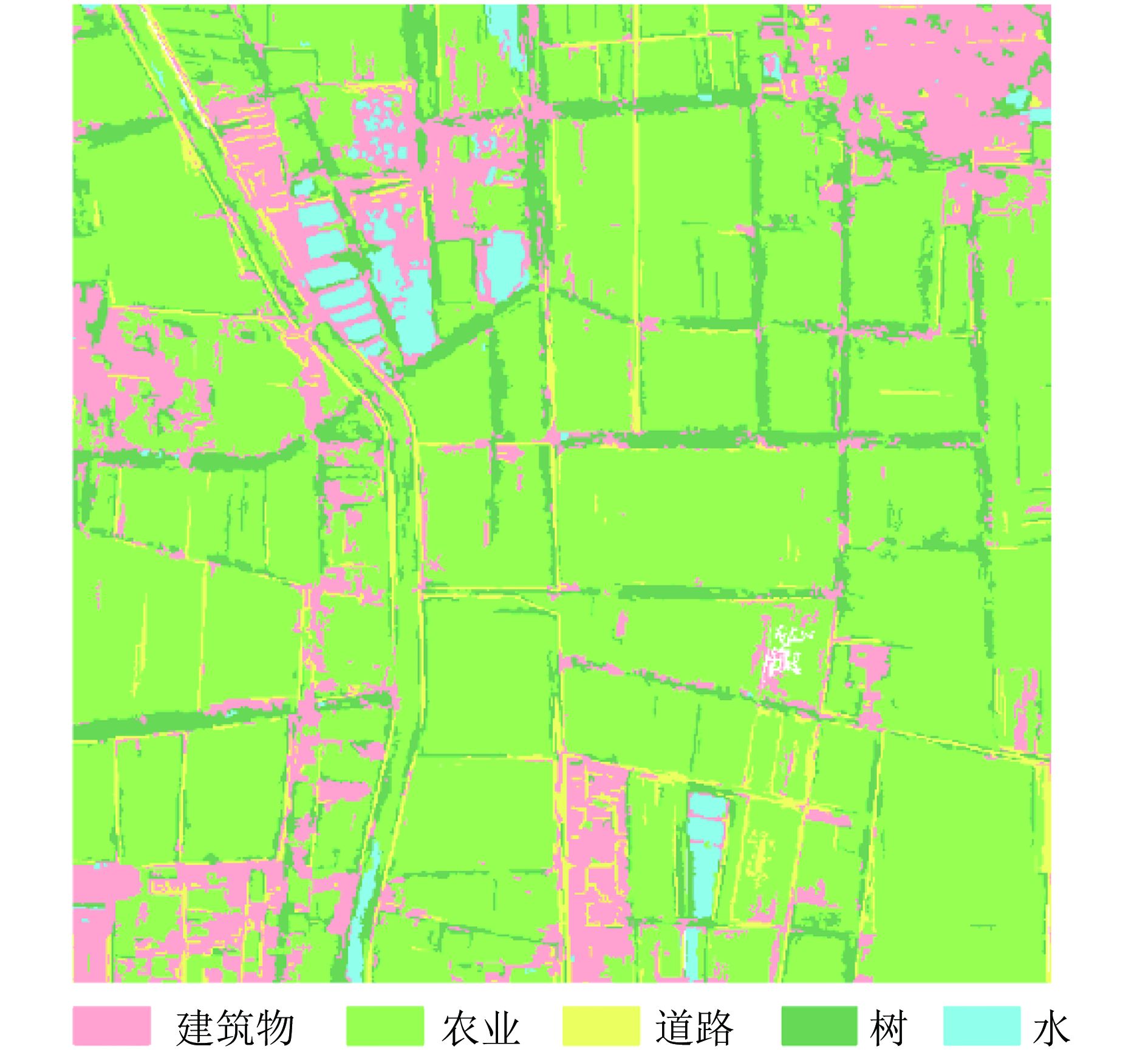
农田实验区土地利用分类图(shape=0，scale parameter=25)(图21)。

图 21 农田实验区土地利用分类图(shape=0，scale parameter=10)

Fig. 21 Land use classification map of farmland (shape=0，scale parameter=10)

6 结　论

空间尺度参数和属性尺度参数是具有普适意义的遥感影像分割尺度参数，运用原始影像的空间统计学特征来估计这些尺度参数对于面向对象影像分析及遥感尺度认知具有重要意义。本文将该思想应用于分形网络演化分割算法，结合ECognition软件对于参数的描述，提出软件层面与算法层面的空间尺度分割参数的联系，并对其分割尺度进行分类验证。实验结果显示，本文提出的尺度估计方法可以一定程度上保证最终的面向对象影像分类的精度。此外，不同于以往分割后评价的尺度选择方法会需要大量的运算量，本文提出的方法不需要先验知识的参与，且在分割前就可以自适应地估计出相对较为合适的尺度参数，提高了面向对象信息提取的自动化程度。

对于本组实验来说，建筑实验区相较于农田实验区所得实验结果较为符合本文方法计算的预期结果。之所以建筑实验区能得到的曲线相对波动较少，整体趋势明显、易于分析，原因在于其影像本身类别内部均质性很高，通过目视解读，就能较好的将各类地物区分，混合像元较少，类别内地物较为相似，类间地物差别较为明显。而对于农田实验区，影响其分类精度的主要因素并不是农作物区，因为其面积较大，无论分割结果是否理想，最后终将归到一类。对于本组实验来说，建筑区、道路和树木这样的地物对于尺度较为敏感。

对于形状异质度参数来说，由于道路和房屋的形状较为规则，形状异质度参数对其分类精度有一定的影响；而农作物区而言，虽然其形状较为规整，但是因为其面积较大，无论先开始分割是什么样子，最后再分类是都将归为一类，所以农田对于形状异质度参数不敏感，影像对象内部自身的均质性成为异质性估计的影响因素，需要在实践中加以考虑。

也正是由于影像对象内部存在异质性或可变性，实际上在研究区域范围较大且景观类型较为复杂的情况下，绝对的最优的尺度是不存在的，基于本文的思路采用分层处理策略，针对影像不同局部子区计算一个理论上的最优尺度，进而进行多个局部子区最优尺度信息提取结果的综合，将能提高面向对象遥感影像处理与分析的精细化程度，这是本研究未来要尝试的一个方向。

参考文献(References)

Atkinson P M and Aplin P. 2004. Spatial variation in land cover and choice of spatial resolution for remote sensing. International Journal of Remote Sensing, 25 (18): 3687–3702. [DOI: 10.1080/01431160310001654383]

Baatz M and Schäpe A. 2000.Multiresolution segmentation: an optimization approach for high quality multi-scale image segmentation//AngewandteGeographischeInformationsverarbeitung XII: Beiträgezum AGIT-Symposium. Salzburg: Herbert Wichmann Verlag.

Benz U C, Hofmann P, Willhauck G, Lingenfelder I and Heynen M. 2004. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS Journal of Photogrammetry and Remote Sensing, 58 (3/4): 239–258. [DOI: 10.1016/j.isprsjprs.2003.10.002]

Blaschke T and Hay G J. 2001. Object-oriented image analysis and scale-space: theory and methods for modeling and evaluating multi-scale landscape structure. International Archives of Photogrammetry and Remote Sensing, 34 : 22–29.

Blaschke T, Hay G J, Kelly M, Lang S, Hofmann P, Addink E, Feitosa R Q, van der Meer F, van der Werff H, van Coillie F and Tiede D. 2014. Geographic object-based image analysis-towards a new paradigm. ISPRS Journal of Photogrammetry and Remote Sensing, 87 : 180–191. [DOI: 10.1016/j.isprsjprs.2013.09.014]

Chen J, Deng M, Xiao P F, Yang M H, Mei X M and Liu H M. 2011. Optimal spatial scale choosing for high resolution imagery based on texture frequency analysis. Journal of Remote Sensing, 15 (3): 492–511. [DOI: 10.11834/jrs.20110100] ( 陈杰, 邓敏, 肖鹏峰, 杨敏华, 梅小明, 刘慧敏. 2011. 纹理频谱分析的高分辨率遥感影像最佳尺度选择. 遥感学报, 15 (3): 492–511. [DOI: 10.11834/jrs.20110100] )

Comaniciu D. 2003. An algorithm for data-driven bandwidth selection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 25 (2): 281–288. [DOI: 10.1109/TPAMI.2003.1177159]

Definiens AG.2007. Definiens Developer 7 User Guide, version 7.0.2.936, 23.

Drăgut L, Tiede D and Levick S R. 2010. ESP: a tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. International Journal of Geographical Information Science, 24 (6): 859–871. [DOI: 10.1080/13658810903174803]

Dronova I, Gong P, Clinton N E, Wang L, Fu W, Qi S H and Liu Y. 2012. Landscape analysis of wetland plantfunctional types: the effects of image segmentation scale, vegetation classes and classification methods. Remote Sensing of Environment, 127 : 357–369. [DOI: 10.1016/j.rse.2012.09.018]

Feng X, Qin K, Cui W H, Chen Y X and Li X H. 2014. Multiscale description and recognition of target shape in high-resolution remote sensing images. Journal of Remote Sensing, 18 (1): 90–104. [DOI: 10.11834/jrs.20133056] ( 冯霞, 秦昆, 崔卫红, 陈一祥, 李向辉. 2014. 高分辨率遥感影像目标形状特征多尺度描述与识别. 遥感学报, 18 (1): 90–104. [DOI: 10.11834/jrs.20133056] )

Hay G J, Castilla G, Wulder M A and Ruiz J R. 2005. An automated object-based approach for the multiscale image segmentation of forest scenes. International Journal of Applied Earth Observation and Geoinformation, 7 (4): 339–359. [DOI: 10.1016/j.jag.2005.06.005]

Johnson B and Xie Z X. 2011. 2011. Unsupervised image segmentation evaluation and refinement using a multi-scaleapproach. ISPRS Journal of Photogrammetry and Remote Sensing, 66 (4): 473–483. [DOI: 10.1016/j.isprsjprs.2011.02.006]

Jung C R. 2007. Combining wavelets and watersheds for robust multiscale image segmentation. Image and Vision Computing, 25 (1): 24–33. [DOI: 10.1016/j.imavis.2006.01.002]

Kim M, Madden M and Warner T.2008. Estimation of optimal image object size for the segmentation of foreststands with multispectral IKONOS imagery//Blaschke T, Lang S and Hay G J, eds. Object-based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications. Berlin: Springer: 291–307 [DOI: 10.1007/978-3-540-77058-9_16]

Ming D P, Ci T Y, Cai H Y, Li L X, Qiao C and Du J Y. 2012. Semivariogram-based spatial bandwidth selection for remote sensing image segmentation with mean-shift algorithm. IEEE Geoscience and Remote Sensing Letters, 9 (5): 813–817. [DOI: 10.1109/LGRS.2011.2182604]

Ming D P, Li J, Wang J Y and Zhang M. 2015. Scale parameter selection by spatial statistics for GeOBIA: using mean-shift based multi-scale segmentation as an example. ISPRS Journal of Photogrammetry and Remote Sensing, 106 : 28–41. [DOI: 10.1016/j.isprsjprs.2015.04.010]

Ming D P, Wang Q and Yang J Y. 2008. Spatial scale of remote sensing image and selection of optimal spatial resolution. Journal of Remote Sensing, 12 (4): 529–537. [DOI: 10.11834/jrs.20080470] ( 明冬萍, 王群, 杨建宇. 2008. 遥感影像空间尺度特性与最佳空间分辨率选择. 遥感学报, 12 (4): 529–537. [DOI: 10.11834/jrs.20080470] )

Ming D P, Zhou W and Wang M. 2016. Scale parameter estimation based on the spatial and spectral statistics in high spatial resolution image segmentation. Journal of Geo-Information Science, 18 (5): 622–631. ( 明冬萍, 周文, 汪闽. 2016. 基于谱空间统计特征的高分辨率影像分割尺度估计. 地球信息科学学报, 18 (5): 622–631. )

Myint S W, Gober P, Brazel A, Grossman-Clarke S and Weng Q H.. 2011. Per-pixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sensing of Environment, 115 (5): 1145–1161. [DOI: 10.1016/j.rse.2010.12.017]

Nogueira K, Penatti O A B and dos Santos J A. 2017. Towards Better Exploiting Convolutional Neural Networks for Remote Sensing Scene Classification. Pattern Recognition, 61 : 539–556. [DOI: 10.1016/j.patcog.2016.07.001]

Pinheiro P O, Collobert R and Dollar P. 2015. Learning to segment object candidates//Proceedings of the Advances in Neural Information Processing Systems 28. Montreal, Canada: Neural Information Processing Systems

Ševo I and Avramović A. 2016. Convolutional neural network based automatic object detection on aerial images. IEEE Geoscience and Remote Sensing Letters, 13 (5): 740–744. [DOI: 10.1109/LGRS.2016.2542358]

Walter V. 2000. Automatic change detection of GIS databases based on classification of multispectral data. International Archives of Photogrammetry and Remote Sensing, 33 : 1138–1145.

Walter V. 2004. Object-based classification of remote sensing data for change detection. ISPRS Journal of Photogrammetry andRemote Sensing, 58 (3/4): 225–238. [DOI: 10.1016/j.isprsjprs.2003.09.007]

Woodcock C E and Strahler A H. 1987. The factor of scale in remote sensing. Remote Sensing of Environment, 21 (3): 311–332. [DOI: 10.1016/0034-4257(87)90015-0]

Woodcock C E, Strahler A H and Jupp D L B. 1988. The use of variograms in remote sensing: I. Scene models and simulated images. Remote Sensing of Environment, 25 (3): 323–348. [DOI: 10.1016/0034-4257(88)90108-3]

Yang J, Li P J and He Y H. 2014. A multi-band approach to unsupervised scale parameter selection for multi-scale image segmentation. ISPRS Journal of Photogrammetry and Remote Sensing, 94 : 13–24. [DOI: 10.1016/j.isprsjprs.2014.04.008]

Yang J, He Y H, Caspersun J and Jones T. 2015. A discrepancy measure for segmentation evaluation from the perspective of object recognition. ISPRS Journal of Photogrammetry and Remote Sensing, 101 : 186–192. [DOI: 10.1016/j.isprsjprs.2014.12.015]

Zhang X L, Xiao P F, Feng X Z, Feng L and Ye N. 2015. Toward evaluating multiscale segmentations of highspatialresolution remote sensing images. IEEE Transactions on Geoscience and Remote Sensing, 53 (7): 3694–3706. [DOI: 10.1109/TGRS.2014.2381632]

Zhang Y J. 1997. Evaluation and comparison of different segmentation algorithms. Pattern Recognition Letters, 18 (10): 963–974. [DOI: 10.1016/S0167-8655(97)00083-4]

Zhao W Z and Du S H. 2016a. Learning multiscale and deep representations for classifying remotely sensed imagery. ISPRS Journal of Photogrammetry and Remote Sensing, 113 : 155–165. [DOI: 10.1016/j.isprsjprs.2016.01.004]

Zhao W Z and Du S H. 2016b. Spectral-spatial feature extraction for hyperspectral image classification: adimension reduction and deep learning approach. IEEE Transactions on Geoscience and Remote Sensing, 54 (8): 4544–4554. [DOI: 10.1109/TGRS.2016.2543748]

摘要

关键词