出版日期: 2017-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176273
2017 | Volumn21 | Number 4
上一篇 | 下一篇

混沌蜂群优化的NSST域多光谱与全色图像融合

吴一全^1,2,3,4,5,6 , 王志来¹

1. 南京航空航天大学电子信息工程学院，南京 210016

2. 南京信息工程大学江苏省大数据分析技术重点实验室，南京210044

3. 浙江工业大学浙江省信号处理重点实验室，杭州 310023

4. 广西师范大学广西多源信息挖掘与安全重点实验室，桂林 541004

5. 成都理工大学国土资源部地学空间信息技术重点实验室，成都 610059

6. 中国地质科学院矿产资源研究所国土资源部成矿作用与资源评价重点实验室，北京 100037

收稿日期: 2016-08-12

基金项目: 国家自然科学基金(编号：61573183)；南京信息工程大学，江苏省大数据分析技术重点实验室开放基金(编号：KXK1403)；浙江省信号处理重点实验室开放基金(编号：ZJKL_6_SP-OP2014-02)；广西多源信息挖掘与安全重点实验室开放基金(编号：MIMS16-01)；国土资源部地学空间信息技术重点实验室开放基金(编号：KLGSIT2015-05)；国土资源部成矿作用与资源评价重点实验室开放基金(编号：ZS1406)

第一作者简介: 吴一全(1963—　)，男，教授，研究方向为遥感图像处理、分析与理解，目标检测与识别等。E-mail：nuaaimage@163.com

中图分类号: O433.4；TP751

文献标识码: A

摘要

为有效融合多光谱图像的光谱信息和全色图像的空间细节信息，提出了一种基于混沌蜂群优化和改进脉冲耦合神经网络(PCNN)的非下采样Shearlet变换(NSST)域图像融合方法。首先对多光谱图像进行Intensity-Hue-Saturation(IHS)变换，全色图像的直方图按照多光谱图像亮度分量的直方图进行匹配；然后分别对多光谱图像的亮度分量和新全色图像进行NSST变换，对低频分量使用改进加权融合算法进行融合，以互信息作为适应度函数，利用混沌蜂群算法找到最优加权系数。对高频分量采用改进脉冲耦合神经网络(PCNN)方法进行融合，再经NSST逆变换和IHS逆变换得到融合图像。本文方法在主观视觉效果和信息熵、光谱扭曲度等客观定量评价指标上优于基于IHS变换、基于非下采样Contourlet变换(NSCT)和非负矩阵分解(NMF)、基于NSCT和PCNN等5种融合方法。本文方法在提升图像空间分辨率的同时，有效地保留了光谱信息。

关键词

图像融合, 多光谱与全色图像, 非下采样Shearlet变换, 混沌蜂群优化, 改进的脉冲耦合神经网络

Multispectral and panchromatic image fusion using chaotic Bee Colony optimization in NSST domain

WU Yiquan^1,2,3,4,5,6 , WANG Zhilai¹

1.College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

2.Jiangsu Key Laboratory of Big Data Analysis Technology/B-DAT, Nanjing University of Information Science & Technology, Nanjing 210044, China

3.Zhejiang Province Key Laboratory for Signal Processing, Zhejiang University of Technology, Hangzhou 310023, China

4.Guangxi Key Laboratory of Multi-Source Information Mining and Security, Guangxi Normal University, Guilin 541004, China

5.Key Laboratory of Geo-Spatial Information Technology, Ministry of Land and Resources, Chengdu University of Technology, Chengdu 610059, China

6.MLR Key Laboratory of Metallogeny and Mineral Assessment Institute of Mineral Resources, Chinese Academy of Geological Sciences, Beijing 100037, China

Abstract

The rapid development of remote sensing technology provides an effective technical approach for humans to understand living environments and to utilize natural resources. Various remote sensing sensors exist, and the images formed by different image sensors have various characteristics, thereby resulting in multi-source remote sensing images, such as multi-spectral and panchromatic images. Fusing the multi-source remote sensing images of the same scene is necessary to efficiently and comprehensively deal with these image data. The multi-spectral image has high spectral resolution and rich spectral information; however, the spatial resolution of this image is low due to the limitations of physical devices. The panchromatic image has high spatial resolution and clear spatial detail; however, its spectral resolution is low. The fusion of multi-spectral and panchromatic images is the integration of the spatial detail information of the panchromatic image into the multi-spectral image to generate an image with high spatial resolution and spectral resolution, which benefit subsequent image processing. A method for the fusion of multi-spectral and panchromatic images using chaotic artificial bee colony optimization and improved Pulse Coupled Neural Network (PCNN) in a Non-Subsampled Shearlet Transform (NSST) domain is proposed. First, Intensity Hue Saturation (IHS) transform is performed on the multi-spectral image. The histogram of the panchromatic image is matched to the histogram of the intensity component of the multi-spectral image. The intensity component of the multispectral image and the new panchromatic image are then decomposed by NSST. Next, the low-frequency component is fused with the improved weighted fusion algorithm. Recently, artificial bee colony algorithm is one of the effective swarm intelligence optimization algorithms, which can adaptively determine the weighted coefficient. Chaotic bee colony optimization algorithm is designed by introducing the tent mapping chaotic sequence to avoid premature phenomena. The chaotic bee colony optimization algorithm has high convergence precision and rapid convergence speed in global optimization. By exploiting this property, the optimal improved weighted coefficient is determined by the chaotic artificial bee colony optimization algorithm. Mutual information is used as the fitness function. The improved PCNN method is adopted for the fusion of high-frequency components. Finally, the fused image is obtained by inverse NSST and inverse IHS transform. Many multi-spectral and panchromatic remote sensing images from LANDSAT TM, IKONOS, and SPOT 4 satellites are tested. Qualitative and quantitative evaluation results are obtained to verify the feasibility and effectiveness of the proposed method. The proposed method outperforms five other kinds of fusion methods: the IHS method, the method of Non-Subsampled Contourlet Transform (NSCT) combined with Non-negative Matrix Factorization (NMF),the method of NSCT combined with PCNN in the subjective visual effect, and the objective quantitative evaluation indexes, such as information entropy and spectral distortion. The proposed method can effectively preserve the spectral information of the multispectral image, while the details of panchromatic images are injected into the fused image as much as possible, effectively improving the spatial resolution of the fused image.

Key words

image fusion, multispectral image and panchromatic image, non-subsampled shearlet transform, chaotic artificial bee colony optimization, improved pulse coupled neural network

1 引　言

遥感图像融合是指将取自相同区域中同一目标的不同光谱与空间信息的遥感图像数据通过一定的算法整合到一幅图像(Dong 等，2015)。多光谱图像富含光谱信息，但空间清晰度不高。全色图像能够反映图像的空间细节信息，但光谱信息贫乏。将两者融合以保证光谱和空间信息的最大化，从而便于后续处理，在多源信息挖掘、大数据分析、地质资源勘探等领域起着重要作用。如何有效地将多源卫星遥感图像进行融合是当今遥感图像处理领域的研究热点之一。

现有的多光谱图像和全色图像融合方法主要包括基于分量替代、基于多尺度分解、基于非负矩阵分解(NMF)及基于神经网络等方法。基于IHS变换(Chien和Tsai，2014)、基于主成分分析(PCA)(夏余和曲仕茹，2014)等方法属于基于分量替代的方法。这类方法能够有效提升图像的空间分辨率，然而当多光谱与全色图像波段的光谱范围不同时，会导致融合结果出现光谱失真现象。基于多尺度分解的融合方法则包括基于Curvelet (蒋年德等，2008)、基于小波变换(郭雷等，2011)、基于Contourlet变换(刘坤和李晖晖，2013)等融合方法。其中，基于小波变换的融合方法是较为典型的多尺度分解方法。然而，小波变换受方向局限的限制无法更稀疏地表示图像中的线段、轮廓等细节信息。为此，人们相继提出了Contourlet变换、非下采样Contourlet变换(NSCT)(Da Cunha 等，2006)、Shearlet变换(Guo和Labate，2007)等更稀疏的信号表示方法。Shearlet变换作为一种高维信号稀疏表示方法，能更有效地捕捉图像的细节信息。但上述变换都不具备平移不变性，容易使融合图像在边缘处出现伪吉布斯现象。非下采样Shearlet变换(NSST)(Easley 等，2008)由Shearlet变换改进而来，并具有平移不变特性。文献(Gao 等，2013；Kong 等，2015)都证明了基于NSST比基于其他多尺度分解的融合结果包含更多的细节信息。在NSST域进行多光谱与全色图像融合，所得融合效果更佳。继上述多尺度分解融合算法之后出现的基于非负矩阵分解的图像融合算法(颜建军等，2007)，对整体特征的提取能力较强，但其无法在图像尺度空间上对图像细节信息进行跟踪，使得融合后图像常常存在细节不清晰甚至丢失等问题。脉冲耦合神经网络(PCNN)(Johnson和Padget，1999)是一类单层的神经网络，具有全局的脉冲同步性和耦合性，可实现区域内灰度相似的像素同步点火，利用其进行融合能达到增强图像局部空间细节的目的(Zhang 等，2014)，因此被广泛地应用于图像融合。

多尺度分解融合规则设计中，往往涉及图像分量的加权融合。利用群智能优化算法可以自适应地确定加权系数。人工蜂群算法(Karaboga和Basturk，2007)作为近年来有效的群智能优化算法之一，相比传统群智能算法，其参数较少，全局搜索能力优越。但算法性能易受最大迭代次数的影响，且可能因遍历性不够出现“早熟”现象。为此，将Tent映射的混沌序列引入人工蜂群算法构成混沌蜂群优化算法，利用其自动搜寻图像融合的加权系数，可望增强融合算法的自适应性以获得更好的融合效果。

为达到融合后图像多光谱信息和空间信息的最大化，本文提出了一种基于混沌蜂群优化和改进PCNN的NSST域多光谱和全色图像融合方法。首先把多光谱图像变换至IHS空间，将全色图像的直方图依照其亮度分量的直方图进行匹配；再对这两幅图像分别进行NSST变换，采用改进的PCNN融合规则对高频分量进行融合；使用改进的加权融合规则对低频分量进行融合，引入混沌蜂群优化算法优化两幅图像低频分量的加权系数，以互信息作为适应度，寻找全局最优加权系数。最后，将本文方法与基于IHS变换、基于NSCT和NMF(Wu 等，2012)、基于NSCT和PCNN(李新娥等，2013)等5种融合方法的实验结果进行了比较，验证了本文方法的优越性。

2 NSST及改进PCNN

2.1 NSST

Shearlet变换是一种新的多尺度分解，通过对基本函数的一系列仿射变换生成基函数，在各个尺度和方向能够近乎最优地表示富含方向信息的图像，且具有较低的冗余度和计算复杂度。当维数为2时，根据能量有限函数生成的仿射系统为：

$\begin{aligned}{{{M}}_{AB}}(\psi ) = & \{ {\psi _{j,l,k}}(x) = |\det {{A}}{|^{j/2}}\psi ({{{B}}^l}{{{A}}^j}x - k)\\& j,l \in {\bf{{Z}}},k \in {{\bf{{Z}}}^2}\} \end{aligned}$

(1)

式中， $\psi \in {L^2}\left( R \right)$ ，通过对基本函数 ${\psi _{j,l,k}}(x)$ 进行旋转、剪切和平移变换，构成仿射系统；A、B为2×2的可逆矩阵，j为分解尺度，l表示方向数，k为平移。若 $\forall f \in {L^2}\left( {{R^2}} \right)$ ，满足Parseval框架 $\sum\limits_{j,l,k} {\left| { < f,{\psi _{j,l,k}} > } \right|} = $ $ {\left\| f \right\|^2}$ ，则 ${{{M}}_{AB}}(\psi )$ 是合成小波。合成小波具有多分辨分析的特性，这意味着它和小波一样，可在各个尺度、位置和方向上构造基元素的Parseval框架。Shearlet则是合成小波的特例，矩阵A为各向异性膨胀矩阵，此时 ${{A}} = {{{A}}_0} = \left( {\begin{array}{*{20}{c}}4&0\\0&2\end{array}} \right)$ ，与变换的尺度相关，控制Shearlet变换的尺度；矩阵B为剪切矩阵，此时 ${{B}} = {{{B}}_0} = \left( {\begin{array}{*{20}{c}}1&1\\0&1\end{array}} \right)$ ，与旋转、剪切等几何变换相关，控制Shearlet变换的方向。

相较Shearlet变换，NSST具有平移不变特性，能够更准确地捕获图像中的轮廓、边缘、细节等信息。NSST变换包括多尺度分解和方向局部化两部分，具体步骤如下：首先在空间域采用非下采样金字塔分解源图像，获得低频、高频分量；然后通过改进的剪切滤波器(SF)实现高频分量的方向局部化。它能够将Shearlet中的标准剪切滤波器从Pseudo-Polar坐标系映射到Cartesian坐标系，取消了降采样操作，使得NSST具有移不变特性；最后，通过傅里叶逆变换进行2维卷积，得到NSST系数。

2.2 改进的PCNN

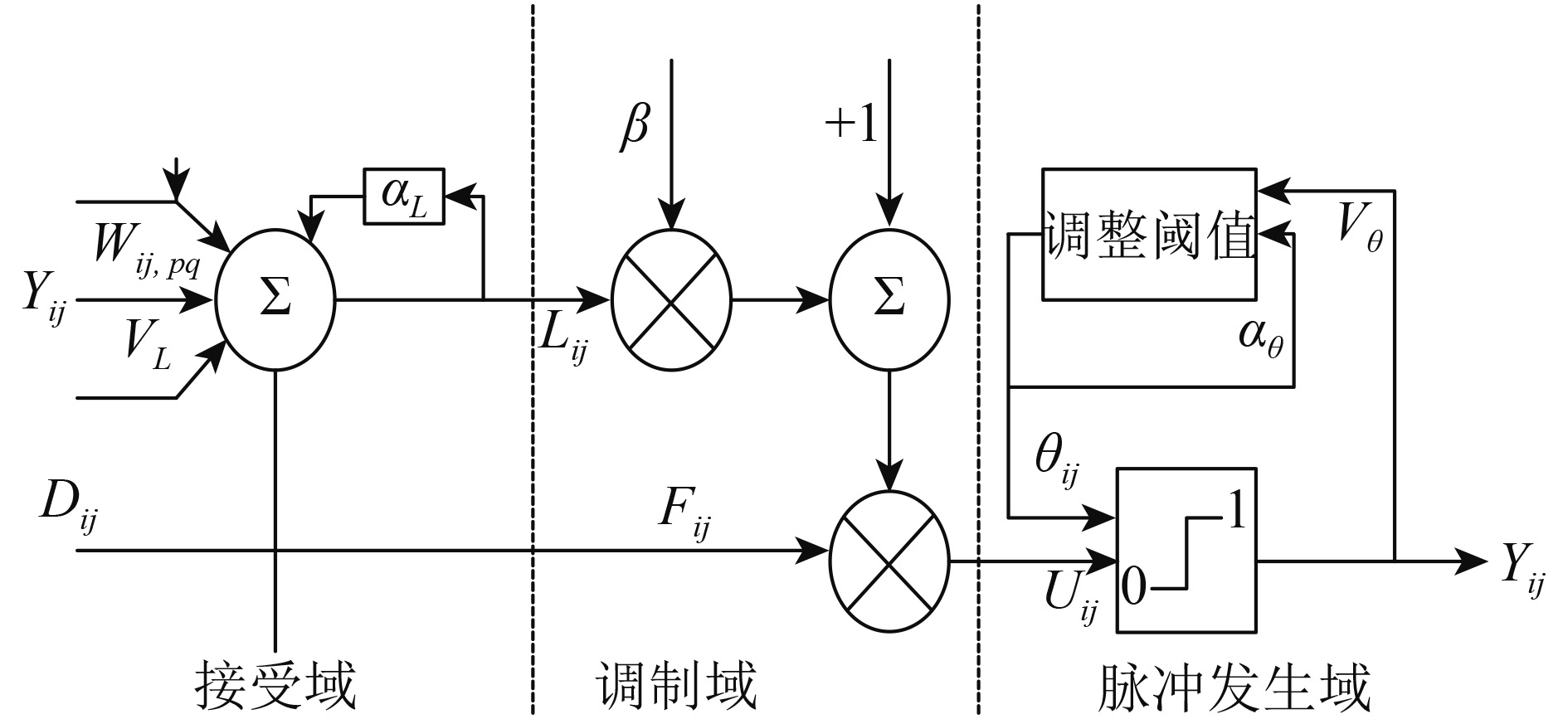
PCNN是一种由若干神经元相互链接而形成的反馈网络，每个神经元由3部分组成，接受域、调制域和脉冲发生部分。原始PCNN模型用于图像处理时，需调整参数较多。简化PCNN的模型如图1所示(Blasch，1999)，数学模型可以由式(2)来描述：

$\left\{ \begin{aligned}& {F_{ij}}(n) = {D_{ij}}\\& {L_{ij}}(n) = {L_{ij}}(n - 1) \times \exp ( - {\alpha _L}) + {V_L}\sum\limits_{pq} {{\omega _{ij,pq}}{Y_{pq}}(n - 1)} \\& {U_{ij}}(n) = {F_{ij}}(n)(1 + \beta {L_{ij}}(n))\\& {\theta _{ij}}(n) = {\theta _{ij}}(n - 1) \times \exp ( - {\alpha _\theta }) + {V_\theta }{Y_{ij}}(n - 1)\\& {Y_{ij}}(n) = step({U_{ij}}(n) - {\theta _{ij}}(n))\end{aligned} \right.$

(2)

式中， $\left( {i,j} \right)$ 为像素位置； ${D_{ij}}$ 为外部输入；n为迭代次数； ${F_{ij}}$ 为神经元输入； ${L_{ij}}$ 为链接输入； ${V_L}$ 为链接输入的放大倍数； ${U_{ij}}$ 为神经元的内部活动项； ${\alpha _L}$ 、 ${\alpha _\theta }$ 为时间衰减常数；β为链接强度； ${\omega _{ij,pq}}$ 为神经元的突触连接权系数； ${\theta _{ij}}$ 表示动态阈值； ${V_\theta }$ 表示阈值放大系数； ${Y_{ij}}(n)$ 表示PCNN的输出。 ${Y_{ij}}(n) = 1$ 或0分别表示神经元是否被激活。

图 1 PCNN简化模型

Fig. 1 Simplified PCNN model

基于PCNN的图像融合算法中，融合规则都是依据输入经PCNN点火次数的多少来选取融合图像的系数，由于PCNN使用的是硬限幅函数，不能体现出点火幅度的差异，故对其进行改进(廖勇等，2014)。在PCNN的输出中，通过Sigmoid连续函数计算点火输出幅度，并将其总和的大小作为高频系数的选取依据。为了描述点火输出幅度的差异，输出重定义如下：

${T_{ij}}\left( n \right) = \frac{1}{{1 + {{\rm e}^{{\theta _{ij}}\left( n \right) - {U_{ij}}\left( n \right)}}}}$

(3)

式中， ${T_{ij}}\left( n \right)$ 是图像 $\left( {i,j} \right)$ 位置的点火输出幅度，取值范围为[0, 1]。n次的点火输出幅度总和为

${Z_{ij}}\left( n \right) = {Z_{ij}}\left( {n - 1} \right) + {T_{ij}}\left( n \right)$

(4)

3 低频和高频分量融合规则

针对多光谱和全色图像融合的特点进行融合规则设计，提出了一种基于混沌蜂群优化和改进PCNN的NSST域多光谱和全色图像融合方法。

3.1 基于混沌蜂群优化的改进加权低频分量融合

低频分量是在低分辨率下对源图像的近似。现改进加权融合规则对低频分量进行融合，即：基于区域能量取大和利用混沌蜂群算法优化其中的加权系数。源图像经NSST变换后，图像的绝大部分能量集中在低频分量。由于无法通过单个像素评判图像区域特征的优劣，故需要邻域内多个像素点的共同体现。基于区域能量取大的融合规则既增强了图像区域内像素的相关性又保留了图像的细节信息，且可反映图像明显的亮度突变(宋梦馨和郭平，2012)。令 ${E_k}\left( {i,j} \right)$ $\left( {k = 1,2} \right)$ 表示图像k中以点 $\left( {i,j} \right)$ 为中心的5×5小块的区域能量，每小块的区域能量 $E = \sum\limits_{i = 1}^5 {\sum\limits_{j = 1}^5 {[f\left( {i,j} \right)} } {]^2}$ ，其中 $f\left( {i,j} \right)$ 为灰度值。由于低频分量聚集了较多的光谱信息，因此对低频分量的首要处理原则是尽可能多地保留多光谱图像的光谱信息。若多光谱图像低频分量的区域能量小于全色图像的区域能量，则采用式(5)的改进加权融合规则，将全色图像的空间细节信息与多光谱图像光谱信息加权融合，融入空间细节的同时兼顾光谱信息的保留；反之，直接将多光谱图像的低频分量作为融合图像的低频分量，以保留更多的光谱信息。改进的加权公式为

${F^l}\left( {i,j} \right) = \left\{ \begin{aligned}& \omega I_A^l\left( {i,j} \right) + (1 - \omega )I_B^l\left( {i,j} \right)\\[3pt]& E_A^l\left( {i,j} \right) > E_B^l\left( {i,j} \right)\\[3pt]& I_B^l\left( {i,j} \right) \;\;\;\;\;\;\;\;\;\;\; \text{其他} \end{aligned} \right.$

(5)

式中， ${F^l}\left( {i,j} \right)$ 表示融合后的低频分量系数， $I_A^l\left( {i,j} \right)$ 和 $I_B^l\left( {i,j} \right)$ 分别表示全色图像P与多光谱图像亮度分量I的低频分量系数， $E_A^l\left( {i,j} \right)$ 和 $E_B^l\left( {i,j} \right)$ 表示相应的低频分量区域能量， $\omega $ 表示加权系数。

进行图像融合时，需要保证融合后图像能从两幅源图像中继承更多的信息。若使用固定加权方法选取某个特定的加权系数进行低频分量的融合，无法保证融合图像自适应地从源图像中继承较多的有效信息。融合图像与源图像之间的互信息是衡量融合后图像质量的一个重要指标。互信息衡量的是融合图像从两幅源图像中继承信息的多少，互信息越大，融合图像从两幅源图像中获取的信息越丰富，融合效果越好，故以互信息作为适应度函数，在低频分量融合中使用混沌蜂群优化算法对加权系数 $\omega $ 进行寻优，进而找到最大互信息所对应的加权系数。当两幅图像的低频分量与其融合后的低频分量互信息和最大时，得到的 $\omega $ 即为最优加权系数。

人工蜂群算法模仿自然蜂群的采蜜行为，由侦察蜂、引领蜂、追随蜂交流合作来搜寻最优蜜源(亦即搜索的最优加权系数)。鉴于人工蜂群优化算法存在易陷入局部最优解的缺点，现考虑使用结合Tent映射混沌序列的人工蜂群算法实现上述加权系数的优化。利用Tent混沌序列的随机性、遍历性强的特性，增强搜索最优蜜源 ${X_{{\rm{best}}}}$ 的遍历性，可有效削弱其对初值的敏感性，减少“早熟”现象出现的几率，得到全局最优解。结合Tent映射的混沌蜂群优化算法的具体步骤描述如下：

(1) 从每次搜索得到的候选加权系数集中选出使得互信息最大的最优加权系数 ${X_{{\rm{best}}}}$ 。

(2) 按照式(6)生成Tent混沌序列 ${w_i}$ ：

${w_{i + 1}} = \left\{ \begin{array}{l}2{w_i}\;\;\;\;\;\;\;\;\;0 \leqslant {w_i} \leqslant 0.5\\[5pt]2(1 - {w_i})\;\;\;0.5 \leqslant {w_i} \leqslant 1\end{array} \right.$

(6)

式中， $i = 1,2,\cdots,K$ ， ${w_1}$ 是由均匀分布生成的(0，1)内随机数，且 ${w_i} \ne $ 0.25、0.5和0.75，K表示混沌序列的长度。

(3) 在加权系数集可能出现的范围内定义区间 $[L,H]$ ，由于所需优化的参数是加权系数，应取[0, 1]。按照式(7)将混沌序列w_i映射到区间 $[L,H]$ 内的混沌变量W_i：

${W_i} = L + 0.1 \times {w_i} \times \left( {H - L} \right)\;\;\;\;\;\;i = 1,2,\cdots,K$

(7)

(4) 按照式(8)将混沌变量W_i与互信息最大下的加权系数 ${X_{{\rm{best}}}}$ 进行线性组合，产生新的候选加权系数V_i：

${V_i} = {X_{{\rm{best}}}} + \lambda {W_i}\;\;\;\;\;\;i = 1,2,\cdots,K$

(8)

$\lambda = \frac{{{C_{\rm{M}}} - c + 1}}{{{C_{\rm{M}}}}}$

(9)

式中， $\lambda $ 为收缩因子， ${C_{\rm{M}}}$ 为最大迭代次数，c为当前迭代次数。

(5) 将 ${V_i}$ 下的互信息值与已有的最优加权系数 ${X_{{\rm{best}}}}$ 下的互信息值进行比较，若 ${V_i}$ 下的互信息值大于 ${X_{{\rm{best}}}}$ 下的互信息值，则选择 ${V_i}$ 作为新的最优加权系数 ${X_{{\rm{best}}}}$ ，否则保留原来的，局部搜索结束；或者当混沌序列达到设定长度K时，局部搜索也结束。返回引领蜂操作阶段，开始新一轮的搜索迭代过程，当迭代次数超过最大迭代次数时，迭代终止。

3.2 基于改进PCNN的高频分量融合

图像经NSST分解得到的高频分量反映图像的细节信息，如图像的区域边界、边缘、纹理细节等。基于PCNN的常规融合方法中将单个像素值作为PCNN的输入，而人眼对单个像素并不敏感，所以将单个像素值作为输入不太合适。拉普拉斯能量和能够恰当表示图像边缘细节信息，故将区域改进拉普拉斯能量和(SML)作为改进PCNN的输入。用 $f\left( {i,j} \right)$ 表示图像 $\left( {i,j} \right)$ 处的系数，SML定义如下：

$\begin{aligned} {S_{{\rm{SML}}}} = & |2f\left( {i,j} \right) - f\left( {i - g,j} \right) - f\left( {i + g,j} \right)| + \\& |2f\left( {i,j} \right) - f\left( {i,j - g} \right) - f\left( {i,j + g} \right)|\end{aligned}$

(10)

式中，g表示可变的空间距离，本文取g=1。

PCNN模型参数中的链接强度 $\beta $ ，为中心神经元与周围神经元链接的强度。 $\beta $ 值对融合效果的影响较大，其他模型参数的影响相对较小。基于PCNN的常规融合方法中，全部神经元的 $\beta $ 值都相同，但人眼对特征显著区域要比不显著区域的反应更敏锐，每个神经元的 $\beta $ 值应该不同。依据区域特征自适应地调整 $\beta $ 值，获得的视觉效果更佳。空间频率是一种反映图像总体活跃程度的区域特征，其值越大说明图像越清晰。为此，采用一种改进的区域空间频率 ${F_{{\rm{MSF}}}}$ 并将其归一化作为PCNN的 $\beta $ 值。 ${F_{{\rm{MSF}}}} = \sqrt {F_{{\rm{RF}}}^2 + F_{{\rm{CF}}}^2 + F_{{\rm{DF}}}^2 + F_{{\rm{SF}}}^2} $ ，其中 $F_{{\rm{RF}}}^{}$ 和 $F_{{\rm{CF}}}^{}$ 分别为行、列频率， $F_{{\rm{DF}}}^{}$ 和 $F_{{\rm{SF}}}^{}$ 分别为主、次对角频率。

$F_{{\rm{RF}}}^{} = \sqrt {\frac{1}{{M(N - 1)}}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left( {{f_{m,n + 1}} - {f_{m,n}}} \right)}^2}} } } $

(11)

$F_{{\rm{CF}}}^{} = \sqrt {\frac{1}{{(M - 1)N}}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left( {{f_{m + 1,n}} - {f_{m,n}}} \right)}^2}} } } $

(12)

$F_{{\rm{DF}}}^{} = \sqrt {\frac{1}{{(M - 1)(N - 1)}}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left( {{f_{m + 1,n + 1}} - {f_{m,n}}} \right)}^2}} } } $

(13)

$F_{{\rm{SF}}}^{} = \sqrt {\frac{1}{{(M - 1)(N - 1)}}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left( {{f_{m,n + 1}} - {f_{m + 1,n}}} \right)}^2}} } } $

(14)

采用Sigmoid函数将 $\beta $ 值归一化到[0, 1]： $\beta = \displaystyle\frac{1}{{1 + {{\rm e}^{ - {F_{{\rm{MSF}}}}}}}}$ 。基于改进PCNN的高频分量具体融合步骤为：

(1) 采用3×3窗口遍历多光谱图像I分量和全色图像P，计算其NSST域高频分量的 ${S_{{\rm{SML}}}}$ 并归一化到[0, 1]，将其输入PCNN模型。

(2) 令最大迭代次数为N_max。PCNN的初值设定为 ${L_{ij}}\left( 0 \right) = {U_{ij}}\left( 0 \right) = {\theta _{ij}}\left( 0 \right) = 0$ 。

(3) 根据式(2)计算所有的中间结果，并计算点火输出幅度总和 ${Z_{ij}}\left( n \right) = {Z_{ij}}\left( {n - 1} \right) + {T_{ij}}\left( n \right)$ ，其中， ${Z_{ij}}\left( 0 \right) = 0$ 。

(4) 当迭代次数 $n < {N_{\max }}$ 时，重复执行步骤(3)，直到迭代次数满足 $n = {N_{\max }}$ 时，停止迭代。

(5) 得到决策矩阵: ${{H}}(i,\!j) \!\!=\!\! \left\{ \begin{array}{l}\!\!\!\!\! 1,Z_{ij}^{\mathop{\rm I}\nolimits} \! \left( \! {{N_{\max }}} \! \right)\! > \!Z_{ij}^{\mathop{\rm P}\nolimits} \! \left( \! {{N_{\max }}} \! \right)\\\!\!\!\!\! 0,{\mathop{\rm else}\nolimits} \end{array} \right.$ ，并根据决策矩阵确定融合图像的高频分量: ${C^{\rm{F}}}\!(i,j) \!=\! $ $\left\{ \begin{array}{l}\!\!\! {C^{\rm{I}}}(i,j),\;\;\;\;\left( {{{H}}\left( {i,j} \right) = 1} \right)\\\!\!\! {C^{\rm{P}}}(i,j),\;\;\;\;\left( {{{H}}\left( {i,j} \right) = 0} \right)\end{array} \right.$ 。

式中， ${C^{\rm{I}}}(i,j)$ ， ${C^{\rm{P}}}(i,j)$ 分别表示NSST域多光谱I分量和全色图像的高频分量。

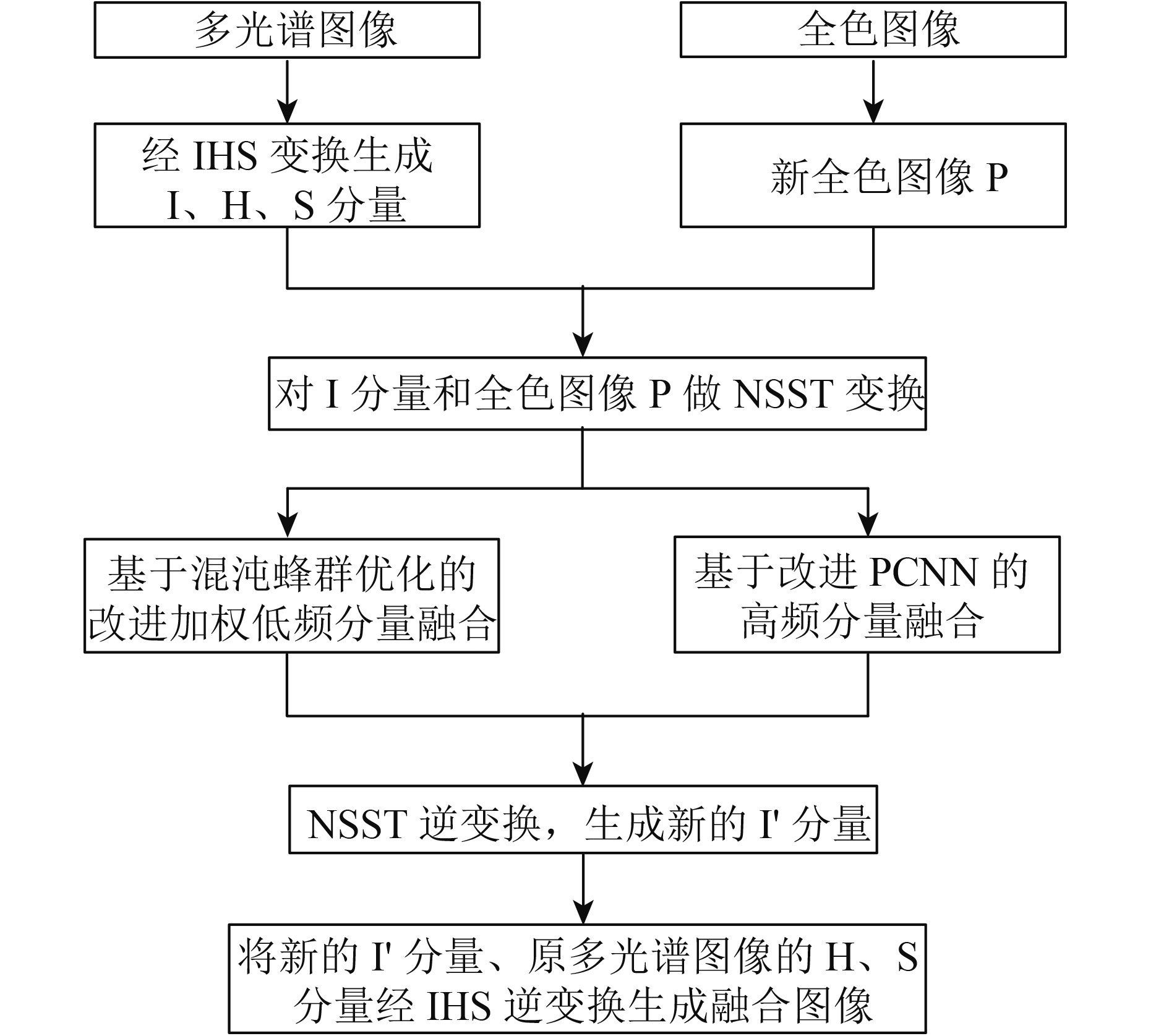
3.3 本文方法流程图和具体融合步骤

本文融合步骤如下：

(1) 将多光谱图像转换至IHS空间；

(2) 将全色图像的直方图依照多光谱图像的亮度分量的直方图进行匹配，得到新全色图像P；

(3) 对I分量及新全色图像P分别进行NSST多尺度分解；

(4) 采用改进加权融合规则对低频分量进行融合，利用改进PCNN算法对中高频分量进行融合，最高频分量使用绝对值取大算法进行融合；

(5) 对处理后的低频和高频分量进行NSST逆变换，得到融合后的新亮度分量I′；

(6) 将原多光谱图像的H、S分量和新亮度分量逆变换至RGB空间，获得融合图像。

融合方法流程图如图2。

图 2 本文方法的流程图

Fig. 2 Flow chart of the proposed method

4 实验结果与分析

为验证本文方法的有效性，利用上述提出的基于混沌蜂群优化和改进PCNN的NSST域多光谱和全色图像融合方法，对大量图像进行了融合实验，并与基于IHS变换以及近年来提出的基于NSCT和PCNN、基于NSCT和NMF、低频固定加权和高频改进PCNN、低频改进加权和高频PCNN等5种图像融合方法的结果进行了比较。由于篇幅所限，现以两组大小分别为256×256和512×512的全色图像和多光谱图像为例加以说明。如图3所示，第1组图像为LANDSAT TM卫星拍摄的某地区3个波段合成的多光谱图像和SPOT 4卫星拍摄的同一地区的全色图像；第2组图像为IKONOS卫星拍摄的某地区3个波段合成的多光谱图像及同一地区的全色图像。图4和图5为利用上述6种融合方法分别针对这2组图像所得到的融合结果。经大量实验，实验参数选取如下效果最优：NSST中，多尺度分解滤波器为“maxflat”，尺度分解层数为3，每层剖分的方向数为[2, 2, 2]。改进的PCNN的参数选取如下： ${N_{\max }} = 200$ ， ${\alpha _L} \!=\! 1.0$ ， ${\alpha _\theta } \!=\! 0.2$ ， ${V_L} \!=\! 1.0$ ， ${V_\theta } \!=\! 20$ ，ω = $ \left[ {\begin{array}{*{20}{c}}{0.707}&1&{0.707}\\1&0&1\\{0.707}&1&{0.707}\end{array}} \right]$ 。混沌蜂群优化算法的参数设置如下：蜂群总数为10，最大迭代次数为30，侦察蜂和引领蜂的数量各占一半，适应度函数搜索参数数量为1，选取局部最优解的迭代次数为3。

图 3 两组多光谱图像和全色图像

Fig. 3 Two groups of multispectral image and panchromatic image

图 4 第1组图像的融合结果

Fig. 4 Fusion results on the images of groupⅠ

图 5 第2组图像的融合结果

Fig. 5 Fusion results on the images of groupⅡ

从主观视觉效果上来看，图4(a)和图5(a)为基于IHS变换方法的融合图像，其清晰程度较原多光谱图像有较大提高，但某些区域的光谱失真现象较明显。图4(b)和图5(b)为NSCT与NMF相结合方法的融合图像，保持了多光谱图像的光谱信息，但在轮廓、边缘、纹理细节表现方面较模糊。图4(c)和图5(c)为NSCT与PCNN相结合方法的融合结果，空间分辨率和NSCT与NMF相结合的方法相比有明显提升。图4(d)和图5(d)为低频固定加权(未使用优化算法)和高频改进PCNN方法所得融合结果，其空间分辨率得到了提升，但融合图像仍存在一定程度上的光谱畸变。由于光谱信息主要聚集在图像的低频分量中，对低频分量如何融合直接影响着光谱畸变的程度，可见导致光谱畸变程度较高的原因是该方法在低频分量融合中不能自适应地加权融合。图4(e)和图5(e)为低频改进加权(使用本文优化算法)和高频PCNN方法所得融合结果，空间分辨率在某种程度上得到了提高，融合图像的光谱信息损失变小。图4(f)和图5(f)为本文方法所得融合结果，可以看出空间细节表现能力得到了有效提高，同时融合图像光谱畸变程度变小，边缘、轮廓更为清晰，视觉效果更佳。值得注意的是，原始多光谱图像在建筑物北面存在阴影，而融合图像中对应部分呈现出绿色的光谱信息。由于少量隐藏的光谱信息集中在高频分量，这说明本文高频分量的融合规则设计(对PCNN进行改进，将区域改进拉普拉斯能量和作为改进PCNN的输入，采用一种改进的区域空间频率 ${F_{{\rm{MSF}}}}$ 并将其归一化作为改进PCNN的 $\beta $ 值)能够将隐藏的光谱细节信息挖掘并凸显出来，使得最后的融合图像涵盖更丰富的光谱信息。

为了能够客观地定量评价融合图像的效果，选取平均梯度、信息熵、相关系数、空间频率和光谱扭曲度作为客观定量评价指标(安振宇和史振威，2013)。平均梯度表征图像纹理的变化及细节的反差，其值越高则图像更清晰；信息熵用来衡量图像所携带的信息量，其值越大，图像携带的信息更多；相关系数体现了融合图像与多光谱图像的相关程度，其值越小，则融合图像的光谱信息相比源多光谱图像光谱信息的变化越大；图像的总体活跃程度可以通过空间频率来度量，其值越大，图像视觉效果更好；光谱扭曲度表示图像的光谱畸变程度，其值越小，说明图像失真越轻微。表1给出了上述6种融合方法对第1组图像的客观定量评价结果。

表 1 6种图像融合方法的定量评价结果
Table 1 Quantitative evaluation results of six image fusion methods

下载CSV

融合方法	波段	平均梯度	信息熵	相关系数	空间频率	光谱扭曲度
IHS变换方法	R	19.7148	7.3253	0.7263	26.4573	25.8817
	G	18.2596	7.5014	0.7552	24.6952	23.5544
	B	15.4998	7.4687	0.8453	21.5514	18.2749
NSCT和NMF方法	R	18.5418	7.4393	0.8413	24.3589	21.2594
	G	17.0986	7.3952	0.8639	22.5070	19.2081
	B	14.7535	7.4940	0.9245	19.6233	13.9206
NSCT和PCNN方法	R	21.1270	7.5586	0.7930	27.5982	23.1101
	G	19.4281	7.5237	0.8146	25.4923	20.9900
	B	16.1772	7.4803	0.8882	21.7991	16.0306
低频固定加权和高频改进PCNN方法	R	21.6652	7.5635	0.8150	28.3952	22.5109
	G	19.8382	7.5219	0.8367	26.1582	20.4289
	B	16.3980	7.4873	0.8976	22.2801	15.6879
低频改进加权和高频PCNN方法	R	21.6408	7.5661	0.8092	28.1582	22.1948
	G	19.8560	7.5244	0.8315	25.9705	20.1406
	B	16.4602	7.4837	0.8958	22.1535	15.4899
本文方法	R	21.6721	7.5624	0.8322	28.3985	21.0743
	G	19.9261	7.5204	0.8523	26.1607	19.1260
	B	16.6002	7.4883	0.9085	22.4182	14.6928

基于IHS变换的融合方法，运算时间最少，但光谱扭曲度最大。NSCT和NMF相结合的方法融合速度较慢，所得融合图像在相关系数指标上最高，但平均梯度和空间频率最低，这说明NMF算法能够有效提取图像整体特征，但在捕捉细节、纹理方面表现不佳。NSCT和PCNN相结合方法融合速度稍快，所得融合结果的平均梯度和空间频率较高，但相关系数较低，反映了该方法能提升图像的空间表现能力，但无法很好地保持图像的光谱信息。低频固定加权和高频改进PCNN方法融合速度稍快，其平均梯度和空间频率有所提高，但光谱扭曲度仍较高。低频改进加权和高频PCNN方法融合速度稍快，在光谱扭曲度指标上有所降低，但空间细节信息还有待增强。本文提出的融合方法与低频改进加权和高频PCNN方法所需时间相当，相比其他未优化的方法融合速度稍慢，但在融合效果上有较为明显的优势，尤其在平均梯度、空间频率、光谱扭曲度这3项指标上都表现最佳，表明图像的光谱信息得到了很好的保持，同时空间分辨率获得了有效提升。NSST能够更稀疏地表示图像信息，低频分量采用基于混沌蜂群优化的改进加权规则可以很好地保留多光谱图像丰富的光谱信息，高频分量利用改进的PCNN能够有效提升图像的空间分辨率，使得融合结果能够在保持光谱分辨率的同时，边缘、纹理等空间细节信息也有效注入融合图像。本文提出的基于混沌蜂群优化的NSST域图像融合方法与未使用优化的融合方法相比在融合效果上具有较为明显的优势，但这一优势是以牺牲运算时间为代价的，图像融合效果的提高更为关键。综合来看，本文方法在主观和客观方面的总体效果都要优于其他5种方法。

5 结　论

本文提出了基于混沌蜂群优化和改进PCNN的NSST域多光谱图像和全色图像融合方法。该方法利用了NSST的多尺度分解、分解后系数的稀疏性等性质，针对多光谱图像和全色图像的低频及高频分量的融合，在低频分量中，利用混沌蜂群优化算法在全局寻优中收敛精度高等特性，优化两幅源图像的加权系数；对高频分量采用改进的PCNN算法进行融合。大量实验结果表明，本文提出的图像融合方法在图像呈现出的边缘细节、光谱畸变等视觉效果及定量评价指标上均优于基于IHS变换、基于NSCT和NMF、基于NSCT和PCNN等方法，在进一步提升融合图像空间分辨率的同时，能更好地保留光谱信息，是一种行之有效的多光谱和全色图像融合方法。

参考文献(References)

An Z Y and Shi Z W. 2013. Hyperspectral image fusion via sc-NMF. Infrared and Laser Engineering, 42 (10): 2718–2723. [DOI: 10.3969/j.issn.1007-2276.2013.10.024] ( 安振宇, 史振威. 2013. 基于sc-NMF的高光谱图像融合. 红外与激光工程, 42 (10): 2718–2723. [DOI: 10.3969/j.issn.1007-2276.2013.10.024] )

Blasch E P. 1999. Biological information fusion using a PCNN and belief filtering//International Joint Conference on Neural Networks. Washington, DC: IEEE: 2792–2795 [DOI: 10.1109/IJCNN.1999. 833523]

Chien C L and Tsai W H. 2014. Image fusion with no gamut problem by improved nonlinear IHS transforms for remote sensing. IEEE Transactions on Geoscience Remote Sensing, 52 (1): 651–663. [DOI: 10.1109/TGRS.2013.2243157]

Da Cunha A L, Zhou J P and Do M N. 2006. The nonsubsampled contourlet transform: theory, design, and applications. IEEE Transactions on Image Processing, 15 (10): 3089–3101. [DOI: 10.1109/TIP.2006.877507]

Dong L M, Yang Q X, Wu H Y, Xiao H C and Xu M L. 2015. High quality multi-spectral and panchromatic image fusion technologies based on Curvelet transform. Neurocomputing, 159 (c): 268–274. [DOI: 10.1016/J.NEUCOM.2015.01.050]

Easley G, Labate D and Lim W Q. 2008. Sparse directional image representations using the discrete shearlet transform. Applied and Computational Harmonic Analysis, 25 (1): 25–46. [DOI: 10.1016/J.ACHA.2007.09.003]

Gao G R, Xu L P and Feng D Z. 2013. Multi-focus image fusion based on non-subsampled shearlet transform. IET Image Processing, 7 (6): 633–639. [DOI: 10.1049/IET-IPR.2012.0558]

Guo K H and Labate D. 2007. Optimally sparse multidimensional representation using shearlets. Siam Journal on Mathematical Analysis, 39 (1): 298–318. [DOI: 10.1137/060649781]

Guo L, Gong C and Zhao T Y. 2011. A new and effective multi-focus image fusion algorithm based on wavelet transforms and neighborhood features. Journal of Northwestern Polytechnical University, 29 (3): 454–459. ( 郭雷, 程塨, 赵天云. 2011. 基于小波变换和邻域特征的多聚焦图像融合算法. 西北工业大学学报, 29 (3): 454–459. )

Jiang N D, Wang Y N and Mao J X. 2008. Research on remote sensing image fusion based on Curvelet transform. Chinese Journal of Scientific Instrument, 29 (1): 61–66. ( 蒋年德, 王耀南, 毛建旭. 2008. 基于Curvelet变换的遥感图像融合研究. 仪器仪表学报, 29 (1): 61–66. )

Johnson J L and Padgett M L. 1999. PCNN models and applications. IEEE Transactions on Neural Networks, 10 (3): 480–498. [DOI: 10.1109/72.761706]

Karaboga D and Basturk B. 2007. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. Journal of Global Optimization, 39 (3): 459–471. [DOI: 10.1007/s10898-007-9149-x]

Kong W W, Wang B H and Lei Y. 2015. Technique for infrared and visible image fusion based on non-subsampled shearlet transform and spiking cortical model. Infrared Physics and Technology, 71 : 87–98. [DOI: 10.1016/j.infrared.2015.02.008]

Li X E, Ren J Y, Lv Z M, Sha W, Zhang L G and He B. 2013. Fusion method of multispectral and panchromatic images based on improved PCNN and region energy in NSCT domain. Infrared and Laser Engineering, 42 (11): 3096–3102. [DOI: 10.3969/j.issn.1007-2276.2013.11.040] ( 李新娥, 任建岳, 吕增明, 沙巍, 张立国, 何斌. 2013. NSCT域内基于改进PCNN和区域能量的多光谱和全色图像融合方法. 红外与激光工程, 42 (11): 3096–3102. [DOI: 10.3969/j.issn.1007-2276.2013.11.040] )

Liao Y, Huang W L, Shang L and Li P. 2014. Image fusion based on Shearlet and improved PCNN. Computer Engineering and Applications, 50 (2): 142–146. ( 廖勇, 黄文龙, 尚琳, 李鹏. 2014. Shearlet与改进PCNN相结合的图像融合. 计算机工程与应用, 50 (2): 142–146. )

Liu K and Li H H. 2013. An image fusion algorithm based on likelihood function of HMT in Contourlet domain. Journal of Optoelectronics: Laser, 24 (10): 2031–2037. ( 刘坤, 李晖晖. 2013. 基于Contourlet域HMT似然概率的图像融合方法. 光电子: 激光, 24 (10): 2031–2037. )

Song M X and Guo P. 2012. A combinatorial optimization method for remote sensing image fusion with Contourlet and HSI transform. Journal of Computer-Aided Design and Computer Graphics, 24 (1): 83–88. ( 宋梦馨, 郭平. 2012. 结合Contourlet和HSI变换的组合优化遥感图像融合方法. 计算机辅助设计与图形学学报, 24 (1): 83–88. )

Wu Y Q, Wu C and Wu S H. 2012. Fusion of multispectral image and panchromatic image based on NSCT and NMF. Journal of Beijing Institute of Technology, 21 (3): 415–420.

Xia Y and Qu S R. 2014. Color image fusion framework based on improved (2D)²PCA . Acta Optica Sinica, 34 (10): 69–76. ( 夏余, 曲仕茹. 2014. 改进(2D)²PCA的彩色图像融合框架 . 光学学报, 34 (10): 69–76. )

Yan J J, Xia C M and Zheng J R. 2007. Multi-spectral image and panchromatic image fusion method based on non-negative matrix factorization. Computer Engineering, 33 (21): 169–171. [DOI: 10.3969/j.issn.1000-3428.2007.21.060] ( 颜建军, 夏春明, 郑建荣. 2007. 基于NMF的多光谱图像和全色图像融合方法. 计算机工程, 33 (21): 169–171. [DOI: 10.3969/j.issn.1000-3428.2007.21.060] )

Zhang B H, Zhang C, Liu Y Y, Wu J S and He L. 2014. Multi-focus image fusion algorithm based on compound PCNN in Surfacelet domain. Optik-International Journal for Light and Electron Optics, 125 (1): 296–300. [DOI: 10.1016/j.ijleo.2013.07.002]

摘要

关键词