|
收稿日期: 2016-02-01; 修改日期: 2016-11-17; 优先数字出版日期: 2016-12-24
基金项目: 国家自然科学基金(编号:41171270);山东省杰出青年基金(编号:JQ201211);山东科技大学研究生科技创新基金(编号:YC150206)
第一作者简介: 贾臣(1991— ),男,硕士研究生,主要研究方向为气溶胶遥感。E-mail:jiachen_1991@163.com
中图分类号: TP701
文献标识码: A
|
摘要
针对传统气溶胶类型确定方法的局限性以及当前气溶胶类型确定存在的困难,提出一种使用多波段气溶胶光学厚度数据确定气溶胶类型的方法。基于大气颗粒物的散射与吸收特性分析,通过构建查找表的方法实现气溶胶类型的确定。该方法利用Mie散射理论通过正向模拟不同类型气溶胶粒子数量与多波段光学厚度之间的关系来构建查找表,基于该查找表,使用440 nm、670 nm、870 nm及1020 nm 4个波段的气溶胶光学厚度确定气溶胶类型。使用模拟的多波段气溶胶光学厚度数据开展了气溶胶类型的确定实验,分析了不同波段气溶胶光学厚度误差对气溶胶类型确定结果的影响。结果表明,该方法可根据4个波段的气溶胶光学厚度以较高的精度确定出沙尘性、水溶性和煤烟3种气溶胶粒子的数量,从而确定气溶胶类型。
关键词
气溶胶类型, 气溶胶光学厚度, Mie散射, 查找表方法
Abstract
The high-precision determination of aerosol models is crucial for analyzing the environmental impact of aerosols and for the remote sensing of Aerosol Optical Depth (AOD). However, the determination of aerosol type remains difficult, hence severely restricting highly accurate AOD retrieval and the application of aerosol optical products in environmental monitoring. A high-precision method for estimating aerosol models is proposed in this paper. The determination of aerosol type plays a vital role in the analysis of aerosol optical properties and is also an essential part of highly accurate AOD retrieval. Conventional methods, which utilize aerosol optical properties to determine aerosol types, are based on the relationship between the AOD of a single band and different aerosol types. However, due to the complex absorption and scattering properties of aerosols, it is difficult to obtain highly accurate aerosol types from AOD data with a single band. Hence, multiband AODs were introduced to enhance the accuracy of determining aerosol types. None the less, the current methods for estimating aerosol types with multiband AODs are iterative with complex and slow calculation processes. A new method to determine aerosol type with multiband AOD data was proposed to overcome the existing difficulties of current methods. Aerosol type is determined based on a lookup table, which is built using the forward simulation of relations between the particle numbers of different aerosol types and multiband AOD data based on Mie scattering theory. AOD at the wavebands of 440, 670, 870, and 1020 nm are adopted to determine aerosol type. The method was used to estimate aerosol types with multiband AOD. To evaluate the effectiveness of the proposed method, multiband AODs are simulated and applied in the validation experiment. Dust, water-soluble, and soot aerosol types are estimated with high precision. The effects of multiband AOD error on aerosol type determination are also analyzed. Results show that the proposed method can determine aerosol types with high stability. Compared with the current real-time determination method of aerosol types, the approach proposed in this paper is fast and can be used to estimate aerosol type from pixel-scale satellite data with multiband AODs. Furthermore, this method can improve the inversion accuracy of aerosol optical thickness, as well as promote the application of aerosol optical products in environmental pollution monitoring.
Key words
aerosol type, Aerosol Optical Depth (AOD), Mie-scattering, look-up table method
1 引 言
大气气溶胶通过直接吸收和散射太阳辐射,能够改变地气辐射传输能量平衡,影响全球或区域气候变化(Andreae和Crutzen,1997;Ramanathan 等,2001);粒径较小的气溶胶颗粒能够直接进入人体,对人体健康造成严重危害(Charlson 等,1992)。准确了解气溶胶空间分布对研究其气候效应、评价大气颗粒物污染等具有重要意义。
遥感技术可以在气溶胶监测中发挥重要作用,从而了解其气候和环境效应。气溶胶光学厚度AOD (Aerosol Optical Depth)是遥感监测气溶胶的一个重要的光学特性参量,而气溶胶类型是影响气溶胶光学厚度遥感反演精度以及基于光学厚度数据分析颗粒物污染的重要因素之一(Kaufman和Sendra,1988;King 等,1992)。故反演气溶胶光学厚度时,先确定与研究地区相符合的气溶胶类型是非常必要的。
1983年,国际大气物理协会提出标准辐射大气SRA (Standard Radiation Atmosphere)气溶胶模型(Deepak和Gerber,1983),SRA模型把对流层气溶胶按组成成分分为水溶性、沙尘性、海洋性和煤烟性4种粒子,同时定义了大陆型、城市/工厂型和海洋型3种基本气溶胶模型;D’Almeida等人(1991)在全球范围内总结气溶胶气候学,通过对大量数据的分析,列出与经度、纬度和季节有关的对流层气溶胶的主要类型,为不同地区气溶胶类型的选择提供了参考;MODIS数据在进行全球气溶胶光学厚度产品生产时,利用全球的AERONET站点地基观测数据,通过聚类分析得到不同季节的全球气溶胶类型分布(Levy,2007)。由于实时确定气溶胶类型比较困难,当前在气溶胶光学厚度遥感反演时,通常是依据区域的气候特点以及工业发展情况,参照SRA等现有的气溶胶模型来确定不同区域的气溶胶类型。气溶胶来源的复杂性,使得气溶胶类型处于不断地变化中,而不同的气溶胶类型对辐射的影响具有明显的差异(陈好 等,2013;王中挺 等,2012;Sun 等,2016)。研究表明,气溶胶的化学组分会决定了其吸湿性、光学特性等(Cappa 等,2011;Che 等,2015)。气溶胶的化学组分复杂,不同类型气溶胶可能包含无机化合物(硫酸盐、硝酸盐、氨、氢离子、水分)、元素碳及有机化合物等(美国环境保护局,2008),无机物、不吸光的有机物趋向于散射可见光,而元素碳、吸光的有机物具有强烈吸收太阳福射的能力。气溶胶类型的遥感研究很大程度上受限制于其化学组分的判定(Sreekanth,2014)。因此,依据区域和季节特点划分气溶胶类型不能真实反映出气溶胶类型的空间分布状况。实时的气溶胶类型确定对于提高气溶胶光学厚度的遥感反演精度具有重要的意义。
遥感方法的气溶胶类型确定主要是利用特定尺度范围内的气溶胶的光学特性,但气溶胶的空间分布和传输过程具有很大的不确定性,其特定尺度范围内的光学特性因环境条件差异会急剧变化(Nicolae 等,2015)。同时,气溶胶光学特性的获取受很大限制:遥感的方法受限于精度,而地基设备测量受限于空间覆盖率(Tan 等,2015),故利用气溶胶的光学特性实现气溶胶类型的实时确定,存在一定困难和挑战。在气溶胶类型的实时确定方面国内外众多学者开展了大量的研究。Kaskaoutis等人(2007;2009)选择长时间序列的AERONET站点实测AOD和Ångström指数数据,对二者关系进行协同分析,通过统计分析设置不同气溶胶类型对应的AOD和Ångström指数阈值,实现了Alta Floresta等地区的气溶胶类型确定工作,并对气溶胶类型的季节变化进行分析。在Kaskaoutis等人(2007;2009)方法的基础上,Pathak等人(2012)、Rama等人(2015)、Tan等人(2015)结合不同地区的气溶胶光学特性分析,确定出Dibrugarh、Anantapur、Singapore等地区自定义的气溶胶类型。Lee等人(2010)对不同气溶胶的散射、吸收等光学特性差异进行分析,利用单次散射反照率(SSA)来区分吸收和非吸收特性气溶胶,利用细粒子百分比(FMF)来确定气溶胶模式中占主导地位的为粗粒子或细粒子,最后,运用单次散射反照率和细粒子百分比将陆地气溶胶分为沙尘、强散射类型细粒子为主、弱吸收类型细粒子等7种气溶胶类型。Srivastava等人(2014)运用Lee等人(2010)的方法,确定出2009年Delhi地区的4种气溶胶类型:污染的沙尘型(48%)、污染的大陆型(32%)、黑碳为主(11%)、有机碳为主(9%)。Amiridis等人(2011)应用拉曼激光雷达对2001年—2005年Thessaloniki的气溶胶进行观测,得到实测站点的后向散射率(LR),并通过辐射传输计算对应时间的单次散射反照率(SSA),选择有效的LR和SSA数据绘制散点图,结合气溶胶来源的分析,确定不同气溶胶类型对应LR和SSA的阈值,实现Thessaloniki地区气溶胶类型确定。Kumar等人(2015)联合应用2003年—2013年的MODIS、MISR和OMI卫星数据,分析气溶胶特性,分析了AOD、Ångström指数(AE)、气溶胶指数(AI)的月份、季节变化,最终通过设置AOD和AE的阈值,确定出Durban地区不同季节的5种气溶胶类型:海洋型、大陆型、生物燃烧和城市混合型、沙尘型、混合型。在国内,胡方超等人(2009)联合应用MODIS遥感数据和太阳光度计CE318数据,结合地面准同步的光谱测量,确定出太湖地区不同季节的气溶胶类型。范娇等人(2015)基于实际观测的气溶胶浓度比例,提出了一种气溶胶各组分体积百分比确定的数学模型,得到了杭州地区自定义的气溶胶类型。
当前基于气溶胶光学特性确定气溶胶类型的方法,主要是基于单波段气溶胶光学厚度或单一气溶胶光学参数与不同气溶胶类型的相关参数构建相关模型,从而确定出气溶胶类型,而由于气溶胶散射及吸收特性的复杂性,单一波段或单一参数难以精确表达不同气溶胶类型体现出的综合的光学特性。所以多波段气溶胶光学参数的应用有助于提高气溶胶类型的确定精度,胡方超等人(2009)开展了类似的研究,但使用的是迭代求解的计算方法,该方法但计算过程较为复杂、迭代运算较多,计算速度较慢,应用受到很大的局限。
针对上述问题,本文以气溶胶光学厚度的计算表达式为基础,分析并建立不同类型的气溶胶粒子数量与多波段气溶胶光学厚度之间的对应关系。基于Mie散射理论和气溶胶的相关物理性质,通过正向模拟,构建气溶胶粒子数量与气溶胶光学厚度的查找表。考虑到既保证查找表精度,又避免过分冗余造成计算效率降低,选择440 nm、670 nm、870 nm及1020 nm 4个波段的气溶胶光学厚度构建查找表。通过该查找表实现了基于多波段气溶胶光学厚度的气溶胶类型确定方法,确定出沙尘性、水溶性和煤烟3种气溶胶粒子的数量。
2 原理与方法
气溶胶光学厚度定义为介质的消光系数在垂直方向上的积分,表征气溶胶粒子对光的削弱作用,考虑k个波段,波长λk处气溶胶光学厚度,由下式计算得出:
| $\begin{aligned}{\rm{\tau }}\left( {{\lambda _k}} \right) = & \mathop \sum \limits_{i = 1}^3 \int\limits_{{r_{\rm{min}}}}^{{r_{\rm{max}}}} {{n_i}\left( r \right)\pi {r^2}{Q_{\rm{ext}}}\left( {r,{\lambda _k}} \right)} {\rm d}r = \\ &\mathop \sum \limits_{i = 1}^3 {n_i}\int\limits_{{r_{\rm{min}}}}^{{r_{\rm{max}}}} {{f_i}\left( r \right)\pi {r^2}{Q_{\rm{ext}}}\left( {r,{\lambda _k}} \right)} {\rm d}r\end{aligned}$ | (1) |
式中,Qext(r,λk)为气溶胶的消光效率因子,可通过Mie散射计算得出;r为粒子半径,ni(r)为气溶胶尺度分布,fi(r)为谱分布函数,为重要的气溶胶物理性质。式(1)说明不同类型气溶胶粒子数量与多波段光学厚度之间存在对应关系,通过正向模拟这种关系,构建关于光学厚度与气溶胶粒子数量的查找表,可实现气溶胶类型的确定。但确定气溶胶类型,首先需要确定Qext(r,λk)、r、ni(r)和fi(r)4个参数。
2.1 Mie散射理论的计算
Qext(r,λk)为气溶胶的消光效率因子,表示为:
| ${Q_{{\rm{ext}}}}\left( {r,{\lambda _k}} \right) = \frac{2}{{{\alpha ^2}}}\mathop \sum \limits_{n = 1}^\infty \left( {2n + 1} \right)Re\left( {{a_n} + {b_n}} \right)$ | (2) |
式中,an、bn为Mie散射系数。Qext(r,λk)及an、bn可根据Mie散射理论计算得到。Mie散射(Mie,1908)是粒子散射相关计算最常用、最基础的算法,是麦克斯韦方程对处在均匀介质中的均匀颗粒在平面单色波照射下的严格数学解。对所有的微粒尺度和任何波长,Mie散射的角度特性用两个强度分布函数i1和i2表示,其函数为
| ${i_1}\left( {\alpha ,m,\theta } \right) = {\left| {{S_1}} \right|^2} = {\left| {\sum\limits_{n = 1}^\infty {\frac{{2n + 1}}{{n\left( {n + 1} \right)}}\left( {{a_n}{\pi _n} + {b_n}{\tau _n}} \right)} } \right|^2}$ | (3) |
| ${i_2}\left( {\alpha ,m,\theta } \right) = {\left| {{S_2}} \right|^2} = {\left| {\sum\limits_{n = 1}^\infty {\frac{{2n + 1}}{{n\left( {n + 1} \right)}}\left( {{a_n}{\tau _n} + {b_n}{\pi _n}} \right)} } \right|^2}$ | (4) |
式中,S1和S2为散射波的无量钢复振幅值,an、bn是复振幅系数,an、bn、
| ${a_n} = \frac{{{\varphi _n}(\alpha ){{\varphi '}_n}(m\alpha ) - m{{\varphi '}_n}(\alpha )\varphi (m\alpha )}}{{{\xi _n}(\alpha ){{\varphi '}_n}(m\alpha ) - m{{\xi '}_n}(\alpha )\varphi (m\alpha )}}$ | (5) |
| ${b_n} = \frac{{m{\varphi _n}(\alpha ){{\varphi '}_n}(m\alpha ) - {{\varphi '}_n}(\alpha ){\varphi _n}(m\alpha )}}{{m{\xi _n}(\alpha ){{\varphi '}_n}(m\alpha ) - {{\xi '}_n}(\alpha ){\varphi _n}(m\alpha )}}$ | (6) |
| ${\pi _n} = {p_n}({\rm{cos}}\theta )/{\rm{sin}}\theta $ | (7) |
| ${\tau _n} = \frac{d}{{d\theta }}{p_n}({\rm{cos}}\theta )$ | (8) |
| ${\varphi _n}(\alpha ) = {(\frac{{\alpha {\rm{\pi }}}}{2})^{\frac{1}{2}}}{J_n}(\alpha )$ | (9) |
| ${\xi _n}(\alpha ) = {(\frac{{\alpha {\rm{\pi }}}}{2})^{\frac{1}{2}}}{H_n}(\alpha ) = {(\frac{{\alpha {\rm{\pi }}}}{2})^{\frac{1}{2}}}\left[ {{J_n}(\alpha ) + {\rm i}{Y_n}(\alpha )} \right]$ | (10) |
式中,Jn(α)、Yn(α)、Hn(α)分别为第1类贝塞尔函数、第2类贝塞尔函数和汉克尔函数,pn为勒让德函数。α=2
2.2 气溶胶的物理性质
2.2.1 气溶胶粒子谱分布
气溶胶尺度分布ni(r)是气溶胶非常重要的物理性质,是研究大气气溶胶对大气辐射传输影响的重要参数。对于大气气溶胶中的沙尘性、水溶性、煤烟3种粒子,若每种成分总粒子数为ni(沙尘性为n1,水溶性为n2,煤烟为n3),谱分布函数对应为fi(r),假设谱分布函数与高度无关,则有:
| ${n_i}\left( r \right) = {n_i}{f_i}\left( r \right)$ | (11) |
通常采用对数正态分布来描述气溶胶粒子的尺度谱(Lekhtmakher和Shapiro,2005),则谱分布函数为
| ${f_i}\left( r \right) = \frac{1}{{r\sqrt {2{\rm{\pi }}} {\rm{ln}}{\sigma _i}}}\exp \left[ { - \frac{{{{({\rm{ln}}r - {\rm{ln}}{R_i})}^2}}}{{2{{({\rm{ln}}{\sigma _i})}^2}}}} \right]$ | (12) |
式中,Ri为第i种粒子的中值半径,lnσi是第i种粒子lnr的标准差,均为常数。这些常数值可在SRA气溶胶模型对数正态分布的参数表中查找,进而确定出谱分布函数。不同类型气溶胶的中值半径、标准差不同,使得谱分布函数不同,故粒子谱会存在差异。
2.2.2 复折射指数
在Mie散射理论的计算中,需确定气溶胶粒子的复折射指数,沙尘性、水溶性、煤烟粒子的复折射指数均可在SRA气溶胶模型中进行确定。复折射指数一般记为m=mr+imi,表征气溶胶粒子对辐射的吸收和散射作用,其中实部mr代表了对辐射的散射作用、虚部mi代表吸收作用。
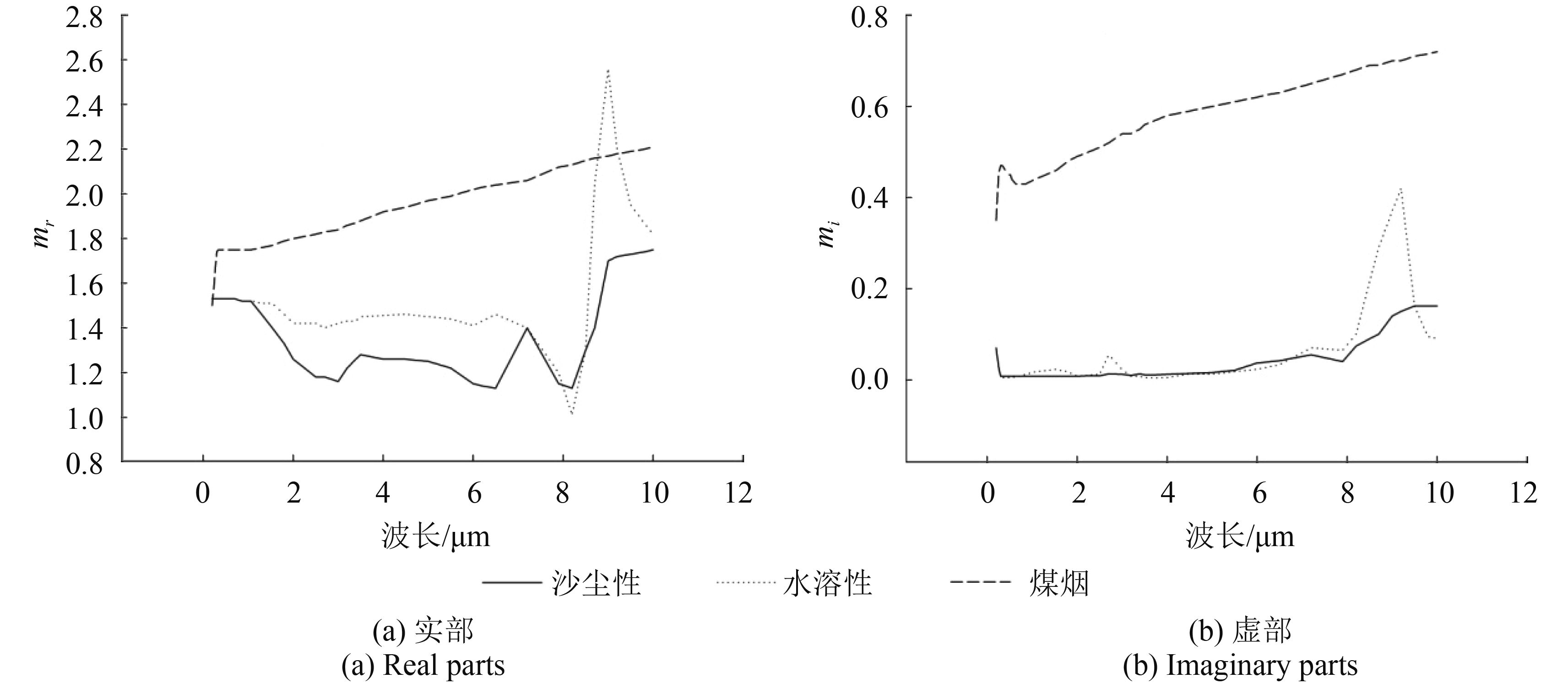
复折射指数由构成气溶胶粒子的化学组成决定。不同类型气溶胶的复折射指数变化很大,造成了不同种类的气溶胶对太阳和长波辐射的吸收和散射特性的不同。同时,大部分气溶胶的复折射指数是波长的函数,图1为沙尘性、水溶性、煤烟气溶胶的复折射指数随波长的变化情况。
从图1可以看出,气溶胶粒的复折射指数具有较为明显的波长依赖关系。在可见光到近红外波段,气溶胶复折射指数随波长的变化比较平缓;相反,在中远红外波段,随波长的变化起伏剧烈;煤烟具有最大的复折射指数,特别是虚部,说明它的吸收作用明显大于其他气溶胶粒子;除煤烟外,在可见光和近红外波段,气溶胶粒子的虚部极小,但随着波长的变化,虚部显著增大,该些粒子对长波辐射的吸收特性显著增大。
3 查找表构建
3.1 查找表法原理
根据式(1),理论上可由观测得到的k个波段的气溶胶光学厚度(记为τk),确定出各成分的粒子总数(记为ni)。选取440 nm、670 nm、870 nm及1020 nm 4个波段的气溶胶光学厚度数据τk=1,4,可建立关于ni=1,3(沙尘性为n1,水溶性为n2,煤烟为n3)的方程组:
| ${\tau _{k = 1,4}} = \mathop \sum \limits_{i = 1}^3 {n_i}\mathop \smallint \limits_{{r_{{\rm{min}}}}}^{{r_{{\rm{max}}}}} {f_i}\left( r \right){\rm{\pi }}{r^2}{Q_{\rm{ext}}}\left( {r,{\lambda _k}} \right){\rm{d}}r$ | (13) |
设
| ${\tau _{k = 1,4}} = \mathop \sum \limits_{i = 1}^3 {n_i}{A_{ik}}$ | (14) |
该方程组有4个方程、3个未知数ni=1,3,其中的Aik可根据气溶胶物理性质和Mie散射理论的相关计算得出,故该方程组是一个超定方程组。超定方程组可以利用数学方法中的最小二乘法求解。但经实践证明,利用最小二乘法对该方程组求解得到的结果ni,经常出现无意义的负值,方程组是无法直接求解的。
分析该方程组发现,若已知ni=1,3,通过式(14)可计算对应的τk=1,4,说明对于任意的ni=1,3,有唯一的τk=1,4与其对应。故可以通过正向模拟,及给出所有气溶胶类型组合下的ni=1,3并通过式(14)计算τk=1,4,建立二者之间的查找表,利用查找表方法可实现多波段光学厚度确定粒子数量。
但考虑到气溶胶类型组合的复杂性,建立查找表存在困难。故考虑利用相关变量代替气溶胶粒子数量和光学厚度建立查找表,以简化计算过程和查找表。所以引入气溶胶粒子总数和沙尘性、水溶性、煤烟粒子占总数的比例,并引入每个波段光学厚度占4个波段光学厚度总和的比例,研究它们之间的关系并建立查找表。
假设气溶胶总粒子数为N,3种气溶胶占总数比例分别为
| $\mathop \sum \limits_{i = 1}^3 {p_{{n_i}}} = 1$ | (15) |
| ${n_i} = {p_{{n_i}}}N$ | (16) |
假设每个波段光学厚度占4个波段光学厚度总和的比例pτk,则有:
| ${p_{{\tau _k}}} = \frac{{{\tau _k}}}{\displaystyle{\sum\limits_{k = 1}^4 {{\tau _k}} }}$ | (17) |
| $\mathop \sum \limits_{k = 1}^4 {p_{{\tau _k}}} = 1$ | (18) |
利用pni对式(14)进行变换可得:
| ${\tau _{k = 1,4}} = \mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}N{A_{ik}} = N\mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}{A_{ik}}$ | (19) |
根据上式,τk=1,4和
| ${\tau _1}\!:\!{\tau _2}\!:\!{\tau _3}\!:\!{\tau _4} = \mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}{A_{i1}}\!:\!\mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}{A_{i2}}\!:\!\mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}{A_{i3}}\!:\!\mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}{A_{i4}}$ | (20) |
显然有
| $\begin{aligned}& {p_{{\tau _1}}}:{p_{{\tau _2}}}:{p_{{\tau _3}}}:{p_{{\tau _4}}} = \\ & \mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}{A_{i1}}:\mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}{A_{i2}}:\mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}{A_{i3}}:\mathop \sum \limits_{i = 1}^3 {p_{{n_i}}}{A_{i4}}\end{aligned}$ | (21) |
上式说明
3.2 查找表构建方法
本文构建的气溶胶类型查找表共包含7个变量,分别为440 nm、670 nm、870 nm及1020 nm 4个波段的气溶胶光学厚度占总气溶胶光学厚度的比例
首先模拟不同类型组合的
但查找表构建的关键在于对
根据SRA模型,在一般情况下,大陆地区沙尘性、水溶性、煤烟3种气溶胶成分按一定数密度百分比组成如表1所示。
表 1 对流层的SRA大陆气溶胶模型
Table 1 Tropospheric continental aerosol model (SRA)
| /% | |||
| 成分 | 沙尘性 | 水溶性 | 煤烟 |
| 数浓度百分比 | 2.27×10–4 | 93.876 | 6.123 |
表1给出的是典型情况,然而大气气溶胶的成分和比例是随时间和地点而变化的,但整体变化不大,可以假设沙尘性的比例不会超过0.1%,煤烟性的比例不会超过10%,且3种粒子的比例都大于0。故
| $\left\{ {\begin{array}{*{20}{c}}{0 < {p_{{n_1}}} \leqslant 0.1\% }\\{0 < {p_{{n_2}}} < 100\% }\\{0 < {p_{{n_3}}} \leqslant 10\% }\\{{p_{{n_1}}} + {p_{{n_2}}} + {p_{{n_3}}} = 100\% }\end{array}} \right.$ | (22) |
根据约束条件,设置粒子比例最大值的1/1000作为步长,在区间(0,0.1%]上以步长0.001%取点作为
根据设置的约束条件和步长,模拟不同类型组合的
3.3 查找方法
对于一组光学厚度值τk=1,4,通过查找表进行查找确定气溶胶粒子比例
利用式(17)由τk=1,4计算出
| $R = \mathop \sum \limits_{k = 1}^4 {(p_{{\tau _k}}' - {p_{{\tau _k}}})^2}$ | (23) |
4 实验结果与分析
4.1 实验过程
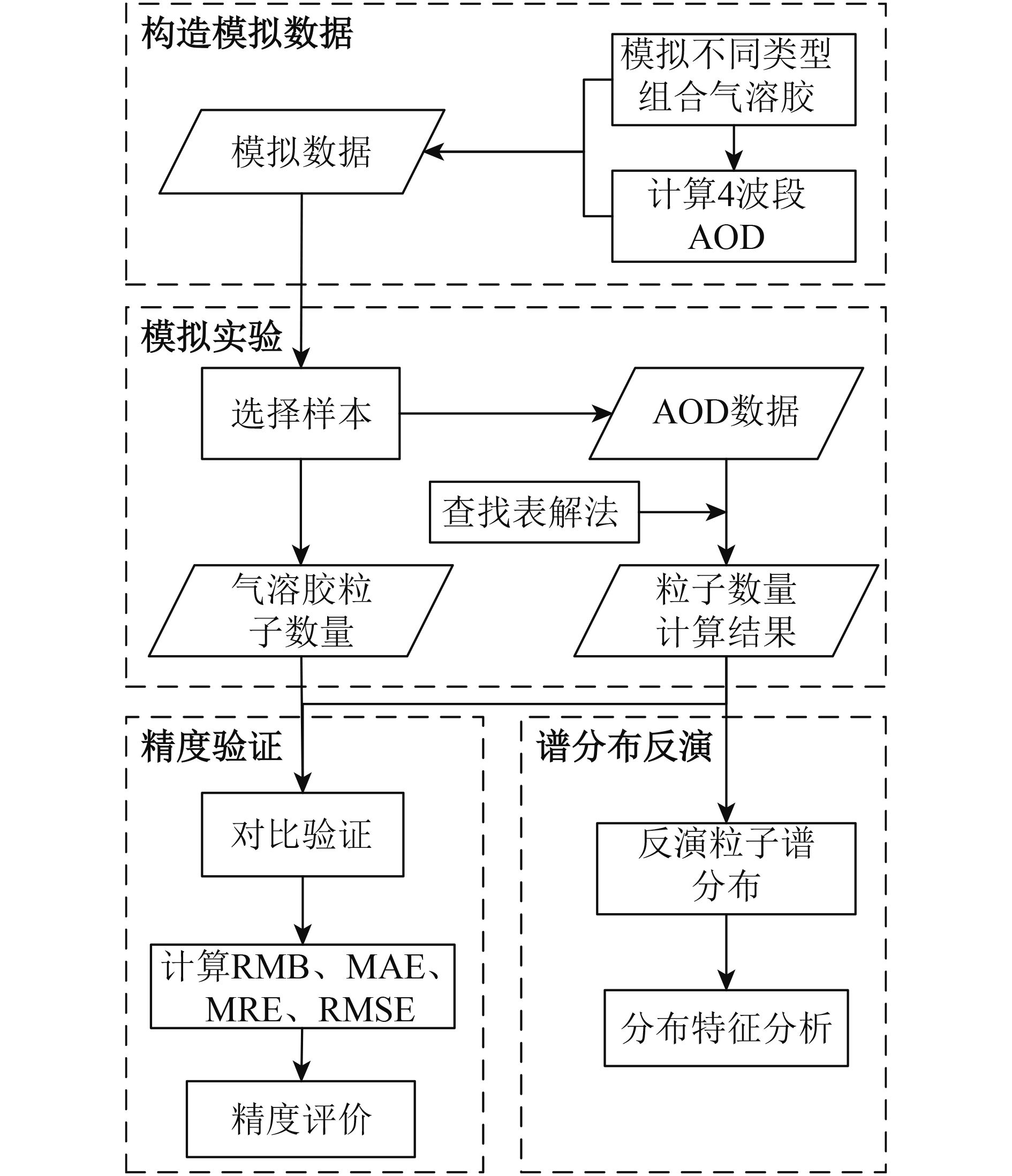
为验证方法的有效性,构造模拟数据进行实验,对气溶胶类型确定方法进行验证,实验的流程图如图2所示。
首先,根据光学厚度有效值的范围,设定沙尘性、水溶性、煤烟3种气溶胶粒子数量的最小值
然后,从模拟数据中随机选择样本。根据样本中的AOD数据,依查找表解法求解气溶胶粒子数量并与样本中的粒子数量数据对比验证,进行精度评价。同时根据粒子数量计算结果,反演粒子谱分布,对比分析3种粒子的分布特征。
最后,分析算法的稳定性;并进行误差分析,分析不同波段的气溶胶光学厚度误差对不同气溶胶类型确定的影响。
4.2 实验结果
从模拟数据中随机选取500组样本对本文方法进行验证。根据光学厚度τk,计算3种粒子的数量ni,与模拟数据中气溶胶粒子数量验证。选取RMB、平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)4个指标,验证计算结果的精度。RMB、MAE、MRE、RMSE的计算式如下:
| ${\rm{RMB}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{n_{({\rm{retrievals}})i}}/{n_{({\rm{data}})i}}} \right|} $ | (24) |
| ${\rm{MAE}} = \frac{{\rm{1}}}{n}\sum\limits_{i = 1}^n {\left| {{n_{({\rm{retrievals}})i}} - {n_{({\rm{data}})i}}} \right|} $ | (25) |
| ${\rm{MRE}} = \frac{{\rm{1}}}{n}\sum\limits_{i{\rm{ = 1}}}^n {(\left| {{n_{({\rm{retrievals}})i}} - {n_{({\rm{data}})i}}} \right|/{n_{({\rm{data}})i}})} $ | (26) |
| ${\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {({n_{({\rm{retrievals}})i}} - {n_{({\rm{data}})i}})} } $ | (27) |
式中,n=500,为样本个数;n(retrievals)i为反演的粒子数量;n(data)i模拟数据中粒子数量。计算500组样本数据的RMB、MAE、MRE、RMSE,结果如下表。
表 2 样本数据结果精度验证
Table 2 Accuracy of sample data results
| 气溶胶粒子 | 样本个数(n) | RMB | MAE | MRE | RMSE |
| 沙尘性 | 500 | 1.0011 | 97.76 | 1.34×10–3 | 3.83×10–3 |
| 水溶性 | 500 | 1.0028 | 1787535 | 3.27×10–3 | 5.44×10–3 |
| 煤烟 | 500 | 0.9942 | 411002 | 6.76×10–3 | 1.12×10–3 |
| 总粒子 | 500 | 1.0011 | 1378857 | 2.46×10–3 | 3.83×10–3 |
由表2可以看出,计算得到的沙尘性、水溶性、煤烟粒子的RMB分别为1.0011、1.0058、0.9942,都接近于1;3种气溶胶粒子及总粒子的MRE小于0.01,RMSE小于0.02,MRE和RMSE整体较小;然而除沙尘性粒子以外,MAE相对较大,原因是气溶胶粒子数量的数量级较大。整体来看,基于查找表方法,使用多波段气溶胶光学厚度确定得到的粒子数量精度较高,能够较为准确地反映出气溶胶类型的组合。说明该方法可以用于多波段光学厚度的气溶胶类型识别。
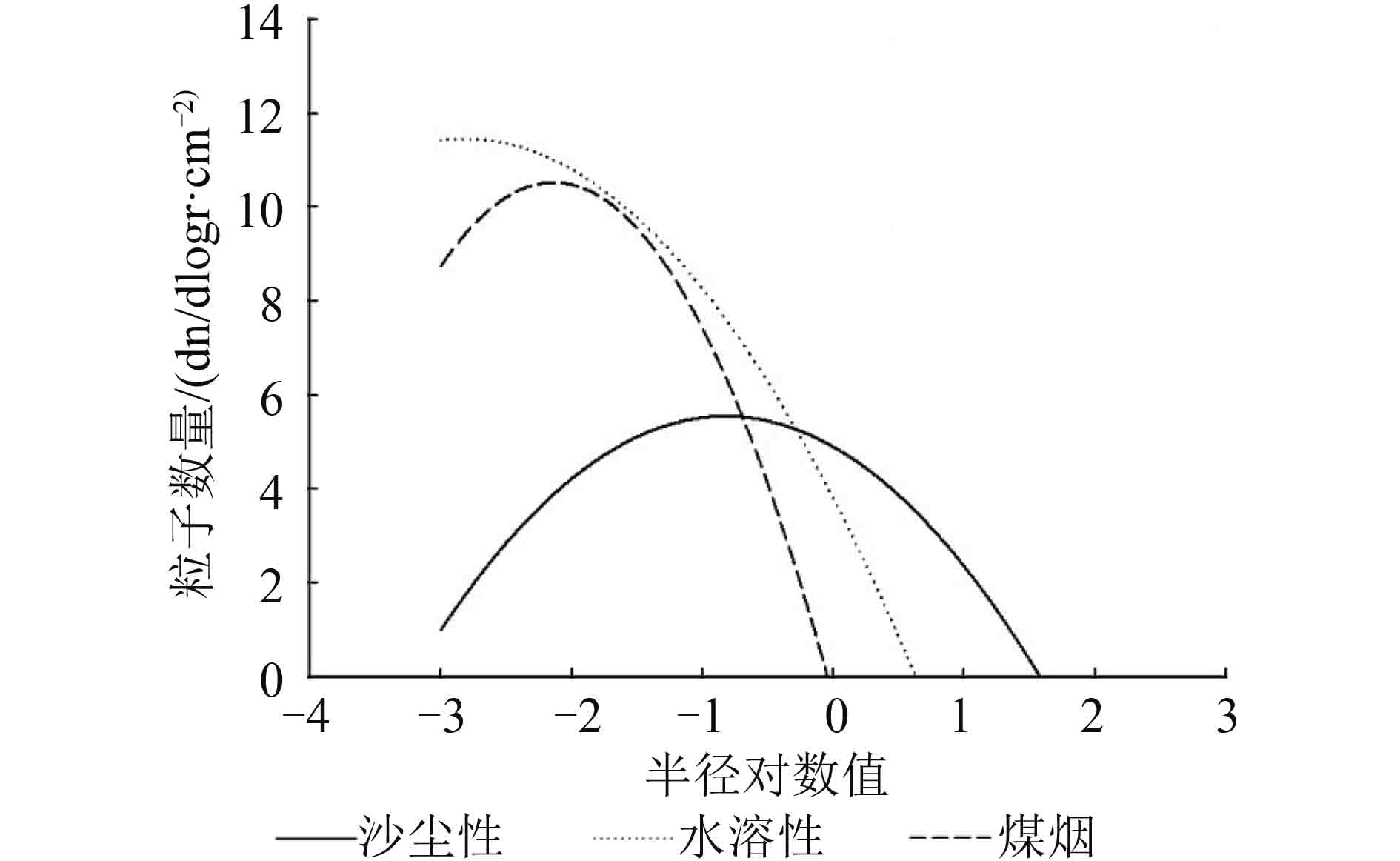
选取某样本数据及其计算结果,根据对数正态分布函数,计算得出不同类型气溶胶的粒子谱分布,并分析粒子谱的差异。图3为沙尘性、水溶性、煤烟型3种气溶胶的数浓度粒子谱分布图,由于气溶胶粒子的尺度跨几个量级且粒子数量很大,故采用对数坐标。
对比不同粒子的谱分布,可得到3种粒子的半径大小范围(表3)。沙尘性粒子的半径分布范围最广,但粒子总数量最低,粒子谱峰值在中值半径(r)为0.5 μm左右,说明煤烟粒子的大部分集中分布在r=0.5 μm左右;煤烟型粒子的半径分布范围最窄,且集中分布在r≤0.01 μm的范围内,说明煤烟型粒子的半径较小;水溶性粒子总数量最大,粒子谱的峰值在r=0.005 μm左右,说明水溶性粒子大部分集中分布在半径很小的范围内。
表 3 沙尘性、水溶性、煤烟气溶胶粒子半径的大小范围
Table 3 Radius range of atmospheric aerosol particles
| /μm | |||
| 气溶胶类型 | 沙尘性 | 水溶性 | 煤烟 |
| 半径范围 | 10–3—102 | 10–3—10 | 10–3—1 |
4.3 算法稳定性分析
设计实验对算法稳定性进行分析。对样本数据中的光学厚度设定一定数值的相对误差(分别取1%、3%、5%、10%、20%、30%、40%和50%)。根据携带误差的光学厚度,计算3种粒子的数量ni,与模拟数据中气溶胶粒子数量验证。并计算平均相对误差(MRE)指标,验证计算结果的精度。MRE结果如表4所示。
表 4 平均相对误差(MRE)结果
Table 4 The result of Mean Relative Error (MRE)
| /(%) | ||||||||
| 光学厚度相对误差值 | 1 | 3 | 5 | 10 | 20 | 30 | 40 | 50 |
| 沙尘性粒子数量MRE | 1.14 | 3.13 | 5.14 | 10.15 | 20.16 | 30.18 | 40.19 | 50.20 |
| 水溶性粒子数量MRE | 1.34 | 3.35 | 5.36 | 10.37 | 20.41 | 30.44 | 40.48 | 50.51 |
| 煤烟粒子数量MRE | 0.88 | 2.38 | 4.26 | 9.22 | 19.15 | 29.07 | 39.00 | 48.93 |
| 粒子总数量MRE | 1.24 | 3.24 | 5.25 | 10.26 | 20.28 | 30.30 | 40.33 | 50.35 |
由表4可知,随着光学厚度误差的增长,粒子数量的误差没有无限增长,并得到一定的控制,证明算法是稳定的。即光学厚度的误差在一定范围之内,粒子数量的计算结果是可接受的。算法的稳定性说明本文方法可以较高精度计算气溶胶粒子数量,确定气溶胶类型。
4.4 误差分析
若气溶胶光学厚度存在误差,会造成反演出的气溶胶粒子数量出现一定偏差,影响气溶胶类型的确定精度,因此,分析不同波段的气溶胶光学厚度误差对不同气溶胶类型确定的影响是必要的。
设第k个波段光学厚度误差为ετk,ετk对第i种粒子数量的计算结果所造成的误差最大值为εik,根据式(16)可得两者之前存在如下关系
| ${\varepsilon _{ik}}{A_{ik}} = {\varepsilon _{{\tau _k}}}$ | (28) |
式中,Aik的值用矩阵形式表示如下:
| ${ A} \!\! = \!\! \left[ {\begin{array}{*{20}{l}}\!\!\!\! {2.51 \times {{10}^{ - 6}}} \!\!&\!\! {2.62 \times {{10}^{ - 6}}} \!\!&\!\! {2.78 \times {{10}^{ - 6}}} \!\!&\!\! {2.94 \times {{10}^{ - 6}}} \!\!\!\! \\\!\!\!\! {1.34 \times {{10}^{ - 9}}} \!\!&\!\! {5.89 \times {{10}^{ - 10}}} \!\!&\!\! {3.73 \times {{10}^{ - 10}}} \!\!&\!\! {3.01 \times {{10}^{ - 10}}} \!\!\!\! \\\!\!\!\! {6.34 \times {{10}^{ - 9}}} \!\!&\!\! {3.25 \times {{10}^{ - 9}}} \!\!&\!\! {2.27 \times {{10}^{ - 9}}} \!\!&\!\! {1.90 \times {{10}^{ - 9}}} \!\!\!\! \end{array}} \right]$ | (29) |
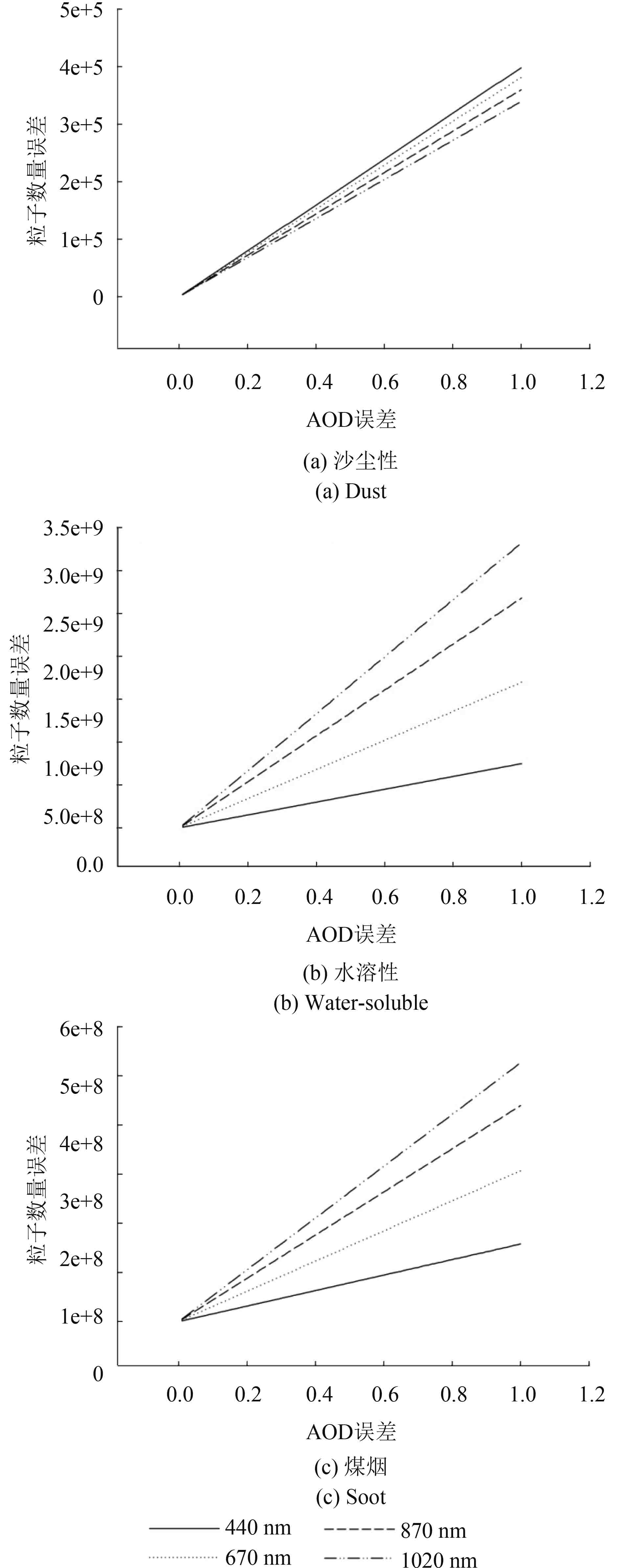
根据式(28),计算不同波段光学厚度的误差在0.1—1之间变化时,对不同类型粒子数量的计算结果造成误差最大值的变化,图4为计算结果误差随光学厚度误差的变化,
由图4可知,3种粒子计算结果受不同波段光学厚度误差的影响程度是不同的。当气溶胶光学厚度的误差在0.1—1之间时,沙尘性粒子的误差均在105的数量级上,4个波段的差别不大;而水溶性和煤烟粒子的情况比较相似,随着波长的降低,粒子的误差逐渐降低,且4个波段的误差相差较大,其中1020 nm处气溶胶光学厚度的误差所造成的两种粒子数量误差分别达到了109和108数量级。
整体来看,440 nm处气溶胶光学厚度的误差对沙尘性粒子数量的确定造成较大的误差;1020 nm处气溶胶光学厚度误差对水溶性、煤烟粒子数量确定造成的误差较大;而670 nm和870 nm介于之间。这说明气溶胶光学厚度的精度对气溶胶类型的确定有重要影响。
5 结 论
本文分析了不同类型气溶胶粒子数量与多波段光学厚度之间的关系,引入两者对应的比例参与相关计算。根据气溶胶光学厚度的计算表达式,建立粒子数量比例与气溶胶光学厚度比例间的对应关系,基于Mie散射理论和气溶胶的物理性质通过正向模拟两者间关系构建气溶胶类型确定的查找表。在查找表构建过程中,依据SRA模型针对临界情况设置控制条件,并设置合适步长对气溶胶粒子数量比例取值,考虑到了不同组合的气溶胶类型,在保证一定精度的前提下,简化查找表以提高计算速度。通过查找表的方法实现多波段光学厚度确定气溶胶类型,可根据440 nm、670 nm、870 nm及1020 nm 4个波段的光学厚度确定出沙尘性、水溶性和煤烟3种气溶胶粒子的数量。
构造模拟数据进行实验,对气溶胶类型确定方法进行验证。结果表明本文提出的气溶胶类型确定方法能够以较高精度确定气溶胶粒子数量,较为准确的得出气溶胶类型的组合。同时通过计算不同波段光学厚度的误差在0.1—1之间变化时,对不同类型粒子数量的计算结果造成误差最大值的变化,得出不同波段气溶胶光学厚度误差对3种粒子造成的影响程度有所差异。说明气溶胶光学厚度的精度对气溶胶类型的确定影响较大。
本文提出的气溶胶类型确定方法克服了传统气溶胶类型确定方法的局限性,实现了气溶胶类型的实时确定。基于气溶胶的光学特性确定类型,理论上比SRA等现有气溶胶模型更加符合实际地区情况。与现有的基于地基测量和卫星遥感数据的实时气溶胶类型确定方法相比,对数据的要求低,根据4个波段的气溶胶光学厚度数据即可实现不同地区的气溶胶类型确定;通过查找表的方法实现,保证较高精度且计算速度较快。本研究下一步的主要内容为利用更多实测数据对方法进行验证和改进。
参考文献(References)
-
Andreae M O and Crutzen P J. 1997. Atmospheric aerosols: biogeochemical sources and role in atmospheric chemistry. Science, 276 (5315): 1052–1058. [DOI: 10.1126/science.276.5315.1052]
-
Cappa C D, Che D L, Kessler S H, Kroll J H and Wilson K R. 2011. Variations in organic aerosol optical and hygroscopic properties upon heterogeneous OH oxidation. Journal of Geophysical Research: Atmospheres, 116 (D15): D15204 [DOI: 10.1029/2011JD015918]
-
Charlson R J, Schwartz S E, Hales J M, Cess R D, Coakley Jr J A, Hansen J E and Hofmann D J. 1992. Climate forcing by anthropogenic aerosols. Science, 255 (5043): 423–430. [DOI: 10.1126/science.255.5043.423]
-
Che H Z, Zhao H J, Wu Y F, Xia X G, Zhu J, Dubovik O, Estelles V, Ma Y J, Wang Y F, Wang H, Wang Y Q, Zhang X Y and Shi G Y. 2015. Application of aerosol optical properties to estimate aerosol type from ground-based remote sensing observation at urban area of northeastern China. Journal of Atmospheric and Solar-Terrestrial Physics, 132 : 37–47. [DOI: 10.1016/j.jastp.2015.06.015]
-
Chen H, Gu X F, Cheng T H, Yu T and Li Z Q. 2013. Characteristics of aerosol types over China. Journal of Remote Sensing, 17 (6): 1559–1571. [DOI: 10.11834/jrs.2013r13028] ( 陈好, 顾行发, 程天海, 余涛, 李正强. 2013. 中国地区气溶胶类型特性分析. 遥感学报, 17 (6): 1559–1571. [DOI: 10.11834/jrs.2013r13028] )
-
D’Almeida G A, Koepke P and Shettle E P. Atmospheric Aerosols: Global Climatology and Radiative Characteristics. Hampton, Va: A Deepak Pub, 1991.
-
Deepak A and Gerber H.1983. Report of the Experts Meeting on Aerosols and their Climatic EffectsWilliamsburg, VA, 28-30March 1983. Williamsburg: World Meteorological Organization, 1983.
-
Du H. 2004. Mie-scattering calculation. Applied Optics, 43 (9): 1951–1956. [DOI: 10.1364/AO.43.001951]
-
Fan J, Guo B F and He H C. 2015. Retrieval of aerosol optical thickness with MODIS data over Hangzhou. ActaOpticaSinica, 35 (1): 101001 [DOI: 10.3788/AOS201535.0101001] ( 范娇, 郭宝峰, 何宏昌. 2015. 基于MODIS数据的杭州地区气溶胶光学厚度反演. 光学学报, 35 (1): 101001 [DOI: 10.3788/AOS201535.0101001] )
-
Hu F C, Wang Z H, Zhang B and Li J S. 2009. Study on method for determining atmospheric aerosol type using remote sensing experimental data. Chinese Journal of Lasers, 36 (2): 312–317. [DOI: 10.3788/CJL20093602.0312] ( 胡方超, 王振会, 张兵, 李俊生. 2009. 遥感试验数据确定大气气溶胶类型的方法研究. 中国激光, 36 (2): 312–317. [DOI: 10.3788/CJL20093602.0312] )
-
Kaskaoutis D G, Kambezidis H D, Hatzianastassiou N, Kosmopoulos P G and Badarinath K V S. 2007. Aerosol climatology: on the discrimination of aerosol types over four AERONET sites. Atmospheric Chemistry and Physics, 7 (3): 6357–6411. [DOI: 10.5194/acpd-7-6357-2007]
-
Kaskaoutis D G, Badarinath K V S, Kharol S K, Sharma A R and Kambezidis H D. 2009. Variations in the aerosol optical properties and types over the tropical urban site of Hyderabad, India. Journal of Geophysical Research: Atmospheres, 114 (D22): D22204 [DOI: 10.1029/2009JD012423]
-
Kaufman Y J and Sendra C. 1988. Algorithm for automatic atmospheric corrections to visible and near-IR satellite imagery. International Journal of Remote Sensing, 9 (8): 1357–1381. [DOI: 10.1080/01431168808954942]
-
King M D, Kaufman Y J, Menzel W P and Tanré D. 1992. Remote sensing of cloud, aerosol, and water vapor properties from the moderate resolution imaging spectrometer (MODIS). IEEE Transactions on Geoscience and Remote Sensing, 30 (1): 2–27. [DOI: 10.1109/36.124212]
-
Kumar K R, Yin Y, Sivakumar V, Kang N, Yu X N, Diao Y W, Adesina A J and Reddy R R. 2015. Aerosol climatology and discrimination of aerosol types retrieved from MODIS, MISR and OMI over Durban (29.88°S, 31.02°E), South Africa. Atmospheric Environment, 117 : 9–18. [DOI: 10.1016/j.atmosenv.2015.06.058]
-
Lee J, Kim J, Song C H, Kim S B, Chun Y, Sohn B J and Holben B N. 2010. Characteristics of aerosol types from AERONET sunphotometer measurements. Atmospheric Environment, 44 (26): 3110–3117. [DOI: 10.1016/j.atmosenv.2010.05.035]
-
Lekhtmakher S and Shapiro M. 2005. About randomness of aerosol size distributions. Journal of Aerosol Science, 36 (12): 1459–1467. [DOI: 10.1016/j.jaerosci.2005.04.004]
-
Levy R C. 2007. Retrieval of Tropospheric Aerosol Properties over Land From Visible and Near-Infrared Spectral Reflectance: Application over Maryland. Washington: University of Maryland, College Park.
-
Mie G. 1908. Beiträgezur OptiktrüberMedien, speziellkolloidaler Metallösungen. Annalen der Physik, 330 (3): 377–445. [DOI: 10.1002/andp.19083300302]
-
Nicolae D, Belegante L, Talianu C and Vasilescu J. 2015. Using artificial neural networks to retrieve the aerosol type from multi-spectral lidar data//EGU General Assembly Conference Abstracts. Vienna, Austria: EGU: 9793.
-
Pathak B, Bhuyan P K, Gogoi M and Bhuyan K. 2012. Seasonal heterogeneity in aerosol types over Dibrugarh-North-Eastern India. Atmospheric Environment, 47 : 307–315. [DOI: 10.1016/j.atmosenv.2011.10.061]
-
Rama G K, Arafath S M, Balakrishnaiah G, Raja O R K, Siva K R N, Lingaswamy A P, Pavan K S, Uma D K, Reddy R R and Suresh B S. 2015. Columnar-integrated aerosol optical properties and classification of different aerosol types over the semi-arid region, Anantapur, Andhra Pradesh. Science of the Total Environment, 527-528 : 507–519. [DOI: 10.1016/j.scitotenv.2015.04.086]
-
Ramanathan V, Crutzen P J, Lelieveld J, Mitra A P, Althausen D, Anderson J, Andreae M O, Cantrell W, Cass G R, Chung C E, Clarke A D, Coakley J A, Collins W D, Conant W C, Dulac F, Heintzenberg J, Heymsfield A J, Holben B, Howell S, Hudson J, Jayaraman A, Kiehl J T, Krishnamurti T N, Lubin D, McFarquhar G, Novakov T, Ogren J A, Podgorny I A, Prather K, Priestley K, Prospero J M, Quinn P K, Rajeev K, Rasch P, Rupert S, Sadourny R, Satheesh S K, Shaw G E, Sheridan P and Valero F P J. 2001. Indian Ocean experiment: an integrated analysis of the climate forcing and effects of the great Indo-Asian haze. Journal of Geophysical Research: Atmospheres, 106 (D22): 28371–28398. [DOI: 10.1029/2001JD900133]
-
Sreekanth V. 2014. On the classification and sub-classification of aerosol key types over south central peninsular India: MODIS–OMI algorithm. Science of the Total Environment, 468-469 : 1086–1092. [DOI: 10.1016/j.scitotenv.2013.09.038]
-
Srivastava A K, Yadav V, Pathak V, Singh S, Tiwari S, Bisht D S and Goloub P. 2014. Variability in radiative properties of major aerosol types: a year-long study over Delhi—an urban station in Indo-Gangetic Basin. Science of the Total Environment, 473-474 : 659–666. [DOI: 10.1016/j.scitotenv.2013.12.064]
-
Sun L, Wei J, Bilal M, Tian X P, Jia C, Guo Y M and Mi X T. 2016. Aerosol optical depth retrieval over bright areas using landsat 8 OLI images. Remote Sensing, 8 (1): 23 [DOI: 10.3390/rs8010023]
-
Tan F Y, Lim H S, Abdullah K, Yoon T L and Holben B. 2015. AERONET data-based determination of aerosol types. Atmospheric Pollution Research, 6 (4): 682–695. [DOI: 10.5094/APR.2015.077]
-
U.S. Environmental Protection Agency. 2008. Air Quality Criteria for Particulate Matter. Beijing: China Environmental Science Press: 11–103 (美国环境保护局. 2008. 颗粒物环境空气质量USEPA基准(上卷). 北京: 中国环境科学出版社: 11–103)
-
Wang Z T, Li Q, Wang Q, Li S S, Chen L F, Zhou C Y, Zhang L J and Xu Y J. 2012. HJ-1 terrestrial aerosol data retrieval using deep blue algorithm. Journal of Remote Sensing, 16 (3): 596–610. [DOI: 10.11834/jrs.20121148] ( 王中挺, 厉青, 王桥, 李莘莘, 陈良富, 周春艳, 张丽娟, 徐拥军. 2012. 利用深蓝算法从HJ-1数据反演陆地气溶胶. 遥感学报, 16 (3): 596–610. [DOI: 10.11834/jrs.20121148] )