出版日期: 2017-05-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176251
2017 | Volumn21 | Number 3
上一篇 | 下一篇

技术方法

DT-CWT结合MRF的遥感图像变化检测

范奎奎^1,2 , 王中元¹ , 欧阳斯达² , 汪汇兵² , 史绍雨²

1. 中国矿业大学环境与测绘学院，徐州 221116

2. 国家测绘地理信息局卫星测绘应用中心，北京 100048

收稿日期: 2016-07-01; 修改日期: 2016-12-01; 优先数字出版日期: 2016-12-08

基金项目: 国家自然科学基金(编号：51374209，41271394)

第一作者简介: 范奎奎(1991—　)，男，硕士研究生，研究方向为遥感影像变化检测、小波变换图像处理。E-mail：fkk@cumt.edu.cn

通讯作者简介: 王中元(1977—　)，男，副教授，研究方向为3S集成及其应用、大比例尺地形图更新。E-mail：wzy95002@163.com

中图分类号: TP751.1

文献标识码: A

摘要

为了解决多尺度遥感图像变化检测在降噪时丢失大量高频信息及单一像素孤立性的问题，提出了一种双树复小波变换DT-CWT(Dual-tree Complex Wavelet Transform)和马尔可夫随机场MRF(Markov Random Field)相结合的非监督遥感图像变化检测算法，首先采用DT-CWT对差异图像进行多尺度分解，并根据MRF模型分割算法提取高频区域的变化特征，然后进行相应层的高、低频重构，再对重构后的各层建立MRF模型并根据贝叶斯最大后验概率准则MAP(Maximum A Posterior)进行最终分割，最后对各层分割结果进行求交融合，得到最终的变化检测结果掩膜图。对比实验结果表明，该方法在去除杂点和噪声的同时能够较好地保留高频信息，并且边缘检测更加平滑，具有较高的变化检测精度和很好的鲁棒性。

关键词

变化检测, 双树复小波变换DT-CWT, MRF模型, 多尺度分解

Change detection of remote sensing images through DT-CWT and MRF

FAN Kuikui^1,2 , WANG Zhongyuan¹ , OUYANG Sida² , WANG Huibing² , SHI Shaoyu²

1.School of Environmental Science and Spatial Informatics, China University of Mining & Technology, Xuzhou 221116, China

2.Satellite Surveying and Mapping Application Center, Beijing 100048, China

Abstract

Image change detection uses an algorithm that is based on multiscale analysis and Markov Random Field (MRF) model. The algorithm is widely used owing to time–frequency wavelet characteristics and the good expression to spatial correlation of the MRF model. To address the significant loss of high-frequency information during noise reduction and pixel independence in change detection of multiscale remote sensing images, this paper proposes an unsupervised change detection algorithm based on the combined dual-tree complex wavelet transform (DT-CWT) and MRF. The algorithm can be divided into the following steps. First, to enhance detail expression and objective image edges, the difference image is decomposed on a multiscale by DT-CWT. Second, the change characteristics in high-frequency regions are extracted by setting the high-frequency components of the first layer to zero and performing MRF segmentation to the other levels. Third, the high- and low-frequency sub-bands of each layer are reconstructed, and the maximum a posteriori probability is estimated by the Iterative Condition Model (ICM) based on the K-means segmentation algorithm, which fully obtains the correlation between pixels. Finally, the segmentation results of each layer are fused to obtain the mask of the final change detection result. To verify the effectiveness and stability of the proposed algorithm, the DT-CWT–Bayes, MRF–Bayes, DWT-MRF–Bayes methods, and the proposed algorithm are comparatively tested and analyzed. The contrast experiment proves that compared with the other methods, the proposed method produces change detection results for edges that subjectively look smoother and more delicate with less noise. In addition, as shown in the table of evaluation indices of the four change detection methods, the proposed method has the least total number of errors and the highest accuracy rate. Thus, the proposed method balances the reduction of tiny spots and noise and the retention of high frequency information. Moreover, the proposed method has high precision for change detection and predominant robust properties. The proposed algorithm fully uses the multidirectional expression, anisotropy, and multiscale properties of DT-CWT, which helps the expression and analysis of image information. In addition, the extraction of the change characteristics in high-frequency regions based on the segmentation algorithm of ICM better balances between noise reduction and retention of high frequency information. Finally, the final iteration and segmentation based on the MRF segmentation algorithm determines the correlation between pixels with considerably reduced false alarm rates while avoiding the influence of registration error. However, the proposed algorithm takes more time due to the existence of some iterative processes.

Key words

change detection, DT-CWT, MRF, multi-scale decomposition

1 引　言

随着遥感数据获取手段不断提高和更新周期不断缩短，变化检测技术作为遥感图像处理与分析中的一项重要应用，已广泛应用于土地利用和土地覆盖变化监测，森林或植被变化检测，灾害救援与治理、城镇和道路变化、地理数据库更新等众多领域(Wu 等，2013；佃袁勇等，2014；孙晓霞等，2011)。由于无监督变化检测方法除了利用两时相的原始图像外，不需要任何额外的先验知识就能得到最终变化检测结果，方法较为高效，故成为众多学者研究的热点(Celik和Ma，2010)。通常无监督变化检测是基于像素差异的变化检测，可分为阈值法(Bruzzone和Prieto，2000；佃袁勇等，2016)、变换法(Marchesi和Bruzzone，2009；吴一全等，2015；陈忠辉等，2011；辛芳芳等，2012)、图像建模法(Kasetkasem和Varshney，2002；李长春等，2013，2014)等。阈值法是通过选择合适的阈值来区分差异图像中的变化类与非变化类像素，从而得到最终的变化区域。贝叶斯最优阈值法(Bruzzone和Prieto，2000)具有简单直观的优点，但是往往只进行单一尺度的分割，难免会引起过度分割或不完全分割，同时检测结果严重依赖于选取的阈值。变换法主要是多尺度变换法和统计分析的方法，如小波变换WT(Wavelet Transform)(Celik和Ma，2010)、主成分分析PCA变换(Principal Component Analysis)(Marchesi和Bruzzone，2009)、核独立成分分析KICA变换(Independent Component Analysis)(吴一全等，2015)等，这类方法较好地克服了传感器噪声、配准误差等因素的影响，但未考虑像素间的相关性，检测边缘粗糙，误检像素较多。图像建模法是通过建立模型来模拟空间上下文相关的分布信息(Kasetkasem和Varshney，2002；李长春等，2013，2014)，此类方法考虑了邻域内像素之间的相互影响，较好地克服了孤立像素问题，但突变和细节信息表达较弱，伪变化检测较多。为了解决上述方法存在的问题，很多学者提出了将多尺度变换与马尔可夫随机场MRF (Markov Random Field)相结合的遥感图像变化检测方法(陈忠辉等，2011；辛芳芳等，2012)，这些方法利用了小波变换的时频分析能力并且考虑了像素的空间相关性，较好地克服了单一像素孤立性、噪声和配准误差等因素引起的伪变化，但是由于在融合过程中直接舍弃了高频信息，只取低频信息进行实验，难免造成信息的损失，加之小波变换存在着方向选择性和平移敏感性，使得变化检测细节仍表达不足。

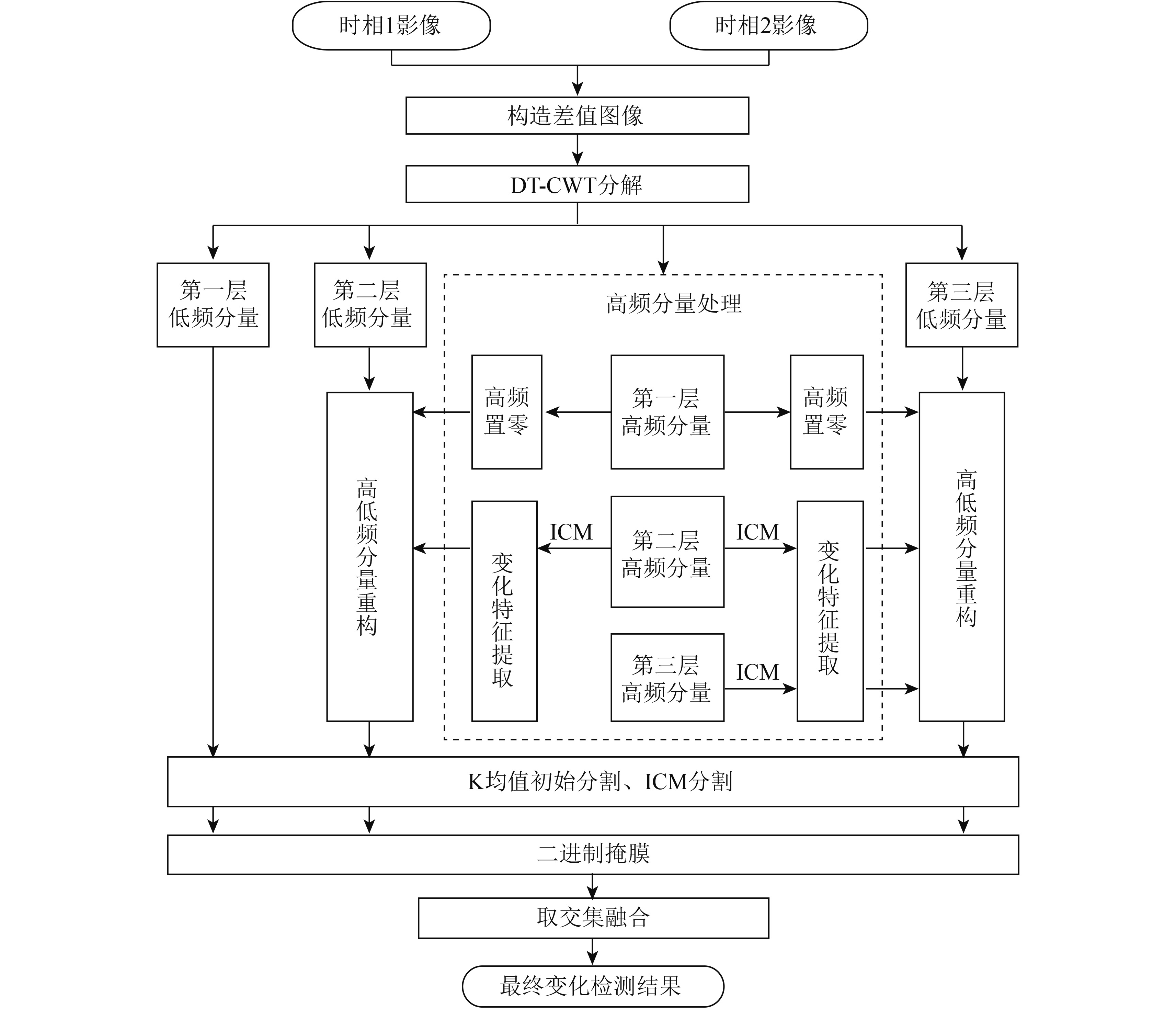
针对上述方法存在的问题，本文提出了一种基于双树复小波变换DT-CWT(Dual-tree Complex Wavelet Transform)与MRF模型相结合的非监督遥感图像变化检测方法，简称为DTCWT-MRF-Bayes，该方法首先采用DT-CWT对差值图像进行多尺度分解，并利用MRF模型分割算法提取出高频区域的变化特征，然后进行相应层的高、低频重构，再对重构后各层建立MRF模型并在贝叶斯框架下根据最大后验概率准则MAP(Maximum A Posterior)进行最终分割，最后对分割后的各层结果进行求交融合，得到最终的变化检测结果。

2 DT-CWT和MRF分割模型

2.1 DT-CWT分解

DT-CWT不仅保持了传统离散小波变换DWT(Discrete Wavelet Transform)良好的时频分析能力，而且还具有近似的平移不变性、良好的方向选择性、有限的数据冗余以及完全重构等特点(Kingsbury，1998)。为了克服奇/偶(odd/even)滤波器因严格线性相位引起的采样结构差异的缺点，本文采用Kingsbury(2001)提出的基于正交变换的Q-Shift(Quarter Sample Shift)滤波器组对图像进行2维DT-CWT分解，每层分解可以得到一个低频子带和6个方向(±15°，±45°，±75°)的高频子带。如图1为三层DT-CWT分解树状图，X为原始图像，X_(n)，(n=1，2，3)为第n层分解的高、低频子带，其中阴影部分为低频子带，空白部分为高频子带。

图 1 三层DT-CWT分解树状图

Fig. 1 Three level DT-CWT decomposition tree

2.2 MRF分割模型

由于马尔可夫随机场(MRF)能够很好地刻画图像信息的空间相关性和有效建立上下文的先验模型，因此被广泛应用于遥感影像分类以及变化检测之中(张斌，2013)。MRF图像分割模型是在贝叶斯框架下进行推理的，其建立通常由两个随机场描述，一个是标记场W={W|w₁，w₂，…，w_n}，用来对待测图像的像素进行跟踪分类标记；另一个是特征场F={F|f₁，f₂，…，f_n}，常以标记场为前提进行特征分析。假设F=f表示从一个随机图像X=x中提取的特征向量，W=w是基于特征向量F=f的分割结果，根据Bayes准则，图像的分割问题可以表示为

$P({W} = {w}{\rm{|}}{F} = {f}) = \frac{{P({F} = {f}{\rm{|}}{W} = {w})P({W} = {w})}}{{P({F} = {f})}}$

(2)

一个图像最优分割问题就是要找到观察图像的最佳标记场$\mathop { W}\limits^{\frown} $，使得后验概率函数P(W=w| F=f)取得最大值(魏小莉和沈未名，2010)，这即为典型的MAP-MRF问题。基于MAP准则，图像分割的全局最优估计$ \mathop { W}\limits^{\frown} $可表示为

$\mathop { W}\limits^{\frown} = \arg \max P({F} = {f|W} = {w})P({W} = {w})$

(3)

由于式(2)$ \mathop { W}\limits^{\frown} $计算非常复杂，基于MRF和吉布斯随机场GRF(Gibbs Random Field)的等价性(Geman和Geman，1984)，MRF-MAP问题可以转化为GRF最小能量函数迭代优化问题，该问题可以用条件迭代模型ICM(Iterative Condition Model)算法来实现，由于ICM很容易收敛到局部最优解，分割效果非常依赖初始分割条件，通常做法是选择K均值聚类分割算法作为图像的初始分割方法。由于经过归一化后进行DT-CWT分解得到的各高、低频子带系数都很小，由灰度直方图来获取K均值初始分割阈值不仅比较困难而且效果不佳，故本文选择自适应Bayes阈值来作为K均值聚类分割的初始阈值，基于K均值初始分割的ICM算法的具体步骤如下：

(1)由“0”和自适应Bayes阈值t来作为初始聚类中心，进行K均值初始聚类分割，分割结果对应的标记场为W_m，m表示迭代次数；

(2)基于MRF和GRF的等价性，由能量函数${ U}({x}) = \sum\limits_{c \in { C}} {{V_c}({x_1},{x_2})} $(只考虑二阶邻域系统，其中c为势团，C为二阶势团集合)计算每个像素的标记场能量U_m(w)；

(3)根据初始分割状态求特征场的参数均值μ_m和方差$\sigma _m^2$，由能量函数${U_m}({{w}},{{f}}) = \sum\limits_{s \in { S}} {{\rm{ln}}(\sqrt {2\pi } {\sigma _m})} +$$\displaystyle\frac{{{{(f - {\mu _m})}^2}}}{{2\sigma _m^2}}$(其中S为所有像素集合，s属于S)计算当前分割每个像素的特征场能量，根据能量最小原则${E_m} = {\rm{min}}({U_m}({w}) + {U_m}({w},{f}))$，更新标记场W_m；

(4)判断循环终止条件，重复步骤(2)、(3)不断对标记场进行迭代更新，达到最终的MRF-MAP最优分割。

基于DT-CWT的MRF分割模型，即是将DT-CWT分解的各个层的高、低频子带看作一个马尔可夫随机场，各子带的像素都具有马尔可夫性，故可以利用上述的MRF分割算法来进行各子带的最优分割。

3 基于DTCWT-MRF-Bayes的变化检测算法

3.1 算法流程

综合考虑算法的精确度和效率，选择进行3层DT-CWT分解和MRF结合进行实验，算法流程图如图2所示。

图 2 基于DT-CWT和MRF的变化检测流程图

Fig. 2 Flowchart of change detection based on DT-CWT and MRF

假设X₁(i，j)、X₂(i，j)均是大小为m×n的经过精确配准的两期同区域的遥感影像X₁、X₂对应的灰度图像矩阵，具体算法实现步骤如下：

(1)采用差值法：${D}(i,j) = \left| {{{X}_2}(i,j) - {{X}_1}(i,j)} \right|$，(m≤i、j≤n)对影像X₁、X₂求取差值图像D；

(2)对差值图D进行三层DT-CWT分解，每层分解可分别得到1个低频子带记为{L₁，L₂，L₃}带和6个方向的高频子带记为H_{k, l}，(k=1，2，3；l=±15°，±45°，±75°)；

(3)由“0”和自适应Bayes阈值t来作为初始聚类中心，分别对各高频子带H_{k, l}，(k=1，2，3；l=±15°，±45°，±75°)进行K均值初始聚类分割，得到初始分割状态${H}_{k,l}^m$，(k=1，2，3；l=±15°，±45°，±75°)和标记场为${W}_{k,l}^m$，其中m表示迭代次数；

(4)基于MRF与GRF的等价性，利用ICM模型不断迭代更新标记场${W}_{k,l}^m$，达到最终的MRF-MAP最优分割；

(5)对最终分割结果进行二进制掩膜，记掩膜图变化类为C，未变化类为U，则将各高频子带H_{k, l}对应的C类像素值保持不变，U类对应的像素值置零，得到提取特征后的各高频带为${\hat H}_{k,l}$，(k=1，2，3；l=±15°，±45°，±75°)；

(6)舍去第一层高频信息${\hat H}_{1,l}$，并取第一层分解得到的低频子带L₁不变作为C₁，取二层分解得到的低频子带L₂与${\hat H}_{2,l}$，(l=±15°，±45°，±75°)进行重构作为C₂，取三层分解得到的低频子带L₃与${\hat H}_{k,l}$，(k=2，3；l=±15°，±45°，±75°)进行重构作为C₃；

(7)分别对C₁、C₂、C₃重复步骤(3)、(4)，即进行K均值初始分割和MRF-MAP最优分割，并且进行二进制掩膜，得到的最终掩膜图像分别为Z₁、Z₂、Z₃；

(8)对Z₁、Z₂、Z₃进行${Z} = {{Z}_1} \cap {{Z}_2} \cap {{Z}_3}$求交融合，得到最终的变化检测二进制掩膜图Z。

算法中，K均值循环终止条件选择为相邻两次循环聚类中心差值均小于0.005，ICM最大迭代次数设置为30次，由于步骤(3)、(4)、(7)中存在循环和迭代过程，可以预知本文所提算法比较耗时。

3.2 融合规则

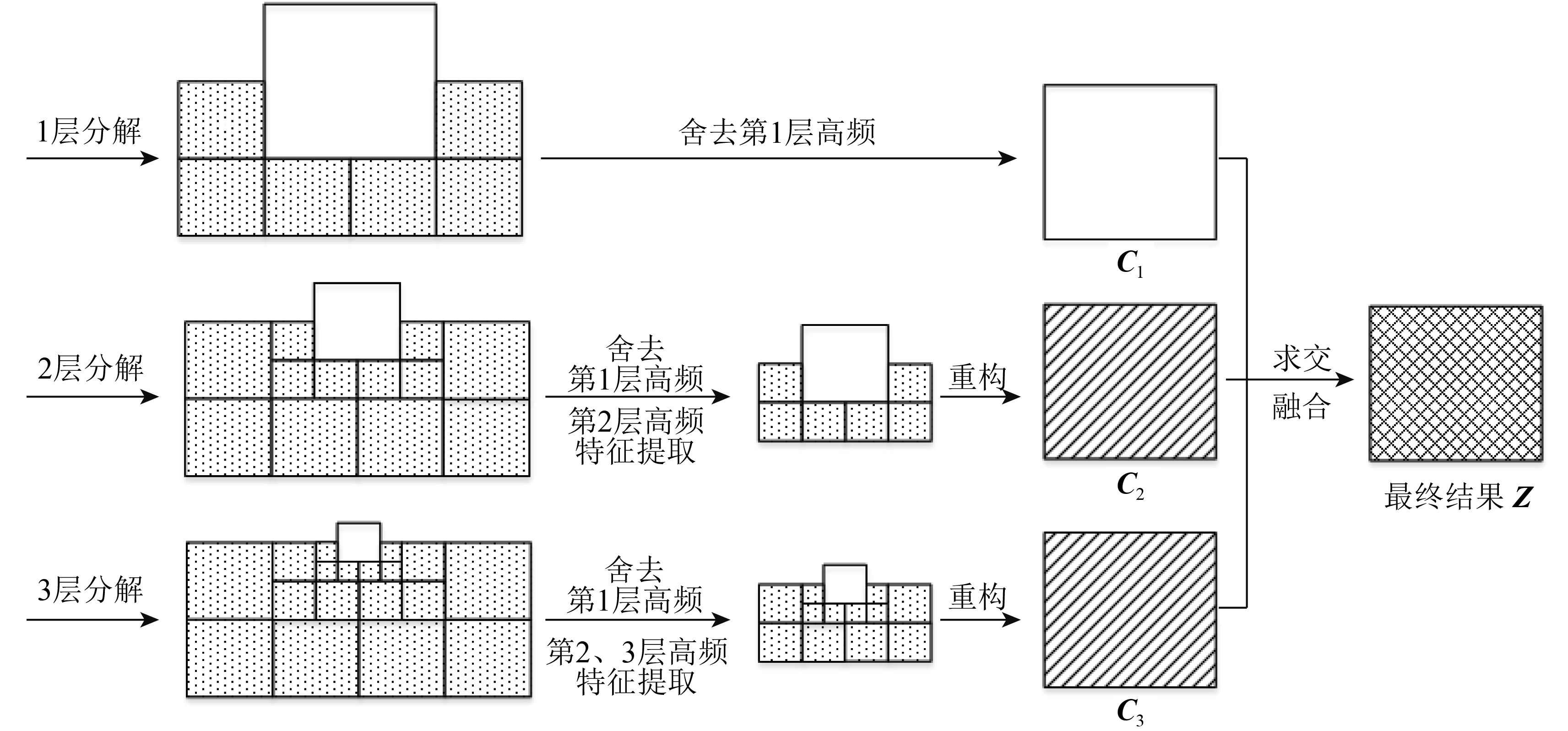
为了进行不同尺度间的融合，运用重构的思想来使得各层分量具有和原图同样的大小，以3层DT-CWT分解为例，具体做法是取分解的第1层低频分量作为第1层C₁，第2层低频分量与提取变化特征的第2层高频分量重构作为第2层C₂，第3层低频分量与提取变化特征的第3层高频分量重构作为第3层C₃，并通过求交融合3层重构后的变化检测结果来得到最终的变化检测结果Z，融合规则示意图如下图3，图中空白部分为低频带，点状阴影部分为高频带(从外圈到内圈依次为第1、2、3层)。由于经过多尺度分解后的遥感图像的低频分量包含图像的主要信息，高频分量包含主要的突变信息(包括细节信息和噪声)，并且噪声绝大部分存在于低分解层(张晗等，2016)，本文通过舍去第1层高频信息并利用MRF模型分割算法预先提取出其他层高频域的变化特征，来达到在去除噪声的同时较好地保留高频细节信息的目的。

图 3 融合规则示意图

Fig. 3 Diagram of fusion rules

4 实验与分析

4.1 数据源

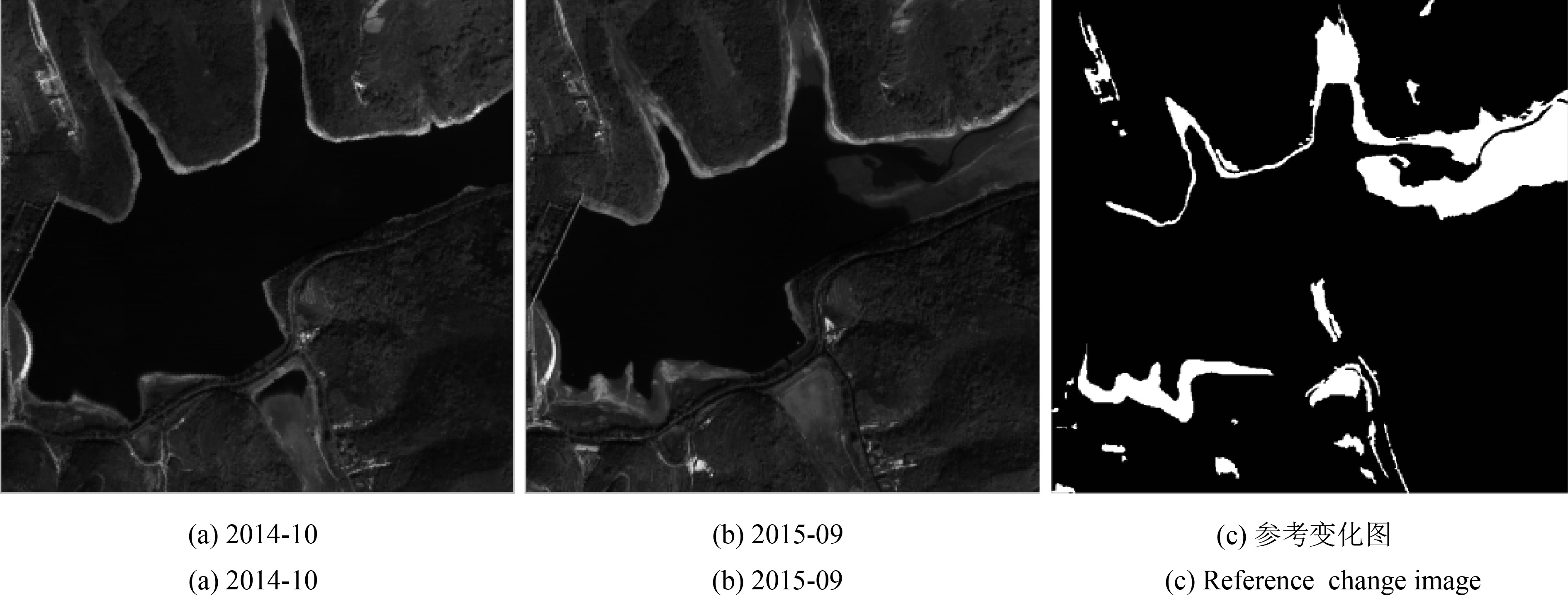
由于不同时期的地表覆盖变化比较复杂，通常选用覆盖区的高分辨率遥感影像进行实验。为了检验所提算法DTCWT-MRF-Bayes的变化检测精度和稳定性，分别选用多种传感器的高分辨率的光学遥感影像进行实验，其中两组资源3号卫星影像分别编号为Ⅰ、Ⅱ，具体数据信息如下表1。

表 1 数据信息
Table 1 Data information

下载CSV

数据类型	时间	地点	大小	波段
ZY-3影像Ⅰ	2014-12	黄港水库/天津市	448×640	全色
ZY-3影像Ⅰ	2015-12	黄港水库/天津市	448×640	全色
ZY-3影像Ⅱ	2014-10	北大河/辽宁省	576×576	全色
ZY-3影像Ⅱ	2015-09	北大河/辽宁省	576×576	全色
TM5影像	2000-07	朗多尼亚州/巴西	512×512	多通道 (4、3、2波段)
TM5影像	2006-07	朗多尼亚州/巴西	512×512	多通道 (4、3、2波段)
Quickbird影像	2012-04	兖州市/山东省	320×320	第3波段
Quickbird影像	2012-09	兖州市/山东省	320×320	第3波段

由于现实中参考变化图很难获得，本实验中各参考变化图是通过直接观察两副图像之间的差异和差异图像人工提取的。各组实验影像集如图4—图7所示，两时相的配准误差均小于1个像素。

图 4 天津市黄港水库ZY-3影像集

Fig. 4 ZY-3 images of Huang Gang Reservoir in TianJin

图 5 辽宁北大河ZY-3影像集

Fig. 5 ZY-3 images of Liaoning North River

图 6 巴西朗多尼亚州TM5影像集

Fig. 6 TM5 images of Rondonia state in Brazil

图 7 山东省兖州市Quickbird影像集

Fig. 7 Quickbird images of Yanzhou city Shandong province

4.2 实验关键环节

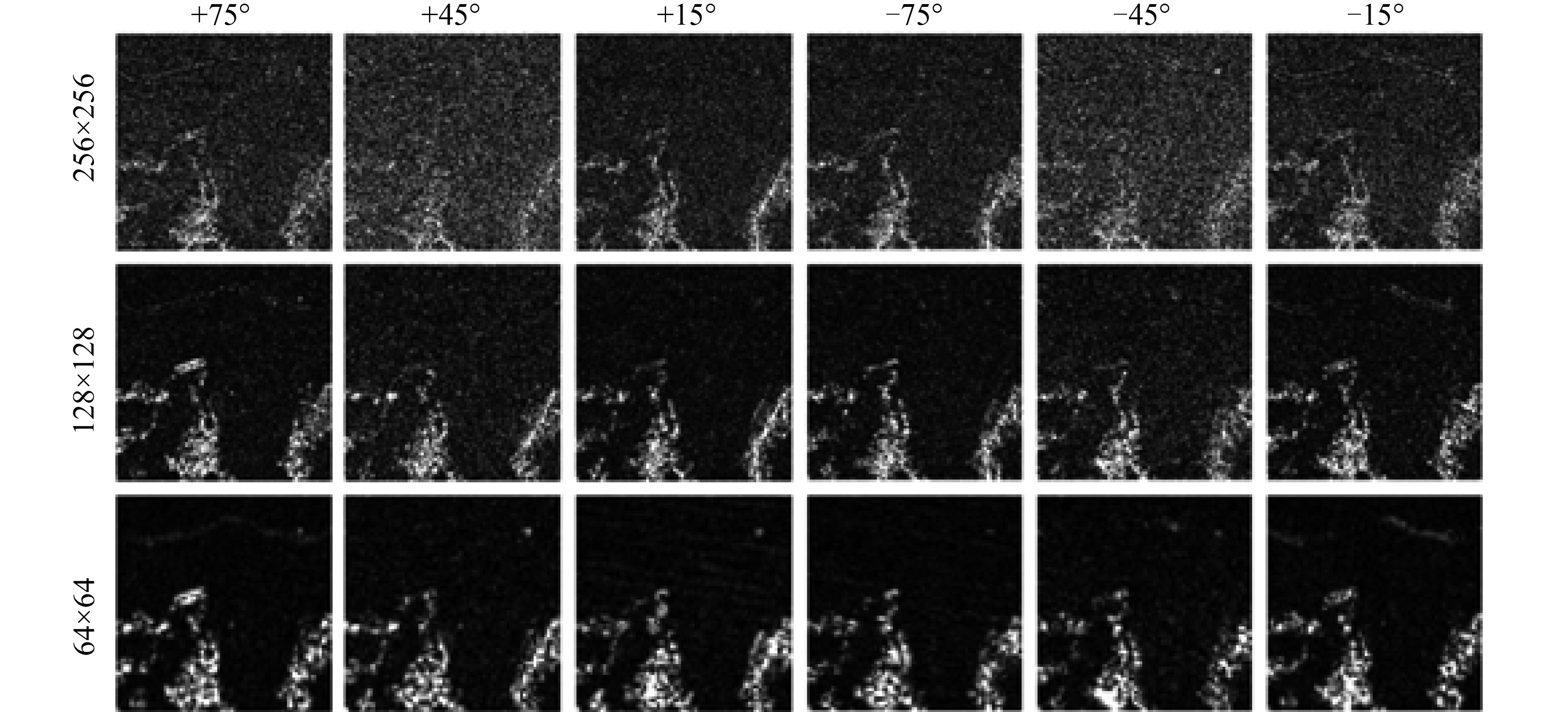
4.2.1 多尺度分解

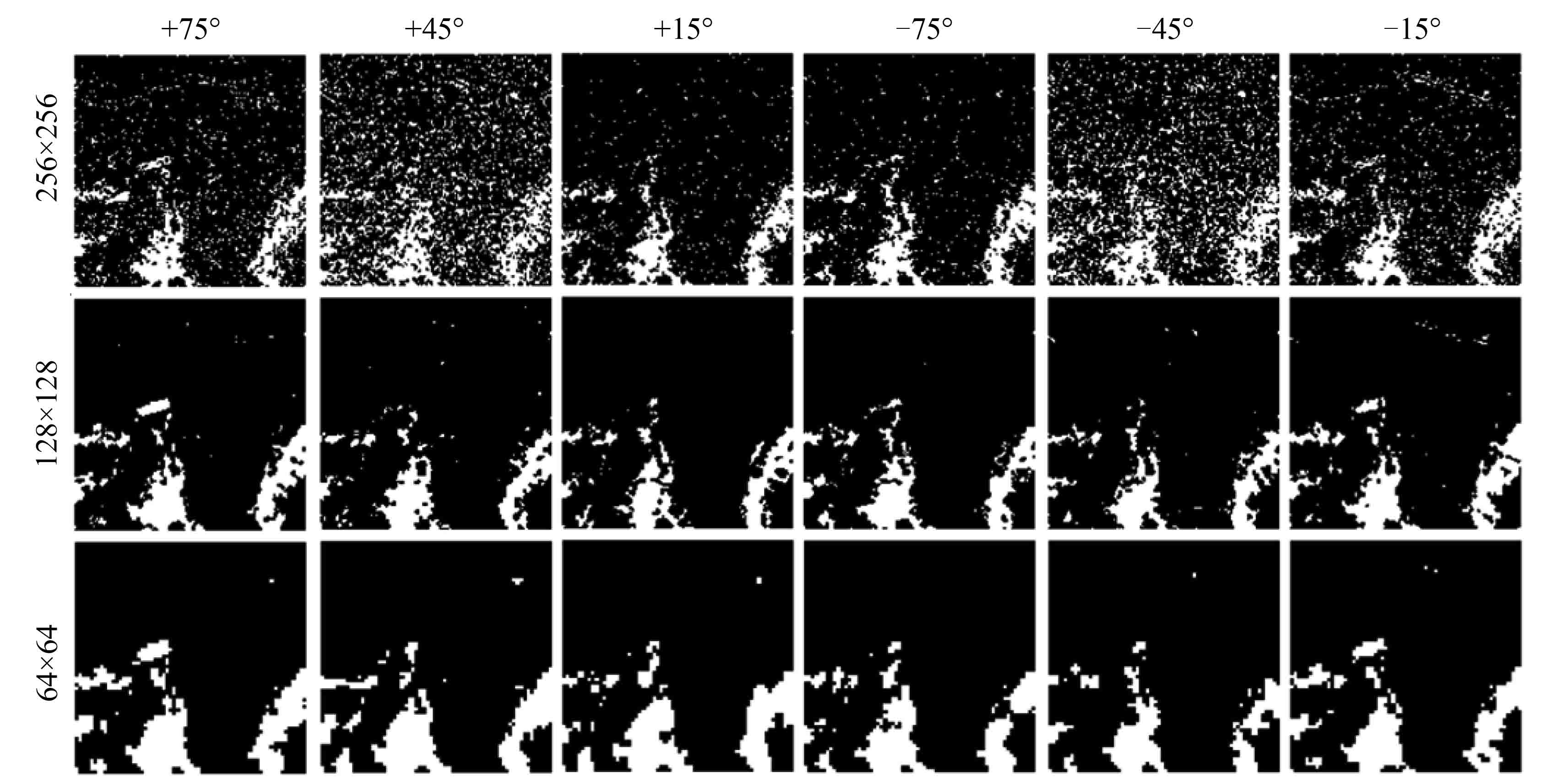
以4.1节中巴西朗多尼亚州TM5卫星影像为例，如图8为两期影像的差值图像经过3层DT-CWT分解后的高频子带图像，从上到下每层图像大小依次为256×256、128×128、64×64，从左到右依次代表+75°、+45°、+15°、–75°、–45°、–15°方向的分量，可以看出DT-CWT具有很好的细节分析能力和多方向表达能力，另外可以看出杂点主要存在于低分解层，且随层数增加逐渐减少。

图 8 3层DT-CWT分解高频子带图像

Fig. 8 Highpass subimages for three level DT-CWT decomposition

4.2.2 高频信息MRF分割

图9为图8通过MRF模型分割算法提取变化特征并经过掩膜得到的二进制图像，可以明显看出提取特征后的结果中杂点主要存在于第1层中，另外可以看出提取结果呈块状随层数增加越明显，故可以通过舍去第1层高频信息和保留其他层高频信息来达到平衡噪声去除和高频信息保留的目的。

图 9 经过ICM分割后的3层高频子带图像

Fig. 9 Three level highpass subimages by ICM

4.3 检测结果分析与评价

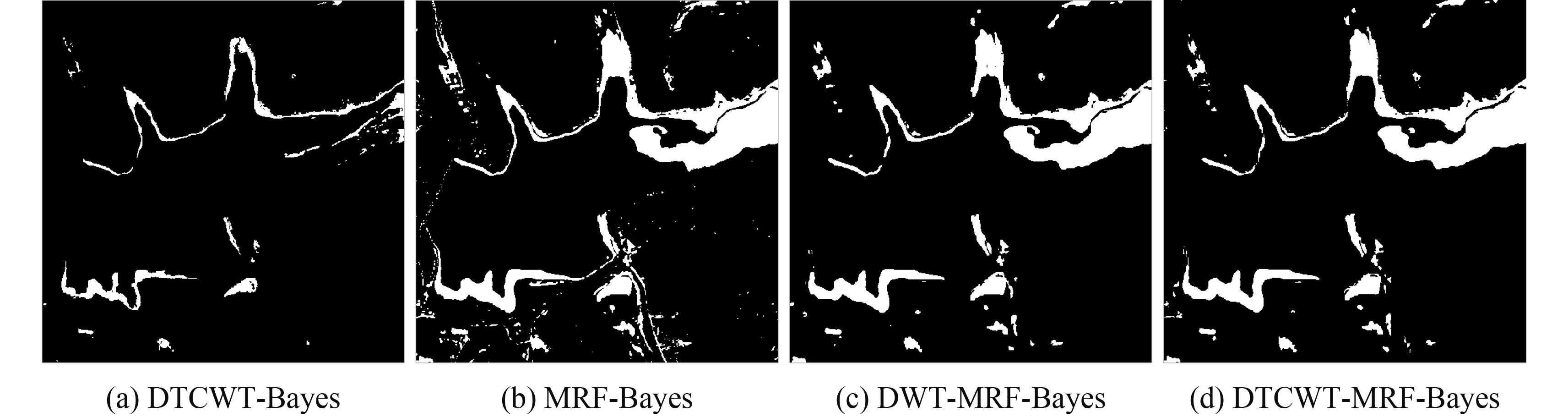
为了验证所提算法的有效性，分别选用DTCWT-Bayes法、MRF-Bayes法、DWT-MRF-Bayes法和文中所提算法DTCWT-MRF-Bayes进行多组实验和对比分析，所有算法运行环境均为Intel(R)Core(TM)i7，2.67 GHz主频，8 GB内存，Matlab2012a。如图10—图13分别为4.1节中各组遥感数据集的变化检测结果。

图 10 天津市黄港水库ZY-3影像变化检测结果

Fig. 10 Change detection results of ZY-3 images of Huang Gang Reservoir in Tianjin

图 11 辽宁北大河ZY-3影像变化检测结果

Fig. 11 Change detection results of ZY-3 images of Liaoning North River

图 12 巴西朗多尼亚地区TM5影像变化检测结果

Fig. 12 Change detection results of TM5 images of Rondonia state in Brazil

图 13 山东省兖州市Quickbird影像变化检测结果

Fig. 13 Change detection results of Quickbird images of Yanzhou city Shandong province

(1)图10—图13可以明显看出DTCWT-Bayes法边缘检测粗糙呈现凹凸状，且从图11(a)和图12(a)可以明显看出有大量漏检区域，由于DT-CWT的多尺度特性，杂点较少，较好克服了传感器噪声、但是由于未考虑像素空间相关性，检测边缘粗糙，错检像素较多；

(2)图10—图13可以看出MRF-Bayes法变化检测结果图中离散点和线条检测较多，这是由于未进行多尺度处理分析，突变信息表达不足，使得伪变信息较多；

(3)4组模拟实验中所有DWT-MRF-Bayes和DTCWT-MRF-Bayes方法和检测结果可以看出变化区域的孤立点明显减少，边缘检测更加平滑细腻，很好的克服了传感器噪声和配准误差的影响，具有很好的鲁棒性，同时可以看出DTCWT-MRF-Bayes方法组较DWT-MRF-Bayes的边缘和微小突变信息检测更加精准，一方面是由于所提的算法DTCWT-MRF-Bayes中，DT-CWT具有比DWT更多的方向表达性，另一方面由于DWT-MRF-Bayes算法在融合规则中直接舍去所有高频信息，虽然较好地去除了噪声，但也造成了信息的损失。综上所述，从主观上看，所提出的算法变化检测总体性能最好。

为了进行客观的评价，以虚警数FA(False Alarms)、漏检数MA(Missed Alarms)、总错误数OE(Overall Error)、正确率OR(Overall Right)以及运行时间T作为性能评价指标，设参考变化图为R(i，j)，检测结果变化图为Z(i，j)，总像素数为S，各评价指标的计算式为

$FA = \sum {({R}(i,j) = 0{\rm{\& }}{Z}(i,j) = 1)} $

(4)

$MA = \sum {({R}(i,j) = 1 {\rm{\& }} {Z}(i,j) = 0)} $

(5)

$OE = FA + MA$

(6)

$OR = (S - OE)/S$

(7)

T为各算法变化检测实际运行时间，各组变化检测结果性能见表2。从表2可以看出：

表 2 4种变化检测结果性能比较
Table 2 Comparison of four change detection results

下载CSV

数据类型	方法	虚警数(FA)	漏检数(MA)	总错误数(OE)	正确率(OR/%)	时间(T/s)
ZY-3影像Ⅰ	DTCWT-Bayes	983	10762	11700	95.92	3.8
	MRF-Bayes	8975	639	9614	96.65	3.6
	DWT-MRF-Bayes	2388	1472	3860	98.65	11.0
	DTCWT-MRF-Bayes	2382	1005	3387	98.82	17.6
ZY-3影像Ⅱ	DTCWT-Bayes	213	23485	23698	92.86	4.4
	MRF-Bayes	4464	226	4690	98.59	4.4
	DWT-MRF-Bayes	1582	3998	5580	98.32	12.7
	DTCWT-MRF-Bayes	1328	2703	4031	98.79	19.9
TM5影像	DTCWT-Bayes	41	19555	19596	92.52	3.5
	MRF-Bayes	1103	1598	2701	98.97	3.8
	DWT-MRF-Bayes	566	1718	2284	99.13	10.0
	DTCWT-MRF-Bayes	415	699	1114	99.58	16.4
Quickbird影像	DTCWT-Bayes	156	575	731	99.29	1.8
	MRF-Bayes	678	25	703	99.31	1.5
	DWT-MRF-Bayes	160	169	329	99.68	3.7
	DTCWT-MRF-Bayes	88	116	203	99.80	5.7

(1) Quickbird组影像实验中方法DTCWT-Bayes虚警数略高于本文所提方法，除此之外DTCWT-Bayes虚警数最小，另外可以看出4组影像集实验中，方法DTCWT-Bayes漏检数和总错误数均远远高于其他3种方法，说明将DT-CWT引入到变化检测算法中可以降低伪变化的检测，但是漏检较为严重；

(2) 4组实验结果中，MRF-Bayes法虚警数最高，且除TM5实验组中漏检数稍高于本文所提方法外，MRF-Bayes法漏检数最少，说明利用MRF的空间像素相关性可以大大降低漏检区域的检测，但同时伪变区域检测较多；

(3) 不考虑DTCWT-Bayes法，另外3种方法中DWT-MRF-Bayes法的漏检数最大，这是由于其在算法融合规则中直接将高频信息舍去造成的；

(4) 引入MRF的3种方法中，方法DTCWT-MRF-Bayes虚警数最小，引入多尺度处理的3种方法中，方法DTCWT-MRF-Bayes漏检数最小，并且4组实验结果中方法DTCWT-MRF-Bayes的总错误数最小，正确率最高，而从运算速度上看，本文所提算法耗时最长，DWT-MRF-Bayes法次之，DTCWT-Bayes和MRF-Bayes法相当，耗时最短，这是由于DWT-MRF-Bayes法没有进行高频信息处理与DTCWT-Bayes和MRF-Bayes法只利用单一方法进行变化检测的缘故。

综上所述，在不考虑运行时间情况下，本文所提算法DTCWT-MRF-Bayes的变化检测性能最优。综合主、客观来看，所提算法能够较准确地获取变化区域，同时能够很好地去除杂点和保持变化区域的边缘信息，具有较强的鲁棒性和较好的视觉效果。

5 结　论

本文提出了一种基于DT-CWT与MRF模型相结合的非监督遥感图像变化检测方法，首先利用DT-CWT的多方向表达性、各向异性和多尺度特性对差值图像进行多尺度分解，有助于图像信息的表达与分析，提高变化检测的精度；然后通过MRF分割算法提取出高频域变化特征并重构去除第一层高频分量后的各层高、低频信息，较好地平衡了噪声的去除和高频信息的保留；最后再次利用MRF分割算法对重构的各层信息进行最终的迭代分割，充分利用了像素间的相关性，不仅大大降低了误检率，而且能够很好地去除了配准误差的影响。对比实验结果表明：基于DT-CWT与MRF相结合的变化检测方法较其他3种方法边缘检测更加平滑细腻，检测杂点相对较少，且总错误数最小，正确率最高，具有较高的变化检测精度和较强的鲁棒性。由于算法中存在迭代过程，耗时较长检测效率较低，对于如何提高算法检测效率和算法复杂度分析需要进一步的研究。

参考文献(References)

Bruzzone L and Prieto D F. 2000. Automatic analysis of the difference image for unsupervised change detection. IEEE Transactions on Geoscience and Remote Sensing, 38 (3): 1171–1182. [DOI: 10.1109/36.843009]

Celik T and Ma KK. 2010. Unsupervised change detection for satellite images using dual-tree complex wavelet transform. IEEE Transactions on Geoscience and Remote Sensing, 48 (3): 1199–1210. [DOI: 10.1109/TGRS.2009.2029095]

Chen Z H, Wang W X, Yu T C and Lin L Q. 2011. Remote sensing image variation detection on multi-scale MRF fusion. Journal of Sichuan University(Engineering Science Edition), 43 (3): 104–108. ( 陈忠辉, 王卫星, 于天超, 林丽群. 2011. 基于多尺度马尔科夫随机场融合的遥感图像变化检测. 四川大学学报(工程科学版), 43 (3): 104–108. )

Dian Y Y, Fang S H and Yao C H. 2014. The geographic object-based method for change detection with remote sensing imagery. Geomatics and Information Science of Wuhan University, 39 (8): 906–912. [DOI: 10.13203/j.whugis20130053] ( 佃袁勇, 方圣辉, 姚崇怀. 2014. 一种面向地理对象的遥感影像变化检测方法. 武汉大学学报(信息科学版), 39 (8): 906–912. [DOI: 10.13203/j.whugis20130053] )

Dian Y Y, Fang S H and Yao C H. 2016. Change detection for high-resolution images using multilevel segment method. Journal of Remote Sensing, 20 (1): 129–137. [DOI: 10.11834/jrs.20165074] ( 佃袁勇, 方圣辉, 姚崇怀. 2016. 多尺度分割的高分辨率遥感影像变化检测. 遥感学报, 20 (1): 129–137. [DOI: 10.11834/jrs.20165074] )

Geman S and Geman D. 1984. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-6 (6): 721–741. [DOI: 10.1109/TPAMI.1984.4767596]

Kasetkasem T and Varshney P K. 2002. An image change detection algorithm based on Markov random field models. IEEE Transactions on Geoscience and Remote Sensing, 48 (8): 1815–1823. [DOI: 10.1109/TGRS.2002.802498]

Kingsbury N. 1998. The dual-tree complex wavelet transform: a new efficient tool for image restoration and enhancement//Proceedings of the9th European Signal Processing Conference. Rhodes: IEEE, 319–322.

Kingsbury N. 2001. Complex wavelets for shift invariant analysis and filtering of signals. Applied and Computational Harmonic Analysis, 10 (3): 234–253. [DOI: 10.1006/acha.2000.0343]

Li C C, Qi X D and Zhang G S. 2013. A study on SAR image change detection based on Markov Random Field models. Modern Radar, 35 (7): 31–35. [DOI: 10.3969/j.issn.1004-7859.2013.07.009] ( 李长春, 齐修东, 张光胜. 2013. 基于MRF模型的SAR图像变化检测研究. 现代雷达, 35 (7): 31–35. [DOI: 10.3969/j.issn.1004-7859.2013.07.009] )

Li C C, Zhang G S, Li H D and Li D D. 2014. A study on SAR image change detection based on improved Markov random field models. Modern Radar, 36 (9): 36–39. [DOI: 10.3969/j.issn.1004-7859.2014.09.009] ( 李长春, 张光胜, 李昊东, 李东东. 2014. 基于改进MRF模型SAR图像变化检测研究. 现代雷达, 36 (9): 36–39. [DOI: 10.3969/j.issn.1004-7859.2014.09.009] )

Marchesi S and Bruzzone L. 2009. ICA and kernel ICA for change detection in multispectral remote sensing images//Proceedings of 2009 IEEE International Geoscience and Remote Sensing Symposium. Cape Town: IEEE, 2: II-980-II-983 [DOI: 10.1109/IGARSS.2009.5418265]

Sun X X, Zhang J X, Yan Q and Gao J X. 2011. A summary on current techniques and prospects of remote sensing change detection. Remote Sensing Information (1): 119–123. [DOI: 10.3969/j.issn.1000-3177.2011.01.023] ( 孙晓霞, 张继贤, 燕琴, 高井祥. 2011. 遥感影像变化检测方法综述及展望. 遥感信息 (1): 119–123. [DOI: 10.3969/j.issn.1000-3177.2011.01.023] )

Wei X L and Shen W M. 2010. Gabor-MRF model based on color texture image segmentation. Geomatics and Information Science of Wuhan University, 35 (8): 955–958. ( 魏小莉, 沈未名. 2010. 一种基于马尔科夫随机场模型的彩色纹理图像分割. 武汉大学学报(信息科学版), 35 (8): 955–958. )

Wu C, Du B and Zhang L P. 2013. Slow feature analysis for change detection in multispectral imagery. IEEE Transactions on Geoscience and Remote Sensing, 52 (5): 2858–2874. [DOI: 10.1109/TGRS.2013.2266673]

Wu Y Q, Cao Z Q and Tao F X. 2015. Change detection of remote sensing images by multi-scale geometric analysis and KICA. Journal of Remote Sensing, 19 (1): 126–133. [DOI: 10.11834/jrs.20153254] ( 吴一全, 曹照清, 陶飞翔. 2015. 结合多尺度几何分析和KICA的遥感图像变化检测. 遥感学报, 19 (1): 126–133. [DOI: 10.11834/jrs.20153254] )

Xin F F, Jiao L C, Wang G T and Wan H L. 2012. Change detection in multi-temporal remote sensing images based on the wavelet-domain hidden Markov chain model. Journal of Xidian University(Natural Science), 39 (3): 43–49. [DOI: 10.3969/j.issn.1001-2400.2012.03.007] ( 辛芳芳, 焦李成, 王桂婷, 万红林. 2012. 利用小波域HMC模型进行遥感图像变化检测. 西安电子科技大学学报(自然科学版), 39 (3): 43–49. [DOI: 10.3969/j.issn.1001-2400.2012.03.007] )

Zhang B. 2013. Research on the Sar Image Classification and Change Detection Based on the Markov Random Field. Wuhan: Wuhan University (张斌. 2013. 基于MRF的SAR图像分类与变化检测应用研究. 武汉: 武汉大学)

Zhang H, Ni W P, Yan W D, Bian H, Wu J Z, Li S and Jin X. 2016. Mid and low resolution SAR image change detection based on fractal and multi-scale analysis. Geomatics and Information Science of Wuhan University, 41 (5): 642–648. [DOI: 10.13203/j.whugis20140375] ( 张晗, 倪维平, 严卫东, 边辉, 吴俊政, 李莎, 金骁. 2016. 利用分形和多尺度分析的中低分辨率SAR图像变化检测. 武汉大学学报(信息科学版), 41 (5): 642–648. [DOI: 10.13203/j.whugis20140375] )

摘要

关键词