出版日期: 2017-05-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176127
2017 | Volumn21 | Number 3
上一篇  |  下一篇
技术方法 
高分辨率遥感影像中建筑物轮廓信息矢量化
expand article info 孙金彦1,2 , 黄祚继1,2 , 周绍光4 , 徐南3 , 钱海明1,2 , 王春林1,2
1. 安徽省(水利部淮河水利委员会)水利科学研究院，合肥 230088
2. 安徽省大禹水利工程科技有限公司，合肥 230088
3. 清华大学 地球系统科学研究中心，北京 100084
4. 河海大学 地球科学与工程学院，南京 210098
收稿日期: 2016-05-12; 修改日期: 2017-01-11; 优先数字出版日期: 2017-01-17
基金项目: 国家自然科学基金(编号：41271420/D010702)
第一作者简介: 孙金彦(1988—　)，女，硕士研究生，研究方向为水环境遥感、图像解译和机器学习。E-mail： sun_jin_yan@126.com
通讯作者简介: 周绍光(1966—　)，男，副教授，研究方向为摄影测量与遥感和数字图分析。E-mail： zhousg1966@126.com
中图分类号: TP701
文献标识码: A

摘要

针对高分辨率遥感影像的特点，提出了基于多类分割与模板匹配的建筑物轮廓矢量化方法：首先对影像进行多尺度SVM分割获取建筑物候选点；然后在Radon变换结合主轴分析获取建筑物主方向的基础上，引入多类分割思想，构建用于分割的能量函数，基于α-扩展算法解算能量函数，将轮廓线分割为3类边缘线段；接着构建形状先验的边缘模板，进行精确定位以获取边缘线的实际位置，去除锯齿状变形，降低提取结果的影响；最后相邻边缘线相正交得到拐角点，依次连接每一个拐角点，得到规则化的建筑物轮廓。相比于同类其他方法，此方法考虑了边缘点的方向信息和相邻边缘点趋于同一类的先验知识，可得到近似全局最优的边缘线段分割结果，避免了规则化过程中选择初始点和处理顺序的麻烦和不利影响，同时充分利用了影像特征，对边缘线段进行精确定位，减弱建筑物提取结果误差的影响。对不同影像的实验结果证明此方法可得到规则化的建筑物外轮廓线，不考虑提取过程中遗漏的建筑物，矢量化结果平均准确度为89%、完整度98%、几何形状相似性87%、整体质量85%。

关键词

遥感影像, 建筑物矢量化, 建筑物外轮廓, α-扩展, 模板匹配, 规则化

Building outline vectorization from high spatial resolution imagery
expand article info SUN Jinyan1,2 , HUANG Zuoji1,2 , ZHOU Shaoguang4 , XU Nan3 , QIAN Haiming1,2 , WANG Chunlin1,2
1.Anhui & Huaihe River Institute of Hydraulic Research, Hefei 230088, China
2.Anhui Dayu Project Construction Supervision and Consult Co., Ltd., Hefei 230088, China
3.Center for earth system science, Tsinghua university, Beijing 100084, China
4.School of Earth Science and Engineering, Hohai University, Nanjing 210098, China

Abstract

The extraction of building outlines from high spatial resolution imagery is a key element of numerous geospatial applications and has been addressed by various approaches. However, the final extraction results are always irregular or inaccurate owing to the boundary regularization algorithm and variability of building shape. This paper proposes a new method for the regularization and vectorization of two dimensional building outlines from high spatial resolution imagery. To accomplish this task, we utilize image segmentation to detect the two main orientations (θ and θ+90°) of the building blobs. To effectively refine boundaries, we then divide the boundary points, which were obtained clockwise, into the first principal, second principal, and unknown orientation classes. Then, we use least square template matching to precisely position the edge to reduce accuracy loss. Finally, the building outlines are generated by connecting the corner points with intersecting adjacent lines. In addition to the omission buildings, experimental results confirm the ability of the presented system to effectively and steadily extract building outlines with an overall average correctness of 89%, completeness of 98%, shape accuracy of 87%, and quality of 85%. This method can be widely used in various applications. Specifically, our method can work with a relatively low-accuracy image segmentation. Therefore, it can be applied for the vector quantization of large-area building outlines. However, our method only focuses on building outlines and does not consider the internal structure of the building. In the future, more attention should be givento solve this issue.

Key words

remote sensing image, building vectorization, building outline, α-expansion, template matching, regularization

1 引　言

建筑物轮廓信息对违章建筑的监管、地图的更新、房地产评估、智慧城市的构建等具有重要意义。遥感技术的不断进步，使得自动矢量化提取高分辨率遥感影像中建筑物轮廓信息成为可能。如何高精度、自动化地从高分辨率遥感影像中提取建筑物轮廓信息成为学者们研究的热点(Ok，2013)。

目前，高分辨率遥感影像中建筑物矢量化提取方法可以大致分为基于细化的方法、基于角点检测的方法和基于直线边缘检测的方法。基于细化的方法较为费时，不能直接提取图形的线宽等信息(吴秀芸，2011)。基于角点检测的方法有两个处理方向：一是角点(拐角点)来自于建筑物边缘线，按照角点之间的几何关系(角度、距离等)进行后续的处理(Maas和Vosselman，1999；Zhang 等，2006；Sampath和Shan，2007；沈蔚 等，2008；Dutter，2007；孟亚宾，2007)；这类方法直接对基础数据(建筑物提取结果)进行处理，没有充分利用影像特征，且对基础数据的质量有较高的要求。二是角点来自影像，结合匹配方法获取最终结果(周绍光 等，2015)；或者先充分利用地物几何特征及图像特征(HSV，纹理等)得到准确建筑物角点的基础上，结合变分水平集演化得到最终结果(Cote和Saeedi，2013)，其缺点在于房屋的整体几何约束信息及直线边缘没有充分利用，由于某些角点被遮蔽或模糊等原因，引起角点匹配和提取错误，可能导致整个提取的失败。基于直线边缘检测的方法则在利用边缘检测算法得到边缘点后，结合直线检测方法(Hough变换、Radon变换等)获取直线边缘，再通过连接及其他手段得到建筑物轮廓(杨化超 等，2006)；但该方法易受噪声、阴影和墙面等因素的干扰，从而导致提取的边缘轮廓不准确。

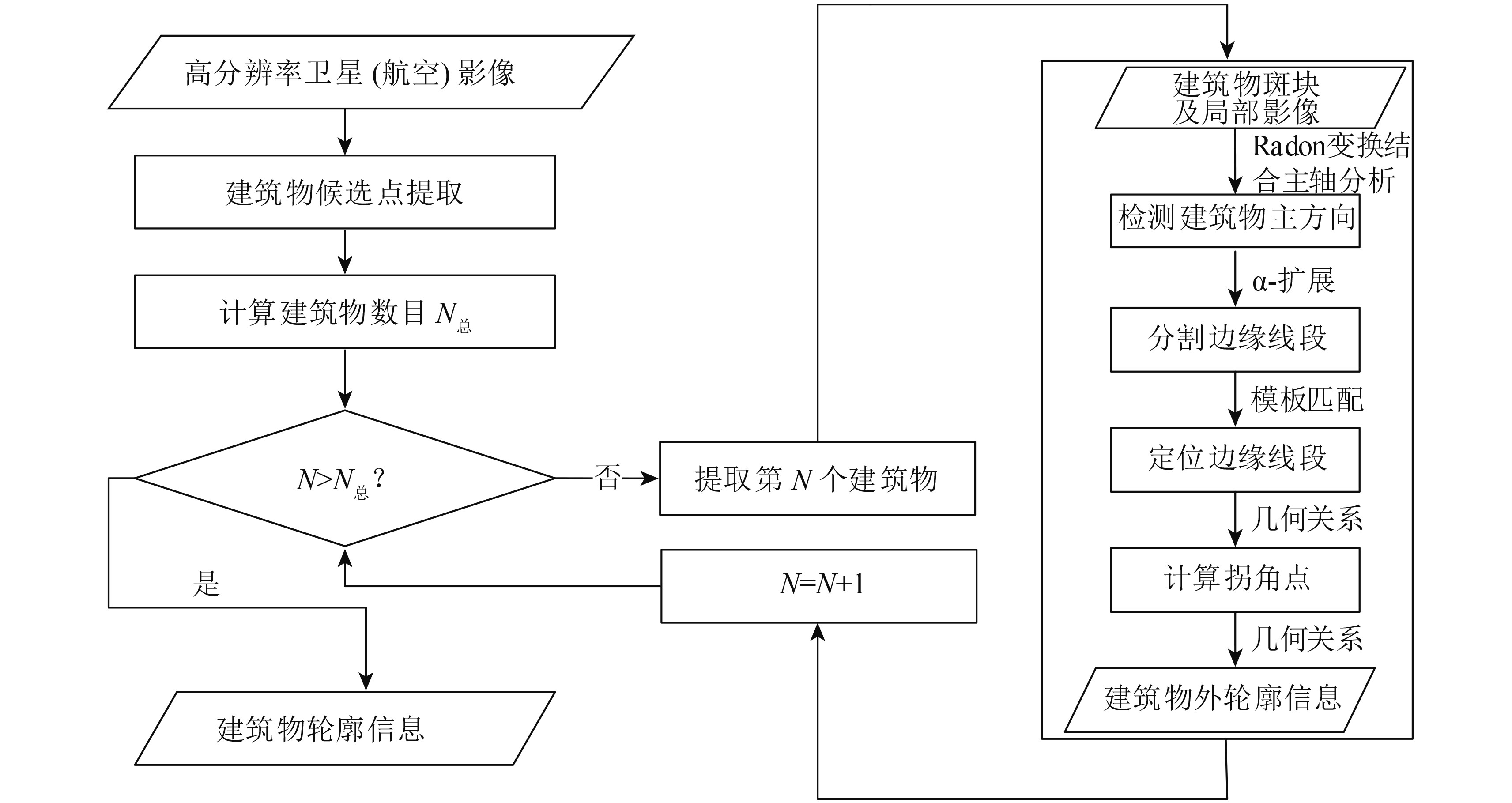
鉴于此，本文提出了一种基于多类分割与模板匹配的建筑物轮廓信息矢量化方法：(1)引入多类分割思想，将边缘线分段问题转换为能量函数的最小化问题，提出了基于α-扩展算法的边缘线分类方法。既考虑了每一个边缘点的方向信息，也利用了相邻边缘点趋于同一类的这一先验知识，可以实现近似全局最优的分类结果，同时此方法避免了选择初始点和处理顺序的麻烦和不利影响。(2)借助模板匹配理论，充分利用影像特征，对于边缘线段进行精确定位，以减弱建筑物提取结果误差的影响。技术路线见图1。


图 1 建筑物轮廓信息矢量化流程
Fig. 1 Flowchart of the proposed building outlines vectorization methodology

2 建筑物候选点提取

高分辨率影像可展现大量的地物特征：地物的颜色、尺寸、形状、纹理以及地物之间的布局关系，空间几何信息异常丰富。然而，高分辨率影像包含太多的非建筑物的光谱和纹理信息，同时噪声(例如墙面、阴影、树木等)的大量存在，也增加了建筑物信息提取的难度。Gabor滤波器在分析数字图像局部区域的频率特征和方向特征方面都具有非常优异的性能，所以文中首先采用一维Gabor滤波器获取高分辨率遥感影像的角度纹理特征和方向特征，同时结合光谱特征构造待分割的特征矢量；然后从单个像元开始，自下而上对特征矢量进行多尺度分割：在人工选择各地物样本的基础上，结合支持向量机(SVM)方法将图像分割为建筑物信息和非建筑物信息；最后结合建筑物的几何特征，结合数学形态学方法得到用于建筑物矢量化的建筑物候选点集(也就是建筑物斑块)。

3 建筑物矢量化

3.1 建筑物主方向检测

通常大部分建筑物都具有垂直结构，这些垂直结构均由两条直线轴构成。依据这一特征，学者们提出很多获取这两个主方向(最大轴和最小轴)的方法，具有代表性的有主成分分析法(陆见微，2006)，最小二乘方法(Chaudhuri和Samal，2007)，改进Hough变换方法(Rau和Chen，2003)。本文采用一种简单的方式-Radon原理结合主轴分析来获取建筑物的主方向：

(1) 对初始轮廓线图像进行Radon变换得到一个累加数列，投影角度θ为0°—179°。累加数列中，行表示投影角度θ，列表示投影累计值；

(2) 去除每一列中小于2的累计值(包含最大值)；

(3) 将每一列的最大值和次大值相加作为这一列的的最终值，生成一个1×180的数组；

(4) 将数组分成两组：一组角度范围是0°—89°，另一组角度范围是90°—179°。接着将第2部分的投影累计值与对应的第1部分投影累计值相加，即0°+90°，1°+91°，…，89°+179°，从而得到第1部分0°—89°新的角度累计值；

(5) 最后依据角度累加值对角度θ(0°—89°)进行重新排序，取最大值θmax作为第1主方向，此时第2主方向为θmax+90°。

采用实验验证方法的有效性结果如表1所示。

表 1 建筑物主方向检测结果比较
Table 1 Evaluation results of four methods

下载CSV 
方法 0°—1° 1°—5° 5°—9° 9°以上
本文方法 33 5 2 1
主成分分析法 4 6 6 25
最小二乘方法 4 5 14 18
改进的霍夫变换 29 8 2 2

从表1可以看出，文中方法检测的建筑物主方向无偏差数目为33个，远大于主成分分析法和最小二乘方法，其他3种情况数目分别为5，2，1，这表明该方法计算的正确率高于其他算法。

3.2 建筑物边缘线段分割

3.2.1 边缘线段分割方法的设计

理论上，建筑物的矢量化应该跟起始点的位置和处理边缘线段的顺序无关，但实际上，如果选择不同的起始点或者不同的边缘线段处理顺序，目前很多的算法可能得到不同的处理结果，例如管子算法、道格拉斯-普克DP(Douglas-Peukcer)算法结合直线逼近等矢量化方法，而选择最佳起始点和最佳的处理顺序是非常耗时的。本文将边缘线进行分类可以避免最佳初始点或最佳处理顺序的选择问题，且为随后的边缘线段精确定位打下基础。

α-扩展算法是将ICM算法循环迭代的思想进入Graph Cuts方法，适用于图像分割，模型拟合等问题的算法(Boykov 等，2001；Boykov和Kolmogorov，2004)。本文采用α-扩展算法思想对边缘线进行分割：在获取建筑物两个主方向的基础上，对建筑物边缘线进行多类分割，从而将建筑物边缘线分割成3类：第1主方向类，第2主方向类以及不定方向类。采用的分割能量函数为：

${E}\left( {f} \right) = \mathop \sum \limits_{p \in { S}} {{{D}}_p}\left( {{{f}_p}} \right) + \mathop \sum \limits_{\left\{ {p,q} \right\} \in { N}} {{V}_{p,q}}\left( {{{f}_p},{{f}_q}} \right)$ (1)

式中， S表示一栋建筑物所有边缘点的集合， N为边缘点的邻域系统，采用八邻域； f是边缘线的一种分割结果； fp为边缘点p所属类别； fp有3个标记值：“1”、“2”、“3”，分别表示第1主方向类、第2主方向类、不定方向类；${{{D}}_p}\left( {{{f}_p}} \right)$为数据项(data cost)，体现了边缘点p与某一类别的相似性。${V_{p,q}}\left( {{{f}_p},{{f}_q}} \right)$为平滑项(smooth cost)，体现了相邻边缘点之间的相似性。相邻两个边缘点距离越近、特征值越近似，该项值越大，这两个边缘点就越有可能被分为一类，利用α-扩展对边缘线进行分类的主要步骤：

(1) 构建用于分割轮廓线的能量函数；

(2) 对轮廓线进行任意的分割得到初始分割结果f；

(3) 随机设置α类的顺序，α$ \in \! {{L}}$，${{L}} \!=\! \left\{ {{{{L}}_1},{{{L}}_2},{{{L}}_\alpha }} \right\}$，令success=0；

(4) 对与每一个α类，构建图，求解图的最小割${C} = argmin\left( {{ E}\left( {{{{f}'}^c}} \right)} \right)$；

(5) 依据最小割，更新分割结果$\hat {{f}},\hat {{f}}= argmin$$ \left( {{E}\left( {{f}'} \right)} \right)$；

(6) 如果${ E}\left( \hat {{f}} \right) < { E}\left( {f} \right)$，则令${f} \!=\! \hat {{f}},{E}\left( {f} \right) \!=\! {E}\left( \hat {{f}} \right)$，success=1；

(7) success=1，重新返回步骤3，重复进行；

(8) 如果success=0，即${E}\left( \hat {{f}} \right) \geqslant {E}\left( {f} \right)$，输出最终分割结果$\hat {{f}}$。

图2为边缘线段分割的主要流程。


图 2 边缘线段分割流程图
Fig. 2 Flowchart of the boundary segmentation

对每一个α类，首先对所有边缘点建立能量函数图，标记为α类的边缘点将被固定为α类；然后通过最大流最小割算法对能量函数图进行“割”。“割”的结果是其中部分原标记值不为α的边缘点被重新标记为α，剩余边缘点仍然保持原有类别不变。通过不断循环修改每个边缘点的标记值，使得能量函数逐渐收敛，最终收敛到全局最小值。

3.2.2 图的构建和解算

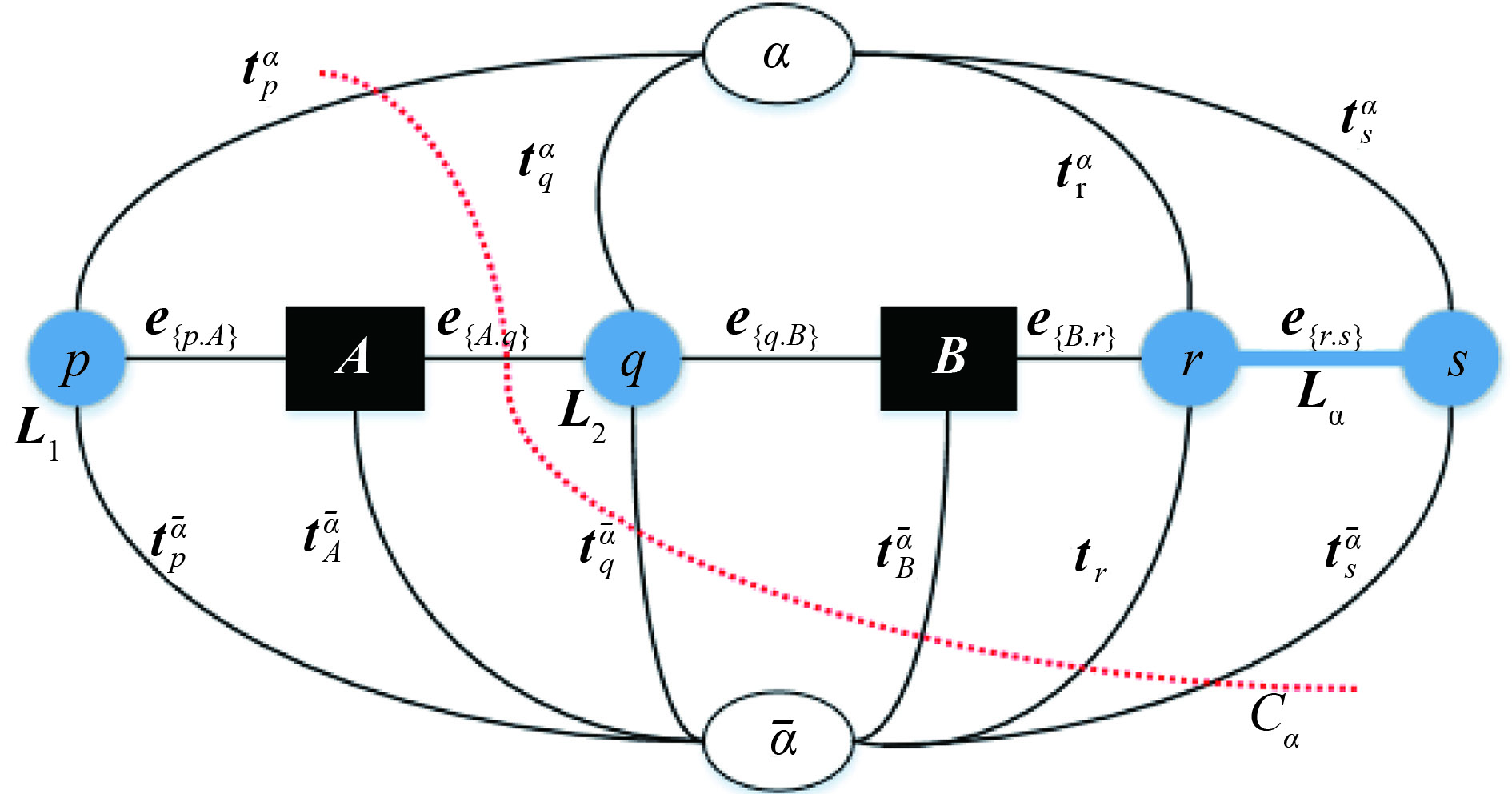
图3为一栋建筑物轮廓线(边缘点数目为Num)上部分边缘点与两个类别顶点α和${\bar \alpha }$之间构成的图${{G}_\alpha },{{G}_\alpha } = \left\{ {{{{V}}_\alpha },{{E}_\alpha }} \right\}$。红色虚线${{C}_\alpha }$，${{C}_\alpha } \subset {{E}_\alpha }$即为该图${{G}_\alpha }$的割，割将边缘点分成了两部分，使得一部分边缘点属于目标顶点${\bar \alpha }$。剩下的边缘点则属于${\bar \alpha }$类，即保持原来的类别不变。


图 3 一条边缘线段的图${{ {{G}}}_\alpha }$
Fig. 3 Graph${{{{ G}}}_\alpha }$

图3中边缘点${{P}} = \left\{ {p,q,r,s} \right\}$，${{P}} \in {{S}}$，类别${{L}} = \left\{ {{{{L}}_1},{{{L}}_2},{{{L}}_\alpha }} \right\}$，其中，${{{L}}_1} \!=\! \left\{ p \right\}$，${{{L}}_2} \!=\! \left\{ q \right\}$，${{{L}}_\alpha } \!=\! \left\{ {r,s} \right\}$，辅助点${{A}} = {A_{\left\{ {p,q} \right\}}}$，${{B}} = {B_{\left\{ {q,r} \right\}}}$。根据相邻的边缘点$\left\{ {p,q} \right\} \in {{S}}$趋于同一类的特征，如果相邻的边缘点$\left\{ {p,q} \right\} \in {{S}}$属于不同类，即${L_{\rm{p}}} \ne {L_{\rm{q}}}$，则在p，q之间引入一个辅助节点${A_{\left\{ {p,q} \right\}}}$。图 Gα中所有的顶点数目可以表示为

${{{V}}_\alpha } = \left\{ {{\rm{\alpha }},\bar \alpha ,{{P}},\mathop \cup \limits_{\begin{array}{*{20}{c}}{\left\{ {p,q} \right\} \in {{S}}}\\{{{{L}}_{\rm{p}}} \ne {{{L}}_{\rm{q}}}}\end{array}} {A_{\left\{ {p,q} \right\}}}} \right\}$ (2)

每一个点p∈ P都通过T链(${{t}}_p^{\alpha }$，${{t}}_p^{\bar \alpha }$)分别与顶点α和$\bar \alpha $相连接。如果相邻的边缘点$\left\{ {p,q} \right\} \in {{S}}$属于同一类，即${{ L}_{\rm{p}}} = {{ L}_{\rm{q}}}$，则通过N链(如${{ e}_{\left\{ {p,q} \right\}}}$)相连接；如果相邻的边缘点$\left\{ {p,q} \right\} \in {{S}}$属于不同类，即${{L}_{\rm{p}}} \ne {{L}_{\rm{q}}}$，则利用一个由3条链组成的${{E}_{\left\{ {p,q} \right\}}} = \left\{ {{{ e}_{\left\{ {p,{ A}} \right\}}},{{ e}_{\left\{ {{ A},q} \right\}}},{{t}}_A^{\bar \alpha }} \right\}$表示，A为p，q之间辅助节点。图 Gα中所有链 Eα可以表示为

${{E}_\alpha } = \left\{ {\mathop \cup \limits_{p \in {{P}}} \left\{ {{{t}}_p^\alpha ,{{t}}_p^{\bar \alpha }} \right\},\mathop \cup \limits_{\begin{array}{*{20}{c}}{\left\{ {p,q} \right\} \in {{S}}}\\{{{{L}}_{\rm{p}}} \ne {{{L}}_{\rm{q}}}}\end{array}} {{ E}_{\left\{ {p,q} \right\}}},\mathop \cup \limits_{\begin{array}{*{20}{c}}{\left\{ {p,q} \right\} \in {{S}}}\\{{{{L}}_{\rm{p}}} = {{{L}}_{\rm{q}}}}\end{array}} {{ e}_{\left\{ {p,q} \right\}}}} \right\}$ (3)

至此，建立一个关于边缘线的图${{G}_\alpha } = \left\{ {{{{V}}_\alpha },{{E}_\alpha }} \right\}$。下面将给图 Gα中所有的链 Eα赋予权重，从而得到用以边缘线分类的能量函数图。每条链的权重按照基本情况的不同，权重也不同如表2所示。

表 2 图Gα中所有链Eα的权重(以点p为例)
Table 2 The weight of the edges for graph

下载CSV 
链 基本情况 权重
${{t}}_p^{\bar \alpha }$ $p \in {{{L}}_\alpha }$ ∞
${{t}}_p^{\bar \alpha }$ $p \notin {{{L}}_\alpha }$ ${{{D}}_p}\left( {{{L}_p}} \right)$
${{t}}_p^\alpha $ $p \in {{P}}$ ${{{D}}_p}\left( \alpha \right)$
${{ e}_{\left\{ {p,q} \right\}}}$ $\left\{ {p,q} \right\} \in {{S}},{{L}_{\rm{p}}} = {{L}_{\rm{q}}}$ ${{V}}\left( {{{L}_p},\alpha } \right)$
${{ e}_{\left\{ {p,A} \right\}}}$ ${{V}}\left( {{{L}_p}{\rm{,\alpha }}} \right)$
${{ e}_{\left\{ {A,q} \right\}}}$ $\left\{ {p,q} \right\} \in {{S}},{{L}_{\rm{p}}} \ne {{L}_{\rm{q}}}$ ${{V}}\left( {\alpha ,{{L}_q}} \right)$
${{t}}_A^{\bar \alpha }$ ${{V}}\left( {{{L}_p},{{L}_{\rm{q}}}} \right)$

为了完成图 Gα的构建，需要确定表2中所有链的权重。首先获取以下两种数据：(1)建筑物的两个互相垂直的主方向角度(θ，θ+90°)，每一个角度都对应于一个边缘线类别中心；(2)每一个边缘点的局部方向。

在3.1节已经得到了建筑物的两个主方向角度(θ，θ+90°)，下面将说明如何获取每一个边缘点的局部方向：在边缘追踪得到有序的建筑物边缘点的基础上，本文获取每一个边缘点局部方向的思路为：采用以当前点为中心，依次取与其相邻的半径R范围内的轮廓点，即2R+1个点进行主成分分析PCA(Principal Components Analysis)，以第一主成分计算当前点的局部方向。

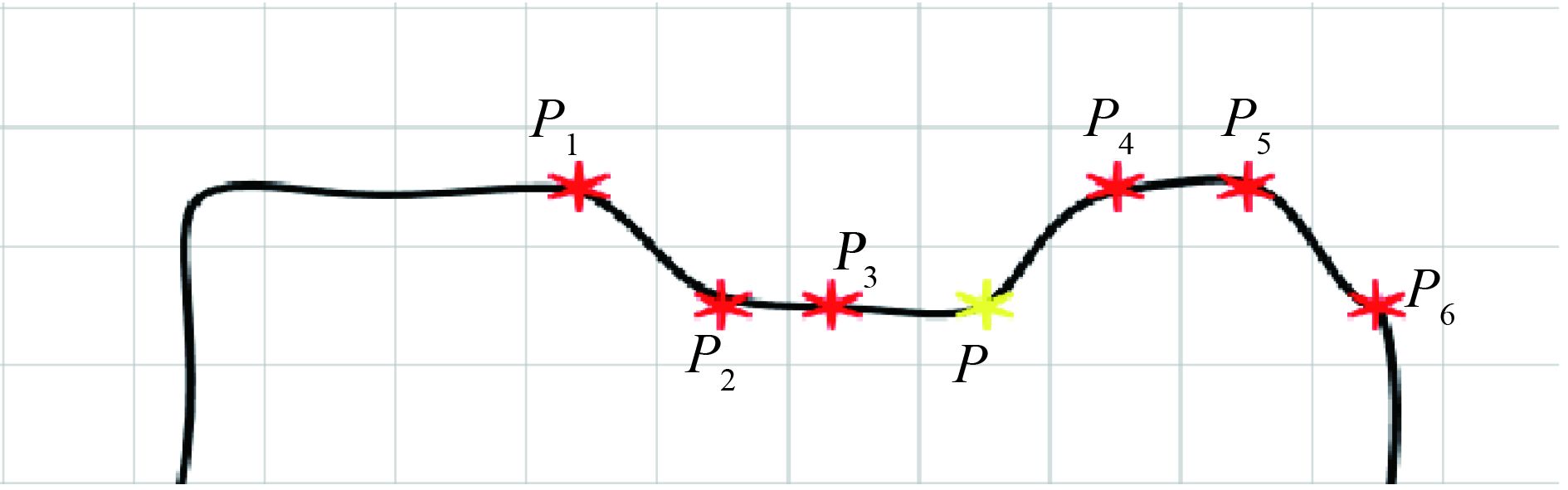
图4所示，要获取点P的局部方向，取以P为中心，半径R=3范围内的7个点(点P，P1—6)，以这7个点坐标(x，y)作为2维向量 S， S7×2=(x，y)T，构建局部协方差矩阵，采用特征值分解求得协方差矩阵的两个特征值，并将最大特征值对应的特征向量(即第一主成分)作为当前点P的法向量(a，b)。最后根据式(4)计算当前点的局部方向$loca{l_{{\rm{direc}}}}\left( p \right)$，公式如下：

$loca{l_{{\rm{direc}}}}\left( p \right) = {\rm{arctan}}\left( {\frac{b}{a}} \right)$ (4)

在获取每个边缘点的局部方向的基础上，计算连接每一个边缘点分别与两个顶点(θ，θ+90°)的T链的权重，公式如下：

${{\rm{D}}_p}\left( \theta \right) = {\lambda _1} - \left[ {{\lambda _1}{{\rm{e}}^{ - \frac{{\left| {loca{l_{{\rm{direc}}}}\left( p \right) - \theta } \right|}}{{ksif}}}}} \right]$ (5)
${{\rm{D}}_p}\left( {\theta + 90^\circ } \right) = {\lambda _1} - \left[ {{\lambda _1}{{\rm{e}}^{ - \frac{{\left| {loca{l_{\rm{direc}}}\left( p \right) - \left( {\theta + 90} \right)} \right|}}{{ksif}}}}} \right]$ (6)

式中，${{\rm{D}}_p}\left( \theta \right)$和${{\rm{D}}_p}\left( {\theta + 90^\circ } \right)$分别为点p属于第一主方向θ类和第二主方向θ+90°类需要付出的代价。系数${\lambda _1}$为断开T链的一个惩罚系数。参数ksif为常数。


图 4 边缘点局部方向的获取
Fig. 4 Local direction of the point P.

计算连接点p与不确定类的T链的权重为

${{\rm{D}}_p}\left( {{\rm{unknown}}} \right) = {\lambda _2}$ (7)

式中，由于这一类的方向是不确定的，我们以一个固定值${\lambda _2}$作为断开点p与不确定类连接需要付出的代价。

根据相邻边缘点趋于同一类的这一先验知识，如果相邻边缘点被分为同一类，这两点之间的N链并没有被破坏，那么N链的权重为0；如果相邻边缘点没有被分为同一类，则必须进行惩罚，惩罚值与这两个点的局部方向密切相关，相应的计算公式如下

${\rm{V}}\left( {{L_p},{L_q}} \right) = \left\{ {\begin{array}{*{20}{c}}{0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{L}_{\rm{p}}} = {{L}_{\rm{q}}}}\\{{\lambda _3} - \left[ {{\lambda _3}{{\rm{e}}^{ - \frac{{\left| {loca{l_{{\rm{direc}}}}\left( p \right) - loca{l_{\rm{direc}}}\left( q \right)} \right|}}{{ksif}}}}} \right]\;\;\;\;\;\;\;\;{{L}_{\rm{p}}} \ne {{L}_{\rm{q}}}}\end{array}\left\{ {p,q} \right\} \in {{N}}} \right.$ (8)

式中，系数λ3为相邻边缘点没有被分为同一类的惩罚系数，也是引入辅助节点的惩罚系数。V(Lp，Lq)即为将相邻边缘点分成不同类别需要付出的代价。

至此，给出了所有链的权重，完成了图的构建。在此基础上，将建筑物边缘线分为3个类别。

图5(a)为建筑物，图5(b)为分割结果的彩色展示，图5(b)中蓝色和红色箭头为分割后建筑物的两个主方向，可以看出分割结果较好。


图 5 边缘线段分割实验
Fig. 5 An example to show the results of the boundary segmentation

3.3 边缘线段的精确定位

现有建筑物轮廓信息规则化方法大多是先进行边缘线的简化(道格拉斯算法或折线逼近，管子算法等)，之后按照一定的法则(正交，模型)进行规则化。虽然这样处理后的建筑物相对于初始提取结果更规则，但是可能会导致提取结果精度的降低，且可能存在规则化形状与建筑物实际形状不太吻合的情况。

考虑到高分辨率影像在边缘处有更高的水平采样率，本文在以前的研究成果基础上，引入了模板匹配的思想，充分利用影像信息，通过构建不同的边缘模板，利用改进的最小二乘模板匹配精确定位建筑物边缘线(Gruen和Agouris，1994)。

在精确定位过程中，边缘模板非常重要。模板的合适与否对实验结果影响程度较大。由于每条边缘线段周围的场景均不相同，所以相应模板的具体形状也不相同。但是同一条边缘线上，边缘点周围的场景变化差异较小。因此实验中针对每一条边缘线，依照以下规则来建立动态的边缘模型。

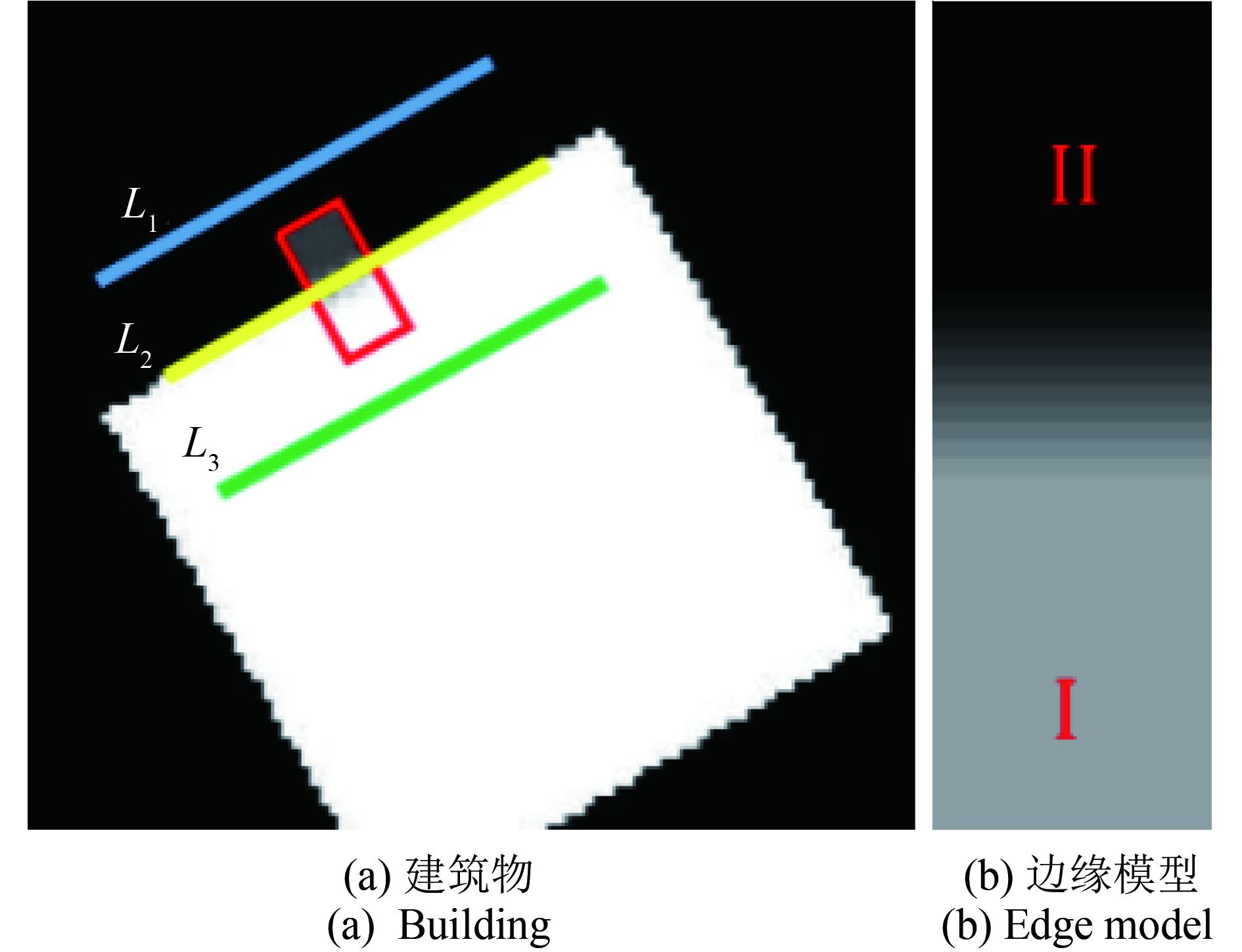
根据建筑物的边缘线特征，在高斯边缘模板的帮助下，建立如下图6(b)所示的边缘模板。假设，图6(a)中白色矩形为一栋建筑物，要建立起边缘线段L2的边缘模板，则首先以L2为中心，R=2 m为半径，建立边缘缓冲区。接着以边缘缓冲区的边界线L1和L3分别给模板相应区域赋值。


图 6 模板的构建
Fig. 6 The Gaussian blurred edge template generation for an edge

图6(a)中模板(红色矩形)上的灰色区域为对应图像中的背景，其像素值为缓冲区边界线L1上所有像素值的平均值；白色区域为对应图像中的前景，其像素值为缓冲区边界线L3上所有像素值的平均值；模板中心区域为对应的边缘，值取边缘线L2上所有像素值的平均值。构建的模板结构如图6(b)所示，Ⅱ区域为背景，Ⅰ区域为前景，两区域的交界处即为模板中边缘线的实际位置。实验中，实验模板的大小不宜过大，长宽比要适中，太宽容易遗漏短边缘，太窄则受噪声的影响越严重，容易将非边缘点识别为边缘点。当分辨率为0.13 m时，模板大小为15×7，15×5，13×7较好。此外，“类斜坡”长度根据具体情况可以调整。实际应用中，应根据建筑物实际情况，建立与边缘类似的模板。

因边缘点之间的偏差情况不同，本文通过对每一条边缘线段(第一主方向类和第二主方向类)上的所有边缘点在其法方向上进行模板匹配，在半径R范围内寻找最佳匹配点来完成对轮廓线的精确定位(Hu 等，2009)。

$R = \left[ {\frac{1}{{SR}}} \right]$ (9)

式中，SR为影像分辨率，当SR=0.13时，R=8。差值dif用于判断最佳匹配位置，可表示为

$dif = \left[ {\frac{1}{{{N_{\rm \text{Ⅰ}}}}}\sum\limits_{i = 1}^{{N_{\rm \text{Ⅰ}}}} {{f_{\rm \text{Ⅰ}}}} \left( {x,y} \right) - \frac{1}{{{N_{\rm \text{Ⅱ}}}}}\sum\limits_{i = 1}^{{N_{\rm \text{Ⅱ}}}} {{f_{\rm \text{Ⅱ}}}} \left( {x,y} \right)} \right]$ (10)

式中，NⅠ，NⅡ分别表示图6(b)模板Ⅰ和Ⅱ区域对应的局部图像区域的像素个数。f是图像窗口。fⅠ和fⅡ分别表示图像窗口中与模板Ⅰ和Ⅱ区域对应的像素集合。

在进行最小二乘模板匹配的过程中，假设一条边缘线段上的点全部被移除，也就是均没有找到符合条件的匹配点，如果这条边缘线段同时满足以下3个条件，则保留其原始边缘点坐标：

(1) 该边缘线段的长度大于$\displaystyle\frac{{1.5}}{{SR}}$，(即1.5 m)；

(2) 该边缘线段与相邻的边缘线段属于不同类；

(3) 其相邻的两个边缘线段属于同一类。

最后，在获取准确边缘线段 (线段方向已知)的基础上，计算相邻边缘线的拐角点，连接拐角点以得到规则化的建筑物外轮廓。

3.4 精度评价

采用两种方式评价提取结果的质量：一是定性比较，即将提取结果叠加到原图上与本文建筑物提取结果及人工识别结果比较；二是定量比较，采用基于像素的4个衡量参数(Zeng 等，2013)：准确度(Cr)，完整度(Cm)，整体质量(Qoq)、一个几何形状相似度参数(Ssh)进行评价。

${C_{\rm{r}}} = \frac{{TP}}{{TP + FP}}$ (11)
${C_{\rm{m}}} = \frac{{TP}}{{TP + FN}}$ (12)
${Q_{\rm{oq}}} = \frac{{TP}}{{TP + FP + FN}}$ (13)
${S_{\rm{sh}}} = 1 - \frac{{\left| {{A_{\rm{r}}} - {A_{\rm{e}}}} \right|}}{{{A_{\rm{r}}}}}$ (14)

式中，TP表示提取结果中准确的建筑物像素点；FP表示提取结果中错误的建筑物像素点；FN表示被遗漏的建筑物像素点；Ae表示提取的所有建筑物总面积，Ar表示参数数据总面积。4个衡量参数的最佳值均为“1”，即100%。

4 实验与分析

图7中第1列为原始影像，分别标记为a、b、c，a为假彩色卫星影像，大小为111×222 pixels、b为Geo Eye-1全色影像(Li 等，2014)，大小为618×467 pixels、c为“真”正射航空影像，大小为329×341 pixels，空间分辨率分别为0.6 m/pixel，0.5 m/pixels和0.25 m/pixel。第2列图像中蓝色线为本文所提方法实验结果；第3列图像中红色线为Zhou (2015)中方法实验结果；第4列图像中绿色线为Douglas-Peukcer(DP)算法结合直线逼近方法实验结果。最后一列为参考数据(ground truth)。


图 7 实验比较
Fig. 7 Comparison of experimental

对比图7中各图，从外形上看，相较于Zhou(2015)方法和本文方法，DP直线逼近方法受建筑物提取结果影响较大，矢量化结果与参考数据相差最大；Zhou(2015)方法通过匹配建筑物拐角点，所提结果与参考数据较为相符，但是此方法易受建筑物本身及其周围地物的影响，容易出现误匹配点，导致矢量化结果存在局部不规则现象；本文方法充分利用了边缘线段几何特征(方向、中心点、长度、相似性等)和影像特征，提取结果与参考数据吻合。表3是上述3种方法的实验结果的定量比较。

表 3 3种方法实验结果
Table 3 Quantitative evaluation results of three methods

下载CSV 
/%
属性 完整度 正确度 几何位置相似性 总体精度
图像编号 a b c a b c a b c a b c
DP直线逼近 97.79 96.47 98.65 94.24 98.33 94.59 92.28 94.83 93.38 91.82 94.92 93.00
Zhou 98.87 96.79 98.70 99.54 98.67 94.92 98.42 95.49 93.75 98.41 95.55 93.42
本文方法 100 98.01 99.30 95.46 99.46 94.72 95.24 97.47 93.77 95.46 97.48 94.10

从表3可以看出，相对于其他两种方法，本文方法提取结果完整度最好，而对于矢量化结果的正确度、几何位置相似性和总体精度，3种方法相差不明显。如果将DP直线逼近方法和强制正交化结合使用可以获取更接近实际形状的建筑物，但是这种方法对图像分割精度的精度要求很高，难以满足，因此，这种方法目前只用于有LiDAR数据或DEM参与提取的建筑物轮廓规则化。Zhou(2015)中方法是本文方法的前身，适合环境干扰因素较少的建筑物轮廓信息提取，实际应用中建筑物周围往往很复杂，故此方法对大范围，不同数据源的建筑物轮廓信息提取适用性不好。

图8为本文方法在其他数据源上的实验。图8(a)、(b)为卫星影像，大小分别为306×428和386×667，空间分辨率分别为0.5 m/pixel和0.7 m/pixel，图8(e)(f)为航空影像，大小分别为729×957、1133×1372，分辨率均为0.09 m/pixel。


图 8 其他实验实例
Fig. 8 Other examples

图8(a)(b)(e)(f)中蓝色线为本文方法实验结果，图8(c)(d)(g)(h)为相应的参考数据。黄色椭圆线包围区域为漏提取得建筑物。对比两类图像可以看出，从外形的角度，本文方法提取结合较为准确，且适合大面积矢量化建筑物。不包含漏提取的建筑物，表4为对图8所示各实验图建筑物提取结果和矢量化结果的精度分析。从表4可以发现，相对于建筑物提取结果，矢量化结果的精度有所提高，说明本文方法可以在规则化建筑物的同时，提取矢量化结果的精度，减弱部分建筑物提取结果误差的影响。

表 4 3种方法实验结果
Table 4 Quantitative evaluation results of three methods

下载CSV 
/%
图像编号 建筑物数目 建筑物提取 矢量化结果
Cm Cr Qoq Ssh Cm Cr Qoq Ssh
(d) 5 96.70 95.44 92.43 92.08 95.55 91.11 87.40 86.22
(e) 22 96.55 78.72 76.57 70.46 99.48 86.91 86.52 84.50
(f) 3 98.54 94.67 93.36 92.99 99.47 93.08 92.63 92.08
(g) 7 97.04 94.01 92.28 91.80 97.54 94.83 92.62 92.22
其他 28 87.63 91.96 81.39 79.96 97.86 87.88 86.22 84.36
平均值 93.07 88.06 82.47 79.71 98.28 88.90 87.52 85.91

5 结　论

本文对基于影像所提取的建筑物进行矢量化(规则化)，对分割所得建筑物边缘线利用Radon变换结合主轴分析以确定建筑物的两个主方向，然后采用多类分割的思想将边缘线分割为3类边缘线段，在此基础上，对边缘线段进行精确定位，通过相邻边缘线段相正交得到拐角点，连接角点得到规划化建筑物轮廓。相较于Douglas-Peukcer(DP)算法结合直线逼近方法和Zhou(2015)的方法，此方法的适用性更广，对图像分割的精度要求有所降低，可用于大范围的建筑物外轮廓矢量化(模型化)。方法的优点在于：

(1) Radon变换和主轴分析相结合，实现了两个建筑物主方向的可靠检测。

(2) 引入多类分割思想，将边缘线分段问题转换为能量函数的最小化问题，既考虑了每一个边缘点的方向信息，也利用了相邻边缘点趋于同一类的这一先验知识，可以实现近似全局最优的分类结果，同时此方法避免了选择初始点和处理顺序的麻烦和不利影响。

(3) 借助模板匹配理论，充分利用影像特征，对于边缘线段进行精确定位，减弱了建筑物提取结果误差的影响。

(4) 本方法适用于所有影像(卫星、航空、无人机影像)中建筑物的矢量化。

本文方法目前仅针对与建筑物的外轮廓，未考虑建筑物的内部结构，今后将在这一方面进行深入研究。

参考文献(References)

  • Boykov Y, Veksler O and Zabih R. 2001. Fast approximate energy minimization via graph cuts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 23 (11): 1222–1239. [DOI: 10.1109/34.969114]
  • Boykov Y and Kolmogorov V. 2004. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. IEEE Transactions on Pattern Analysis and Machine Intelligence, 26 (9): 1124–1137. [DOI: 10.1109/TPAMI.2004.60]
  • Chaudhuri D and Samal A. 2007. A simple method for fitting of bounding rectangle to closed regions. Pattern Recognition, 40 (7): 1981–1989. [DOI: 10.1016/j.patcog.2006.08.003]
  • Cote M and Saeedi P. 2013. Automatic rooftop extraction in nadir aerial imagery of suburban regions using corners and variational level set evolution. IEEE Transactions on Geoscience and Remote Sensing, 51 (1): 313–328. [DOI: 10.1109/TGRS.2012.2200689]
  • Dutter M. 2007. Generalization of building footprints derived from high resolution remote sensing data. Pennsylvania State:The Pennsylvania State University CiteSeerX Archives
  • Gruen A and Agouris P. 1994. Linear feature extraction by least squares template matching constrained by internal shape forces//Proceedings of SPIE 2357, ISPRS Commission III Symposium: Spatial Information from Digital Photogrammetry and Computer Vision. Munich, Federal Republic of Germany: SPIE:316[DOI: 10.1117/12.182860]
  • Hu X Y, Zhang Z X and Li J. 2009. Linear feature extraction using adaptive least-squares template matching and a scalable slope edge model. International Journal of Remote Sensing, 30 (13): 3393–3407. [DOI: 10.1080/01431160802562198]
  • Li Z B, Liu Z Z and Shi W Z. 2014. A fast level set algorithm for building roof recognition from high spatial resolution panchromatic images. IEEE Geoscience and Remote Sensing Letters, 11 (4): 743–747. [DOI: 10.1109/LGRS.2013.2278342]
  • Lu J W. 2006. A Study of Building Extraction from High Resolution Remote Sensing Images.Beijing: University of Chinese Academy of Sciences (陆见微. 2006. 高分辨率遥感图像中建筑物外形自动提取方法研究. 北京: 中国科学院研究生院)
  • Maas H G and Vosselman G. 1999. Two algorithms for extracting building models from raw laser altimetry data. ISPRS Journal of Photogrammetry and Remote Sensing, 54 (2/3): 153–163. [DOI: 10.1016/S0924-2716(99)00004-0]
  • Meng Y B. 2007. Study on the building contour extraction from high resolution satellite image. Fuxin: Liaoning Technical University (孟亚宾. 2007. 高分辨率卫星影像建筑物轮廓提取方法研究. 阜新: 辽宁工程技术大学)
  • OkAO. 2013. Automated detection of buildings from single VHR multispectral images using shadow information and graph cuts. ISPRS Journal of Photogrammetry and Remote Sensing, 86 : 21–40. [DOI: 10.1016/j.isprsjprs.2013.09.004]
  • Rau J Y and Chen L C. 2003. Fast straight lines detection using Hough transform with principal axis analysis. Journal of Photogrammetry and Remote Sensing, 8 (1): 15–34. [DOI: 10.6574/JPRS.2003.8(1).2]
  • Sampath A and Shan J. 2007. Building boundary tracing and regularization from airborne lidar point clouds. Photogrammetric Engineering and Remote Sensing, 73 (7): 805–812. [DOI: 10.14358/PERS.73.7.805]
  • Shen W, Li J, Chen Y H, Deng L and Peng G X. 2008. Algorithms study of building boundary extraction and normalization based on lidar data. Journal of Remote Sensing, 12 (5): 692–698. [DOI: 10.3321/j.issn:1007-4619.2008.05.003] ( 沈蔚, 李京, 陈云浩, 邓磊, 彭光雄. 2008. 基于LIDAR数据的建筑轮廓线提取及规则化算法研究. 遥感学报, 12 (5): 692–698. [DOI: 10.3321/j.issn:1007-4619.2008.05.003] )
  • Wu X Y. 2011. Research on Extraction and Contour Vectorizationof Buildings from High-Resolution Remote Sensed Images. Nanjing: Nanjing University (吴秀芸. 2011. 基于高分辨率遥感影像的建筑物提取及轮廓矢量化研究. 南京: 南京大学)
  • Yang H C, Deng K Z and Zhang S B. 2006. Semi-automated extraction from aerial image using improved Hough transformation. Science of Surveying and Mapping, 31 (6): 93–94, 97. [DOI: 10.3771/j.issn.1009-2307.2006.06.032] ( 杨化超, 邓喀中, 张书毕. 2006. 基于Hough变换的航空影像建筑物半自动提取. 测绘科学, 31 (6): 93–94, 97. [DOI: 10.3771/j.issn.1009-2307.2006.06.032] )
  • Zeng C Q, Wang J F and Lehrbass B. 2013. An evaluation system for building footprint extraction from remotely sensed data. IEEE Journal ofSelected Topics in Applied Earth Observations and Remote Sensing, 6 (3): 1640–1652. [DOI: 10.1109/JSTARS.2013.2256882]
  • Zhang K, Yan J and Chen S C. 2006. Automatic construction of building footprints from airborne LIDAR data. IEEE Transactions on Geoscience and Remote Sensing, 44 (9): 2523–2533. [DOI: 10.1109/TGRS.2006.874137]
  • Zhou S G, Sun J Y, Fan L, Xiang J and Chen C. 2015. Extraction of building contour from high resolution images. Remote Sensing for Land and Resources, 27 (3): 52–58. [DOI: 10.6046/gtzyyg.2015.03.10] ( 周绍光, 孙金彦, 凡莉, 向晶, 陈超. 2015. 高分辨率遥感影像的建筑物轮廓信息提取方法. 国土资源遥感, 27 (3): 52–58. [DOI: 10.6046/gtzyyg.2015.03.10] )
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体