搭载在Terra和Aqua两颗卫星上的中分辨率成像光谱仪(MODIS)是美国地球观测系统(EOS)计划中用于观测全球生物和物理过程的重要仪器。它采集的数据具有信息丰富，获取速度快、覆盖范围广等特点，广泛应用于对地检测、云分类、气候研究等领域。但由于传感器的限制和外在干扰，MODIS图像分辨率仍然局限在一定水平上。在MODIS 36个中等分辨率水平 (0.25—1 um)的光谱波段中(Aumann 等，2003)，有2个波段的空间分辨率是250 m，5个波段为500 m，另29个波段为1000 m。超分辨率重建(SR)可以增强MODIS图像的空间细节，去除图像噪声，保持图像边缘。

Harris(1964)首次提出了图像超分辨率的概念，图像超分辨率指利用一幅或多幅低分辨率图像重建高分辨率图像，主要方法可分为3类：基于插值的方法(Jain，1989；Parker 等，1983)，基于重建的方法(Irani和Peleg，1991；Schultz和Stevenson，1994)以及基于学习的方法(Yang 等，2008；Zeyde 等，2010；Dong 等，2011；Zhu 等，2014)。基于插值的方法主要有双线性插值，双三次方插值等，这类方法虽计算效率较高，但往往难于获得理想的重构图像；最大后验概率(MAP)图像超分辨率是典型的基于重建的方法，该方法通过对超分辨率重建这个病态问题进行正则化，具有降噪能力强、解唯一等优点，但存在正则化参数难于确定的问题，沈焕锋等人(2006)利用迭代重建的中间结果，提出了一种自适应选择正则化参数的方法；基于学习的方法通过学习高低分辨率图像之间的映射关系来重建图像，主要有基于例子的方法、基于稀疏表示的方法等；近年来，随着过完备字典稀疏表示理论的发展，基于稀疏表示的图像超分辨率引起了国内外众多研究者的关注(沈焕锋 等，2006；Shen 等，2016；刘哲 等，2015；潘宗序 等，2015；Li 等，2016)；Yang等人(2008)通过训练一对高低分辨率字典，并利用高低分辨率图像在相应字典下有相同系数的特点来重建图像；Zeyde等人(2010)使用K-SVD进行字典训练，提高了字典的训练速度；Li等根据高光谱图像(HSI)在空域和光谱域的自相似性，提出一种采用组稀疏策略的HIS图像超分辨率方法(Li 等，2016)；Dong等人(2011)基于图像的自相似性，提出基于稀疏表示的非局部正则化方法，提升了重建效果；Shen等人(2016)提出了一种适用于正则化图像超分辨的范数自适应选择方法，从而可以在图像超分辨率时优选保真项和正则化项的范数，这对基于稀疏表示的图像超分辨率有一定的指导作用。纵观图像超分辨率的最新研究成果，基于过完备字典稀疏表示的方法已逐渐成为图像超分辨率的主流。本文从MODIS图像的特点出发，基于稀疏表示理论，力图研究一种适用于MODIS图像的超分辨率方法。

由于不同传感器获取的MODIS图像，具有多种空间分辨率、光谱分辨率，包含了云层结构、土地覆盖等丰富的信息；相比于普通图像，MODIS图像具有精细的纹理结构和清晰的边缘轮廓，且图像的不同部分，纹理结构和边缘轮廓往往具有不同的特性，如果能针对MODIS图像的局部特性，对不同的图像区域进行分类，采用自适应的超分辨率方法，将有望提高重建效果；然而，传统基于稀疏表示的超分辨率方法大都没有考虑图像块之间的结构差异，从而采用对不同的图像块分类训练字典的方案，难于适应MODIS图像的特点。鉴于主题模型在图像分类中的成功应用，同时考虑到人类的视觉系统对自然图像的高频部分比较敏感，且传统超分辨率方法对图像纹理等高频部分的重建结果往往比较模糊的缺点，本文提出一种采用主题学习和稀疏表示的MODIS图像超分辨率重建方法。该方法首先通过双边滤波器将MODIS图像分解为平滑分量和纹理分量，将得到的纹理分量作为字典的训练样本；然后通过主题模型将训练样本图像划分为多个主题，每个主题训练一对高低分辨率字典，同时在字典训练阶段，运用改进的K-SVD字典更新方法，仅对字典和稀疏表示中的非零系数进行更新，以提高计算效率，减小表示误差；在图像重建阶段，同样用双边滤波器将待重建的低分辨率MODIS图像分解为平滑部分和纹理部分，平滑部分采用双三次方插值重建，而对于纹理部分的每个图像块，则通过主题模型自适应地选择相应的字典，结合稀疏系数重建出高分辨率纹理图像；最后，根据重建的平滑部分和纹理部分得到高分辨率MODIS图像。实验结果表明，重建的高分辨率MODIS图像在PSNR等客观指标及视觉效果上均优于传统方法。

由于图像中包含着大量的结构和纹理信息，而纹理部分包含着图像的丰富细节，因此，本文采用双边滤波器提取图像的纹理部分，然后进行稀疏表示和重建，而对平滑部分直接插值重建，最后结合两部分得到高分辨率图像。

在Yang等人(2008)提出的图像超分辨率模型中，训练样本的低分辨率图像由高分辨率图像降采样产生，然后训练图像被划分为图像块，组成大量的高低分辨率图像块对，同时训练这些图像块对可以得到高低分辨率字典D^h 和D^l ，并基于高低分辨率图像在对应字典上具有相同的稀疏系数进行超分辨率重建。因此，Yang等人(2008)的研究目的是学习高低分辨率图像块之间一对一的映射关系，利用一个低分辨率图像块对高分辨率图像块进行预测。然而，自然图像中，高分辨率图像块和低分辨率图像块之间是多对一的映射关系，即给定一个低分辨率图像块，对应的高分辨率图像块有多种可能性，所以我们的方法是对这些可能性进行预测，重建出最优的高分辨率图像块。本文结合主题模型，对纹理部分采用多字典学习的方法重建高分辨率MODIS图像。

人类视觉对平滑图像并不具有很强的敏感性，因此，本文在对图像进行稀疏表示之前，先提取图像的纹理细节。首先使用双边滤波获取图像的平滑部分，双边滤波器是由几何空间距离决定滤波器系数和像素差值决定滤波器系数的两个函数构成，图像的平滑部分表示为

$\begin{array}{l}{{X}_c}\left( {i,j} \right) = \displaystyle\frac{1}{{\gamma \left( {i,j} \right)}}\sum\limits_{\left( {i',j'} \right) \in {{ S}_{i,j}}} {{g_s}\left( {i - i',j - j'} \right)} \\*{g_r}\left( {{{X}_{in}}\left( {i,j} \right)} \right) - {{X}_{in}}\left( {i',j'} \right){{X}_{in}}\left( {i',j'} \right)\end{array}$

(1)

式中，(i′,j′)∈ S _i,j表示像素(i′,j′)和(i,j)是相邻像素， S _i,j代表模板域，g_s 是定义域的高斯核函数，可表示为

${g_s}(i - {i'},j - {j'}) = \exp ( - \frac{{{{(i - {i'})}^2} + {{(i - {i'})}^2}}}{{2\sigma _s^2}})$

(2)

g_r 是值域的高斯核函数：

$\begin{aligned}{g_r}({{X}_{in}}(i,j)) - {{X}_{in}}({i'},{j'})) = \\\exp ( - \frac{{{{\left\| {{{X}_{in}}(i,j) - {{X}_{in}}({i'},{j'})} \right\|}^2}}}{{2\sigma _r^2}})\end{aligned}$

(3)

X (i,j)代表原始图像。γ是归一化参数：

$\begin{array}{l}\gamma (i,j) = \displaystyle\sum\limits_{({i'},{j'}) \in {{ S}_{i,j}}} {{g_s}(i - {i'},j - {j'})} \\ * {g_r}({{X}_{in}}(i,j) - {{X}_{in}}({i'},{j'}))\end{array}$

(4)

用 X_d 表示需要提取的图像纹理部分，则纹理部分可由原始图像减去平滑部分得到：

${{X}_d} = {X}(i,j) - {{X}_c}(i,j)$

(5)

主题模型可以发现一个低分辨率图像块对应的多个高分辨率图像块之间的语义(主题)关系，因此，给出一组图像集合，目标是确定每一部分图像归属哪一个主题。为了使主题模型应用到MODIS图像的超分辨率重建中，划分和定义如下：假设图像由N个局部区域组成，即有 ${ D} = ({{ d}_1},{{ d}_2}, \cdots ,{{ d}_N})$ ，每个区域我们称之为一个“文档”。N个“文档”被划分M个“词语” ${ W} = ({{ w}_1},{{ w}_2}, \cdots ,{{ w}_M})$ ，每个“词语”即为一个小的图像块。“主题” ${ z} \in { Z} =\{ {{ z}_1},{{ z}_2}, \cdots ,{{ z}_K}\}$ 是根据文档中“词语”的共现所形成的“文档”的集合(Purkait和Chanda，2013)。在我们提出的方法中，使用主题模型对图像块进行主题划分，每一个主题中，都训练一对高低分辨率字典。

文档所属主题的确定可以通过概率潜在语义分析(pLSA)(Hofmann，1999a)来实现。通过已知的文档集合 ${ D} = ({{ d}_1},{{ d}_2}, \cdots ,{{ d}_N})$ 和词语集合 ${ W} = ({{ w}_1},{{ w}_2}, \cdots ,{{ w}_M})$ 建立一个M×N的共生表 f ( w_i , d_j )，矩阵 f ( w_i , d_j )表示在文档 d_j 中词语 w_i 出现的频率。N和M分别表示文档和词语矩阵维数的大小。pLSA是一个将潜在语义变量 z_k ，可视的词语 w_i 和文本 d_j 联系起来的统计模型，pLSA的模型如下式所示：

${P}({{w}_i},{{d}_j}) = {P}({{d}_j}){P}({{w}_i}/{{d}_j})$

(6)

${P}({{w}_i}/{{d}_j}) = \sum\limits_{k = 1}^K {{P}({{z}_k}/{{d}_j})P({{w}_i}/{{z}_k})} $

(7)

式中， P ( w_i , d_j )表示文档和词语的联合概率分布， P ( d_j )是第j篇文档发生的概率。 P ( z_k / d_j )表示在文档 d_j 中潜在语义变量 z_k 的概率分布， P ( w_i / z_k )表示在主题 z_k 中词语 w_i 发生的概率，根据最大似然估计原则，pLSA模型的参数可以通过求取如下对数似然函数的极大值来计算：

$L = \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{ f}({{ w}_i},{{ d}_j})} } \log { f}({{ w}_i},{{ d}_j})$

(8)

最大似然估计求解的经典算法是EM算法(Hofmann，1999b)。使用随机数初始化之后，交替使用E步骤和M步骤进行迭代计算。在E步骤中，计算每个潜在变量的后验概率：

${P}{\mathbf{(}}{{z}_k}{\mathbf{/}}{{w}_i}{\mathbf{,}}{{d}_j}{\mathbf{)}} = \frac{{{P}{\mathbf{(}}{{z}_k}{\mathbf{)}}{P}{\mathbf{(}}{{d}_j}{\mathbf{/}}{{z}_k}{\mathbf{)}}{P}{\mathbf{(}}{{w}_i}{\mathbf{/}}{{z}_k}{\mathbf{)}}}}{{\displaystyle\sum\limits_{l = 1}^K {{P}{\mathbf{(}}{{z}_l}{\mathbf{)}}{P}{\mathbf{(}}{{d}_j}{\mathbf{/}}{{z}_l}{\mathbf{)}}{P}{\mathbf{(}}{{w}_i}{\mathbf{/}}{{z}_l}{\mathbf{)}}} }}$

(9)

在M步骤中，对参数进行估计：

${P}({{w}_i}/{{z}_k}) = \frac{{\displaystyle\sum\limits_{j = 1}^N {{f}({{w}_i},{{d}_j})} {P}({{z}_k}/{{w}_i},{{d}_j})}}{{\displaystyle\sum\limits_{t = 1}^M {\displaystyle\sum\limits_{j = 1}^N {{f}({{w}_t},{{d}_j})} {P}({{z}_k}/{{w}_t},{{d}_j})} }}$

(10)

${P}({{d}_i}/{{z}_k}) = \frac{{\displaystyle\sum\limits_{i = 1}^M {{f}({{w}_i},{{d}_j})} {P}({{z}_k}/{{w}_i},{{d}_j})}}{{\displaystyle\sum\limits_{j = 1}^N {\displaystyle\sum\limits_{t = 1}^M {{f}({{w}_t},{{d}_j})} {P}({{z}_k}/{{w}_t},{{d}_j})} }}$

(11)

${P}({{z}_k}/{{d}_j}) = \frac{{{P}({{d}_j}/{{z}_k}){P}({{z}_k})}}{{\displaystyle\sum\limits_{l = 1}^K {{P}({{d}_j}/{{z}_l}){P}({{z}_l})} }}$

(12)

式(9)—式(12)反复迭代直至收敛，可以得到主题k中文档的分布 P ( d_j / z_k )和词语的分布 P ( w_i / z_k )，通过 ${P}({{z}_k}/{{d}_j}) = \displaystyle\frac{{{P}({{d}_j}/{{z}_k}){P}({{z}_k})}}{{\displaystyle\sum\limits_{l = 1}^K {{P}({{d}_j}/{{z}_l}){P}({{z}_l})} }}$ 计算文档中主题的概率，最终根据概率最大化原则 ${{z}_0} = \mathop {\max }\limits_{{{{z}}_k}} {P}({{z}_k}/{{z}_j})$ 确定文档归属的主题。图1展示了3个不同主题下文档的集合。

从图1可以看出，pLSA方法将有相似结构特征的文档集合在一个主题下，显然，左边主题下的文档的边缘比右边的更加锐利，细节也更加丰富。因此，分主题训练字典和重建的方法将有效地表达图像的特征结构。

传统的基于图像块的超分辨率重建方法，低分辨率图像样本块由高分辨率图像样本块产生，组成图像样本对，训练一对高低分辨率字典。在本篇模型当中，我们通过主题模型，将样本块分为 K 个不同的主题，每个主题训练一对高低分辨率字典 ${D}_k^l$ 和 ${D}_k^h$ 。根据稀疏表示理论，字典学习问题即为求解如下优化问题：

$\mathop {\arg \min }\limits_{{D},{A}} \left\| {{X} - {DA}} \right\|_F^2{\rm {s.t.}}{\left\| {{{\alpha }_i}} \right\|_0} \leqslant \varepsilon $

(13)

式中， ${X} = \left[ \begin{array}{l} {X}_d^h\\ {X}_d^l \end{array} \right]$ ， ${D} = \left\| \begin{array}{l} {{D}^h}\\ {{D}^l} \end{array} \right\|$ ，阈值ε表示稀疏测度， ${X}_d^h$ 是高分辨率训练样本集， ${X}_d^l$ 为低分辨率训练样本集。K-SVD求解式(13)时，首先找一个合适的初始化字典，然后固定字典 D ，更新稀疏系数 A ，接下来固定系数矩阵 A ，对 D 进行逐列更新(Aharon 等，2006；Smith和Elad，2013)。K-SVD算法更新字典原子时，先选出稀疏矩阵中的非零元素组成集合，然后获取非零集合对应的样本子集和系数子集，最后逐列更新字典原子。因此，从K-SVD求解的思路出发，我们改进的目标仍然是更新字典 D 和 A 中的非零系数，所以转为求解如下优化方程：

$\left\{ {\hat { D},{ A}} \right\} = \mathop {{\rm{Arg}}\min }\limits_{{ D},{ A}} \left\| {{ X} - { {DA}}} \right\|_F^2 {\rm{s}}.{\rm{t}}.{ A} \odot { M} = 0$

(14)

式中， A ⊙ M 表示两个相同维度矩阵的Schur积， M 是由元素0和1组成的矩阵，矩阵 M 和 A 的关系如下，如果 A (i,j)=0，那么有 M (i,j)=1，否则 M (i,j)=0。 A ⊙ M =0的约束条件可以求出标记矩阵 M ，使得 A 中所有的零元素被标记下来，避免了K-SVD算法构建非零元素集合对 A 的结构的破坏。在字典更新阶段，只用使 A 中的零元素保持不变，同时对非零元素进行更新，随着迭代次数的增加， A 中的零元素不断增多从而变得更加稀疏，以获得式(14)更好的近似结果，相比于传统的K-SVD字典更新方法，移除了构建非零元素集合的步骤，从而使 A 的原支撑集保持不变，降低了表示误差。式(14)仍然是一个难以求解的非凸问题，不过它的求解比过完备字典更为简单。我们可以用多种方法迭代求解式(14)的约束问题。

接下来讨论改进K-SVD方法的具体策略。首先，将 DA 表示n个矩阵的和，式(14)转化为如下结果：

$\left\{ {\hat { D},{ A}} \right\} = \mathop {{\rm{arg}}\min }\limits_{{ D},{ A}} \left\| {{ X} - \sum\limits_{j = 1}^n {{{ d}_j}{ a}_j^{\rm T}} } \right\|_F^2 {\rm{s}}.{\rm{t}}.{{ m}_j} \odot {{ a}_j} = 0$

(15)

式中， d_j 是字典 D 的第j个列向量， ${a}_j^{\rm T}$ 和 ${m}_j^{\rm T}$ 分别表示矩阵 A 和矩阵 M 的第j行( a_i 不同于 a_j ， a_i 表示 A 的第i列)。使用块下降法对式(15)进行求解，并对字典原子 d_j 和系数 a_j 进行更新。运用SVD方法对 ${{E}_j} = ({X} - \sum\limits_{i \ne j} {{{d}_i}a_i^{\rm T}} ) \odot ({{1}_d} \cdot {m}_j^{\rm T})$ 分解。 ${{1}_d} \cdot {m}_j^{\rm T}$ 表示掩膜矩阵，它的作用是在 ${X} - \displaystyle\sum\limits_{i \ne j} {{{d}_i}{a}_i^{\rm T}} $ 中移除对第j个原子没有贡献的列向量。

通过上述方法的迭代计算，使得对字典和稀疏系数的更新更加准确和简便，同时降低了表示误差。

通过上面的主题模型和改进的K-SVD训练方法，可以将训练样本归类为多个主题并每个主题训练一对高低分辨率字典 $[{D}_k^l;{D}_k^h]$ 。下面讨论根据字典重建高分辨率图像。

首先将待重建的低分辨率MODIS图像划分为多个重叠的文档，文档再用同样的方式被划分为多个重叠的块。低分辨率图像的文档归属于哪一个主题可以由pLSA算法求解，因此对于每一个低分辨率图像块y_i ，对应的主题和字典就被确定，求解它在该字典下的表示系数如下：

${{\alpha }_i} = \mathop {\arg \min }\limits_{{{\mathbf{\alpha }}_i}} \left\| {{D}_k^l{\alpha } - {{y}_i}} \right\|_2^2 + {\lambda _i}{\left\| {{{\alpha }_i}} \right\|_1}$

(16)

式中，λ_i 是正则化参数。求解式 (16) 这一优化问题，收敛后得到最优解 ${\alpha }_k^*$ ，从而重建的高分辨率图像块为 ${{x}^*} = {D}_k^h{\alpha }_k^*$ 。在所有的文档中我们重复上面的重建步骤，再利用重叠的部分得到高分辨率MODIS图像。

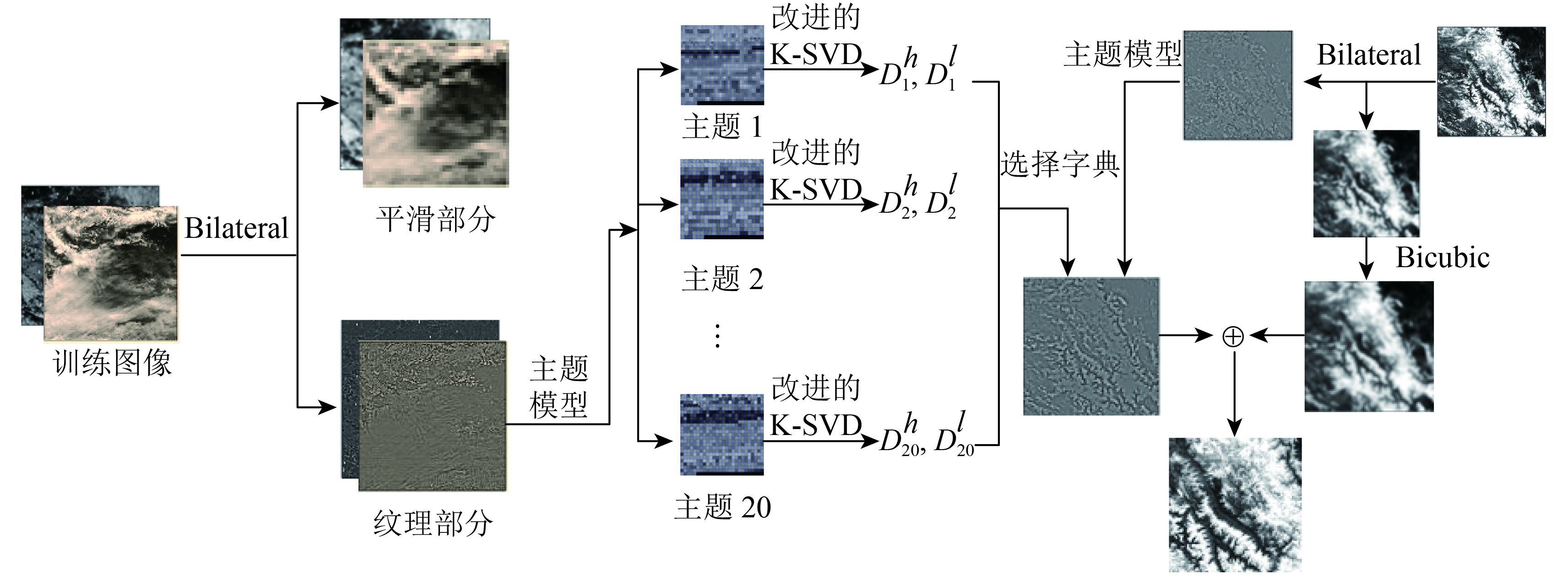
基于主题学习和稀疏表示的MODIS图像超分辨率重建可以归纳为以下两个步骤：(1)学习阶段，在训练样本中，通过pLSA模型确定文档所属的主题，然后用每个主题的图像块训练高低分辨率字典。(2)重建阶段，确定每个低分辨率块所属的主题，利用第一阶段中每个主题训练的高低分辨率字典重建高分辨率MODIS图像。图2为本文方法流程图，算法分为训练阶段和重建阶段。

采用双边滤波器将MODIS图像分解为平滑部分 X_c 和纹理部分 X_d ，其中 X_d 作为高分辨率训练样本，记为 ${X}_s^h$ 。

(1)对高分辨率训练样本 ${X}_s^h$ 进行降采样，产生低分辨率训练样本 ${X}_s^l$ ，并组成训练样本对 ${{X}_s} = \left[ \begin{array}{l} {X}_s^h\\ {X}_s^l \end{array} \right]$ 。

(2)将高低分辨率训练样本对划分为m×m大小的重叠文档，再将文档划分为n×n大小的重叠图像块。

(3)对由训练图像生成的所有文档，应用pLSA来进行训练，通过EM算法迭代公式(9)(10)(11)(12)直至收敛，从而得到 P ( z / d )，确定文档归属的主题。

(4)对于每个主题下的文档，用2.3节训练字典的方法生成每个主题的一对独立字典 $[{D}_k^l;{D}_k^h]$ 。

(5)保存文档—主题分布矩阵，以及重建所需的高低分辨率字典。

(1)待重建的低分辨率MODIS图像通过双边滤波器分解为平滑部分 ${X}_c^l$ 和纹理部分 ${X}_d^l$ 。

(2)将纹理部分图像 ${X}_d^l$ 划分为m×m大小的重叠文档，再将文档划分为n×n大小的重叠图像块。

(3)对于测试图像划分的所有文档，同样应用pLSA来进行训练，通过EM算法迭代公式(9)(10)(11)(12)直至收敛，从而得到 P ( z / d )，确定文档归属的主题。

(4)根据文档所属主题选择对应的高低分辨率字典对 $[{D}_k^l;{D}_k^h]$ ，结合2.4节求解的稀疏表示系数重建高分辨率纹理图像块，并由所有重建的高分辨率图像块组成高分辨率纹理图像 ${X}_d^h$ 。

(5)对低分辨率平滑图像 ${X}_c^l$ 采用双三次方插值，重建出高分辨率平滑图像 ${X}_c^h$ 。

(6)结合重建的高分辨率纹理部分和平滑部分获得最终的高分辨率MODIS图像 ${X} = {X}_c^h + {X}_d^h$ 。

实验在Windows7系统下进行，硬件配置为Intel Core(TM) i5-3740 CPU @ 3.2 GHz，8 GB内存。测试数据来自2016-03-02 7:57 AQUA卫星接收的MODIS 1B数据，地理区域为东经97.8151°到东经134.6207°，北纬46.3421°到97.8151°；选取其中第2、6—7、17—19、22—26、31—36波段的MODIS图像组成训练样本。实验中，将训练样本划分为20000个大小为50×50的文档，图像块的大小为7×7。为了减少算法的计算复杂度并提高重建效果，实验参数设置如下，pLSA模型主题数K=20，训练字典大小L=500。测试阶段，选取MODIS数据中第1、2、18、22、23、26波段的图像作为测试图像。为了客观评价本文方法的超分辨率重建效果，截取图像的一个区域，并进行下采样和模糊处理后作为待重建的低分辨率图像，实验选用峰值信噪比(PSNR)和结构相似度(SSIM)进行不同方法重建结果的客观评价指标，一般而言，PSNR和SSIM越高，表明重建结果越好。实验中，首先采用本文方法进行1.6倍(s=1.6)超分辨率重建，表1列举了双三次方插值方法(Parker 等，1983)、SCSR方法(Yang 等，2008)和本文方法重建图像的PSNR和SSIM值；然后进行2倍(s=2)超分辨率重建，并与双三次方插值方法、SCSR方法、ASDS方法(Dong 等，2011)的重建效果进行对比，表2列举了不同方法重建的客观评价指标；同时，选取波段2图像比较不同方法进行2倍重建的视觉效果，结果如图3所示。

从表1和表2可以看出，采用主题学习和稀疏表示的超分辨率方法所得的重建结果比其他方法具有更高的PSNR和SSIM，具体来说，本文方法的PSNR比双三次方插值高1 dB左右，比ASDS方法高0.2 dB到0.4 dB左右；这说明将主题模型应用到图像超分辨率重建可以获得了较好的复原效果。从图3视觉效果上进行观察，双三次方插值使图像产生了模糊，SCSR方法和ASDS方法也出现了明显的振铃效应，而本文方法重建图像更加清晰，恢复了更多的纹理细节，云和植被的轮廓更加明显，很好地表达了MODIS图像的纹理特征。

为了衡量不同方法的计算效率，截取波段1中大小为256×256和128×128的图像作为测试图像，记录不同方法所需的重建时间，结果如表3所示。从表3可以看出，双三次方插值法计算效率最高，这主要是由于该方法无需迭代过程，然而结合表1和表2可知，它的重建效果是最差的；在采用字典学习的同类方法中，本文方法的重建速度明显快于Yang的SCSR方法；同时，由于本文方法增加了多字典自适应选择阶段，造成重建速度比ASDS略慢，但重建耗时尚可接受。总体而言，相比传统基于学习的超分辨率方法，本文方法在提高重建效果的同时，仍能保持较高的计算效率。

下面比较本文方法与双三次方插值方法、SCSR方法对实际图像的超分辨率重建效果，由于ASDS方法在重建过程中将模糊算子作为已知条件，而在实际处理中模糊算子往往难于估计，因此本文就不进行ASDS方法重建效果的比较。为方便处理，我们选取MODIS数据中波段1图像并截取出部分区域，它的原始分辨率为每像素250 m。我们采用不同方法进行2倍插值重建，重建图像的分辨率提高到每像素125 m，重建结果如图4所示，从不同方法重建结果的主观视觉效果来看，本文方法重建的图像具有较高对比度，保留了更多的纹理细节。

为了检验本文方法的噪声鲁棒性，我们模拟噪声对超分辨率重建效果的影响，并对比了不同重建方法的抗噪性能。实验截取波段2图像作为原始高分辨率测试图像，加入方差为1，不同均值的随机噪声，然后经过下采样及模糊处理后作为待重建的低分辨率图像。采用双三次方插值方法、SCSR方法、ASDS方法和本文方法对待重建的低分辨率图像进行超分辨率处理，不同方法重建结果的PSNR如图5所示。从图5可以看出，随着噪声均值的不断增大，4种方法的PSNR均会不同程度下降，但本文方法在不同噪声强度下，重建图像的PSNR仍高于其他方法，说明本文方法的噪声鲁棒性相对较强。由于MODIS卫星在成像及传输过程中均会受到系统内部噪声及外界噪声等的影响，所得到的MODIS图像难以避免噪声干扰，本文算法较强的噪声鲁棒性也显示了其实际应用价值。

受制于成像传感器分辨率的限制，MODIS图像的超分辨率研究具有重要的现实意义。由于MODIS图像具有精细的纹理结构和清晰的边缘轮廓，且图像的不同部分往往具有不同的特性，本文通过双边滤波分离MODIS图像的平滑及纹理部分，并将纹理部分看成是由若干文档组成的训练样本，结合潜在语义分析确定文档所属的主题，针对每个主题所对应的图像块，采用改进的K-SVD方法训练若干适用于不同主题的高低分辨率字典对，构造出一种局部自适应的超分辨率方法。从实验结果来看，本文方法不仅使得重建图像的视觉效果优于传统方法，而且在PSNR和SSIM等客观评价指标上，也比传统方法有明显的提升，这表明本文所提出的方法不仅适用于MODIS图像纹理细节丰富的特点，而且通过采用多主题多字典方案，克服了传统基于稀疏表示的超分辨率方法难于根据MODIS图像的局部特性自适应选择合理字典的问题，从而可以更加稀疏地表示MODIS图像，增强重建图像的细节信息。由于字典学习及稀疏编码所带来的计算开销，基于稀疏表示的超分辨率方法往往耗时较多，下一步将研究字典训练及图像重建的改进算法，并合理优化算法的迭代过程，以提高图像超分辨率算法的计算效率。