|
收稿日期: 2016-02-17; 修改日期: 2016-06-10; 优先数字出版日期: 2016-06-17
基金项目: 中国地质调查局地质矿产调查评价国家专项工作项目(编号: 12120113095400)
第一作者简介: 刘夯(1990— ),男,硕士研究生,研究方向为微波遥感应用、计算机视觉。E-mail:
liuhang326@163.com
中图分类号: TP751.1
文献标识码: A
|
摘要
针对指数加权均值比(ROEWA)边缘检测算子无法准确确定边缘位置和边缘方向的问题,对其表达式进行了改进。重新定义了反转的、带符号的、归一化最小指数加权均值比(IROEWA),作为边缘强度指标,来量化描述边缘的跃变程度,并在此基础上准确计算出边缘的方位。同时将改进的非极大值抑制算法应用到边缘检测流程中,对IROEWA得到的边缘强度图进行后处理。针对自然SAR图像和仿真SAR图像的实验都表明,改进算法能够得到比ROEWA加分水岭分割的原始算法更好的边缘检测结果。利用接收者操作特征(ROC)曲线,对改进算法进行量化评价,其曲线下面积(AUC)可达0.97570,非常接近理想的检测器;在其ROC曲线的最优点处,检测率可达0.95232,而虚警率仅为0.00214左右。
关键词
合成孔径雷达图像, 边缘检测, 指数加权均值比, 非极大值抑制, 接收者操作特征曲线
Abstract
This paper reports on a method to improve the Ratio Of an Exponentially Weighted Averages (ROEWA) edge detector, so that the improved edge detector can accurately determine the positions and directions of edges for Synthetic Aperture Radar (SAR) images. We attempt to build an optimal edge detector for SAR images to obtain better results of edge detection. The edge strength index is redefined as an inverted, signed, and normalized minimum ROEWA (IROEWA), which is utilized to quantitatively describe the phase step of edges. A new method that accurately calculates edge direction is developed based on the edge strength map from IROEWA. We can obtain the possible values of edge directions in this manner, which continuously distributes from 0 degrees to 180 degrees. Therefore, we must improve the Non-Maximum Suppression (NMS) algorithm, so that it can process sub-pixels. Finally, the improved NMS algorithm is also added into the edge detection workflow. This improved edge detection algorithm is called IROEWA & NMS. We conducted two experiments for IROEWA & NMS: one employed nature SAR images, whereas the other adopted a simulation SAR image. Experiment results show that the IROEWA & NMS outperforms the original ROEWA with watershed thresholding. The IROEWA operator is faster than the ROEWA operator under the same conditions. We applied a Receiver Operating Characteristic (ROC) curve to evaluate the IROEWA & NMS and determined that its Area Under the Curve (AUC) is 0.97570; thus, it approximates the ideal optimal detector. The detection rate at the position of the optimal point in the ROC curve of the IROEWA & NMS is as high as 0.95232, whereas the false alarm rate is as low as 0.00214. The IROEWA & NMS exhibits suitable performance on both the detection and false alarm rates. It has significant application value in several fields, such as the segmentation and edge detection for SAR images.
Key words
SAR images, edge detection, ROEWA, Non-Maximum Suppression(NMS), Receiver Operating Characteristic(ROC)
1 引 言
边缘检测是图像处理和计算机视觉中的基本问题,是提取线性特征和识别线性目标的基础。然而,一般基于加性噪声模型的边缘检测算子,对于合成孔径雷达SAR图像的检测不具有恒虚警(Constant False Alarm)性,会出现保留虚假边缘、遗漏真实边缘的情况(赵凌君 等,2007)。对此,Bovik(1988)基于乘性噪声模型和单边缘模型提出了均值比率算子,即RoA (Ratio of Averages);而Zaman和Moloney (1993)提出了改进的RoA算子,即MRoA (Modified Ratio of Averages);后来,Fjørtoft等人(1998)又基于乘性噪声模型和多边缘模型,提出了指数加权均值比率算子,即ROEWA (Ratio Of Exponentially Weighted Averages)。
ROEWA算子虽然对SAR图像具有恒虚警性,但其边缘定位精度差,单边缘有多次响应的现象。对此国内颇有一些改良研究:贾承丽和匡纲要(2007)利用Gabor方位估计器处理ROEWA的边缘强度图,估算出边缘方位,首次将Canny (1986)的边缘检测算法思想应用到ROEWA算法的改进中,利用非极大值抑制,即NMS (Non-Maximum Suppression)算法,处理ROEWA边缘强度图,提高了边缘定位精度;后来,吴禹昊等人(2010)利用方位模板估算边缘方位,做了类似改进;安成锦等人(2011)和杨道莲等人(2013),分别利用Radon和Hough方位估计器估算边缘方位,也做了类似改进。
针对该问题,本文对ROEWA原始算子的两个表达式进行了修改,在此基础上直接计算出更准确的边缘方位,改进并应用了亚像元处理级别非极大值抑制算法,获得了更好的边缘检测结果。
2 ROEWA的算法原理
ROEWA算子是一种基于线性最小均方误差滤波器(Linear MMSE Filter)的指数加权均值比率算子。在1维情况下,该滤波器f表达式为
| $f(x) = C{{\rm e}^{ - \alpha \left| x \right|}}$ | (1) |
在离散情况下,滤波器f可以用因果滤波器f1和非因果滤波器f2来实现,则滤波器f离散表示为
| $f(n) = \frac{1}{{1 + b}}{f_1}(n) + \frac{b}{{1 + b}}{f_2}(n - 1)$ | (2) |
式中,
根据f(x,y)=f(x)f(y)将滤波器f推广到2维空间。那么,对于水平方位,先使用滤波器f对图像强度I进行逐列滤波,然后分别用f1和f2进行逐行滤波,即可分别获得因果和非因果指数加权均值:
| ${\hat u_{{X_{1}}}}(x,y) = {f_{1}}(x) * [f(y) \odot I(x,y)]$ | (3) |
| ${\hat u_{{X_2}}}(x,y) = {f_2}(x) * [f(y) \odot I(x,y)]$ | (4) |
式中,*表示水平方位卷积运算,⊙表示竖直方位卷积运算。同理,可得竖直方位的因果和非因果指数加权均值。式(3)和式(4)中,输入信号与f1和f2的卷积运算可以简化成递归运算。假设滤波器f1和f2输入信号为e1和e2,则卷积s1和s2递归式如下:
| ${s_{1}}(n) = a[{e_{1}}(n) - {s_{1}}(n - 1)] + {s_{1}}(n - 1),n = 1,...,N$ | (5) |
| ${s_2}(n) = a[{e_2}(n) - {s_2}(n + 1)] + {s_2}(n + 1),n = N,...,1$ | (6) |
于是,水平和竖直方位上的4种指数加权均值均可由上述递归算法联合式(2)求得。此时,ROEWA算子在水平和竖直方位上的边缘强度分量分别为
| ${r_{{X_{\max }}}}(x,y) = \max \left[\frac{{{{\hat u}_{{X_1}}}(x - 1,y)}}{{{{\hat u}_{{X_2}}}(x + 1,y)}}, \frac{{{{\hat u}_{{X_2}}}(x + 1,y)}}{{{{\hat u}_{{X_1}}}(x - 1,y)}} \right]$ | (7) |
| ${r_{{Y_{\max {\kern 1pt} }}}}(x,y) = \max \left[\frac{{{{\hat u}_{{Y_{1}}}}(x,y - 1)}}{{{{\hat u}_{{Y_{2}}}}(x,y + 1)}}{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{{\hat u}_{{Y_{2}}}}(x,y + 1)}}{{{{\hat u}_{{Y_{1}}}}(x,y - 1)}}\right] $ | (8) |
类似于向量模的计算,可求得2维空间中的总体边缘强度为
| ${r_{2{D_{\max }}}}(x,y) = \sqrt {r_{{X_{\max }}}^2(x,y) + r_{{Y_{\max }}}^2(x,y)} $ | (9) |
3 本文的改进算法
3.1 边缘方位求算问题及改进算法
ROEWA算子是Fjørtoft等人(1998)在研究SAR图像分割问题时提出的,他们直接运用分水岭分割算法(Watershed Thresholding)和一种伪边缘区域融合算法,处理边缘强度图(Edge Strength Map),所以并不需要确定边缘方位。但在一些国内的SAR图像线性目标识别研究中,参考了Canny(1986)边缘检测的算法思想,将非极大值抑制应用到改进算法中,用以优化边缘形态和提高边缘定位精度;而非极大值抑制算法必须确定(与边缘延伸方位相互垂直的)边缘跃变方位才能实现。
杨道莲等人(2013)在研究ROEWA的改进算法时,将确定边缘方位的方法总结为3类:(1)直接参照梯度方位算法计算方位,(2)利用方位模板匹配判定方位,(3)使用方位估计器估算方位。然而,不论是方位模板还是方位估计器,其本质都是一种原始ROEWA的后处理:先利用原始的ROEWA算子处理SAR图像,得到的边缘强度图;然后将边缘强度图输入到一个给定的判定函数,得出判定指标,判定边缘最可能属于哪个既定方位;最后应用非极大值抑制,优化边缘检测结果。
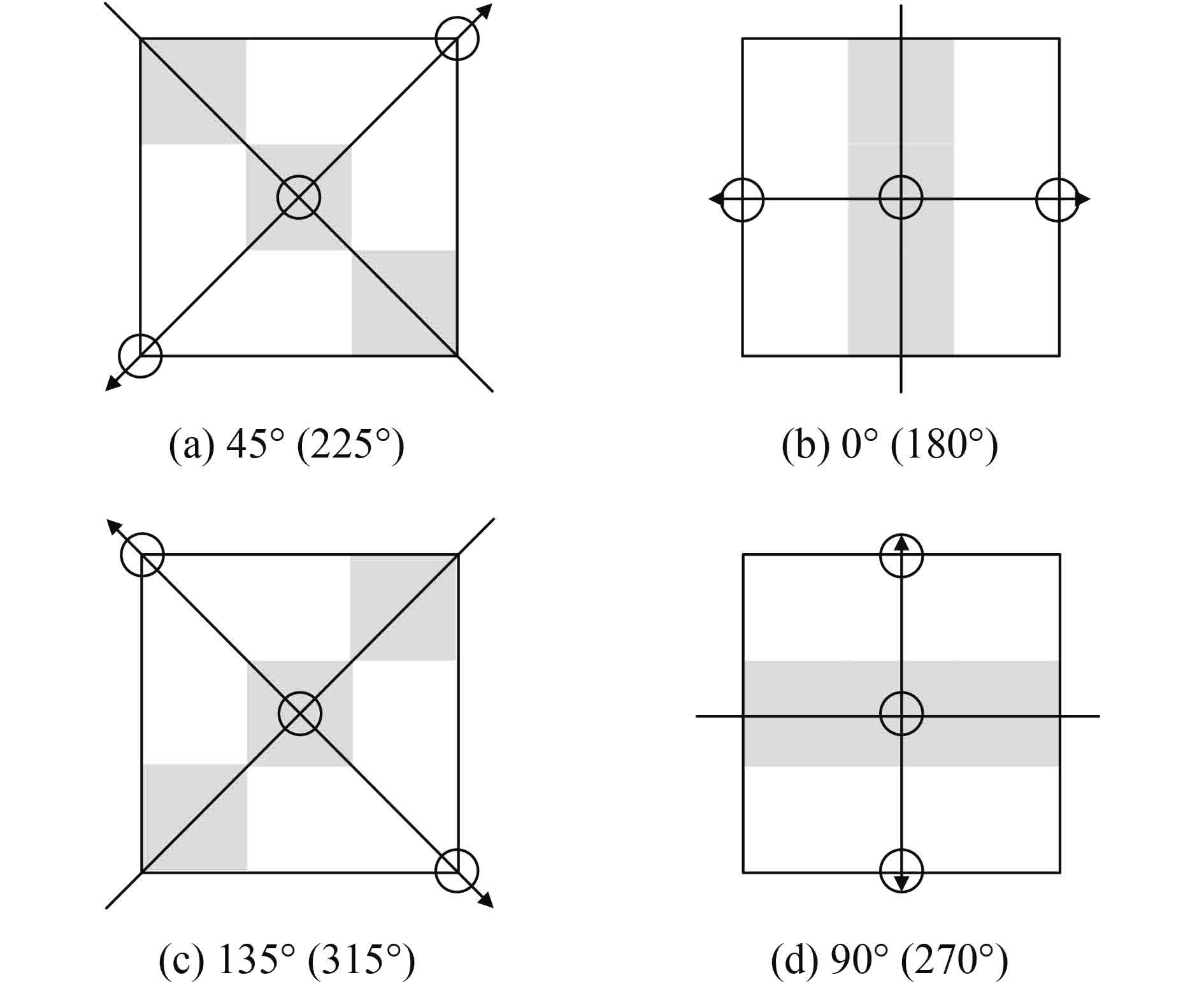
一般地,这种后处理将圆周等分为4方位(即8方向)的“米”字形式,凡是位于(–22.5°,22.5°)之间的边缘就判定为0°(180°)方位,位于(22.5°,67.5°)之间的边缘就判定为45°(225°)方位,其他情况以此类推。显然,使用方位匹配模板或方位估计器得出的方位角,只能把边缘估算到有限个既定方位上,显然是不够准确的。而梯度方位算法本质是向量运算,在2维平面空间内,任意向量
Paillou(1997)较早提出了参照梯度方位的改进算法,直接将指数加权均值比等同于梯度分量,利用反正切函数求边缘方位:
| $D(x,y) = \arctan [{r_Y}(x,y)/{r_X}(x,y)]$ | (10) |
贾承丽和匡纲要(2007)针对性地指出,这种方法所得方位角仅在[0, π/2)内,缺失了(π/2, π)范围内的角度,显然是不正确的;并认为最直接的改进思路就是将定义边缘强度分量的式(7)和式(8)改写成:
| ${r_{\max }} = \left\{ {\begin{array}{*{20}{c}}{ - \max ({{\hat u}_1}/{{\hat u}_2},{{\hat u}_2}/{{\hat u}_1}),{{\hat u}_1} > {{\hat u}_2}}\\{\max ({{\hat u}_1}/{{\hat u}_2},{{\hat u}_2}/{{\hat u}_1}),{{\hat u}_1} \leqslant {{\hat u}_2}}\end{array}} \right.$ | (11) |
但其同时指出,实验结果表明这种方法无法得到正确结果,并猜想可能是比值代替差分后,不再符合梯度定义的缘故;于是,其改用2维Gabor滤波器来估算方位,并用非极大值抑制算法细化边缘和磁滞门限法确定分割阈值。事实上,式(11)中的
本文以反转的、带符号的、归一化最小均值比r1–min来表示边缘强度分量。r1–min能够取到反正切函数定义域[0, ∞)内所有值;当r1–min=0的时候,表示当前点处于同质区域;且r1–min与边缘跃变程度呈正相关,r1–min越大则边缘跃变程度越大。用以代替式(7)和式(8)的边缘强度分量定义如下:
| ${r_{1 - \min }} = \left\{ {\begin{array}{*{20}{c}}{ - [1 - \min ({{\hat u}_1}/{{\hat u}_2},{{\hat u}_2}/{{\hat u}_1})],{{\hat u}_1} > {{\hat u}_2}}\\{1 - \min ({{\hat u}_1}/{{\hat u}_2},{{\hat u}_2}/{{\hat u}_1}),{{\hat u}_1} \leqslant {{\hat u}_2}}\end{array}} \right.$ | (12) |
由此,提出一种准确的边缘方位计算方法:根据式(10)求得(–π/2, π/2)内的方位角,并判断方位角D<0时,令D←D+π,从而使方位角值域归化到[0, π)。
相应地,总体边缘强度则定义为
| ${r_{2{D_{1 - \min }}}}(x,y) = \sqrt {r_{{X_{1 - \min }}}^2(x,y) + r_{{Y_{1 - \min }}}^2(x,y)} $ | (13) |
3.2 改进的非极大值抑制算法
非极大值抑制对于虚假边缘去除、边缘细化和精确定位都有良好的效果。简而言之,非极大值抑制算法就是判断当前点的梯度值在该点梯度方位上是不是局部最大值:先构建一个空间与边缘强度图等大的边缘点集合,将所有像元点作为待定的边缘点;如果当前点是梯度方位上局部最大值,则将当前点作为边缘点保留;如果不是,则将当前点从边缘点集合中去除。如图1所示,为3×3窗口中既定方位的非极大值抑制算法,只需取出当前点对应方位上的3个像元值,进行比较并判断取舍。
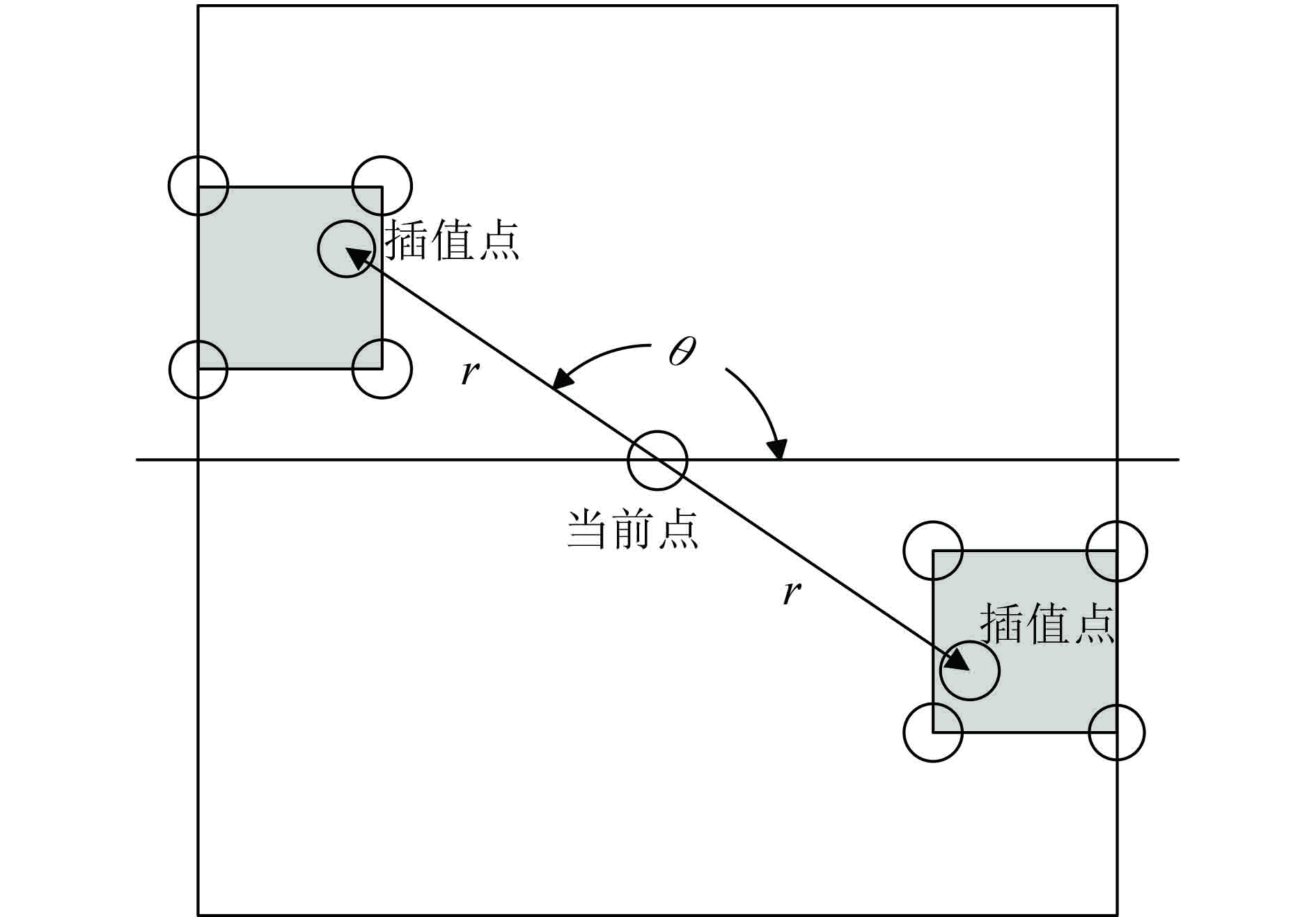
由于本文改进算子得到的边缘方位有无限个连续的可能取值,所以还需要将既定方位的非极大值抑制算法,改进成亚像元级别的处理方法。如图2所示,亚像元级别的非极大值抑制算法,其改进思路为:给定一个可以不为整数的邻域半径r,并根据当前点的边缘方位,计算出两个邻域点的坐标;如果邻域点的横纵坐标不全为整数,则需插值计算其边缘强度;插值计算时,分别对邻域点的横纵坐标向上向下取整,两两组合可得4个整数坐标的点,然后根据这4个点进行线性插值;最后,比较当前点与邻域点的边缘强度大小,若当前点的边缘强度小于任何一个领域点的,则将当前点从边缘点集中剔除。
4 实验结果与分析
为便于描述,本文将改进的指数加权均值比率算子IROEWA(Improved Ratio of Exponentially Weighted Averages);而带非极大值抑制的改进算法称为IROEWA & NMS。如图3所示,本文边缘检测技术路线为:(1)输入灰度图像;(2)用IROEWA算子进行边缘检测,得到边缘强度图和边缘方位;(3)根据边缘强度图和边缘方位进行非极大值抑制;(4)执行阈值选取、二值分割和形态学滤波等后处理;(5)输出边缘检测结果图。
本文的算法,是基于Emgu CV库中的Matrix类实现的,利用Matrix类很容易在.NET平台上实现对图像数据的矩阵操作。Emgu CV库是一个跨平台的OpenCV封装库,其依托.NET框架,支持C#、VB等多种语言,并能在各种操作系统上运行。
4.1 自然SAR图像的边缘检测实验
如图4所示,本实验以440×440某岸线城市SAR图像作为测试图,以2.60 GHz英特尔i5-3230 M处理器、4.00 GB内存、32位Win7操作系统作为测试平台,对ROEWA、IROEWA,及IROEWA & NMS分别进行10次测试,求取平均耗时。
如表1所示,对比测试结果可知:本文设计的IROEWA耗时比原始的ROEWA略少;考虑到前人的改进算法(贾承丽和匡纲要,2007;吴禹昊 等,2010;安成锦 等,2011;杨道莲 等,2013)流程为ROEWA→方位估计器(或方位模板)→NMS,所以在相同条件下IROEWA & NMS理论上的运行速度要比上述改进算法快。
表 1 3种测试对象运行耗时
Table 1 Run time for three test objects
| /ms | |
| 测试对象 | 运行耗时 |
| ROEWA | 364.4 |
| IROEWA | 321.2 |
| IROEWA & NMS | 852.4 |
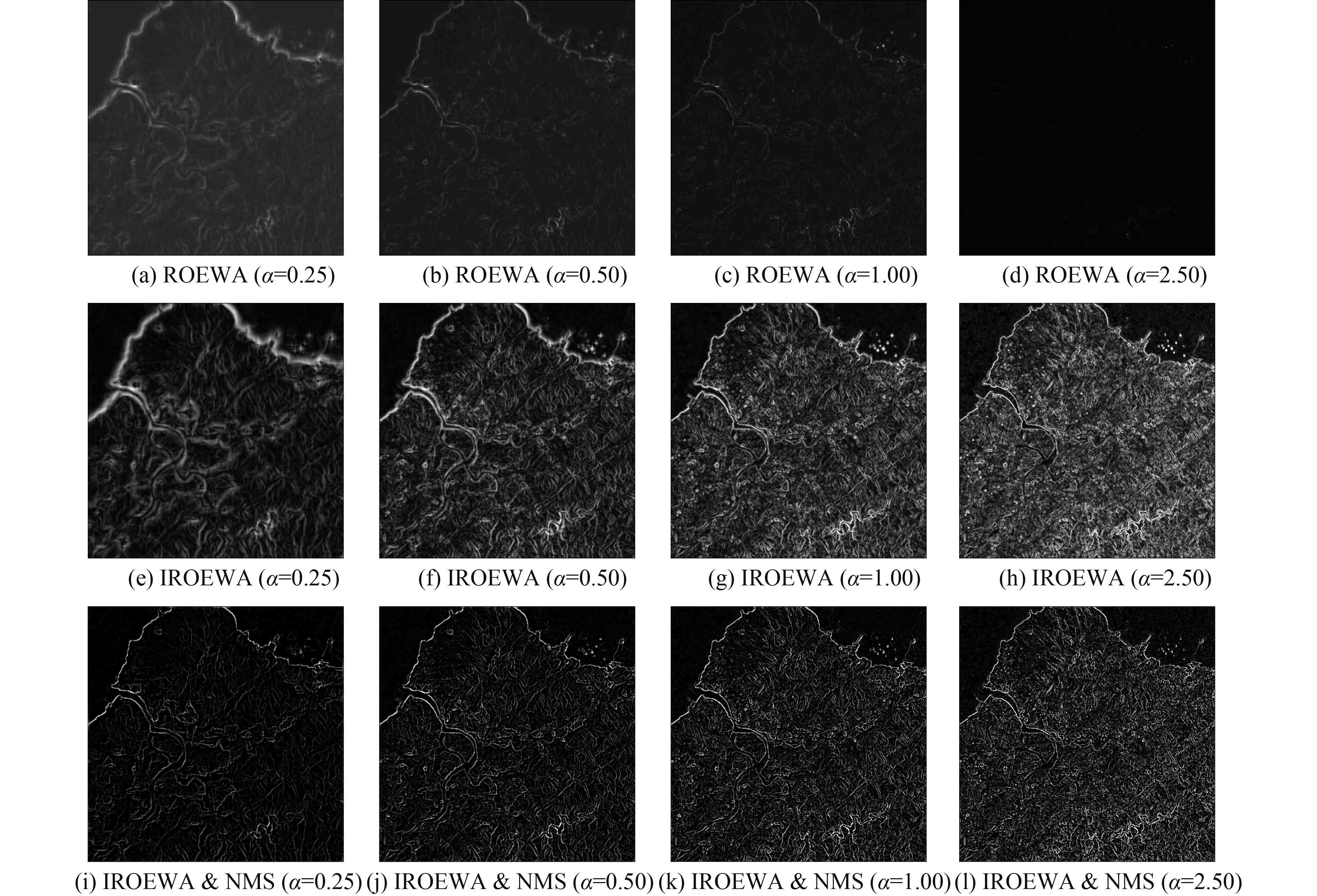
本实验着重对比如图5(a)—(d)所示的ROEWA、如图5(e)—(h)所示的IROEWA和如图5(i)—(l)所示的IROEWA & NMS对应的边缘强度图,得出以下结论:(1)不论是原始的ROEWA算子,还是本文的IROEWA算子,其滤波器f的参数α越大,其边缘就越细、定位越准确,且形态质量越高,但同时检出的虚假边缘也越多;(2)边缘形态的高质量和虚假边缘的低检出,两者是此消彼长、难以兼顾的关系;(3)ROEWA的边缘检测结果会随着α增大而逐渐淡化在暗背景中,而本文的IROEWA却没有淡化现象,展现了良好的性能;(4)非极大值抑制在边缘细化方面有明显的效果,能有效提高边缘形态质量;(5)在α参数较小时,本文的IROEWA & NMS算法能使边缘形态的高质量和虚假边缘的低检出得以兼顾。
4.2 仿真SAR图像的边缘检测实验
仿真SAR图像需要根据某种乘性噪声模型来生成,本实验采用Lee(1986)在研究SAR图像斑点噪声抑制算法时提出的乘性噪声模型:
| $I(x,y) = s(x,y) \cdot n(x,y)$ | (14) |
式中,I(x,y)是SAR回波信号;s(x,y)是无噪声的原始信号;n(x,y)代表随机噪声,服从期望为1且标准差为(4/π–1)1/2≈0.522的瑞利分布。
参考Fjørtoft等人(1998)仿真实验用图,编写Matlab程序生成明暗相间的竖直条带图,其条带宽度从3个像元逐一递增到18个像元;并根据上述乘性噪声模型,为其添加服从瑞利分布的乘性噪声,得到如图6(a)所示的测试用图。编写Matlab程序生成如图6(b)所示的边缘检测结果参考图。图6(c)是原始ROEWA算子在α=0.20时得到的边缘强度图;图6(d)是IROEWA & NMS在在α=0.20时得到的边缘强度图;图6(e)是图6(b)经过分水岭分割得到的边缘图;图6(f)是图6(d)经过二值分割得到的边缘图。
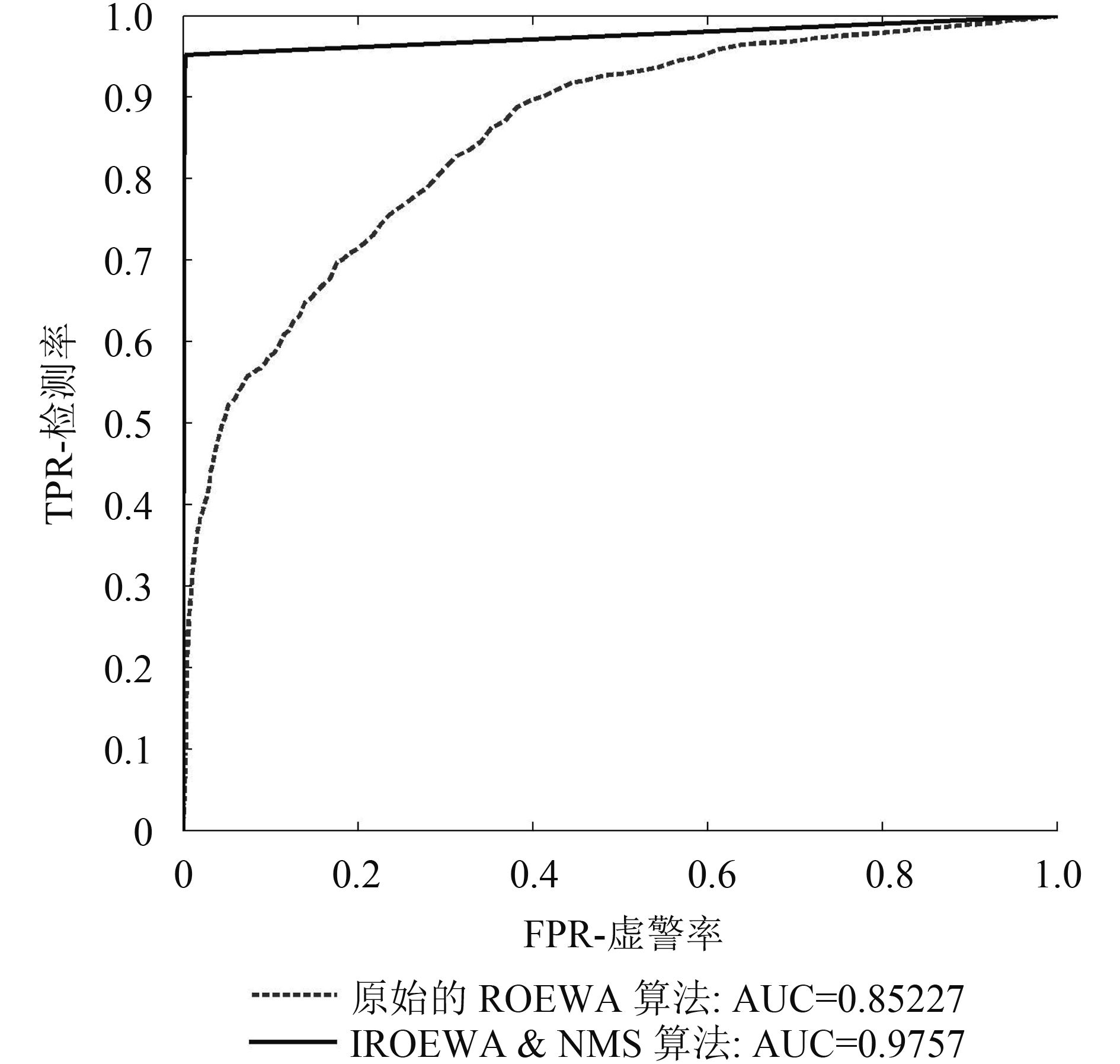
本实验利用仿真SAR图像,对原始ROEWA和IROEWA & NMS分别进行测试。先求得两者边缘强度图的唯一值序列vi ,通过循环设置阈值T=vi ,对边缘强度图进行一系列二值分割,得到边缘检测结果;然后利用接收者操作特征,即Receiver Operating Characteristic (ROC),来量化评价边缘检测结果,计算并绘制出ROC曲线,以曲线下面积,即Area under the Curve (AUC)作为指标,来量化评价算法的总体性能(Mason和Graham,2002)。
ROC曲线的x坐标代表虚警率,y坐标代表检测率;故当虚警率为零,检测率为1时,是检测器的最优状态;曲线上最接近(0, 1)的点即最优点,对应最优的分割阈值;而点(0, 0)到点(0, 1),再到点(1, 1)的连线,即理想检测器的ROC曲线(孙长亮,2006)。如图7所示,ROEWA的AUC仅为0.85227,而IROEWA & NMS的AUC高达0.97570。由此可见,IROEWA & NMS已经非常接近理想的检测器了。
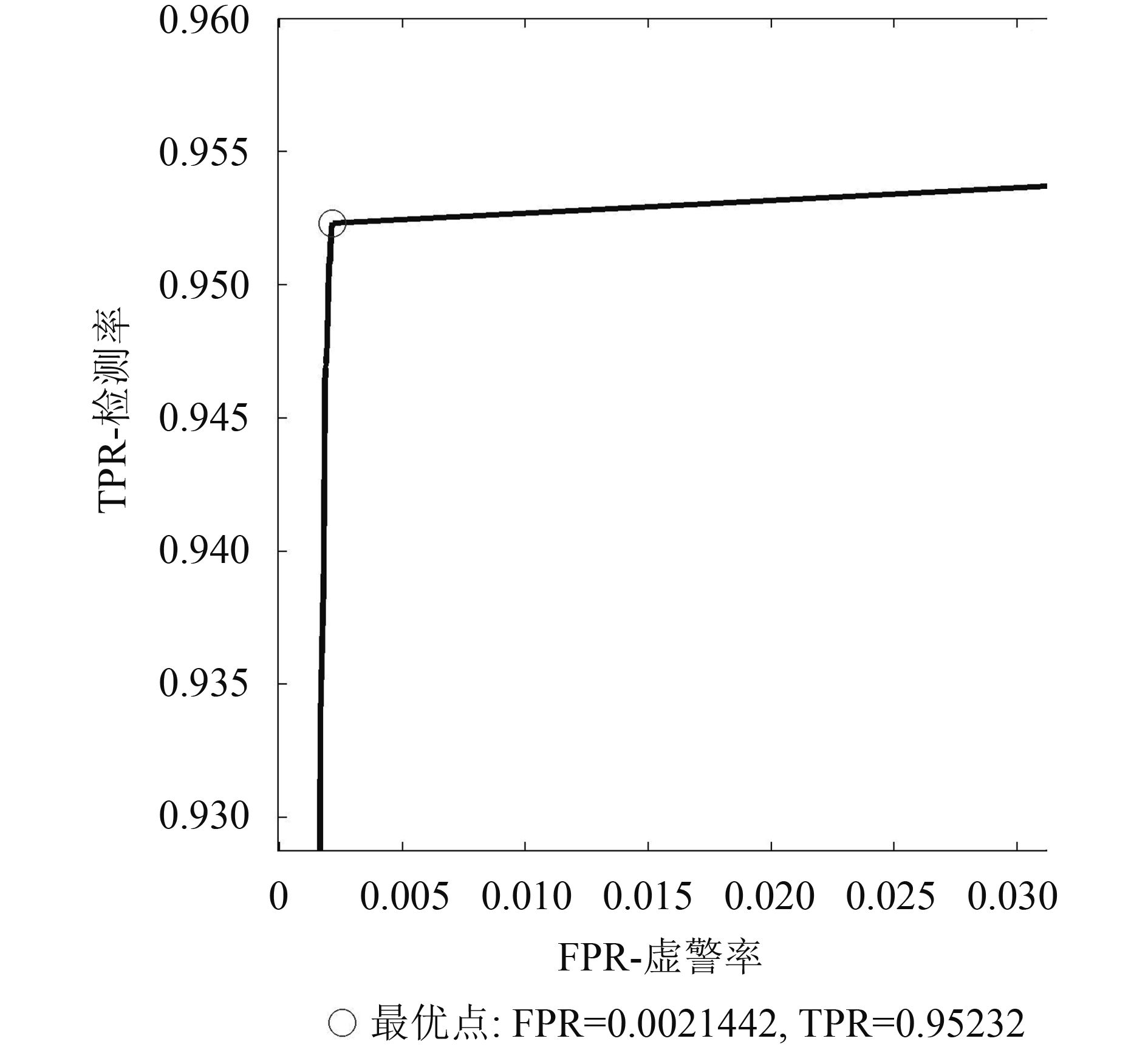
如图8所示,在IROEWA & NMS算法ROC的局部图中,最优点处对应的检测率为0.95232,虚警率约为0.00214。
5 结 论
本文针对ROEWA算子和国内已有的ROEWA改进算法不能准确计算边缘方位的问题,仅仅通过简单修改ROEWA算子的两个表达式,就重新定义了边缘强度分量,并据此设计出一种简单而准确的边缘方位计算方法,以至于不必再使用复杂而繁琐的方位估计器或方位模板去估算边缘方位。根据准确计算的边缘方位,应用改进到亚像元处理级别的非极大值抑制算法,处理边缘强度图后,能得到更好的边缘检测结果。针对自然SAR图像和仿真SAR图像的算法测试实验表明:本文改进的IROEWA & NMS边缘检测算法,在兼顾高检测率和低虚警率方面有良好的表现,通过ROC曲线的量化评价来看,其性能已经很接近理想的检测器,而且运行速度快。这种改进算法在SAR图像分割和SAR图像边缘检测领域,特别是在诸如道路、河流、海岸线等线性目标的检测任务中是很有应用价值的。本文目前主要完成了该算法的改进和评价,在算法的自动化方面还存在不足,下一步研究应该着眼于如何利用ROC曲线自动化地选取参数并进行边缘检测方面。
参考文献(References)
-
AnC J, XinY L and ChenZ P. 2011. Edge detection algorithm for SAR image based on improved ROEWA. Journal of Image and Graphics, 16 (8): 1483–1488. ( 安成锦, 辛玉林, 陈曾平. 2011. 基于改进ROEWA算子的SAR图像边缘检测方法. 中国图象图形学报, 16 (8): 1483–1488. )
-
BovikA C. 1988. On detecting edges in speckle imagery. IEEE Transactions on Acoustics, Speech, and Signal Processing, 36 (10): 1618–1627. [DOI: 10.1109/29.7550]
-
CannyJ F. 1986. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-8 (6): 679–698. [DOI: 10.1109/TPAMI.1986.4767851]
-
FjørtoftR . 1998. An optimal multiedge detector for SAR image segmentation. IEEE Transactions on Geoscience and Remote Sensing, 36 (3): 793–802. [DOI: 10.1109/36.673672]
-
JiaC L and KuangG Y. 2007. An improved edge detection algorithm for SAR images. Journal of Electronics and Information Technology, 29 (2): 379–382. ( 贾承丽, 匡纲要. 2007. 一种改进的SAR图像边缘检测方法. 电子与信息学报, 29 (2): 379–382. )
-
LeeJ S. 1986. Speckle suppression and analysis for synthetic aperture radar images. Optical Engineering, 25 (5): 636–643. [DOI: 10.1117/12.7973877]
-
MasonS J and GrahamN E. 2002. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: statistical significance and interpretation. Quarterly Journal of the Royal Meteorological Society, 128 (584): 2145–2166. [DOI: 10.1256/003590002320603584]
-
Paillou P. 1997. Detecting step edges in noisy SAR images: a new linear operator. IEEE Transactions on Geoscience and Remote Sensing, 35 (1): 191–196. [DOI: 10.1109/36.551947]
-
Sun C L. 2006. Study of ATR Algorithm Performance Evaluation Method based on ROC Curve. Changsha: National University of Defense Technology: 28–31 (孙长亮. 2006. 基于ROC曲线的ATR算法性能评估方法研究. 长沙: 国防科学技术大学: 28–31)
-
Wu Y H, Chen T Z and Shu Y. 2010. Road extraction from high resolution SAR images based on the directional ROEWA detector. Computer Engineering and Science, 32 (8): 71–74. ( 吴禹昊, 陈天泽, 粟毅. 2010. 基于方向ROEWA算子的高分辨率SAR图像道路提取. 计算机工程与科学, 32 (8): 71–74. )
-
Yang D L, Lu C H, Zhang J L, Yang K and Chen X T. 2013. Edge detection in SAR images based on ROEWA and Hough transform. Journal of Electronic Measurement and Instrument, 27 (6): 543–548. ( 杨道莲, 鲁昌华, 张金良, 杨凯, 陈晓婷. 2013. 基于ROEWA与Hough变换的SAR图像边缘检测. 电子测量与仪器学报, 27 (6): 543–548. )
-
Zaman M R and Moloney C R. 1993. A comparison of adaptive filters for edge-preserving smoothing of speckle noise // Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing. Minneapolis, MN, USA: IEEE: 77–80 [DOI: 10.1109/ICASSP.1993.319751]
-
ZhaoL J, JiaC L and KuangG Y. 2007. Overview of edge detection in SAR images. Journal of Image and Graphics, 12 (12): 2042–2049. ( 赵凌君, 贾承丽, 匡纲要. 2007. SAR图像边缘检测方法综述. 中国图象图形学报, 12 (12): 2042–2049. )