出版日期: 2017-03-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176234
2017 | Volumn21 | Number 2

技术方法

遥感影像主特征线检测

戴激光^1,2 , 张力² , 朱恩泽¹ , 廖健驰¹ , 方鑫鑫¹ , 李晋威¹

1. 辽宁工程技术大学测绘与地理科学学院，阜新 123000

2. 中国测绘科学研究院，北京 100039

收稿日期: 2016-06-20; 修改日期: 2016-09-02; 优先数字出版日期: 2016-11-28

基金项目: 国家自然科学基金(编号：41271374，61540056，41401535)，对地观测技术国家测绘地理信息局重点实验室开放基金项目(编号： K201402)；资源与环境信息系统国家重点实验室开放基金

第一作者简介: 戴激光(1978—　)，男，在站博士后，副教授，研究方向为高分辨率影像特征提取理论研究。E-mail： daijg03@163.com

通讯作者简介: 张力(1970—　)，男，研究员，研究方向为数字摄影测量与遥感及计算机视觉理论和应用。E-mail： zhangl@casm.ac.cn

中图分类号: P237

文献标识码: A

摘要

受到成像规律性差，背景纹理复杂及强烈噪声的影响，直线检测方法通常难以适应遥感影像处理的需求。有鉴于此，论文提出一种具有视觉显著性的遥感影像主特征线检测方法。论文首先论证了利用已提取直线为基元，基于格式塔法则构建主特征线的可行性；其次对直线在主特征线上的复杂投影情况进行了详细的剖析，并给出了主特征线的定义；接着建立了主特征线累计权重矩阵及直线统计矩阵，依据格式塔原则分析直线权重分布规律，以此构建了直线的权重模型，同时探讨不同直线在同一主特征线上权重分配规律；最后依据上述分析结果提出了具体的算法步骤。通过多幅含有强烈噪声的光学与SAR遥感卫星影像实验结果表明，相对于其他聚类算法，论文算法能够在杂乱无序的直线集中提取较为清晰的主特征线，并且实验效果基本符合人工视觉感知，便于机器对遥感影像的清晰理解。

关键词

主特征线, 格式塔法则, 视觉显著性, 累计权重矩阵, 直线统计矩阵

Principal line detection in remote sensing image

DAI Jiguang^1,2 , ZHANG Li² , ZHU Enze¹ , LIAO Jianchi¹ , FANG Xinxin¹ , LI Jinwei¹

1.School of Geomatics, Liaoning Technical University, Fuxin 123000, China

2.Chinese Academy of Surveying and Mapping, Beijing 100039, China

Abstract

The linear detection method is usually difficult to adapt to the demand of remote sensing image processing because of it exhibits poor imaging regularity, complex background texture, and strong noises. To address these problems, we proposed a new method that possesses visual saliency in the remote sensing image and can detect principal features. First, the possibility of constructing principal lines according to the Gestalt laws and the use of extracted lines as geometric primitives were analyzed. The complex projection of the lines in the principal lines was then examined, and the definition of the principal lines was provided. Furthermore, the cumulative weight matrix of the principal line and linear statistical matrix were constructed. Meanwhile, the distribution regularity of the short line weight was studied according to the Gestalt laws, and the model of the short linear weight was constructed. Accordingly, the weight allocation pattern of the different lines in the same principal line was also discussed. Finally, detailed algorithm steps were proposed according to these analyses.The key algorithm steps were described as follows: first, the chain code marshaling algorithms were employed to extract the straight lines. Second, the accumulative weighted matrix and linear statistical matrix of the principal lines were constructed. Third, the lines were sorted on the basis of their spatial positions. Fourth, according to linear weight distribution regularity, all the lines were elected to a cumulative weight matrix according to the linear weight model and distribution rules, and the results were recorded in the linear statistical matrix. Fifth, the local maximum value of the accumulative matrix was obtained to prevent parallel overlapping among the principal lines. Sixth, constraint analysis on the continuity and purity of the accumulative weighted matrix and linear statistical matrix was conducted to prevent the appearance of false principal lines. Finally, the parameters of the principal lines were obtained according to the sorting results of the weight voting matrix and weight values. Meanwhile, the principal line was obtained through its endpoints.The results of multiple SAR and optical remote sensing satellite images with strong noises showed that the traditional line extraction method can obtain only the disordered linear information, which is not clear and useful for image processing. In this study, our proposed method obtained clear principal lines by using Gestalt law on the basis of traditional linear extraction algorithm, and the results were basically in agreement with artificial visual perception. Meanwhile, the results suggest that our algorithm is superior to the traditional cluster algorithm in terms of operation efficiency and experimental effects. The experimental results indicate the potential application of our method in various fields, such as road extraction, image matching, and object recognition. However, this method also presents several shortcomings. First, the extraction results of the principal lines rely heavily on previous results. In addition, whether the linear-weighted Gaussian model established in this study is in full compliance with the Gestalt law requires further investigation. Finally, several parameter settings are experience values acquired by a large number of experiments. Thus, we hope to achieve the adaptive processing of these parameters in our future research.

Key words

principal lines, Gestalt laws, visual saliency, cumulative weight matrix, linear statistical matrix

1 引　言

直线作为一种重要的几何信息，在立体匹配、图像压缩、变化检测等领域具有极大的应用价值。目前直线检测的方式主要分为两类：自上而下的方法及自下而上的方法。基于Hough变换的算法是最为经典的自上而下方法(Ballard，1981)。这种方法利用图像和参数空间的点线对偶关系，通过聚类的方式获取直线相关参数。其优点是具有较好的容错性及抗噪性；缺点是计算复杂度高、参数难以选择、缺乏局部特性、直线端点定位难度大，容易产生虚假直线及漏检问题(Chung 等，2004；王竞雪等，2014b；Xu 等，2015)。自下而上的方法包括链码跟踪(Freeman，1970)和相位编组(Burns 等，1986)的直线提取方法，这类方法通常采用一定约束规则进行八邻域或八邻域外边缘跟踪(Von Gioi 等，2010；王竞雪等，2014a)，利用边缘跟踪结果采取最小二乘(Cuneyt和Cihan，2012)、合并与分裂(Wu 等，2012)等算法完成对直线的拟合。该类算法的优点是计算量小并且实时性好，直线效果与实际地物轮廓信息具有较好的吻合度；但其缺点在于采用局部跟踪方式进行直线拟合，跟踪过程极易受到局部噪声及约束规则的影响。例如白噪声易引发连续边缘跟踪过程的终止，而相位编组方法中相位分区的选择及链码跟踪方向的确定都会导致部分连续边缘发生断裂，同一直线经常被割裂为多条直线。

综上所述，现有的直线检测方法都存在各自的优势及缺点，并且均试图完整检测图像中所有直线信息，以此提高对图像的理解。但在遥感卫星影像中，由于成像规律性差，背景纹理复杂且噪声大，线状地物在不同影像上表现出不同的灰度分布形态，苛求对所有直线的理想检测效果并不现实。因此一些学者尝试提取一些具有视觉显著性的特征线，通常这一类线称为主特征线。已有的研究分别通过边缘点(Barni 等，1996；Tsuda 等，1996)、目标直线(陈仁杰等，2010；Stahl和Wang，2008)进行聚类分析，以此进行直线拟合。但这类方法一方面受到起始聚类中心位置准确性的制约，另外一方面没有对聚类体进行局部有效分析，形成的主特征线是穿过影像中的一条轨迹，没有端点信息，因而检测效果并不理想。

格式塔法则是计算机视觉中一个重要的理论，其目的是模拟生物在面对复杂地物时对显著信息的识别能力，已应用于图像分割(曾接贤和王玉，2015)、图像重建(徐威等，2015)及路面图像裂缝检测(李翠华等，2011)等领域。有鉴于此，论文依据格式塔法则，针对主特征线的特点，以检测到的直线为处理基元(为与主特征线区别，以下均称短直线)，提出一种具有端点信息的遥感影像主特征线检测方法。

2 格式塔法则

格式塔法则是以知觉心理为主(曾接贤和王玉，2015)。该法则强调结构的整体作用和产生知觉的组成成分之间的联系，即人类具有无需学习的组织倾向，便能在视觉环境中组织排列事物的位置，感受和知觉出环境的整体与连续信息。因此基于SAR影像数据，论文以具有视觉显著性的主特征线与形成主特征的短直线集为研究目标，分析主特征线与短直线集的排列关系，对格式塔法则中部分原则进行探讨：

(1) 图形与背景的关系原则(figured out)。是指图形与背景间具有强烈的对比性，因而图形能够被清晰识别。如图1(a)所示，在SAR影像中人眼能够清晰识别白带边缘信息，可将作为影像中的主要显著特征。但是在实际影像处理中，由于SAR影像存在大量的相干斑噪声，因而图1(b)在白带边缘附近利用直线提取算法仅能得到一系列具有不同角度、长度的蓝色直线集。

(2) 相似原则(fimilarity)。当刺激物的形状、大小、颜色、强度等物理属性方面比较相似时，这些刺激物就容易被组织起来而构成一个整体。如图1(b)所示，利用直线检测方法获得的蓝色直线集在主特征线附近表现出角度相似性及相同性，故可视为一个相似整体。

(3) 接近或邻近原则(proximity)。即距离较近的各部分趋向于组成一个整体。如图1(b)所示，短直线端点间距离较小，符合接近或邻近原则。

(4) 连续性原则(continuity)。如果一个图形的某些部分可以被看作是连接在一起的，那么这些部分就相对容易被视为是一个整体。如图1(b)所示，蓝色短直线集在主特征线附近表现出连续规律性排列特点，因而如图1(c)所示易被识别为的红色主特征线。

综上所述，短直线与主特征线间的空间关系符合格式塔原理，故可将其作为主特征线提取的基元。反之，如果直接利用边缘信息提取主特征线，如图1(d)所示为SAR影像主特征附近提取的边缘信息，过多的噪声信息将直接影响提取主特征线的精度及效率，并且边缘点空间位置关系也难以度量，进而影响主特征线的检测效果。因而论文选取短直线作为主特征线的检测基元，以此减少噪声对主特征线的影响。

图 1 主特征线示意图

Fig. 1 Flow chart of the principal line

3 算法原理

3.1 短直线投影分析与主特征线定义

受到成像方式、光照、噪声、遮挡等多种因素的影响，短直线在主特征线附近的位置排列方式存在一些差异，为定量化建立基于格式塔法则的主特征线模型，需要对短直线集在主特征线上的投影关系进行分析：

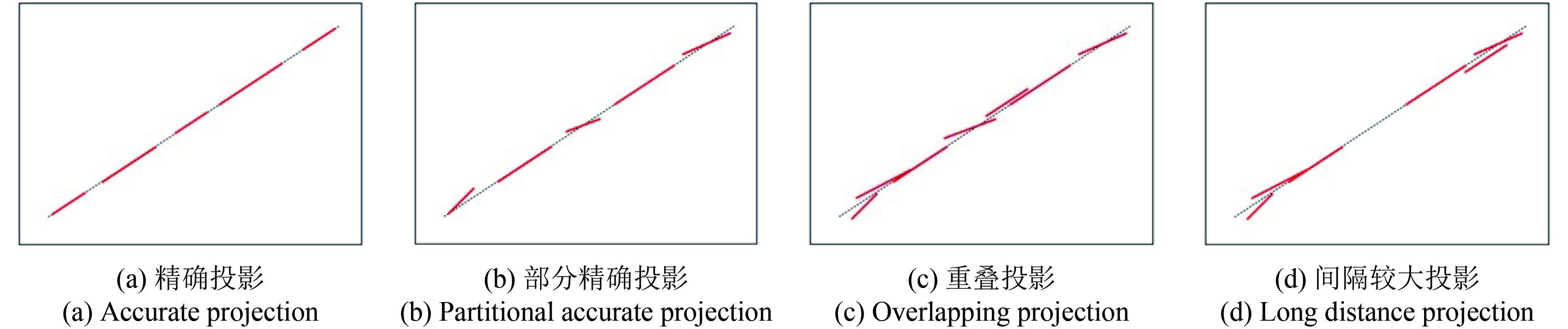
情况1 短直线集精确投影于主特征线。如图2(a)所示，短直线(红色直线，下同)均遵循主特征线(虚线，下同)位置约束，短直线端点间存在一定距离。这种情况下，短直线符合相似原则及接近原则，但不完全符合连续性原则。例如影像地物目标受到其他地物遮挡时，这种断裂投影情况极易发生。

情况2 部分短直线精确投影于主特征线。当短直线集不完全遵循主特征线约束，即部分短直线与主特征线间存在较小的夹角。如图2(b)所示，短直线集虽然符合接近原则，但存在较弱的角度相似性。例如在光学卫星影像道路信息提取过程中，路面两侧栽种的树木易引发边缘点的误判，进而降低道路两侧直线信息的提取精度。

情况3 短直线在主特征线上重叠投影。如图2(c)所示，在主特征两侧形成具有角度差异的短直线集，并且短直线集在线条边缘附近存在一定的交错投影。在光学卫星影像和SAR影像线条边缘处这一现象非常普遍。

情况4 短直线集间隔距离较大投影。如图2(d)所示构成主特征线的短直线集之间存在较大的距离间隔，连续性弱成为制约短直线集构成主特征的主要障碍。这类情况在光学卫星与SAR影像中均有明显呈现，例如在光学卫星影像中，线状地物周围噪声大、信息对比度小极易引发连续性边缘的破裂。在SAR影像中，受到强烈相干斑噪声的影响，线特征亦多有断裂情况发生。

针对短直线集在主特征线上投影的复杂情况，以建立主特征线的模型方法为切入点，对具有视觉显著性的主特征线进行定义：主特征线是以多条具有较小角度差异、连续性较强、有规律排列的短直线集合为处理基元，通过一系列数据建模分析形成具有视觉显著性的长直线。

图 2 短直线在主特征线上投影示意图

Fig. 2 The projection of lines on principal line

3.2 权重模型

依据上述主特征线定义及短直线投影情况，可利用格式塔法则对短直线进行相似性、邻近性及连续性分析，通过刻画短直线对主特征线的权重累加值，突出主特征线的视觉显著性。因此，首先需要建立权重矩阵，其次对短直线的权重分布规律进行分析，进而建立短直线权重模型，最后对主特征线上短直线权重分配规律进行分析。

3.2.1 权重矩阵

在定量化提取主特征线的过程中，权重矩阵的构建是一个关键的环节，通过权重矩阵中的权值可确定主特征线的参数以及构成主特征的短直线信息集。因此论文权重矩阵包括两个矩阵：主特征线累计权重矩阵及短直线统计矩阵，具体设置如下：

(1) 主特征线累计权重矩阵 M ₁(简称矩阵 M ₁，下同)。该矩阵构建类似于Hough变换中的投票器，如下所示：

$\begin{array}{c}{{M}_1} = \left( {\begin{array}{*{20}{l}}{{m_{00}}} & \cdots & {{m_{0j}}} & \cdots & {{m_{0\theta }}}\\ \vdots & \ddots & {} & {} & \vdots \\{{m_{i0}}} & {} & {{m_{ij}}} & {} & {{m_{i\theta }}}\\ \vdots & {} & {} & \ddots & \vdots \\{{m_{\rho 0}}} & \cdots & {{m_{\rho j}}} & \cdots & {{m_{\rho \theta }}}\end{array}} \right)\\\rho = 2 \times r\end{array}$

(1)

式中，m_ij 记录参数(i,j)累计权重值，i∈[1,ρ]，j∈[1,θ]，r为当前影像对角线长度，θ=180。参数(i,j)与主特征线关系如式(2)所示：

$i = {x_i} \times \cos j + {y_i} \times \sin j + 8$

(2)

式中，i是影像空间坐标原点到主特征线的垂直距离，单位为像素；j为主特征线垂线与影像空间x轴夹角，单位为度；(x_i ,y_i )为影像空间主特征线上任意点坐标。

(2) 短直线统计矩阵 M ₂(简称矩阵 M ₂，下同)。该矩阵大小与 M ₁一致，其下标意义与 M ₁相同，但矩阵元素不再记录数值，而是程序设计中的容器。

${{M}_2} = \left( {\begin{array}{*{20}{l}}{Ve{c_{00}}} & \cdots & {Ve{c_{0j}}} & \cdots & {Ve{c_{0\theta }}}\\ \vdots & \ddots & {} & {} & \vdots \\{Ve{c_{i0}}} & {} & {Ve{c_{ij}}} & {} & {Ve{c_{i\theta }}}\\ \vdots & {} & {} & \ddots & \vdots \\{Ve{c_{\rho 0}}} & \cdots & {Ve{c_{\rho j}}} & \cdots & {Ve{c_{\rho \theta }}}\end{array}} \right)$

式中，Vec_ij 是记录对参数(i,j)权重投票的短直线信息集容器，该容器保存投票短直线及权重投影信息，以便对矩阵 M ₁进行短直线空间位置分析。

3.2.2 短直线权重分布规律

在权重投票过程中，受格式塔相似原则的限制，短直线仅能对位置近似的主特征线进行投票，通常位置近似包括角度和距离接近，故论文设定短直线初始旋转阈值α₀与初始平移阈值ε₀，以此分析短直线权重分布规律。理论上两种阈值设定后，应满足如下关系

${\varepsilon _0} =0.5 \times Le{n_0} \times \sin {\alpha _0}$

(3)

式中，Len₀为理想情况下短直线长度。该公式表示在短直线长度Len₀不变情况下，初始旋转阈值α₀与初始平移阈值ε₀之间的对应关系。

但由于短直线长度Len差异较大，采用统一的阈值并不恰当，并且式(3)也不成立，因此需要设定当前短直线的有效阈值。假定Len×sinα₀大于ε₀，这说明当前短直线长度Len较大，初始旋转阈值α₀并不适用，故设定当前短直线平移阈值ε=ε₀，角度阈值α=arcsin((2×ε₀)/Len)。而当短直线长度Len较小，即Len×sinα₀小于ε₀时，设定当前短直线角度阈值α=α₀，平移阈值ε=Len×sinα₀。利用这一方式，论文针对短直线长度不同的特点，设定不同短直线的旋转阈值α与平移阈值ε，以此确定短直线权重分布范围。

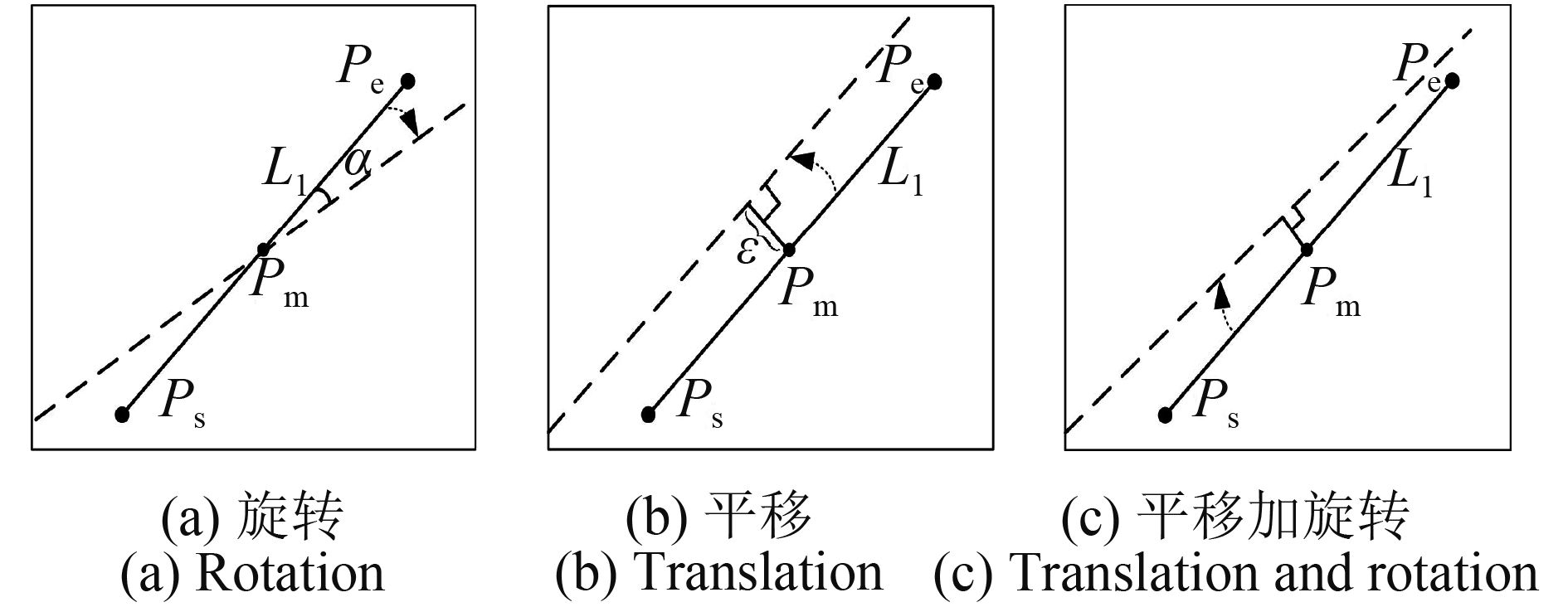
如图3所示，假设从影像中提取短直线L₁属性为(Len,ω,P_m,P_s,P_e)，其投影主特征线如虚线所示。其中，Len,ω表示长度、角度，P_m,P_s,P_e为直线L₁的中点、两个端点坐标，y轴较大的为P_s。依据上述旋转阈值α与平移阈值ε的设定，直线L₁权重分布范围包括如图3(a)(b)所示L₁旋转与平移后形成的不同主特征线，同时也涵盖如图3(c)所示以P_m为中心平移加旋转后的主特征线。进而可以定义，短直线的投影权重分布范围应是以P_m为中心两侧旋转弧度α构成的旋转直线集，和以旋转集直线为中心两侧平移距离范围为ε像素的直线集，即以L₁为中心的(2ε+1)×(2(α/β)+1)条主特征线集合，其中β为单位旋转参数。

图 3 短直线权重分布规律示意图

Fig. 3 The weight distribution rule of line

3.2.3 短直线权重模型

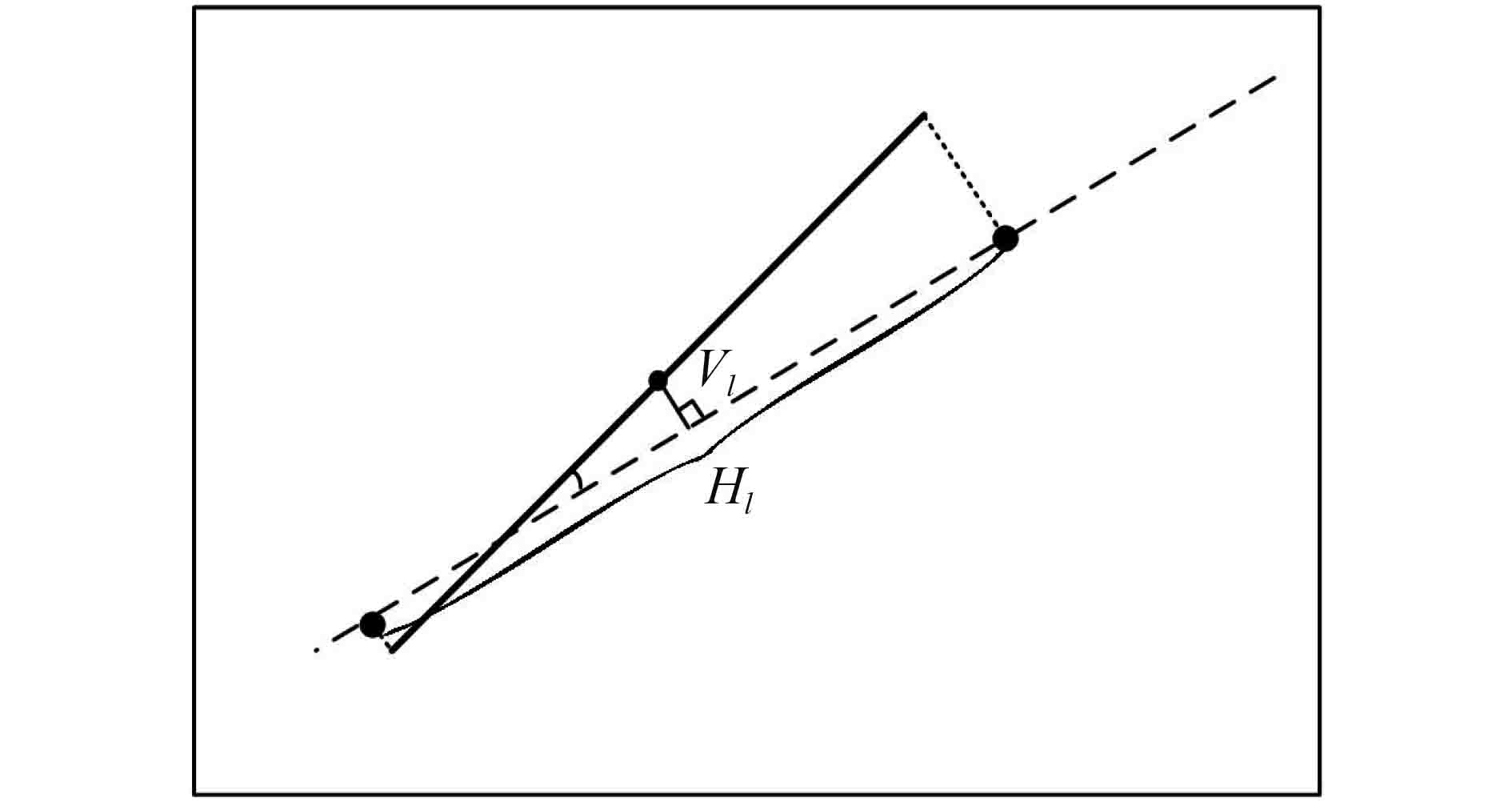
依据格式塔相似原则，短直线与主特征线空间位置上越接近其权重应该越大。具体空间位置参数分析如下：垂直距离，即短直线中心点至投影主特征线的垂直距离；重叠距离，投影直线在主特征线上的覆盖范围。通过对大量遥感影像的分析发现，线状地物由于受到影像锯齿问题的影响，易发生较小的角度旋转，但人眼易将其视为同一直线。与之相反的是，当短直线与主特征线存在一定的垂直距离时，人眼倾向于将其视为不同直线。有鉴于此，构建的短直线权重模型如下所示：

$W = {H_l} \times \exp \left( { - \left( {V_l^2/{\sigma ^2}} \right)} \right)$

(4)

式中，W为权重， $\exp \left( { - \left( {V_l^2/{\sigma ^2}} \right)} \right)$ 为当前短直线单位权重，如图4所示V_l 为短直线(实线)中点距离主特征(虚线)的垂直距离，σ为尺度因子，H_l 为短直线在主特征线上的重叠距离。对式(4)分析表明，垂直距离的增大权重W呈指数型下降趋势，其分布为高斯分布，符合人工视觉。

图 4 权重模型

Fig. 4 Weight model

3.2.4 短直线信息集权重分配规律

在图2(c)中，短直线信息集在主特征线同一区域易出现重叠投影问题。而依据格式塔连续原则，主特征线上同一区域内仅能有一条短直线进行投影。为了解决这一问题，需要对构成主特征的短直线信息集权重进行分配，具体如下：

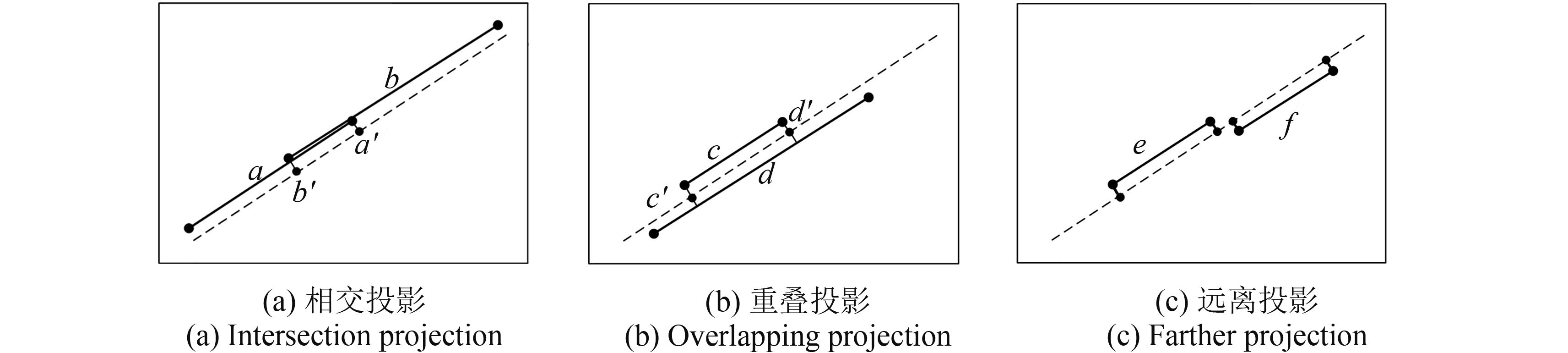
情况1 如图5(a)所示短直线a、b平移后，可在主特征虚线上进行权重投票，但存在投影重叠区域a′b′，假定短直线a单位权重为W_a 大于短直线b单位权重W_b ，则矩阵 M ₁主特征线坐标上加入短直线a、b权重，但需去掉短直线b重叠区域权重值，矩阵 M ₂相应坐标上记录短直线a投影信息及短直线b投影变化信息。

情况2 如图5(b)所示短直线c、d在主特征虚线投影存在重叠区域c′d′，假定短直线c单位权重W_c 小于直线d单位权重W_d ，则短直线c在矩阵 M ₁主特征线坐标上不进行权重投票，矩阵 M ₂相应坐标上不记录短直线c信息。

情况3 如图5(c)所示，当短直线e、f在主特征线上没有交叉投影，则将短直线e、f权重直接累加至矩阵 M ₁主特征线坐标上，并在矩阵 M ₂相应坐标上记录短直线e、f信息。

图 5 短直线间投影空间位置拓扑关系

Fig. 5 Spatial position topological relations between line projections

3.3 算法步骤

依据权重模型进行主特征线的提取，具体步骤如下：

(1) 短直线提取。由于相位编组的直线提取方法受到边缘相位的限制，使得这类方法在SAR影像中很难获取较好的直线效果，因此论文选取链码跟踪方式进行短直线提取，即利用Canny算法提取影像边缘图，采用链码跟踪方式进行短直线拟合，确保直线拟合边缘精度为亚像素。

(2) 矩阵 M ₁与矩阵 M ₂建立，将矩阵 M ₁权值置零，同时将矩阵 M ₂元素容器置空。

(3) 短直线排序。依据端点y轴坐标对步骤(1)获取的短直线进行位置排序，以便矩阵 M ₂记录的短直线信息集有位置规律性，有利于后续权重分配。

(4) 短直线权重投票。对所有短直线按照排列顺序进行权重投票。以任意短直线L_i 为例，首先，计算影像空间原点与L_i 的距离i及L_i 垂线与x轴夹角j；其次，依据短直线权重分布规律，确定L_i 在矩阵 M ₁中投票坐标范围，是以左上角坐标为(i–ε,j–α/β)，右下角坐标为(i+ε,j+α/β)的子矩阵 M_i 。然后，利用式(4)计算L_i 在子矩阵 M_i 不同坐标上投票权重，同时依据短直线信息集权重分配规律及子矩阵 M_i 坐标值，分析L_i 与矩阵 M ₂相应坐标上原有短直线信息集之间的空间位置关系，避免主特征线上同一区域重复投票问题的发生。最后，根据L_i 在子矩阵 M_i 不同坐标上的权重结果，将权重累计至矩阵 M ₁对应坐标上，并将短直线L_i 、相应权重及旋转平移数值记录到矩阵 M ₂对应坐标短直线信息集。

(5) 局部极值点确定。步骤(4)完成后，对矩阵 M ₁进行八邻域分析，保留局部极大值，将局部极值点周围八邻域置零，同时清空矩阵 M ₂相应坐标短直线信息集，防止主特征线出现重叠现象。

(6) 短直线归属关系分析。依据格式塔法则，一条短直线仅属于一条主特征线，故需利用矩阵 M ₁和矩阵 M ₂确定所有短直线归属关系。首先对矩阵 M ₁进行权重排序后，根据权重越大主特征线概率越大的假设，当一条短直线在矩阵 M ₁的权重高坐标上投票，那么在矩阵 M ₁其他坐标上不能进行权重投票，如已投票则在矩阵 M ₁和矩阵 M ₂其他坐标上剔除其权重值及短直线信息，以此防止虚假、平行、近似主特征线出现。

(7) 主特征线邻近分析。依据格式塔接近或邻近原则，构成整体的各部分距离接近。因此论文对矩阵 M ₂所有坐标上短直线信息集进行邻近分析，将短直线信息集内直线间存在较大间隔，并且间隔距离大于邻近约束参数μ的短直线信息集进行重新梳理。由于短直线权重投票顺序是依据其坐标排序的，因此直线集内直线端点坐标间也必然存在坐标顺序，故只需统计相邻短直线端点距离是否大于邻近约束参数μ即可。如大于参数μ，则分裂短直线信息集，选取其中权重最大的作为矩阵 M ₂当前位置直线信息集，同时改变矩阵 M ₁相应坐标上权值。如低于参数μ，则矩阵 M ₁和矩阵 M ₂相应坐标不做修改。

(8) 主特征线纯度分析。在构成主特征线过程中，短直线通过旋转、平移在主特征线上投票。而根据格式塔相似原则，精确符合主特征线的短直线长度应保证在一定比例之上，以此避免检测出来的主特征线仅由多条短直线角度旋转、平移而形成。因此论文对矩阵 M ₂所有坐标上短直线信息集进行分析，当短直线信息集内精确投影短直线长度(较小的平移与旋转)与短直线信息集总长度比值低于纯度阈值λ时，则矩阵 M ₂当前坐标上短直线信息集清空，矩阵 M ₁相应坐标上权重置零，高于纯度阈值λ则不做改动。

(9) 主特征线输出。对矩阵 M ₁依据权重大小进行排序，利用排序次序确定主特征线参数，主特征线端点可依据矩阵 M ₂相应坐标上短直线信息集端点范围确定。

4 实验结果处理与分析

4.1 参数分析及设定

由于论文算法涉及多个阈值参数，因此需要进行讨论分析：

(1) 初始平移参数ε₀。通常短直线不能完全位于主特征线轨迹中。例如在道路两侧连续性边缘，由于受到成像过程导致的影像退化问题影响，提取的短直线经常会位于连续性边缘的两侧，而初始平移参数就是为了适应这一问题而设定的，这有助于提高主特征线的容错性。在设定初始平移参数ε₀时，数值不易过大，如果过大一方面降低了算法运算速度，另一方面可能将无关短直线引入到当前主特征线中来，造成主特征线的误提取。因此，论文将该参数设定为4像素。

(2) 初始旋转参数α₀。该参数主要是为了适应在成像过程中影像出现的模糊失真问题。该问题将引发连续性边缘发生方位偏差，导致提取的短直线角度发生变形。因此通过实验分析，确定α₀为π/4弧度，单位旋转参数β为π/16弧度。

(3) 邻近约束参数μ。光学影像的遮挡和SAR影像的相干斑噪声是制约遥感实际应用的关键瓶颈问题，同样这一问题也会造成短直线的断裂，邻近约束参数μ就是为此而设定的。根据光学与SAR影像受该类问题影响的程度，通过大量实验的分析，确定μ在光学卫星影像中为50像素，SAR影像为100像素。

(4) 纯度参数λ。该参数是为了分析精确符合主特征线的短直线长度比值。相对于SAR影像，光学影像受到噪声的影响相对低一些，故该参数设为0.4，而SAR影像λ设为0.3。

(5) 尺度因子σ。尺度因子参照高斯分布中的通用值，即σ=1.414。

4.2 主特征线实验结果与分析

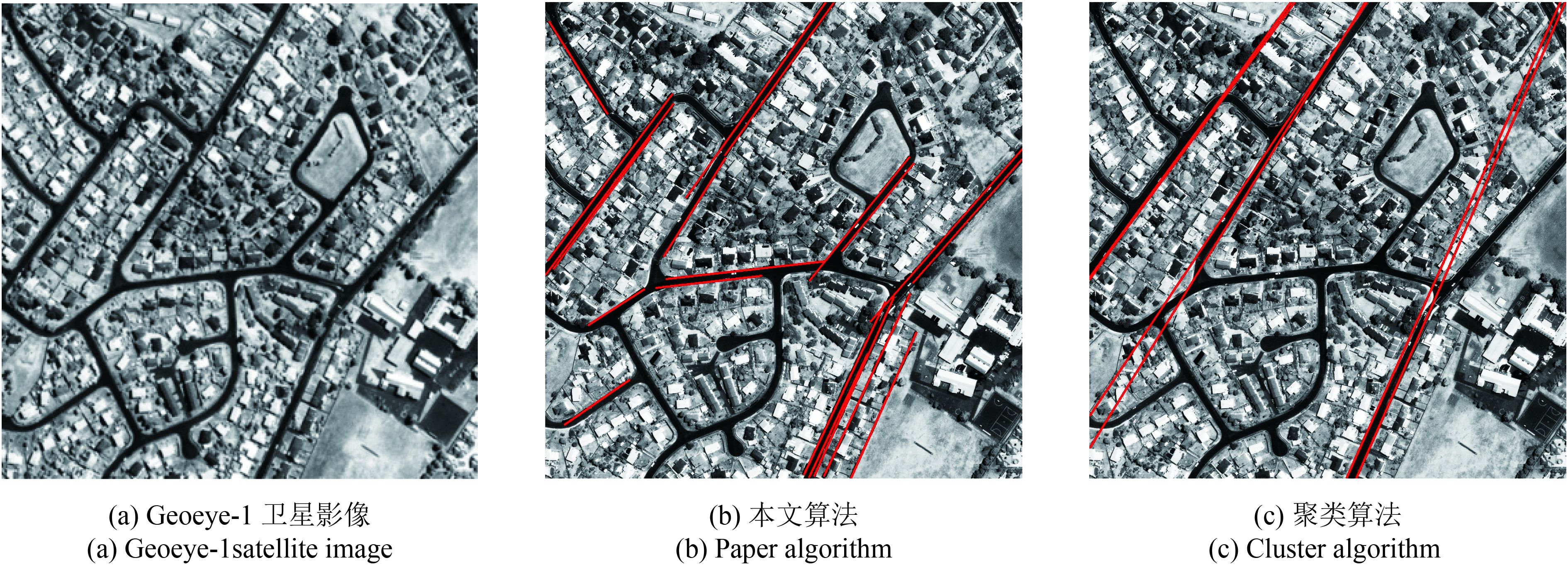
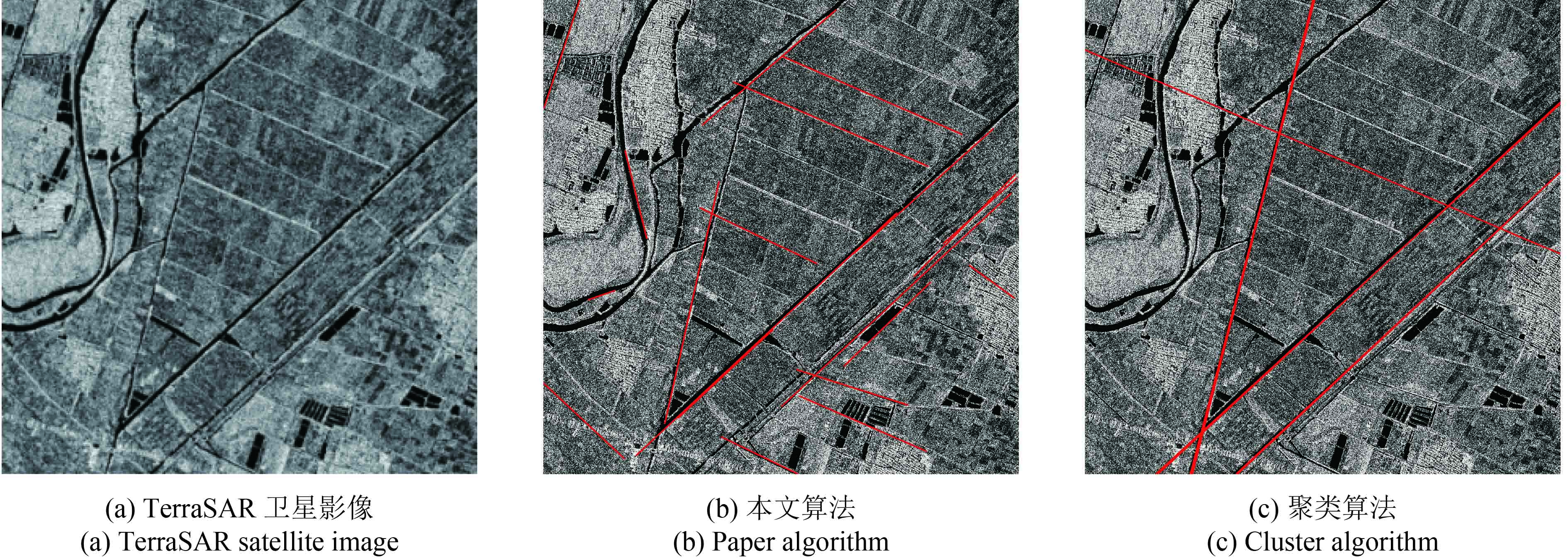
为了充分验证本文算法的可靠性，论文以VS2010作为处理平台，对论文算法进行单进程编程，并采用基于聚类的主特征线方法(陈仁杰等，2010)(以下简称聚类算法)进行对比分析，由于该算法仅能提供穿过影像的几条轨迹线，故论文只对其提出的轨迹线进行对比分析。在实验中，由于篇幅所限选取具有代表性的两幅光学和两幅SAR影像进行实验分析。

为定量化验证论文实验数据的有效性，论文利用影像信噪比SNR(Signal-to-Noise Ratio)对遥感影像数据进行分析，具体公式(Fiete和Tantalo，2001)如下：

${\rm{SNR}} = 20\log \frac{{{I_{{\rm{mean}}}}}}{{{\sigma _{\rm{I}}}}}$

(5)

式中，I_mean为影像灰度均值，σ_I为噪声标准差，信噪比单位为分贝(db)。

4.2.1 实验1

图 6 IKONOS影像主特征线提取示意图

Fig. 6 Principal lines extraction for IKONOS image

表 1 不同算法主特征线提取结果
Table 1 Principal line extraction results by different algorithms

下载CSV

数据	SNR/db	论文算法			聚类算法
数据	SNR/db	提取直线数目	错误直线数目	耗时/s	提取直线数目	错误直线数目	耗时/s
图6	4.74	20	2	54.16	3	1	50.92
图7	4.75	20	0	73.46	7	2	69.23
图8	1.21	20	0	91.23	5	1	150.67
图9	4.83	5	1	24.23	2	0	20.79

4.2.2 实验2

图 7 Geoeye-1影像主特征线提取示意图

Fig. 7 Principal lines extraction for Geoeye-1 image

4.2.3 实验3

图 8 TerraSAR影像主特征线提取示意图

Fig. 8 Principal lines extraction for TerraSAR image

4.2.4 实验4

在算法耗时方面，如表1可以观察到论文算法与聚类算法耗时相差不大，唯一出现较大差距的出现图8实验中。通过分析发现，在图8中提取短直线数量较大(24165条)，聚类算法在运行过程中需要进行多次类更新，而每条直线均需要参与多次类分析，因此该实验耗时较长。

图 9 ASAR影像主特征线提取示意图

Fig. 9 Principal lines extraction for ASAR image

综上所述，论文方法相对于聚类算法，在算法效率、提取效果等方面均有较大优势，其关键原因在于论文算法进行了有效的局部短直线分析，使得检测的主特征线不仅含有端点信息，并且符合视觉显著性特点。但论文算法也存在效率较低、耗时较长等缺点，通过分析主特征线提取算法的各个阶段结果表明：短直线的权重分配、纯度分析等工作占了算法耗时的绝大部分，但这也是算法空间位置分析的主要环节，由于算法目前采用单进程编写，未来将进行多进程处理以提高算法效率。

5 结　论

论文提出了一种新的基于格式塔法则的遥感影像主特征线检测方法。为了弱化噪声、复杂背景等因素对边缘信息的影响，论文以已提取直线为基元，依据格式塔法则对主特征线进行定义，并对形成主特征线的短直线进行规律分析。在此基础上，建立了主特征线累计权重矩阵和短直线统计矩阵，探讨了短直线权重分布规律，构建了短直线权重模型，对短直线信息集在同一主特征线上的权重分配规律进行了分析，最后给出了完整的主特征线具体实现步骤。通过实验结果对比分析表明，本文算法能够在含有大量噪声的光学卫星影像和SAR影像中提取具有视觉显著性的主特征线，效果基本满足人的视觉感知，实验结果有望应用于道路提取、影像匹配、物体识别等领域。当然作为一种新的算法，论文也存在一些不足，如主特征线提取结果严重依赖于前期直线提取结果。同时论文所建立的短直线权重模型，是否完全符合格式塔法则，仍有待于进一步研究。另外，论文的部分参数设定是通过大量实验求得的经验值，未来的工作希望能找到一种高效的自适应参数算法。

参考文献(References)

BallardD H. 1981. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognition, 13 (2): 111–122. [DOI: 10.1016/0031-3203(81)90009-1]

Barni M, Cappellin V, Paoli A and Mecocci A. 1996. Unsupervised detection of straight lines through possibilistic clustering // Proceedings of the International Conference on Image Processing. Lausanne, Switzerland: IEEE: 963–966

Burns J B, Hanson A R and Riseman E M. 1986. Extracting straight lines. IEEE Transaction on Pattern Analysis and Machine Intelligent, PAMI-8(4): 425–455 [DOI: 10.1109/TPAMI.1986.4767808]

ChenR J, LiuL G and DongG C. 2010. Detection of principal lines in images. Journal of Image and Graphics, 15 (3): 403–408. [DOI: 10.11834/jig.20100308] ( 陈仁杰, 刘利刚, 董光昌. 2010. 图像主特征直线的检测算法. 中国图象图形学报, 15 (3): 403–408. [DOI: 10.11834/jig.20100308] )

ChungK L, ChenT C and YanW M. 2004. New memory- and computation-efficient Hough transform for detecting lines. Pattern Recognition, 37 (5): 953–963. [DOI: 10.1016/j.patcog.2003.09.008]

Cuneyt A and Cihan T. 2011. EDLines: a real-time line segment detector with a false detection control. Pattern Recognition Letters, 32 (13): 1633–1642. [DOI: 10.1016/j.patrec.2011.06.001]

Fiete R D and Tantalo T. 2001. Comparison of SNR image quality metrics for remote sensing systems. Optical Engineering, 40 (4): 574–585. [DOI: 10.1117/1.1355251]

Freeman H. 1970. Boundary encoding and processing // Picture Processing and Psychopictorics. New York: Academic Press: 241–266

Li C H, Shi H, Dai P Y, Chen J, Du X F, Qu Y Y and Xie Y. 2011. Super-resolution image reconstruction based on gestalt theory. Journal of Xiamen University (Natural Science), 50 (2): 261–270. ( 李翠华, 施华, 戴平阳, 陈婧, 杜晓凤, 曲延云, 谢怡. 2011. 引入格式塔理论的超分辨率图像重建技术. 厦门大学学报(自然科学版), 50 (2): 261–270. )

Stahl J S and Wang S. 2008. Globally optimal grouping for symmetric closed boundaries by combining boundary and region information. IEEE Transactions on Pattern Analysis and Machine Intelligence, 30 (3): 395–411. [DOI: 10.1109/TPAMI.2007.1186]

Tsuda K, Minoh M and Ikeda K. 1996. Extracting straight lines by sequential fuzzy clustering. Pattern Recognition Letters, 17 (6): 643–649. [DOI: 10.1016/0167-8655(96)00029-3]

Von Gioi R G, Jakubowicz J, Morel J M and Randall G. 2010. LSD: a fast line segment detector with a false detection control. IEEE Transactions on Pattern Analysis and Machine Intelligent, 32 (4): 722–732. [DOI: 10.1109/TPAMI.2008.300]

WangJ X, SongW D, ZhaoL K and WangW X. 2014a. Application of improved freeman chain code in edge tracking and straight line extraction. Journal of Signal Processing, 30 (4): 422–430. [DOI: 10.3969/j.issn.1003-0530.2014.04.008] ( 王竞雪, 宋伟东, 赵丽科, 王伟玺. 2014a. 改进的Freeman链码在边缘跟踪及直线提取中的应用研究. 信号处理, 30 (4): 422–430. [DOI: 10.3969/j.issn.1003-0530.2014.04.008] )

Wang J X, Zhu Q, Wang W X and Zhao L K. 2014b. Straight line extraction algorithm by Hough transform combining edge grouping. Journal of Remote Sensing, 18 (2): 378–389. [DOI: 10.11834/jrs.20143127] ( 王竞雪, 朱庆, 王伟玺, 赵丽科. 2014b. 结合边缘编组的Hough变换直线提取. 遥感学报, 18 (2): 378–389. [DOI: 10.11834/jrs.20143127] )

Wu B, Zhang Y S and Zhu Q. 2012. Integrated Point and Edge Matching on Poor Textural Images Constrained by self-adaptive triangulations. ISPRS Journal of Photogrammetry and Remote Sensing, 68 : 40–55. [DOI: 10.1016/j.isprsjprs.2011.12.005]

Xu W, Tang Z M, Xu D and Wu G X. 2015. Integrating multi-features fusion and gestalt principles for pavement crack detection. Journal of Computer-Aided Design and Computer Graphics, 27 (1): 147–156. ( 徐威, 唐振民, 徐丹, 吴国星. 2015. 融合多特征与格式塔理论的路面裂缝检测. 计算机辅助设计与图形学学报, 27 (1): 147–156. )

Xu Z Z, Shin B S and Klette R. 2015. Accurate and robust line segment extraction using minimum entropy with Hough transform. IEEE Transactions on Image Processing, 24 (3): 813–822. [DOI: 10.1109/TIP.2014.2387020]

Zeng J X and Wang Y. 2015. Natural image segmentation method based on Gestalt rules. Journal of Image and Graphics, 20 (8): 1026–1034. [DOI: 10.11834/jig.20150805] ( 曾接贤, 王玉. 2015. 结合格式塔完形规则的自然图像分割. 中国图象图形学报, 20 (8): 1026–1034. [DOI: 10.11834/jig.20150805] )

摘要

关键词