出版日期: 2017-03-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176257
2017 | Volumn21 | Number 2

技术方法

3维块匹配小波变换的极化SAR非局部均值滤波

刘留 , 杨学志 , 周芳 , 郎文辉

合肥工业大学计算机与信息学院，合肥 230009

收稿日期: 2016-07-04; 修改日期: 2016-11-15; 优先数字出版日期: 2016-11-22

基金项目: 国家自然科学基金(编号：61371154，61271381，61503111)；安徽省自然科学基金(编号：1608085QF142)；中央高校基本科研业务费专项资金资助(编号：2015HGBZ0106,2015HGQC0005)；国家博士后科学基金(编号：2016M592045)

第一作者简介: 刘留(1991—　)，男，硕士研究生，研究方向为极化合成孔径雷达图像处理。E-mail： liuliu@mail.hfut.edu.cn

通讯作者简介: 杨学志(1970—　)，男，教授，研究方向为图像处理，模式识别及合成孔径雷达图像解译。E-mail： hfut.cv@gmail.com

中图分类号: TP751

文献标识码: A

摘要

极化合成孔径雷达(SAR)图像受相干斑噪声的影响，难以很好地保持结构特性，针对这个问题提出了一种采用3维块匹配小波变换的非局部均值滤波算法NL-3DWT (Nonlocal Filter based on 3-D Patch Matching Wavelet Transform)。该算法使用块匹配的3维非抽样小波变换对极化总功率图进行预滤波，在此基础上使用边界对齐窗提取结构相似像素，同时使用Sigma范围选择极化SAR数据的散射相似像素，共同构成相似像素集合；构建结构保持权重函数增大图像结构信息在块相似性度量时的权重，最终实现极化SAR图像结构保持的相干斑抑制。该算法增强了图像结构特征的表达，提高了结构相似像素选择的准确性，机载极化SAR数据实验结果表明，NL-3DWT算法能够在抑制相干斑噪声的同时，更有效地保持极化SAR图像的结构特性和极化散射特性。

关键词

极化SAR, 相干斑抑制, 非局部均值, 小波变换, 结构保持

Non-local filtering for polarimetric SAR data based on three dimensional patch matching wavelet transform

LIU Liu , YANG Xuezhi , ZHOU Fang , LANG Wenhui

School of Computer and Information, Hefei University of Technology, Hefei 230009, China

Abstract

The Polarimetric Synthetic Aperture Radar (PolSAR) system has unique advantages in observing the Earth’s surface at different times and weather conditions. However, PolSAR data restricted to an inherent imaging mechanism are corrupted by speckle noise. The presence of speckle increases the difficulty of image understanding and decreases the accuracy of subsequent image segmentation and classification. Thus, the research on the algorithms of PolSAR image speckle reduction has important theoretical significance and practical value.A non-local filter based on the three dimensional patch matching wavelet transform (NL-3DWT) was proposed to solve the problem of preserving the structural characteristics in the despeckling of PolSAR images. First, the algorithm combined an undecimated wavelet transform with the three dimensional patch group that consists of similar patches and then applied the combination to the span (or total power) image. Local linear minimum mean square error estimation was subsequently utilized to shrink the coefficients in the wavelet domain before the inverse three dimensional wavelet transform to obtain the updated span image. Second, the edge-aligned windows selected the structural similar pixels in the updated span image. The Sigma range selected the scattering similar pixels by employing the original PolSAR data. These similar pixels were adopted to construct a pixel set to participate in the final non-local means filtering. Third, the structural similarity index based on the similar pixels set was introduced to calculate the structural preserving weight function, which was utilized in the non-local means filtering with the original PolSAR data.Two sets of PolSAR data detected by the airborne AIRSAR system were adopted to verify the effectiveness of the proposed algorithm in terms of three aspects: speckle reduction, structural features preservation, and polarimetric features preservation. Considering its relevance to this study, the NL-3DWT algorithm was compared with the classical refined PolSAR filtering method of Lee and two types of the latest PolSAR nonlocal filter methods (i.e., NL-Pretest and NL-HPP). The three methods all employed the parameters derived from their respective studies to yield convincing results.The resulting images or evaluation indexes, such as Equivalent Number of Looks (ENL), Blind/Referenceless Image Spatial Quality Evaluator (BRISQUE), and Edge Preservation Index (EPI), show that the NL-3DWT method effectively lowered the speckle and retained edge details in the speckle reduction and structural features preservation processes. In contrast, the Refined Lee still had residual speckle. Furthermore, the NL-Pretest resulted in over-filtering that appeared as false targets, although it suppressed the speckle noise. The NL-3DWT algorithm also more effectively preserved the polarimetric scattering mechanisms than the NL-HPP in terms of the H-Alpha scatter plots in the polarimetric features preservation.The proposed method can increase the accuracy of structurally similar pixel selection, enhance the expression of image structure features, and improve the weight of image structural information in the similarity measurement between patches. Test results demonstrate that the NL-3DWT algorithm effectively lower the speckle and retains the structural characteristics and polarimetric scattering characteristics in PolSAR images. However, the algorithm complexity causes difficulties in the real-time processing of PolSAR images. Hence, studying the fast algorithm must be considered.

Key words

polarimetric SAR, speckle reduction, nonlocal means, wavelet transform, structure preserving

1 引　言

极化SAR由于受自身成像机制约束不可避免地带有相干斑噪声(Lee和Pottier，2009)。它的存在增加了极化SAR图像解译的难度，降低了后续图像分割和分类的准确性(Kersten 等，2005)，因此，研究极化SAR图像相干斑抑制算法具有重要的理论意义和实用价值。

极化SAR图像相干斑抑制的基本准则是在有效去除相干斑噪声的同时尽可能地保持原有结构特性和极化散射特性。早期的Refined Lee滤波(Lee 等，1999)使用边缘方向窗，类似的，还有基于区域增长技术的IDAN滤波(Vasile 等，2006)和自适应方向窗滤波(Lang 等，2015)都是在一定邻域内自适应地选择同质像素参与滤波，减少了滤波过程中结构信息的损失。但这些方法只使用了图像的局部结构特征，也没有充分利用像素的极化散射特性。研究者为了在更大范围内选择结构相似像素，将非局部均值滤波推广到了极化SAR领域(Chen 等，2011；Deledalle 等，2015；Hu 等，2015；Liu和Zhong，2014)，这类方法基于图像块模型将像素结构相似性度量的范围理论上扩大到了整个图像，具有良好的相干斑去噪能力和结构保持能力，但该类方法仍没有充分利用极化散射信息。

基于散射模型的滤波(Lee 等，2004,2006)和Lee等人(2009,2015)提出的精改Sigma滤波都是在极化协方差矩阵上选择散射相似像素进行滤波，有效改善了极化信息的保持，但结构信息的保持不充分。双边滤波(D’Hondt 等，2013；Alonso-González 等，2013)同时在像素的空间邻域和极化邻域选择相似像素，取得了一定的相干斑抑制和特性保持效果。但该类方法使用固定的矩形邻域参与滤波，对于含有丰富结构信息的图像可能会因无法自适应选择邻域大小而降低结构保持性能。

以上方法都没有考虑到在较大范围内同时提取极化SAR图像的结构信息和极化散射信息用于相干斑抑制。杨学志等人(2015)提出的基于同质像素预选择的非局部均值滤波算法(NLHPP)，在搜索窗范围内利用边界对齐窗提取结构信息的同时结合Sigma范围提取散射信息以构建同质像素集合参与滤波，在获得显著相干斑抑制效果的同时，很好地保持了极化SAR图像的结构特性和散射特性。但该算法是直接在原始极化数据生成的极化总功率(Span)图上提取信息，因而不可避免地受到相干斑噪声的影响，使得结构特性和极化散射特性的保持仍然不充分。

为了进一步解决极化SAR图像结构信息保持的难题，提高结构相似像素选择的准确性，本文提出一种采用3维块匹配小波变换的非局部均值滤波算法NL-3DWT (Nonlocal Filter based on 3-D Patch Matching Wavelet Transform)。该算法将3维块匹配小波变换与结构相似像素选择相结合，并构建结构保持权重函数以提高结构信息在非局部均值滤波像素相似性度量时的比重。NL-3DWT算法的优势如下：

(1)由多个相似图像块构成的图像块组能够克服单一图像块模型对极化数据结构特征描述不准确的缺陷，基于图像块组的3维非抽样小波变换能够利用小波框架分解的结构特性分离信号与噪声，克服相干斑噪声对结构特征提取的影响。相比原有的图像块模型，采用3维块匹配的小波变换不仅有效减弱了噪声的干扰，还能更突出地表达结构特征，提高结构相似像素选取的准确性。

(2)在结构相似性指数(SSIM)(易子麟等，2012)的基础上构建非局部均值滤波算法的结构保持权重函数，更加突出结构特征对像素相似性度量的贡献，使结构相似的像素被赋予更大的权值，增大结构信息在滤波过程中的比重，在抑制相干斑噪声的同时，进一步保持像素的结构特性。

2 采用3维块匹配小波变换的极化SAR非局部均值滤波

2.1 极化SAR非局部均值滤波

极化SAR非局部均值滤波将图像块的相似性度量由像素值推广到了极化矩阵，根据矩阵数据的统计特性来衡量块间的相似性，并通过加权平均来估计图像块中心像素矩阵的值，在有效抑制相干斑噪声的同时保持结构信息的完整(Chen 等，2011；Deledalle 等，2015；Hu 等，2015；Liu和Zhong，2014)。其形式为

$\hat { C}(s) = \frac{{\displaystyle \sum {{ w}(s,t){ C}(t)} }}{{\displaystyle \sum {{ w}(s,t)} }}$

(1)

${w}(s,t) = \exp \left( { - \frac{{{\mathop d \nolimits} ({{C}_{{{\rm{p}}_s}}},{{C}_{{{\rm{p}}_t}}})}}{h}} \right)$

(2)

式中， $\hat { C}(s)$ 是待滤波像素s处协方差矩阵的估计值， C (t)是以s为中心一定搜索范围内其余像素的协方差矩阵。 w (s,t)是根据以s，t为中心的图像块p_s ，p_t 的相似性分配的权重， $d({{C}_{{p_s}}},{{C}_{{p_t}}})$ 是两个图像块之间的距离度量函数，用来描述块间的相似性，本文使用最大后验概率的形式来表示(Liu和Zhong，2014)，h是指数函数的参数，用于控制滤波平滑程度。

2.2 3维块匹配小波变换预滤波

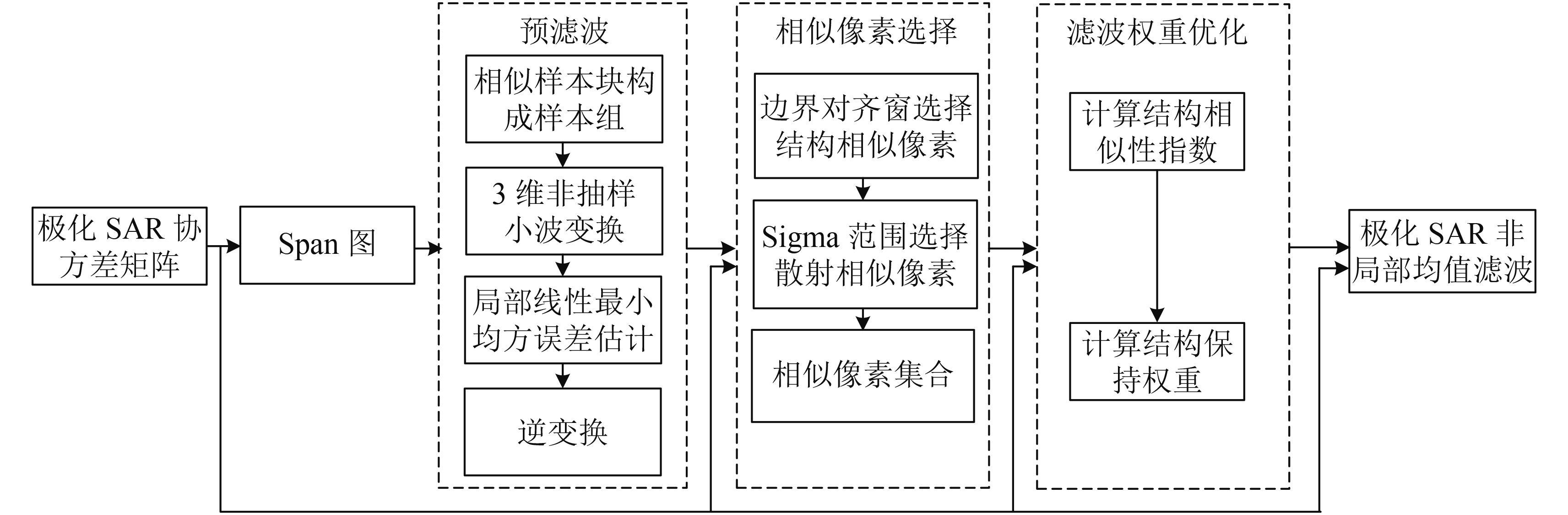
图1为NL-3DWT滤波算法的流程框图，主要由3部分组成。首先对极化SAR协方差矩阵生成的Span图进行预滤波；其次根据预滤波结果并结合极化SAR协方差矩阵选择相似像素参与滤波；最后根据选择出的相似像素再结合原始极化SAR协方差矩阵，优化滤波权重，加权求和完成极化SAR非局部均值滤波处理。本节将从这3方面详细介绍算法的实现过程。

图 1 NL-3DWT滤波算法流程图

Fig. 1 Flow of NL-3DWT algorithm

对Span图进行3维块匹配非抽样小波变换的预滤波，能够降低相干斑噪声对结构相似像素选取的干扰，从而准确表达极化SAR图像的结构特征(Dabov 等，2007；Parrilli 等，2012)。

算法首先在Span图上选择若干相似样本块组成样本组，其次使用3维非抽样小波变换，再经过适合SAR乘性噪声的局部线性最小均方误差(LLMMSE)(Dabov 等，2007)估计后进行逆变换，构成新的Span图，具体步骤如下：

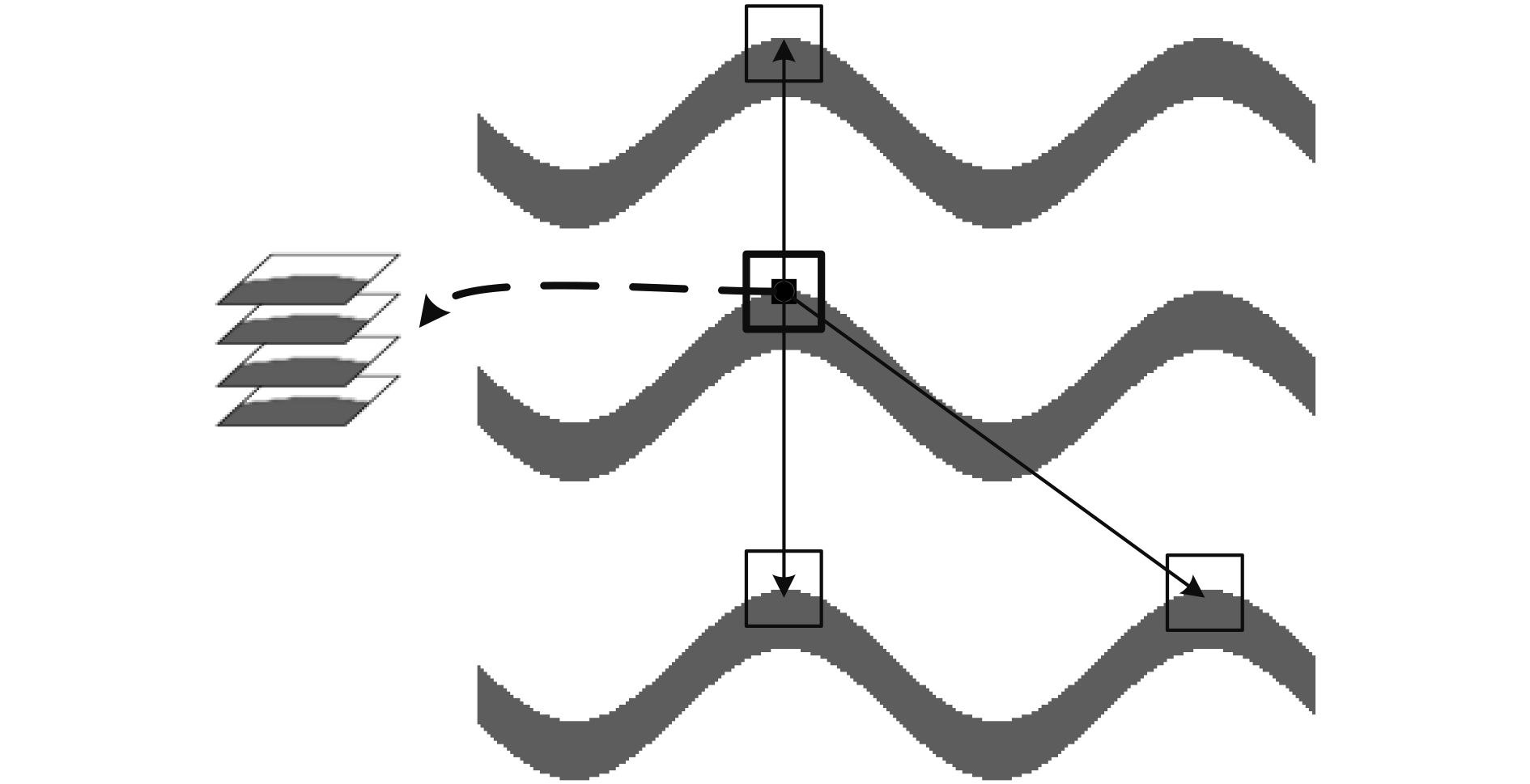
(1) 在Span图上以步长step选取中心点，选取n×n的图像块，在s×s的搜索窗范围内，使用基于概率估计的图像块相似(PPB)距离(Deledalle 等，2009)度量以每个像素点为中心的参考块和中心块的权重，选择权重最大即最相似的m个参考块组成样本组，如图2所示。

图 2 3维块匹配示意图

Fig. 2 Sketch of three dimensional patch matching

(2) 对3维样本组先进行level级2维非抽样小波变换，再进行level级1维非抽样小波变换；

(3) 对(2)得到的高频小波域系数按下式使用LLMMSE：

$\mathop X\limits^ \wedge (i) = \max \left( {0,\frac{{{{\overline {{Z^2}} }_{{\rm{sb}}(i)}} - \displaystyle \frac{{\sigma _{\rm{u}}^2}}{{1 + \sigma _{\rm{u}}^2}}{{\overline {{Z^2}} }_{\rm{g}}}}}{{{{\overline {{Z^2}} }_{{\rm{sb}}(i)}}}}} \right)Z(i)$

(3)

式中，Z(i)表示小波变换后第i个高频子带的观测值， $\mathop X\limits^ \wedge (i)$ 表示小波变换后第i个高频子带无噪信号的估计值， ${\overline {{Z^2}} _{{\rm{sb}}(i)}}$ 表示第i个高频子带观测值平方的均值， ${\overline {{Z^2}} _{\rm{g}}}$ 表示整个样本组观测值平方的均值， $\sigma _{\rm{u}}^2$ 表示噪声方差。

(4) 对上述收缩后的系数进行逆变换，得到经过信噪分离的m个相似图像块的估计值，取平均后选择块的中心像素点构成新的Span图。

2.3 相似像素选择

NL-3DWT滤波算法采用与文献(Yang 等，2015)相同的相似像素选择方法，将结构特性和极化散射特性选择相结合，弥补从单一方面选择相似像素不准确的缺陷。具体步骤如下：

(1) 选取Span图上一定大小的矩形窗划分成9个可以重合的邻域。计算各邻域的均值，构成3×3的矩阵。

(2) 将4种边缘检测算子与3×3矩阵对应元素相乘求和，选取值最大者为边缘方向。由于每个边缘方向有两个反向的边界对齐窗，进一步根据矩阵中心值与边缘方向上相邻位置的接近程度选择对齐窗作为结构相似像素集合。

(3) 在协方差矩阵3个主对角线元素的强度图上选择3×3的邻域，使用最小均方误差估计均值后再与Sigma范围(I₁，I₂)相乘得到3个Sigma强度选择范围(C_meanI₁，C_meanI₂)。不同视数，Sigma范围也不同，文献(Lee 等，2015)给出了计算公式。

(4) 选择同时处于3个Sigma强度范围和结构相似集合的像素参与滤波。

2.4 滤波权重优化

NL-3DWT滤波算法基于SSIM来度量SAR图像块间的结构相似性，建立与结构特征的联系，计算结构保持权重来增大结构信息在权值分配上的比重。首先在相似像素集合上计算SSIM(易子麟等，2012)：

${\rm{SSIM}}(s,t) = \frac{{(2{\mu _s}{\mu _t} + {\eta _1})(2{\sigma _{st}} + {\eta _2})}}{{(\mu _s^2 + \mu _t^2 + {\eta _1})(\sigma _s^2 + \sigma _t^2 + {\eta _2})}}$

(4)

式中，μ_s 和σ_s 分别表示以像素点s为中心的图像块p_s 的灰度均值和标准差，μ_t 和σ_t 分别表示以像素t为中心的图像块p_t 的均值和方差。σ_st 表示块p_s 和p_t 中灰度的协方差，η₁和η₂是为了防止计算溢出而设定的非0极小常数。

SSIM的绝对值越大，则两个图像块越相似。为了与原有极化SAR非局部均值滤波权重函数一致，我们将基于结构相似性指数的函数与原图像块间的距离相乘，改进图像块相似性度量的方法，增大结构信息在滤波过程中的比重，定义如下结构保持权重函数：

${w_{\rm{p}}}(s,t) = \exp \left( { - \frac{{d({C_{{{\rm{p}}_s}}},{C_{{{\rm{p}}_t}}})}}{h} \times \frac{{1 - {\rm{SSIM}}(s,t)}}{2}} \right)$

(5)

上式与原有极化SAR非局部均值滤波权值函数w(s,t)单调性一致，图像块越相似，权值越大。经过上述改进后，将式(5)代替式(2)，应用到极化SAR非局部均值滤波中。

2.5 NL-3DWT实现过程

结构特性和极化散射特性选择的准确性直接关系到极化SAR图像滤波的效果。为降低相干斑噪声对相似像素选择的干扰，本文提出的NL-3DWT算法将3维非抽样小波变换和结构相似像素选择相结合，提高对结构相似像素选择的准确性，并融入结构保持权重函数，进一步增强算法对结构信息的保持能力。

通过图1及上文的分析，NL-3DWT算法的实现步骤描述如下：

(1) 在Span图上构造3维图像块样本组，使用3维非抽样小波变换并利用式(3)进行系数收缩，再逆变换重构更新Span图。

(2) 在更新的Span图上利用边界对齐窗提取结构信息，对原始极化SAR协方差数据利用Sigma范围选取散射相似像素构成相似像素集合参与滤波。

(3) 根据相似像素集合在更新的Span图上计算结构相似性指数并结合原始极化SAR协方差数据以确定滤波结构保持权重w_p(s,t)，之后代入式(1)进行非局部均值滤波。

3 实验结果与分析

本文对两组机载极化SAR数据进行实验。一组是AIRSAR系统获取的San Francisco海湾数据，截取512×512个像素，视数为4。另一组也是该系统获取的Flevoland地区的数据，参数相同。将从相干斑抑制、结构特性保持和极化散射特性保持3个方面与Refined Lee滤波(Lee 等，1999)，NLPretest滤波(Chen 等，2011)和NLHPP滤波(杨学志等，2015)等算法进行对比分析。为了使结果真实可信，均使用其推荐的滤波参数，Refined Lee滤波使用7×7的搜索窗，NLPretest滤波、NLHPP滤波搜索窗大小为15×15，相似窗大小为3×3，NLHPP的迭代次数设置为3。根据Matlab小波工具箱的设置，本文算法设置图像块大小为4×4；为了减少计算量，分析比较多次实验结果，设置搜索窗尺寸为21×21，步长为4，选取最相似的8个块构成样本组；根据小波基和SAR图像的特性并结合文献(Dabov 等，2007；Parrilli 等，2012)的实验结果，选择小波基函数为Daubechies-8，设置非抽样小波变换的层数level为3。

3.1 相干斑抑制

图3列出了滤波前后极化SAR数据pauli分解生成的伪彩色合成图。视觉上可以看出，4种滤波方法都能对相干斑进行有效抑制。图3(b)和图4(b)的Refined Lee滤波虽然抑制了部分噪声，但在San Francisco的海洋区域和Flevoland的平坦区域均出现了块效应，模糊了边缘细节。NLPretest滤波结构细节保持上相比Refined Lee滤波有明显改善，但在San Francisco的城市区域(图3(c))出现了“亮斑”，在Flevoland的匀质区域(图4(c))出现了“伪影”(红色箭头标出)，说明在这些区域存在过度的平滑。NLHPP滤波和NL-3DWT滤波相比前两种滤波算法，不仅有效抑制了相干斑噪声，细节信息保持的也更好，没有出现过平滑的现象。

图 3 San Francisco滤波前后的伪彩色合成图

Fig. 3 Comparison of speckle filtering algorithms based on false color image of San Francisco

图 4 Flevoland滤波前后的伪彩色合成图

Fig. 4 Comparison of speckle filtering algorithms based on false color image of Flevoland

为客观衡量4种滤波算法相干斑抑制的性能，本文使用两种评价指标：等效视数(ENL) (Dellepiane和Angiati，2014)和无参考图像质量评价(BRISQUE) (Mittal 等，2012)。ENL值越大表示滤波后的图像越平滑，去除的噪声越多，BRISQUE越小，说明滤波后图像的保真度越高，细节信息丢失的少。因此，通过这两个指标可以综合评价滤波算法的相干斑抑制能力。

表1列出了两组测试数据在不同滤波算法下Span图上的ENL和BRISQUE值。从表1中可以看出，NL-3DWT滤波算法的ENL值较大，BRISQUE值最低，说明拥有良好的噪声抑制能力，图像整体结构保持的也最好，这与主观评价一致。原因是该算法将多个相似图像块构成图像块组克服了单一图像块模型对极化数据结构特征描述不准确的缺陷，在此基础上使用3维非抽样小波变换能够利用小波框架分解的结构特性分离信号与噪声，克服相干斑噪声对结构特征提取的影响。相比原有的图像块模型，不仅有效减弱了噪声的干扰，更突出表达了像素结构特征，提高了结构相似像素选取的准确性。

表 1 不同滤波算法在两幅Span图上的ENL值和BRISQUE值
Table 1 Comparison of ENL and BRISQUE values on two Span images

下载CSV

		Original data	Refined Lee	NLPretest	NLHPP	NL-3DWT
San Francisco	ENL	15.88	50.32	88.43	82.24	90.40
San Francisco	BRISQUE	26.16	15.19	14.44	13.88	12.96
Flevoland	ENL	21.24	126.39	198.80	190.29	197.75
Flevoland	BRISQUE	38.94	16.94	11.23	8.14	5.44

3.2 结构特性保持

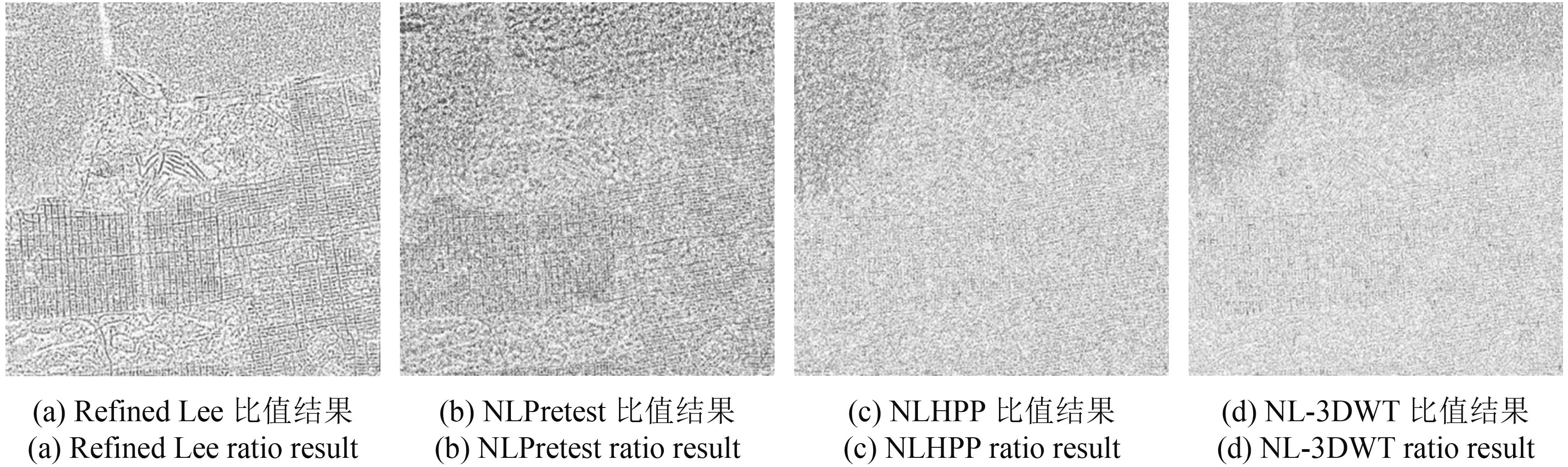
通过去噪后生成的Span图与未滤波时的Span图进行相除得到的比值图能够粗略反映原始图像结构信息的损失情况(Hebar 等，2009)，比值图中所含的结构信息越少，说明滤波算法的结构保持能力越强。

视觉上可以看出NL-3DWT滤波(图5(d)、图6(d))和NLHPP滤波(图5(c)、图6(c))得到的比值图更为模糊。相比NLHPP滤波，NL-3DWT滤波的比值图中包含更少的细节，说明其在滤波过程中保持了更多的结构信息。

图 5 San Francisco不同滤波算法得到的比值图

Fig. 5 Comparison of different speckle filtering results based on ratio image of San Francisco

图 6 Flevoland不同滤波算法得到的比值图

Fig. 6 Comparison of different speckle filtering results based on ratio image of Flevoland

边缘保持是结构保持必不可少的一部分，本文使用边缘保持指数(EPI)(Ding 等，2013)来客观评价滤波后极化SAR图像的边缘保持能力。EPI的值越小，说明算法的边缘保持能力越弱。

表2中的区域1、2是San Francisco图中的森林和城市区域，区域3、4是Flevoland地区图中的道路交叉口，都属于结构信息十分丰富的区域。在这些区域上计算EPI的值，能充分验证算法的边缘保持能力。可以看出，在区域1、2和4，NL-3DWT滤波取得的EPI值都是最大的，只在区域3略低于NLHPP，说明NL-3DWT对边缘结构的保持能力优于其他3类算法。原因是其利用3维块匹配小波变换对相似样本块重构以准确利用边缘结构特征并且在降噪过程中利用结构相似性指数得到更优化的块的结构相似性度量权重，因而能更好地保持结构信息。

表 2 不同滤波方法在Span图上的标记区域的EPI值
Table 2 Comparison of EPI values from the marked regions on Span image

下载CSV

	Refined Lee	NLPretest	NLHPP	NL-3DWT
区域1	0.63	0.72	0.77	0.81
区域2	0.65	0.71	0.76	0.79
区域3	0.45	0.62	0.72	0.68
区域4	0.39	0.66	0.56	0.67

3.3 极化散射特性保持

极化SAR数据的极化散射特性对于极化SAR图像的分割和分类有重要的参考价值，极化SAR滤波的基本原则就是在抑制相干斑噪声的同时尽可能多的保持原始数据的结构特性和极化散射特性。由于San Francisco图像中海洋面积较大，表面散射居多，树木植被等森林区域多为体散射，城市街区由于人造结构和地面间相互作用造成二次散射居多，也存在不少镜面散射，因此本节以该典型数据来验证不同滤波算法对极化特性的保持能力。

图7是San Francisco地区红色标记区域的H-Alpha散点分布图(Lee 等，2004)，分别代表了海洋、城市、森林3种不同的散射机制。极化熵H和平均Alpha角是表征地物目标极化散射特性的两个重要参数。原始数据中的3类散射点(图7(a))由于受到相干斑噪声的影响在H-Alpha平面上呈随机分布，如图7(b)所示。图7(c)—图7(f)是4种算法滤波后的H-Alpha散点分布图。NL-3DWT滤波相比其他3种算法在海洋和城市区域散射点更加聚集，森林区域有相对更高的极化熵值，符合散射机制的一般规律。这说明NL-3DWT算法通过3维块匹配小波变换提高了Sigma范围选择相似散射机制像素的准确性，更加有效地保持了极化散射特性。

图 7 海洋、森林和城市区域的H-Alpha散点分布图

Fig. 7 Scatter plots for H-Alpha in ocean, city and forest regions

4 结　论

极化SAR图像像素的相似性不仅包括边缘、纹理等结构属性相似，还包括极化散射特征相似，所以极化SAR图像相干斑抑制的难点在于准确地选取相似像素参与滤波。之前的学者主要集中研究了在单一方面提取相似像素，在综合考虑结构特性和散射特性方面仍存在不足。

本文针对这一问题提出了一种改进的极化SAR图像非局部均值滤波算法。本算法将3维块匹配小波变换与Span图相结合，在对Span图进行预滤波的基础上采用边界对齐窗提取极化SAR图像的结构属性，利用Sigma范围提取其散射特性，将二者共同选择出的像素作为相似像素，参与非局部均值滤波并构建结构保持权重函数以进一步保持像素的结构特性。

NL-3DWT的优势主要表现在以下两个方面：(1)3维块匹配的小波变换在原有2维图像块模型的基础上，利用图像块匹配技术构建3维图像块组，强化了对结构属性的表达，同时在小波域里实现了信号与噪声的分离，不仅有效减弱了相干斑噪声的干扰，还能增强像素的结构特征，提高在Span图上选取结构相似像素的准确性；(2)构建结构保持权重函数，增大结构信息在非局部均值滤波权值分配上的比重，更加突出结构特性对像素相似性度量的贡献，同时结合散射相似像素选择，实现相似像素更加准确地选取。

相比Refined Lee(Lee 等，1999)、NLPretest (Chen 等，2011)分别从单一结构特征和统计特性上选择相似像素，NLHPP(杨学志等，2015)综合考虑了结构特性和散射特性，但Span图上的相干斑噪声严重干扰了结构相似像素选取的准确性，阻碍了该算法结构保持能力的提高；在此基础上本文提出的NL-3DWT算法不仅能有效抑制相干斑噪声，还能进一步保持极化SAR图像的结构信息和极化散射信息。然而，算法的复杂度对图像实时处理带来了困难，因此如何对算法进行快速计算是下一步需要研究的问题。

参考文献(References)

Alonso-GonzálezA P. 2013. Bilateral distance based filtering for polarimetric SAR data. Remote Sensing, 5 (11): 5620–5641. [DOI: 10.3390/rs5115620]

Chen J, Chen Y L, An W T, Cui Y and Yang J. 2011. Nonlocal filtering for polarimetric SAR data: a pretest approach. IEEE Transactions on Geoscience and Remote Sensing, 49 (5): 1744–1754. [DOI: 10.1109/TGRS.2010.2087763]

D’HondtO . 2013. Iterative bilateral filtering of polarimetric SAR data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 6 (3): 1628–1639. [DOI: 10.1109/JSTARS.2013.2256881]

Dabov K, Foi A, Katkovnik V and Egiazarian K. 2007. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing, 16 (8): 2080–2095. [DOI: 10.1109/TIP.2007.901238]

Deledalle C A, Denis L and Tupin F. 2009. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights. IEEE Transactions on Image Processing, 18 (12): 2661–2672. [DOI: 10.1109/TIP.2009.2029593]

DeledalleC A. 2015. NL-SAR: a unified nonlocal framework for resolution-preserving (Pol)(In)SAR denoising. IEEE Transactions on Geoscience and Remote Sensing, 53 (4): 2021–2038. [DOI: 10.1109/TGRS.2014.2352555]

Dellepiane S G and Angiati E. 2014. Quality assessment of despeckled SAR images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (2): 691–707. [DOI: 10.1109/JSTARS.2013.2279501]

Ding Z G, Zeng T, Dong F, Liu L S, Yang W F and Long T. 2013. An improved PolSAR image speckle reduction algorithm based on structural judgment and hybrid four-component polarimetric decomposition. IEEE Transactions on Geoscience and Remote Sensing, 51 (8): 4438–4449. [DOI: 10.1109/TGRS.2013.2270036]

HebarM . 2009. Autobinomial model for SAR image despeckling and information extraction. IEEE Transactions on Geoscience and Remote Sensing, 47 (8): 2818–2835. [DOI: 10.1109/TGRS.2009.2013697]

Hu J, Guo R, Zhu, X, Baier G and Wang Y. 2015. Non-local means filter for polarimetric SAR speckle reduction-experiments using Terrasar-X data // Joint ISPRS Conference on Photogrammetric Image Analysis and High Resolution Earth Imaging for Geospatial Information. Munich, 71–77 [DOI: 10.5194/isprsannals-II-3-W4-71-2015]

KerstenP R, LeeJ S and AinsworthT L. 2005. Unsupervised classification of polarimetric synthetic aperture radar images using fuzzy clustering and EM clustering. IEEE Transactions on Geoscience and Remote Sensing, 43 (3): 519–527. [DOI: 10.1109/TGRS.2004.842108]

Lang F K, Yang J and Li D R. 2015. Adaptive-window polarimetric SAR image speckle filtering based on a homogeneity measurement. IEEE Transactions on Geoscience and Remote Sensing, 53 (10): 5435–5446. [DOI: 10.1109/TGRS.2015.2422737]

Lee J S, Grunes M R and de Grandi G. 1999. Polarimetric SAR speckle filtering and its implication for classification. IEEE Transactions on Geoscience and Remote Sensing, 37 (5): 2363–2373. [DOI: 10.1109/36.789635]

Lee J S, Grunes M R, Pottier E and Ferro-Famil L. 2004. Unsupervised terrain classification preserving polarimetric scattering characteristics. IEEE Transactions on Geoscience and Remote Sensing, 42 (4): 722–731. [DOI: 10.1109/TGRS.2003.819883]

Lee J S, Grunes M R, Schuler D L, Pottier E and Ferro-Famil L. 2006. Scattering-model-based speckle filtering of polarimetric SAR data. IEEE Transactions on Geoscience and Remote Sensing, 44 (1): 176–187. [DOI: 10.1109/TGRS.2005.859338]

Lee J S and Pottier E. 2009. Polarimetric Radar Imaging: from Basics to Applications. Boca Raton: CRC Press: 157–160

LeeJ S, WenJ H, AinsworthT L, ChenK S and ChenA J. 2009. Improved sigma filter for speckle filtering of SAR imagery. IEEE Transactions on Geoscience and Remote Sensing, 47 (1): 202–213. [DOI: 10.1109/TGRS.2008.2002881]

LeeJ S, AinsworthT L, WangY T and ChenK S. 2015. Polarimetric SAR speckle filtering and the extended sigma filter. IEEE Transactions on Geoscience and Remote Sensing, 53 (3): 1150–1160. [DOI: 10.1109/TGRS.2014.2335114]

Liu G C and Zhong H. 2014. Nonlocal means filter for polarimetric SAR data despeckling based on discriminative similarity measure. IEEE Geoscience and Remote Sensing Letters, 11 (2): 514–518. [DOI: 10.1109/LGRS.2013.2271321]

Mittal A, Moorthy A K and Bovik A C. 2012. No-reference image quality assessment in the spatial domain. IEEE Transactions on Image Processing, 21 (12): 4695–4708. [DOI: 10.1109/TIP.2012.2214050]

Parrilli S, Poderico M, Angelino C V and Verdoliva L. 2012. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage. IEEE Transactions on Geoscience and Remote Sensing, 50 (2): 606–616. [DOI: 10.1109/TGRS.2011.2161586]

VasileG S. 2006. Intensity-driven adaptive-neighborhood technique for polarimetric and interferometric SAR parameters estimation. IEEE Transactions on Geoscience and Remote Sensing, 44 (6): 1609–1621. [DOI: 10.1109/TGRS.2005.864142]

Yang X Z, Chen J, Zhou F, Lang W H, Zheng X and Li G Q. 2015. Polarimetric SAR image despeckling using non local means filter based on homogeneous pixels preselection. Journal of Electronics and Information Technology, 37 (12): 2991–2999. [DOI: 10.11999/JEIT150314] ( 杨学志, 陈靖, 周芳, 郎文辉, 郑鑫, 李国强. 2015. 基于同质像素预选择的极化SAR图像非局部均值滤波. 电子与信息学报, 37 (12): 2991–2999. [DOI: 10.11999/JEIT150314] )

Yi Z L, Yin D, Hu A Z and Zhang R. 2012. SAR image despeckling based on non-local means filter. Journal of Electronics and Information Technology, 34 (4): 950–955. ( 易子麟, 尹东, 胡安洲, 张荣. 2012. 基于非局部均值滤波的SAR图像去噪. 电子与信息学报, 34 (4): 950–955. )

摘要

关键词