|
收稿日期: 2016-04-07; 修改日期: 2016-09-13; 优先数字出版日期: 2017-01-25
基金项目: 国家自然科学基金(编号:41371362,41371359)
第一作者简介: 张立福(1967-), 男, 研究员, 研究方向为高光谱遥感。E-mail:zhanglf@radi.ac.cn
中图分类号: TP701
文献标识码: A
文章编号: 1007-4619(2017)01-0062-12
|
摘要
卫星遥感技术为我们研究全球变化提供了时间、空间、光谱多维度的海量遥感大数据,目前还没有一种针对遥感数据的多维度的特性设计的一体化存储结构。本文提出了一种多维遥感数据的组织方式,设计了SPAtial-Temporal-Spectral(SPATS)时空谱多维遥感数据一体化存储结构,定义了5种多维数据存储格式:Temporal Sequential in Band(TSB)、Temporal Sequential in Pixel(TSP)、Temporal Interleaved by Band(TIB)、Temporal Interleaved by Pixel(TIP)和Temporal Interleaved by Spectrum(TIS),设计了Multi-dimensional Data Analysis(MDA)多维数据分析模块,实现了长时间序列遥感影像的时空谱多维一体化存储,并能够进行不同维度的数据分析与显示,构建了基于不同光谱指数的时间谱影像立方体,为时空谱多维遥感数据的综合与表征提供数据组织解决方案。
关键词
遥感技术 , 一体化存储 , 多维数据结构 , SPATS , MDA
Abstract
The techniques of satellite remote sensing has been providing massive remote sensing data, however there's no integrated storage structure specially designed for the characters of remote sensing's multi-dimensions. In this context, a method of organizing multi-dimensional remote sensing data is proposed, and an integrated storage structure of SPAtial-Temporal-Spectral (SPATS) multi-dimensional remote sensing images is designed with five multi-dimensional storage format defined:Temporal Sequential in Band (TSB)、Temporal Sequential in Pixel (TSP)、Temporal Interleaved by Band (TIB)、Temporal Interleaved by Pixel (TIP) and Temporal Interleaved by Spectrum (TIS). In addition, Based on this structure, a multi-dimensional data analysis module, namely MDA, is designed, which could implement the SPATS integrated storage of long time-series remote sensing imagery, perform data analysis and display, and build temporal image cubes of a variety of spectral indices, providing a solution of organizing data for the synthesis and characterization of SPATS multi-dimensional remote sending images.
Key words
remote sensing , integrated storage , multi-dimensional data structure , SPATS , MDA
1 引言
遥感卫星长时间连续对地观测,积累了大量有价值的长时间序列遥感数据,如Landsat系列卫星获取了长达40多年高质量的地球陆表数据(Irons等,2012;Wulder等,2012),MODIS传感器积累了大约15年的每天全球观测数据(Mouillot等,2014),这些长时间序列数据集被广泛用于全球变化研究。例如,Landsat长时间序列数据被广泛应用于森林扰动和恢复的趋势变化监测(Kennedy等,2010)、森林扰动历史数据自动化重建(Huang等,2010)、地表森林生物量变化定量分析(Powell等,2010),以及土地覆盖变化监测(Margono等,2012;Townsend等,2009)等研究;MODIS长时间序列数据大量被应用于农作物物候监测(Galford等,2008;Sakamoto等,2005)、洪水空间范围变化(Sakamoto等,2007),以及火灾区域制图(Roy等,2005)等研究。
随着遥感技术的发展以及应用研究的不断深入,时间维的遥感信息越来越多地受到重视,数据组织与利用正在由空间-光谱一体化向着时间-空间-光谱一体化发展。然而,现在已有的遥感数据格式采用离散文件的方式组织长时间序列遥感影像,给时空谱一体化分析应用带来极大不便,迫切需要设计一种新的数据结构来组织这种多维数据,实现时空谱一体化数据的高效处理与分析。目前用于时间序列分析的遥感数据集通常是以一种常用格式的文件为基本存储单元,如Tagged Image File Format (Geo-TIFF)、Hierarchical Data Format (HDF)(Group 2014),以及遥感商用软件自带格式(如ENVI和ERDAS)。其中ENVI和ERDAS软件自带数据格式只能存储3维立方体数据,每个文件对应一个时间的数据;HDF和Geo-TIFF数据格式有所不同,内部采用更加复杂的数据结构(树状结构或链表结构),可以将几个时间的3维立方体影像组织在一个文件中,当组织长时间序列遥感影像数据时,首先将长时间序列按时间分成若干组,每一个组包含一个或多个时间,每个组对应一个HDF文件存储,每个文件中采用树状结构或链表结构组织在一起。采用这种方式组织方式,提取时谱数据时需要读取多个文件,且针对每个文件遍历其中树状结构或者链表结构中的各个节点数据。根据这些数据格式的特点可知,在处理过程中存在大量重复的步骤,过程烦琐,且难以通过交互式操作完成对应研究工作。究其原因,目前遥感影像的存储是基于3维立方体模型,数据处理的对象在逻辑上实际是一些离散的3维立方体数据,而目前还没有研究提出一种4维立方体模型来组织长时间序列遥感数据,不能将这些具有空间、时间和光谱4个维度的数据集构建成一个4维立方体,在4维立方体数据的基础上完成时间序列分析。
本文提出了一种将遥感数据时间-空间-光谱4个维度一体化组织管理的SPAtial-Temporal-Spectral (SPATS)数据结构,SPATS采用4维立方体存储结构,其中根据数据存储方式的不同,定义了5种多维数据格式,分别面向不同场景的应用类型。为了能够处理SPATS数据结构的Multi-Dimensional Dataset (MDD)数据集,设计了一个遥感数据多维分析软件模块Multi-dimensional Data Analysis (MDA),作为遥感多维分析软件Multi-dimensional Analysis for Remote Sensing (MARS)主要的功能模块。MDA模块能够将长时间序列遥感影像构建成一个时空谱一体化的多维数据集,并能够进行不同维度的数据分析与显示,构建时间谱并提取时谱特征,满足遥感时空谱多特征关联分析的需求。
2 SPATS数据结构设计
2.1 五种多维存储结构定义
传统的成像光谱数据立方体的存储方式有3种:BSQ,BIP,BIL。根据SPATS数据集的存储方式的不同,定义了5种常用的多维数据的存储结构。
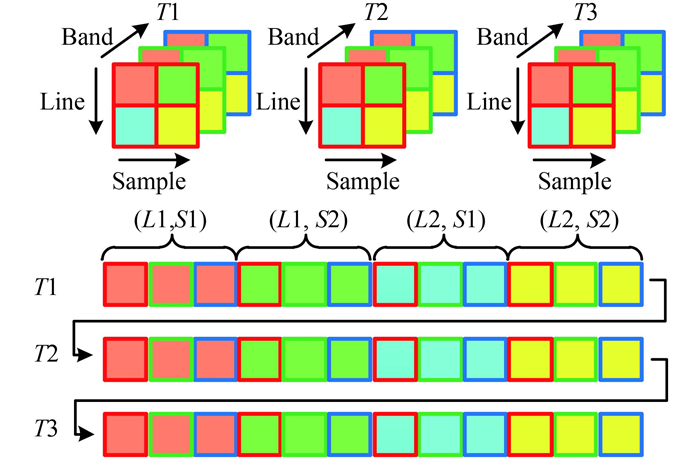
(1) Temporal Sequential in Band (TSB)。如图 1所示,假设多时相遥感数据集包含
TSB存储格式首先将
| $ {P_{{\rm{TSB}}}} = {F_{{\rm{TSB}}}}\left( 1 \right) + {F_{{\rm{TSB}}}}\left( 2 \right) + \cdots + {F_{{\rm{TSB}}}}\left( T \right) $ | (1) |
式中,
| $ {F_{{\rm{TSB}}}}\left( t \right) = {B_{{\rm{TSB}}}}\left( {t,1} \right) + {B_{{\rm{TSB}}}}\left( {t,2} \right) + \cdots + {B_{{\rm{TSB}}}}\left( {t,S} \right) $ | (2) |
式中,
| $ \begin{array}{l} \!\!{B_{{\rm{TSB}}}}\left( {t,s} \right) = A\left( {t,s,1 \! : \! C,1} \right) + A\left( {t,s,1 \! : \! C,2} \right) + \cdots + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; A\left( {t,s,1 \! : \! C,R} \right) \end{array} $ | (3) |
式中,
(2) Temporal Sequential in Pixel (TSP)。如图 2所示,TSP存储格式首先是将第一个时间的立方体数据按照波段方向采取光谱维优先的原则存储第一个像元的光谱信息,然后各个像元点的光谱再按照“先行后列”的顺序进行存储,最后依据上述规则将多个时间的立方体数据按时间顺序存储,这种存储结构可以表示为
| $ {P_{{\rm{TSP}}}} = {F_{{\rm{TSP}}}}\left( 1 \right) + {F_{{\rm{TSP}}}}\left( 2 \right) + \cdots + {F_{{\rm{TSP}}}}\left( T \right) $ | (4) |
式中,
| $ \begin{array}{l} {F_{{\rm{TSP}}}}\left( t \right) = A\left( {t,1:S,1,1} \right) + A\left( {t,1:S,2,1} \right) + \cdots + \\ A\left( {t,1:S,C,1} \right) + A\left( {t,1:S,1,2} \right) + A\left( {t,1:S,2,2} \right) + \\ \;\;\;\;\;\;\;\;\; \ldots + A\left( {t,1:S,C,2} \right) + \cdots A\left( {t,1:S,1,R} \right) + \\ \;\;\;A\left( {t,1:S,2,R} \right) + \cdots + A\left( {t,1:S,C,R} \right) \end{array} $ | (5) |
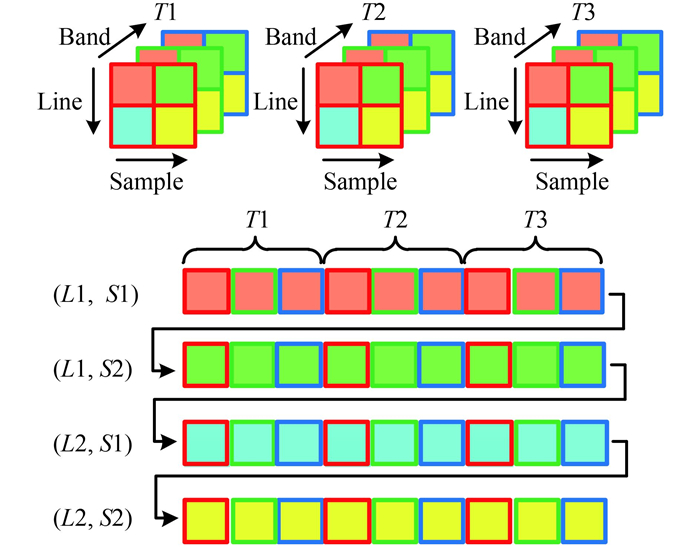
(3) Temporal Interleaved by Band (TIB)。如图 3所示,TIB存储格式首先将第一个波段的第一个时间的像元按照“先行后列”的顺序存储,然后将第一个波段在不同时间上的所有数据按时间顺序组织在一起,最后依据上述规则将所有时间的每个波段依次按照波段的顺序存储,这种存储结构可以表示为
| $ {P_{{\rm{TIB}}}} = {F_{{\rm{TIB}}}}\left( 1 \right) + {F_{{\rm{TIB}}}}\left( 2 \right) + \ldots + {F_{{\rm{TIB}}}}\left( S \right) $ | (6) |
式中,
| $ {F_{{\rm{TIB}}}}\left( s \right) = {B_{{\rm{TIB}}}}\left( {1,s} \right) + {B_{{\rm{TIB}}}}\left( {2,s} \right) + \ldots + {B_{{\rm{TIB}}}}\left( {T,s} \right) $ | (7) |
式中,
| $ \begin{array}{l} \!\!{B_{{\rm{TIB}}}}\left( {t,s} \right) = A\left( {t,s,1:C,1} \right) + A\left( {t,s,1:C,2} \right) + \ldots + \\ \;\;\;\;\;\;\;\;\;\;\;\;\; A\left( {t,s,1:C,R} \right) \end{array} $ | (8) |
(4) Temporal Interleaved by Pixel (TIP)。如图 4所示,TIP首先将第一个波段的第一个像元点在不同时间的数据按时间顺序优先组织在一起,然后所有时间的第一个波段内的像元数据再按“先行后列”的原则顺序存储,最后依据上述规则将所有波段数据按照波段顺序进行存储, 这种存储结构可以表示为
| $ {P_{{\rm{TIP}}}} = {F_{{\rm{TIP}}}}\left( 1 \right) + {F_{{\rm{TIP}}}}\left( 2 \right) + \ldots + {F_{{\rm{TIP}}}}\left( S \right) $ | (9) |
式中,
| $ \begin{array}{l} {F_{{\rm{TIP}}}}\left( s \right) = A\left( {1:T,s,1,1} \right) + A\left( {1:T,s,2,1} \right) + \\ \ldots + A\left( {1:T,s,C,1} \right) + A\left( {1:T,s,1,2} \right) + \\ A\left( {1:T,s,2,2} \right) + \ldots + A\left( {1:T,s,C,2} \right) + \ldots \\ A\left( {1:T,s,1,R} \right) + A\left( {1:T,s,2,R} \right) + \ldots + \\ A\left( {1:T,s,C,R} \right) \end{array} $ | (10) |
(5) Temporal Interleaved by Spectrum (TIS)。如图 5所示,TIS存储格式首先将第一个像元点所有时间的光谱维数据优先存储,然后依据这一规则将其他像元点按照空间上“先行后列”的原则依次进行存储, 这种存储结构可以表示为
| $ \begin{array}{l} {P_{{\rm{TSP}}}} = {B_{{\rm{TIS}}}}\left( {1,1} \right) + {B_{{\rm{TIS}}}}\left( {2,1} \right) + \ldots + \\ {B_{{\rm{TIS}}}}\left( {C,1} \right) + {B_{{\rm{TIS}}}}\left( {1,2} \right) + {B_{{\rm{TIS}}}}\left( {2,2} \right) + \ldots + \\ {B_{{\rm{TIS}}}}\left( {C,2} \right) + \ldots + {B_{{\rm{TIS}}}}\left( {1,R} \right) + {B_{{\rm{TIS}}}}\left( {2,R} \right) + \ldots + \\ {B_{{\rm{TIS}}}}\left( {C,R} \right) \end{array} $ | (11) |
式中,
| $ \begin{array}{l} {B_{{\rm{TIS}}}}\left( {c,r} \right) = A\left( {1,1:S,c,r} \right) + A\left( {2,1:S,c,r} \right) + \ldots + \\ A\left( {T,1:S,c,r} \right) \end{array} $ | (12) |
2.2 5种结构之间转换
本文提出的5种多维数据存储结构在不同应用中各具优势,5种数据结构之间需要相互转换。这5种结构两两之间的转换方式有10种,其中有些转换方式的转换过程比较复杂,效率很低,这种情况下完全可以先转化成为其他格式作为过度的一种格式,然后再将这种过度格式转化成为最终需要的结构。要实现这种间接的格式转换,首先需要根据这5种数据存储结构的特点,找到一组基本的转换关系,在后面实际的转换过程中利用这一组转换关系进行组合从而实现任意两种格式之间的转换。基本的转换关系包括下面4种方式:
(1) TSB与TSP之间的转换
/* TSP- > TSB */
FOR
FOR
FOR
FOR
END
END
END
END
/* TSB- > TSP */
FOR
FOR
FOR
FOR
END
END
END
(2) TSP与TIS之间的转换
/* TSP- > TIS */
FOR
FOR
FOR
END
END
END
/* TIS- > TSP */
FOR
FOR
FOR
END
END
(3) TSB与TIB之间的转换
/* TSB- > TIB */
FOR
FOR
END
END
/* TIB- > TSB */
FOR
FOR
END
END
(4) TIB与TIP之间的转换
/* TIB- > TIP */
FOR
FOR
FOR
FOR
END
END
END
END
END
/* TIP->TIB */
FOR
FOR
FOR
FOR
END
END
END
END
这4种基本的转换关系是充分考虑了5种数据存储结构内在的特点,使计算机在存储空间中寻找目标数据片段的次数尽可能少,从而减少数据转换过程中花费的时间。在这4种基本转换方式的基础上,可以实现另外6种转换,它们分别是:
(1) TIP与TSB之间的转换。通过TIP↔TIB↔TSB这种顺序依次转换实现。
(2) TIP与TSP之间的转换。通过TIP↔TIB↔TSB↔TSP这种顺序依次转换实现。
(3) TIP与TIS之间的转换。通过TIP↔TIB↔TSB↔TSP↔TIS这种顺序依次转换实现。
(4) TIB与TSP之间的转换。通过TIB↔TSB↔TSP这种顺序依次转换实现。
(5) TIB与TIS之间的转换。通过TIB↔TSB↔TSP↔TIS这种顺序依次转换实现。
(6) TSB与TIS之间的转换。通过TSB↔TSP↔TIS这种顺序依次转换实现。
2.3 数据格式分析
定义的5个格式内部存储结构各不相同,每个格式都对应于一种或者多种最高效的数据操作类型,它们分别对应不同的应用场景。在特定应用场景下,选择合适数据存储格式对提高数据处理的效率具有重要意义。
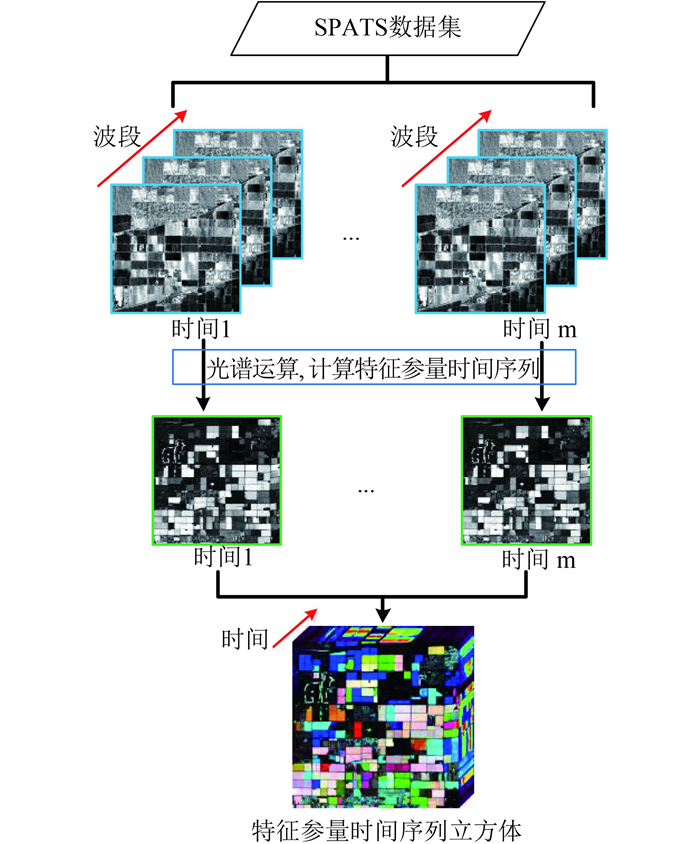
(1) TSB格式。从前面格式的存储结构示意图中可以看出,TSB格式将每一个时间的所有波段数据组织在一起,因此这种格式最适合于对一个时间的若干个波段数据进行操作,以及对波段在空间维的处理。TSB格式比较典型应用场景包括:提取一个或多个时间所有波段组成的光谱立方体数据,光谱运算和空间域滤波等。
图 6展示了TSB格式用于提取特征参量的时间序列立方体数据的应用场景。该格式支持以最快的方式提取多个时间整个波段数据,因此基于该格式读取波段数据,通过光谱运算计算特征参量,能够最高效地提取不同时间特征参量组成的时间序列立方体数据。
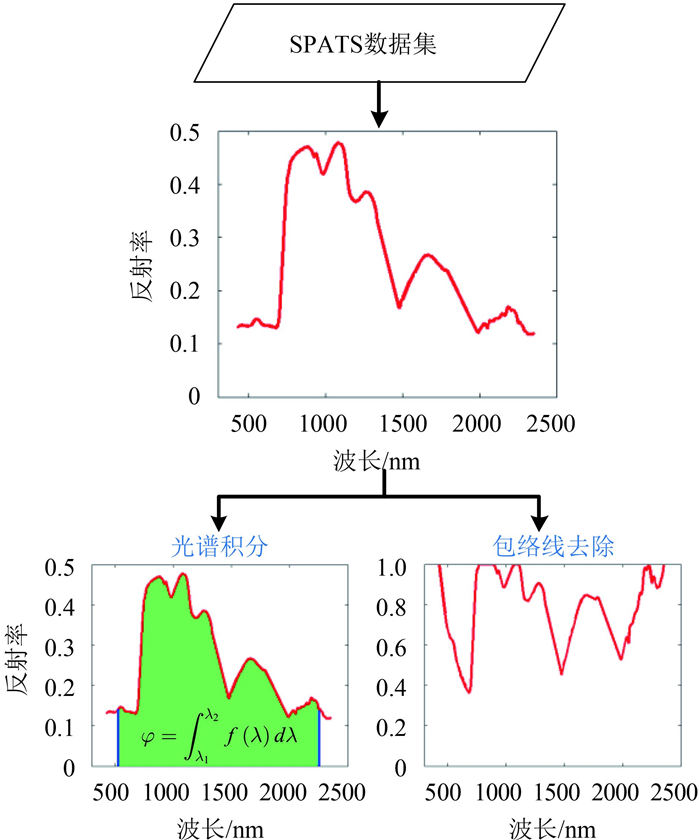
(2) TSP格式。TSP格式的特点是将每个时间影像的光谱数据组织在一起,因此这种格式最适合于对一个时间的光谱数据进行操作。TSP格式比较典型应用场景包括:提取一个像元或者一片区域的光谱曲线,以及对不同时间的影像进行光谱特征化,例如计算光谱斜率和坡向、光谱二值编码、光谱吸收指数、光谱倒数和积分等。
图 7展示了TSP格式用于提取和显示光谱曲线,光谱维积分和包络线去除这两种光谱特征化的场景。该格式支持以最快的方式提取光谱数据,因此基于该格式能够最高效地完成对光谱维的分析操作。
(3) TIB格式。TIB格式的特点是将一个波段所有时间数据组织在一起,因此这种格式最适合于提取某个波段的时间序列立方体数据。TIB格式与TSB不同,前者是将相同波段、不同时间组织在一起,而后者是将相同时间、不同波段数据聚集在一起。TIB格式典型应用场景包括:提取一个波段的时间序列立方体,以及针对某个波段,选择3个时间的数据用于假彩色合成显示。
图 8展示了从SPATS数据集中,确定一个特定波段后,提取一个时间序列的立方体数据。
(4) TIP格式。TIP格式最大的特点是将图像中像元的时谱数据组织在一起,因此这种格式最适合于对像元的时间谱进行处理与分析。TIP格式比较典型的应用场景包括:提取一个像元或者一片区域在某个波段的时谱曲线,在时间维进行平滑和滤波处理,对时间谱曲线进行拟合,以及进行预测分析等。
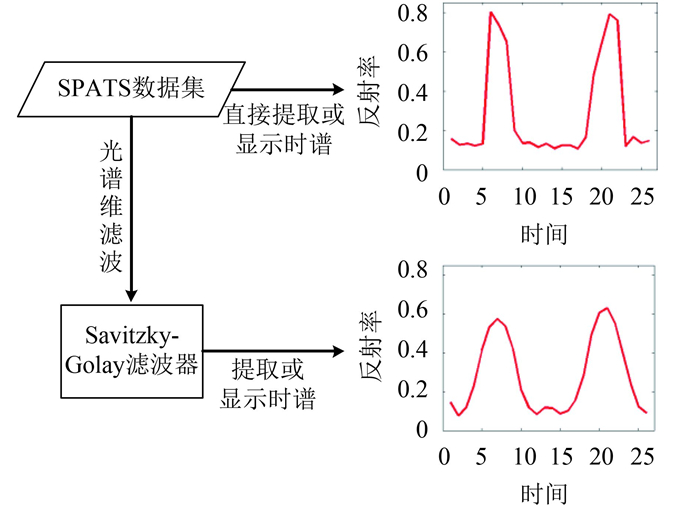
图 9具体展示了TIP格式用于提取和显示一个波段的时谱曲线,以及在光谱维进行Savitzky-Golay滤波,对时谱进行处理。
(5) TIS格式。TIS格式的特点是将每一个像元在整个时间序列上的光谱数据组织在一起,因此这种格式最适合于提取像元光谱曲线的时间序列数据。典型的应用场景是抽取某一个像元在一个时间范围内的所有光谱曲线,然后对这些曲线进行3维可视化,并分析该像元的光谱随着时间变化的情况。
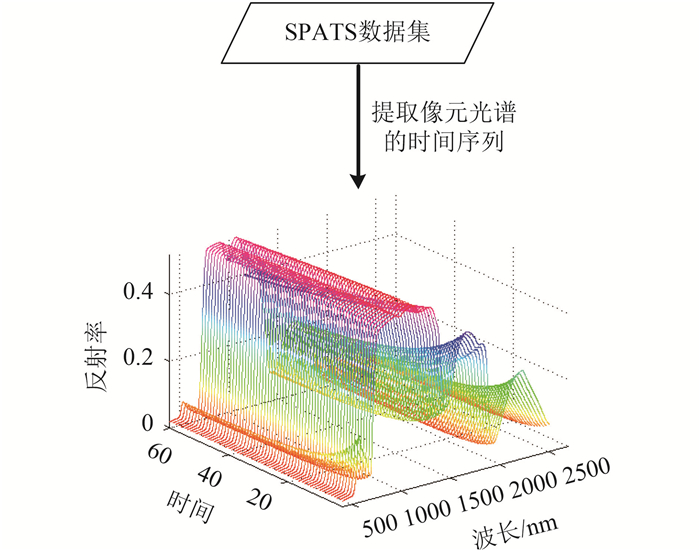
图 10展示了TIS格式用于提取一个像元光谱曲线的时间序列数据,3维可视化后便于直接观察光谱曲线随时间的变化。
3 多维分析模块构建
3.1 文件结构设计
SPATS结构数据由两部分组成:数据文件和头文件。数据文件是实际存储影像数据的文件,影像数据以TSB、TSP、TIP、TIB、和TIS中的一种格式存储在这个文件中,头文件既记录了影像数据本身的信息,包括空间、光谱和时间维的大小、数据存储格式、数据类型,也记录了关于影像数据附加的描述信息,包括坐标投影和仿射变换系数、光谱维和时间维的名称以及文件名称和类型、数据偏移等描述,如图 11。采用这种头文件与数据文件分离的方式使得数据的使用更加灵活,使用者可以利用外部工具打开头文件,查看和修改关于数据文件的信息。设计的头文件后缀名为mdr,数据文件后缀名为mdd。
单个时相的遥感数据预处理后一般以BSQ或者BIP格式存储,那么在构建SPATS结构数据时也分别对应两种格式。具体的讲,如果待构建的数据格式是BSQ则构建成TSB格式,如果是BIP则构建成TSP格式。之所以首先构建成这两种格式是考虑到BSQ与TSB、BIP与TSP在单个立方体内部采用相同的存储方式,在构建过程中对预处理的文件采用逐个读取的方式,避免了同时打开多个文件并在多个文件之间来回读取,减少了计算机在SPATS构建过程中的资源和时间开销。
3.2 模块介绍
基于多维组织结构构建了一套MDA多维数据分析软件模块,实现的功能包括:MDD数据构建、打开、转换,时谱、光谱和光谱特征参量立方体提取,以及不同维度的分析与显示功能。该模块能够将经过预处理后的长时间序列的遥感立方体数据构建成MDD存储结构的数据集,由于数据集内部的5种存储格式分别针对不同的应用,因此为了快速有效地进行多维分析、提取与显示,可以通过该模块的转换功能进行格式转换,然后再进行后续操作。在构建的MDD数据集的基础上,可以利用光谱特征参量提取功能批量计算一个时间序列影像的光谱特征参量(如NDVI等),构成特征参量立方体,进而可以以灰度或者假彩色合成对特征参量进行显示,以及交互式显示任一像元特征参量时谱曲线。也可以通过光谱立方体或者时间立方体提取功能从MDD时空谱4维立方体中提取3维立方体数据,导出成常用遥感软件支持格式来进行数据的相关处理与分析。
该多维分析模块能够嵌入至一些遥感软件平台中,例如ENVI,其中关键是需要拓展软件平台的数据格式,使其支持SPATS的五种数据格式。本研究在自主开发的MARS多维遥感数据处理分析软件中增加了SPATS的5种数据格式,并嵌入多维分析模块(Mdd analysis),包括Mdd数据的构建(Mdd builder)、打开(Mdd open)、格式转换(Mdd conversion)和数据提取(Data extraction)等。
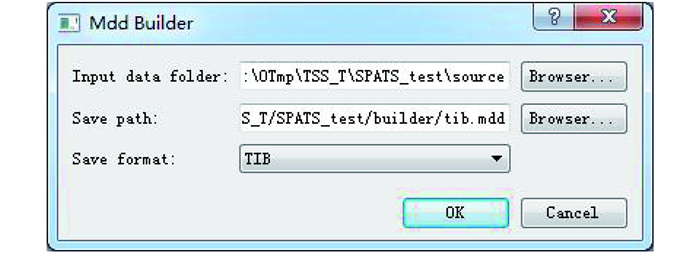
(1) MDD数据构建及打开。MDD多维数据需要利用经过预处理后的时间序列遥感影像来构建,预处理过程主要包括影像的配准与裁剪,该过程可以由MDA多维分析软件自动完成。预处理过的影像在空间覆盖范围以及像元大小上完全一致,每一个时间的影像是由多个波段组成数据立方体,通常立方体内部存储格式是BSQ或者BIP,每个立方体文件的文件名以时间命名,例如:2002011、2002035、2002043等(表示影像获取的年份以及Day of Year (DOY)),并存放在一个文件夹中。图 12为MDD构建界面,首先指定源数据存放的文件夹路径,同时指定输出文件的文件名、路径,以及构建数据的格式。在确认输入输出之后,构建模块根据文件名自动生成指定格式的MDD数据。
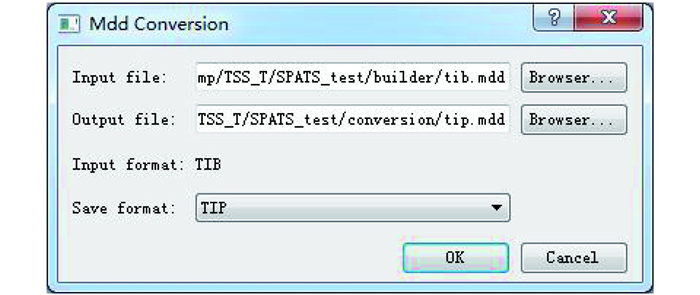
(2) 格式转换。初始构建MDD数据的格式不一定适用于具体的应用,此时需要进行格式转换,尽可能减少数据提取和分析中的时间。图 13为格式转换界面,首先指定格式转换的输入和输出数据,模块会根据输入数据的头文件自动判断待转换格式;然后指定输出格式,在确定输入输出后便自动完成转换。通过格式转换,在以后相关操作中就能最大限度的减少计算时间。
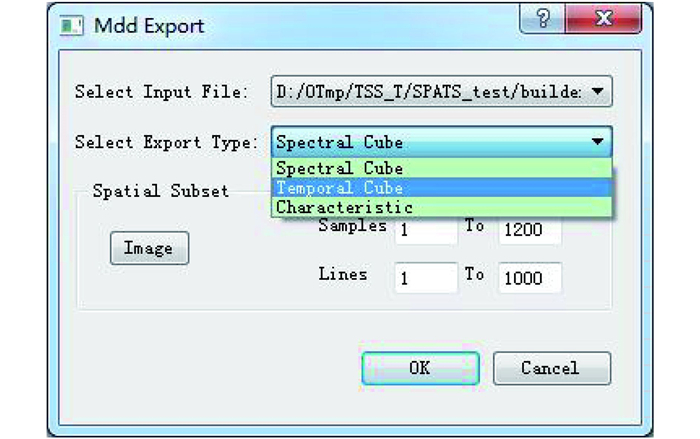
(3) 数据提取。数据提取功能支持3种数据的提取,第一种是时谱特征参量的提取,它是首先进行光谱运算然后输出,另外两个分别是时间立方体提取和光谱立方体提取,它们是直接从时-空-谱4维数据中提取3维数据立方体。如图 14界面所示,首先指定待导出数据的路径,然后指定导出数据的空间范围以及类型,如果选择类型为特征参量立方体,首先需要输入特征参量计算表达式,并且指定表达式中各个变量对应的波段,进一步选择提取的时间序列和输出路径,确认之后模块会自动完成提取过程。如果在图 14界面中选择提取类型为光谱立方体,此时选择一个时间和多个待输出的波段,并指定输出路径。再者如果图 14中选择提取类型为时间立方体,与光谱立方体不同的是,此时是选择一个波段以及多个时间。
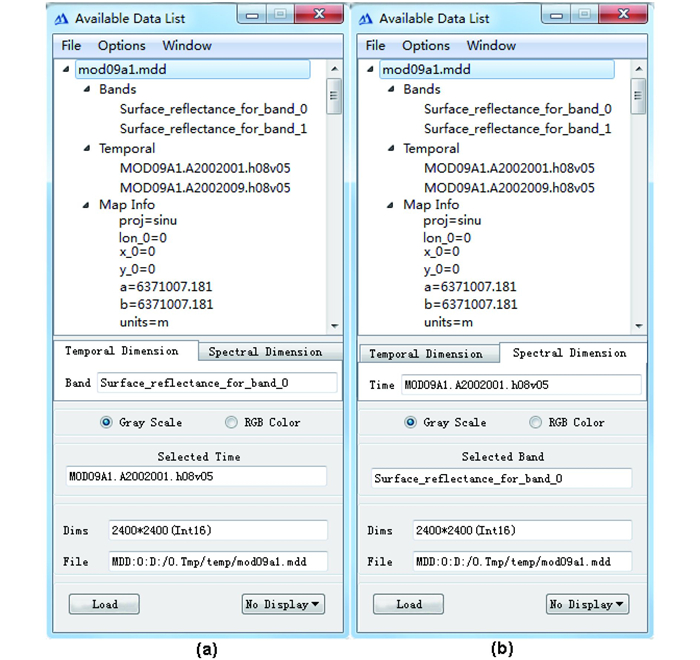
(4) 数据列表与显示。如图 15所示,构建或打开MDD数据后会在available data list中出现该数据集的对应信息,包括:波段(bands)、时间(temporal),以及图像坐标信息(map info)。“temporal dimension”和“spectral dimension”两个选项卡可以来回切换,它们分别表示图像显示时第3个维度(第1、2是平面的2维度)是时间维或光谱维。具体来说,如果选择“temporal dimension”(如图 15(a)),表示第3维为时间,这时需要选择一个波段的一个时间来进行灰度图显示,或者选择这个波段的3个时间来进行假彩色合成显示,在图中“band”位置选择1个波段,然后在“selected time”中选择1个或3个时间(gray scale时选择一个时间,RGB时选择3个时间),最后加载显示;同理,如果选择“spectral dimension”(如图 15(b)),这时在“time”位置选择1个时间,然后在“selected band”中选择1个或3个波段加载显示。
3.3 处理流程分析
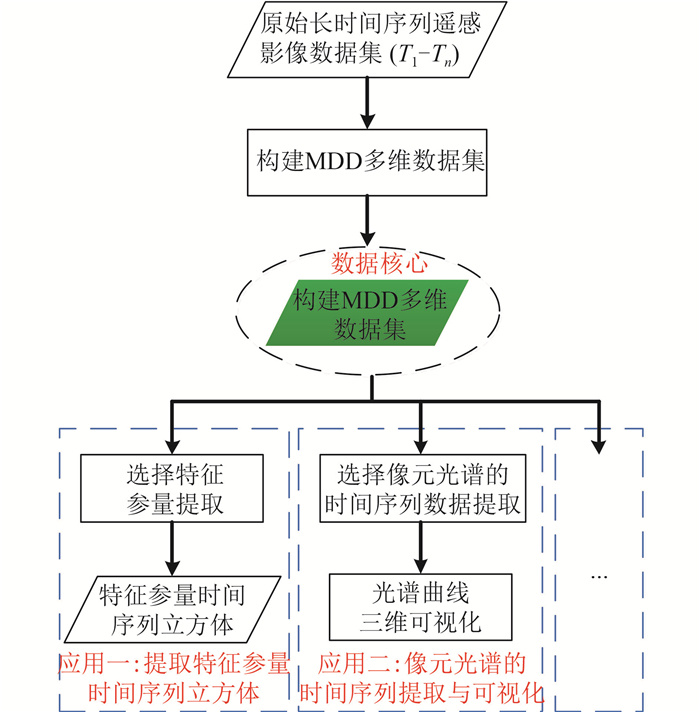
利用MDA多维分析模块进行数据处理与分析的流程如图 16所示,首先获取
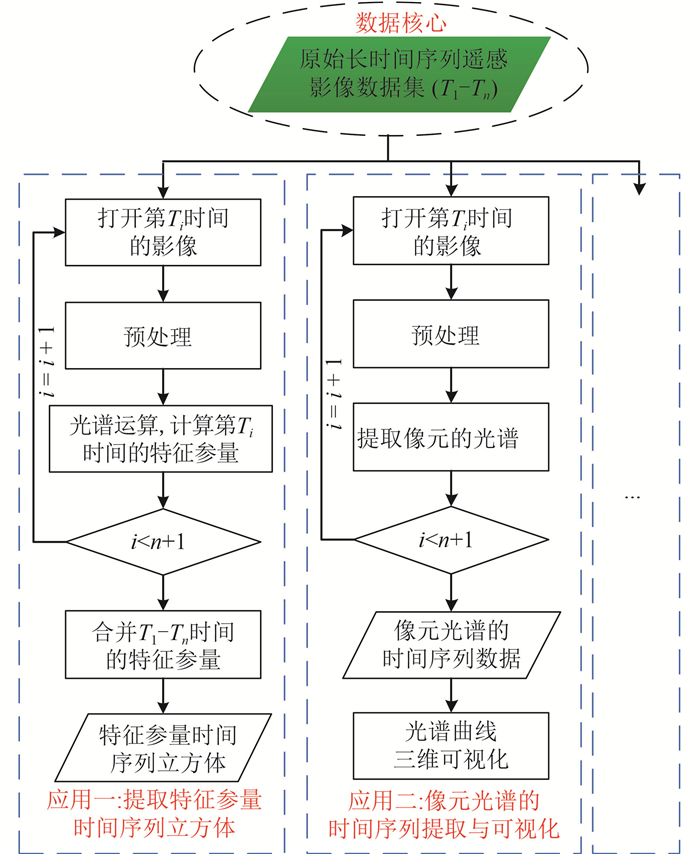
图 17是不使用MDA多维分析模块的情况下,时空谱多维数据应用处理的一般流程,图中包含两个应用:提取特征参量时间序列立方体和像元光谱的时间序列提取与可视化,这两个应用都是以原始获取的长时间序列遥感数据集为核心数据,以循环的方式对每一个时间的遥感数据作处理后,获得最终结果。与图 16中采用MDA模块处理的流程相比,前者的处理流程明显更加烦琐。这两种处理方式差异的根本原因在于图 17中的处理流程是以原始的长时间遥感数据集为数据核心展开的应用处理,由于原始数据没有统一组织,给数据的应用带来了不必要的烦琐流程;而图 16中则是以构建的MDD多维数据集为数据核心,这种结构数据将原始的时空谱遥感数据经过预处理后重新组织成一个一体化多维存储结构,所有应用都是以MDD数据展开,同时定义的5种格式保证了不同应用场景下处理的效率。因此采用MDA模块进行多维分析应用不仅流程简单,而且处理速度快,提高了不同应用场景下的效率。
3.4 时谱分类应用
这里运用一个构建时间序列数据并用于分类的实例来验证多维分析模块的应用效果。实验区位于美国西南部亚利桑达州的凤凰城附近,中心坐标为33°26.68′N,112°17.43′W,区域大小为3.18 km×3.18 km,该区域主要地物覆盖类型是作物,形状规则的田块种植有不同的作物类型。实验数据是2002年全年Landsat TM/ETM+的26幅无云影像,对应条带号为Path 37/Row 37。
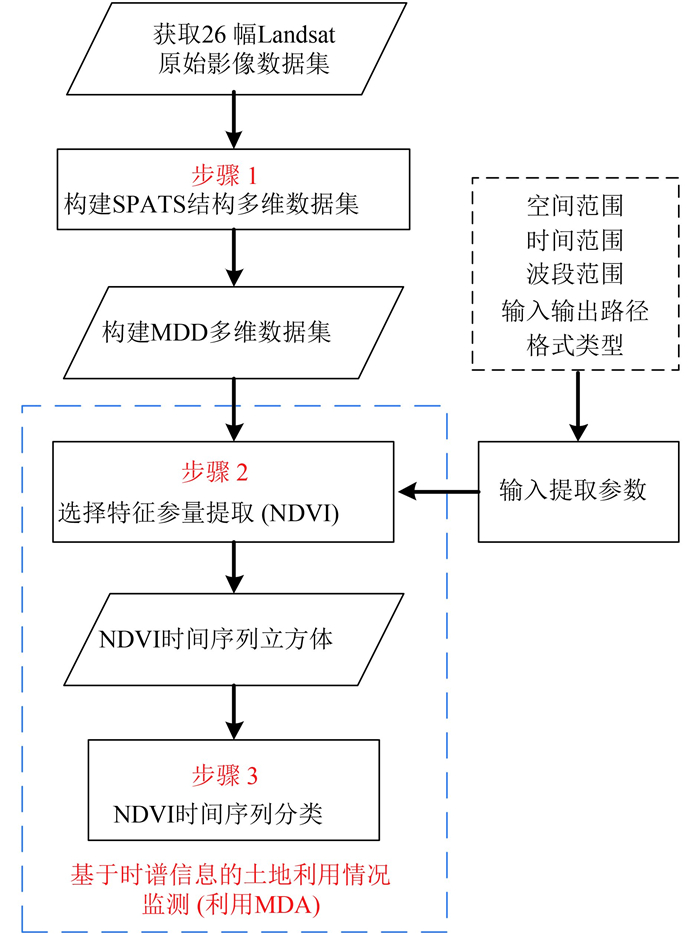
图 18是利用MDA基于时谱信息的土地检测流程,从图中可以看出首先将获取的26幅Landsat原始影像数据集构建成MDD数据结构,然后输入参数(空间范围、时间范围、波段范围、输入和输出路径和格式类型)通过光谱运算计算特征参量,输出NDVI时间立方体数据,最后利用这个立方体数据进行时谱分类。图 19是利用ENVI软件手动操作的操作流程,首先对第一个时间的影像进行预处理(主要是空间裁剪),根据输入的特征参量表达式计算这个时间的特征参量(NDVI),然后进行下一个时间的计算直至26个时间全部计算完成,之后将这26个时间的NDVI组合成特征参量立方体,最后同样进行时谱分类。
对以上两种方式的操作步骤和所花费的平均时间(表 1)进行比较,可以看出利用MDA,不仅操作步骤少,而且所花费的总时间少很多。在整个时间序列分类过程中,由于利用了多维分析模块(MDA),使得利用NDVI时间序列立方体数据的生成流程变得异常简洁,很大程度上提高了分类效率。以上测试中对比所用软件是ENVI 4.8 32 bit,MARS与ENVI运行环境使用的是HP6200P电脑,CPU为Intel Pentium Dual-lore,2.7 GHz,RAM是4 GB Disk and file system:500 G,NTFs file system;OS为Windows 7 Professional。
表 1 操作步骤与花费时间对比
Table 1 The comparison for processing steps and spending time
| 利用ENVI | 利用MDA | |||
| 步骤编号 | 平均花费时间/s | 步骤编号 | 平均花费时间/s | |
| 1 | 21 | 1 | 42 | |
| 2 | 15 | |||
| 3 | 21 | 2 | 25 | |
| 4 | 15 | |||
| …… | 3 | 120 | ||
| 51 | 21 | |||
| 52 | 10 | |||
| 53 | 33 | |||
| 54 | 120 | |||
| 步骤总数 | 总平均时间 | 步骤总数 | 总平均时间 | |
| 54 | 1089 | 3 | 187 | |
4 结论
本文针对时-空-谱多维数据分析的迫切需求,研究了多维数据组织方式,设计了SPATS多维遥感数据一体化存储结构,定义了5种多维数据存储格式,构建了一套MDA多维数据分析软件模块,并通过实际应用对多维数据组织效果进行了验证,得出以下结论:
(1) SPATS多维结构在设计理念上不同于目前现有的组织方式,它不是将一个多维立方体数据通过降维然后用多个低维立方体来表示,而是直接将4维遥感数据当作一个整体,组织成一个4维超立方体数据集。SPATS真正实现了时-空-谱4维遥感数据的一体化组织。
(2) 本文构建的多维分析模块不仅仅是一个时-空-谱4维遥感数据组织的工具,它更是一个以SPATS数据结构为核心,针对多维分析应用的开放平台,无论是空间维分析,还是光谱维或者时间维分析都可以基于这个平台展开。
(3) SPATS数据结构内部定义了5种数据存储格式,分别针对不同的数据分析应用而设计,在具体分析应用的处理速度方面具有优势。
参考文献(References)
-
Galford G L, Mustard J F, Melillo J, Gendrin A, Cerri C C, Cerri C E.2008.Wavelet analysis of MODIS time series to detect expansion and intensification of row-crop agriculture in Brazil. Remote Sensing of Environment, 112 (2): 576–587[DOI: 10.1016/j.rse.2007.05.017]
-
Huang C Q, Goward S N, Masek J G, Thomas N, Zhu Z L, Vogelmann J E.2010.An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sensing of Environment, 114 (1): 183–198[DOI: 10.1016/j.rse.2009.08.017]
-
Irons J R, Dwyer J L, Barsi J A.2012.The next Landsat satellite:the Landsat data continuity mission. Remote Sensing of Environment, 122 : 11–21[DOI: 10.1016/j.rse.2011.08.026]
-
Kennedy R E, Yang Z Q, Cohen W B.2010.Detecting trends in forest disturbance and recovery using yearly Landsat time series:1. LandTrendr-Temporal segmentation algorithms. Remote Sensing of Environment, 114 (12): 2897–2910[DOI: 10.1016/j.rse.2010.07.008]
-
Margono B A, Turubanova S, Zhuravleva I, Potapov P, Tyukavina A, Baccini A, Goetz S, Hansen M C.2012.Mapping and monitoring deforestation and forest degradation in Sumatra (Indonesia) using Landsat time series data sets from 1990 to 2010. Environmental Research Letters, 7 (3): 034010 [DOI: 10.1088/1748-9326/7/3/034010]
-
Mouillot F, Schultz M G, Yue C, Cadule P, Tansey K, Ciais P, Chuvieco E.2014.Ten years of global burned area products from spaceborne remote sensing-A review:analysis of user needs and recommendations for future developments. International Journal of Applied Earth Observation and Geoinformation, 26 : 64–79[DOI: 10.1016/j.jag.2013.05.014]
-
Powell S L, Cohen W B, Healey S P, Kennedy R E, Moisen G G, Pierce K B, Ohmann J L.2010.Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data:acomparison of empirical modeling approaches. Remote Sensing of Environment, 114 (5): 1053–1068[DOI: 10.1016/j.rse.2009.12.018]
-
Roy D P, Jin Y, Lewis P E, Justice C O.2005.Prototyping a global algorithm for systematic fire-affected area mapping using MODIS time series data. Remote Sensing of Environment, 97 (2): 137–162[DOI: 10.1016/j.rse.2005.04.007]
-
Sakamoto T, Van Nguyen N, Kotera A, Ohno H, Ishitsuka N, Yokozawa M.2007.Detecting temporal changes in the extent of annual flooding within the Cambodia and the Vietnamese Mekong Delta from MODIS time-series imagery. Remote Sensing of Environment, 109 (3): 295–313[DOI: 10.1016/j.rse.2007.01.011]
-
Sakamoto T, Yokozawa M, Toritani H, Shibayama M, Ishitsuka N, Ohno H.2005.A crop phenology detection method using time-series MODIS data. Remote Sensing of Environment, 96 (3/4): 366–374[DOI: 10.1016/j.rse.2005.03.008]
-
Townsend P A, Helmers D P, Kingdon C C, McNeil B E, de Beurs K M, Eshleman K N.2009.Changes in the extent of surface mining and reclamation in the Central Appalachians detected using a 1976-2006 Landsat time series. Remote Sensing of Environment, 113 (1): 62–72[DOI: 10.1016/j.rse.2008.08.012]
-
Wulder M A, Masek J G, Cohen W B, Loveland T R, Woodcock C E.2012.Opening the archive:how free data has enabled the science and monitoring promise of Landsat. Remote Sensing of Environment, 122 : 2–10[DOI: 10.1016/j.rse.2012.01.010]