出版日期: 2017-01-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176021
2017 | Volumn21 | Number 1

国产卫星

M-估计法广义变分同化FY-3B/IRAS通道亮温

王根¹ , 唐飞² , 刘晓蓓¹ , 邱康俊¹ , 温华洋¹

1. 安徽省气象信息中心, 合肥 230031

2. 南京信息工程大学大气科学学院资料同化研究与应用中心, 南京 210044

收稿日期: 2016-01-06; 修改日期: 2016-06-01; 优先数字出版日期: 2017-01-25

基金项目: 公益性行业（气象）科研专项（编号：GYHY201406028）；淮河流域气象开放研究基金（编号：HRM201407）；安徽省气象局科技发展基金（编号：RC201506）

第一作者简介: 王根(1983-), 男, 博士, 工程师, 研究方向为卫星资料同化、GRAPES数值模拟和多源数据融合。E-mail:203wanggen@163.com

中图分类号: P407

文献标识码: A

文章编号: 1007-4619(2017)01-0052-10

摘要

采用FY-3B/IRAS亮温资料进行广义变分同化研究。广义变分同化结合了经典变分同化和稳健M-估计两者的优点。区别于经典变分同化依赖于先前的质量控制并要求误差服从高斯分布，把M-估计法耦合到经典变分同化框架中，得到广义变分同化，其弱化了同化前的质量控制和误差服从高斯分布这两个条件。目标能量泛函包含M-估计以保证对离群值具有稳健性，从而能够得到较好的同化结果。对比变分同化前后的FNL资料湿度与GDAS湿度相关系数作为同化结果检验评价。具体操作过程在FNL作为背景场的基础上分别采用经典和M-估计不同的权重因子变分同化FY3B/IRAS资料，把得到的分析场与GDAS进行相关性比较，由于湿度具有较强的非高斯性，文中首先评估了安徽省13个站GPS/PWV和积分相关湿度廓线得到大气可降水量（即GDAS/PWV和FNL/PWV资料）的相关性，进一步基于信息熵自由度思想进行了近一个月IRAS 20个通道对分析场的影响贡献率诊断研究。

关键词

广义变分同化 , M-估计 , NCEP/FNL , 大气可降水量 , 信息熵自由度

Application of M-estimators method on FY-3B/IRAS channel brightness temperature generalized variational assimilation

WANG Gen¹ , TANG Fei² , LIU Xiaobei¹ , QIU Kangjun¹ , WEN Huayang¹

1.Anhui Meteorological Information Centre, Hefei 230031, China

2.Center of Data Assimilation for Research and Application, School of Atmospheric Science, Nanjing 210044, China

Abstract

This study adopts the Infrared Atmospheric Sounder of Feng-Yun and the 3rd (B) Weather Satellite (FY-3B/IRAS) brightness temperature to investigate the generalized variational assimilation, which combines the advantages of classical variational assimilation and robust M-estimators. Classical variational assimilation is based on the model variables and satellite observations of the brightness temperature to yield a quadratic functional minimization. The observational errors are needed to follow a Gaussian distribution and subsequently apply the least-square principle. The least-squares method is sensitive to outliers; if the analyzed data contain gross errors, the parameter estimation will be inaccurate. The classical variational assimilation consists of two stages. First, an appropriate algorithm is used to identify and address outliers in the data and then, the assimilation. This approach may result in the loss of useful data because the outliers are not always harmful; some outliers may represent new information, such as weather phenomena. At present, the quality control is generally based on a certain threshold value if the subjective uncertainty is too strong. If outliers persist after the quality control, the optimal parametric results that are obtained through classical variational assimilation become meaningless. M-estimators are added to the framework of classical variational assimilation to obtain a generalized variational assimilation, which is coupled with quality control in the process of assimilation. The main idea is to use the weight factor of M-estimators to re-estimate the contribution rate of the observation items to the objective function in each process of objective function minimization based on classical variational assimilation. The cost function consists of M-estimators to guarantee the robustness to outliers. Thus, the assimilation results are improved. Humidity is an important dynamic variable in the NWP model. It does not only determine the occurrence of precipitation but also changes the temperature through evaporation and condensation, and it also influences the wind field by changing the pressure gradient. In addition, the nonlinearity of humidity is stronger than temperature, which causes the humidity to follow a stronger non-Gaussian distribution. Thus, humidity was used as an assimilation experiment effect validation, and the correlation coefficient of humidity was compared with FNL and GDAS, which are assimilated by different M-estimator weights. The specific operation process that is based on the FNL as the background field adopts classical and different weight factors of M-estimators to the variational assimilation of FY-3B/IRAS. In addition, the correlation between the analyzed field, and the GDAS is compared. The correlation between 13 GPS/PWV stations of Anhui province and the integral humidity profile of the relevant field from both GDAS/PWV and FNL/PWV is evaluated. Furthermore, based on the information entropy of freedom degrees, the contribution of IRAS 20 channels were determined to analyze the field for nearly a month. Preliminary results demonstrate the potential application value of the generalized variational assimilation.

Key words

generalized variational assimilation , M-estimators , NCEP/FNL , precipitable water vapor , freedom degrees of information entropy

1 引言

数值天气预报NWP (Numerical Weather Prediction)是一个初/边值问题。卫星资料的使用提高了数据资料的空间和时间分辨率，从而对提高NWP预报精度起到关键的作用(王根，2014)。

近年来针对卫星资料的使用主要有两种方法。一是间接法，对卫星通道的观测亮温首先进行反演得到温度、湿度和地面风场信息等。由于反演是一对多的问题，间接法会导致反演的不适定性，可能带来错误的结果。二是直接法，采用变分同化的方法，变分同化是基于极小化模式变量模拟值和卫星观测亮温二次泛函。二次泛函通常包括两项：背景项和观测项。背景项定义为模式空间中背景场变量和同化变量之间的差值；观测项定义为卫星观测空间中观测亮温和模拟亮温的差值(张华，2004)。通用的变分同化方法在文中记为经典变分同化。

经典变分同化要求误差服从高斯分布，目的是应用最小二乘理论(Wang和Zhang，2014)。最小二乘法对离群值敏感，如果数据包含过失误差，导致估计的参数不准确。采用经典变分同化时则需要分两步进行：首先使用合适的算法识别和处理数据中的离群值，然后再进行变分同化。与此同时较多有用的数据将会丢失，因为离群值并不总是有害的。一些离群值可能代表新的信息(如天气现象等)。加上质量控制通常是基于一些经验阈值的给定，主观和不确定性较强。如果在质量控制后还存在离群值，则会导致经典变分同化得到的最优参数估计结果没有意义。因此需要考虑误差服从非高斯分布，对离群值不敏感的稳健统计方法。

最初研究稳健统计的学者有Tukey (1960)、Huber (1964, 1967)和Hampel (1971, 1974)。Huber (1981)提出了稳健统计的定义，稳健统计方法必须能够较好且合理地处理假设模型。当模型有较小偏离时，得到的结果只应有较小破坏；当模型有较大偏离时，结果也不会有破坏性或致命的影响。误差满足高斯分布只是理论上的假设，但实际个例较多误差不满足高斯分布，如AIREP、无线电探空仪、温度、METAR地表气压(Lsaksen，2010)。一般认为，由于水汽具有较快的时空变化特征，大气湿度观测误差的非高斯分布特性更明显(Zhang等，2013；Li等，2011)。国外一些学者很早进行了非高斯误差变分研究，Dharssi等(1992)提出了非高斯变分方法。Ingleby和Lorenc (1993)基于贝叶斯理论使用多元正态分布进行质量控制。Anderson和Järvinen (1999)采用了变分质量控制法有效地拒绝或采用(执行过程中对观测数据赋予权重)偏差很大的观测数据。Andersson (2003)采用重大误差和高斯误差的组合进行了一些研究。Lsaksen (2010)得到经过Huber norm质量控制后的观测数据对分析场有正影响效果。

朱江(1995)用简单的模式试验基于4维变分框架，通过计算“误差均差比”识别并订正重大误差，但严格质量控制的缺点是倾向于剔除较多极端但正确的观测，导致错过重要的天气现象。郝民等人(2013)把变分质量控制的方法用于中国自主研发的区域GRAPES-3DVAR中，同化后得到的湿度场和水汽输送强度更接近实况，同时也提高了模式对降水强度和落区的预报能力。Bewley等人(2000)通过考虑初始条件作为控制变量，把其应用到资料同化中，与“变分质量控制”重要不同是该算法并不需要假定重大误差分布，而是显示把误差作为目标泛函自变量的一部分。Tachim Medjo (2002)用简单的模式进行了Bewley等人(2000)的算法的测试，得到了较好的收敛性。但目前还没有看到此方法应用在气象相关领域的文献，尤其在国内相关的文献较少。

基于上述Bewley等人(2000)算法前瞻性的思想和Wang和Zhang (2014)前期研究的基础，文中把M-估计法(Wang和Zhang，2014；Huber，1981；Bhar，2007；Liu和Qi，2005)的权重函数(如L2-估计，Huber-估计，L1-估计和Cauchy-估计等)耦合到经典变分同化中得到广义变分同化。广义变分同化对离群值具有稳健性，在极小化迭代执行过程中耦合了质量控制，动态调整观测资料对目标泛函的权重值。文中采用FY3B/IRAS亮温资料进行广义变分同化试验，试验过程中选取不同M-估计法和经典变分同化NCEP (National Centers for Environmental Prediction)的FNL分析资料进行对比，考虑到湿度非高斯性较强，采用FNL和GDAS湿度相关系数进行度量。首先评估FNL/PWV (可降水量PWV，Precipitable Water Vapor)、GDAS/PWV和GPS/PWV的相关性，进一步采用信息熵自由度进行IRAS通道亮温资料对分析场影响贡献率诊断研究。

2 经典变分同化回顾

在卫星遥感和数据同化中一般都是极小化二次目标泛函，以得到较好的大气状态估计。

经典变分同化定义为下面的目标泛函(张华等，2004)：

总能量泛函：

$ \mathop {\min }\limits_{\boldsymbol{x} \in {{\left[ {{\boldsymbol{x}_b} - {{\boldsymbol{\delta}} _x},{\boldsymbol{x}_b} + {{\boldsymbol{\delta}} _x}} \right]}^n}} J\left( \boldsymbol{x} \right) = \min \left( {{J_b}\left( \boldsymbol{x} \right) + {J_o}\left( \boldsymbol{x} \right)} \right) $

(1)

背景项：

$ {J_b}\left( \boldsymbol{x} \right) = \frac{1}{2}{\left( {\boldsymbol{x} - {\boldsymbol{x}_b}} \right)^{\rm T}}{\boldsymbol{B}^{ - 1}}\left( {\boldsymbol{x} - {\boldsymbol{x}_b}} \right) $

(2)

观测项：

$ {J_o}\left( \boldsymbol{x} \right) = \frac{1}{2}{\left( {\boldsymbol{H}\text{′} \!\!\!\! \left( \boldsymbol{x} \right) - {\boldsymbol{y}_{{\rm{obs}}}}} \right)^{\rm T}}\boldsymbol{R}_{{\rm{obs}}}^{ - 1}\left( {H\left( \boldsymbol{x} \right) - {\boldsymbol{y}_{{\rm{obs}}}}} \right) $

(3)

式中，$\boldsymbol{x}$是控制变量；$\boldsymbol{x}_b$是背景场又称第一猜测场(包含温度、湿度、压力和风场等信息)；背景和观测误差协方差矩阵分别为$\boldsymbol{B}$和$\boldsymbol{R}_{\rm{obs}}$。上标“T”和“-1”分别表示矩阵转置和逆。$\boldsymbol{y}_{\rm{obs}}$是观测亮温。$\boldsymbol{H}$′是观测算子，对于卫星资料而言，也称为快速辐射传输模式，$\boldsymbol{H}$′在文中采用Tiros业务垂直探测器辐射传输模式RTTOV (Radiative Transfer for Tirosn Operational Vertical Sounder)进行计算(Hocking等，2010)。经过推导，则有：

$ \boldsymbol{x} = {\boldsymbol{x}_b} + \boldsymbol{B}{\boldsymbol{H}^{\rm T}}{\left( {\boldsymbol{HB}{\boldsymbol{H}^{\rm T}} + {\boldsymbol{R}_{{\rm{obs}}}}} \right)^{ - 1}}\left( {{\boldsymbol{y}_{{\rm{obs}}}} - \boldsymbol{H}\text{′} \!\!\!\!(\boldsymbol{x}) {\boldsymbol{x}_b}} \right) $

(4)

极小化后的$\boldsymbol{x}$即为分析场$\boldsymbol{x}_a$，$\boldsymbol{H}=∂ \boldsymbol{H}′/∂ \boldsymbol{x}$是Jacobi矩阵($∂$是求偏导符号标记)，表示卫星各通道观测或模拟亮温对待同化大气温度和湿度等的敏感性，又称为温度和湿度Jacobi等(王根，2014)。

3 广义变分同化理论分析

文中基于M-估计法对离群值有较强的稳健性，采用广义变分同化框架期望获得更好的同化结果。区别经典变分同化依赖于变分之前资料的质量控制和观测误差服从高斯分布，广义变分同化降低了这些要求。

3.1 广义变分同化目标泛函

广义变分同化观测项目标泛函定义为(Wang和Zhang，2014)：

$ \! {J_{o'}}(\boldsymbol{x},\boldsymbol{w}) = \frac{{\rm{1}}}{{\rm{2}}}{\left[ {\boldsymbol{H}\text{′}\!\!\!\!(\boldsymbol{x}) - {\boldsymbol{y}_{{\rm{obs}}}}} \right]^{\rm{T}}}\boldsymbol{w}(\boldsymbol{r})\boldsymbol{R}_{{\rm{obs}}}^{ - {\rm{1}}}\left[ {\boldsymbol{H}\text{′}\!\!\!\!(\boldsymbol{x}) - {\boldsymbol{y}_{{\rm{obs}}}}} \right] $

(5)

需要说明的是广义变分同化只是观测项的目标泛函构造和经典变分同化有所不同，背景目标泛函则相同。式(5)中，$\boldsymbol{w}\left( \boldsymbol{r} \right)$是权重因子，作为观测资料对目标泛函的影响权重值。其他变量与式(3)相同。

3.1.1 权重因子分析

定义：

$ \boldsymbol{w}(\boldsymbol{r}) = \left( {1/\boldsymbol{r}} \right){\rm{\cdot}}\left( {{\rm d}\rho (\boldsymbol{r})/{\rm d}r} \right) $

(6)

式中，$ρ$($r$)是M-估计的代价函数(见表 1)。d是求导标记。$\boldsymbol{w}$($\boldsymbol{r}$)是对角矩阵，元素为$w$($r_i$)，$r_i$=[$y_i$-$H′_i$($x$)]/$σ_i$。权重因子$\boldsymbol{w}$具有自适应加权的功能。当偏差较大时，观测资料对目标泛函的影响会减小，当偏差无限大时，相应的观测资料影响会被抑制，也就是说广义变分同化减小了小概率数据对同化结果的影响(Bhar，2007)。$y_i$是通道$i$的观测亮温。$H′_i$($x$)是通道$i$的模拟亮温。$σ_i$是观测误差协方差矩阵的元素。

表 1定义了常用M-估计的代价函数$ρ$($r$)、影响函数$φ$($r$)、权重函数$w$($r$)和稳健尺度$c$(表 1中给出了一般参考文献中给定的值)，$r$值与式(5)一致，具体见参考文献(Bhar，2007；Wang和Zhang，2014)。

表 1 常用M-估计介绍
Table 1 List of common M-estimators

下载CSV

M估计法类型	代价函数$ρ$($r$)	影响函数$φ$($r$)	权重函数$w$($r$)	稳健尺度$c$
$L^2$	$r^2$/2	$r$	1	1
$Welsch$	${\left( {{ c^2}/2} \right)\left[ {1 - \exp \left( { - {{\left( {r/c} \right)}^2}} \right)} \right]}$	${r\exp \left( { - {{\left( {r/c} \right)}^2}} \right)}$	${\exp \left( { - {{\left( {r/c} \right)}^2}} \right)}$	$c$=2.9846
$Beaton - Tukey\begin{array}{{20}{c}} {\left\{ {\begin{array}{{20}{c}} {if\|r\| \leqslant c}\\ {if\|r\| > c} \end{array}} \right.} \end{array}$	$\left\{ {\begin{array}{*{20}{c}} {\left( {{c^2}/6} \right)\left( {1 - {{\left[ {1 - {{\left( {r/c} \right)}^2}} \right]}^3}} \right)}\\ {\left( {{c^2}/6} \right)} \end{array}} \right.$	$\left\{ {\begin{array}{*{20}{c}} {r{{\left[ {1 - {{\left( {r/c} \right)}^2}} \right]}^2}}\\ 0 \end{array}} \right.$	$\left\{ {\begin{array}{*{20}{c}} {{{\left[ {1 - {{\left( {r/c} \right)}^2}} \right]}^2}}\\ 0 \end{array}} \right.$	$c$=4.6851
$L_p$	$\|r{\|^c}/c$	${\mathop{\rm sgn}} \left( r \right)\|r{\|^{c - 1}}$	$\|r{\|^{c - 2}}$	$c$=1.2
$L_1$	$\|r\|$	${\mathop{\rm sgn}} (r)$	${\rm{1/}}\|r\|$
$L_1$-$L_1$	$2\left( {\sqrt {1 + {r^2}/2} - 1} \right)$	$r/\sqrt {1 + {r^2}/2} $	$1/\sqrt {1 + {r^2}/2} $
$Huber\begin{array}{{20}{c}} {\left\{ {\begin{array}{{20}{c}} {if\|r\| \leqslant c}\\ {if\|r\| > c} \end{array}} \right.} \end{array}$	$\left\{ {\begin{array}{*{20}{c}} {{r^2}/2}\\ {c\left( {\|r\| - r/2} \right)} \end{array}} \right.$	$\left\{ {\begin{array}{*{20}{c}} r\\ {c{\mathop{\rm sgn}} \left( r \right)} \end{array}} \right.$	$\left\{ {\begin{array}{*{20}{c}} 1\\ {c/\|r\|} \end{array}} \right.$	$c$=1.345
$German-Maclure$	$\left[ {\left( {{r^2}/2} \right)/\left( {1 + {r^2}} \right)} \right]$	$r/{\left( {1 + {r^2}} \right)^2}$	$1/{\left( {1 + {r^2}} \right)^2}$
$Fair$	${c^2}\left[ {\|r\|/c - \ln \left( {1 + \|r\|/c} \right)} \right]$	$r/\left( {1 + \|r\|/c} \right)$	$1/\left( {1 + \|r\|/c} \right)$	$c$=1.3998
$Cauchy$	$\left( {{c^2}/2} \right)\left[ {\ln \left( {1 + {{\left( {r/c} \right)}^2}} \right)} \right]$	$r/\left[ {1 + {{\left( {r/c} \right)}^2}} \right]$	$1/\left[ {1 + {{\left( {r/c} \right)}^2}} \right]$	$c$=2.3849

需要说明的是：具体选择M-估计权重因子时应该满足一些约束。最重要约束是在变量空间要求单个函数为凸函数，以保证最终结果收敛到唯一解。从表 1中的Huber影响函数(图略)可以看出，区别于$L_2$($L_2$为经典变分同化法)影响函数呈直线增长；Huber超过某阈值时其影响值就不再增长而为一常数。投影到相应的权重函数时，$L_2$权重函数值始终为1；Huber权重函数在稳健尺度(表 1中$c$为稳健尺度值)范围内为1，范围外随着偏差的增大权重减小(图略)(Wang和Zhang，2014)。

3.1.2 离群值分析

广义变分同化不仅依赖于权重因子的给定，也依赖于离群值的阈值(文中也称为稳健尺度)。离群值的阈值可由通道亮温偏差的中位数求得：

$ {c_i} = med\left[ {\left| {y_i^{{\rm{obs}}} - y_i^{{\rm{sim}}}} \right|,i = ch{\rm{01}},ch{\rm{02}},\cdots,ch{\rm{20}}} \right] $

(7)

式中，${y_i^{{\rm{obs}}}}$和${y_i^{{\rm{sim}}}}$分别是通道$i$的观测和模拟亮温，$med$表示绝对偏差中位数。

3.1.3 广义变分同化目标泛函梯度分析

每次极小化迭代过程中权重因子的权值都被更新以实现观测项对目标泛函影响的动态重估计。

目标泛函梯度定义为

$ {\nabla _x}J = {\nabla _x}{J_b}\left( \boldsymbol{x} \right) + {\nabla _x}{J_{{o'}}}\left( {\boldsymbol{x},\boldsymbol{w}} \right) $

(8)

背景项梯度：

$ {\nabla _x}{J_b}\left( \boldsymbol{x} \right) = {\boldsymbol{B}^{ - 1}}\left( {\boldsymbol{x} - {\boldsymbol{x}_b}} \right) $

(9)

观测项梯度：

$ \begin{array}{l} {\nabla _x}{J_{o'}}\left( {\boldsymbol{x},\boldsymbol{w}} \right) = {\boldsymbol{H}^{\rm T}}\left[ {\boldsymbol{w}\left( \boldsymbol{r} \right)\boldsymbol{R}_{{\rm{obs}}}^{ - 1}\left( {\boldsymbol{H}{\text{′}} \!\!\!\! \left( \boldsymbol{x} \right) - {\boldsymbol{y}_{{\rm{obs}}}}} \right)} \right]+ \\ {\boldsymbol{H}^{\rm T}}\left[ {\frac{1}{2}{{\left( {\boldsymbol{H}{\text{′}}\!\!\!\! \left( \boldsymbol{x} \right) - {\boldsymbol{y}_{{\rm{obs}}}}} \right)}^{\rm T}}\left( {\boldsymbol{w}'\left( \boldsymbol{r} \right)/{\sigma _0}} \right)\boldsymbol{R}_{{\rm{obs}}}^{ - 1}\left( {\boldsymbol{H}'\left( \boldsymbol{x} \right) - {\boldsymbol{y}_{{\rm{obs}}}}} \right)} \right] \end{array} $

(10)

3.2 广义变分同化算法步骤介绍

文中采用FY3B/IRAS通道亮温资料进行广义变分同化研究，广义变分同化数值算法步骤如下：

(1) 输入背景资料后采用RTTOV计算卫星通道模拟亮温。$y_i^{{\rm{sim}}} = {H_i}\left( {{\boldsymbol{x}_b}} \right)$

(2) 统计每个通道亮温偏差(偏差定义为卫星观测和模拟亮温之间的差值)，由式(7)计算每个通道的离群值阈值。

(3) 计算广义变分同化目标泛函和梯度。此步骤需要选取相应的M-估计法(参考表 1)。

$ \begin{array}{l} J({\boldsymbol{x}_k}) = {J_b}({\boldsymbol{x}_k}) + {J_{o'}}({\boldsymbol{x}_k},{\boldsymbol{w}_k})\\ {\nabla _{{x_k},{w_k}}}J({\boldsymbol{x}_k}) = {\nabla _{{x_k}}}{J_b}({\boldsymbol{x}_k}) + {\nabla _{{\boldsymbol{x}_k},{\boldsymbol{w}_k}}}{J_{o'}}({\boldsymbol{x}_k},{\boldsymbol{w}_k}) \end{array} $

(4)调用极小化算法进行求解，得到控制变量$\boldsymbol{x}_k$，$ {\boldsymbol{x}_k} = {\boldsymbol{x}_b} + \delta {\boldsymbol{x}_k}$。$k$表示迭代次数。

(5)如果$||{\boldsymbol{x}_k} - {\boldsymbol{x}_{k - 1}}|{|_2} < \varepsilon $或$ k < {n_{\max }}$，则停止迭代，否则转到(3)进行下一次迭代。$ε$是迭代停止阈值。$n_\rm{max}$是极小化迭代中的最大迭代次数。

4 其他公式介绍

4.1 大气可降水量介绍

大气可降水量PWV是指地面上垂直气柱中含有的水汽总量，假定这些水汽全部凝结，并积聚在气柱的底面上时所具有的液态水深度。利用混合比计算PWV (丁金才，2009)：

$ {\rm{PWV}} = \frac{1}{{{\rho _{{\rm{water}}}}}}\int\limits_{{P_0}}^0 {\frac{q}{g}{\rm{d}}p} $

(11)

式中，$ρ_{water}$为液态水密度，$P_0$为地面气压，$p$为气压，$q$为混合比，$g$为重力加速度。

4.2 基于信息熵自由度的资料影响率诊断分析

文中基于信息熵信号自由度思想进行FY3B/IRAS资料对同化分析场的影响诊断研究(与Zhang私下交流)。信息熵自由度定义为

$ DFS = Tr(\boldsymbol{KH}) $

(12)

式中，$ \boldsymbol{KH}$定义为分析场对观测资料的敏感性。$ \boldsymbol{K}$为增益矩阵，$\boldsymbol{K} = \boldsymbol{B}{\boldsymbol{H}^{\rm T}}{(\boldsymbol{HB}{\boldsymbol{H}^{\rm T}} + {\boldsymbol{R}_{{\rm{obs}}}})^{{\rm{ - 1}}}}$，$Tr$表示矩阵迹，通过转换则有：

$ DFS = Tr\left( {\partial \boldsymbol{H}'(x){\boldsymbol{x}_a}/\partial {\boldsymbol{y}_{\rm obs}}} \right) $

(13)

式中，$H$′($x$)为观测算子；$\boldsymbol{x}_a$为分析场；$\boldsymbol{y}_{\rm{obs}}$是通道观测亮温。∂表示偏导标记。

在计算信息熵自由度时采用数值逼近方法，分3步进行：

(1) 计算原始的分析场$\boldsymbol{x}_a$。

$ {\boldsymbol{x}_a} = {\boldsymbol{x}_b} + \boldsymbol{K}\left( {{\boldsymbol{y}_{\rm obs}} - \boldsymbol{H}({\boldsymbol{x}_b})} \right); $

(2) 计算对通道观测亮温扰动后的$\boldsymbol{x}_{a^*}$。

$ {\boldsymbol{x}_{a * }} = {\boldsymbol{x}_b} + \boldsymbol{K}({\boldsymbol{y}_{{\rm{obs}} * }} - \boldsymbol{H}({\boldsymbol{x}_b})) $

(14)

(3)利用数值逼近则有信息熵自由度定义：

$ Tr(\boldsymbol{KH}) \approx {\left( {{\boldsymbol{y}_{{\rm{obs}}*}} - {\boldsymbol{y}_{{\rm{obs}}}}} \right)^{\rm T}}{\boldsymbol{R}^{ - {\rm{1}}}}\boldsymbol{H}({{+ \boldsymbol{x}}_{a*}} - {\boldsymbol{x}_a}) $

(15)

5 广义变分同化FY3B/IRAS试验

因为PWV是通过湿度计算得到，首先进行GPS/PWV、GDAS/PWV和FNL/PWV相关性研究，考虑到广义变分同化对高斯和非高斯均有较好的同化效果(Wang和Zhang，2014；Zhang等，2013；Liu和Qi，2005)，文中主要进行广义变分算法应用研究，采用同化FNL前/后的分析场湿度值与GDAS湿度进行相关研究作为最终同化效果验证，并进一步基于信息熵信号自由度进行IRAS资料影响诊断研究，最后给出了Huber权重函数极小化迭代过程中权重值的趋势分布图。

5.1 FY3B/IRAS仪器介绍

风云三号气象卫星B星(FY-3B)是中国第2代极轨气象卫星，于2010年11月5日发射，共携带11个探测器，文中只考虑同化红外分光计IRAS (Infrared Atmospheric Sounder)资料(陆其峰，2011)。IRAS共有26个通道，文中只同化20个红外通道(波数范围在669-2660 cm^-1)。

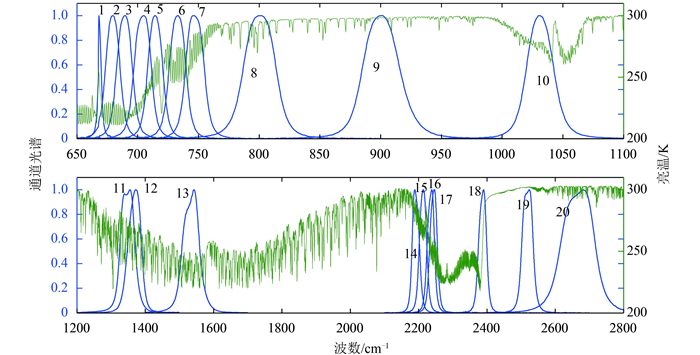
图 1分别给出了FY3B/IRAS 20个通道归一化后的光谱响应函数分布图，图中蓝色曲线表示IRAS 20个通道光谱响应函数分布，背景线(绿色)为亮温值(由国家卫星气象中心提供)(Qi等，2012)。

图 1 FY3B/IRAS 20个红外通道光谱响应函数分布(引自Qi等，2012)

Fig. 1 The response function distribution of 20 infrared channel spectrum detected by FY3B/IRAS (Cite:Qi, et al., 2012)

5.2 相关模型介绍

文中涉及的模型有2个：(1) 快速辐射传输模式RTTOV，用于通道亮温模拟(Hocking等，2010)；(2) 变分同化系统。文中变分同化系统是基于欧洲卫星数值天气预报应用研究小组开发的1维变分同化模型(杜华栋等，2008)。在原模型的基础上，进行了如下修改：

(1) 关闭其他变量(云廓线等)，只考虑温度、湿度、O₃(气候态)等廓线和2 m温度、2 m湿度、u、v风场、地表气压、地表温度。

(2) 添加广义变分同化和相应的M-估计法代码。

(3) 改写目标泛函和相应泛函梯度的程序接口。

5.3 数据准备

文中涉及的数据包括3类：(1) 作为计算PWV值的FNL和GDAS数据；(2) 作为变分同化观测资料的IRAS实际观测亮温；(3) 作为评估FNL和GDAS湿度积分可信度的GPS/MET水汽反演资料(即GPS/PWV资料)，下面分别进行介绍。

NCEP的FNL资料来源于国家气象中心数值预报中心，FNL资料每天有4个时次(分别为00时、06时、12时和18时，世界时)。对FNL资料：首先进行FNL数据解码，其次提取并进行相应的插值(水平和垂直插值)得到RTTOV所需的信息(温度、湿度等廓线以及地表信息)；GDAS (Global Data Assimilation System)资料从威斯康辛大学网站下载，GDAS每天也有4个时次，资料具体操作与FNL类似；IRAS资料来源于国家卫星气象中心数据室。GPS/PWV资料由国家大气探测中心实时下发，文中只考虑安徽省13个站(宿州，阜阳，寿县，蚌埠，金寨，桐城，合肥，马鞍山，太湖，东至，铜陵，宣城和黄山市)资料。

5.4 变分同化不同M-估计权重因子结果分析比较

气象资料变分同化是根据“最优”统计方法将各种已知信息(包括模式模拟和观测)融合在一起，以得到“最好”的用来描述给定分辨率的大气条件下的最优场。

文中观测资料考虑IRAS前20个对数值天气预报起作用的通道。在具体同化过程中，IRAS前20个通道全部进入同化系统，不考虑通道选择和组合情况。采用FNL同化前/后的背景场/分析场湿度资料与GDAS湿度资料进行相关性度量作为同化效果检验。

输入：模式空间包括FNL的温度、湿度和气压等；观测空间为IRAS观测亮温。

输出：模式空间和观测空间最优的同化结果，包括分析场的温度和湿度廓线等。

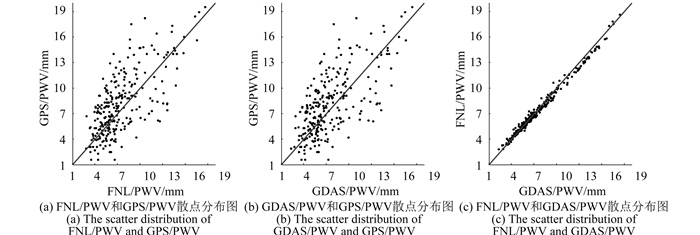
过程：使用RTTOV进行IRAS通道亮温模拟；使用控制变量$x$，观测亮温obs和模拟亮温sim计算目标泛函及相应的梯度，调用极小化算法进行迭代，直到满足迭代停止条件，完成变分同化。

图 2给出了不同背景场(FNL和GDAS)计算出的大气可降水量与GPS/PWV实际值比较结果。统计时间从2012-12-24T18:00-2013-01-13T18:00。GPS/PWV资料理论上是每个时次都有观测，但考虑到在解算过程中涉及星历等，导致安徽省13个站点GPS/PWV存在大量缺测。图 2给出了3种资料FNL/PWV、GDAS/PWV和GPS/PWV (包含站号58122、58203、58221、58306和58319资料)散点分布图。

图 2 FNL/PWV、GDAS/PWV和GPS/PWV散点分布图

Fig. 2 The scatter distribution of FNL/PWV, GDAS/PWV and GPS/PWV respectively

考虑到水汽资料时空变化较大(Zhang等，2013；Li等, 2011)，并且不同分析场是通过不同同化系统同化不同种类资料得到。图 2中，FNL/PWV和GPS/PWV相关系数为0.690；GDAS/PWV和GPS/PWV相关性系数为0.677；此过程中GPS/PWV资料没有进行相应的质量控制。GDAS/PWV和FNL/PWV相关系数为0.995，从而说明FNL和GDAS两种资料在计算PWV值时较接近，与GPS/PWV也有较好的相关性。

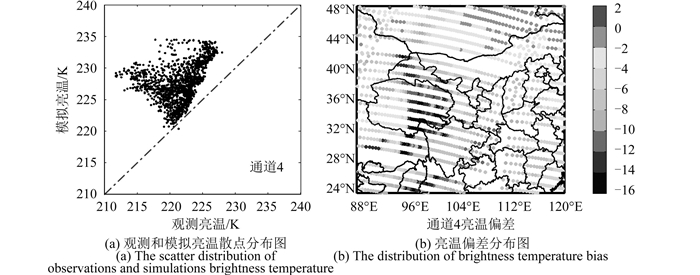
图 3给出了FY-3B/IRAS通道4在2012-12-26T 6:00观测和模拟亮温散点图(图 3(a))以及亮温偏差O-B图(图 3(b))，单位均为K。

图 3 观测和模拟以及亮温偏差散点分布图

Fig. 3 The scatter distribution of observations and simulations and the distribution of brightness temperature bias

从图 3中可以看出，IRAS亮温偏差在某些视场点FOV (Field-Of-View)存在较大的偏差。分析原因：在给出的例子中IRAS资料没有进行相应的偏差订正和云检测研究(王根，2014)。在模拟通道亮温时考虑到不同通道光谱信息不同，当FOV有云时，由通道光谱信息可知，中低层通道亮温偏差值较大，这一点参考文献(朱文刚等，2013)可以验证，进一步说明文中对通道亮温模拟效果较好。

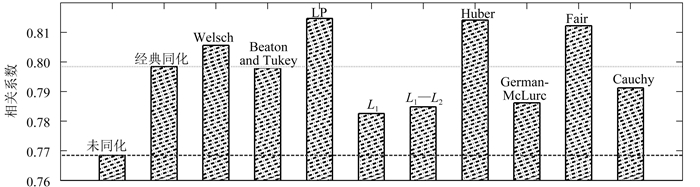
图 4给出了在不同M-估计权重因子下变分同化FY3B/IRAS资料后的FNL湿度和GDAS湿度相关系数均值分布。统计时间从2012-12-24T18:00-2013-01-13T18:00。图中“No assimilation”为未同化FY3B/IRAS资料；“Classical assimilation”为经典变分同化法(即采用$L_2$权重因子)，其他为添加相应的M-估计权重因子得到的结果。需要说明的是：此处相关系数分析考虑湿度在垂直层次上的分布，即整层廓线，而非某一特定层(如500 hPa)。

图 4 估计权重后的FNL与GDAS湿度相关系数

Fig. 4 The correlation coefficient between humilities from FNL and GDAS which are assimilated by different M-estimators weight

从图 4可以看出，$L_1$、$L_1$-$L_2$、German-McLurc和Cauchy同化后的FNL分析场湿度相关系数低于经典变分同化($L_2$)，其他权重因子同化后相关系数均高于经典变分同化得到的相关系数，Huber权重因子具有较好的效果，此过程中剔除了极小化迭代失败、不收敛的视场点FOV (张思勃和官莉，2015)，说明广义变分同化IRAS通道观测亮温可行，但要选择合适的权重因子。

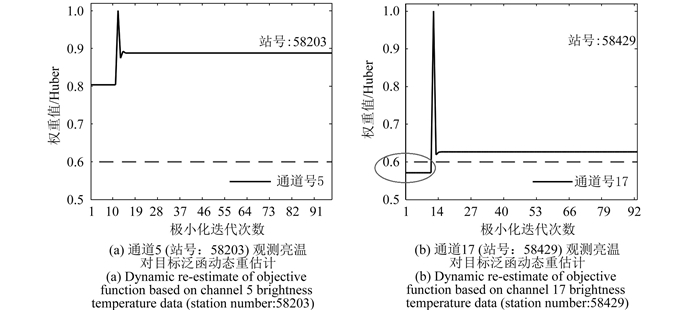
下面进一步给出了M-估计权重值动态重估计过程分析。图 5给出了2013-01-13T18:00采用Huber权重函数衡量通道观测亮温对目标泛函权重值重估计迭代过程。给出了IRAS通道5(波数为716 cm^-1)和通道17(波数为2245 cm^-1)极小化迭代情况，迭代次数分别为98和93次。执行广义变分同化当某通道观测亮温权重值小于60%时，此通道的亮温在此次迭代过程中不使用(灰线表示60%)。

图 5 观测项对目标泛函动态重估计

Fig. 5 Dynamic re-estimate of objective function based on observation data

从图 5可以看出，在初始迭代时，由于通道观测亮温偏差很大，很多通道的权重值都比较小(如通道17的亮温在前11次极小化迭代时，不参与变分同化)。在以后的每次迭代过程中对背景廓线进行有效的修正，亮温偏差较小，贡献率较大；当迭代停止时，权重值趋向于某一常数。

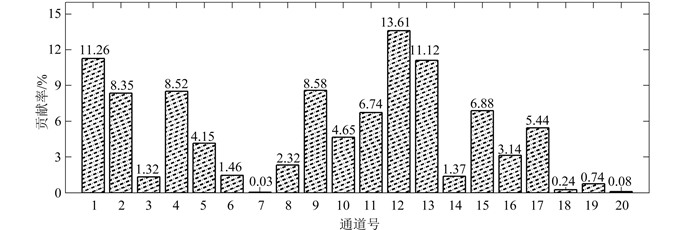
在前面研究的基础上，图 6给出了IRAS 20个通道33个时次(研究时间段为FY-3B经过安徽境内，统计时间从2012-12-25T6:00-2013-01-13T 18:00)信息熵自由度衡量的累计贡献率所占比例。

图 6 IRAS 20个通道累计贡献率比例分布

Fig. 6 The ratio distribution of cumulative contribution of 20 channels detected by IRAS

从图 6可以看出，本试验中高层通道(如通道1权重函数峰值在30 hPa，受云的影响较小)和H₂O通道(如通道12权重函数峰值在700 hPa和通道13峰值在500 hPa)对此分析过程中分析场的贡献率较大。水汽通道不仅提供温度更能提供湿度信息(Zhang等，2013；Li等，2011)，从而对分析场的影响较大。一些地表通道(如通道19权重函数值在地表)对同化后分析场影响较小，主要是文中对通道亮温进行模拟时未考虑地表发射率等因素的影响导致O-B偏差较大(Qi等，2012)，采用M-估计时对分析场的影响较小，进而导致贡献率较小。窗区通道9对分析结果具有一定的影响，后期进行深入的研究。

区别于经典变分同化需要进行严格的质量控制剔除所谓的离群值，这些数据一经剔除在之后的极小化过程中将不再使用。广义变分同化在极小化的过程中耦合了质量控制，被拒绝的通道观测亮温还可能再次被同化使用。由M-估计的特性，广义变分同化在应用中还有一些不确定性，需要根据不同的问题进行研究，要求在实际应用中尽可能综合使用经典和广义变分同化法。

6 结论

考虑到误差服从高斯分布只是一种理论上的假设，研究实际数据非高斯广义变分同化具有前瞻性和必要性。文中结合了经典变分和M-估计的优点，构建广义变分同化目标泛函及相应的梯度并进行了FY3B/IRAS通道亮温同化研究，耦合M-估计一些权重因子得到了较好的同化效果。本文主要进行算法的研究，与温度相比，湿度、水汽和大气可降水量的时空变化较大，具有较强的非高斯性，从而文中选择湿度相关性进行同化结果验证，具体结论如下：

(1) 通过变量转换积分混合比廓线进行了两种资料(FNL和GDAS)评估，得到两种资料在计算大气可降水量值时较接近，与GPS/PWV有较好相关性。

(2) 在经典变分同化目标泛函中耦合$L_1$、$L_1$-$L_2$、German-McLurc和Cauchy估计同化后的分析场湿度相关系数低于经典变分同化，其他权重因子则反之，Huber权重因子具有较好的效果。通道观测亮温权重值在广义变分同化极小化迭代过程中动态变化。广义变分同化的方法可行，但依赖于M-估计权重因子的选取。

(3) 基于信息熵自由度进行IRAS通道亮温对分析场影响诊断，得到在本文试验中高层通道和H₂O通道对分析场的贡献率较大，此结论需进一步进行大量试验并深入研究。此算法为后期卫星资料同化对湿度预报精度的提高和高光谱大气红外探测器(如AIRS)通道的选择提供一种新的思路。

文中不足之处，研究的卫星通道观测视场点FOV较少；对于FY-3B/IRAS资料没有考虑云检测和偏差订正。文中的方法为我们后期变分同化卫星水汽通道和GPS/PWV提供一种新的思路。在后续的工作中，将根据不同数据的特性给定比较符合不同问题的权重因子，并把广义变分同化的思想用于WRFDA (Weather Research and Forecasting Model Data Assimilation)进行大量实际个例的应用研究。

参考文献(References)

Anderson E. 2003. Variational quality control[EB/OL]. http://www.ecmwf.int/newsevents/training/meteor-ological_presentations/pdf/DA_Andersson3.pdf

Anderson E, Järvinen H.1999.Variational quality control. Quarterly Journal of the Royal Meteorological Society, 125 (554): 697–722 [DOI: 10.1002/qj.49712555416]

Bewley T R, Temam R, Ziane M.2000.A general framework for robust control in fluid mechanics. Physica D:Nonlinear Phenomena, 138 (3/4): 360–392[DOI: 10.1016/S0167-2789(99)00206-7]

Bhar L. 2007. Robust regression[EB/OL]. http://iasri.res.in/design/ebook/EBADAT/3-Diagnostics%20and%20Remedial%20Measures/5-ROBUST%20REGRESSION1.pdf

Dharssi I, Lorenc A C, Ingleby N B.1992.Treatment of gross errors using maximum probability theory. Quarterly Journal of the Royal Meteorological Society, 118 (507): 1017–1036[DOI: 10.1002/qj.49711850709]

Ding J C. GPS Meteorology and Application. Beijing: Meteorological Press 2009: 54-55. ( 丁金才. 2009. GPS气象学及其应用. 北京: 气象出版社 : 54 -55. )

Du H D, Huang S X, Shi H Q.2008.Method and experiment of channel selection for high spectral resolution data. Acta Physica Sinica, 57 (12): 7685–7692 ( 杜华栋, 黄思训, 石汉青. 2008. 高光谱分辨率遥感资料通道最优选择方法及试验. 物理学报, 57 (12): 7685–7692)[DOI: 10.3321/j.issn:1000-3290.2008.12.045]

Hampel F R.1971.A general qualitative definition of robustness. The Annals of Mathematical Statistics, 42 (6): 1887–1896[DOI: 10.1214/aoms/1177693054]

Hampel F R.1974.The influence curve and its role in robust estimation. Journal of the American Statistical Association, 69 (346): 383–393[DOI: 10.1080/01621459.1974.10482962]

Hao M, Zhang H, Tao S W, Gong J D.2013.Application of variational quality control to regional GRAPES-3DVAR. Plateau Meteorology, 32 (1): 122–132 ( 郝民, 张华, 陶士伟, 龚建东. 2013. 变分质量控制在区域GRAPES-3DVAR中的应用研究. 高原气象, 32 (1): 122–132)[DOI: 10.7522/j.issn.1000-0534.2012.00013]

Hocking J, Rayer P, Saunders R, Matricardi M, Geer A and Brunel P. 2010. RTTOV v10 Users Guide. NWPSAF-MO-UD-023, , Darmstadt, Germany:EUMETSAT

Huber P J.1964.Robust estimation of a location parameter. The Annals of Mathematical Statistics, 35 (1): 73–101[DOI: 10.1214/aoms/1177703732]

Huber P J. 1967. The behavior of maximum likelihood estimates under nonstandard conditions//Proceedings of the 5th Berkeley Symp osium on Mathematical Statistics and Probability, Volume 1:Statistics. Berkeley, CA:University of California Press:221-233

Huber P J. Robust Statistics. New York: John Wiley and Sons, Inc 1981.

Ingleby N B, Lorenc A C.1993.Bayesian quality control using multivariate normal distributions. Quarterly Journal of the Royal Meteorological Society, 119 (513): 1195–1225[DOI: 10.1002/qj.49711951316]

Li H, Liu J J, Fertig E, Kalnay E, Kostelich E, Szunyogh I.2011.Improved analyses and forecasts with AIRS temperature retrievals using the local ensemble transdorm kalman filter. Journal of Tropical Meteorology, 17 (1): 43–49

Liu Z Q and Qi C L. 2005. Robust variational inversion:with simulated ATOVS radiances[EB/OL]. http://cimss.ssec.wisc.edu/itwg/itsc/itsc14/proceedings/

Lsaksen L. 2010. Variational quality control[EB/OL]. http://www.ecmwf.int/newsevents/training/meteorological_presentations/pdf/DA/VarQC.pdf

Lu Q F.2011.Initial evaluation and assimilation of FY-3A atmospheric sounding data in the ECMWF System. Science China Earth Sciences, 54 (10): 1453[DOI: 10.1007/s11430-011-4243-9] ( 陆其峰. 2011. 风云三号A星大气探测资料数据在欧洲中期天气预报中心的初步评价与同化研究. 中国科学:地球科学, 54 (10): 1453)[DOI: 10.1007/s11430-011-4243-9]

Qi C L, Chen Y, Liu H, Wu C Q, Yin D K.2012.Calibration and validation of the InfraRed Atmospheric Sounder onboard the FY3B satellite. IEEE Transactions on Geoscience and Remote Sensing, 50 (12): 4903–4914[DOI: 10.1109/TGRS.2012.2204268]

Tachim Medjo T.2002.Iterative methods for a class of robust control problems in fluid mechanics. SIAM Journal on Numerical Analysis, 39 (5): 1625–1647[DOI: 10.1137/S0036142900381679]

Tukey J W. 1960. A survey of sampling from contaminated distributions//Olkin I. Contributions to Probability and Statistics. Stanford, CA:Stanford University Press

Wang G. 2014. FY3B/IRAS Data Bias Correction, Cloud Detection, Quality Control and Assimilation Test.Nanjing:Nanjing University of Information Science and Technology (NUIST) (王根. 2014. FY3B/IRAS资料偏差订正、云检测、质量控制和同化测试.南京:南京信息工程大学)

Wang G, Zhang J W.2014.Generalised variational assimilation of cloud-affected brightness temperature using simulated hyper-spectral atmospheric infrared sounder data. Advances in Space Research, 54 (1): 49–58[DOI: 10.1016/j.asr.2014.03.009]

Zhang H. 2004. Study on ATOVS Radiation Data Directly Assimilation Method and Application.Lanzhou:Lanzhou University, 2004 (张华. 2004. ATOVS辐射率资料的直接同化方法及应用研究.兰州:兰州大学)

Zhang H, Xue J S, Zhuang S Y, Zhu G F, Zhu Z S.2004.Idea experiments of GRAPES three-dimensional variational data assimilation system. Acta Meteorologica Sinica, 62 (1): 31–41 ( 张华, 薛纪善, 庄世宇, 朱国富, 朱宗申. 2004. GRAPES三维变分同化系统的理想试验. 气象学报, 62 (1): 31–41)[DOI: 10.3321/j.issn:0577-6619.2004.01.004]

Zhang J W, Wang G, Yang Y, Zhong X, Wang J.2013.Study on hyper-spectral atmospheric infrared sounder assimilation. International Journal of Hybrid Information Technology, 6 (1): 123–128

Zhang S B and Guan L. 2015. Effect of AMSR-E data interference on the retrieval of land surface parameters. China Environmental Science, 35(1):260-268 (张思勃, 官莉. 2015. AMSR-E观测资料干扰对反演地表参数的影响.中国环境科学, 35(1):260-268)

Zhu J.1995.Four-dimensional data quality control:variational method. Acta Meteorologica Sinica, 53 (4): 480–487 ( 朱江. 1995. 观测资料的四维质量控制:变分法. 气象学报, 53 (4): 480–487)[DOI: 10.11676/qxxb1995.054]

Zhu W G, Li G, Zhang H, Jin D Z, Wang G, Zhong Y M.2013.Study on application technique of cloud detection and clear channels hyperspectral atmospheric infrared detector AIRS data. Meteorological Monthly, 39 (5): 633–644 ( 朱文刚, 李刚, 张华, 金大智, 王根, 钟亦鸣. 2013. 高光谱大气红外探测器AIRS资料云检测及晴空通道应用技术初步研究. 气象, 39 (5): 633–644)[DOI: 10.7519/j.issn.1000-0526.2013.05.012]