出版日期: 2017-01-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176003
2017 | Volumn21 | Number 1

国产卫星

风云静止卫星地表温度产品空值数据稳健修复

刘紫涵¹ , 吴鹏海¹ , 吴艳兰¹ , 沈焕锋² , 曾超³

1. 安徽大学资源与环境工程学院, 安徽省地理信息工程中心, 合肥 230601

2. 武汉大学资源与环境科学学院, 武汉 430079

3. 清华大学水沙科学与水利水电工程国家重点实验室, 北京 100084

收稿日期: 2016-01-13; 修改日期: 2016-08-30; 优先数字出版日期: 2017-01-25

基金项目: 国家自然科学基金（编号：41501376）；安徽省自然科学基金面上项目（编号：1608085MD83，1308085MD52）；地理国情监测国家测绘地理信息局重点实验室开放基金（编号：2014NGCM05）；安徽大学研究生学术创新研究强化项目（编号：yqh100254）

第一作者简介: 刘紫涵(1990-), 男, 硕士研究生, 研究方向为遥感图像处理与应用。E-mail:rs312lzh@yeah.net

通讯作者简介: 吴鹏海(1987-), 男, 讲师, 研究方向为遥感信息处理与应用的研究。E-mail:wuph@ahu.edu.cn

中图分类号: TP79

文献标识码: A

文章编号: 1007-4619(2017)01-0040-12

摘要

静止卫星地表温度数据是研究昼夜气候和环境变化的重要参数。但现有发布的静止卫星地表温度数据由于受到云等大气因素的影响，往往出现数值缺失现象。针对该问题，提出基于昼夜变化模型的风云静止卫星地表温度空值数据的稳健修复方法。由多项式、傅里叶函数和高斯函数构建新的昼夜变化模型，并利用Levenberg-Marquardt算法进行模型参数的求解与优化，进而实现空值修复。以风云2号F星数据（FY-2F）为例，模拟不同类型的像元缺失情况进行修复，并将不同模型修复结果与真实温度值比较，同时也对真实数据进行了测试。结果表明：本文提出的修复方法能有效对温度空值数据修复，且优于传统方法。

关键词

地表温度数据 , 静止卫星 , 温度日变化模型 , 稳健回归 , 风云2号F星(FY-2F)

Robust reconstruction of missing data in Feng Yun geostationary satellite land surface temperature products

LIU Zihan¹ , WU Penghai¹ , WU Yanlan¹ , SHEN Huanfeng² , ZENG Chao³

1.School of Resources and Environment Engineering, Anhui University, Hefei 230601, China

2.School of Resource and Environmental Sciences, Wuhan University, Wuhan 430079, China

3.State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China

Abstract

Land Surface Temperature (LST) derived from geostationary satellites (GEO-LST) is one of the key parameters in analyzing diurnal climate and environment changes. Compared with polar-orbiting satellite data, the LST of geostationary satellites has become increasingly attractive because of its high temporal resolution. GEO-LST has been widely applied in meteorological, climatological, and hydrological studies. However, the existing GEO-LST products can suffer from cloud cover, cloud contamination, and atmospheric disturbance, resulting in missing data. The objective of this study is to develop a new method for reconstructing Feng Yun geostationary satellite (FY-2F) LSTs based on Diurnal Temperature Cycle (DTC) and robust regression. The hourly LSTs from FY-2F with 5 km spatial resolution are adopted for this study, and different types of missing pixels are simulated and reconstructed based on a new model. This model is composed of polynomial, Fourier, and Gaussian functions (PFG), and a robust regression called Levenberg-Marquardt (LM) algorithm is adopted for solving and optimizing the modelparameters. A performance test is conducted by comparing the PFG model based on the LM algorithm with the other two methods implemented on FY-2F data, namely, a method based on Least Square (LS) algorithm modeling of the previous model (van den Bergh. F VAN2006) and a method based on LS algorithm modeling of the PFG. Moreover, the new method is also tested for real LST products (with missing data). By comparing the reconstructed results of different methods (LM-PFG, LS-PFG, and LS-VAN2006) with the real LST values, the simulated experiment indicates that the LM-PFG method obtains the lowest root mean square compared with the other two methods. The stability analysis of these methods shows that LM-PFG is the least sensitive to missing samples, which validates that LM-PFG is more stable than LS-PFG and LS-VAN2006. Simultaneously, experimental results show that LM-PFG can also reconstruct the missing values with high accuracy and better than the other methods. In this study, an approach for reconstructing GEO-LSTs based on DTC and robust regression is proposed. The method is evaluated using simulated and real FY-2F LST products and can obtain high scores on quantitative evaluation and visual connectivity. Further work can be conducted to expand this method to other potential GEO-LSTs, such as Meteosat Second Generation Spinning Enhanced Visible and Infrared Imager LSTs or Geostationary Operational Environmental Satellite Imager LSTs. Similar to previous studies, the reconstructed LST values of the proposed method are estimated under cloud-free conditions. LSTs under cloudy conditions should be investigated in future studies.

Key words

land surface temperature , geostationary satellite , diurnal temperature cycle , robust regression , FY-2F

1 引言

地表温度LST (Land Surface Temperature)是研究区域和全球地表过程中的关键因子，在地-气交互及能量交换中起重要作用(Li等，2013；Zhan等，2013；宋挺等，2015)。基于热红外遥感反演的地表温度数据已广泛用于水文学、气候学和生态学等方面的研究。与极轨卫星相比，具有高时间分辨率的静止卫星地表温度数据在研究昼夜气候和环境变化方面具有明显的优势(Keramitsoglou等，2013；Wu等，2015)。然而，由于卫星传感器受大气密度、云层变化、气溶胶等影响较大，现有发布的静止卫星地表温度产品(如风云卫星)往往存在空值现象(欧阳晓莹和贾立，2011)，导致空间不连续。因此，如何修复地表温度空值数据是当前热红外遥感应用等面临的重要问题(周义等，2014)。

针对遥感LST空间不连续问题，研究比较多的是极轨卫星温度产品，主要的修复方法是空间内插，但该类方法由于仅利用了空间信息，精度往往不高(刘梅，2012)。为了提高修复精度，有学者引入高程等相关因子提出协克里金等修复方法(Ke等，2013；蔡迪花等，2009)。而对于静止卫星温度产品的空值数据，主要利用温度昼夜变化模型DTC (Diurnal Temperature Cycle)进行空值修复，修复结果取决于DTC模型精度。早期的模型主要由两个函数构成：正弦函数和指数函数(Parton和Logan，1981)、余弦函数和指数函数(Göttsche和Olesen，2001，2009；Schädlich等，2001)，后来发展到三段函数，如van den Bergh等人(2006)将白天的温度变化过程分成两个部分，提出由两个余弦函数及一个指数函数组成的DTC模型，并利用该模型对静止卫星空值数据进行有效修复(van den Bergh等，2006)。近年来，关于DTC模型精度的比较研究也备受关注。如Duan等人在晴空条件下对六种DTC模型的模拟效果进行比较和评估，结果表明“VAN2006”、“GOT2009”和“JNG2006”模型具有普遍适用性(Duan等，2012，2014)。此外，其他修复方法，如再生核希尔伯特空间等统计分析方法也取得较好的效果(Udahemuka等，2007；Coops等，2007)。总的来说，虽然在DTC建模方面已取得了很大的进展(Huang等，2014)，但Duan等(2012)同时指出地表环境对传统的DTC模型的拟合能力有较大影响，DTC模型的精度和稳健性不够；此外，DTC模型在增加自由参量的条件下，拟合效果会相应提高，而增加参数势必会导致修复效率下降，而且最优参数的选取目前依然是DTC模型的重要研究内容(Udahemuka等，2007)。因此，本文在前人研究的基础上，提出一种面向风云静止卫星地表温度产品空值数据稳健修复方法，一方面通过构建不同的分段函数来提高DTC模型精度，另一方面利用列文伯格-马夸尔特法，LM (Levenberg-Marquardt)稳健拟合技术优化模型参数(Finsterle和Kowalsky，2011；Wilamowski和Hao，2010；Gavin，2016)，进而提高模型稳健性和修复效率，实现空值像元的高精度、高效率修复。并在模拟实验和真实实验下测试算法的性能。

2 FY-2F地表温度数据产品

风云2号F星(FY-2F)是风云二号(03批)卫星中的第一颗卫星，也是中国第4颗业务静止气象卫星，于2012年1月发射成功，运行于东经123.5°、赤道上空。FY-2F主要有效载荷为红外和可见光自转扫描辐射器VISSR，包含1个可见光通道和4个红外通道。近年来随着风云卫星数据使用推广，其反演的各类遥感定量产品需求也不断提高。目前，FY-2F卫星可提供包括地表温度数据等在内18种产品，一景地表温度影像数据可以实现获取覆盖地球表面约三分之一的全圆盘图像(韦飞等，2013)。本文试验数据采用风云静止卫星标称格式LST产品(FY-2F LST)，可从风云卫星遥感数据服务网免费下载(http://www.nsmc.cma.gov.cn/[2016-01-13])，该数据星下点空间分辨率为5 km，时间分辨率为1 h，一天可以获取24景。

3 模型建立与优化

3.1 VAN2006昼夜变化模型

van den Bergh等人(2016)在前人提出的DTC模型基础上，通过对余弦函数半周期宽度的改变将白天的地表温度变化分为两段，建立三段函数的DTC模型，并成功应用于静止卫星空值数据的修复。为方便描述，本文命名该模型为“VAN2006”，表达式如下：

$\begin{aligned} {{T_{{\rm{day1}}}}\left( t \right) = {T_0} + {T_{{\rm{a}}}}{\rm cos}\left( {\frac{{\rm{\pi }} }{{{\omega _1}}}\left( {t - {t_{\rm{m}}}} \right)} \right),t} { \leqslant {t_{\rm{m}}}}\\ {{T_{{\rm{day2}}}}\left( t \right) = {T_0} + {T_{{\rm{a}}}}{\rm cos}\left( {\frac{{\rm{\pi }} }{{{\omega _2}}}\left( {t - {t_{\rm{m}}}} \right)} \right),{t_{\rm{m}}} \leqslant t} { \leqslant {t_{\rm{s}}}}\\ {{T_{{\rm{night}}}}\left( t \right) = {T_0} + {T_{{\rm{a}}}}{\rm cos}\left( {\frac{{\rm{\pi }} }{{{\omega _2}}}\left( {{t_{\rm{s}}} - {t_{\rm{m}}}} \right)} \right){{\rm{e}}^{\frac{{ - \left( {t - {t_{\rm{s}}}} \right)}}{d}}},t \geqslant {t_{\rm{s}}}} \end{aligned}$

(1)

式中，左边表示3个不同时间段的温度值，右边$T_0$、$T_{\rm a}$、${t_{\rm m}}$和${t_{\rm s}}$分别表示为日出时分地表残余温度、温度变化幅度、最大温度对应的时刻和温度自由衰减的起始时刻，t表示时间。$d$为衰减系数，可以由模型在时刻${t_s}$所满足的连续性解出，求解结果如式(2)所示。参数${\omega _1}$和${\omega _2}$表示余弦函数的半周期宽度，由已知地表温度数据拟合而得到。因此，模型VAN2006所表示的地表温度变化曲线可以由6个自由参量共同描述，即$T_0$，$T_{\rm a}$，${t_{\rm m}}$，${t_{\rm s}}$，${\omega _1}$及${\omega _2}$，具体参数含义见表 1。Duan等人(2012)在晴空条件下对6种DTC模型的模拟效果进行比较和评估，结果表明VAN2006模型具有普遍适用性，但该模型是假定晴空条件下的插值估计，且具有6个自由参量，因此要求像元一天24小时的时间序列中至少存在6个非空点，才足以建立模型。

$d = \frac{{{\omega _2}}}{{\rm{\pi }} }{\tan ^{ - 1}}\left({\frac{{\rm{\pi }} }{{{\omega _2}}}\left({{t_{\rm s}} - {t_{\rm m}}} \right)} \right)$

(2)

表 1 参数的意义
Table 1 The meaning of parameters

下载CSV

参数	意义
T₀/℃	近似日出时分地表残余温度
T_α/℃	温度变化幅度
t_m	最大温度对应的时刻
t_s	温度自由衰减的起始时刻
ω₁、ω₂	余弦函数的半周期宽度
d	衰减系数

3.2 PFG模型

实现静止卫星地表温度产品空间连续的关键在于建立精确的地表温度昼夜变化曲线拟合函数。传统的地表温度昼夜变化模型尽管物理意义明确，但稳健性和精度不够。本文在研究不同的温度昼夜变化模型基础上，根据地表温度日变化特点，并结合温度最高点和衰减时刻构建地表温度昼夜变化分段函数，提出利用多项式(Polynomial)、傅里叶函数(Fourier)和高斯函数(Gaussian)建立面向空值修复的分段函数模型(PFG)，其中PFG命名原则为3种函数的英文首字母组合，PFG函数物理量之间的近似函数关系如式(3)所示。

${P_n}(x) = \left\{ \begin{array}{l} \!\!\! \sum\limits_{k = 0}^M {{a_k}{x^k} \;\; k = 0,1, \cdots, M \;\;\; \;\;\;\;\;\; \; \; {t_0} \leqslant x \leqslant {t_{\rm{m}}}} \\ \!\!\! {a_0} + \sum\limits_{k = 1}^n {({a_k}{\rm cos}(k\omega x) + } \\ \!\!\! {b_k}\sin (k\omega x)) \;\; k = 1,2, \cdots, n \;\;\; \; \;\; {t_{\rm{m}}} \leqslant x \leqslant {t_{\rm s}}\\ \!\!\! \sum\limits_{k = 1}^n {{a_k} \cdot {{\rm e}^{ - {{\left( {\frac{{x - {b_k}}}{{{c_k}}}} \right)}^2}}}} \;\; k = 1,2, \cdots, n \;\; {t_{\rm s}} \leqslant x \leqslant {t_0} + 24 \end{array} \right.$

(3)

式中，${P_n}\left( x \right)$为所求的昼夜变化模型，t₀为日出时刻，t_m为最大温度对应的时刻，t_s为温度自由衰减的起始时刻，$\omega $为正余弦函数的半周期宽度，${a_0},{a_k},{b_k},{c_k}$为拟合系数。与简单的正余弦函数相比，式(3)傅里叶函数中${a_k}$和${b_k}$也存在解析的三角函数表达，可以计算针对任意频率点上的频谱值，具有明显的拟合优势(景月岭等，2008)。参数$m,n$大小随静止卫星传感器类型与分段函数选择的不同而变化，经大量实验验证，设定面向风云数据的PFG模型中参数$M = 6$，$n = 2$，并且${t_0} = {t_{\mathop{\rm m}\nolimits} } - \omega /2$，${t_{\rm s}} = {t_{\mathop{\rm m}\nolimits} } + \omega /2$。

正余弦函数的半周期宽度可以由式(4)求解得出(Elagib等，1999)。

$\omega = \frac{2}{{15}}{\cos ^{ - 1}}(\frac{{\cos 85}}{{\cos \varphi \cos \sigma }} - {\rm tan}\varphi \cdot \tan \sigma )$

(4)

式中，参数$\varphi $表示研究点的纬度数据，参数$\sigma $是黄赤交角，可以由关于位于该年天数的方程计算而得，如式(5)所示，$DOY$表示数据源所处该年的天数(Elagib等，1999)。

$\sigma = 23.45\sin \left( {\frac{{360}}{{365}}\left( {284 + DOY} \right)} \right)$

(5)

首先PFG函数模型仍以指数型函数(Gaussian)模拟地表温度夜间的变化趋势，其次由于Schädlich等(2001)认为地表温度于上午增长、下午下降的变化趋势不同。对于白天地表温度下降过程，热反应包括来自太阳的辐射以及地表的反射等，由于热传导过程比较复杂，仅用一个正弦函数或余弦函数难以表达该过程，需要用多个正弦函数和余弦函数的叠加表示，因此提出利用多个正弦函数或余弦函数叠加表示的傅里叶函数模拟下降过程。傅里叶谱通常假定信号为平稳或分段平稳，如果以傅里叶谱定义白天全局会导致频率能量谱分布的失真(李静和罗奇峰，2013)，考虑到传统傅里叶谱的缺陷，不宜使用傅里叶函数模拟白天的整个过程。对于白天温度增长主要来自太阳的辐射，且增长趋势类似线性增长，根据导热理论及有效温度数据大量实验验证，提出用多项式拟合地表温度变化曲线，一方面简化算法的复杂性，另一方面有研究指出对于正弦特性曲线多项式拟合能得到较高的精度，获得理想的拟合曲线(司少玲和关永，2006)，但拟合次数并非越高越好，大量实验验证6次拟合曲线能较好地对原始温度曲线进行近似。

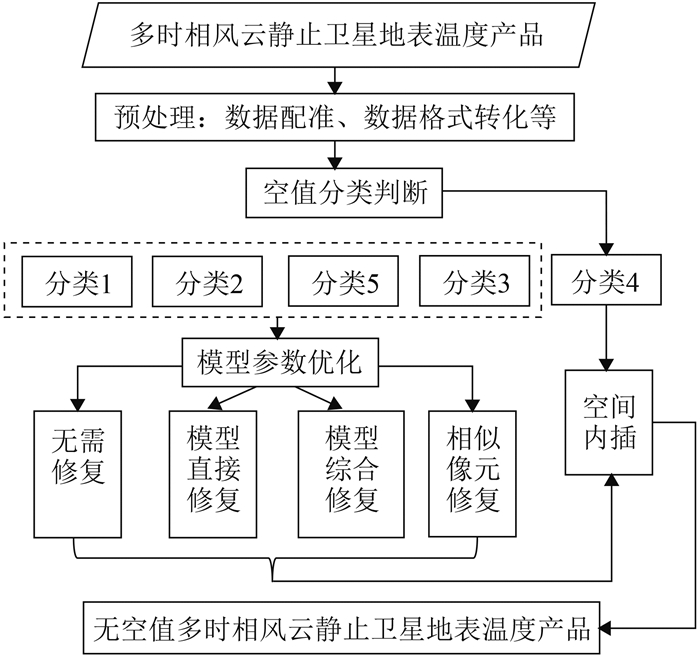
本文所采用的技术路线如图 1所示。

图 1 风云静止卫星地表温度产品空值修复技术路线图

Fig. 1 The flowchart followed to reconstruct invalid FY-2F LSTs

3.3 参与拟合数据点的确定

在PFG模型下，参与拟合的数据点影响着模型参数求解精度，进而影响着空值修复效果；因此，参与拟合数据点的确定显得尤为重要。拟合点如何确定与所采用静止卫星数据有关，由于FY-2F卫星时间分辨率为1小时，一天可以获取24景数据。针对某一像元，其所在24个时相的空值数介于0-24。

此外，由于云层等天气条件的变化，FY-2F LST影像中空值位置具有随机性；且鉴于本文提出的模型分为3个时间段，对于当前待修复像元所在时间序列的每一时间段内空值像元数量不等，且有可能某个时间段内全为空值等情况，加大了模型参数的求解复杂性。因此本文假定当前待修复像元在白天温度上升，温度下降，夜间至次日日出前这3个时间段内的空值数量分别为s₁，s₂，s₃，按照如下几类情况确定参与拟合的数据，具体分类如下：

(1)若时间序列所有像元没有空值，即满足式(6)，无需进行修复。

${s_1} = {s_2} = {s_3} = 0$

(6)

(2)针对FY-2F LST，在大量实验基础上权衡模型拟合与过拟合影响之后，设定在白天温度上升，温度下降，夜间至次日日出前这3个时间段内模型参数都为6个，即方程(3)模型中的参数$M = 6$，$n = 2$。由方程组求解原理可知，求解6个参数，至少需要6个有效点，因此由于每个时间段含有的非空值个数不能少于模型参数，满足如式(7)所示条件，才足以建立模型，对于此种情况则直接利用模型进行空值修复。式(7)中${t_0}$为日出时刻，(${t_{{\rm m} }}+ 1$)为最大温度的下一半点时刻，(${t_{{\rm s}}} + 1 $)为温度自由衰减时的下一半点时刻，(${t_{{\rm s}}} - 1$)为温度自由衰减时的上一半点时刻。以白天温度上升时间段为例，$(({t_{{\rm m}}} + 1) - {t_0})$为区间长度，${s_1}$为空值点个数，$(({t_{{\rm m}}} + 1) - {t_0}) - {s_1}$是这一时间段的有效点(非空点)个数。

$\left\{ \begin{array}{l} \left| {(({t_{\rm m}} + 1) - {t_0}) - {s_1}} \right| \geqslant 6\\ \left| {(({t_{\rm s}}+ 1) - {t_{\rm m}}) - {s_2}} \right| \geqslant 6\\ \left| {({t_0} + 24 - {t_{{\rm s} - 1}}) - {s_3}} \right| \geqslant 6 \end{array} \right.$

(7)

(3)若整个时间序列只有少数的非空值，无论是本文提出的模型，还是VAN2006模型，待求参数至少为6个，鉴于此种情况，由于FY-2F卫星LST产品一天有24景数据，所以当时间序列中空值数大于18时，3个时间段中的任何一种模型都无法建立，因此本文提出相似性像元的原理：对待修复空值像元建立3×3邻域窗口，邻域内每个像元进行相似像元筛选的计算，直至使式(8)等式左侧参数ε最小作为相似像元，待相似像元确定后，利用相似像元构建时序上DTC模型，将待修复像元的空值时刻带入DTC模型，求解空值时刻对应的温度，待修复像元24时刻中非空值继续保留，综合起来作为修复结果。其中空值分布满足式(9)。

$\varepsilon = \sqrt {\frac{{\sum\limits_i^M {{{({Y_i} - {Z_i})}^2}} }}{M}} $

(8)

式中，${Z_i}$为待修复像元一天24时刻中第$i$个非空值，${Y_i}$为对应领域像元一天24时刻中第$i$个非空值，M为参与计算的非空值数量。

$18 < {s_1} + {s_2} + {s_3} < 24$

(9)

(4)若整个时间序列都是空值，如式(10)所示，此种极端情况，建议在能够利用DTC模型修复的空值处理之后，利用邻域空间内插技术进行修复。

${s_1} + {s_2} + {s_3} = 24$

(10)

(5)整个时间序列空值不满足上述的任何一种分类，利用模型综合技术，即本文所提出的模型与VAN2006的组合进行空值修复研究。

3.4 参数求解与优化

当确定参与拟合的数据之后，则进行模型参数的求解与优化，常规的最小二乘法，LS (Least Square)常遇到模型求解停止或参数为负的问题，而非线性最小二乘法如高斯-牛顿最小二乘法对迭代初始值的选取要求很严格，若初始值选择不当，求解常陷入局部极值，或者迭代不收敛(Madsen等，2004)，最为关键的是最小二乘法法并不考虑系数矩阵中的噪声扰动，稳健性不够(张鸿燕和耿征，2009)。而本文使用的LM算法是解决非线性拟合问题的有效方法，也是目前非线性方程求解领域研究和使用最频繁的方法之一(Finsterle和Kowalsky，2011)。该方法利用迭代方法计算残差平方和，并以此作为模型是否达到最佳拟合效果的评估标准，当残差平方和达到最小值时，迭代过程结束，得出的即为拟合公式的最优结果。其目标函数为：

$ \begin{aligned} & {\chi ^2}({a_0},{a_1}{\rm{,}} \cdots ,{a_k}) = \frac{1}{{N - Nc}} \\ & \sum\limits_i {\sum\limits_j^{} {{\varpi _{ji}}{{\left[ {{P_n}({x_i},{a_0},{a_1}{\rm{,}} \cdots ,{a_k}) - {y_i}} \right]}^2}} } \end{aligned} $

(11)

式中，χ²为残差平方和；N为总实验点数；Nc为参数个数，$({a_0},{a_1},\cdots ,{a_k})$为待求参数。LM算法实际上是梯度下降法和高斯-牛顿法(Gauss-Newton)的结合(Gavin，2016)。该算法实现过程中引入一个非负调节参数$\lambda $，从而获得高阶的训练速度，如果$\lambda = 0$就变成高斯-牛顿法；如果$\lambda $很大，即成为负梯度下降法。LM算法中调节参数$\lambda $选取和修正方法具体见参考文献(Fan，2003；Ma和Jiang，2007)，算法收敛准侧和误差界设定参照文献(杨柳和陈艳萍，2005，2008)。这种方法可快速、有效地对离散试验数据进行拟合，提高地表温度变化曲线数据分析的精度和工作效率。

4 实验与分析

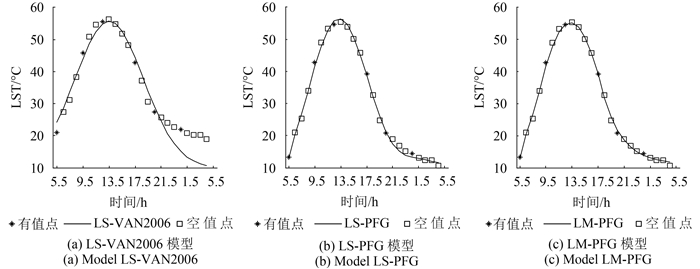
得益于“VAN2006”模型的分段思想，本文提出利用多项式、傅里叶函数和高斯函数建立面向空值修复的分段函数模型(PFG)，得到物理量之间的近似函数关系，并在此基础上引入LM算法进行参数的优化，并与传统最小二乘法(LS)下的VAN2006和PFG进行比较。为了便于区分，以上3个模型在本文分别命名为：LM-PFG、LS-PFG和LS-VAN2006。此外对于特定情况VAN2006与LS-PFG，VAN2006与LM-PFG的综合运用分别命名为V-LS-PFG和V-LM-PFG。

4.1 模拟实验1与分析

在模拟实验1中，本文下载2013年6月13日的24景FY-2F LST数据，并在每一景影像中截取大小为50×50像素的同一区域作为实验数据。由于静止卫星地表温度产品空间分辨率较低(Duan等，2014)，每一个像素单元的地表覆盖类型不同，致使热反应情况不相同，因而描述各个像元的参数也各有差异，所以本文选取7个位置不同的研究点。对这7个位置点所在时序的24个温度值按上述空值分类进行人为随机剔除，以模拟空值像元，再根据空值情况确定修复方法，并进行模型参数求解与优化。待模型参数求解后，将模拟的空值所在时间点带入模型求解，得到修复结果。为了定量评价不同模型在模拟实验中的性能，本文采用模拟值与真实值之间建立的RMSE作为模型优劣的判断标准，如式(12)所示：

${\rm RMSE} = \sqrt {\frac{{\sum\limits_i^m {{{({{\rm O}_i} - {F_n}({x_i};A))}^2}} }}{m}} $

(12)

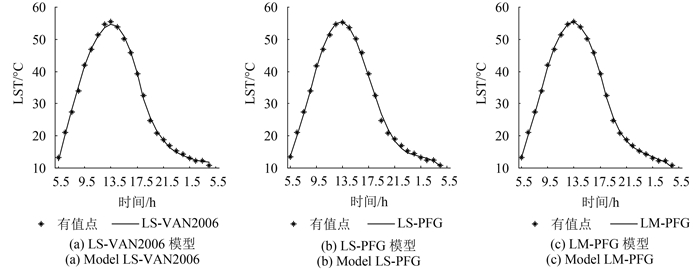
式中，${{\rm O}_i}$为真实值，${F_n}({x_i};A)$为分类对应方法所求值，${x_i}$为自变量，$A$为模型参数向量。

为比较无空值情况下(符合分类1)的各模型精度，表 2列出7个不同位置点时间序列建立的DTC模型与真实值间的RMSE信息。以RMSE作为模型效果判断标准，从表 2可知，LS-VAN2006方法在地点1和地点6的RMSE分别为0.2311和0.2707，在其他5个地点的RMSE更大些；LS-PFG方法在所有位置点的RMSE都比LS-VAN2006方法小，且在0.2-0.3；而本文提出的LM-PFG在7个位置点的RMSE都小于0.2，甚至地点1的RMSE低到0.0624。因此，在没有空值情况下，本文提出的LM-PFG优于LS-PFG，更强于LS-VAN2006，图 2示出地点5在时间序列无空值条件下3种模型的拟合效果。

表 2 FY-2F LST数据DTC模型RMSE (分类1)
Table 2 The RMSE of DTC model for FY-2F imagery (Classification 1)

下载CSV

	地点1	地点2	地点3	地点4	地点5	地点6	地点7
LS-VAN2006	0.2311	0.4374	0.4617	0.3317	0.4351	0.2707	0.4066
LS-PFG	0.2265	0.2443	0.2722	0.2371	0.2076	0.2567	0.2809
LM-PFG	0.0624	0.1764	0.1936	0.1483	0.1517	0.1393	0.1446

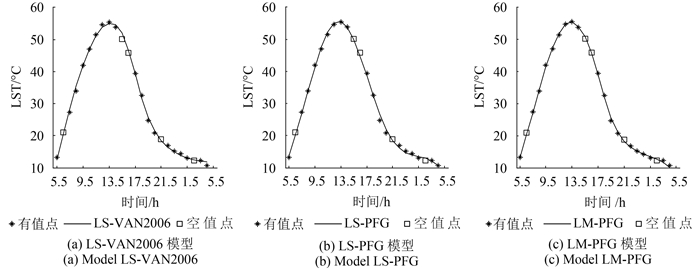
图 2 3种模型拟合效果(分类1)，RMSE=(0.4351，0.2076，0.1517)

Fig. 2 The effects of three models (classification 1), RMSE=(0.4351, 0.2076, 0.1517)

表 3列出7个不同位置点时间序列中含有5个随机空值点建立的DTC模型与真实值间的RMSE信息，空值分布情况符合分类2。表 3与表 2相比可知，3种模型在7个位置点对应的RMSE都在增大，说明由于空值的出现，模型的拟合效果降低。从地点5的3种模型拟合效果图(图 3)可知：相比其他两模型，LM-PFG在整个时间序列尤其夜间时段都达到很好的模拟效果，说明该模型稳健性较强。

表 3 FY-2F LST数据DTC模型RMSE (分类2)
Table 3 The RMSE of DTC model for FY-2F imagery (Classification 2)

下载CSV

	地点1	地点2	地点3	地点4	地点5	地点6	地点7
LS-VAN2006	0.4954	0.5080	0.6778	0.4953	0.5023	0.5663	0.5806
LS-PFG	0.2573	0.3019	0.4985	0.4810	0.3989	0.4381	0.3717
LM-PFG	0.1797	0.2520	0.3082	0.3076	0.2225	0.2960	0.2044

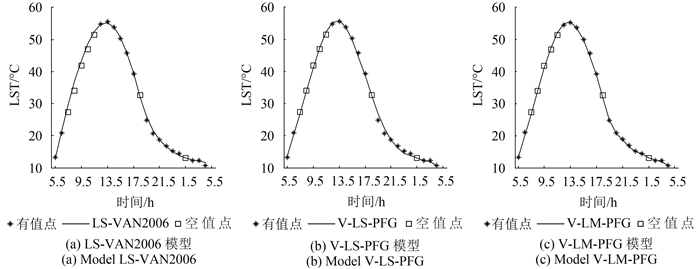
图 3 3种模型拟合效果(分类2)，RMSE=(0.5023，0.3989，0.2225)

Fig. 3 The effects of three models (classification 2), RMSE=(0.5023, 0.3989, 0.2225)

表 4列出7个不同位置点时间序列中含有7个随机空值点建立的DTC模型与真实值间的RMSE信息，空值分布情况符合分类5。由于白天温度上升阶段空值点较多且连续，导致该时段本文提出的模型无法建立，只能利用LS-VAN2006模型拟合求解，而在另外两个时段仍采用本文提出的模型，得到V-LM-PFG和V-LS-PFG的综合模型。从图 4和表 4可以看出：当空值点多且连续，导致难以建立模型时，V-LM-PFG综合模型同样优于其他两种模型。

表 4 FY-2F LST数据DTC模型RMSE (分类5)
Table 4 The RMSE of DTC model for FY-2F LSTs (Classification 5)

下载CSV

	地点1	地点2	地点3	地点4	地点5	地点6	地点7
LS-VAN2006	0.8513	0.7801	0.8332	0.7403	0.8111	0.7587	0.6392
V-LS-PFG	0.3201	0.3654	0.3748	0.3677	0.3866	0.3334	0.3736
V-LM-PFG	0.2771	0.3152	0.2756	0.2966	0.3056	0.2654	0.3044

图 4 3种模型拟合效果(分类5)，RMSE=(0.8111，0.3866，0.3056)

Fig. 4 The effects of three models (classification 5), RMSE=(0.8111, 0.3866, 0.3056)

表 5列出7个不同位置点时间序列中只有若干非空值点建立的DTC模型与真实值间的RMSE信息，空值分布情况符合分类3。表 5与表 4相比，LS-VAN2006模型在7个位置点的RMSE增长幅度很大，最小值已超过1.53。这是由于能够参与模型拟合的有效点减少，引起模型拟合效果变差，进一步影响空值修复。而本文提出寻找相似像元代入模型的方法得到较低的RMSE，再一次表明LM-PFG稳健性强于LS-PFG和LS-VAN2006。如图 5所示，VAN2006在整个时间序列模拟都存在偏差，而LS-PFG在温度最大值与温度自由衰减时刻前后的模拟有一定偏差，LM-PFG在整个时间序列的模拟都较理想。

表 5 FY-2F LST数据DTC模型RMSE (分类3)
Table 5 The RMSE of DTC model for FY-2F LSTs (Classification 3)

下载CSV

	地点1	地点2	地点3	地点4	地点5	地点6	地点7
LS-VAN2006	1.9082	1.7441	1.8628	1.7369	1.6501	1.5580	1.5315
LS-PFG	0.5816	0.4794	0.5777	0.4636	0.4856	0.4631	0.5798
LM-PFG	0.4894	0.3634	0.3968	0.3102	0.3518	0.3759	0.3545

图 5 3种模型拟合效果(分类3)，RMSE=(1.6501，0.4856，0.3518)

Fig. 5 The effects of three models (Classification 3), RMSE=(1.6501, 0.4856, 0.3518)

4.2 模拟实验2与分析

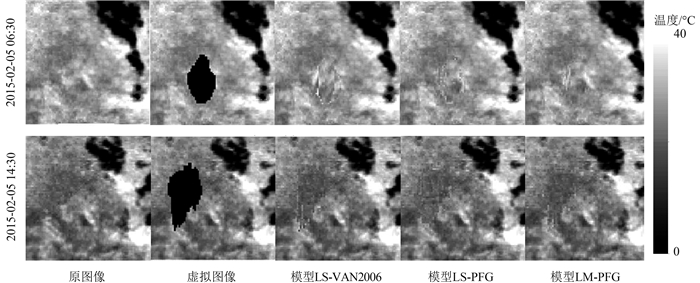
由于模拟实验1只是选了若干像素点时间尺度上进行模型的验证，而随机点位的选择无法准确说明区域性空值是否对模型的精度有影响。因此在模拟实验2中，本文下载2015年2月5日的24景FY-2F LST数据，在日内24副影像中的两幅影像(6:30和14:30)中随机截取80×80像素的相同区域，并人为去掉其中的某些值，虚拟出大片的空值，然后采用不同的方法修补，并与真实影像进行对比。

图 6第1排和第2排从左至右分别是2015年2月5日6:30和14:30两个时间点裁剪区域原图像、虚拟出大片空值的图像、LS-VAN2006、LS-PFG和LM-PFG方法修复后结果。在目视上，对比不同方法的修复痕迹可以看出：LS-VAN2006方法对应的修复痕迹最明显，LM-PFG方法图像纹理比较平滑，修复痕迹不明显，而LS-PFG方法的修复痕迹明显程度介于LS-VAN2006和LM-PFG之间。模拟实验2表明在大片空值的情况下，LM-PFG方法的修复效果同样优于LS-PFG和LS-VAN2006方法的修复效果。在定量上，表 6列出两幅虚拟影像(2015年2月5日6:30和14:30)利用3种方法修复结果与真实值之间的平均RMSE (空值区域所有点对应RMSE的平均值)信息。由表 6可知，每一幅虚拟影像中3种方法对应的RMSE值，LS-VAN2006最大，LS-PFG次之，LM-PFG最小，再次说明LM-PFG修复精度高于LS-PFG和LS-VAN2006。

图 6 3种方法修复结果对比

Fig. 6 Comparison of the reconstructing effects of three methods

表 6 3种修复方法RMSE (模拟实验2)
Table 6 The RMSE of three reconstructing methods (Simulation experiment 2)

下载CSV

时间	空值点数	LS-VAN2006	LS-PFG	LM-PFG
6:30	389	0.4115	0.2869	0.2151
14:30	586	0.4274	0.3033	0.2365

4.3 真实实验与分析

真实实验中，随机截取80×80像素的区域作为真实实验所需数据，首先利用matlab软件读取24景数据，经相应编程处理得到24景数据的空值分布矩阵，根据数据空值标记结果选择不同处理方法，对空值标记后的静止卫星LST数据时间序列中非空值像元建立昼夜变化曲线，求解拟合系数并优化处理，将空值对应时间点带入模型求解，得到修复结果。由于篇幅限制，本文选取若干时相修复前后数据，如图 7所示。

图 7 2013年6月13日4：30、17：30、23：30和2013年6月15日12：30修复前后图像

Fig. 7 The images before and after reconstruction acquired at 4:30, 17:30 and 23:30 on June 13, 2013 and at 12:30 on June 15, 2013, respectively

图 7第1排从左至右分别是裁剪区域2013年6月13日4:30、17:30、23:30和2013年6月15日12:30的温度数据，第2排分别为对应的修复后结果。该图所示的4幅图像左起至右，所包含的空值由少至多，由离散到聚集，与之对应的是修复难度由简单到复杂。通过修复前后图像对比可以看出，对于图像中含有少数离散空值点，LM-PFG模型修复结果很理想；随着空值点增多，分布更加集中，修复后图像隐约可见修复痕迹(见17:30和23:30的修复结果)，这是因为对于空值附近的非空像元并没有修复，而这些像元很可能是由于温度产品生产过程中对薄云等检测误差导致。针对大面积的空值(如12:30的数据)，其修复效果也比较好，这往往是传统空间内插技术难以完成的。

5 结论

针对静止卫星温度产品的空值现象，本文通过多项式、傅里叶函数、高斯函数建立面向空值修复的分段函数模型，并引入Levenberg-Marquardt算法进行参数的优化，从而实现空值像元修复。在模拟实验1中，选取不同时空条件下的7个试验点作为研究对象，根据不同的空值分布情况进行模型参数拟合与优化，并与传统最小二乘法下VAN2006和PFG进行比较。结果表明：本文提出的LM-PFG模型具有拟合误差低，精度高、稳健性强等特点。在模拟实验2中，人为去掉日内的24副影像中两幅影像的某些值，虚拟出大片的空值，然后将不同方法的修补结果与真实影像进行对比，结果再次验证LM-PFG强于LS-PFG和LS-VAN2006。在真实实验方面，利用本文提出的方法能够得到较好的修复结果，尤其是针对大面积空值实现理想修复，解决大面积空值难以修复的问题。

本文提出的LM-PFG模型对于静止气象卫星地表温度数据的插补具有一定的应用价值，但该模型仍然存在一些不足：(1)本文模型为分段函数，当待修复像元时间序列空值数量较多时，可能会导致分段函数无法建立，这时需要综合其他方法进行静止气象卫星地表温度数据插补的研究；(2)本文模型中的部分参数与数据相关性较高，如模型中多项式系数是面向风云数据的，因此该系数可能并不适用于其他类型数据，这时需要进行统计实验来确定新的系数，所以如何构建一体化模型，即每种数据类型都存在一个可供选择的准确系数将是下一步的重要研究内容；(3)本文构建的DTC模型均是假设在晴空条件下，这种假设下的修复结果与真实云(尤其厚云)下地表温度必然存在一定误差。若研究区域内存在站点温度数据，利用该站点温度数据对修复结果进行约束，可在一定程度上提高修复精度。此外，在实验设计方面，针对小面积的空值像元，本文并没有比较空间内插结果与基于DTC模型的结果，这也将是下一步研究的重点，而且本文针对时间序列所有像元均为空值的情况并没有深入研究，只是提出在所有能够修复的空值处理完之后，采用空间内插技术进行修复，但由于静止卫星时间分辨率很高，这种情况很难出现。

参考文献(References)

Cai D H, Guo N, Li C W.2009.Interpolation of air temperature based on DEM over eastern region of Gansu. Journal of Arid Meteorology, 27 (1): 10–17 ( 蔡迪花, 郭铌, 李崇伟. 2009. 基于DEM的气温插值方法研究. 干旱气象, 27 (1): 10–17)

Coops N C, Duro D C, Wulder M A, Han T.2007.Estimating afternoon MODIS land surface temperatures (LST) based on morning MODIS overpass, location and elevation information. International Journal of Remote Sensing, 28 (10): 2391–2396 [DOI: 10.1080/01431160701294653]

Duan S B, Li Z L, Wang N, Wu H, Tang B H.2012.Evaluation of six land-surface diurnal temperature cycle models using clear-sky in situ and satellite data. Remote Sensing of Environment, 124 : 15–25 [DOI: 10.1016/j.rse.2012.04.016]

Duan S B, Li Z L, Tang B H, Wu H, Tang R L, Bi Y Y, Zhou G Q.2014.Estimation of diurnal cycle of land surface temperature at high temporal and spatial resolution from clear-sky MODIS data. Remote Sensing, 6 (4): 3247–3262[DOI: 10.3390/rs6043247]

Elagib N A, Alvi S H, Mansell M G.1999.Day-length and extraterrestrial radiation for Sudan:a comparative study. International Journal of Solar Energy, 20 (2): 93–109[DOI: 10.1080/01425919908914348]

Fan J Y.2003.A modified Levenberg-Marquardt algorithm for singular system of nonlinear equations. Journal of Computational Mathematics, 21 (5): 625–636

Finsterle S, Kowalsky M B.2011.A truncated Levenberg-Marquardt algorithm for the calibration of highly parameterized nonlinear models. Computers and Geosciences, 37 (6): 731–738[DOI: 10.1016/j.cageo.2010.11.005]

Gavin H P. 2016. The Levenberg-Marquardt Method for Nonlinear Least Squares Curve-Fitting Problems. Durham:Department of Civil and Environmental Engineering, Duke University:1-18

Göttsche F M, Olesen F S.2001.Modelling of diurnal cycles of brightness temperature extracted from METEOSAT data. Remote Sensing of Environment, 76 (3): 337–348[DOI: 10.1016/S0034-4257(00)00214-5]

Göttsche F M, Olesen F S.2009.Modelling the effect of optical thickness on diurnal cycles of land surface temperature. Remote Sensing of Environment, 113 (11): 2306–2316[DOI: 10.1016/j.rse.2009.06.006]

Huang F, Zhan W F, Duan S B, Ju W M, Quan J L.2014.A generic framework for modeling diurnal land surface temperatures with remotely sensed thermal observations under clear sky. Remote Sensing of Environment, 150 : 140–151[DOI: 10.1016/j.rse.2014.04.022]

Jing Y L, Li J B, Lin G.2008.Research on numerical conversion algorithms of structure dynamic analysis in time and frequency domains. Journal of Dalian University of Technology, 48 (6): 875–880 ( 景月岭, 李建波, 林皋. 2008. 结构动力数值分析的时频域转换算法研究. 大连理工大学学报, 48 (6): 875–880)

Ke L H, Ding X L, Song C Q.2013.Reconstruction of time-series MODIS LST in Central Qinghai-Tibet Plateau using geostatistical approach. IEEE Geoscience and Remote Sensing Letters, 10 (6): 1602–1606[DOI: 10.1109/LGRS.2013.2263553]

Keramitsoglou I, Kiranoudis C T, Weng Q H.2013.Downscaling geostationary land surface temperature imagery for urban analysis. IEEE Geoscience and Remote Sensing Letters, 10 (5): 1253–1257[DOI: 10.1109/LGRS.2013.2257668]

Li J and Luo Q F. 2013. Study on estimation of LST under cloudy region in MODIS images//The Thirty Year Academic Conference of the Seismological Society of China. Beijing:Seismological Society of China (李静, 罗奇峰. 2013. HHT变换的特点及其优越性分析//中国地震学会成立三十年学术研讨会.北京:中国地震学会)

Li Z L, Tang B H, Wu H, Ren H Z, Yan G J, Wan Z M, Trigo I F, Sobrino J A.2013.Satellite-derived land surface temperature:current status and perspectives. Remote Sensing of Environment, 131 : 14–37[DOI: 10.1016/j.rse.2012.12.008]

Liu M. 2012. Study on Estimation of LST under Cloudy Region in MODIS Images. Nanjing:Nanjing University (刘梅. 2012. MODIS影像中云覆盖像元地表温度的估算研究.南京:南京大学)

Ma C F, Jiang L H.2007.Some research on Levenberg-Marquardt method for the nonlinear equations. Applied Mathematics and Computation, 184 (2): 1032–1040[DOI: 10.1016/j.amc.2006.07.004]

Madsen K, Nielsen H B, Tingleff O.2004.Methods for non-linear least squares problems (2nd ed.). SIAM Journal on Optimization, 16 (1): 487–490

Ouyang X Y and Jia L. 2011. Retrieval of land surface temperature time series based on geostationary meteorological satellite FY-2C/SVISSR//5th Annual Symposium of Remote Sensing on Both Sides of the Taiwan Straits. Harbin:The Geographical Society of China (欧阳晓莹, 贾立. 2011.基于静止气象卫星FY-2C/SVISSR的地表温度时间序列反演研究//第五届海峡两岸遥感遥测会议.哈尔滨:中国地理学会)

Parton W J, Logan J A.1981.A model for diurnal variation in soil and air temperature. Agricultural Meteorology, 23 : 205–216[DOI: 10.1016/0002-1571(81)90105-9]

Schädlich S, Göttsche F M, Olesen F S.2001.Influence of land surface parameters and atmosphere on METEOSAT brightness temperatures and generation of land surface temperature maps by temporally and spatially interpolating atmospheric correction. Remote Sensing of Environment, 75 (1): 39–46[DOI: 10.1016/S0034-4257(00)00154-1]

Si S L, Guan Y.2006.Determination of optimal power of data fitting to characteristic curve of trigonometric function. Computer Engineering and Design, 27 (24): 4660–4662 ( 司少玲, 关永. 2006. 三角函数曲线数据拟合最佳次数的确定. 计算机工程与设计, 27 (24): 4660–4662 )

Song T, Duan Z, Liu J Z, Shi J Z, Yan F, Sheng S J, Huang J, Wu W.2015.Comparison of four algorithms to retrieve land surface temperature using Landsat 8 satellite. Journal of Remote Sensing, 19 (3): 451–464 ( 宋挺, 段峥, 刘军志, 石浚哲, 严飞, 盛世杰, 黄君, 吴蔚. 2015. Landsat 8数据地表温度反演算法对比. 遥感学报, 19 (3): 451–464 )

Udahemuka G, van den Bergh F, van Wyk B J and van Wyk M A. 2007. Robust fitting of diurnal brightness temperature cycle//18th Annual Symposium of the Pattern Recognition Association of South Africa (PRASA). Pietermaritzburg, Kwazulu-Natal, South Africa

van den Bergh F, van Wyk M A and van Wyk B J. 2006. A Comparison of data-driven and model-driven approaches to brightness temperature diurnal cycle interpolation//Proceeding of the 17th Annual Symposium of the Pattern Recognition Association of South Africa. Parys, South Africa:252-256

Wei F, Wang S J, Liang J B, Wang Y, Zhang S Y, Jing T, Zhang H X, Zhang B Q, Leng S.2013.Next generation Space Environment Monitor (SEM) for FY-2 satellite series. Chinese Journal of Geophysics, 56 (1): 1–11 ( 韦飞, 王世金, 梁金宝, 王月, 张申毅, 荆涛, 张焕新, 张斌全, 冷双. 2013. 风云二号03批卫星空间环境监测器. 地球物理学报, 56 (1): 1–11)[DOI: 10.6038/cjg20130101]

Wilamowski B M, Yu H.2010.Improved computation for Levenberg-Marquardt training. IEEE Transactions on Neural Networks, 21 (6): 930–937[DOI: 10.1109/TNN.2010.2045657]

Yang L, Chen Y P.2005.On the convergence of a new Levenberg-Marquardt method. Mathematica Numerica Sinica, 27 (1): 55–62. ( 杨柳, 陈艳萍. 2005. 一种新的Levberg-Marquardt算法的收敛性. 计算数学, 27 (1): 55–62. )

Wu P H, Shen H F, Zhang L P, Göttsche F M.2015.Integrated fusion of multi-scale Polar-orbiting and geostationary satellite observations for the mapping of high spatial and temppral resolution land surface temperature. Remote Sensing of Enviroment, 156 : 169 [DOI: 10.1016/j.rse.2014.09.013]

Yang L, Chen Y P.2005.A new globally convergent Levenberg-Marquardt method for solving nonlinear system of equations. Mathematica Numerica Sinica, 17 (1): 55-62 ( 杨柳, 陈艳萍. 2008. 求解非线性方程组的一种新的全局收敛的Levberg-Marquardt算法. 计算数学, 17 (1): 55-62 )

Zhan W F, Chen Y H, Zhou J, Wang J F, Liu W Y, Voogt J, Zhu X L, Quan J L, Li J.2013.Disaggregation of remotely sensed land surface temperature:literature survey, taxonomy, issues, and caveats. Remote Sensing of Environment, 131 : 119–139[DOI: 10.1016/j.rse.2012.12.014]

Zhang H Y, Geng Z.2009.Novel interpretation for Levenberg-Marquardt algorithm. Computer Engineering and Applications, 45 (19): 5–8 ( 张鸿燕, 耿征. 2009. Levberg-Marquardt算法的一种新解释. 计算机工程与应用, 45 (19): 5–8 )

Zhou Y, Qin Z H, Bao G.2014.Progress in retrieving land surface temperature for the cloud-covered pixels from thermal infrared remote sensing data. Spectroscopy and Spectral Analysis, 34 (2): 364–369 ( 周义, 覃志豪, 包刚. 2014. 热红外遥感图像中云覆盖像元地表温度估算研究进展. 光谱学与光谱分析, 34 (2): 364–369 )