Print

出版日期: 2017-01-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176023
2017 | Volumn21 | Number 1





                              上一篇|





下一篇
技术方法
城市交通网络分形维数的不确定性估计、控制与分析
expand article info 李畅 , 李桂娥 , 朱昱佳
华中师范大学城市与环境科学学院 地理过程分析与模拟湖北省重点实验室, 武汉 430079
收稿日期: 2016-01-28; 修改日期: 2016-06-17; 优先数字出版日期: 2017-01-25
基金项目: 国家自然科学基金（编号：41101407，61301278）；湖北省自然科学基金（编号：2014CFB377，2010CDZ005）；华中师范大学中央高校基本科研项目（编号：CCNU15A02001）；武汉市晨光计划（编号：2016070204010137）；华中师范大学中央高校基本科研业务费项目（编号：CCNU16JCZX09）
第一作者简介: 李畅(1982-), 男, 副教授, 研究方向为地理信息科学、数字摄影测量与遥感的理论、技术和地学应用研究。E-mail:lcshaka@126.com; lichang@mail.ccnu.edu.cn
中图分类号: N93
文献标识码: A
文章编号: 1007-4619(2017)01-0074-10

摘要

长度-半径维数模型作为描述城市交通网络复杂不确定性现象的一种分形分维方法，其自身存在的不确定性往往被忽视，且相关研究更是鲜见报道。故针对该模型在分形维数测算全过程中存在的不确定性问题，本文率先开展了系统剖析、定量估计和质量控制研究。首先对数据源、矢量化处理、测算中心、尺度选择、以及分维数模型估计等一系列环节进行了不确定性估计与分析，其中首次给出了分形维数在一定置信水平下的不确定性度量区间，并依据误差传播理论对误差的传递和累积进行了描述；然后着重提出了基于LMedS（Least Median of Squares）的质量控制方法。最后通过对拉萨市的算例实验表明：道路的矢量化过程、测算中心和测算尺度的选择都会导致分维的不确定性；并在对数据质量进行控制的基础上，通过置信区间对长度-半径维数模型的不确定性进行了在一定概率水平下的首次度量；同时结合区域现状对研究结果给出了合乎实际的解释。本文在描述表征不确定性问题的分形几何和分形维数的基础上，系统地揭示了其自身不确定性的本质，不仅进一步丰富了分形分维理论，为控制其质量奠定理论基础，而且可为城市交通网络分形维数的地学应用提供可靠的科学依据。

关键词

交通网络 , 长度-半径维数模型 , 不确定性 , LMedS , 质量控制 , 误差传播

Uncertainty estimation, control, and analysis of fractal dimension for urban traffic network
expand article info LI Chang , LI Gui'e , ZHU Yujia
Key Laboratory for Geographical Process Analysis and Simulation, Hubei Province, College of City and Environmental Science, Central China Normal University, Wuhan 430079, China

Abstract

Finding the ideal fractal of the objective world based on pure mathematics is difficult, but the statistical significance of random fractal is an objective existence such that fractal and fractal dimension has some uncertainty. The length-radius dimension model is a fractal dimension method used to describe the complex and uncertain phenomenon of urban traffic network. However, the uncertainty of the model is frequently neglected, and related research are rarely reported. Therefore, theories and methods of uncertainty for fractal dimension should be developed and improved urgently. Aiming at the uncertainty existing in the measuring process of length-radius dimension model, we first systematically conduct research on the analysis, quantitative estimation, and quality control of fractal dimension for the urban traffic network.

The uncertainty estimation and analysis of this model are conducted from the aspects of data source, vector processing, measuring center, scale selection, and fractal dimension estimation. In particular, the uncertainty measurement interval of fractal dimension (i.e., the corresponding regression coefficient) under a certain confidence level is first provided quantitatively. Then, based on the theory of error propagation, we describe the propagation and accumulation of errors. Meanwhile, a method of quality control is proposed using least median of squares (LMedS) to remove the gross error (i.e., outliers) and to determine the scale less range simultaneously.

In this study, the experimental data were selected from the traffic network distribution map of Lhasa City in 2011, which is the map of the Lhasa road network with a scale of 1:370000 published by the China Cartographic Publishing House. The main road includes national, provincial, county, and township roads. The Lhasa City traffic network distribution map was acquired by registration and vectorization using ArcGIS. Experimental results show that vectorization of the traffic network and selection of the measuring center and scale cause uncertainty in the fractal dimension. The road is vectorized under different scale environments, e.g., 1:1000, 1:10000, cdots, 1:500000. Thus, the uncertainty for roads can be obviously observed. Transportation hub and geometric centers are employed to verify the uncertainty of fractal dimension. The uncertainty of the length-radius dimension model is controlled at a certain level of probability, and the uncertainty of this model is measured by calculating the confidence interval for the first time. To be exact, the confidence interval of the fractal dimension is (1.633, 1.707) under the confidence level of 95%. Furthermore, the corresponding table of the original data and data processed by LMedS proves that the proposed method is reliable, that is, the coefficient of determination R2 is improved from 0.9931 to 0.9989.

From the description of the uncertainty of fractal geometry and fractal dimension, this study systematically reveals the uncertain essence of the model. The proposed methods of uncertainty, quality control, and analysis are not only applicable to the length-radius dimension model but also to the branch dimension that is similar to the calculation method. The model can also provide references for the statistical significance of all random fractals in nature. The proposed model not only further enriches fractal dimension theory and establishes the theoretical foundation of its quality control but also provides reliable scientific basis for the geoscience applications of fractal dimension for the urban traffic network.

Key words

traffic network , length-radius dimension model , uncertainty , LMedS , quality control , error propagation

1 引言

正是因为客观世界难以找到纯数学的理想分形，但统计意义下的随机分形却是客观存在的，因而分形理论成了描述复杂、非线性空间分布的有力工具(Mandelbrot和Aizenman，1979)。分形理论的精妙在于把一个不确定性的分形几何问题转换成为了一个确定性的维数问题，如Cantor集、Koch曲线等，一旦尺度确定，就可以得到确定性的分形维数，例如Cantor集尺度与对应份数的关系(尺度，份数)为(1/3, 2)、(1/9, 4)、(1/27, 8)…、(1/${3^n}$, ${2^n}$)，其对应的Hausdorff维数为log (2)/log (3)=log (4)/log (9)=log (8)/log (27)=…=log (${2^n}$)/log (${3^n}$)=0.6309，取对数后的点对(log${3^i}$，log${2^i}$)严格成比例，即共线；然而，自然当中存在的统计意义下的分形几何问题，在不同尺度下得到的对应的分维数是不确定的，需做回归分析才可得到一个相对确定的维数，例如经典的海岸线长度问题，以中国海岸线为例，尺度与长度的点对关系(尺度，长度)为(马建华 等，2015)：(400，4156)、(200，4776)、(100，5486)、(50，6304)、…，然而对其取对数后的点对(log400，log4156)…(log50，log6304)并不共线，故需进行回归分析。剖析上述问题的本质原因在于研究对象自相似性的程度，自然界中事物的非规则本质使得无规分形无法获得绝对意义上的事物的确定性分形特征，并在测算过程中不可避免产生不确定性，且必须进行回归分析，这正是无规分形具有不确定性的根源所在，同时这也是激发本研究--分形维数不确定性的理论关键动机。

综上所述，分形理论自身同样存在不确定性，而且已经引起少数学者的思考，当前学者对于分形不确定性的研究已涉及对盒子维数的测量算法(梁东方 等，2002)、河流(李静静 等，2010)和海岸线(马建华 等，2015)长度的测算等方面，且有学者对分形不确定性进行了计算机模拟(李德毅 等，2004)，相关研究多着眼于测量尺度选择对于分形分维的影响，对本研究也无不启迪，在此基础上我们对其开展了系统性的不确定性研究。鉴于分形分维理论在地学应用研究中对交通网络分形特征的分析较为经典(Benguigui和Daoud，1991；Benguigui，1992；柏春广和蔡先华，2008；Li 等，2012)，因而本文拟以此为研究对象分析常用于描述其分形特征的长度-半径维数的不确定性。回顾以往学者的研究，对于城市交通网络长度-半径维数的不确定性分析仅有少量文献(刘妙龙和黄佩蓓，2003；刘承良 等，2013)在研究过程中指出测算中心和尺度选取不同，会对解算交通网络的真实分维值产生影响，但并未对其不确定性进行系统研究和剖析。基于此，本文尝试对城市交通网络分形分维开展不确定性来源分析、度量及其质量控制的研究，以期丰富分形分维的相关理论与质量控制方法，并为全面、客观分析研究对象的分形分维特征提供可靠依据。

2 分形维数的不确定性分析原理与质量控制

本文拟以经典的长度-半径维数模型为例对其计算过程中的不确定性进行分析与度量。因此，首先回顾一下该模型(Frankhauser，1990; 陈彦光，2008)。一般地，对于一个几何体，设长度为$L$，面积为$S$，体积为$V$，则有

$ {L^{1/1}} \propto {S^{1/2}} \propto {V^{1/3}} $ (1)

借助广义体积$M$，则(1)的广义化形式可以表示成：

$ {L^{1/1}} \propto {S^{1/2}} \propto {V^{1/3}} \propto {M^{1/D}} $ (2)

式中，$D$表示欧氏维数，倘若几何体的某个测度具有分形特征，则其相应的$D$值为非整数。

如果一个面积为$S$的区域，其中的交通网络具有分形特征，则其总长$L$($S$)与面积之间应该具有如下关系

$ L{\left( S \right)^{1/D}} \propto {S^{1/2}} $ (3)

当所选区域为圆形时，$S \propto {r^2}$，则式(3)可表示为以下形式

$ L\left( r \right) = {L_1}{r^D} $ (4)

式中，$r$为以某枢纽为中心的回旋(转)半径，$L$($r$)为半径为$r$的区域范围内的道路网络总长度，${L_1}$为常系数，幂指数$D$即分维，Frankhouser将其命名为半径维数(radial dimension)，也可称之为长度-半径维数。

从中不难发现，在对城市道路网络进行长度-半径维数测算时，道路网络的数据选择与预处理、测算中心和测算尺度的选择、分形维数模型本身都将成为该模型的不确定性来源对真实分维值的测算产生影响。所以，本文将从(1) 数据源、(2) 矢量化处理、(3) 测算中心及尺度选择、(4) 分维数模型估计等环节对其进行不确定性分析，并基于误差传播的累积效应，在一定概率水平下通过置信区间对长度-半径维数模型的不确定性进行首次度量，同时，基于LMedS (Least Median of Squares)提出相应的质量控制方法。

2.1 分形维数的不确定性分析原理

(1) 数据源的不确定性。对于研究学者而言，城市交通道路网的基础数据源主要来自于对纸质或电子地图的矢量化并同时辅助其他工具对数据进行完善。从数据获取源来看，影响数据质量的因素主要包括地图测量误差、绘制误差，图纸变形误差(柳宗伟 等，2002)，地图要素本身的密度和复杂程度以及地图综合(王桥 等，1998; 艾廷华 等，2007; Li，2007)过程中对于地物的取舍程度等。

(2) 数据转换的不确定性。从城市交通道路矢量数据处理方式来看，数字化以及数字化操作人员的熟练程度及操作方式、数据格式转换等同样存在不确定性。对于同一区域，不同比例尺的地图对分维数会产生影响(陈杰和马素媛，2012)，即使是同一比例尺的地图，在不同比例的矢量化环境下，其结果也不相同，从而导致不确定性。故，矢量化的结果，例如：点、线、面皆存在不确定性，其中点的不确定性可以由误差椭圆来描述；线的不确定性可以由G-带误差模型进行概括；面的不确定性则可通过讨论多边形组成顶点的不确定性和基于多边形边界的误差带两种方法对其不确定性进行度量(Shi，2009)。

(3) 测算中心和测算尺度的不确定性。对交通道路网的长度-半径维数进行测算时需要选择测算中心和测算尺度。从当前学者的研究工作来看，测算中心或为城市交通网络的枢纽或为城市的几何中心亦或是重心，不同的选择所获得结果也不尽相同，故在中心选择上存在认知的不确定性。即使同是选择城市道路网的交通枢纽中心，也会因研究者不同，而有差别，即相应测算中心都存在一个点位误差(测算点与真实点)，可用点位误差椭圆(Shi，2009)来衡量。对于测算尺度的选取，就目前而言，没有固定的标准，多数学者都是结合研究区域的特征选取合适的尺度进行测算，这也为测算区域交通网络的分维值增加了多样性。

(4) 分形维数估计的不确定性度量。对于分形维数模型，有些不确定性可以通过对数据重新定位、浏览、查错等进行降低，而有些则是无法避免且随处理过程进行误差传播累积。对于此类不确定性可通过计算分维数的置信区间进行定量估计。

对式(4)作对数变换，则可得到：

$ \ln L\left( r \right) = \ln {L_1} + D\ln r $ (5)

为了表示方便，在以下公式中，凡涉及点对(ln$r$，ln$L$($r$))均用(${x_i}$，${y_i}$)代换，ln${L_1}$用$a$代换，分维数(即回归系数)用$b$表示，则文中长度-半径对应的点列的回归方程可用下式表示：

$ {y_i} = \hat b{x_i} + \hat a + {\varepsilon _i} $ (6)

式中，${\hat a}$表示一元线性回归模型截距($a$)的最大似然估计值，${\hat b}$表示$b$(回归系数)的最大似然估计值，(${x_i}$，${y_i}$)表示上述代换后对应的样本点对，${\varepsilon _i}$表示随机误差。在以下公式中凡涉及到样本的个数均用$n$表示，为了计算上的方便，特引入下述记号

$ \left\{ \begin{array}{l} {S_{xx}} = \sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} = \sum\limits_{i = 1}^n {x_i^2} - \frac{1}{n}{\left( {\sum\limits_{i = 1}^n {{x_i}} } \right)^2}\\ {S_{yy}} = \sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} = \sum\limits_{i = 1}^n {y_i^2} - \frac{1}{n}{\left( {\sum\limits_{i = 1}^n {{y_i}} } \right)^2}\\ {S_{xy}} = \sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)} = \sum\limits_{i = 1}^n {{x_i}{y_i}} - \frac{1}{n}\left( {\sum\limits_{i = 1}^n {{x_i}} } \right)\left( {\sum\limits_{i = 1}^n {{y_i}} } \right)\\ \bar x = {\displaystyle\frac{1}{n}}\sum\limits_{i = 1}^n {{x_i}} \\ \bar y = {\displaystyle\frac{1}{n}}\sum\limits_{i = 1}^n {{y_i}} \end{array} \right. $ (7)

这样，$a$，$b$的最大似然估计值就可以表述为

$ \left\{ \begin{array}{l} \hat b = \displaystyle \frac{{{S_{xy}}}}{{{S_{xx}}}}\\ \hat a = {\displaystyle{\frac{1}{n}}}\sum\limits_{i = 1}^n {{y_i}} - \left( {{\displaystyle{\frac{1}{n}}}\sum\limits_{i = 1}^n {{x_i}} } \right)\hat b \end{array} \right. $ (8)

为了更有效地描述随机变量之间的相关关系，特引入残差(残差为某样本点观测值与拟合值之差)平方和，记为${Q_e}$，${\hat y}$则表示样本对应的回归方程值，则

$ {Q_e} = \sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} = \sum\limits_{i = 1}^n {{{\left( {{y_i} - \hat a - \hat b{x_i}} \right)}^2}} $ (9)

将样本中的${y_i}$改为${Y_i}$($i$=1，2，…，$n$)(${Y_i}$是指相互独立的随机变量)，则

$ {Q_e} = {S_{YY}} - \hat b{S_{xY}} $ (10)

若残差平方和${Q_e}$服从分布，且令${\sigma ^2}$表示均方误差：

$ \frac{{{Q_e}}}{{{\sigma ^2}}} \sim {\chi ^2}\left( {n - 2} \right) $ (11)

则

$ E\left( {\frac{{{Q_e}}}{{{\sigma ^2}}}} \right) = n - 2 $ (12)

这样就可以得到${\sigma ^2}$的无偏估计量

$ {{\hat \sigma }^2} = \frac{{{Q_e}}}{{n - 2}} = \frac{1}{{n - 2}}\left( {{S_{YY}} - \hat b{S_{xY}}} \right) $ (13)

将道路长度和半径长度标绘在双对数坐标图上，判别其回归效果，若回归效果显著，则可以对分维数作区间估计。事实上，可由下式得到$b$(即分维数$D$)的置信水平为1-$\alpha $的置信区间为

$ \left( {\hat b \pm {t_{\alpha /2}}\left( {n - 2} \right)\frac{{\hat \sigma }}{{\sqrt {{S_{xx}}} }}} \right) $ (14)

式中，$t$表示学生分布，${t_{\alpha /2}}\left( {n - 2} \right)$表示自由度为($n$-2)的$t$分布在$\alpha $/2下对应的分位点。分维数存在满足一定置信水平的置信区间，表明了分维数的不确定性，该不确定性的来源一方面包括数据处理的累积误差，另一方面包括回归模型分析本身具有的误差，因而该置信区间可以用于对分维数进行不确定性度量。

在实际问题求解中，为了更直观地表示回归直线的不确定性，需要对该直线的不确定性误差带进行界定和描述。本文对长度-半径的双对数回归直线的不确定性误差带可由对回归直线中自变量的某一指定值(${x_0}$)满足一定置信水平的置信区间的求解引申而来。则对于$\mu \left( {{x_0}} \right) = \hat b{x_0} + \hat a$置信水平为1-$\alpha $的置信区间为

$ \left( {\hat a + \hat b{x_0} \pm {t_{\alpha /2}}\left( {n - 2} \right)\hat \sigma \sqrt {\frac{1}{n} + \frac{{{{\left( {{x_0} - \bar x} \right)}^2}}}{{{S_{xx}}}}} } \right) $ (15)

式中，$t$的含义与式(14)相同。由上式可知：该置信区间的长度是${x_0}$的函数，且与$\left| {{x_0} - \bar x} \right|$有关，即随着该值的增加而增加，因此对于回归直线的不确定性误差带曲线则可通过上式推导出其对应的置信上限和下限函数将其进行绘制。

(5) 分形分维的不确定性传播描述。客观世界是一个复杂、多元、非线性的巨系统，其不确定性具有多样性且普遍存在，而确定性则是有条件的。在实验数据获取和分析的过程中，由于基础数据、处理技术、分析方法等的限制，在每一个环节都有可能会产生难以预料的系统误差和随机误差，且这些误差将以不同的权重不断累积，对实验结果产生影响。因此，为了将不确定性所带来的风险降到最低，需要分析、控制和管理不确定性。结合Shi (2009)和杨元喜(2012)等对于误差传播和累积的分析，本文拟采用下式对城市交通网络分形维数的不确定性进行误差估计。若在测算城市交通网络分形维数(fractal dimension)的过程中，其不确定性是由以下独立误差所致：底图数据(map data)(用$\sigma _{{\rm{MD}}}^2$表示，对应2.1节中的(1)对应的误差来源)、矢量化(vectorization)(用$\sigma _{{\rm{V}}}^2$表示，对应2.1节中的(2)对应的误差来源)、测算中心(measuring centre)(用$\sigma _{{\rm{MC}}}^2$表示，对应2.1节中的(3)的测算中心误差来源)、测算尺度(measuring scale)(用$\sigma _{{\rm{MS}}}^2$表示，对应2.1节中的(3)的测算尺度误差来源)、拟合误差(fitting error)(2.1节式(13)中的${\sigma ^2}$，用$\sigma _{{\rm{FE}}}^2$表示)、数据误差(data error)(用$\sigma _{{\rm{DE}}}^2$表示，对应2.2节中的误差来源)、其他(other)(是指在测算分形维数的过程中其他不确定性因素引起的误差)。则有

$ {\sigma _{{\rm{FD}}}} = \sqrt {\sigma _{{\rm{MD}}}^2 + \sigma _{\rm{V}}^2 + \sigma _{{\rm{MC}}}^2 + \sigma _{{\rm{MS}}}^2 + \sigma _{{\rm{FE}}}^2 + \sigma _{{\rm{DE}}}^2 + \sigma _{\rm{O}}^2} $ (16)

在实际问题分析过程中，可以假设以上各过程是相互独立的，但是各过程产生的不确定性误差对于总误差的贡献并非等权，但鉴于权重系数很难确定，故本文假设是等权，城市交通网络分形维数的不确定性误差正是以这种各类误差代数和开方的方式传播、累积进而影响最终的实验结果。

2.2 基于LMedS的质量控制

基于客观条件的限制，在确定两组变量之间的相关关系时，有些数据存在异常观测值，即模型的外点，这些数据会对真实结果产生很大影响，另外还必须确定无标度区，而2.1中的第(4)部分的分维数测算方法并不能处理这些问题，因而需要对拟合数据进行质量控制。最小平方中值估计法(Rousseeuw，1984)(Least Median of Squares，LMedS)作为一种鲁棒性比较强的回归方法，因其比其他鲁棒方法如RANSAC等限制更为严格，因此基本上可以消除所有的异常值，因此本文选取该方法对数据质量进行控制LMedS的崩溃点高达50%，其求解模型参数${\hat \beta }$(本研究是指${\hat a}$和${\hat b}$)使得：

$ \mathop {\min }\limits_{\hat \beta } \left[ {\mathop {{\rm{med}}}\limits_i \left( {r_i^2} \right)} \right] $ (17)

式中，${r_i}$表示样本点到抽样直线的距离(而不是残差)以提高可靠性，med (·)为中值运算，将该式运用到本文所研究的问题中，可以得到如下算法：(1) 从样本子集中随机抽取两个样本点(即模型的必要观测数，两个点可确定一条回归直线)；(2) 计算每个样本子集的模型参数；(3) 计算每个模型中，各个样本点(除去样本子集)与该模型的偏差(距离)，并记录偏差居中(中位数)的样本偏差Med；(4) 重复多次迭代运算(需满足抽取到两个内点样本的最小概率)；(5) 从多个Med偏差中挑选出最小的一个${M_J}$，其对应的模型参数就是最终的模型参数的估计值；(6) 计算该鲁棒方法的标准差，用${{\hat \sigma }_S}$表示：

$ {{\hat \sigma }_S} = 1.4826\left( {1 + \frac{5}{{\left( {n - p} \right)}}} \right)\sqrt {{M_J}} $ (18)

式中，$n$表示样本点的总数，$p$为模型的必要观测数(该模型取$p$=2)，常数1.4826是为了达到高斯噪声时与最小二乘法同样效率的校正系数，5/($n$-$p$)是为了补偿小数集的效应；(7) 计算样本点到抽样直线的距离；(8) 通过制定相应的权重即可确定模型的内点和外点：

$ {W_i} = \left\{ \begin{array}{l} 1\;\;\;\;r_i^2 \leqslant {\left( {2.5{{\hat \sigma }_S}} \right)^2}\\ 0\;\;\;\; \text{其他} \end{array} \right. $ (19)

对于该模型，当${W_i}$=0时为模型的外点，则可去除异常数据点，从而获得无标度区的点集，最后按最小二乘法鲁棒估计出最终参数。

当前，对数据质量进行控制的鲁棒方法主要包括M估计法、RANSAC、LMedS以及基于以上3种的变形和改进算法。从各类算法的基本思想来看，M估计法对于初值的依赖性比较强，且对异常值需满足总体上平摊的条件；RANSAC算法对于错误率较高的数据仍然具有很好的处理效果，但在应用时需要给定数据的错误率和正确拟合模型的误差容限，而且每次计算出的结果随机性很大。综合来看，LMedS算法是在RANSAC算法的基础上发展而来，相比于M估计法，其理论更为严密，而与RANSAC相比，不用设置拟合模型的误差阈值，且计算的结果更为稳定。故，基于LMedS的质量控制方法更具有应用优势。

3 算例与分析

3.1 数据简介

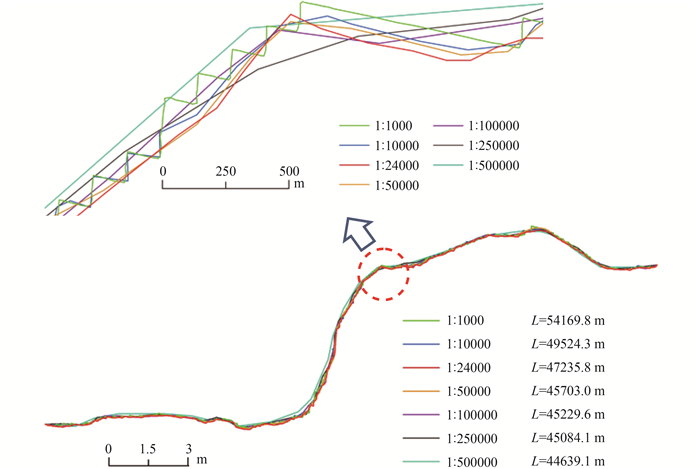
拉萨市是一座海拔3650 m的高原城市，具有1300多年的发展历史，是西藏及西南经济区的政治、经济、文化中心和西部大开发的轴心之一，同时也是世界著名的高原城市和全区的交通枢纽；并且拉萨市拥有丰富的旅游资源，其旅游态势也是逐年上升，这些客观条件使得拉萨市的地位异常显著。但就目前来看，对于该市交通网络发展状况的相关研究较少。基于以上原因，本文选取拉萨为实验区，由于受数据源限制，通过对所获得数据进行质量对比，最终选定了2011年的数据。拉萨市的交通网络分布图，其为中国地图出版社编制的比例尺为1:370000的拉萨市道路网络分布图。道路主要包括国道、省道、县道、乡道(该市国道、省道很少)，并在ArcGIS中对其分布图进行了配准、矢量化等，获得了该市交通网络分布图如图 1所示。


图 1 拉萨市2011年交通网络分布图
Fig. 1 The traffic network distribution of Lhasa in 2011

3.2 实验结果与分析

长度-半径维数模型的不确定性体现在整个数据处理流程中，它们作为不可避免的误差，通过传播累积到实验结果当中。现以拉萨市交通网络为例，对分维数测算过程中产生的显著不确定性进行说明。

(1) 矢量化过程中的不确定性。在获取基础数据时，有些客观因素导致的不确定性是无法避免的，但有些却是可以人为控制的。在对拉萨市道路矢量化过程中发现：对于同一交通网络，不同比例尺的矢量化环境中得到的道路长度差别很大。本文以国道318在达孜县的一段进行矢量化为例，选择同样的起始点和矢量化边界(道路的南侧边界)，在不同比例尺的矢量化环境下对其进行了矢量化，其结果如图 2所示。


图 2 不同比例尺矢量化环境下的道路长度和局部道路放大图
Fig. 2 The road length and partial enlarged details under different scale vectorization environment

从实验结果来看，不同比例尺矢量环境下的道路长度存在很大差别，1:1000与1:500000差距达到了9530.7 m，差距较小的1:100000与1:250000相比，也有145.5 m的差别。矢量化过程中道路长度的差距是惊人的，这对于整个实验结果的影响是不容小觑的，倘若对全区域的道路进行矢量化，但不对矢量化环境的比例尺进行控制，其结果将会产生很大的误差，进而不能真实地反映区域交通网络的密度分布情况。因此，为减小矢量化过程中的不确定性则需选择恰当的比例尺矢量环境，并规定所有道路的矢量规则，尽可能将矢量化带来的不确定性降到最低。

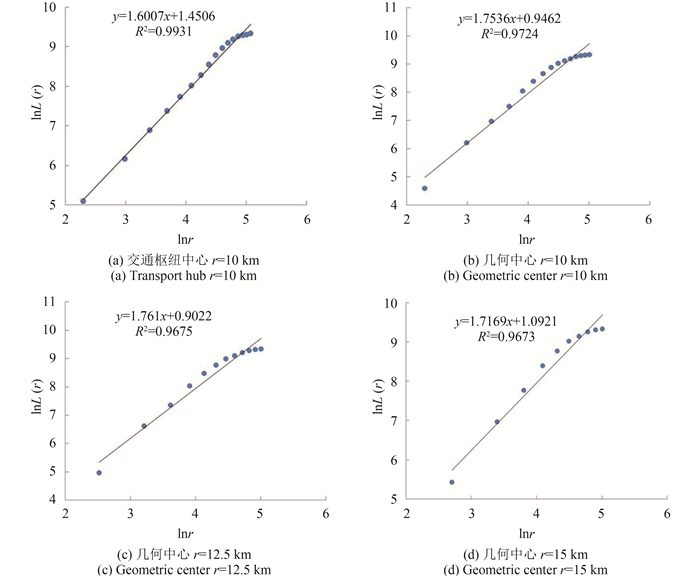
(2) 测算中心不同所引起的分维数的差异。在对拉萨市交通网络分维数进行测算时，不同测算中心和测算尺度测得的分维数存在一定差异。结合拉萨市交通网络的分布特征，分别以拉萨市(城关区)交通枢纽中心和拉萨市的几何中心为测算中心，对其分维数进行测定。在测算尺度选择方面，以交通枢纽为测算中心的数据以$r$=10 km进行处理，以几何中心为测算中心的数据分别以$r$=10 km、$r$=12.5 km、$r$=15 km进行处理，获得了相应的点列(ln$r$，ln$L$($r$))，并对其进行拟合，其结果如图 3所示。


图 3 不同测算中心和测算尺度下的拉萨市交通网络长度
Fig. 3 The ln-ln plots on the lengths of traffic network against radial distances of Lhasa under different measuring center and measuring scale

通过实验结果可知，不同的测算中心对于分维值会产生很大的影响。刘承良等人(2013)在对长三角都市圈城乡道路网进行研究时发现：若将测算中心选在沪-宁-杭三市围成的三角形几何中心时，其维数值超过2；若测算中心为上海市中心城区几何中心，其维数值则小于2，这两者的结果对于描述从测算中心到周围路网的密度分布情况是相反的。如此大的差别足以说明测算中心选取的不确定性对于城市交通网络的描述会产生很大的影响。尽管很多异常现象可以用道路网的实际分布情况对其进行解释，但其间包含的不确定性却是不可被忽视的。另一方面，不同的测算尺度对于分维值的影响可由图 3(b)(c)(d)对比得出，它不仅会影响对城市道路网分形程度的判别，还会影响长度-半径之间的相关性程度。从另一个层面来看，测算尺度的不同，还会影响分形维数的“无标度区”范围，进而影响交通网络的分维数。

(3) 基于LMedS的数据质量控制。在实验数据的获取过程中，受各种条件限制，再加上数据本身也存在很大的不确定性，故数据有可能存在异常值，所以在对拉萨市交通网络的数据进行拟合之前，本文首先对拟合数据做了基于LMedS的数据质量控制。借助MATLAB编写的程序对以交通枢纽为中心的数据进行了处理。数据处理结果如表 1、表 2所示。

表 1 原始数据
Table 1 The original data

下载CSV 
标号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
ln$r$ 2.303 2.996 3.401 3.689 3.912 4.094 4.248 4.382 4.500 4.605 4.700 4.787 4.868 4.942 5.011 5.075
ln$L$($r$) 5.092 6.160 6.882 7.376 7.734 8.012 8.272 8.546 8.786 8.958 9.093 9.187 9.260 9.287 9.308 9.325

表 2 基于LMedS处理之后的数据
Table 2 Data processed by LMedS

下载CSV 
标号 1 2 3 4 5 6 7 8 9 10 11 12 13
ln$r$ 2.303 2.996 3.401 3.689 3.912 4.094 4.248 4.382 4.500 4.605 4.700 4.787 4.868
ln$L$($r$) 5.092 6.160 6.882 7.376 7.734 8.012 8.272 8.546 8.786 8.958 9.093 9.187 9.260

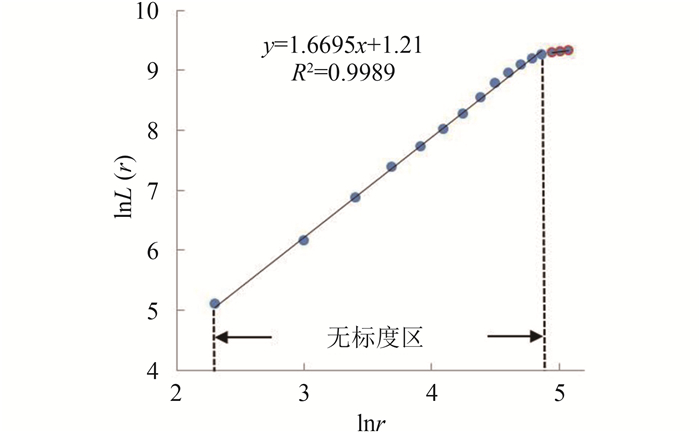
从数据处理结果来看，该组数据整体回归效果很好，只是在数据的尾部存在异常值，对于这样的数据剔除结果，则需要根据研究区域的实际情况做客观分析。剔除异常值后的数据拟合效果如图 4所示。


图 4 基于LMedS数据处理之后的拉萨市交通网络长度-半径双对数坐标图
Fig. 4 The ln-ln plot on the lengths of traffic network against radial distances of Lhasabased on LMedS

将图 4和图 3(a)的数值结果对比来看，图 4中的可决系数${R^2}$为0.9989，而图 3(a)为0.9931，可见去除异常值之后的数据相关性更高，变量之间的回归效果也更好，则从理论层面来讲：基于LMedS理论对数据进行处理，其鲁棒性更好，可见，该算法对于去除异常值可以取得一定的效果。从拉萨市交通网络的实际分布情况来看，从第14个点，即回转半径取到140 km之后，道路网络的分形分维特征不再明显，这一方面与研究区域的边界有关，另一方面则与拉萨市的独特地理环境有关，由此可见出现这种现象从实际的角度分析是合理的。

此外，在利用长度-半径维数对城市交通网络进行研究时，往往会因为研究区域的边界问题而需要在对数据做回归分析时划分“无标度区”，本文利用LMedS处理之后的数据竟与按照常规经验方法划分的“无标度区”一致，可见该数据质量控制方法还可用于划分“无标度区”。

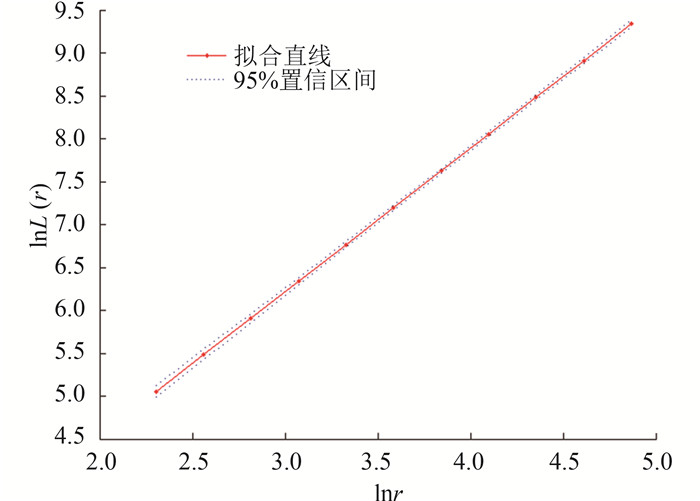
(4) 分维数的不确定性度量。对城市交通网络分布图进行了矢量化、选取测算中心、建立缓冲区、数据异常值去除等基本数据处理之后，按照长度-半径维数模型对其分维数进行测算。本文以拉萨市交通枢纽中心为测算中心，并根据式(14)对其分维数的不确定性进行了度量，根据式(15)对回归直线的置信域进行了求解和绘制出图，则在满足置信水平95%的情况下分形维数的置信区间为(1.633，1.707)，其对应的分布情况如图 5所示。


图 5 长度-半径维数模型回归函数的置信区间
Fig. 5 The confidence interval of regression function of the length-radius dimension model

由图 5可以看出：长度-半径维数模型回归函数的置信区间呈现中间窄两头较宽的表现形式，且置信区间的上限和下限差距较小，可见，LMedS对数据质量进行了良好的控制。结合上图和分形维数的置信区间的结果来看，点列的分布与拟合直线的拟合情况良好，但其分维数的差别还是达到了0.074，看起来差别不大的数字，在对其交通网络的分布进行认识和界定时，却相差很大。若拉萨市的交通网络分维数为1.707，则其分维数已略高于1.7的普适性的分形分维值(刘妙龙和黄蓓佩，2004)，说明其交通网络的发育状况良好，已相对较为成熟；但若其分形维数为1.633，只能说明拉萨市的交通网络发育程度较好，且仍有一定的发展空间，其交通网络仍需不断完善。由此可见，该实验过程在数据处理和建立长度-半径维数模型这一过程中引入了很多不确定性因素，以至对真实实验结果会产生很大影响，从另外一个角度来看，这同时也表明本方法对长度-半径维数模型进行不确定性度量是可行的。

分形维数的一点变化，有可能会影响到研究区域交通网络未来发展策略的改变，因而探寻交通网络分形维数的不确定性极为重要。分形维数的不确定性来源包括很多方面，其不确定性是多重不确定性误差传播累积的结果，且其误差的传输和累积可以用式(16)概括表示。通过全面了解其不确定性，在实验过程中将人为产生的不确定性降到最低，并对其不确定性进行度量估计与分析，可以为更全面真实地了解城市交通网络的分布状况服务。

4 结论

长度-半径维数模型作为将复杂的不确定性交通网络分布变得简单的研究，将自相似的分形几何转换到分形维数后，并不是一个问题确定性的终结，这恰恰是其自身不确定性的开始，而且其不确定性包括很多方面，且有些无法避免，并在测算过程的各个环节都有可能引入。最后对长度-半径维数模型在测算过程中的不确定性及其质量控制总评如下：

(1) 从不确定性来源来看，主要包括道路网的选择和路网的矢量化过程、测算中心和测算尺度的选取、实验数据的不确定性、模型本身具有的不确定性等方面。

(2) 对分维数的测算过程是一个完整连续的过程，依据误差传播累积理论，可以首先基于LMedS去除异常值数据从而提高可靠性，继而通过计算分维数满足一定置信水平的置信区间对其不确定性进行度量，用于辅助分析城市交通网络的分形分维情况。

本文提出的不确定性分析度量方法不仅适用于长度-半径维数模型，而且对于与其测算方法类似的分枝维数可完全适用，甚至对于统计学意义上自相似性的所有分形几何问题，即：需拟合求解分维值的方法(例如，如盒子维数等模型)，在数据质量控制和不确定性度量方面同样具有借鉴和推广价值。当然，此项研究也有其局限性，本文指出了分形维数的不确定性来源并对其进行了测算，但并未对其误差贡献进行量化；另一方面，本文只探讨了城市交通网络分形维数的不确定性，而在其他应用领域中的不确定性尽管存在与本研究相同的共性问题，但还存在差异性的个性问题，值得进一步深入研究。因此，如何将每种来源的不确定性因素在度量过程中进行量化、如何制定统一的测算标准、分形分维理论在其他领域应用中的不确定性探讨是下一阶段研究的重点。

参考文献(References)

数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献