|
收稿日期: 2016-05-15; 修改日期: 2016-07-01;
优先数字出版日期: 2016-09-25
基金项目: 国家自然科学基金项目(编号:41231170,41501406)
第一作者简介:
李召良(1964-), 男, 研究员, 研究方向为热红外定量遥感反演。E-mail:lizhaoliang@caas.cn
中图分类号: TP79
文献标识码: A
文章编号: 1007-4619(2016)05-0899-22
|
摘要
地表温度是表征地表过程变化的一个非常重要的特征物理量,是地表-大气能量交换的直接驱动因子,广泛地用于地表能量平衡、气候变化和资源环境监测等研究领域。本文系统地评述了热红外地表温度遥感反演方法,包括单通道算法、多通道算法、多角度算法、多时相算法和高光谱反演算法。回顾了地表温度反演的基础理论和方法;并在此基础上,进一步综述了地表温度遥感反演的验证方法,以及地表温度的时间和角度归一化方法;最后对未来提高地表温度反演精度的研究方向提出了建议。
关键词
地表温度 , 热红外数据 , 反演 , 验证
Abstract
Land Surface Temperature (LST) is a key parameter in the physical processes of surface energy and water balance at local and global scales. Knowledge of LST provides information on the temporal and spatial variations of the surface equilibrium state and is of fundamental importance in many applications. This paper systematically surveys the methods for LST derived from thermal infrared remotely sensed data. These methods include single-channel, multi-channel, multi-angle, multi-temporal, and hyperspectral retrieval methods. To provide potential LST users with reliable information regarding the quality of the LST product and to provide feedback to the developers of LST retrieval algorithms for future improvement, assessing the accuracy of the retrieved LST is necessary. We review the methods used to validate LST derived from thermal infrared remotely sensed data, including temperature-based, radiance-based, and inter-comparison methods. The advantages and disadvantages of these methods are discussed. Furthermore, we review the temporal and angular normalization methods of satellite-derived LST. Finally, we present suggestions for future research to improve the accuracy of satellite-derived LST.
Key words
land surface temperature , thermal infrared data , retrieval , validation
1 引言
地表温度LST(Land Surface Temperature)是区域和全球尺度上陆地表层系统过程的关键参数,它综合了地表与大气的相互作用以及大气和陆地之间能量交换的结果(Anderson等,2008;Brunsell和Gillies,2003;Karnieli等,2010;Kustas和Anderson,2009;Zhang等,2008)。地表温度作为众多基础学科和应用领域的一个关键参数,能够提供地表能量平衡状态的时空变化信息,在数值预报、全球环流模式以及区域气候模式等研究领域得到广泛的应用。精确的地表温度不仅有助于评估地表能量与水文平衡、热惯量和土壤湿度,而且有助于获取全球表面温度及掌握其长期的变化(Arnfield,2003;Bastiaanssen等,1998;Hansen等,2010;Kalma等,2008;Kogan,2001;Su,2002;Voogt和Oke,2003;Weng,2009;Weng等,2004)。因此,国际地圈生物圈计划将地表温度列为优先测定的参数之一(Townshend等,1994)。由于影响地表温度的表面状态参数,例如反照率、土壤的物理和热特性以及植被等具有较强的空间非均匀性(Liu等,2006;Neteler,2010),地表温度在时空领域里变化相当快(Prata等,1995;Vauclin等,1982)。要获取区域和全球尺度上地表温度的时空分布,常规的地面定点观测难以实现,而卫星遥感是唯一可能的手段(Dash等,2002;Li等,2013;Prata等,1995)。
利用热红外遥感数据反演地表温度最早可追溯到20世纪70年代(McMillin,1975)。为了更好地了解区域尺度的地球系统以及获得精度优于10%的蒸散发数据,地表温度的反演误差必须在1K以内(Wan和Dozier,1996)。然而星载热红外辐射计所接收的波谱信息,不仅受地球表面参数(温度,比辐射率)的影响,而且还受到从地球表面到辐射计之间电磁波传输路径上大气成分和热结构的影响。因此利用星载热红外遥感获取地表温度必须解决两个问题:首先进行大气校正,即消除大气的干扰,其次是考虑地表发射率的影响。为了实现卫星热红外数据地表温度反演,国内外学者进行了大量研究,并提出了不同的方法来消除发射率和大气的影响(Becker和Li,1990;Gillespie等,1998;Jiménez-Muñoz和Sobrino,2003;Kealy和Hook,1993;Kerr等,1992;Vázquez等,1997;Price,1983,1984;Qin等,2001;Susskind等,1984;Tonooka,2001;Wan和Dozier,1996;Wan和Li,1997)。本文系统地回顾了热红外地表温度遥感反演方法的研究进展,并指明了未来提高反演精度的研究方向。
2 红外辐射传输基础理论
根据普朗克定律(Planck’s law),绝对温度大于0 K的任何物体都会向外以电磁波的形式辐射能量。处于热平衡状态下的黑体在温度T和波长λ处的辐射能量可以用普朗克定律表示,即
| $ {B_\lambda }(T)= \frac{{{C_1}}}{{{\lambda ^5}\left[ {{\rm{exp}}\left({{C_2}/{C_2}\lambda T - \lambda T} \right)- 1} \right]}} $ | (1) |
式中,
由于绝大多数自然地物都是非黑体,它们的热辐射需要在式(1)中加入地表发射率ε的影响。地表发射率可定义为地物的实际热辐射与同温同波长下黑体热辐射的比值。自然地物的热辐射可以用地表发射率乘以式(1)的普朗克函数得到。显然,如果大气对卫星获取的辐亮度信号没有影响,那么在已知地表发射辐射和发射率的情况下,地表温度就能根据式(1)反演得到。
黑体在特定温度T(K)下单色辐射强度的极大值所对应的波长λmax可以用维恩位移定律表示,即
| $ T{\lambda _{\max }} = 2897.9{\rm{\mu m}} $ | (2) |
根据这一性质,对于温度在250—330 K的地表来说,其峰值波长λmax主要处于热红外波长范围(8.8—11.6 μm),而对于诸如火灾、火山喷发的高温地表,其温度可高于800 K,那么它们的峰值波长λmax主要处于中红外波长范围(3—5 μm)。因此,可以根据不同的需求选择不同的波长范围来探测地表热辐射状况。
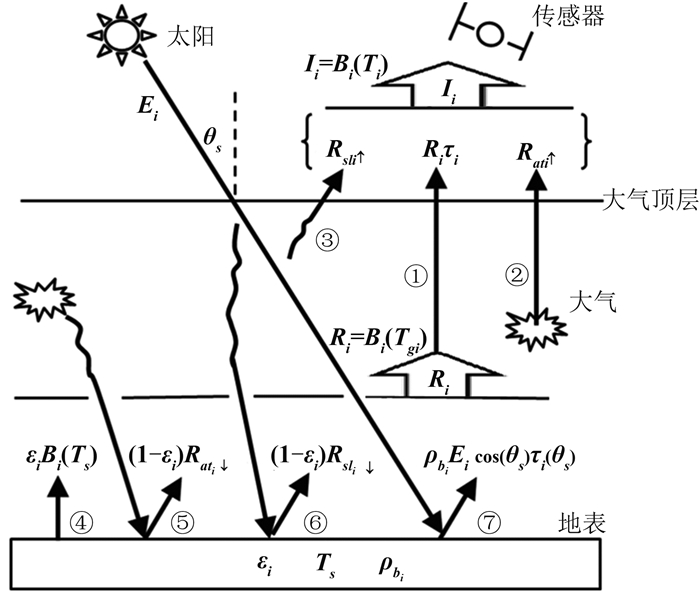
卫星红外传感器能够接收到视线方向上来自地表经大气传输的辐射信息。在局地热平衡的晴空无云条件下,根据辐射传输方程,传感器在大气顶部所接收到的通道辐亮度Ii可以表示为
| $ {I_{{i}}}{\text{(}}\theta {\text{,}}\varphi {\text{)=}}{R_i}(\theta {\text{,}}\varphi){\tau _i}(\theta {\text{,}}\varphi)\!+\! {R_{a{t_i} \uparrow }}(\theta {\text{,}}\varphi)\!+\! {R_{s{l_i} \uparrow }}(\theta {\text{,}}\varphi)$ | (3) |
式中,地表辐亮度
| $ \begin{aligned} {R_i}(\theta {\text{,}}\varphi){\text{ =}} & {\varepsilon _i}(\theta {\text{,}}\varphi){B_i}({T_s})+ [1 - {\varepsilon _i}(\theta {\text{,}}\varphi)]{R_{a{t_i} \downarrow }} {\text{+ }} \\ & [1 - {\varepsilon _i}(\theta {\text{,}}\varphi)]{R_{s{l_i} \downarrow }} + {\rho _{bi}}(\theta {\text{,}}\varphi{\text{,}}{\theta _s}{\text{,}}{\varphi _s})\times \\ & {E_i}\cos({\theta _s}){\tau _i}({\theta _s}{\text{,}}{\varphi _s})\hfill \\ \end{aligned} $ | (4) |
式中,θ和φ分别表示观测天顶角和观测方位角(图 1)。为简单起见,观测天顶角和方位角在之后公式中将被忽略。τi是通道i的大气等效透过率。
为了方便和数学简写起见,大气顶部辐亮度
| $ {B_i}({T_i})= {I_i}{\text{,}}\;{B_i}({T_{gi}})= {R_i} $ | (5) |
值得注意的是,式(3)—(5),除了角度变量(
| $ {X_i} = \frac{{\int_{{\lambda _1}}^{{\lambda _2}} {{g_i}(\lambda){X_\lambda }{\rm{d}}\lambda } }}{{\int_{{\lambda _1}}^{{\lambda _2}} {{g_i}(\lambda){\rm{d}}\lambda } }} $ | (6) |
式中,
3 热红外地表温度遥感反演方法
过去几十年里,利用卫星热红外数据进行地表温度反演已经得到了显著的发展。国内外研究者对辐射传输方程和地表发射率使用了不同的假设和近似,针对不同卫星搭载的不同传感器,提出了多种反演算法,这些算法大致可以分为5类:单通道算法、多通道算法、多角度算法、多时相算法、高光谱反演算法。
3.1 单通道算法
热红外单通道算法,利用卫星接收的位于大气窗口的单通道数据,使用大气透过率/辐射程序对大气的衰减和发射进行校正,需要输入大气廓线数据。然后在已知地表发射率的条件下,将式(3)和式(4)反向计算,得到地表温度(Ottlé和Vidal-Madjar,1992;Price,1983;Susskind等,1984)。使用这种方法精确反演地表温度需要高质量的大气透过率/辐射程序来估算式(3)和式(4)中的大气参数,还需要已知通道发射率和准确的大气廓线,并且需要考虑地形的影响(Sobrino等,2004b)。
通常,大气透过率/辐射程序的精度主要受到程序中所使用的大气辐射传输模型以及大气分子吸收系数和气溶胶吸收系数不确定性的影响(Wan,1999)。最常见的大气辐射传输模型,如MODTRAN系列模型和4A/OP模型,已经被广泛用于大气校正或卫星热红外数据模拟。研究表明,在大气窗口内,如3.4—4.1 μm和8—13 μm,不同大气辐射传输模型的精度在0.5%—2%之间,这将造成反演的地表温度误差在0.4—1.5 K之间(Wan,1999)。值得注意的是,即使大气辐射传输模型本身完全没有误差,在对大气的吸收和程辐射进行校正时,所用的大气廓线本身的不完整性也会造成一个严重的问题(Gillespie等,2011)。相关研究还表明,地表发射率1%的误差在湿热大气下会对地表温度造成0.3 K的误差,而在干冷大气下误差更是高达0.7 K(Dash等,2002)。由于单通道的波长范围通常在10 μm左右,在这个范围内大多数的地表发射率在百分之几以内,而发射率的不确定性会造成地表温度1—2 K的误差。然而,如果某个波长的地表发射率已知,那么反演误差就完全来自于大气校正。大气廓线通常是由地面无线探空设备、卫星垂直探测仪和气象预测模型测量得到。由于大气水汽会随着时间和空间发生剧烈变化,利用地面无线探空设备探测远离目标区域的大气或探测远离卫星过境时刻的大气可能都会对地表温度反演结果造成较大误差(Cooper和Asrar,1989)。
为了减少对探空数据的依赖性,过去10年内已经提出了多种单通道算法,利用卫星遥感数据在发射率已知的条件下反演地表温度。Qin等人(2001)提出了一种基于Landsat-5 TM数据的单通道地表温度反演算法,该算法利用了大气透过率和水汽含量之间以及平均大气温度和近地表空气温度之间的经验线性关系,仅仅需要近地表空气温度和水汽含量,而不需要知道大气廓线。Jiménez-Muñoz和Sobrino(2003)以及Jiménez-Muñoz等人(2009)发展了一种通用型单通道算法,该方法适用于任何半高全宽约1 μm的热红外通道数据,前提是需要已知地表发射率和总大气水汽含量。这种通用型单通道算法只需要最少的输入数据,可应用于使用相同方程和系数的不同热红外传感器。Cristóbal等人(2009)也发现在单通道算法中使用近地面空气温度和大气水汽含量可以提高地表温度反演精度,尤其是在水汽含量较高的情况下。Sobrino等人(2004b)、Sobrino和Jiménez-Muñoz(2005)、Jiménez-Muñoz和Sobrino(2010)分析比较了上述算法,并指出所有使用经验关系的单通道算法在高水汽含量情况下精度较差,这是因为在高水汽浓度下,算法中使用的经验关系都是不稳定的。
需要注意的是,单通道算法是对辐射传输方程的简单变形,前提是地表发射率和大气廓线已知。这些方法虽然在理论上能够精确反演地表温度,但高精度的地表发射率在实际应用中很难获取。
3.2 多通道算法
正如3.1节中所强调的,使用单通道算法需要已知每个像元的地表发射率、大气辐射传输模型以及精确的大气廓线。这些条件在绝大多数的实际情况中很难或者不可能满足。为了利用卫星热红外数据获取全球或区域尺度下高精度的地表温度,必须发展其他方法。一种用于海洋温度反演的方法(即分裂窗算法),利用了中心波长在11—12 μm之间的两个通道水汽吸收不同的特点,最早是由McMillin(1975)提出的,这种方法不需要任何大气廓线信息。在此之后,多种分裂窗算法被提出并修改,成功用于海面温度反演(Barton等,1989;Deschamps和Phulpin,1980;França和Carvalho,2004;Llewellyn-Jones等,1984;McClain等,1985;Niclòs等,2007;Sobrino等,1993)。受到分裂窗算法成功用于海面温度遥感反演的启发,从20世纪80年代开始,国内外学者努力尝试将其扩展用于地表温度反演(Atitar和Antonio Sobrino,2009;Becker,1987;Becker和Li,1990;Coll等,1994;Prata,1994a,b;Price,1984;Sobrino等,1991,1994,1996;Tang等,2008;Ulivieri等,1994;Wan和Dozier,1996)。
3.2.1 线性分裂窗算法
线性分裂窗算法利用10—12.5 μm之间相邻通道的对水汽吸收特性不同的特点,根据温度或波长对辐射传输方程进行线性化处理。这种方法将地表温度表达为两个热红外通道亮度温度的线性组合(McMillin,1975)。一种典型的线性分裂窗算法可以写为
| $ LST = {a_0} + {a_1}{T_i} + {a_2}({T_i} - {T_j})$ | (7) |
式中,ak(k=0,1,2)主要与两个通道的光谱响应函数
| $ {a_k} = {f_k}({g_i}{\text{,}}{g_i}{\text{,}}{\varepsilon _i}{\text{,}}{\varepsilon _i}{\text{,}}WV{\text{,}}VZA)$ | (8) |
需要指出的是,这种地表温度反演方法的精度有赖于系数ak的正确选择,这些系数可以通过对模拟数据的回归或者比较卫星数据和实测地表温度数据之间的经验关系来确定。要在卫星像元尺度上(几平方公里)获得与卫星观测同步的有代表性的地面实测温度数据是极其困难的。因此,利用辐射传输方程如MODTRAN(Berk等,2003)来模拟大气顶部的亮度温度是一种有效的方式,通过比较模拟卫星数据与模型中预设的地表温度,可以准确地确定系数ak。过去几十年里,已经发展了多种线性分裂窗算法,这些算法形式上都比较相似,只是对系数ak的参数化不同。但总的来说,这些系数都被参数化为地表发射率、水汽含量和观测天顶角的线性或非线性组合。
3.2.2 非线性分裂窗算法
由于对辐射传输方程线性处理以及分裂窗算法中的近似处理会产生误差,如把大气透过率近似处理为水汽含量的线性函数,最终导致如式(7)中的线性分裂窗算法反演的地表温度在湿热的大气条件下误差较大。为了提高反演精度,发展了一种非线性分裂窗算法,即
| $ LST = {c_0} + {c_1}{T_i} + {c_2}({T_i} - {T_j})+ {c_3}{({T_i} - {T_j})^2} $ | (9) |
式中,系数ck(k=0,···,3)如式(7)中的系数ak一样,利用不同大气和地表参数下的模拟数据,根据式(8)拟合回归得到。
在最近几十年里,已经发展了多种形式相似的非线性分裂窗算法(Atitar和Antonio Sobrino,2009;Coll和Caselles,1997;François和Ottlé,1996;Sobrino和Raissouni,2000;Sobrino等,1994)。与线性分裂窗算法一样,有的非线性分裂窗算法将地表发射率加入到ck的表达式中,有的则同时考虑了发射率和水汽含量,有的还考虑了观测天顶角。
3.2.3 线性或非线性多通道算法。
当有3个或多个热红外通道时,使用类似上述分裂窗算法的方法,将这些通道大气顶部的亮度温度进行线性或非线性组合来反演地表温度(Sun和Pinker,2003,2005,2007)。例如,Sun和Pinker(2003)等发展了一种三通道线性算法,利用GOES数据反演夜间地表温度。在该方法中,假设3个通道的地表发射率可以根据地表类型估算得到。此外,利用3.9 μm处中红外通道Ti1的特点提高夜间大气校正的精度,3个通道线性方程的参数由通道发射率组成,没有考虑水汽含量和观测天顶角,即
| $ \begin{split} LST = & {d_0} \!+\!({d_1} \!+\! {d_2}\frac{{1 - {\varepsilon _i}}}{{{\varepsilon _i}}}){T_i} \!+\!({d_3} \!+\! {d_4}\frac{{1 - {\varepsilon _j}}}{{{\varepsilon _j}}}){T_j} {\text{+ }} \\ &({d_5} + {d_6}\frac{{1 - {\varepsilon _{i1}}}}{{{\varepsilon _{i1}}}}){T_{i1}} \end{split} $ | (10) |
式中,dk(k=0,···,6)是常数,与大气和观测天顶角无关。与已有的分裂窗算法(Becker和Li,1990;Wan和Dozier,1996)比较结果表明,这种三通道算法能够获得最好的地表温度值,均方根误差是1 K(Sun和Pinker,2003)。此外,Sun和Pinker(2007)还提出了一种基于SEVIRI(Spinning Enhanced Visible and Infrared Imager)数据的四通道非线性地表温度反演算法,算法考虑了地表发射率的影响,系数与地表类型有关。对于夜间的地表温度反演,算法可以写为
| $ \begin{split} LST = & {e_0} + {e_1}{T_i} + {e_2}({T_i} \!-\! {T_j})+ {e_3}({T_{i1}} \!-\! {T_{i2}})+ \\ & {e_4}{({T_i} \!-\! {T_j})^2} {\text{+ }} {e_5}(\sec VZA - 1)\end{split} $ | (11) |
式中,下标i2表示8.7 μm处的热红外通道,系数ek(k=0,···,5)与地表类型有关。为了计算白天中红外通道i1地表反射的太阳直射辐射,太阳校正项
需要注意的是,卫星在白天大气顶部接收到的中红外数据包括地表反射的太阳直射辐射以及地表和大气自身的发射辐射,而太阳校正项的误差也会影响最终地表温度的反演精度,特别是在中红外波段反射率较高的干旱和半干旱地区。另外,多增加一个通道也会随之带来增加测量误差的代价。此外,与测量仪器噪声和其他不确定性有关的误差也会影响最终地表温度的反演精度。在中红外通道和8.7 μm通道,自然和人造地表的发射率范围以及各种不确定性要比传统分裂窗算法中使用的通道更高(Trigo等,2008b),这也进一步限制了这些通道在业务应用中的广泛使用。
3.2.4 温度发射率分离法(TES)
Gillespie等人(1996)利用大气校正后的先进星载热发射和反射辐射仪(ASTER)数据,率先提出了温度发射率分离法。这一方法基于光谱反差和最小发射率之间的经验关系来增加方程的数目(等价于减少未知数的个数),使不可解的反演问题变得可解。TES算法由3个成熟的模块组成:发射率归一化方法(NEM)(Gillespie,1995)、光谱比值(SR)、最大最小表观发射率差值法(MMD)(Matsunaga,1994)。
NEM模块最早被用来估计初始的地表温度值和从大气校正后的辐射值中得到的归一化后的地表发射率值(Gillespie等,1996)。SR模块用来计算归一化后的发射率值与它们均值的比值,尽管SR模块不能直接获得真实的地表发射率值,但即使地表温度是由NEM模块粗略估计出的,发射率光谱的形状还是能得到很好的描述。最后,在SR模块结果的基础上,MMD模块用来找出N个通道的光谱差异(即MMD),接着利用N个通道的最小发射率值(LSEmin)和MMD之间的经验关系估算出最小的地表发射率。一旦估算出最小发射率值,其他通道的发射率也可以直接通过SR得到,接着便可以估算出地表温度并使之完善(Gillespie等,1998)。
TES的主要优势是结合了3个前驱具有吸引力的特征并且利用了N个通道的发射率范围和最小发射率值之间的经验关系来反演地表温度和发射率。因此,该方法可以适用于任何类型的自然下垫面,特别是类似于岩石和土壤的具有较大光谱反差的发射率的下垫面,并且不需要考虑发射率中的光谱差异(Gillespie等,1998;Sobrino等,2008)。数值模拟和一些实验场的验证表明当大气校正精度较高时,TES算法反演地表温度的精度可以达到±1.5 K以内,发射率的精度可以达到±0.015以内(Gillespie等,1996,1998;Sawabe等,2003)。另外,Hulley和Hook(2011)优化了LSEmin和MMD之间的关系,使得TES算法能够适用于MODIS的3个热红外通道(29,31,32)。
有些研究表明对于具有较小光谱反差的发射率的下垫面(比如水,雪和植被),和在湿热的大气条件下,TES算法在地表温度和发射率反演中会引入显著的误差(Coll等,2007;Gillespie等,1996,2011;Hulley和Hook,2009,2011;Sawabe等,2003)。Sabol等人(2009)指出在TES的原始版本中,低发射率反差和高发射率反差会被区别对待。因此,在该版本中,对于在LSEmin和MMD的散点图回归线上方的地物(比如土壤、植被、水体(雪)),反演出的地表发射率较低,而地表温度较高。这也解释了为什么有些研究指出对于裸土而言,不精确的大气校正可能在温度反演中产生2 K—4 K的误差(Dash等,2002)。对于温暖潮湿的大气,显著误差的来源是不同的。大气校正中的不确定性会导致较大的明显的发射率差异,对于灰体表面,将会有更大的影响(Hulley和Hook,2011)。为了尽可能减小大气校正的误差,Gillespie等人(2011)利用Tonooka(2005)提出的水汽缩放法(WVS)来改善TES算法。
正如数值模拟中显示的那样,当通道数减少时,地表温度和反射率反演的不确定性会增大,使得TES算法不适用于绝大多数正在运行的传感器(Sobrino等,2008)。传感器定标误差和热红外通道噪声也可能对地表温度和发射率的反演产生不确定性(Gillespie等,2011;Jiménez-Muñoz和Sobrino,2006;Sobrino等,2008)。另外,TES算法对于低差异和高差异的地表是区别对待的,这使得在灰体边缘会出现不连续的情况,比如水体、森林和庄稼(Sobrino等,2007)。为了解决这些问题,Sabol等人(2009)将初始的TES算法中的LSEmin和MMD之间的幂函数关系替换为线性表达式,并将这一新关系应用于所有的地物来减小这种不连续性。研究表明这一修改对于岩石表面和灰体来说,精度会有一点下降,但对近灰体表面来说,却可以提高其精度。
3.3 多角度算法
多角度算法是建立在同一物体由于从不同角度观测时所经过的大气路径不同而产生的大气吸收不同的基础上。由于大气吸收体的相对光学物理特性在不同观测角度下保持不变,大气透过率仅随角度的变化而变化。与分裂窗算法的基本原理类似,大气的作用可以通过特定通道在不同角度观测下所获得亮温的线性组合来消除(Chedin等,1982;Li等,2001;Prata,1993,1994a,1994b;Sobrino等,1996,2004a)。
这种算法主要基于第一代双角度模式卫星,即搭载在第一代欧洲遥感卫星(ERS-1)上的沿轨扫描辐射计(ATSR)发展而来。ATSR能够在2 min内对同一片地表区域进行双角度观测。一个是垂直观测,天顶角范围是0°—21.6°,另一个是前向观测,天顶角范围是52°—55°。假设地表温度和海面温度与观测天顶角无关,大气状况在水平方向是均一的并且在观测时间内稳定不变,Prata(1993,1994a)提出了一种基于ATSR数据的双角度算法反演地表温度和海面温度。Sobrino等人(1996)提出了一种改进型的双角度算法,考虑了垂直观测时的发射率εn和前向观测时的发射率εf
| $ LST = {T_n} + {p_1}({T_n} - {T_f})+ {p_2} + {p_3}(1 - {\varepsilon _n})+ {p_4}({\varepsilon _n} - {\varepsilon _f})$ | (12) |
式中,pk(k=1,···,4)是与垂直和前向观测角度下大气透过率和平均等效空气温度有关的参数;Tn和Tf分别是垂直和前向观测时的亮度温度。这种算法仅与发射率有关,而与水汽含量无关。Sobrino等人(2004a)发展了一种非线性双角度算法来减少大气水汽含量对地表温度反演结果的影响,即
| $ \begin{split} LST = & {T_n} + {q_1}({T_n} - {T_f})+ {q_2}{({T_n} - {T_f})^2} + \\ &({q_3} + {q_4}WV)(1 - {\varepsilon _n})+ \\ &({q_5} + {q_6}WV)\Delta \varepsilon + {q_0} \end{split} $ | (13) |
式中,qk(k=0,···,6)是与传感器有关的常量,可以利用模拟数据拟合回归确定。利用模拟热红外数据,Sobrino和Jiménez-Muñoz(2005)比较了如式(13)所示的双角度算法,并考虑了地表发射率、水汽含量和观测天顶角的非线性分裂窗算法。结果表明,在地表发射率的光谱和角度变化已知情况下,双角度算法精度要优于分裂窗算法。
值得注意的是,尽管多角度(双角度)算法能够比分裂窗算法提供更好的结果,但是双角度算法应用于卫星数据时有几个实际困难(Sobrino和Jiménez-Muñoz,2005)。多角度算法中的一个重要现象是发射率的角度相关性,因为在卫星空间分辨率尺度下,自然地表的角度效应是未知的,如裸土和岩石(Sobrino和Cuenca,1999)。地表温度的角度相关性也是一个问题。除了需要大气晴空无云并且水平均一,还必须要求在不同斜程路径下的多角度测量有明显差异。否则,不同角度下的测量会高度相关,导致算法不稳定,并对仪器噪声极其敏感(Prata,1993,1994a)。此外,在不同观测角度下对同一目标地物进行观测会覆盖不同的传感器区域(即像元)。即使可能会观测到同样的像元大小,但由于地物的3维结构,在不同观测角度下观测到的地物仍可能明显不同。最后,不同观测角度像元的配准不好会导致地表温度反演结果的巨大误差。所以,多角度算法仅适用于理想大气条件下的均质区域(如海洋表面或浓密森林植被),而不适用于非均质地表。
3.4 多时相算法
多时相算法是在假定地表发射率不随时间变化的前提下利用不同时间的测量结果来反演地表温度和发射率的,其中比较有代表性的是两温法(Watson,1992)和日夜双时相多通道物理反演法(Wan和Li,1997)。
3.4.1 两温法
两温法的思路是通过多次观测来减少未知数的个数。假设热红外通道已经经过精确的大气校正并且发射率不随时间而发生变化,那么如果地表被N个通道两次观测,2N次测量将会有N+2个未知数(N个通道的发射率以及2个地表温度)。因此,当N≥2时,这N个地表发射率和2个地表温度可以从2N个方程中同时得到(Watson,1992)。注意到地表发射率不随时间而变化的假设暗示地表是均匀的并且有相对稳定的土壤湿度,所以首先是要减小由于像元大小和观测角度带来的地表发射率的变动,其次要避免地表发射率随土壤湿度的变化而变化,比如要考虑降雨和露水的发生。
两温法的主要优势是它对地表发射率的光谱形状没有作出假设,只是假定发射率是不随时间而变化的。虽然这一方法有一个简单直接的公式,但是由于这2N个方程是高度相关的,因此方程的解可能不稳定,并且对传感器噪声和大气校正产生的误差非常敏感(Caselles等,1997;Gillespie等,1996;Watson,1992)。由于在没有实测大气廓线数据的情况下,很难进行非常精确的大气校正,因此在反演地表温度和发射率时使用近似的廓线可能导致比较大的误差。Peres和DaCamara(2004)发现增加观测的次数和(或)温差可以提高反演的精度,但是这种提高会受到热红外测量高相关性的限制。
除了上面提到的问题外,这一方法还需要在两个不同的时间点对影像进行精确的几何配准(Gillespie等,1996;Watson,1992)。对于下垫面均匀的区域,不精确配准带来的地表温度和发射率误差较小,但对于下垫面不均匀的区域,这一误差将较大(Wan,1999)。卫星观测天顶角的改变会引起地表发射率的改变,因此违背了地表发射率不随时间改变的假设,导致两温法的精度降低(Li等,2013)。
3.4.2 日夜双时相多通道物理反演法
Wan和Li(1997)受到日夜温度无关波谱指数法和两温法的启发,进一步提出了日夜物理反演法,即通过结合白天和晚上的中红外以及热红外数据来同时反演地表温度和发射率。这一方法假定从白天到夜晚地表发射率不会发生太大的改变,并且在中红外波段感兴趣范围角度形式因子的变化很小(<2%),以此减少未知数的个数,从而使反演更加稳定。为了减小反演过程中大气校正残差的影响,引入了两个变量:大气底层的空气温度(Ta)和大气水汽含量(WV),以此来改正反演过程中初始的大气廓线。有了N个通道的两次测量(白天和夜晚),未知数的个数为N+7(N个通道的发射率,2个地表温度,2个Ta,2个水汽含量,1个中红外通道的角度形式因子)。因此,为了使方程可解,N必须大于等于7。
通常来讲,日夜物理反演法是之前提到的使用两次观测的两温法的发展,与之前提到的两温法和日夜温度无关波谱指数法相比,日夜算法在以下几个方面较为突出:
(1)对于中红外通道,白天太阳辐射的存在会显著地减小方程之间的相关性,从而使方程的解更加稳定和精确。日夜温度无关波谱指数法首先需要获得像元的双向反射率,再分别计算地表温度和发射率,然而日夜算法是同时将两者反演出来,避免了逐步反演中误差传播情况的出现。另外,尽管在两次测量中(白天和夜晚)地表温度相同,日夜算法可以获得精确的地表温度和发射率,但只利用到热红外测量的两温法则要求不同温度值之间有显著的差异。
(2)通过考虑初始大气廓线带来的误差,引入两个变量(Ta、WV)后,地表温度和发射率的反演精度得到很大的提高。因此,日夜算法对大气校正的精度并没有要求,这一点与日夜温度无关波谱指数法和两温法很不相同。
(3)日夜算法不需要12小时间隔的测量(白天和夜晚),只要地表发射率不发生大的改变,几天内获得的白天和夜晚的数据也同样可用。
但是,和其他的多时相反演方法类似,日夜算法同样面临着几何配准精度低以及观测天顶角变化等关键问题。为了解决几何配准精度不高的问题,Wan(1999)将MODIS像元从1 km的分辨率聚合为5 km或6 km。与此同时,16组观测天顶角用来保证白天和夜晚观测天顶角分组的质量(Wan和Li,2011)。为了避免最差的解,获得更好的地表温度反演结果,Wan(2008)实现了一系列的优化,这些优化所针对的包括一些并不理想的情况:周围云层和气溶胶的影响、由于雨雪天气以及夜晚露水的出现导致中红外通道和8.75 μm通道在白天和夜晚的地表发射率的值不同(假设31和32通道相对高发射率值受这些情况影响较小,即使是在干旱地区)。这些优化包括:结合使用Terra和Aqua卫星MODIS数据、为白天数据增加权重、完全结合依赖于观测角的通用分裂窗算法和日夜算法作为地表温度差异的紧密成分和相关的约束条件、使用31和32波段发射率的变量、日夜算法中解的迭代里使用WV和Ta、有效地提高31和32波段最高质量数据所占的权重。更多关于MODIS日夜算法的细节可以参考文献(Wan,2008;Wan和Li,1997,2011)。
3.5 高光谱反演算法
高光谱反演算法依靠的是地表发射率固有的光谱特性而不是时相信息,其中比较有代表性的是迭代光谱平滑温度发射率分离法(Borel,2008)和线性发射率约束法(Wang等,2011)。在一些合理的假设和约束下,通过减少未知数的个数或者增加方程的数量,利用这些方法可以使用经过大气校正后的辐射值反演出地表温度和发射率。
3.5.1 迭代光谱平滑温度发射率分离法
高光谱热红外数据可以提供更多的关于大气和地表的详细的光谱信息,Borel(1997,1998,2008)指出典型的发射率光谱和由大气引入的光谱特征相比要平滑的多,根据式(4)给出的辐射传输方程可以知道,如果地表温度没有准确地估计,相应的地表发射率光谱会显示出大气光谱特征,即在估算出的地表发射率波谱上会出现由大气吸收线引起的锯齿。当反演的地表发射率的光谱平滑度达到最大时,反演出的地表温度和发射率是最准确的。在这一属性的基础上,从高光谱热红外数据中反演地表温度和发射的迭代光谱平滑温度发射率分离法被提了出来。学者们提出了包括一阶和二阶等各种平滑标准(Borel,2008;Cheng等,2010;Kanani等,2007;Ouyang等,2010)。事实上,在不考虑平滑函数细节的前提下,这些不同的平滑标准都会得出相同的统计结果。
Ingram和Muse(2001)分析了这一方法对光谱假设和测量噪声的敏感性,发现对典型地物来说,这一假设对反演精度的影响是可以忽略的,但这也依赖于信噪比,即当信噪比较高时反演的精度也较高。和之前提到的绝大部分方法类似,该方法需要精确的大气校正,在众多的影响因素中,大气校正对反演结果的影响是最大的。除此之外,反演精度还对热红外通道中心波长的移动以及波段宽度较为敏感(Borel,2008)。Wang等人(2011)指出当地表温度与大气下行辐射的有效温度接近时,异常点的出现可能会使找到令人满意的解变得困难。
3.5.2 线性发射率约束法
Wang等人(2011)受到最初由Barducci和Pippi(1996)提出的灰体发射率法的启发,提出了从经过大气校正的高光谱热红外数据同时反演地表温度和发射率的新的TES算法。这一算法假定发射率光谱可以被分为M个部分,每一部分的发射率随着波长线性变化。在这种情况下,发射率光谱可以通过获取值为aak,偏差值为bbk(k=1,…,M)的分段线性函数来重新创建。假定方程数N(对应N个通道测量值)大于或等于未知数的个数(2M+1,对应1个地表温度,M个aak,M个bbk),那么地表温度和发射率可以同时获得。由于高光谱热红外传感器有许多窄通道,所以N≥2M+1这一条件很容易满足。
Wang等人(2011)进行了一系列的敏感性分析,发现在选择了好的区段长度的情况下,由发射率线性变化的假设引入的误差可以被忽略,区段长度建议选择10 cm–1。该方法与ISSTE算法相比,产生的异常点更少,白噪声和大气下行辐射的不确定性对其影响更小。由于大气光谱特征在湿热的大气环境中更为显著,所以LECTES方法在湿热大气中要比在干冷大气中的效果更好。该方法与ISSTES类似,它只适合于高光谱热红外数据并且需要精确的大气校正。然而,由于分段线性函数可以使未知数的个数极大减少,所以这一方法显示出同时反演地表温度、地表发射率以及大气廓线的巨大潜力。Paul等人(2012)提出了一种通过红外大气探测干涉仪(IASI)高光谱数据同时反演地表温度和发射率光谱的方法。在这种方法中,地表温度和发射率反演利用了陆地发射率的初估值,这一初估值是通过非线性统计(神经网络)法将6个MODIS通道插值到IASI高光谱范围中得到的。
4 卫星反演地表温度的验证
尽管近几十年来提出了很多算法来从卫星热红外数据中反演地表温度,但是很少有对这一温度进行验证的报道。这是因为在地面测量卫星像元尺度的地表温度较难,而且地表温度自身也存在较大的时间和空间上的变化。在最近几年,一些研究开始验证通过不同传感器得到的地表温度,其中大多是下垫面均匀的。这些传感器验证包括TM/ETM+、ASTER、AVHRR、AATSR、MODIS和SEVIRI数据(Coll等,2005,2010,2012;Hulley和Hook,2009;Niclòs等,2011;Prata,1994b;Sabol等,2009;Sawabe等,2003;Sobrino等,2007;Sòria和Sobrino,2007;Trigo等,2008a,b;Wan,2008;Wan和Li,2008;Wan等,2002,2004)。其中,有3种方法通常被用来验证从遥感数据中反演得到的地表温度值:基于温度的方法(T-based)、基于辐射的方法(R-based)以及交叉验证。
4.1 基于温度的方法(T-based)
基于温度的方法是基于地面的方法,它直接将从卫星数据中反演得到的地表温度与在卫星过境时刻地面测量的温度进行对比(Coll等,2005;Prata,1994b;Slater等,1996;Wan等,2002;Wang等,2008;Li等,2013;Guillevic等,2012;)。然而,在实验场测量地表温度是一项复杂而又困难的工作,这是由于卫星像元(几平方千米)和实验场传感器(几平方米或几平方厘米)的尺度差异造成的。此外,自然地表覆盖和相应的地表温度和发射率值在公里级别上的差异很大。Snyder等人(1997)指出均匀并且平坦的容易被测量和特征化的表面可以作为验证站点,包括内陆水、沙、雪和冰(Coll等,2005;Guillevic等,2012;Sobrino等,2004a;Wan,2008)。验证仪器需要观测的区域大小取决于地表像元间的差异以及几个“端元”可以结合的程度,从而获取卫星像元的代表值。这一过程一直很有挑战性,这是因为在影像中很难找到足够的地表,在地面上进行有代表性的热量的采样也较为困难。
由于在像元尺度上绝大多数地球表面都是不均匀的,高质量的地面温度验证较为缺乏,并且受限于一些均匀的地表类型,比如专用的湖泊、海滩、草地和农田(Coll等,2005,2010,2009;Wan等,2002,2004)。一旦确定了热量均匀的区域,由验证站点地面测量仪器在几个点处测量的地表温度的平均值可以认为是真实的地表温度值,并且可将其与像元尺度上卫星数据反演得到的地表温度值进行比较。许多学者利用这个方法针对不同的传感器进行了地表温度值的验证(Coll等,2005,2010,2009;Peres等,2008;Sabol等,2009;Wan,2008;Wan等,2002)。
基于温度的方法的主要优势在于它提供了直接评估卫星传感器辐射质量和地表温度反演算法改正大气和地表发射率影响的能力。然而,基于温度的方法验证的成功与否主要取决于地面温度测量的精度以及它们能在多大程度上代表像元尺度上的地表温度。由于地表温度会随着时间和空间变化,在几米或者短时间内,地表温度就可以有10 K甚至更大的变化,这取决于地表的本质、太阳辐射的级别以及当地气象条件,因此该方法的验证活动通常会限制于晚上以及均匀下垫面,比如湖泊、浓密草地以及植被区域。另外,即使地面观测可以展开,将地面点测量的尺度转换为卫星传感器视场角下的像元尺度也是一个难点,特别是对于不均匀的下垫面会更难(Wan等,2002),从而导致了仅有少数地表类型适用于基于温度的验证方法,并能使地表测得的地表温度在像元尺度的误差在1 K以内。实测数据的收集也是一个艰苦的任务,并且通常限制于短期的、专门的实验场测量。因此,基于温度的方法不适用于地表温度产品的全球验证。
4.2 基于辐射的方法(R-based)
基于辐射的方法(R-based)是一种高级的用来验证基于空间的地表温度测量的可选择的方法(Coll等,2012;Wan和Li,2008;Wan,2014;Hulley和Hook,2011;Niclòs等,2011)。这一方法不依赖于地面测量的地表温度值,它需要的是发射率光谱和测量的大气廓线,其中发射率光谱可以在实验场中测量得到,也可以通过地表覆盖类型或辅助数据估算得到,大气廓线则是在卫星过境时在验证站点测量得到(Wan,2008;Wan和Li,2008)。这一方法使用的是由卫星数据反演得到的地表温度和之前提到的实测的大气廓线以及作为大气辐射传输方程的初始输入参数的地表发射率,这一方程模拟的是卫星过境时刻大气层顶的辐射值。利用模拟的大气层顶的辐射值与测量的辐射值之间的差值,初始的地表温度值可以得到调整,模拟的辐射值可以通过迭代重计算来匹配卫星测量的辐射值。调整后的地表温度值和初始的由卫星数据反演得到的地表温度值的差值便是地表温度反演的精度。更多有关基于辐射的方法的细节可参考Wan和Li(2008)。
基于辐射的方法不需要地面测量的地表温度值,因此它可以应用到地面测量难以开展的地表,并且可以扩展到均匀的、非同温的表面。该方法使得在白天和晚上对均匀的、非同温的表面而言,卫星反演的地表温度的验证变得可能。然而,这一方法的最大限制是像元尺度测量或估计的典型地物发射率值的使用,检查实际大气是否无云,在观测时刻模拟中用到的廓线能在多大程度上代表实际廓线(Coll等,2012)。该方法的成功与否取决于大气辐射传输方程、大气廓线以及像元尺度地表发射率的精度。
4.3 交叉验证
这一方法使用经过验证的其他卫星数据反演得到的地表温度来进行验证(Trigo等,2008a)。这一验证技术是一种可选的验证地表温度的方法,应用的条件是在没有可用的大气廓线或者地面测量值,或者是基于温度和辐射的验证方法不能采用的情况下。
交叉验证方法是将已经验证好的地表温度产品作为参考,将需要验证的由卫星数据反演得到的地表温度与由其他卫星反演得到的验证过的地表温度进行比较。由于地表温度存在较大的空间和时间上的变化,因此在比较之前,需要进行地理坐标匹配、时间匹配以及观测天顶角的匹配(Qian等,2013;Trigo等,2008a)。这一方法的主要优势在于它可以在没有地面测量的情况下进行验证,并且只要能获得已经验证好的产品,它可以在世界范围内使用。正如之前所提到的那样,这一方法的精度对两次温度测量的空间和时间上的不匹配较敏感,两次观测的时间间隔应该尽可能的短。考虑到地表发射率同样依赖于观测天顶角,在不同的观测角下,两传感器的像元覆盖了不同的区域,包含不同的地表信息,因此只有具有相同或相近的观测天顶角的像元才能被用来进行交叉验证。
5 地表温度的时间和角度归一化方法
5.1 地表温度的时间归一化
地表温度是一个随时间变化的特征物理量,卫星遥感获取的只是对应观测时刻、观测角度下的瞬时地表温度。不同极轨卫星传感器获取的像元温度具有不同的局地观测时间,即使同一极轨卫星传感器,同一天不同像元或同一像元不同天,其局地观测时间也不相同,导致极轨卫星观测数据反演的同一天不同像元或同一像元不同天的地表温度产品之间缺乏可比性(Li等,2013)。为了使得同一天不同像元或同一像元不同天之间的地表温度具有可比性,需要将不同局地观测时间的地表温度归一化到相同的局地观测时间。根据一天中云的分布状况,地表温度的时间归一化方法可分为全天无云和部分有云两种情况。
5.1.1 全天无云情况
在全天无云的情况下,利用地表温度日变化模型拟合卫星遥感获取的地表温度可以模拟得到一天中任意时刻的地表温度,从而实现全天无云状况下极轨卫星地表温度的时间归一化。对于每一天每个地点,极轨卫星最多提供4次观测数据(例如,Terra-MODIS和Aqua-MODIS,白天和晚上的观测数据),而现有的地表温度日变化模型包含了5—6个自由参数(Duan等,2012,2013,2014a;Inamdar等,2008;Jiang等,2006;Schädlich等,2001;Quan等,2014)。在这5—6个自由参数中,有的参数与时间相关(如最大温度出现时刻、温度开始衰减时刻),有的参数与温度相关(如日出时刻附近的初始温度、温度的幅度)。地表温度日变化模型的一般形式可以表示为
| $ {T_{\rm s}}\left(t \right)= f\left({{T_0}{\text{,}}{T_{\rm a}}{\text{,}}{t_{\rm m}}{\text{,}}{t_{\rm s}}{\text{,}}t,\cdots} \right)$ | (14) |
式中,Ts为地表温度,t为时间,T0为日出时刻附近的初始温度,Ta为温度的幅度,tm为最大温度出现时刻,ts为温度开始衰减时刻。
通常假定与时间相关的参数可以通过气候模式(如CCM3/BATS)或者静止卫星数据(如GOES,MSG-SEVIRI)得到,从而确定地表温度日变化的典型模式。结合地表温度日变化典型模式和极轨卫星一天2次或者4次的观测数据,利用地表温度日变化模型可以模拟得到一天中任意时刻的地表温度。
Jin和Dickinson(1999)通过气候模式CCM3/ BATS模拟出不同纬度、不同季节、不同地表覆盖类型条件下的地表温度日变化典型模式,再结合一天2次的NOAA-AVHRR地表温度数据,利用地表温度日变化模型模拟得到一天中任意时刻的地表温度。Sun和Pinker(2005)发展了与Jin和Dickinson(1999)类似的方法估算NOAA-AVHRR的地表温度日变化数据,但是其地表温度日变化典型模式通过静止卫星GOES的地表温度日变化数据获得。Zhou等人(2013)通过静止卫星FY-2C数据得到地表温度日变化典型模式,再结合一天4次的MODIS地表温度数据,利用地表温度日变化模型模拟得到一天中任意时刻的地表温度。
上述方法需要通过气候模式或者静止卫星数据确定地表温度日变化典型模式,并且假定极轨卫星数据具有与典型模式类似的地表温度日变化模式。为了不借助于气候模式或者静止卫星数据,通过数据统计分析假定温度开始衰减时刻ts可以近似为日落前1小时,Duan等人(2014b)发展了4参数地表温度日变化模型。利用4参数地表温度日变化模型拟合一天4次的MODIS地表温度数据,模拟得到一天中任意时刻的地表温度。为了将地表温度日变化模型能够应用于不同观测次数的地表温度数据,Huang等人(2014)发展了一系列不同参数数量(2—12个)的地表温度日变化模型。利用这一系列模型拟合不同观测次数的地表温度数据,模拟得到一天中任意时刻的地表温度,从而实现全天无云状况下极轨卫星地表温度的时间归一化。
5.1.2 部分有云情况
基于地表温度日变化模型的地表温度时间归一化方法只能应用于全天无云情况,而在部分有云情况下(即极轨卫星过境时段无云),该方法无法得以使用。
通过数据统计分析表明,上午时段地表温度随时间呈近似线性变化。基于这一特点,Duan等人(2014c)建立了斜率函数法地表温度时间归一化模型,即
| $ LS{T_{\rm an}}{\text{ = }}\left({{t_{\rm an}} - {t_{\rm bn}}} \right)SLP + LS{T_{\rm bn}} $ | (15) |
式中,SLP为地表温度在极轨卫星上午过境时段内的变化斜率;LSTbn为时间归一化前的地表温度;LSTan为时间归一化后的地表温度;tbn和tan分别为对应LSTbn和LSTan的局地观测时间。
利用斜率函数法地表温度时间归一化模型将地表温度归一化到相同的局地观测时间时,必须要先确定SLP。然而,在极轨卫星上午过境时段内,极轨卫星只能获取1次观测数据,因此不能直接从极轨卫星地表温度数据中获得SLP。静止卫星数据具有高时间分辨率的特点,能够提供每15 min或者30 min的热红外数据,假定极轨卫星数据在卫星上午过境时段内具有与静止卫星数据类似的地表温度变化信息,因此利用静止卫星数据可以估算SLP。
Duan等人(2014c)建立了地表温度变化斜率SLP与3个可获取参量之间的回归关系,即
| $ SLP = {a_1}{\rm NDVI} + {a_2}\cos {\theta _s} + {a_3}{\rm DEM} + {a_0} $ | (16) |
式中,NDVI为归一化植被指数;cos θs为太阳天顶角的余弦值;DEM为地表高程;a0、a1、a2、a3为回归系数。
5.2 地表温度的角度归一化
目前地表温度反演算法常常将地表看做同温均质体,假设温度不随传感器的观测通道发生变化,且多在反演过程忽略地表温度本身的方向性。对于浓密植被和水体来说,这一假设是合理的,并且能够有效地减少未知数的个数。但是,对于3维结构明显(例如稀疏植被、城市建筑)的非同温混合像元,其内部具有复杂组合结构且存在不同的组分,不同组分具有不同的发射率和温度,而不同组分对像元热辐射贡献的有效权重也随着观测角度的变化而变化,因此像元的热辐射往往表现出明显的方向性,导致其温度随着观测通道与观测角度而发生变化,那么将像元当作同温均质体假设将不再成立。研究发现,垂直方向上和倾斜方向上的裸土温差高达5 K,城市地表温差高达10 K,而温度1—3 K的误差将在通量估算结果中引入高达100 W/m2的误差(Lagouarde等,2010,2014)。即使是同温像元,像元内部各组分在不同观测角度下的不同比例以及各个组分间的多次散射也使得像元发射率依赖于观测方向,从而导致同温像元的热辐射也表现出一定的角度效应。对于大角度观测传感器(如MODIS、AVHRR)不同像元对应不同的观测角度,温度的角度效应将导致观测数据反演的同一景影像不同像元或同一像元在不同天的地表温度产品之间缺乏可比性,从而使得温度产品的应用受到很大程度的限制。
将不同方向上的地表温度(或等效温度)纠正到同一方向上(如垂直方向上)以增强不同像元间地表温度的可比性,增加地表温度的适用性。这一过程即是地表温度的角度归一化。像元热辐射的角度效应主要来自于像元发射率的方向性、以及不同温度组分比例随观测角度的变化。Ren等人(2011)在假设同温地表的前提下,将地表温度的角度效应完全归咎于发射率的角度变化,基于MODIS的发射率产品提取了像元尺度多种地类的方向性发射率,并将其应用于劈窗算法实现了地表温度的角度纠正,角度纠正后的地表温度数值与原有的MODIS地表温度相差1—3 K,且差异随着观测天顶角的增大而增大。彭菁菁等人(2011)利用经过大气纠正以后的方向性亮温代替原有核驱动BRDF(Bidirectional Reflectance Distribution Function)模型中的二向性反射率,将核驱动BRDF模型应用到方向性亮温,从而使得在已知不少于3个方向性亮温的前提下,便可拟合出任意方向上的亮温。利用机载多角度热红外数据对模型进行了验证,误差小于1.0 K。在此基础上,Ren等人(2015)深入探讨了核驱动BRDF模型对半球空间方向性热辐射的拟合能力,提出了地表温度角度归一化的局部最优角度组合以及观测天顶角临界值。更进一步,在明确了方向性等效温度与发射率定义的基础上,发展了从机载多角度中红外与热红外数据反演方向性等效温度与发射率的D-TISI模型,并利用核驱动BRDF模型获得所有像元在垂直方向上等效温度。结果表明,垂直方向上与观测倾斜方向上的等效温度存在明显差异,尤其是非植被区,二者温差可达6 K或更高。
然而,尽管多角度热红外数据是实现地表温度角度归一化过程的重要数据源,但是目前仅有ATSR系列卫星平台提供2个角度的热红外数据观测,角度数目和观测时间间隔(2 min)还不足以高精度地实现地表温度角度归一化,因此还需要在方法以及多角度热红外数据源等方面进一步开展研究。
6 展望
在全球尺度上精确获取地表温度对许多领域的研究都很关键,包括地球表面水和能量平衡,陆地生态系统中物质和能量交换以及全球气候变化。学者们提出各种各样的方法来从多光谱或者多角度热红外数据中反演地表温度。由于多光谱数据提供的光谱信息有限,因此所有方法都依赖于辐射传输方程的近似以及不同的假设和限制,以此解决反演自身的病态问题。在某些情况下,这些近似、假设和限制可能并不正确。因此,用户必须考虑传感器的特性、需要的精度、计算的时间、大气温度和水汽廓线的可用性以及地表发射率来选择最佳的从空间中估算地表温度的方法。考虑到最近几十年从多光谱热红外数据估算地表温度有了显著的进步,但如果在遥感数据的获取上没有创新的话,将不会再有明显的进步。为了克服多光谱数据的缺陷,从根本上提高地表温度的反演精度,有必要在遥感领域探索新的想法,开辟新的道路。
高光谱热红外传感器与多光谱热红外传感器相比,由于它有着几千个通道,所以毫无疑问它将更易于获取大气和地表的参数。大量的窄波段通道可以提高大气探测的分辨率(Chahine等,2001),并获得用来进行大气校正的大气特征参数。大气窗口内测量的高光谱热红外数据可以提供更多详细的地表信息,特别是发射率光谱,而不是多光谱数据中离散的发射率值。另外,它还能提供更多合理的假设和限制,从而将地表温度和发射率分离开。这些原因驱动着定量遥感和其他相关学科的发展,利用高光谱热红外数据分离地表温度和发射率以及大气廓线和大气校正中大气特性的反演将成为未来定量遥感研究的热点。
未来的发展将着眼于从多光谱和多时相热红外数据的结合来提取地表温度的新方法,该数据可以从新一代静止卫星上的多光谱传感器上获得,比如SEVIRI,GOES和FY-2系列,它们能够获取每日的地球表面数据,并且能至少每小时以固定的观测天顶角对地表进行扫描。除了两温法、日夜温度无关波谱指数法和日夜双时相多通道物理反演法需要在白天和夜晚进行两次测量,其他所有方法都基于多光谱数据并且不需要考虑时相信息。因此,利用多光谱和多时相热红外数据中的多时相信息来反演地表温度是非常吸引人的。
另外,目前绝大多数可用的地表温度反演方法都是在晴空条件下由极轨卫星提供的多光谱数据瞬时反演的,而并没有适合所有天气状况的长期的地表温度产品。考虑到对被动微波和热红外数据的补充,未来必须发展一个基于物理的模型来从被动微波数据中反演出地表温度,以及一个有效地结合不同地表温度的模型,其中地表温度是从热红外和被动微波卫星数据中反演得到的,以此生产在各种天气条件下的高空间分辨率的地表温度产品。另外,由于极轨卫星搭载的传感器的固有的扫描特性,在某一特定地点从相同的极轨卫星在不同时间反演的地表温度或者是在不同的地点相同时间反演的地表温度与观测时不同当地太阳时和观测天顶角是相符的,更不用说从不同极轨卫星反演的地表温度。由于地表温度随着时间和观测天顶角的变化而变化,不同时间反演的同一像元或者是相同时间反演的不同像元的地表温度并不具有可比性,这也极大地限制了地表温度产品的应用。为了强调这些问题,包括角度归一化和时间归一化的一系列的地表温度模型必须发展起来以生产所有天气条件下的长期的、时间和角度归一化后的持续的地表温度产品。未来的研究应该集中在以下内容上,以此提高基于空间测量的地表温度估算精度。
6.1 高光谱热红外数据同时反演地表温度、发射率和大气廓线的方法
正如Li等人(2013)所阐述,地表发射辐射和大气吸收、散射和发射的耦合使得地表参数(地表温度和发射率)和大气廓线的单独反演变得复杂。从空间中确定地表参数需要大气廓线的知识,反之亦然。因此,虽然很有挑战性,但在没有任何关于地表或大气的先验知识的前提下发展一种同时反演地表温度、发射率和大气廓线的方法也变得自然而然。Ma等人(2000,2002)率先尝试从多光谱热红外测量中反演出这些参数,随着高光谱热红外传感器的出现,上千的窄波段通道可以提供足够的垂直分辨率来提取大气信息,也可以提供更多的物理限制条件,以精确分离地表温度和发射率。尽管近些年来相关的研究较少(Li等,2007;Wang等,2013),但是在未来还是有两点值得注意:一是必须建立迅速而精确的大气传输方程模型来满足反演过程中对精度和速度的要求,二是人工神经网络法和物理反演法都需要进行改进来提高反演的精度。比如,在人工神经网络法中应当考虑更多的细节,包括结构、学习模式、有代表性的训练数据的选择以及使用的通道。同时,另外的限制(如Wang等人(2011)提出的线性发射率限制)、数学方法以及规则化应该引入到基于物理的反演方法中,以此减少与假设相关的不确定性,并使方程的解稳定。人工神经网络法和物理反演法的结合也代表着未来几年人们在地表温度反演方面的选择,因为这两种方法的优势可以互补,即人工神经网络法可以为地表温度、发射率和大气廓线提供初始估计值,物理反演法可以进一步改进这些值。
6.2 新一代静止卫星多光谱和多时相数据同时反演地表温度和发射率的方法
新一代静止卫星相比于极轨卫星在研究地表随时间变化以及大气信息时更有优势,因为尽管它们的分辨率不高,但它们以固定的观测天顶角对地面进行高频率观测。学者们对从多光谱数据中反演地表温度作了很多努力,但对多时相信息的考虑则不多。因此,利用静止卫星多光谱和多时相数据同时反演地表温度和发射率是非常有吸引力的。有了静止卫星数据,时间和角度连续的地表温度可以直接由这些反演方法得出,而不需要进行地表温度的时间和角度归一化。
6.3 考虑气溶胶和卷云影响的地表温度反演算法的改进
大气校正是地表温度反演中最重要的问题之一,大气校正的误差会直接降低最终得到的地表温度的精度。由于在正常晴空条件下,热红外通道气溶胶的透过率较高(对MODIS热红外通道大约为0.95—0.98)(Wan,1999),又缺乏实时估计气溶胶的方法(气溶胶含量、大小分布、类型、散射相函数),因此在第3节介绍的地表温度反演算法中都使用了平均的气溶胶分布以及恒定的气溶胶含量。与水汽相比,气溶胶对地表温度反演的影响较小,但需要高精度的地表温度时,也不能忽略它的影响,在一些特定应用中,较大的气溶胶含量更加不能被忽略(Jiménez-Muñoz和Sobrino,2006)。为了进一步提高地表温度反演精度,现有的反演算法必须进行改善,或者有新的算法来改正气溶胶的影响,尤其是在气溶胶含量较大的时候。
另外,卷云对地表温度反演的影响也应该考虑。卷云在许多地表温度反演算法中经常被认为是云干扰,被卷云遮住的像元通常在数据预处理中被直接去掉。由于热红外波长可以穿过卷云,在有卷云的情况下反演地表温度是有可能的。为此,应该建立新的地表温度算法来消除卷云的影响。
6.4 非均匀像元组分温度的反演
对于非均匀和非等温的像元,观测到的辐射值是几个部分辐射综合的结果(比如土壤和植被)。像元的平均温度并不能反映每一组分的真实温度,假设每一组分是等温的,组分温度与像元平均温度值相比包含了更多的物理意义,并为陆地和大气交界处的热通量提供了更好的参数化。因此,混合像元的组分温度比平均温度值重要很多。然而,组分温度的反演较难,因为包括组分发射率和大气效应的更多的参数需要提前知道。一些学者尝试利用多角度数据反演组分温度(Jia等,2003;Li等,2001;Menenti等,2001)。然而,他们的方法还不是很令人满意,未来还需要改进。另外,进一步的研究应该集中于挖掘空间、时间和光谱数据中的辅助信息。由于不同的观测天顶角可能对应不同的像元大小,所以新的算法可以针对固定观测天顶角的高光谱热红外数据,这是因为该数据中包含有混合像元中各组分温度的信息。
6.5 从被动微波数据以及热红外数据和被动微波数据的结合反演地表温度的方法
热红外数据为地表温度提供了较高的空间分辨率(几千米),但当地表完全或部分被云覆盖时,反演的精度便会降低。相反,微波可以穿过云层,适用于任何天气条件,但分辨率较差(最差几十千米)(Aires等,2004)。因此,热红外数据和微波数据可以互补,两者的结合有希望生产出适合于所有天气条件下的、与热红外数据分辨率一致的长期的地表温度产品。未来的研究可以着眼于以下几点:
(1)建立一个新的利用被动微波数据反演地表温度的物理模型。学者们已经提出了一些利用利用被动微波数据反演地表温度的技术,包括(半)经验统计模型,神经网络以及物理模型(Aires等,2001;Chen等,2011;Mao等,2007;McFarland等,1990;Njoku和Li,1999;Weng和Grody,1998)。然而,通常这些方法的物理机理并不十分清楚,它们考虑发射率和大气效应的假设和简化降低了反演的地表温度的可用性和精度。新模型的建立应该集中于简化辐射传输方程的参数化并建立不同频率和极化发射率之间的关系。一个令人满意的模型应该结合不同频率测量的亮温和极化模式来反演地表温度。
(2)建立从被动微波数据反演表层温度的模型。众所周知,被动微波反演地表温度与热红外不同,前者反应的是从地表到地下一定深度的土壤温度的平均值(取决于用来反演地表温度的频率),后者则是几微米的表层温度。为了结合这两种类型的地表温度并提取出表层温度,必须建立一个能够从被动微波反演的地表温度中提取出表层温度的模型,这一过程需要不同频率被动微波数据反演的地表温度以及土壤的导热系数方程。
(3)建立微波—热红外混合模型。为了生产出所有天气条件下的高空间分辨率的地表温度数据,必须建立混合热红外和被动微波反演地表温度的有效模型,亟待解决的关键问题在于当微波像元完全或部分被云覆盖时,如何在热红外数据的空间分辨率上重新获得地表温度。
6.6 卫星数据反演地表温度的物理意义和应用
地表温度在物理上有着明确的定义,但是由于卫星反演出的温度没有确定的物理意义,因此地表温度的定义并没有达成一致,特别是对于不均匀、非等温的表面。地表温度的定义同样取决于地表发射率的定义,因为在整个辐射中,它们是耦合在一起的。目前发射率定义有几种,比如r发射率(Becker和Li,1995)、e发射率(Norman和Becker,1995)和表观发射率(Li等,1999)。这些定义在热平衡时对均匀下垫面是一样的,但由于自然界中下垫面通常是不均匀的,因此假定地表均匀并且热量平衡通常是与现实情况相违背的,特别是当分辨率较低时。因此,在很多情况下,这些定义的差别也很明显。由于r发射率是可测量的,所以在地表温度和发射率反演中推荐使用r发射率的定义。
不管使用地表温度的哪种定义,卫星反演的地表温度,即辐射温度或表层温度,只能获得地面下较浅深度的热红外辐射信息,因此,它不能直接替代热力学的和空气动力学的温度在估算地表通量和相关应用中的作用。这些温度之间必须建立一种转换,但是目前的研究很少考虑这些差异,不经过任何转换,直接将表层温度视为热力学的和空气动力学的温度。这一简化将给地表通量估算结果带来不确定性,因此,未来需要考虑不同温度的物理定义和相关应用的精度需求来解决这一问题。
6.7 卫星反演地表温度的验证
地表温度验证最重要的问题可能是卫星像元尺度上地面真实值的精度和代表性,尽管基于地面的验证被认为是最值得信赖的验证技术,但在地面上找到卫星像元大小的均匀下垫面和在非均匀景观中采样的代价给地面测量带来了困难。第1个问题可以通过提高热红外数据分辨率来解决,第2个问题需要建立新的采样方法,比如无线网络观测系统或者用相应的新仪器进行多尺度观测。利用从陆地数据同化系统中或者是间接验证地表温度的气候模型中预测的地表温度的尝试必须更加关注提高模型输出的精度和时间与空间上尺度不匹配的问题。对于交叉验证技术,必须建立一个合适的尺度转换程序,以此消除空间、时间和角度效应对地表温度的影响。因此,地表温度的验证仍然是一个需要不断深入研究的内容。
参考文献(References)
-
Aires F, Prigent C, Rossow W B, Rothstein M.2001.A new neural network approach including first guess for retrieval of atmospheric water vapor, cloud liquid water path, surface temperature, and emissivities over land from satellite microwave observations. Journal of Geophysical Research-Atmospheres, 106 (D14): 14887–14907. DOI: 10.1029/2001JD900085.
-
Aires F, Prigent C, Rossow W B.2004.Temporal interpolation of global surface skin temperature diurnal cycle over land under clear and cloudy conditions. Journal of Geophysical Research-Atmospheres, 109 (D4): D04313 DOI: 10.1029/2003JD003527.
-
Anderson M C, Norman J M, Kustas W P, Houborg R, Starks P J, Agam N.2008.A thermal-based remote sensing technique for routine mapping of land-surface carbon, water and energy fluxes from field to regional scales. Remote Sensing of Environment, 112 (12): 4227–4241. DOI: 10.1016/j.rse.2008.07.009.
-
Arnfield A J.2003.Two decades of urban climate research:a review of turbulence, exchanges of energy and water, and the urban heat island. International Journal of Climatology, 23 (1): 1–26. DOI: 10.1002/joc.859.
-
Atitar M, Antonio Sobrino J.2009.A split-window algorithm for estimating lst from meteosat 9 data:test and comparison with in situ data and MODIS LSTs. IEEE Geoscience and Remote Sensing Letters, 6 (1): 122–126. DOI: 10.1109/LGRS.2008.2006410.
-
Barducci A, Pippi I.1996.Temperature and emissivity retrieval from remotely sensed images using the"grey body emissivity"method. IEEE Transactions on Geoscience and Remote Sensing, 34 (3): 681–695. DOI: 10.1109/36.499748.
-
Barton I J, Zavody A M, O'Brien D M, Cutten D R, Saunders R W, Llewellyn-Jones D T.1989.Theoretical algorithms for satellite-derived sea surface temperatures. Journal of Geophysical Research:Atmospheres, 94 (D3): 3365–3375. DOI: 10.1029/JD094iD03p03365.
-
Bastiaanssen W G M, Menenti M, Feddes R A, Holtslag A A M.1998.A remote sensing surface energy balance algorithm for land (SEBAL). 1.Formulation.Journal of Hydrology, 212-213 : 198–212. DOI: 10.1016/S0022-1694(98)00253-4.
-
Becker F.1987.The impact of spectral emissivity on the measurement of land surface temperature from a satellite. International Journal of Remote Sensing, 8 (10): 1509–1522. DOI: 10.1080/01431168708954793.
-
Becker F, Li Z L.1990.Towards a local split window method over land surfaces. International Journal of Remote Sensing, 11 (3): 369–393. DOI: 10.1080/01431169008955028.
-
Becker F, Li Z L.1995.Surface temperature and emissivity at various scales:definition, measurement and related problems. Remote Sensing Reviews, 12 (3/4): 225–253. DOI: 10.1080/02757259509532286.
-
Berk A, Anderson G P, Acharya P K, Hoke M L, Chetwynd J H, Bernstein L S, Shettle E P, Matthew M W and Adler-Golden S M.2003.MODTRAN4 Version 3 Revision 1 USER'S MANUAL.Hanscom, MA:Air Force Research Laboratory
-
Borel C C.1997.Iterative retrieval of surface emissivity and temperature for a hyperspectral sensor//Proceedings of the First JPL Workshop on Remote Sensing of Land Surface Emissivity.Pasadena, California:Jet Propulsion Laboratory:1-5
-
Borel C C.1998.Surface emissivity and temperature retrieval for a hyperspectral sensor//Proceedings of IEEE International Symposium on Geoscience and Remote Sensing (IGARSS).Seattle, WA:IEEE:546-549. [DOI:10.1109/IGARSS.1998.702966]
-
Borel C C.2008.Error analysis for a temperature and emissivity retrieval algorithm for hyperspectral imaging data. International Journal of Remote Sensing, 29 (17/18): 5029–5045. DOI: 10.1080/01431160802036540.
-
Brunsell N A, Gillies R R.2003.Length scale analysis of surface energy fluxes derived from remote sensing. Journal of Hydrometeorology, 4 (6): 1212–1219. DOI: 10.1175/1525-7541(2003)004<1212:LSAOSE>2.0.CO;2.
-
Caselles V, Coll C, Valor E.1997.Land surface emissivity and temperature determination in the whole HAPEX-Sahel area from AVHRR data. International Journal of Remote Sensing, 18 (5): 1009–1027. DOI: 10.1080/014311697218548.
-
Chahine M T, Aumann H H, Goldberg M, McMillin L, Rosenkranz P, Staelin D, Strow L, Susskind J and Gunson M.2001.AIRS-team retrieval for core products and geophysical parameters//Algorithm Theoretical Basis Document.Washington, DC:NASA
-
Chedin A, Scott N A, Berroir A.1982.A single-channel, double-viewing angle method for sea surface temperature determination from coincident Meteosat and TIROS-N radiometric measurements. Journal of Applied Meteorology, 21 (4): 613–618. DOI: 10.1175/1520-0450(1982)021<0613:ASCDVA>2.0.CO;2.
-
Chen S S, Chen X Z, Chen W Q, Su Y X, Li D.2011.A simple retrieval method of land surface temperature from AMSR-E passive microwave data-A case study over Southern China during the strong snow disaster of 2008. International Journal of Applied Earth Observation and Geoinformation, 13 (1): 140–151. DOI: 10.1016/j.jag.2010.09.007.
-
Cheng J, Liang S L, Wang J D, Li X W.2010.A stepwise refining algorithm of temperature and emissivity separation for hyperspectral thermal infrared data. IEEE Transactions on Geoscience and Remote Sensing, 48 (3): 1588–1597. DOI: 10.1109/TGRS.2009.2029852.
-
Coll C, Caselles V, Sobrino J A, Valor E.1994.On the atmospheric dependence of the split-window equation for land surface temperature. International Journal of Remote Sensing, 15 (1): 105–122. DOI: 10.1080/01431169408954054.
-
Coll C, Caselles V.1997.A split-window algorithm for land surface temperature from advanced very high resolution radiometer data:validation and algorithm comparison. Journal of Geophysical Research-Atmospheres, 102 (D14): 16697–16713. DOI: 10.1029/97JD00929.
-
Coll C, Caselles V, Galve J M, Valor E, Niclòs R, Sánchez J M, Rivas R.2005.Ground measurements for the validation of land surface temperatures derived from AATSR and MODIS data. Remote Sensing of Environment, 97 (3): 288–300. DOI: 10.1016/j.rse.2005.05.007.
-
Coll C, Caselles V, Valor E, Niclòs R, Sánchez J M, Galve J M, Mira M.2007.Temperature and emissivity separation from ASTER data for low spectral contrast surfaces. Remote Sensing of Environment, 110 (2): 162–175. DOI: 10.1016/j.rse.2007.02.008.
-
Coll C, Hook S J, Galve J M.2009.Land surface temperature from the advanced along-track scanning radiometer:validation over inland waters and vegetated surfaces. IEEE Transactions on Geoscience and Remote Sensing, 47 (1): 350–360. DOI: 10.1109/TGRS.2008.2002912.
-
Coll C, Galve J M, Sanchez J M, Caselles V.2010.Validation of landsat-7/ETM+thermal-band calibration and atmospheric correction with ground-based measurements. IEEE Transactions on Geoscience and Remote Sensing, 48 (1): 547–555. DOI: 10.1109/TGRS.2009.2024934.
-
Coll C, Valor E, Galve J M, Mira M, Bisquert M, García-Santos V, Caselles E, Caselles V.2012.Long-term accuracy assessment of land surface temperatures derived from the Advanced Along-Track Scanning Radiometer. Remote Sensing of Environment, 116 : 211–225. DOI: 10.1016/j.rse.2010.01.027.
-
Cooper D I, Asrar G.1989.Evaluating atmospheric correction models for retrieving surface temperatures from the AVHRR over a tallgrass prairie. Remote Sensing of Environment, 27 (1): 93–102. DOI: 10.1016/0034-4257(89)90040-0.
-
Cristóbal J, Jiménez-Muñoz J C, Sobrino J A, Ninyerola M, Pons X.2009.Improvements in land surface temperature retrieval from the Landsat series thermal band using water vapor and air temperature. Journal of Geophysical Research-Atmospheres, 114 (D8): D08103 DOI: 10.1029/2008JD010616.
-
Dash P, Göttsche F M, Olesen F S, Fischer H.2002.Land surface temperature and emissivity estimation from passive sensor data:theory and practice-current trends. International Journal of Remote Sensing, 23 (13): 2563–2594. DOI: 10.1080/01431160110115041.
-
Deschamps P Y, Phulpin T.1980.Atmospheric correction of infrared measurements of sea surface temperature using channels at 3.7, 11 and 12 Mm. Boundary-Layer Meteorology, 18 (2): 131–143. DOI: 10.1007/BF00121320.
-
Duan S B, Li Z L, Wang N, Wu H, Tang B H.2012.Evaluation of six land-surface diurnal temperature cycle models using clear-sky in situ and satellite data. Remote Sensing of Environment, 124 : 15–25. DOI: 10.1016/j.rse.2012.04.016.
-
Duan S B, Li Z L, Wu H, Tang B H, Jiang X G, Zhou G Q.2013.Modeling of day-to-day temporal progression of clear-sky land surface temperature. IEEE Geoscience and Remote Sensing Letters, 10 (5): 1050–1054. DOI: 10.1109/LGRS.2012.2228465.
-
Duan S B, Li Z L, Tang B H, Wu H, Tang R L.2014a.Direct estimation of land-surface diurnal temperature cycle model parameters from MSG-SEVIRI brightness temperatures under clear sky conditions. Remote Sensing of Environment, 150 : 34–43. DOI: 10.1016/j.rse.2014.04.017.
-
Duan S B, Li Z L, Tang B H, Wu H, Tang R L.2014b.Generation of a time-consistent land surface temperature product from MODIS data. Remote Sensing of Environment, 140 : 339–349. DOI: 10.1016/j.rse.2013.09.003.
-
Duan S B, Li Z L, Tang B H, Wu H, Tang R L, Bi Y Y, Zhou G Q.2014c.Estimation of diurnal cycle of land surface temperature at high temporal and spatial resolution from clear-sky MODIS data. Remote Sensing, 6 (4): 3247–3262. DOI: 10.3390/rs6043247.
-
França G B, Carvalho W S.2004.Sea surface temperature GOES-8 estimation approach for the Brazilian coast. International Journal of Remote Sensing, 25 (17): 3439–3450. DOI: 10.1080/01431160310001632738.
-
François C, Ottlé C.1996.Atmospheric corrections in the thermal infrared:global and water vapor dependent Split-Window algorithms-Applications to ATSR and AVHRR data. IEEE Transactions on Geoscience and Remote Sensing, 34 (2): 457–470. DOI: 10.1109/36.485123.
-
Gillespie A R.1995.Lithologic mapping of silicate rocks using TIMS.TIMS Data Users'Workshop. Pasadena, CA:NASA Jet Propulsion Laboratory : 29–44.
-
Gillespie A R, Rokugawa S, Hook S J, Matsunaga T, Kahle A B.1996.Temperature/Emissivity Separation Algorithm Theoretical Basis Document, Version 2.4. Maryland, USA:NASA/GSF : 1–64.
-
Gillespie A R, Rokugawa S, Matsunaga T, Cothern J S, Hook S, Kahle A B.1998.A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Transactions on Geoscience and Remote Sensing, 36 (4): 1113–1126. DOI: 10.1109/36.700995.
-
Gillespie A R, Abbott E A, Gilson L, Hulley G, Jiménez-Muñoz J, Sobrino J A.2011.Residual errors in ASTER temperature and emissivity standard products AST08 and AST05. Remote Sensing of Environment, 115 (12): 3681–3694. DOI: 10.1016/j.rse.2011.09.007.
-
Göttsche F M, Olesen F S.2009.Modelling the effect of optical thickness on diurnal cycles of land surface temperature. Remote Sensing of Environment, 113 (11): 2306–2316. DOI: 10.1016/j.rse.2009.06.006.
-
Guillevic P C, Privette J L, Coudert B, Palecki M A, Demarty J, Ottlé C, Augustine J A.2012.Land Surface Temperature product validation using NOAA's surface climate observation networks-Scaling methodology for the Visible Infrared Imager Radiometer Suite (VⅡRS). Remote Sensing of Environment, 124 : 282–298. DOI: 10.1016/j.rse.2012.05.004.
-
Hansen J, Ruedy R, Sato M, Lo K.2010.Global surface temperature change. Reviews of Geophysics, 48 (4): G4004 DOI: 10.1029/2010RG000345.
-
Huang F, Zhan W F, Duan S B, Ju W M, Quan J L.2014.A generic framework for modeling diurnal land surface temperatures with remotely sensed thermal observations under clear sky. Remote Sensing of Environment, 150 : 140–151. DOI: 10.1016/j.rse.2014.04.022.
-
Hulley G C, Hook S J.2009.Intercomparison of versions 4, 4. 1 and 5 of the MODIS Land Surface Temperature and Emissivity products and validation with laboratory measurements of sand samples from the Namib desert, Namibia.Remote Sensing of Environment, 113 (6): 1313–1318. DOI: 10.1016/j.rse.2009.02.018.
-
Hulley G C, Hook S J.2011.Generating consistent land surface temperature and emissivity products between ASTER and MODIS data for earth science research. IEEE Transactions on Geoscience and Remote Sensing, 49 (4): 1304–1315. DOI: 10.1109/TGRS.2010.2063034.
-
Inamdar A K, French A, Hook S, Vaughan G, Luckett W.2008.Land surface temperature retrieval at high spatial and temporal resolutions over the southwestern United States. Journal of Geophysical Research-Atmospheres, 113 (D7): D07107 DOI: 10.1029/2007JD009048.
-
Ingram P M, Muse A H.2001.Sensitivity of iterative spectrally smooth temperature/emissivity separation to algorithmic assumptions and measurement noise. IEEE Transactions on Geoscience and Remote Sensing, 39 (10): 2158–2167. DOI: 10.1109/36.957278.
-
Jia L, Li Z L, Menenti M, Su Z, Verhoef W, Wan Z.2003.A practical algorithm to infer soil and foliage component temperatures from bi-angular ATSR-2 data. International Journal of Remote Sensing, 24 (23): 4739–4760. DOI: 10.1080/0143116031000101576.
-
Jiang G M, Li Z L, Nerry F.2006.Land surface emissivity retrieval from combined mid-infrared and thermal infrared data of MSG-SEVIRI. Remote Sensing of Environment, 105 (4): 326–340. DOI: 10.1016/j.rse.2006.07.015.
-
Jiménez-Muñoz J C, Sobrino J A.2003.A generalized single-channel method for retrieving land surface temperature from remote sensing data. Journal of Geophysical Research-Atmospheres, 108 (D22): 4688 DOI: 10.1029/2003JD003480.
-
Jiménez-Muñoz J C, Sobrino J A.2006.Error sources on the land surface temperature retrieved from thermal infrared single channel remote sensing data. International Journal of Remote Sensing, 27 (5): 999–1014. DOI: 10.1080/01431160500075907.
-
Jiménez-Muñoz J C, Cristobal J, Sobrino J A, Soria G, Ninyerola M, Pons X.2009.Revision of the single-channel algorithm for land surface temperature retrieval from landsat thermal-infrared data. IEEE Transactions on Geoscience and Remote Sensing, 47 (1): 339–349. DOI: 10.1109/TGRS.2008.2007125.
-
Jiménez-Muñoz J C, Sobrino J A.2010.A single-channel algorithm for land-surface temperature retrieval from ASTER data. IEEE Geoscience and Remote Sensing Letters, 7 (1): 176–179. DOI: 10.1109/LGRS.2009.2029534.
-
Jin M L, Dickinson R E.1999.Interpolation of surface radiative temperature measured from polar orbiting satellites to a diurnal cycle:1. Without clouds.Journal of Geophysical Research-Atmospheres, 104 (D2): 2105–2116. DOI: 10.1029/1998JD200005.
-
Kalma J D, McVicar T R, McCabe M F.2008.Estimating land surface evaporation:a review of methods using remotely sensed surface temperature data. Surveys in Geophysics, 29 (4/5): 421–469. DOI: 10.1007/s10712-008-9037-z.
-
Kanani K, Poutier L, Nerry F, Stoll M P.2007.Directional effects consideration to improve out-doors emissivity retrieval in the 3-13 μm domain. Optics Express, 15 (19): 12464–12482. DOI: 10.1364/OE.15.012464.
-
Karnieli A, Agam N, Pinker R T, Anderson M, Imhoff M L, Gutman G G, Panov N, Goldberg A.2010.Use of NDVI and land surface temperature for drought assessment:merits and limitations. Journal of Climate, 23 (3): 618–633. DOI: 10.1175/2009JCLI2900.1.
-
Kealy P S, Hook S J.1993.Separating temperature and emissivity in thermal infrared multispectral scanner data:implications for recovering land surface temperatures. IEEE Transactions on Geoscience and Remote Sensing, 31 (6): 1155–1164. DOI: 10.1109/36.317447.
-
Kerr Y H, Lagouarde J P, Imbernon J.1992.Accurate land surface temperature retrieval from AVHRR data with use of an improved split window algorithm. Remote Sensing of Environment, 41 (2/3): 197–209. DOI: 10.1016/0034-4257(92)90078-X.
-
Kogan F N.2001.Operational space technology for global vegetation assessment. Bulletin of the American Meteorological Society, 82 (9): 1949–1964. DOI: 10.1175/1520-0477(2001)082<1949:OSTFGV>2.3.CO;2.
-
Kustas W, Anderson M.2009.Advances in thermal infrared remote sensing for land surface modeling. Agricultural and Forest Meteorology, 149 (12): 2071–2081. DOI: 10.1016/j.agrformet.2009.05.016.
-
Lagouarde J P, Hénon A, Kurz B, Moreau P, Irvine M, Voogt J, Mestayer P.2010.Modelling daytime thermal infrared directional anisotropy over Toulouse city centre. Remote Sensing of Environment, 114 (1): 87–105. DOI: 10.1016/j.rse.2009.08.012.
-
Lagouarde J P, Dayau S, Moreau P, Guyon D.2014.Directional anisotropy of brightness surface temperature over vineyards:case study over the medoc region (SW France). IEEE Geoscience and Remote Sensing Letters, 11 (2): 574–578. DOI: 10.1109/LGRS.2013.2282492.
-
Li J, Li J L, Weisz E, Zhou D K.2007.Physical retrieval of surface emissivity spectrum from hyperspectral infrared radiances. Geophysical Research Letters, 34 (16): L16812 DOI: 10.1029/2007GL030543.
-
Li X W, Strahler A H, Friedl M A.1999.A conceptual model for effective directional emissivity from nonisothermal surfaces. IEEE Transactions on Geoscience and Remote Sensing, 37 (5): 2508–2517. DOI: 10.1109/36.789646.
-
Li Z L, Stoll M P, Zhang R H, Jia L, Su Z B.2001.On the separate retrieval of soil and vegetation temperatures from ATSR data. Science in China Series D:Earth Sciences, 44 (2): 97–111. DOI: 10.1007/BF02879653.
-
Li Z L, Tang B H, Wu H, Ren H Z, Yan G J, Wan Z M, Trigo I F, Sobrino J A.2013.Satellite-derived land surface temperature:current status and perspectives. Remote Sensing of Environment, 131 : 14–37. DOI: 10.1016/j.rse.2012.12.008.
-
Liu Y B, Hiyama T, Yamaguchi Y.2006.Scaling of land surface temperature using satellite data:a case examination on ASTER and MODIS products over a heterogeneous terrain area. Remote Sensing of Environment, 105 (2): 115–128. DOI: 10.1016/j.rse.2006.06.012.
-
Llewellyn-Jones D T, Minnett P J, Saunders R W, Zavody A M.1984.Satellite multichannel infrared measurements of sea surface temperature of the N. E.Atlantic Ocean using AVHRR/2.Quarterly Journal of the Royal Meteorological Society, 110 (465): 613–631. DOI: 10.1002/qj.49711046504.
-
Ma X L, Wan Z M, Moeller C C, Menzel W P, Gumley L E, Zhang Y L.2000.Retrieval of geophysical parameters from Moderate Resolution Imaging Spectroradiometer thermal infrared data:evaluation of a two-step physical algorithm. Applied Optics, 39 (20): 3537–3550. DOI: 10.1364/AO.39.003537.
-
Ma X L, Wan Z M, Moeller C C, Menzel W P, Gumley L E.2002.Simultaneous retrieval of atmospheric profiles, land-surface temperature, and surface emissivity from Moderate-Resolution Imaging Spectroradiometer thermal infrared data:extension of a two-step physical algorithm. Applied Optics, 41 (5): 909–924. DOI: 10.1364/AO.41.000909.
-
Mao K B, Shi J C, Tang H J, Guo Y, Qiu Y B and Li L Y.2007.A neural-network technique for retrieving land surface temperature from AMSR-E passive microwave data//Proceedings of IEEE International Symposium on Geoscience and Remote Sensing.Barcelona:IEEE:4422-4425 [DOI:10.1109/IGARSS.2007.4423835]
-
Matsunaga T.1994.A temperature-emissivity separation method using an empirical relationship between the mean, the maximum, and the minimum of the thermal infrared emissivity spectrum. Journal of the Remote Sensing Society of Japan, 14 (2): 230–241.
-
McClain E P, Pichel W G, Walton C C.1985.Comparative performance of AVHRR-based multichannel sea surface temperatures. Journal of Geophysical Research:Oceans, 90 (C6): 11587–11601. DOI: 10.1029/JC090iC06p11587.
-
McFarland M J, Miller R L, Neale C M U.1990.Land surface temperature derived from the SSM/I passive microwave brightness temperatures. IEEE Transactions on Geoscience and Remote Sensing, 28 (5): 839–845. DOI: 10.1109/36.58971.
-
McMillin L M.1975.Estimation of sea surface temperatures from two infrared window measurements with different absorption. Journal of Geophysical Research, 80 (36): 5113–5117. DOI: 10.1029/JC080i036p05113.
-
Menenti M, Jia L, Li Z L, Djepa V, Wang J M, Stoll M P, Su Z B, Rast M.2001.Estimation of soil and vegetation temperatures with multiangular thermal infrared observations:IMGRASS, HEIFE, and SGP 1997 experiments. Journal of Geophysical Research-Atmospheres, 106 (D11): 11997–12010. DOI: 10.1029/2000JD900671.
-
Neteler M.2010.Estimating daily land surface temperatures in mountainous environments by reconstructed MODIS LST data. Remote Sensing, 2 (1): 333–351. DOI: 10.3390/rs1020333.
-
Niclòs R, Caselles V, Coll C, Valor E.2007.Determination of sea surface temperature at large observation angles using an angular and emissivity-dependent split-window equation. Remote Sensing of Environment, 111 (1): 107–121. DOI: 10.1016/j.rse.2007.03.014.
-
Niclòs R, Galve J M, Valiente J A, Estrela M J, Coll C.2011.Accuracy assessment of land surface temperature retrievals from MSG2-SEVIRI data. Remote Sensing of Environment, 115 (8): 2126–2140. DOI: 10.1016/j.rse.2011.04.017.
-
Njoku E G, Li L.1999.Retrieval of land surface parameters using passive microwave measurements at 6-18 GHz. IEEE Transactions on Geoscience and Remote Sensing, 37 (1): 79–93. DOI: 10.1109/36.739125.
-
Norman J M, Becker F.1995.Terminology in thermal infrared remote sensing of natural surfaces. Agricultural and Forest Meteorology, 77 (3/4): 153–166. DOI: 10.1016/0168-1923(95)02259-Z.
-
Ottlé C, Vidal-Madjar D.1992.Estimation of land surface temperature with NOAA9 data. Remote Sensing of Environment, 40 (1): 27–41. DOI: 10.1016/0034-4257(92)90124-3.
-
Ouyang X Y, Wang N, Wu H, Li Z L.2010.Errors analysis on temperature and emissivity determination from hyperspectral thermal infrared data. Optics Express, 18 (2): 544–550. DOI: 10.1364/OE.18.000544.
-
Peng J J, Liu Q, Liu Q, Li J H, Ma H Z, Fang L.2011.Kernel-driven model fitting of multi-angle thermal infrared brightness temperature and its application. Journal of Infrared and Millimeter Waves, 30 (4): 361–365, 371. DOI: 10.3969/j.issn.1002-6819.2010.z2.010. ( 彭菁菁, 刘强, 柳钦火, 李加洪, 马红章, 方莉. 2011. 多角度热红外亮温值的模型拟合与应用. 红外与毫米波学报, 30 (4): 361–365, 371. DOI: 10.3969/j.issn.1002-6819.2010.z2.010. )
-
Peres L F, DaCamara C C.2004.Land surface temperature and emissivity estimation based on the two-temperature method:sensitivity analysis using simulated MSG/SEVIRI data. Remote Sensing of Environment, 91 (3/4): 377–389. DOI: 10.1016/j.rse.2004.03.011.
-
Peres L F, Sobrino J A, Libonati R, Jiménez-Muñoz J C, Dacamara C C, Romaguera M.2008.Validation of a temperature emissivity separation hybrid method from airborne hyperspectral scanner data and ground measurements in the SEN2FLEX field campaign. International Journal of Remote Sensing, 29 (24): 7251–7268. DOI: 10.1080/01431160802036532.
-
Prata A J.1993.Land surface temperatures derived from the advanced very high resolution radiometer and the along-track scanning radiometer:1. Theory.Journal of Geophysical Research-Atmospheres, 98 (D9): 16689–16702. DOI: 10.1029/93JD01206.
-
Prata A J.1994a.Validation Data for Land Surface Temperature Determination from Satellites.Technical Paper-CSIRO Division of Atmospheric Research No.33.1-36 [DOI:10.13140/RG.2.1.3880.9441]
-
Prata A J.1994b.Land surface temperatures derived from the advanced very high resolution radiometer and the along-track scanning radiometer:2. Experimental results and validation of AVHRR algorithms.Journal of Geophysical Research-Atmospheres, 99 (D6): 13025–13058. DOI: 10.1029/94JD00409.
-
Prata A J, Caselles V, Coll C, Sobrino J A, Ottlé C.1995.Thermal remote sensing of land surface temperature from satellites:current status and future prospects. Remote Sensing Reviews, 12 (3/4): 175–224. DOI: 10.1080/02757259509532285.
-
Price J C.1983.Estimating surface temperatures from satellite thermal infrared data-A simple formulation for the atmospheric effect. Remote Sensing of Environment, 13 (4): 353–361. DOI: 10.1016/0034-4257(83)90036-6.
-
Price J C.1984.Land surface temperature measurements from the split window channels of the NOAA 7 advanced very high resolution radiometer. Journal of Geophysical Research-Atmospheres, 89 (D5): 7231–7237. DOI: 10.1029/JD089iD05p07231.
-
Qian Y G, Li Z L, Nerry F.2013.Evaluation of land surface temperature and emissivities retrieved from MSG/SEVIRI data with MODIS land surface temperature and emissivity products. International Journal of Remote Sensing, 34 (9/10): 3140–3152. DOI: 10.1080/01431161.2012.716538.
-
Qin Z, Karnieli A, Berliner P.2001.A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. International Journal of Remote Sensing, 22 (18): 3719–3746. DOI: 10.1080/01431160010006971.
-
Quan J L, Chen Y H, Zhan W F, Wang J F, Voogt J, Li J.2014.A hybrid method combining neighborhood information from satellite data with modeled diurnal temperature cycles over consecutive days. Remote Sensing of Environment, 155 : 257–274. DOI: 10.1016/j.rse.2014.08.034.
-
Ren H Z, Yan G J, Chen L, Li Z L.2011.Angular effect of MODIS emissivity products and its application to the split-window algorithm. ISPRS Journal of Photogrammetry and Remote Sensing, 66 (4): 498–507. DOI: 10.1016/j.isprsjprs.2011.02.008.
-
Ren H Z, Yan G J, Liu R Y, Li Z L, Qin Q M, Nerry F, Liu Q.2015.Determination of optimum viewing angles for the angular normalization of land surface temperature over vegetated surface. Sensors, 15 (4): 7537–7570. DOI: 10.3390/s150407537.
-
Sabol Jr D E, Gillespie A R, Abbott E, Yamada G.2009.Field validation of the ASTER Temperature-Emissivity Separation algorithm. Remote Sensing of Environment, 113 (11): 2328–2344. DOI: 10.1016/j.rse.2009.06.008.
-
Sawabe Y, Matsunaga T, Rokugawa S, Hoyano A.2003.Temperature and emissivity separation for multi-band radiometer and validation ASTER TES algorithm. Journal of the Remote Sensing Society of Japan, 23 (4): 364–375.
-
Schädlich S, Göttsche F M, Olesen F S.2001.Influence of land surface parameters and atmosphere on METEOSAT brightness temperatures and generation of land surface temperature maps by temporally and spatially interpolating atmospheric correction. Remote Sensing of Environment, 75 (1): 39–46. DOI: 10.1016/S0034-4257(00)00154-1.
-
Slater P N, Biggar S F, Thome K J, Gellman D I, Spyak P R.1996.Vicarious radiometric calibrations of EOS sensors. Journal of Atmospheric and Oceanic Technology, 13 (2): 349–359. DOI: 10.1175/1520-0426(1996)013<0349:VRCOES>2.0.CO;2].
-
Snyder W C, Wan Z M, Zhang Y L, Feng Y Z.1997.Requirements for satellite land surface temperature validation using a silt playa. Remote Sensing of Environment, 61 (2): 279–289. DOI: 10.1016/S0034-4257(97)00044-8.
-
Sobrino J A, Coll C, Caselles V.1991.Atmospheric correction for land surface temperature using NOAA-11 AVHRR channels 4 and 5. Remote Sensing of Environment, 38 (1): 19–34. DOI: 10.1016/0034-4257(91)90069-I.
-
Sobrino J A, Caselles V, Coll C.1993.Theoretical split-window algorithms for determining the actual surface temperature. IL Nuovo Cimento C, 16 (3): 219–236. DOI: 10.1007/BF02524225.
-
Sobrino J A, Li Z L, Stoll M P, Becker F.1994.Improvements in the split-window technique for land surface temperature determination. IEEE Transactions on Geoscience and Remote Sensing, 32 (2): 243–253. DOI: 10.1109/36.295038.
-
Sobrino J A, Li Z L, Stoll M P, Becker F.1996.Multi-channel and multi-angle algorithms for estimating sea and land surface temperature with ATSR data. International Journal of Remote Sensing, 17 (11): 2089–2114. DOI: 10.1080/01431169608948760.
-
Sobrino J A, Cuenca J.1999.Angular variation of thermal infrared emissivity for some natural surfaces from experimental measurements. Applied Optics, 38 (18): 3931–3936. DOI: 10.1364/AO.38.003931.
-
Sobrino J A, Raissouni N.2000.Toward remote sensing methods for land cover dynamic monitoring:application to Morocco. International Journal of Remote Sensing, 21 (2): 353–366. DOI: 10.1080/014311600210876.
-
Sobrino J A, Jiménez-Muñoz J C, Paolini L.2004a.Land surface temperature retrieval from LANDSAT TM 5. Remote Sensing of Environment, 90 (4): 434–440. DOI: 10.1016/j.rse.2004.02.003.
-
Sobrino J A, Sòria G, Prata A J.2004b.Surface temperature retrieval from Along Track Scanning Radiometer 2 data:algorithms and validation. Journal of Geophysical Research-Atmospheres, 109 (D11): D11101 DOI: 10.1029/2003JD004212.
-
Sobrino J A, Jiménez-Muñoz J C.2005.Land surface temperature retrieval from thermal infrared data:an assessment in the context of the Surface Processes and Ecosystem Changes Through Response Analysis (SPECTRA) mission. Journal of Geophysical Research-Atmospheres, 110 (D16): D16103 DOI: 10.1029/2004JD005588.
-
Sobrino J A, Jiménez-Muñoz J C, Balick L, Gillespie A R, Sabol D A, Gustafson W T.2007.Accuracy of ASTER level-2 thermal-infrared standard products of an agricultural area in Spain. Remote Sensing of Environment, 106 (2): 146–153. DOI: 10.1016/j.rse.2006.08.010.
-
Sobrino J A, Julien Y, Atitar M, Nerry F.2008.NOAA-AVHRR orbital drift correction from solar zenithal angle data. IEEE Transactions on Geoscience and Remote Sensing, 46 (12): 4014–4019. DOI: 10.1109/TGRS.2008.2000798.
-
Sòria G, Sobrino J A.2007.ENVISAT/AATSR derived land surface temperature over a heterogeneous region. Remote Sensing of Environment, 111 (4): 409–422. DOI: 10.1016/j.rse.2007.03.017.
-
Su Z.2002.The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrology and Earth System Sciences, 6 (1): 85–100. DOI: 10.5194/hess-6-85-2002.
-
Sun D L, Pinker R T.2003.Estimation of land surface temperature from a Geostationary Operational Environmental Satellite (GOES-8). Journal of Geophysical Research-Atmospheres, 108 (D11): 4326 DOI: 10.1029/2002JD002422.
-
Sun D L, Pinker R T.2005.Implementation of GOES-based land surface temperature diurnal cycle to AVHRR. International Journal of Remote Sensing, 26 (18): 3975–3984. DOI: 10.1080/01431160500117634.
-
Sun D L, Pinker R T.2007.Retrieval of surface temperature from the MSG-SEVIRI observations:part I. Methodology.International Journal of Remote Sensing, 28 (23): 5255–5272. DOI: 10.1080/01431160701253246.
-
Susskind J, Rosenfield J, Reuter D, Chahine M T.1984.Remote sensing of weather and climate parameters from HIRS2/MSU on TIROS-N. Journal of Geophysical Research-Atmospheres, 89 (D3): 4677–4697. DOI: 10.1029/JD089iD03p04677.
-
Tang B H, Bi Y Y, Li Z L, Xia J.2008.Generalized split-window algorithm for estimate of land surface temperature from chinese geostationary FengYun meteorological satellite (FY-2C) data. Sensors, 8 (2): 933–951. DOI: 10.3390/s8020933.
-
Tonooka H.2001.An atmospheric correction algorithm for thermal infrared multispectral data over land-A water-vapor scaling method. IEEE Transactions on Geoscience and Remote Sensing, 39 (3): 682–692. DOI: 10.1109/36.911125.
-
Tonooka H.2005.Accurate atmospheric correction of ASTER thermal infrared imagery using the WVS method. IEEE Transactions on Geoscience and Remote Sensing, 43 (12): 2778–2792. DOI: 10.1109/TGRS.2005.857886.
-
Townshend J R G, Justice C O, Skole D, Malingreau J P, Cihlar J, Teillet P, Sadowski F, Ruttenberg S.1994.The 1 km resolution global data set:needs of the International Geosphere Biosphere Programme. International Journal of Remote Sensing, 15 (17): 3417–3441. DOI: 10.1080/01431169408954338.
-
Trigo I F, Monteiro I T, Olesen F, Kabsch E.2008a.An assessment of remotely sensed land surface temperature. Journal of Geophysical Research-Atmospheres, 113 (D17): D17108 DOI: 10.1029/2008JD010035.
-
Trigo I F, Peres L F, DaCarnara C C, Freitas S C.2008b.Thermal land surface emissivity retrieved from SEVIRI/meteosat. IEEE Transactions on Geoscience and Remote Sensing, 46 (2): 307–315. DOI: 10.1109/TGRS.2007.905197.
-
Ulivieri C, Castronuovo M M, Francioni R, Cardillo A.1994.A split window algorithm for estimating land surface temperature from satellites. Advances in Space Research, 14 (3): 59–65. DOI: 10.1016/0273-1177(94)90193-7.
-
Vauclin M, Vieira S R, Bernard R, Hatfield J L.1982.Spatial variability of surface temperature along two transects of a bare soil. Water Resources Research, 18 (6): 1677–1686. DOI: 10.1029/WR018i006p01677.
-
Vázquez D P, Reyes F J O, Arboledas L A.1997.A comparative study of algorithms for estimating land surface temperature from AVHRR data. Remote Sensing of Environment, 62 (3): 215–222. DOI: 10.1016/S0034-4257(97)00091-6.
-
Voogt J A, Oke T R.2003.Thermal remote sensing of urban climates. Remote Sensing of Environment, 86 (3): 370–384. DOI: 10.1016/S0034-4257(03)00079-8.
-
Wan Z M, Dozier J.1996.A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Transactions on Geoscience and Remote Sensing, 34 (4): 892–905. DOI: 10.1109/36.508406.
-
Wan Z M, Li Z L.1997.A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Transactions on Geoscience and Remote Sensing, 35 (4): 980–996. DOI: 10.1109/36.602541.
-
Wan Z M.1999.MODIS land-surface temperature algorithm theoretical basis document (LST ATBD) Greenbelt MD, USA:NASA/GSFC
-
Wan Z M, Zhang Y L, Zhang Q C, Li Z L.2002.Validation of the land-surface temperature products retrieved from Terra Moderate Resolution Imaging Spectroradiometer data. Remote Sensing of Environment, 83 (1/2): 163–180. DOI: 10.1016/S0034-4257(02)00093-7.
-
Wan Z, Zhang Y, Zhang Q, Li Z L.2004.Quality assessment and validation of the MODIS global land surface temperature. International Journal of Remote Sensing, 25 (1): 261–274. DOI: 10.1080/0143116031000116417.
-
Wan Z M.2008.New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sensing of Environment, 112 (1): 59–74. DOI: 10.1016/j.rse.2006.06.026.
-
Wan Z, Li Z L.2008.Radiance-based validation of the V5 MODIS land-surface temperature product. International Journal of Remote Sensing, 29 (17/18): 5373–5395. DOI: 10.1080/01431160802036565.
-
Wan Z M and Li Z L.2011.MODIS land surface temperature and emissivity//Ramachandran B, Justice C O and Abrams M J, eds.Land Remote Sensing and Global Environmental Change.New York:Springer:563-577 [DOI:10.1007/978-1-4419-6749-7_25]
-
Wan Z M.2014.New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sensing of Environment, 140 : 36–45. DOI: 10.1016/j.rse.2013.08.027.
-
Wang N, Wu H, Nerry F, Li C R, Li Z L.2011.Temperature and emissivity retrievals from hyperspectral thermal infrared data using linear spectral emissivity constraint. IEEE Transactions on Geoscience and Remote Sensing, 49 (4): 1291–1303. DOI: 10.1109/TGRS.2010.2062527.
-
Wang N, Li Z L, Tang B H, Zeng F N, Li C R.2013.Retrieval of atmospheric and land surface parameters from satellite-based thermal infrared hyperspectral data using a neural network technique. International Journal of Remote Sensing, 34 (9/10): 3485–3502. DOI: 10.1080/01431161.2012.716536.
-
Wang W H, Liang S L, Meyers T.2008.Validating MODIS land surface temperature products using long-term nighttime ground measurements. Remote Sensing of Environment, 112 (3): 623–635. DOI: 10.1016/j.rse.2007.05.024.
-
Watson K.1992.Spectral ratio method for measuring emissivity. Remote Sensing of Environment, 42 (2): 113–116. DOI: 10.1016/0034-4257(92)90094-Z.
-
Weng F Z, Grody N C.1998.Physical retrieval of land surface temperature using the special sensor microwave imager. Journal of Geophysical Research-Atmospheres, 103 (D8): 8839–8848. DOI: 10.1029/98JD00275.
-
Weng Q H, Lu D S, Schubring J.2004.Estimation of land surface temperature-vegetation abundance relationship for urban heat island studies. Remote Sensing of Environment, 89 (4): 467–483. DOI: 10.1016/j.rse.2003.11.005.
-
Weng Q H.2009.Thermal infrared remote sensing for urban climate and environmental studies:methods, applications, and trends. ISPRS Journal of Photogrammetry and Remote Sensing, 64 (4): 335–344. DOI: 10.1016/j.isprsjprs.2009.03.007.
-
Zhang R H, Tian J, Su H B, Sun X M, Chen S H, Xia J.2008.Two improvements of an operational two-layer model for terrestrial surface heat flux retrieval. Sensors, 8 (10): 6165–6187. DOI: 10.3390/s8106165.
-
Zhou J, Chen Y H, Zhang X, Zhan W F.2013.Modelling the diurnal variations of urban heat islands with multi-source satellite data. International Journal of Remote Sensing, 34 (21): 7568–7588. DOI: 10.1080/01431161.2013.821576.