出版日期: 2016-09-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20166241
2016 | Volumn20 | Number 5

论文

黑河遥感试验中尺度上推研究的进展与前瞻

李新¹ , 晋锐¹ , 刘绍民² , 葛咏³ , 肖青⁴ , 柳钦火⁴ , 马明国⁵ , 冉有华¹

1. 中国科学院寒区旱区环境与工程研究所, 甘肃兰州 730000

2. 北京师范大学地理学与遥感科学学院遥感科学国家重点实验室, 北京 100875

3. 中国科学院地理科学与资源研究所, 北京 100101

4. 中国科学院遥感与数字地球研究所遥感科学国家重点实验室, 北京 100101

5. 西南大学地理科学学院, 重庆 400715

收稿日期: 2016-06-30; 修改日期: 2016-07-02; 优先数字出版日期: 2016-09-25

基金项目: 国家自然科学基金委员会重大研究计划“黑河流域生态-水文过程集成研究”集成项目（编号：91425303）；中国科学院西部行动计划三期项目“黑河流域生态-水文遥感产品生产算法研究与应用试验”（编号：KZCX2-XB3-15）；中国科学院创新交叉团队项目资助

第一作者简介: 李新(1969-), 男, 研究员, 研究方向为陆面数据同化、遥感和GIS在冰冻圈和水文水资源研究中的应用、流域集成研究。E-mail:lixin@lzb.ac.cn

中图分类号: TP79

文献标识码: A

文章编号: 1007-4619(2016)05-0921-12

摘要

尺度问题是遥感科学研究的一个关键科学问题，但其理论和方法的发展严重受限于稀缺的多尺度观测数据。黑河生态水文遥感试验（HiWATER）的核心目标之一是开展多尺度观测以支持尺度转换研究。本文综述了HiWATER中定点观测的尺度上推研究进展，内容包括：（1）尝试严格定义了空间平均、空间尺度上推、观测足迹、代表性误差、观测真值等概念；（2）介绍了HiWATER获取的多尺度（单点-像元-区域-流域）生态水文观测数据；（3）发展了基于地统计理论的多尺度采样方法，改进了基于时间稳定性的采样方法；（4）定量评估了辐射、碳通量、土壤水分、地表温度单点观测的代表性误差，实证了异质性地表遥感产品真实性检验的不确定性主要来源于观测的时空代表性；（5）发展了定点观测的尺度上推方法，将克里格方法推广至回归克里格、面到面、不等精度观测等情形，发展了贝叶斯框架下的非线性尺度上推方法，实证了引入遥感观测作为协同信息可显著提高尺度上推的精度。总之，HiWATER初步形成了从采样设计、多尺度观测、代表性误差的度量、尺度上推新方法到真实性检验的研究框架。

关键词

像元尺度 , 代表性误差 , 观测真值 , 采样设计 , 真实性检验 , 黑河流域

Upscaling research in HiWATER: Progress and prospects

LI Xin¹ , JIN Rui¹ , LIU Shaomin² , GE Yong³ , XIAO Qing⁴ , LIU Qinhuo⁴ , MA Mingguo⁵ , RAN Youhua¹

1.Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China

2.State Key Laboratory of Remote Sensing Science, School of Geography and Remote Sensing Science, Beijing Normal University, Beijing 100875, China

3.State Key Laboratory of Resources & Environmental Information System, Institute of Geographical Science and Natural Resources Research, Chinese Academy of Sciences, Datun Road, Beijing 100101, China

4.State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China

5.School of Geographical Sciences, Southwest University, Chongqing 400715, China

Abstract

The scale issue in quantitative remote sensing is a significant challenge that comprises three major problems that need to be addressed:(1) the forward modeling of remote sensing signals for heterogeneous land surfaces, (2) the parameter inversion for heterogeneous land surfaces, and (3) the upscaling of in situ observation for the validation of remote sensing products. This study focuses on the third problem by reviewing the progress of upscaling research in the Heihe Watershed Allied Telemetry Experimental Research (HiWATER). First, we define several basic concepts associated with scaling on the basis of the probability space and data assimilation theory. These concepts include spatial average, spatial upscaling, footprint scale, pixel scale, point scale, representativeness error, observation truth, and validation threshold. Second, we introduce the multiscale observation platform of HiWATER and multiscale observation data, which covers the scales from point to pixels, sub-basins, and the whole river basin. Third, we describe several new developments in the sampling design based on geostatistics and temporal stability analysis. Specifically, a hybrid model-based sampling method without any spatial autocorrelation assumptions is developed to optimize the distribution of eco-hydrological wireless sensor network nodes, a universal coKriging model is proposed to optimize multivariate sampling design, and a stratified block kriging is used to optimize the sampling locations in a spatial heterogeneous area. The temporal stability analysis is improved for the selection of the representative sampling points of the albedo and leaf area index. The stratified temporal stability analysis is proposed to identify the representative sampling points for monitoring long-term soil moisture at the pixel scale in high-intensity irrigated agricultural landscapes. Fourth, the representativeness of the in situ observation of solar radiation, carbon flux, soil moisture, and land surface temperature is evaluated. Results showed that the uncertainty of the validation for remote sensing products in heterogeneous areas mainly comes from the spatial and temporal representativeness of in situ measurements. Fifth, several upscaling methods are developed. The Kriging method is extended to block regression Kriging, area-to-area regression Kriging, spatiotemporal regression block Kriging, and unequal accuracy block Kriging for upscaling the in situ observation from the point-scale or footprint-scale to the pixel scale. Additionally, several case studies show that the Bayesian maximum entropy, a nonlinear method, is capable of providing a generalized theory framework to fuse general knowledge (such as that obtained from a model) and specific knowledge (such as that obtained from direct and indirect observations). The usefulness of high-resolution remote sensing data as auxiliary information in improving the accuracy of upscaling is verified in this work. Overall, the multi-scale observation data collected in HiWATER are helpful in improving our understanding of remote sensing scale problems.

Key words

pixel-scale , representativeness error , true value , sampling design , validation , Heihe River basin

1 引言

尺度转换问题是定量遥感最核心的问题之一，长期困扰着遥感正向模型的发展、遥感反演和遥感产品真实性检验，并引发了国内外遥感科学研究者的广泛讨论(Wu和Li，2009)。目前，遥感研究中的尺度转换问题主要有3类：(1)异质性像元(混合像元)的正向建模，如随机辐射传输模型的发展；(2)异质性像元的参数反演，如反演中的尺度校正；(3)定点观测的尺度上推及遥感产品真实性检验。

本文专门讨论第3类问题，它涉及：(1)异质性地表采样问题，即如何在地表布设点和足迹尺度观测，如何优化空间和时间采样，为尺度上推和真实性检验准备基础数据。(2)点观测和足迹观测的代表性问题，其核心是如何定量代表性误差。(3)像元尺度真值的估计，这是一个尺度上推问题，涉及地面点观测或者足迹观测到像元尺度的转换，高分辨率像元到粗分辨率像元的转换，辅助信息在尺度转换中的应用，以及在尺度上推中如何度量不确定性。

尽管尺度转换问题倍受关注，但这方面研究进展并不大，这一方面是因为几乎没有成熟的理论来指导尺度转换研究，另一方面也是受困于没有真正的多尺度数据(Li等，2013)。面对遥感尺度转换研究的困境，李小文院士曾指出，应结合“自上而下的演绎方法和自下而上归纳方法”，发展普适性的尺度转换方法；同时，应“从数据和方法论两方面促进尺度效应和尺度转换研究”(李小文和王祎婷，2013)。这一思路，和当前国际上一系列多尺度观测试验的出发点是一致的。

2012年启动的黑河生态水文遥感试验(HiWATER)的主要目标之一是推进对于尺度转换问题的理解(李新等，2012；Li等，2013)。在HiWATER所关注的核心问题中，有3个问题和尺度转换问题密切相：(1)异质性(heterogeneity)；(2)不确定性(uncertainty)；(3)尺度转换(scaling)。HiWATER开展以来，在前期试验的基础上，尝试从获取真正的多尺度数据和发展普适性尺度转换方法两方面来推动尺度转换研究，并取得了一定的进展。

2 概念定义

尺度转换问题的研究进展缓慢，和这一领域的若干重要概念不清有关。本文对于定点观测的尺度上推与遥感产品真实性检验研究中若干基本概念进行了定义。借助概率空间和数据同化的理论，力求准确定义，并在全文中使用统一的概念。但对这些概念的更严格定义，需要借助随机微分方程等数学工具，这是我们努力的方向。

2.1 空间平均(spatial average)和空间尺度上推(spatial upscaling)

在概率空间{Ω，F，P}上有定义在空间域A上的随机场Θ，其中，Ω为样本空间，其元素记为ω；F是样本空间Ω的幂集的一个非空子集；P是一个概率测度。

$ {\boldsymbol{\Theta}} :{\boldsymbol{\Omega}} \times {\boldsymbol{A}} \to {{\rm{\mathbb{R}}}^n} $

(1)

参考Ostoja-Starzewski(2006)的工作，定义空间平均为

$ \overline {{\boldsymbol{\Theta}} \left(\omega \right)} \equiv \frac{1}{\boldsymbol{A}}\mathop {\displaystyle\int} \nolimits_A \boldsymbol{\Theta} \left( {\omega {\rm{,}}\mu } \right){\rm{d}}{\boldsymbol{A}} $

(2)

式中，μ为空间中的一个点。把定点观测看做随机空间变量，则求解式(2)的过程即定点观测的空间尺度上推。

系统状态以及观测场都是最常见的空间随机场，本文用X表示系统中的状态向量，Y表示观测向量。

2.2 足迹尺度/像元尺度(footprint-scale/pixel-scale)

足迹又称代表性空间，是指变量的贡献源区的最主要部分。像元是一种特殊的观测足迹，通常指遥感的观测足迹，它可为正方形、矩形、椭圆形或其他形状。

在空间尺度上推中，避免严格的数学定义，足迹尺度可以被看做随机场Θ的空间平均(式(2))的积分区间，即足迹所对应的面积或体积。

2.3 点尺度(point-scale)

所有观测都有其足迹，但为了研究方便，当足迹很小时，通常可忽略足迹内的异质性。定义足迹为0的尺度为点尺度，相应的观测为点观测(point observation)。

2.4 观测的代表性误差(representativeness error)

从一个状态向量到一个观测向量，或者两个不同观测向量之间的映射可以统一表示为

$ H: \boldsymbol{X} \to \boldsymbol{Y} $

(3)

X和Y的足迹可以相同也可以不同，它们可以是同一个物理量也可以不是同一个物理量。H被称为观测算子(observation operator)，其具体实例包括：点观测到足迹观测的空间尺度上推，地表状态变量到点观测的转换，以及把地表状态变量映射到遥感原始观测的辐射传输模型(Li，2014)。观测算子H的误差ε可表示为

$ \boldsymbol{Y} = H\left(\boldsymbol{X} \right)+ \boldsymbol{\varepsilon}, $

(4)

ε可以分解为仪器误差ε_E(instrument error)和代表性误差ε_F，即

$ \boldsymbol{\varepsilon} = {\boldsymbol{\varepsilon} _{_E}} + {\boldsymbol{\varepsilon} _{_F}} $

(5)

仪器(或者更广义地说，观测模型)经过严格的定标后，其数学期望为零，也就是说仪器误差是一个无偏估计。

代表性误差通常更难估计，它既包括尺度转换带来的误差，也包括观测模型的不完美(如物理表达上的欠缺)所带来的误差。通常，定点观测的代表性误差来自于点—足迹或足迹—足迹的尺度转换，遥感观测的代表性误差部分来自于遥感正向模型从微观尺度到像元尺度的尺度转换。

2.5 观测的真值(observation truth)

观测的真值可以定义为无偏最优估计，也就是它的误差的数学期望为零，而其不确定性(如方差)可以被控制在所期望的范围内，即

$ \begin{array}{l} E\left({{{\boldsymbol{\varepsilon}} _i}} \right)= 0，\\ {\rm{Var}}\left({{{\boldsymbol{\varepsilon}} _i}} \right)= {\sigma ^2} < \infty \end{array} $

(6)

式中，下标i表示误差向量的第i个元素。通常，当E(ε_i)时，仪器误差和代表性误差的数学期望同时为0，即E(ε_E，i)=0并且E(ε_F，i)=0。

2.6 检验阈值(validation threshold)

检验阈值δ是一个主观的标准，来自于对于待检验变量的理解及真实性检验中的经验。具体定义为

$ {\left\| \boldsymbol{\varepsilon} \right\|_p} < \delta $

(7)

其数值选取通常应考虑：(1)公认的标准，如土壤水分的检验阈值一般为0.04 m³ m^–3；(2)与目标地物有关，如叶面积指数(LAI)的检验阈值针对不同土地覆被类型而不同，因此常常采用相对值，如10%。

3 HiWATER多尺度观测数据

获得多尺度观测数据是研究尺度转换问题的前提。在尺度转换问题上进展甚少的主要原因之一是过去“实际上不存在可为全面验证已有的尺度上推方法提供足够信息的数据集”(Vereecken等，2007)。近年来，包括HiWATER之内的一系列多尺度观测试验以及无线传感器网络和足迹尺度地面观测技术(Liu等，2011)的发展，为验证和发展新的尺度转换方法提供了前所未有的数据基础。

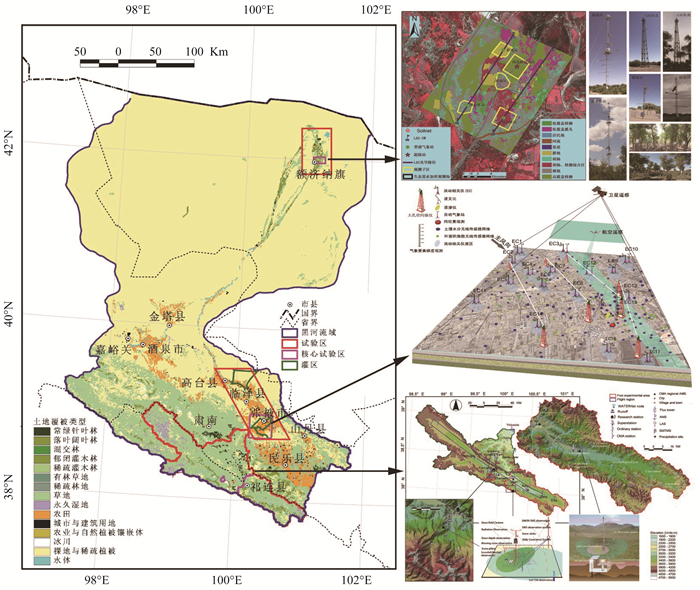
HiWATER非常重视多尺度观测数据的获取，在黑河流域全流域上、中、下游分别布置了多尺度嵌套的水文气象观测网(李新等，2012; Li等，2013)、通量观测矩阵(Xu等，2013; Liu等，2016)、生态水文无线传感器网络(Jin等，2014; Qu等，2014)，并开展了大量航空遥感试验和同步的地面加强观测(图 1)。其中，针对中游绿洲—荒漠系统，布置了分布在绿洲内部农田和湿地以及绿洲外围的戈壁、沙丘和荒漠草原上，由6套涡动相关仪(EC)、自动气象站以及径流等水循环和能量平衡观测设备组成的大矩阵；在绿洲内部，选择典型的农田生态系统，布置了由18套EC、4组大孔径闪烁仪(LAS)、17台自动气象站、野外同位素原位观测系统、200多个土壤温湿度传感器节点、50多个叶面积指数传感器节点构成的小矩阵，并开展了探空、地基遥感、地面配套参数等加强观测。在上游，建成了多尺度嵌套的生态水文观测网络，由全流域水文气象—通量观测站、子流域(八宝河)生态水文传感器网络(40个节点)(晋锐等，2012)以及积雪和冻融超级观测站组成。在下游，建成了由2组LAS，分布于胡杨、柽柳、胡杨/柽柳混交林、农田、裸地上的5套EC与自动气象站，以及土壤水分无线传感器网络组成的多尺度观测系统。在航空遥感方面，搭载激光雷达、光学—近红外—热红外波段成像光谱仪、多角度热红外成像仪、微波辐射计，开展了21个架次，总计约100 h的航空遥感飞行，获取了一套超高分辨率遥感数据。

图 1 黑河生态水文遥感试验(HiWATER)中的多尺度观测

Fig. 1 Multi scale observation system of HiWATER

HiWATER观测数据涵盖的尺度包括：(1)流域尺度：几千到几十万平方公里，包括了整个流域和主要的子流域；(2)汇水区(watershed)和灌区尺度：几十到几百平方公里；(3)千米尺度：与中等分辨率遥感，如MODIS(Moderate Resolution Imaging Spectroradiometer)、MERIS(Medium Resolution Imaging Spectrometer)、中国风云气象卫星的分辨率相对应，也与流域生态与水文模型的网格分辨率相对应；对定点观测而言，千米尺度与LAS的足迹相当；(4)景观尺度：通常几个或几十公顷，与EC的观测足迹相当；(5)米到亚米尺度，与多数土壤水分传感器及LAI传感器的尺度相当；(6)单株植物、叶面、气孔尺度。

4 异质性地表的空间采样

采样是尺度上推的重要基础，从数学角度讲，也是空间尺度上推的一个反问题。优化的采样，不仅能够更好地捕捉到空间异质性，减少采样成本，也更有利于得到足迹尺度的最优估计。

4.1 基于地统计理论的采样

近年来，异质性地表的采样在理论方法上都有了突破性的进展(Wang等，2009，2012)。在此理论基础上，HiWATER发展了多种基于地统计理论的优化采样方法，在采样设计中重点考虑的因素包括：基于景观异质性和生态水文变量时空异质性的分区采样、无偏最优估计、多尺度采样。

针对黑河中游高度异质性条件下多尺度采样的需求，Kang等人(2014)发展了一种混合优化策略的土壤水分采样方案，目标是在无先验知识的条件下，用有限的传感器网络节点，同时满足变异函数估计及统计推断方差最小化的要求。该方法包括两个子策略：一是针对变量空间变异结构建模，使多个尺度的变异性都有足够的样本用于估计，有利于连续空间变异函数的准确拟合；二是有助于减少空间估计的不确定性，使样本空间分布尽量均匀分布。Kang等人(2014)基于以上策略开展了数值试验，采用了15种类型的随机模拟场，对样本代表性、变异函数参数估计精度以及不同像元尺度的估计精度进行了验证。结果表明，经过优化的传感器网络有较好的空间代表性，均值最大绝对偏差为0.12，标准差的最大绝对偏差为0.05；变异结构建模精度较高，最大相对误差不超过6%，平均相对误差为3%。

针对如何利用有限的观测节点捕捉流域生态水文关键变量的空间分布和时间动态特征的问题，Ge等人(2015a)发展了泛协同克里格采样优化模型(UCK model-based sampling)，该方法将观测目标看做多变量空间随机场，首先针对环境协变量和降水、土壤水分及地表温度间的关系进行趋势建模，利用协同区域化模型构建多变量残差之间的空间相关性，再以多变量残差加权估计误差平方和最小为目标，采用空间模拟退火算法优化观测点空间位置和属性分布。这个方法被成功地应用于黑河流域上游八宝河子流域生态水分传感器网络的设计和实施，实现了观测网和多目标对象属性分布的优化以及多要素空间变异特征的捕捉。类似的方法被应用于流域总初级生产力(GPP)的采样方案设计，Wang等人(2014a)利用分层块克里格模型(StrBK)构建目标函数，在确定最佳样本量大小后，通过空间模拟退火优化算法，确定异质表面空间采样最佳方案。数值实验结果表明，对GPP而言，考虑空间异质的采样可以比未考虑异质的采样精度提高约10.1%。

4.2 基于时间稳定性的采样

时间稳定性是指对某一变量在某一空间变量间位置的测量与该在某一区域上的空间结构统计关系的时间不变性(Vachaud等，1985; Kachanoski和De Jong，1988)。如果这种时间不变性存在，则该方法可用于该变量地面长期监测网的采样设计，即通过前期短期的探索性观测，确定代表性观测点的位置，在这几个代表性位置布置长期观测点，可在很大程度上长期代表一定精度水平内的区域空间平均值。后期研究发现，这种时间不变性不同程度地存在于许多生态水文要素中。如今，时间稳定性分析方法已被广泛应用于土壤水分、生态系统生产力、反照率等地表参量代表性观测位置的识别。

在HiWATER中，该方法得到进一步的发展和应用。Ran等人(2016a)针对该方法在高强度灌溉农业景观像元尺度土壤水分代表性监测点识别中的性能及其尺度依赖性开展了系统实验。结果表明，在高强度灌溉的农田景观中，时间稳定性分析的性能受到灌溉和降水不同性质的影响，并存在明显的尺度依赖性。时间稳定性分析对于处理系统误差主导的区域具有明显优势，对于随机误差主导的区域可通过分层来提高代表性观测点的识别性能。同时，对于如何利用瞬时采样(高空间分辨率辅助信息)，如何确定采样期长度和采样点数量给出了具体建议。Wu等人(2015)在同一区域成功利用时间稳定性分析方法识别最有代表性的反照率地面观测点，通过加权平均实现了反照率地面观测向像元平均的尺度转换，为遥感反照率产品验证提供了像元尺度真值。Zeng等人(2015)基于时间稳定性的思想，基于植被类型与植被长势等先验知识，考虑样点在不同时相的空间代表性与属性代表性，提出了一种非均质地表LAI的地面采样方法，该方法在多时相上明显优于传统的随机采样和均匀采样。

综上，基于时间稳定性分析的代表性观测点识别与采样设计，有效地减少了地面观测的代表性误差。基于时间稳定性分析方法的采样设计中蕴含了重要的目标参量的空间结构信息，将代表性观测点与高分辨率遥感或其他观测手段得到的空间结构信息相融合，有望提高尺度上推的精度。

5 定点观测的代表性误差

HiWATER为分析定点观测的代表性误差的来源、尺度依赖、与空间异质性的关系，以及控制和减小代表性误差的途径，提供了前所未有的多尺度观测数据。本节以太阳短波辐射、地表蒸散发、CO₂通量、地表温度(LST)、土壤水分为例，来分析定点观测的代表性误差。

(1)太阳短波入射辐射。一般认为，太阳短波入射辐射具有很高的空间一致性，在几十公里的范围内不会有太大的变化。因此，太阳短波入射辐射的单点观测常被用来直接验证不同时空分辨率的相应遥感产品，而忽略了点观测可能存在的空间代表性不足的问题。那么，对于太阳短波入射辐射，点尺度和遥感产品的足迹尺度(如5 ×5 km或1°×1°)间的空间不匹配性到底有多强？点观测的代表性误差有多大？针对这些问题，依据HiWATER的矩阵观测和高分辨率的黑河流域太阳辐射产品(Huang等，2016a)，Huang等人(2016b)探讨了太阳短波入射辐射点观测在公里和1°×1°网格两种空间尺度上的代表性误差。结果表明，单点地基观测与卫星遥感产品间确实存在空间尺度上的不匹配性，由此而来的代表性误差不仅依赖于它们的时间和空间尺度，而且与即时的大气状况，特别是足迹范围内的云覆盖率有关。例如，在5 km尺度上，当时间尺度从月尺度到瞬时尺度时，代表性误差约为1.4%—8.1%。当时间尺度大于等于日尺度，代表性误差较小可以忽略；然而，当时间尺度小于日尺度时，代表性误差不可忽略，尤其是在瞬时尺度上，代表性误差要远大于仪器误差。在1°×1°网格尺度上，不论时间尺度如何，代表性误差均不可忽略。

(2)CO₂通量。EC所测量的CO₂通量常被用于验证CO₂通量遥感产品和模型结果，然而，由于布置位置、传感器高度及气象条件和下垫面结构的差异，每一个站点的EC通量观测都具有不同的代表性，这种空间代表性对于CO₂通量的尺度转换及遥感和模型估计结果的验证有重要影响。Ran等人(2016b)使用HiWATER通量矩阵5 ×5 km范围内的17个EC观测研究了初级生产力(NPP)、净生态系统生产力(NEP)和生态系统呼吸(Re)的代表性误差，结果表明，CO₂通量具有很大的代表性误差，对于5 ×5 km上的NPP、NEP和Re，单个EC在一个生长季的系统高估可能分别超过25(±14)%、40(±33)%和20(±13)%，由于模型参数的尺度依赖性，这种代表性误差可能通过模型参数标定过程传递到网格尺度上。利用EC源区与目标网格植被指数或精细土地覆被类型结构之间的关系，可以有效地纠正大于20%的代表性误差。

(3)地表温度。热红外辐射计单点观测得到的LST常被用于验证LST遥感产品，而关于其代表性误差的研究甚少。Yu和Ma(2015)选取了HiWATER观测矩阵核心区内，对应于一个MODIS像元(1 ×1 km)的两种不同视角的红外辐射计观测，分析了用LST单点观测验证MODIS LST产品的代表性误差。其中，1个半球视角热红外辐射计安装在6 m高度，对应的足迹直径为44.7 m；7个小视角(半视场角为22°)热红外辐射计安装在4 m高度，对应的足迹直径为3.2 m。代表性误差的分析结果表明，对于小视角热红外辐射计观测，LST单点观测在白天的代表性误差小于1 K的概率只有15.3%，而大于3 K的概率达41.8%。大视角热红外辐射计观测的代表性明显好于小视角观测，其单点观测在白天的代表性误差小于1 K的概率为32.9%，而大于3 K的概率降低为14.9%。此外，地表空间异质性越大，尺度之间的不匹配越显著；白天的代表性误差大于夜间的代表性误差，原因是白天热异质性更强。总之，如果以1 K作为验证阈值，则单点观测在白天不能被用于验证遥感产品的概率远远大于能够被用于验证遥感产品的概率。

(4)土壤水分。土壤水分遥感产品真实性检验的传统思路也是采用单点观测，但这一验证方法近年来受到很大的质疑，原因就在于土壤水分的高度空间异质性导致的单点观测的代表性不强。利用HiWATER的土壤水分无线传感器网络和宇宙射线的土壤水分数据，Li和Liu(2016)研究了定点观测数据验证遥感产品时的代表性问题。他们把0.04 m³ m^–3作为土壤水分产品真实性检验的检验阈值，如果代表性误差大于检验阈值，则认为该估计量不能被用于真实性检验；而代表性误差小于检验阈值的估计量则被分为优( < 0.01 m³ m^–3)、良(0.01—0.02 m³ m^–3)、可用(0.02—0.04 m³ m^–3)3个类别。然后，借助3个数值实验，量化了单点观测、多点观测算术平均以及块克里格(block Kriging)空间均值的代表性误差。实验结果表明，分别只有不超过12%、12%、21%的单点观测可以被视为优、良、可用的足迹尺度真值。当使用多点观测的算术均值时，这个概率有明显的提升；而采用块克里格的空间加权平均则进一步增强了多点观测估计足迹尺度真值的代表性。该研究说明，只有通过恰当的尺度上推方法，才能将点尺度的土壤水分观测上推到足迹尺度，验证该尺度下的数据产品。

6 空间尺度上推方法

像元尺度真值的获取，按照式(2)的定义，即是在某种假设的基础上得到被积函数，再利用通常是空间上离散的观测，数值积分得到空间平均的过程。

在HiWATER中，将尺度转换研究的核心聚焦在中等分辨率(–1 km)异质性像元，原因是：(1)遥感像元的空间表达方式与多数生态或水文模型的空间离散化方式(即网格作为模拟单元)一致；(2)在流域生态水文应用中，中等分辨率遥感起到重要的作用，而其像元分辨率也和流域生态—水文模型的分辨率较为接近(500—1000 m)；(3)中等分辨率像元是一个适中的表征异质性的尺度；(4)与不同宏观尺度的尺度转换方法类似。因此，如果能够把定点观测转换到1 km分辨率的空间尺度上，通常，同类方法也至少适用于相近的尺度，如100 m—10 km。

利用HiWATER数据，针对土壤水分、蒸散发、反照率和叶面积指数，发展了点和足迹尺度定点观测的尺度上推方法。

6.1 克里格(Kriging)框架下的线性尺度上推方法

克里格是最常用的线性尺度上推方法，它假定空间平均(式(2))是多个定点观测的加权和，而权重由点对之间的距离来确定(李新等，2000)。借助HiWATER的多尺度观测，进一步发展和丰富了克里格框架下的线性尺度上推方法，将克里格方法推广至利用协同信息、面到面、时空克里格、不等精度观测等情形。

(1)利用协同信息的块回归克里格(block regression Kriging)。Kang等人(2015)认为具有面覆盖特征的遥感信息可在异质性地表的土壤水分尺度上推研究中发挥重要作用。他们采用回归克里格算法融合了HiWATER土壤水分无线传感器网络多点观测和多种遥感辅助信息，比较了不同分辨率和信息来源的遥感数据对土壤水分尺度上推的贡献，包括90 m分辨率的ASTER植被干燥指数(TVDI)、1000 m分辨率的MODIS TVDI、以及700 m分辨率的机载L波段微波辐射计PLMR亮度温度数据。与普通克里格结果比较表明：引入遥感辅助信息能够显著提高尺度上推的估值精度，而且能反映土壤水分的空间分布模式及其细节信息，尤其是当灌溉破坏了土壤水分的空间连续性时；ASTER TVDI因为与土壤水分的相关性最强且分辨率较高，其估计误差最小；即使引入相关性较弱且分辨率较粗的MODIS TVDI，也能对尺度上推的估计精度起到积极作用。

(2)面到面回归克里格(ATARK)。Ge等人(2015b)根据HiWATER通量矩阵观测中的17套EC和4套LAS观测，将感热通量从EC足迹尺度上推到与中等分辨率遥感像元尺度相匹配的LAS足迹尺度。该方法首先对趋势建模，即建立感热通量和植被覆盖度(FVC)、归一化差值植被指数(NDVI)、LST等遥感产品之间的多元线性回归模型；然后，建立点变异函数，针对样本量少的问题，通过将多时相的残差视为独立的重复试验，在基于残差空间变异结构相似的假设下，结合多时相的残差构建稳定的变异函数，再将构建的变异函数转换到各个时刻；接着，利用面到面克里格对残差建模；最后，根据ATARK估计方程以及感热通量足迹模型计算LAS足迹尺度的感热值。ATARK尺度上推结果方法可改进已有的面积权重法和足迹权重法存在的低估问题，其精度也优于这两种传统方法。该方法为分析EC和LAS足迹尺度之间的关系奠定了基础。

(3)利用协同信息的面到面不等权重回归克里格(WATARK)。在ATARK方法中，对观测源区进行离散化后的点，对于Kriging估计均具有相同的权重；然而在EC和LAS的足迹模型中，源区形状和不同位置的贡献权重是不同的，主要取决于气象条件。因此，Hu等人(2015)在ATARK基础上发展了不等权重的去卷积离散化方法；并利用FVC、NDVI、LST和风速(WS)来对潜热通量观测进行去趋势处理；去除趋势后的残差可看做空间随机场，满足二阶平稳假设条件；在残差估计中引入路径权重函数和通量足迹模型，从而在尺度上推过程中，同时考虑异质性和自相关性，将EC观测尺度上推到LAS观测足迹尺度。结果表明WATARK方法优于面积权重法、足迹权重法，多源线性回归法及ATARK，表现出更加接近1的斜率分布。

(4)时空回归块克里格(STRBK)。土壤水分仪器观测时间和卫星过境时间并不一致，因此，利用卫星过境时刻前后的点观测数据，采用时空克里格模型可以得到像元尺度更为稳健的土壤水分估计，并提高土壤水分的尺度上推精度。Wang等人(2015)使用HiWATER中时间分辨率为1 min的土壤水分无线传感器网络数据，并以多种遥感产品作为辅助信息，利用STRBK方法实现了土壤水分单点观测的尺度上推。与单个时刻的块克里格尺度上推结果相比，时空块克里格的估计方差降低约6%—19.0%，进而证明STRBK方法可以削弱仪器观测误差和观测时刻的影响。

(5)仪器误差不同时的克里格尺度上推方法。传统地统计方法只考虑样本，而不考虑样本误差对插值结果的影响，在实际应用中，意味着没有考虑仪器误差的影响。然而，对于多类型观测而言，仪器误差的不同会对尺度上推结果带来影响。针对该问题，Wang等人(2014b)构建了不等精度块克里格方程组，进而采用蒙特卡洛模拟方法，模拟构建不等精度观测的方差协方差矩阵，最终得到像元尺度土壤水分估计值和估计误差的方差。数值实验结果表明：与简单平均法、等精度块克里格法和不等精度块克里格模拟法进行比较，块克里格的估计误差方差要小于简单平均法的方差；不等精度块克里格法可以同时考虑仪器误差和尺度上推模型误差，更加适用于不等精度观测下土壤水分的估计以及研究尺度上推过程中的误差传递问题。Kang等人(2016a)则进一步考虑观测误差对克里格权重系数的影响，将异质性观测误差引入到块克里格的尺度上推研究中，分析了无仪器误差、同质仪器误差以及异质仪器误差的估计结果及不确定性的影响。结果表明，考虑仪器误差可以降低估计的不确定性，但对于仪器误差相同的数据而言，仪器误差对克里格权重系数并无影响。

6.2 基于贝叶斯估计的尺度上推

如6.1节所述，在空间尺度上推中引入辅助信息可以提高估计的精度，而回归克里格是一种能够融合其他先验信息的线性估计方法。是否存在更广义的融合先验信息的方法呢？贝叶斯估计提供了一种更广义的可用于尺度上推的信息融合理论框架。

贝叶斯最大熵(BME)方法是一种更通用的非线性估计器，并且适用于非正态分布和空间异质性情形(Christakos和Li，1998)。BME通过最大化后验概率分布来融合广义知识(如物理定律、经验方程等)和特定知识，其中，特定知识又分为硬数据和软数据，硬数据一般指器测误差很小可忽略不计的数据，软数据则有较大的不确定性。BME是地统计估计方法的新发展，需要指出的时，克里格只是BME的一个特例。

Gao等人(2014)尝试采用BME来融合HiWATER土壤水分传感器网络观测数据(作为硬数据)和ASTER地表温度数据(作为软数据)，成功实现了土壤水分的尺度上推。同时，比较了BME与普通克里格、普通协同克里格、回归克里格方法的性能，而后两种方法也能融合辅助信息。数值模拟结果表明，BME和回归克里格的估计精度优于普通克里格和普通协同克里格，而BME又略优于回归克里格，这再次证明引入辅助信息能显著提高土壤水分尺度上推的估计精度，而以概率方式融合辅助信息的BME方法不仅性能更优良，也具有更强的适用性。

地统计方法需要大量的地面定点观测估计空间自相关函数，当定点观测分布稀疏时，地统计方法难以得到满意的尺度上推结果，但是，观测的时间序列信息仍可以作为尺度上推的可用信息。针对这一问题，Kang等人(2016b)采用基于贝叶斯线性回归估计的尺度上推方法，通过引入MODIS估算的表观热惯量(ATI)的时间序列信息，建立ATI与定点土壤水分观测之间的关系，进而捕捉尺度上推后的网格尺度土壤水分在时间序列上的变化趋势，在时间窗口内构建网格尺度土壤水分与地面多点观测的关系方程，采用贝叶斯方法估计网格尺度土壤水分和点观测之间的回归系数，从而得到时间窗口内的尺度上推结果。在黑河流域上游的实验结果表明：与克里格等方法相比，该方法对观测点数量要求不高，但要求观测点空间分布相对均匀；它不仅可以获取单个格网的时间连续尺度上推结果以用于遥感产品的真实性检验，也可以获取目标变量的时空连续分布。

需要说明的是，本节所叙述的尺度上推更多指利用有限信息实现区域制图，和6.1节中所讨论的获取足迹尺度真值在概念上有所不同。

6.3 利用结构信息的尺度上推

对于结构性非常强的参量(如LAI)，如果不考虑像元足迹内的土地覆被类型差异，单纯使用足迹内所有点观测的简单或加权算术平均获取尺度上推结果可能带来极大的偏差，而考虑土地覆被分异的面积加权平均则相对可靠和稳健(Hufkens等，2008)。Shi等人(2015)开展了这方面的实证研究，利用HiWATER中游试验中的LAI传感器网络多节点观测数据，分两个步骤实现了LAI从点尺度到像元尺度的尺度上推：

步骤1 使用多个点观测的线性加权计算每一种土地覆被类型的代表性LAI，其中权重由期望最大化算法计算；

步骤2 以足迹范围内各种土地覆被类型的面积比例为权重，加权得到像元尺度上总的LAI。该方法的精度非常高，到LAI观测节点为23个时，LAI的误差仅为0.03，完全能够满足LAI遥感产品真实性检验的需求。Fan等人(2015)利用BME方法融合HiWATER土壤水分传感器网络观测数据、ASTER的土壤蒸发效率、灌溉统计和机载PLMR土壤水分产品，结果表明，通过引入有结构的灌溉信息，有助于提高生长季初期(植被覆盖度低)土壤水分的尺度上推精度，但植被覆盖度较高时的精度依然较差，而通过融合航空PLMR土壤水分产品，则可有效地改善植被覆盖度较高时的精度。从而证实了引入结构信息及高分辨率遥感信息的作用。Peng等人(2015)发展了一个结合地面观测和高分辨率遥感的反照率尺度上推方案，讨论了其不确定性来源及其估计方法，并在黑河流域进行了实证研究。结果表明，通过使用大小样方嵌套采样、根据地面测量校正高分辨率反照率的偏差及几何匹配误差分级等措施，能有效控制尺度上推结果的不确定性及其对遥感产品验证的影响。

7 结论

本文以定点观测的尺度上推为主线，综述了HiWATER在多尺度观测数据获取、异质性地表的空间采样、定点观测的代表性误差度量，以及空间尺度上推方法发展等方面的进展。总结如下：

(1)尝试严格定义了空间平均、空间尺度上推、观测足迹、代表性误差、观测真值等概念。从观测算子误差的角度统一了代表性误差的定义，代表性误差既包括尺度转换带来的误差，也包括观测模型的不完美所带来的误差。观测真值可以定义为无偏最优估计，也就是观测误差的数学期望为零，而其不确定性可以被控制在所期望的范围内。

(2)发展了基于地统计理论的多变量、多尺度采样方法，其优势是在得到全局无偏最优估计的同时，可更好捕捉多尺度的空间变异特征；改进了基于时间稳定性的采样方法，给出了利用瞬时高分辨率辅助信息提高采样精度的方法。

(3)利用HiWATER通量矩阵和传感器网络中的多点—足迹观测数据，研究了辐射、碳通量、土壤水分、LST的代表性误差，证实了对于异质性地表，单点观测的代表性误差不可忽略甚至可能很大，当异质性较强时，单点观测的代表性误差小于真实性检验阈值的概率可能会很小，因此，在遥感产品真实性检验中必须考虑代表性误差；也证明了无论是采用那种空间平均，都可以显著提高像元尺度真值估计的空间代表性。

(4)发展了针对点和足迹尺度定点观测的尺度上推方法，将克里格方法推广至回归克里格(利用协同信息)、面到面回归克里格、时空回归克里格、不等仪器误差等情形，高分辨率遥感(如航空遥感)作为重要的协同信息，可显著提高尺度上推的估计精度。发展了贝叶斯框架下的非线性尺度上推方法，其核心是引入可靠的辅助信息作为尺度上推的约束，这些辅助信息常常来自于和观测变量密切相关的遥感数据。

(5)在观测技术上，传感器网络作为一种新的观测方式，为多点带面获取像元尺度真值提供了可能；此外，大足迹地面观测通常具有更好的空间代表性，将在遥感产品真实性检验中发挥重要作用。

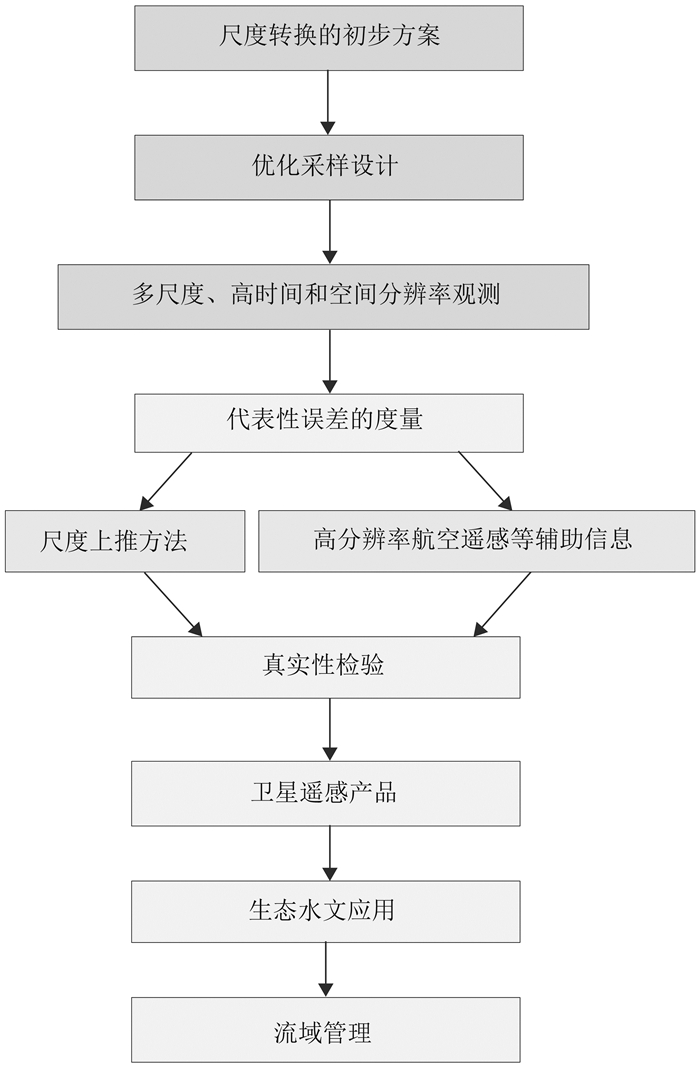
(6)初步形成了从采样设计、多尺度观测、代表性误差的度量、尺度上推到真实性检验的定点观测尺度上推研究框架(图 2)。

图 2 黑河生态水文遥感试验(HiWATER)中的尺度转换研究方法总结

Fig. 2 Upscaling research framework in HiWATER

建立严谨、统一的尺度转换理论是推进遥感尺度研究的前提。本文在理论工作方面的尝试是对空间平均、空间尺度上推、代表性误差、观测真值等若干概念的数学定义。从式(2)可知，空间平均的被积函数是一个随机过程。因此，无论是建立空间平均的普适方法，还是更严格定义与之相关的基本概念，特别是定义尺度和尺度转换，都需要借助随机分析。该方面的尝试将是未来工作的一个主要方向(Liu和Li，2016)。

克里格框架下的尺度上推方法假设空间平均是多点观测的线性加权和，但在真实的地理世界中，所关心的变量的空间、时间变化可能是非常复杂的非线性随机过程。贝叶斯估计虽然提供了融合非线性广义知识的可能，但如何在该框架下实现动态模型和多源观测互相融合的尺度上推，是一个很大的难题。且还未见这方面的实证研究。如果把动力过程引入到定点观测的尺度上推中，则涉及到系综平均(ensemble average)、空间平均、时间平均之间的关系，这是遍历理论所讨论的范畴。

随机分析和遍历理论可能是尺度转换的理论基础和数学工具，而HiWATER等多尺度观测试验的数据宝库也有待进一步发掘。希望下一步“从数据和方法论两方面促进尺度效应和尺度转换研究”(李小文和王祎婷，2013)，推进遥感尺度问题研究向更深层次迈进。

参考文献(References)

Christakos G, Li X Y.1998.Bayesian maximum entropy analysis and mapping:a farewell to kriging estimators?. Mathematical Geology, 30 (4): 435–462. DOI: 10.1023/A:1021748324917.

Fan L, Xiao Q, Wen J G, Liu Q, Jin R, You D Q, Li X W.2015.Mapping high-resolution soil moisture over heterogeneous cropland using multi-resource remote sensing and ground observations. Remote Sensing, 7 (10): 13273–13297. DOI: 10.3390/rs71013273.

Gao S G, Zhu Z L, Liu S M, Jin R, Yang G C, Tan L.2014.Estimating the spatial distribution of soil moisture based on Bayesian maximum entropy method with auxiliary data from remote sensing. International Journal of Applied Earth Observation and Geoinformation, 32 : 54–66. DOI: 10.1016/j.jag.2014.03.003.

Ge Y, Liang Y Z, Wang J H, Zhao Q Y, Liu S M.2015b.Upscaling sensible heat fluxes with area-to-area regression kriging. IEEE Geoscience and Remote Sensing Letters, 12 (3): 656–660. DOI: 10.1109/LGRS.2014.2355871.

Ge Y, Wang J H, Heuvelink G B M, Jin R, Li X, Wang JF.2015a.Sampling design optimization of a wireless sensor network for monitoring ecohydrological processes in the Babao River basin, China. International Journal of Geographical Information Science, 29 (1): 92–110. DOI: 10.1080/13658816.2014.948446.

Hu M G, Wang J H, Ge Y, Liu M X, Liu S M, Xu Z W, Xu T R.2015.Scaling flux tower observations of sensible heat flux using weighted area-to-area regression Kriging. Atmosphere, 6 (8): 1032–1044. DOI: 10.3390/atmos6081032.

Huang G H, Li X, Huang C L, Liu S M, Ma Y F, Chen H.2016b.Representativeness errors of point-scale ground-based solar radiation measurements in the validation of remote sensing products. Remote Sensing of Environment, 181 : 198–206. DOI: 10.1016/j.rse.2016.04.001.

Huang G H, Li X, Ma M G, Li H Y and Huang C L.2016a.High resolution surface radiation products for studies of regional energy, hydrologic and ecological processes over Heihe River Basin, northwest China.Agricultural and Forest Meteorology, in press [DOI:10.1016/j.agrformet.2016.04.007]

Hufkens K, Bogaert J, Dong Q H, Lu L, Huang C L, Ma M G, Che T, Li X, Veroustraete F, Ceulemans R.2008.Impacts and uncertainties of upscaling of remote-sensing data validation for a semi-arid woodland. Journal of Arid Environments, 72 (8): 1490–1505. DOI: 10.1016/j.jaridenv.2008.02.012.

Jin R, Li X, Yan B P, Li X H, Luo W M, Ma M G, Guo J W, Kang J, Zhu Z L, Zhao S J.2014.A nested ecohydrological wireless sensor network for capturing the surface heterogeneity in the midstream areas of the Heihe River Basin, China. IEEE Geoscience and Remote Sensing Letters, 11 (11): 2015–2019. DOI: 10.1109/LGRS.2014.2319085.

Jin R, Li X, Yan B P, Luo W M, Li X H, Guo J W, Ma M G, Kang J, Zhang Y L.2012.Introduction of eco-hydrological wireless sensor network in the Heihe River basin. Advances in Earth Science, 27 (9): 993–1005. ( 晋锐, 李新, 阎保平, 罗万明, 李秀红, 郭建文, 马明国, 亢健, 张艳林. 2012. 黑河流域生态水文传感器网络设计. 地球科学进展, 27 (9): 993–1005. )

Kachanoski R G, de Jong E.1988.Scale dependence and the temporal persistence of spatial patterns of soil water storage. Water Resources Research, 24 (1): 85–91. DOI: 10.1029/WR024i001p00085.

Kang J, Jin R, Li X.2015.Regression kriging-based upscaling of soil moisture measurements from a wireless sensor network and multiresource remote sensing information over heterogeneous cropland. IEEE Geoscience and Remote Sensing Letters, 12 (1): 92–96. DOI: 10.1109/LGRS.2014.2326775.

Kang J, Jin R, Li X, Ma C F, Qin J and Zhang Y.2016b.High spatio-temporal resolution mapping of soil moisture by integrating wireless sensor network observations and MODIS apparent thermal inertia in the Babao River Basin, China.Remote Sensing of Environment, in press.

Kang J, Jin R, Li X and Zhang Y.2016a.Kriging with measurement errors:a case study of spatial prediction of soil moisture in the middle reach of Heihe River Basin.IEEE Geoscience and Remote Sensing Letters, in press.

Kang J, Li X, Jin R, Ge Y, Wang J F, Wang J H.2014.Hybrid optimal design of the eco-hydrological wireless sensor network in the middle reach of the Heihe River Basin, China. Sensors, 14 (10): 19095–19114. DOI: 10.3390/s141019095.

Li X.2014.Characterization, controlling, and reduction of uncertainties in the modeling and observation of land-surface systems. Science China Earth Sciences, 57 (1): 80–87. DOI: 10.1007/s11430-013-4728-9.

Li X, Cheng G D, Liu S M, Xiao Q, Ma M G, Jin R, Che T, Liu Q H, Wang W Z, Qi Y, Wen J G, Li H Y, Zhu G F, Guo J W, Ran Y H, Wang S G, Zhu Z L, Zhou J, Hu X L, Xu Z W.2013.Heihe watershed allied telemetry experimental research (HiWATER):scientific objectives and experimental design. Bulletin of the American Meteorological Society, 94 (8): 1145–1160. DOI: 10.1175/BAMS-D-12-00154.1.

Li X, Cheng G D, Lu L.2000.Comparison of spatial interpolation methods. Advances in Earth Science, 15 (3): 260–265. ( 李新, 程国栋, 卢玲. 2000. 空间内插方法比较. 地球科学进展, 15 (3): 260–265. )

Li X and Liu F.2016.Can point measurements of soil moisture be used to validate a footprint-scale soil moisture product?.IEEE Geoscience and Remote Sensing Letters, in press

Li X, Liu S M, Ma M G, Xiao Q, Liu Q H, Jin R, Che T, Wang W Z, Qi Y, Li H Y, Zhu G F, Guo J W, Ran Y H, Wen J G, Wang S G.2012.HiWATER:An Integrated Remote Sensing Experiment on Hydrological and Ecological Processes in the Heihe River Basin. Advances in Earth Science, 27 (5): 481–498. ( 李新, 刘绍民, 马明国, 肖青, 柳钦火, 晋锐, 车涛, 王维真, 祁元, 李弘毅, 朱高峰, 郭建文, 冉有华, 闻建光, 王树果. 2012. 黑河流域生态-水文过程综合遥感观测联合试验总体设计. 地球科学进展, 27 (5): 481–498. )

Li X W, Wang Y T.2013.Prospects on future developments of quantitative remote sensing. Acta Geographica Sinica, 68 (9): 1163–1169. ( 李小文, 王祎婷. 2013. 定量遥感尺度效应刍议. 地理学报, 68 (9): 1163–1169. )

Liu F and Li X.2016.The stochastic calculus reformulation of data assimilation:on scale.Nonlinear Processes in Geophysics, in press [DOI:10.5194/npg-2016-35]

Liu S M, Xu Z W, Song L S, Zhao Q Y, Ge Y, Xu T R, Ma Y F, Zhu Z L, Jia Z Z and Zhang F.2016.Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces.Agricultural and Forest Meteorology, in press [DOI:10.1016/j.agrformet.2016.04.008]

Liu S M, Xu Z W, Wang W Z, Jia Z Z, Zhu M J, Bai J, Wang J M.2011.A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrology and Earth System Sciences, 15 (4): 1291–1306. DOI: 10.5194/hess-15-1291-2011.

Ostoja-Starzewski M.2006.Material spatial randomness:from statistical to representative volume element. Probabilistic Engineering Mechanics, 21 (2): 112–132. DOI: 10.1016/j.probengmech.2005.07.007.

Peng J J, Liu Q, Wen J G, Liu Q H, Tang Y, Wang L Z, Dou B C, You D Q, Sun C K, Zhao X J, Feng Y B, Shi J.2015.Multi-scale validation strategy for satellite albedo products and its uncertainty analysis. Science China Earth Sciences, 58 (4): 573–588. DOI: 10.1007/s11430-014-4997-y.

Qu Y H, Zhu Y Q, Han W C, Wang J D, Ma M G.2014.Crop leaf area index observations with a wireless sensor network and its potential for validating remote sensing products. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (2): 431–444. DOI: 10.1109/JSTARS.2013.2289931.

Ran Y H, Li X, Jin R, Kang J and Cosh M.2016a.Strengths and weaknesses of temporal stability analysis for monitoring and estimating field-mean soil moisture in a high-intensity irrigated agricultural landscape.Water Resources Research, second review

Ran Y H, Li X, Sun R, Kljun N, Zhang L, Wang X F and Zhu G F.2016b.Spatial representativeness and uncertainty of eddy covariance carbon flux measurements for upscaling net ecosystem productivity to the grid scale.Agricultural and Forest Meteorology, in press [DOI:10.1016/j.agrformet.2016.05.008]

Shi Y C, Wang J D, Qin J, Qu Y H.2015.An upscaling algorithm to obtain the representative ground truth of LAI time series in heterogeneous land surface. Remote Sensing, 7 (10): 12887–12908. DOI: 10.3390/rs71012887.

Vachaud G, Passerat de Silans A, Balabanis P, Vauclin M.1985.Temporal stability of spatially measured soil water probability density function. Soil Science Society of America Journal, 49 (4): 822–828. DOI: 10.2136/sssaj1985.03615995004900040006x.

Vereecken H, Kasteel R, Vanderborght J, Harter T.2007.Upscaling hydraulic properties and soil water flow processes in heterogeneous soils. Vadose Zone Journal, 6 (1): 1–28. DOI: 10.2136/vzj2006.0055.

Wang J F, Christakos G, Hu M G.2009.Modeling spatial means of surfaces with stratified nonhomogeneity. IEEE Transactions on Geoscience and Remote Sensing, 47 (12): 4167–4174. DOI: 10.1109/TGRS.2009.2023326.

Wang J F, Stein A, Gao B B, Ge Y.2012.A review of spatial sampling. Spatial Statistics, 2 : 1–14. DOI: 10.1016/j.spasta.2012.08.001.

Wang J H, Ge Y, Heuvelink G B M, Zhou C H.2014a.Spatial sampling design for estimating regional GPP with spatial heterogeneities. IEEE Geoscience and Remote Sensing Letters, 11 (2): 539–543. DOI: 10.1109/LGRS.2013.2274453.

Wang J H, Ge Y, Heuvelink G B M, Zhou C H.2015.Upscaling in situ soil moisture observations to pixel averages with spatio-temporal geostatistics. Remote Sensing, 7 (9): 11372–11388. DOI: 10.3390/rs70911372.

Wang J H, Ge Y, Song Y Z, Li X.2014b.A geostatistical approach to upscale soil moisture with unequal precision observations. IEEE Geoscience and Remote Sensing Letters, 11 (12): 2125–2129. DOI: 10.1109/LGRS.2014.2321429.

Wu H, Li Z L.2009.Scale issues in remote sensing:a review on analysis, processing and modeling. Sensors, 9 (3): 1768–1793. DOI: 10.3390/s90301768.

Wu X D, Xiao Q, Wen J G, Liu Q, You D Q, Dou B C, Tang Y, Li X W.2015.Optimal nodes selectiveness from WSN to fit field scale albedo observation and validation in long time series in the foci experiment areas, Heihe. Remote Sensing, 7 (11): 14757–14780. DOI: 10.3390/rs71114757.

Xu Z W, Liu S M, Li X, Shi S J, Wang J M, Zhu Z L, Xu T R, Wang W Z, Ma M G.2013.Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. Journal of Geophysical Research-Atmospheres, 118 (23): 13140–1315. DOI: 10.1002/2013JD020260.

Yu W P, Ma M G.2015.Scale mismatch between in situ and remote sensing observations of land surface temperature:implications for the validation of remote sensing LST products. IEEE Geoscience and Remote Sensing Letters, 12 (3): 497–501. DOI: 10.1109/LGRS.2014.2347953.

Zeng Y L, Li J, Liu Q H, Qu Y H, Huete A R, Xu B D, Yin G F, Zhao J.2015.An optimal sampling design for observing and validating long-term leaf area index with temporal variations in spatial heterogeneities. Remote Sensing, 7 (2): 1300–1319. DOI: 10.3390/rs70201300.